第四章

造物主在哪些与行星运动有关的事物中表现了和谐比例，方式为何

• In What Things，and In What Way？ •

向着您，我转过身来，高贵的开普勒，您的智力创造了一个神圣的精神宇宙，在我们的时代里，被视为智慧的东西是什么？是屠杀一切，使高尚的东西变低微，使低微的东西纷纷扬起，甚至使人类精神在机械的法则之下屈服。

——18世纪德国诗人诺瓦利斯用诗句表达了他对开普勒的钦佩和仰慕。

第谷出生地的素描图。

如果把行星逆行和留的幻象除去，使它们在其真实偏心轨道上的自行突显出来，则行星还剩下这样一些特征项：（1）与太阳之间的距离；（2）周期；（3）周日偏心弧；（4）在那些弧上的周日时耗（delay）； ⁽¹⁾ （5）它们在太阳上所张的角，或者相对于太阳上的观测者的视周日弧。在行星的整个运行过程中，除周期以外，所有这些项都是可变的，而且在平黄经处变化最大，在极点处变化最小，此时行星正要从其中的一极转向另一极。因此，当行星位于很低的位置或与太阳相当接近时，它在其偏心轨道上走过一度的时耗很少，而在一天之中走过的偏心弧却很长，从太阳上看运动很快。此后，行星的运动将这样持续一段时间，而不发生明显的改变，直到通过了近日点，行星与太阳的直线距离才渐渐开始增加。同时，行星在其偏心轨道上走过1°的时耗也越来越长，或若考虑周日运动，从太阳上看去，行星每天的行进将越来越少，走得也越来越慢，直至到达高拱点，距离太阳最远为止。此时，行星在偏心轨道上走过1°的时耗最长，而在一天之中走过的弧最短，视运动也是整个运行过程中最小的。

最后，所有这些特征项既可以属于处于不同时间的同一颗行星，又可以属于不同的行星。所以倘若假定时间为无限长，某一行星轨道的所有状态都可以在某一时刻与另一行星轨道的所有状态相一致，并且可以相互比较，则它们的整个偏心轨道之比将等于其半径或平均距离之比。但是两条偏心轨道上被指定为相等或具有同一（度）数的弧却代表不同的真距离，比如土星轨道上1°的长度大约等于木星轨道上1°的长度的两倍。而另一方面，用天文学数值所表示的偏心轨道上的周日弧之比，也并不等于行星在一天之中穿过以太的真距离之比，因为同样的单位度数在上行星较宽的圆上表示较大的路径，在下行星较窄的圆上表示较小的路径。

我们首先考虑前面所列特征项中的第二项，即行星的周期，它等于行星通过整个轨道所有弧段的全部时耗（长的、中等的和短的）之总和。根据从古至今的观测结果，诸行星绕日一周所需时间如下表所示：

①　古人把一天的时间分成60个单位，每一个单位的时间长度为1日分。后面的时间单位“分”均指“日分”。——中译者

因此，这些周期之间并不存在和谐比例。只要把较大的周期连续减半，把较小的周期连续加倍，忽略八度音程，得到一个八度内的音程，就很容易看出这一点。 ⁽²⁾

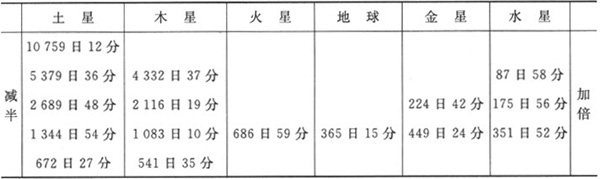
你可以发现，所有最后的数都无法构成和谐比例，或者说构成的比例是无理的。因为如果取120（对弦的分割数）为对火星的日数687的度量，则按照这种单位计算，土星的十六分之一周期为117，木星的八分之一周期小于95，地球的周期小于64，金星的两倍周期大于78，水星的四倍周期大于61。这些数值都不能与120构成和谐比例，但与它们临近的数60、75、80和96却可以；类似的，如果把120取为土星的度量，则木星的值约为97，地球大于65，金星大于80，水星小于63；当木星取为120时，地球小于81，金星小于100，水星小于78；当金星取为120时，地球小于98，水星大于94；最后，当地球取为120时，水星小于116。但如果这种对比例的自由选择是有效的话，它们本应当是绝对完美的和谐比例，而不存在任何盈余或亏缺。于是我们发现，造物主并不希望时耗之和即周期之间构成和谐比例。

尽管行星的体积之比等于周期之比这个猜想很有可能成立（它基于几何学证明以及《火星评注》中关于行星运动成因的学说），从而土星球大约是地球的30倍，木星球是地球的12倍，火星球小于地球的两倍，地球是金星球的一倍半，是水星球的4倍，但即使这样，这些关于体积的比例也不是和谐的。

然而，除非已经受到其他某种必然性定律的支配，否则上帝所创立的任何事物都不可能不具有几何学上的美，所以我们立即可以推出，凭借某种预先存在于原型中的东西，周期已经得到了最合适的长度，运动物体也已经得到了最合适的体积。需要说明的是，这些看似不成比例的体积和周期何以会被设计成这般尺寸。我已经说过，周期是由最长的、中等的和最短的时耗全部加在一起得到的，因此，几何学上的和谐必定可以从这些时耗上，或者从造物主心灵中的某种在先的东西中发现。而时耗之比与周日弧之比有着密切的关系，因为周日弧与时耗成反比。我们还说过，任一行星的时耗与距离之比相等。于是对于同一颗行星来说，（周日）弧、等弧上的时耗、周日弧与太阳之间的距离这三者是一回事。既然对于行星来说，所有这些项都是可变的，那么如果至高的造物主已经通过可靠的设计给行星赋予了某种几何学上的美的话，这种美就一定会在其两极处凭借远日距和近日距实现，而不会凭借两者之间的平均距离实现。极距离之比已定，就不必再把居间的比例也设计成确定的值了，因为根据行星从其中一极通过所有中间点向另一极运动的必然性，它们会自动获取相应的值。

根据第谷·布拉赫极为精确的观测结果以及《火星评注》中所给出的方法，通过17年的苦心研究，我们得到了如下极距离：

距离与谐和音程的比较 ⁽³⁾

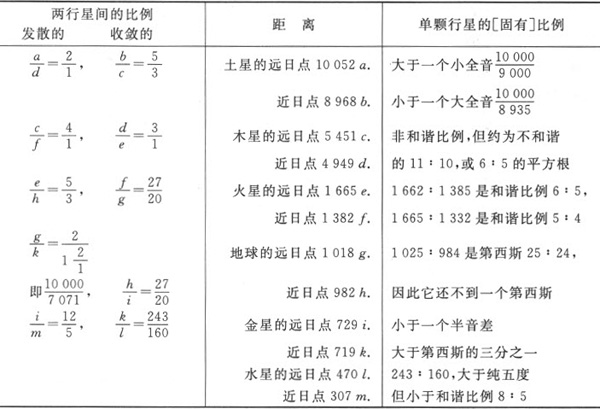
因此，除了火星与水星，其他行星的极距离之比都不接近谐和音程。

然而倘若你把不同行星的极距离进行相互比较，某种和谐的迹象就会显示出来。因为土星与木星的发散极距离之间略大于一个八度，收敛极距离之间是大六度和小六度的平均；木星与火星的发散极距离之间构成约两个八度，收敛极距离之间约为八度加五度；地球与火星的发散极距离之间略大于大六度，收敛极距离之间构成增四度；地球与金星的收敛极距离之间也构成增四度，但发散极距离之间却不能构成任何和谐比例，这是因为它小于半个八度，也就是说小于2∶1的平方根；最后，金星与水星的发散极距离之间略小于八度加小三度，发散极距离之间略大于增五度。

因此，尽管有一个距离与和谐比例偏离较远，但业已取得的成功却激励我们继续探索下去。我的推理如下：首先，由于这些距离都是没有运动的长度，所以它们不适合用来考察和谐比例，因为和谐与运动的快慢联系更为紧密；其次，由于这些距离都是天球半径，所以很容易想见，五种正立体形的比例更可能适用于它们，这是因为几何立体与天球（或被天际物质四处包围，如古人所说的那样，或被累计起来的连续多次旋转所包围）之比，等于内接于圆的平面图形（正是这些图形产生了和谐）与天上的运动圆周之比以及与运动发生的其他区域之比。因此，如果我们要寻找和谐，就不应当在这些天球半径中寻找，而要到运动的度量即实际运动中去寻找。当然，天球的半径只能取成平均距离，而我们这里所讨论的却是极距离。因此，我们所讨论的不是关于天球的距离，而是关于运动的距离。

尽管我已经由此转到了对极运动进行比较，但极运动之比仍与前面所讨论的极距离之比相同，只不过比例的顺序要颠倒一下。因此，前面发现的某些不和谐比例在极运动之间也可以找到。但我认为，得到这样的结果是理所当然的，因为我是在把偏心弧进行比较，它们不是通过同样大小的量度进行表达和计算的，而是通过大小因行星而异的度和分来计算的。而且从我们这里观察，它们的视尺寸绝不会与其数值所指示的一样大，除非是在每颗行星的偏心轨道的中心，而这一中心并没有落在任何东西上；认为在那个位置存在着某种能够把握这种视尺寸的感官或天性，这是令人难以置信的；或者说，如果我想把不同行星的偏心弧与它们在各自中心（因行星而异）所显现出，来的视尺寸进行比较，这是不可能的。然而，如果要对不同的视尺寸进行互相比较，那么它们就应该在宇宙中的同一个位置显现，并使其比较者处在它们共同显现的位置。因此我认为，这些偏心弧的视尺寸或者应从心中排除，或者应以不同的方式来表示。如果我把视尺寸从心中排除，而把注意力转到行星的实际周日行程上去，我就发现不得不运用我在前一章第九条中所给出的规则。 ⁽⁴⁾ 于是，把偏心周日弧乘以轨道的平均距离，我们便得到了如下行程：

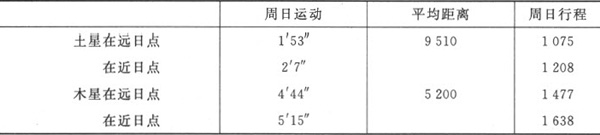
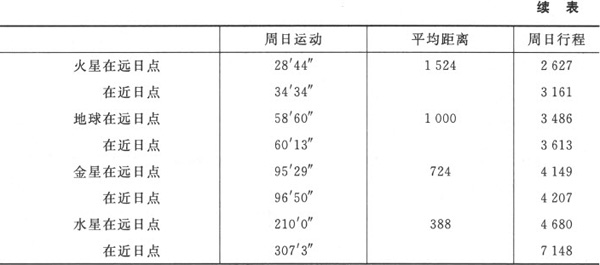
由此我们可以看到，土星的行程仅为水星行程的七分之一。亚里士多德会认为这个结论是符合理性的，因为他在其《论天》（On the Heavens 或De Caelo ）一书的第二卷中曾说， ⁽⁵⁾ 距太阳较近的行星总是要比距太阳较远的行星走更大的距离，而这在古代天文学中是不能成立的。

的确，如果我们认真思索一下就不难理解，最智慧的造物主不大可能会为行星的行程特别建立和谐，因为如果行程的比例是和谐的，那么行星的所有其他方面就会与行星的旅程发生联系并受到限制，从而就没有其他可供建立和谐的余地了。但是谁将从行程之间的和谐获益呢？或者说谁将觉察到这些和谐呢？在大自然中，只有两种东西可以向我们显示出和谐，即光或声：光通过眼睛或与眼睛类似的隐秘感官接受，声则通过耳朵接受。心灵把握住这些流溢出来的东西，或者通过本能（关于这一点，我在第四卷中已经讲得很多了），或者通过天文学的或和谐的推理来把和谐与不和谐区分开。事实上，天空中静寂无声，星辰的运动也不至于同以太产生摩擦而发出噪音。光也是如此。如果光要传达给我们某些关于行星行程的信息，它就会或者传达给眼睛，或者传达给某种与眼睛类似并处于某一特定位置的感官；为了使光能够把信息瞬间传达给我们，这种感官似乎必定就呈现在那里。如此一来，为了使所有行星的运动都能同时呈现给感官，整个世界都将有感官存在。通过观察，通过在几何与算术中长时间地四处游荡，再通过轨道的比例以及其他必须首先了解的东西，最后得到实际的行程，这种路径对于任何天性来说似乎都太长了，为了改变这种状况，引入和谐似乎是合理的。

因此，综合以上所有这些看法，我可以恰当地得出结论说，行星穿过以太的真实行程应当不予考虑，我们应当把目光转向视周日弧，它们在宇宙中的一个确定的显著位置——太阳这个所有行星的运动之源——可以很清楚地显示出来。我们必须看到，不是某一行星距离太阳有多远，也不是它在一天之中走过多少路程（因为这属于推理和天文学，而不属于天性），而是每颗行星的周日运动对太阳所张角度的大小，或者说它在一个围绕太阳的轨道（比如说椭圆）上看起来走过了多大的弧，才能使这些经由光传到太阳的现象，能够与光一起直接流向分有这种天性的生命体，正如我们在第四卷中所说，天上的图式经由光线流入胎儿。 ⁽⁶⁾

因此，如果把导致行星出现留和逆行现象的轨道周年视差从行星的自行中消去，那么第谷的天文学告诉我们，行星在其轨道上的周日运动（在太阳上的观察者看来）如下表所示：

需要注意的是，水星的大偏心率使得其运动之比显著偏离了距离平方之比。 ⁽⁷⁾ 如果令平均距离100与远日距121之比的平方等于远日运动与平均运动245′32″之比，我们便可以得到远日运动为167；如果令100与近日距79之比的平方等于近日运动与同一平均运动之比，就得到近日运动为393。两个结果都比我预想的要大，这是因为平近点角处的平均运动因斜着观测而不会显出245′32″那么大，而是会比它小5′。因此，我们发现远日运动和近日运动也较小。不过根据我在前一章第七条中讲到的欧几里得《光学》的定理8，远日运动（看起来）偏小的程度较小，近日运动偏小的程度较大。

因此，根据前面给出的偏心周日弧的比例，我完全可以在头脑中假想，单颗行星的这些视极运动之间存在着和谐，可以构成谐和音程，因为我发现，和谐比例的平方根在任何地方都起着支配作用，而我知道视运动之比等于偏心运动之比的平方。但事实上，仅凭实际观测，而不用借助推理就可以证明我的结论。正如你在上表中所看到的，行星的视运动之比非常接近和谐比例：土星和木星的比例分别略大于大三度和小三度，前者超出了53∶54，后者超出了54∶55或更小，也就是说约为一个半音差；地球的比例略大于一个半音（超出了137∶138，或者说几乎半个音差）；火星小于一个五度（小于29∶30，接近34∶35或35∶36）；水星的比例比一个八度大了小三度，而不是一个全音，即大约比全音小38∶39（约为两个音差，即34∶35或35∶36）。只有金星的比例小于任何谐和音程，其自身仅为一个第西斯；因为它的比例介于两个音差和三个音差之间，超出了一个第西斯的三分之二，大约为34∶35或35∶36，或者说等于一个第西斯减去一个音差。

对月球也可做这样的考虑。 ⁽⁸⁾ 我们发现它在方照时的每时远地运动（即最慢的运动）是26′26″，而在朔望时的每时近地运动（即最快的运动）是35′12″。这样就刚好构成了纯四度，因为26′26″的三分之一是8′49″，它的4倍等于35′16″。需要注意的是，除此以外，我们在视运动中再没有发现纯四度这个谐和音程了。还应注意，四度谐和音程与月相中的方照之间存在着类似之处。因此，前面所说的那些可以在单颗行星的运动中找到。

然而对于两行星极运动之间的相互比较，无论你所比较的是发散极运动还是收敛极运动，只要我们看一看天体的和谐，便可豁然开朗。因为土星与木星的收敛运动比例恰好是2倍或一个八度，发散运动之比略大于3倍或八度加五度。由于5′30″的三分之一是1′50″，而土星是1′46″，所以行星的运动与谐和音程之间大约相差一个第西斯，即26∶27或27∶28。如果土星在远日点处的运动再小一秒，这个差就将等于34∶35，即金星的极运动之比。木星和火星的发散运动与收敛运动分别构成三个八度和两个八度加三度，不过并非精确，因为38′1″的八分之一是4′45″，木星是4′30″，这两个值之间仍然有18∶19（半音15∶16与第西斯24∶25的平均值）的差距，也就是说接近于一个纯小半音128∶135。 ⁽⁹⁾ 同样，26′14″的五分之一是5′15″，木星是5′30″，因此这里比5倍比例少了21∶22，而比另一个比例多了约一个第西斯24∶25。

构成两个八度加小三度而非大三度的谐和音程5∶24与此相当接近，因为5′30″的五分之一是1′6″，它的24倍等于26′24″，它与26′14″相差不到半个音差。火星与地球被分配了最小的比例，它恰好等于一倍半或纯五度，这是因为57′3″的三分之一是19′1″，它的2倍等于38′2″，这正是火星的值38′11″。它们还被分配了较大的比例5∶12，即八度加小三度，但更不精确，这是因为61′18″的十二分之一是5′6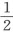 ″，乘以5得25′33″，而火星则是26′14″。因此，这里小了约一个减第西斯，即35∶36。地球与金星被分配的最大和谐比例是3∶5，最小和谐比例是5∶8，即大六度和小六度，但又是不精确的，因为97′37″的五分之一乘以3得58′33″，这要比地球的远日运动大34∶35，行星比例大约超出和谐比例35∶36。94′50″的八分之一是11′51″＋，它的5倍是59′16″，大约等于地球的平均运动，因此这里行星的比例要比和谐比例小29∶30或30∶31，这个值也接近于一个减第西斯35∶36，这个最小比例就是行星比例与纯五度之间的差距。因为94′50″的三分之一是31′37″，它的2倍是63′14″，地球的近日运动61′18″比它略小31∶32，所以行星的比例恰好等于临近和谐比例的平均值。最后，金星和水星被分配的最大比例是两个八度，最小比例是大六度，但不是精确的。这是因为384′的四分之一是96′0″，金星是94′50″，它比4倍比例大约多出了一个音差。164′的五分之一是32′48″，乘以3得98′24″，而金星是97′37″，所以行星的比例大约超出了一个音差的三分之二，即126∶127。

以上就是被赋予行星的各种谐和音程。主要比较（即收敛极运动与发散极运动之间的比较）中的任何一个比例都非常接近于某种谐和音程，所以倘若以这样的比例调弦，耳朵很难分辨出不谐和部分，只有木星与火星之间是个例外。 ⁽¹⁰⁾

接下来，如果我们比较同一侧的运动 ⁽¹¹⁾ ，结果也不应偏离谐和音程太远。如果把土星的4∶5 comp．53∶54与居间比例1∶2复合，得到的结果2∶5 comp．53∶54即为土星与木星的远日运动之比。 ⁽¹²⁾ 把1∶2与木星的5∶6 comp．54∶55复合，得到的结果5∶12 comp．54∶55即为土星与木星的近日运动之比。类似地，把木星的5∶6 comp．54∶55与居间比例5∶24 comp．158∶157复合，我们便得到远日运动之比1∶6 comp．36∶35。 ⁽¹³⁾ 把同样的5∶24 comp．158∶157与火星的2∶3 comp．30∶29复合，得到的结果5∶36 comp．25∶24即125∶864或近似的1∶7即为（木星与火星的）近日运动之比：目前仍然只有这个比例是不和谐的。 ⁽¹⁴⁾ 再把第三个居间比例2∶3 ⁽¹⁵⁾ 与火星的2∶3 comp．30∶29复合，得到的结果4∶9 comp．30∶29或40∶87，即为（火星与地球的）远日运动之比，它是另一个不谐和音程。如果不与火星复合，而与地球的15∶16 comp．137∶138复合，那么就得到（火星与地球的）近日运动之比5∶8 comp．137∶138。 ⁽¹⁶⁾ 如果把第四个居间比例5∶8 comp．31∶30或2∶3 comp．31∶32与地球的15∶16 comp．137∶138复合，得到的结果即为地球与金星的远日运动之比，它的值接近3∶5，这是因为94′50″的五分之一是18′58″，它的3倍是56′54″，而地球是57′3″。 ⁽¹⁷⁾ 如果把金星的34∶35 ⁽¹⁸⁾ 与同一比例进行复合，便得到（地球与金星的）近日运动之比为5∶8，这是因为97′37″的八分之一是12′12″＋，乘以5是61′1″，而地球是61′18″。最后，如果把最后一个居间比例3∶5 comp．126∶127与金星的34∶35复合，得到的结果3∶5 comp．24∶25即为（金星与水星的）远日运动之比，它所对应的音程是不谐和的。如果把它同水星的5∶12 comp．38∶39进行复合，便得到（金星与水星的）近日运动之比为两个八度或1∶4减去大约一个第西斯。

因此，我们可以发现以下谐和音程：土星与木星的收敛极运动之间构成一个八度；木星与火星的收敛极运动之间约为两个八度加小三度；火星与地球的收敛极运动之间是一个五度，其近日运动之间是小六度；金星与水星的收敛极运动之间是大六度，发散极运动或者说近日运动之间是两个八度。因此，余下的那点微小出入似乎可以忽略不计（特别是对于金星和水星的运动），而不会损害主要是基于第谷·布拉赫的观测建立起来的天文学。

然而应当注意的是，木星与火星之间并不存在主要谐和音程，但我只是在那里才发现，正立体形的安放是近乎完美的，因为木星的近日距离约为火星远日距离的3倍，所以这两颗行星力图在距离上获得在其运动上没有达到的完美和谐。

还应注意的是，土星与木星之间的较大行星比例超出3倍这一和谐比例的量，大约等于金星的固有比例；火星与地球的收敛运动和发散运动之间的较大比例也大约少了同样的量。第三点要注意的是，对于上行星来说，谐和音程建立在收敛运动之间，而对于下行星来说，则是建立在同一方向的运动之间。 ⁽¹⁹⁾ 第四点要注意的是，土星与地球的远日运动之间大约为五个八度，这是因为57′3″的三十分之一是1′47″，而土星的远日运动是1′46″。

此外，单颗行星建立的谐和音程与两颗行星之间建立的谐和音程有很大的不同，前者不能在同一时刻存在，而后者却可以；因为当同一颗行星位于远日点时，它就不可能同时位于近日点，但如果是两颗行星，就可以其中一颗在远日点，同时另一颗在近日点。 ⁽²⁰⁾ 这种由单颗行星所构成的和谐比例与两颗行星所构成的和谐比例之间的差别，类似于被我们称为合唱音乐的素歌或单音音乐（古人唯一知晓的音乐种类） ⁽²¹⁾ 与复调音乐——人们晚近发明的所谓“华丽音乐” ⁽²²⁾ ——之间的差别一样。在接下来的第五章和第六章中，我将把单颗行星与古人的合唱音乐相比较，它的性质将在行星运动中得以展示。而在后面的章节中，我将说明两颗行星与现代的华丽音乐之间也是相符的。

————————————————————

(1) 这里显然有误。周日时耗当然就是一日。根据开普勒后来的讨论，他这里本来要说的似乎是“在等弧上的时耗”。后面的“时耗”均指经过相等弧段所需的时间。——中译者

(2) 周期每除以2，音程就提高一个八度；每乘以2，就降低一个八度。例如，土星周期的十六分之一为672.27天，音程提高了四个八度。这个值比上火星的周期大约为117∶120。这个音程在一个八度以内，但显然不是谐和音程。——中译者

(3) 总注：在开普勒的这部著作中，我把concinna和inconcinna分别译为“和谐的”和“不和谐的”。concinna通常被用来指位于音阶的“自然系统”或纯律之内的所有比例，而inconcinna则被用来指这个调音系统之外的所有那些比例。“谐和的”（consonans）和“不谐和的”（dissonans）是指此音乐系统之内的音程（即谐和音）的性质。“和声”（harmonia）有时是在“和谐”（concordance）的意义上使用，有时则在“谐和音程”（consonance）的意义上使用。

genus durum和genus molle或译为“大调”和“小调”，或译为“大音阶”和“小音阶”，或译为“大（音程）”和“小（音程）”。modus用来指教会调式的用法仅在第六章中出现。

由于我们目前所使用的音乐术语对于16和17世纪并非严格适用，所以这里有必要对术语做一些解释。这里的材料选自开普勒《世界的和谐》，第三卷。

小音阶中的一个八度系统（Systema octavae in cantu molli）：

在大音阶中（In cantu duro）

由于在所有音乐中，这些音阶可以在一个或多个八度以上进行重复，所以上面这些比例都可以减半，即

开普勒所考虑的各种音程为：

80∶81　　（季季莫斯）音差［comma（of Didymus）］，大小全音之差（ ）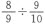

24∶25　　第西斯（diesis）［e-降e、B-降b、或一个半音与一个小全音之差（ ）］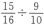

128∶135　小半音（lemma）［一个半音与一个大全音之差（ ）］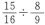

243∶256　柏拉图小半音（Plato's lemma）（在这个系统中没有出现，但在毕达哥拉斯调音系统中出现了）

15∶16　　半音（semitone）小调：降e-d，降b-A；大调：e-d，B-A

9∶10 　　小全音（minor whole tone）小调：f-降e，c-降b；大调：e-b，B-A

8∶9　　　大全音（major whole tone）小调：g-f，d-c，A-G；大调：g-f，d-c，A-G

27∶32　　亚小三度（sub-mlnor tone）大小调：f-d，c-A

5∶6　　　小三度（minor third）小调：e-降-c，降b-G；大调：g-e，d-B

4∶5　　　大三度（major third）小调：g-e-降，d-b-降；大调：e-c，B-G

64∶81　　二全音（ditone）（毕达哥拉斯三度）（大小调：a-f）

243∶320　小不完全四度（lesser imperfect fourth）（“大不完全五度”的转位）见下

3∶4　　　纯四度（perfect fourth）小调：g-d，f-c，降e-降b，d-A，c-G；大调：g-d，f-c，e-B，d-A，c-G

20∶27　　大不完全四度（greater imperfect fourth）小调：降b′-f；大调：a-e

32∶45　　增四度（augmented fourth）小调：a-降e；大调：b-f

45∶64　　减五度（diminished fifth）小调：e-降-A；大调：f-B

27∶40　　小不完全五度（lesser imperfect fifth）小调：f-降b；大调：e-A

2∶3　　　纯五度（perfect fifth）小调：g-c，d-G；大调：g-c，d-G

160∶243　大不完全五度（greater imperfect fifth）（由二全音和小三度复合而成 ）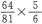

81∶128 　不完全小六度（imperfect mlnor sixth）（大小调：f-A）

5∶8　　　小六度（minor sixth）小调：降e-G；大调：g-B，c′-e

3∶5　　　大六度（major sixth）小调：g-降B，c′-降e；大调：e-G，b-d

64∶27　　大大六度（greater major sixth）小调：d′-f，a-c；大调：d′-f，a-c

1∶2　　　八度（octave）（g-G，a-A，b-B，降b-降B）

所有这些音程都是单音程。当把一个或几个八度加在单音程上时，合成的音程就是一个“复”音程。

1∶3等于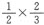 ——一个八度和一个纯五度

3∶32等于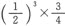 ——三个八度和一个纯四度

1∶20等于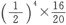 ——四个八度和一个大三度

谐和音程：大小三度和六度、纯四度、纯五度、纯八度

“掺杂”谐和音程：下小三度、二全音、小不完全四度和五度、大不完全四度和五度、不完全小六度、大大六度。

不谐和音程：所有其他音程。

在整部著作中，开普勒沿袭他那个时代的理论家的用法而使用弦长比，而不是像我们今天通常所做的那样使用振动比。当然，弦长比是振动比的倒数，也就是说，弦长比4∶5用振动比来表示就是5∶4。这解释了为什么音阶是降序，而数值却是增序。很有意思的是，开普勒的大小音阶彼此互为逆行，因此当用振动比来表示时，它们的顺序与用弦长比来表示时正好相反：

这里选了任意音高G来定出这些比值。这个g或“gamma”通常是16世纪整个音阶的最低音。——Elliott Carter，Jr．

［Elliott Carter，Jr．，1908—，美国作曲家，拓展了十二音作曲方法——中译者］

(4) 这条规则是要找到一种对所有行星均适用的对真周日行程的公共量度，即真周日弧乘以行星与太阳之间的距离所得到的积。——中译者

(5) Aristotle，De Caelo ，291 a 29—291 b 10．——中译者

(6) 这里开普勒似乎是主张，生命体接受天体的和谐是天性使然。在理解天体和谐的各种可能性中，从太阳上看到的视运动是最适合本能体认的。——中译者

(7) 开普勒已经证明了，对于小偏心率，从太阳上看到的视角速度与行星和太阳之间的距离的平方成反比。参见第三章，第六条。——中译者

(8) 月球视运动的比例被取作地球上的观测值。——中译者

(9) 参见前面对“距离与和谐比例的比较”的注释。——中译者

(10) 开普勒把“耳朵很难辨别出”的不谐和部分的最大值取作一个第西斯24∶25。只有木星的发散运动与火星的发散运动之间的不谐和部分大于一个第西斯，它的实际值是128∶135，即一个第西斯与一个半音的平均值。尽管这些不谐和部分已经相当小了，但它们还没有小到开普勒所希望的程度。因为一个大到第西斯程度的不谐和部分在音乐演奏中是不被允许的，其可以接受的最大不谐和部分为一个音差80∶81，小于第西斯的三分之一。——中译者

(11) 即比较两行星的近日运动或远日运动。——中译者

(12) comp．代表比例或音程之间的“复合”，即两者相乘。开普勒在前面已经说明，土星的远日运动与近日运动之间的比例比大三度4∶5超出了53∶54或一个半音差。而土星的近日运动与木星的远日运动之间几乎恰好相差一个八度1∶2，所以把前者与1∶2复合，就得到了土星与木星的远日运动之比。于是，这两个远日运动之间就比八度加大三度超出了大约一个半音差，它很好地落在了开普勒所能接受的一个第西斯的极限之内。后面的计算也是类似的。——中译者

(13) 即木星与火星的远日运动之比。这个值相当于比两个八度加一个五度小两个音差的音程。——中译者

(14) 木星的近日运动与火星的远日运动之比是5∶24 comp．158∶157，火星的远日运动与木星的近日运动之比是2∶3 comp．30∶29，把这两个值复合起来，便得到木星与火星的近日运动之比，即开普勒所说的不谐和音程1∶7。——中译者

(15) 即火星的近日运动与地球的远日运动之比。——中译者

(16) 于是火星与地球的近日运动之比对应着一个谐和音程，不谐和部分只有半个音差。——中译者

(17) 这里的不谐和部分约为一个音差的四分之一。——中译者

(18) 开普勒已经说明金星的远日运动与近日运动之比对应着一个第西斯减一个音差，即音程34∶35。——中译者

(19) 即两颗行星的远日运动或近日运动之间。——中译者

(20) 由单颗行星所构成的谐和音只能像单线旋律那样连续听到，而两颗行星所构成的谐和音却可以同时听到，就像在开普勒认为是晚近发明的复调音乐中一样。——中译者

(21) 古希腊的合唱音乐是单线的，所有人都演唱同一种旋律。——Elliott Carter，Jr．

(22) 在素歌中，音符的所有时值都大体相等，而在“华丽音乐”中，音符有不同长度的时值，这使作曲家既可以规定不同对位部分组合在一起的方式，又可以制造丰富的表现效果。事实上从这时起，所有旋律都是“华丽音乐”的风格。——Elliott Carter，Jr．