第八章 实立方体中的热运动
·Chapter VIII Of the Movement of Heat in A Solid Cude·
傅立叶早年的文学爱好和他当教师的经历对其理论的成功有很大影响。他的论著具有简洁性、清晰性和普遍性的特征,其中包含有很强的几何直观,而且对每一种数学表示都给出其实际的物理意义。

傅立叶红外显微光谱仪
333 我们仍然需要运用方程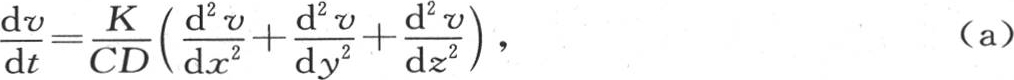 它表示在受空气作用的实立方体中的热运动(第二章第5节)。首先,假定v有一个很简单的值e-mt cosnx cospy cosqz,如果我们把它代进所提出的方程中,那么我们有条件方程m=k(n2 +p2 +q2 ),字母k表示系数
它表示在受空气作用的实立方体中的热运动(第二章第5节)。首先,假定v有一个很简单的值e-mt cosnx cospy cosqz,如果我们把它代进所提出的方程中,那么我们有条件方程m=k(n2 +p2 +q2 ),字母k表示系数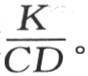 由此得到,如果我们用任意三个量代替n,p,q,并把m取作k(n2 +p2 +q2 ),那么前面的v值就总满足这个偏微分方程。因此我们有方程v=e-k(n2 +p2 +q2 )t cosnx cospy cosqz。这个问题的性质还要求:如果x变号,并且如果y和z保持不变,那么该函数不变;并且这对y或z也应成立:现在这个v值显然满足这些条件。
由此得到,如果我们用任意三个量代替n,p,q,并把m取作k(n2 +p2 +q2 ),那么前面的v值就总满足这个偏微分方程。因此我们有方程v=e-k(n2 +p2 +q2 )t cosnx cospy cosqz。这个问题的性质还要求:如果x变号,并且如果y和z保持不变,那么该函数不变;并且这对y或z也应成立:现在这个v值显然满足这些条件。
334 为了表示表面状态,我们应当运用下面的方程: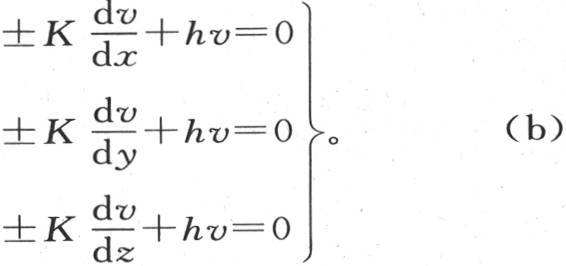
当x=±a,或y=±a,或z=±a时,这些方程应当被满足。 【1】 取立方体的中心为坐标原点:边由a来表示。 【2】
方程(b)的第一个给出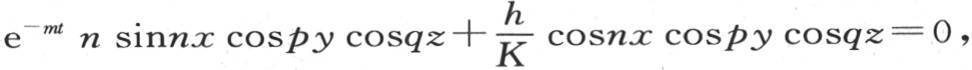 或者是
或者是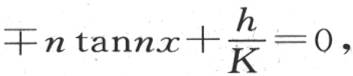 一个在x=±a时必然成立的方程。 【3】
一个在x=±a时必然成立的方程。 【3】
由此得到,n这个量除了应当满足条件 之外,我们不可能对它取任何其他的值。因此,我们应当解给出ε值的定义方程
之外,我们不可能对它取任何其他的值。因此,我们应当解给出ε值的定义方程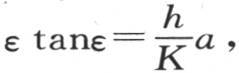 并且取
并且取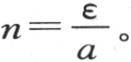 现在ε的这个方程有无数实根;因此我们可以得到n的无数不同的值。用同样的方法,我们可以确定对p和q所能给出的值;它们都由在前一个问题中(第328目 【4】 )曾应用过的作图来表示。用n1 ,n2 ,n3 ,…表示这些根;这样,只要我们用根n1 ,n2 ,n3 ,…中的一个代替n,并且用同样的方式选择p和q,我们就可以对v给出由方程v=e-kt(n2 +p2 +q2 ) cosnx cospy cosqz所表示的特殊值。
现在ε的这个方程有无数实根;因此我们可以得到n的无数不同的值。用同样的方法,我们可以确定对p和q所能给出的值;它们都由在前一个问题中(第328目 【4】 )曾应用过的作图来表示。用n1 ,n2 ,n3 ,…表示这些根;这样,只要我们用根n1 ,n2 ,n3 ,…中的一个代替n,并且用同样的方式选择p和q,我们就可以对v给出由方程v=e-kt(n2 +p2 +q2 ) cosnx cospy cosqz所表示的特殊值。
335 因此我们可以组成无数特殊的v值,并且显然,几个这样的值的和也满足微分方程(a)和定义方程(b)。为了对v给出问题所需要的一般形式,我们可以把与项a e-kt(n2 +p2 +q2 ) cosnx cospy cosqz类似的项合起来。
v的值可以由下面的方程表示:
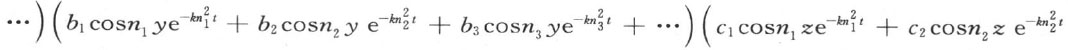
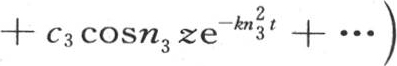 。 【5】
。 【5】
右边由三个水平行中所写的三个因子的积所组成,量a1 ,a2 ,a3 ,…是未知系数。现在根据假定,如果令t=0,那么温度在这个立方体的所有点上都是相同的。因此我们应当确定a1 ,a2 ,a3 ,…,使得无论x,y和z的值如何,只要这些值的每一个都包含在a和-a之间,v的值就是不变的。用1来表示在这个固体所有点的初始温度,我们应当有方程(第323目)1=a1 cosn1 x+a2 cosn2 x+a3 cosn3 x+…,1=b1 cosn1 y+b2 cosn2 y+b3 cosn3 y+…,1=c1 cosn1 z+c2 cosn2 z+c3 cosn3 z+…,其中,需要确定a1 ,a2 ,a3 ,…。在用cosni x乘第一个方程的两边后,从x=0到x=a积分:那么从前面所运用的分析(第325目)得到,我们有方程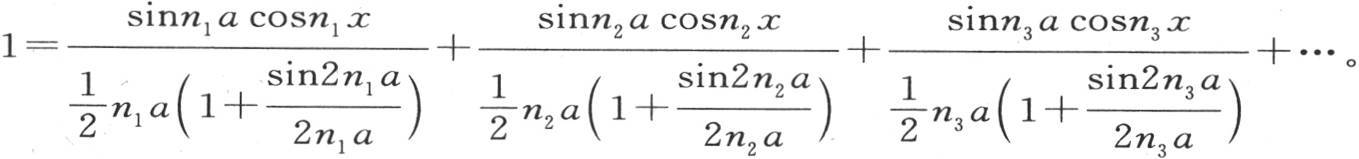
用μi 表示量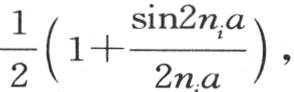 我们有
我们有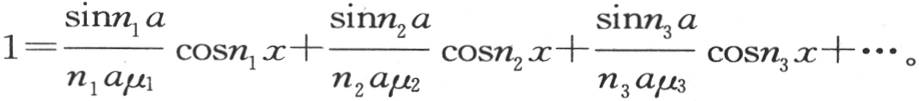
当我们对x给出包含在a和-a之间的值时,这个方程总成立。
由此我们得到v的一般值,它由下面的方程给出: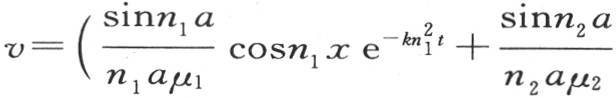
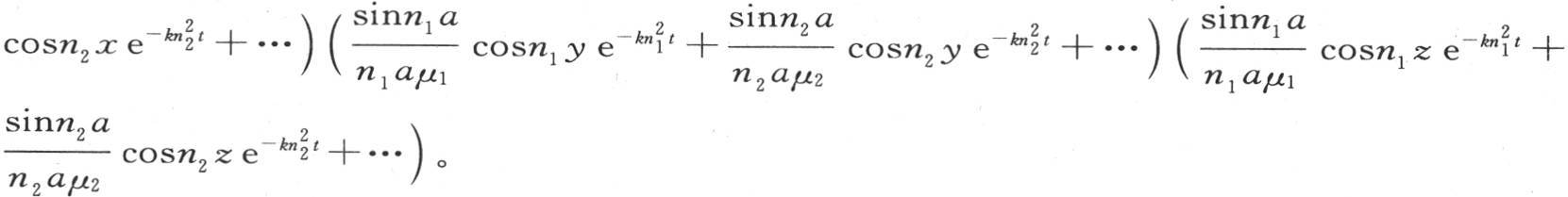
336 因此,v的表达式由三个类似的函数组成,一个是x的函数,另一个是y的函数,第三个是z的函数,这不难直接验证。
事实上,如果在方程 中,我们假定v=XYZ;X表示x和t的函数,Y表示y和t的函数,Z表示z和t的函数,那么我们有
中,我们假定v=XYZ;X表示x和t的函数,Y表示y和t的函数,Z表示z和t的函数,那么我们有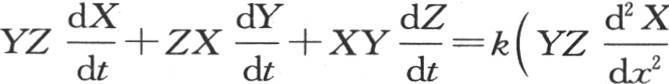
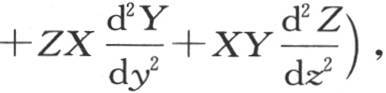 或者是
或者是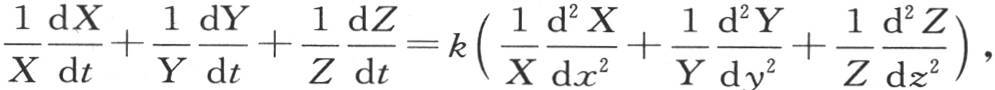 它包含三个独立的方程
它包含三个独立的方程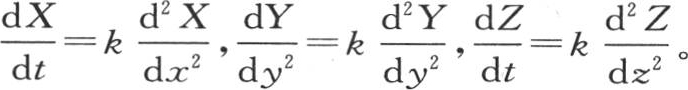
我们必定还有与表面相关的条件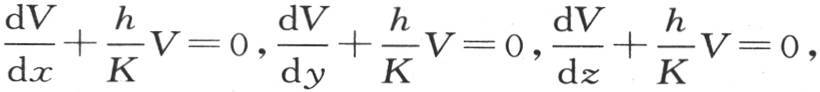 因此我们推得
因此我们推得
由此得到,为了完全解决这个问题,我们只需取方程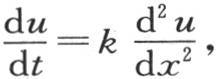 并且对它增加条件方程
并且对它增加条件方程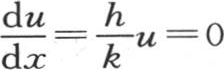 就够了,这个条件方程在x=a时必然成立。然后我们应当或者用y或者用z来代替x,这样,我们就有三个函数X,Y,Z,这些函数的积就是v的一般值。
就够了,这个条件方程在x=a时必然成立。然后我们应当或者用y或者用z来代替x,这样,我们就有三个函数X,Y,Z,这些函数的积就是v的一般值。
因此所提出的问题的解如下:v=φ(x,t)φ(y,t)φ(z,t);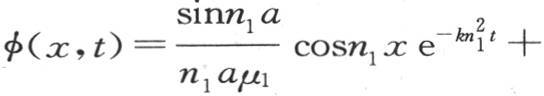
 由下述方程
由下述方程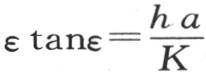 给出,其中,ε表示na,μi 的值是
给出,其中,ε表示na,μi 的值是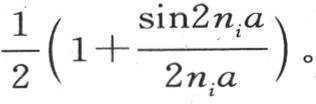
用同样的方法,可以得到函数φ(y,t),φ(z,t)。
337 我们可以确信,v的这个值可以在它的整个范围内解这个问题,并且,为了表示这个固体的温度变化,偏微分方程(a)的完全积分必然取这种形式。
事实上,v的表达式满足方程(a)和与表面有关的条件。因此,在某一时刻内从分子的作用和从空气对表面的作用所产生的温度变化,是我们通过相对时间t微分v的值所得到的温度变化。由此得到,如果函数v在任一时刻的开始表示这个温度系统,那么它仍然表示在后一时刻开始时所成立的那个温度系统,同样可以证明,这个固体的变化状态总是由函数v来表示,其中t的值不断增加。现在这个函数与初始状态一致:因此,它表示这个固体所有的后继状态。所以可以确信,对v给出与前面不同的函数的任一个解都肯定是错的。
338 如果我们假定已经历经的时间t变得很大,那么除v的表达式的第一项外,我们不再非得考虑其他任何项了;因为值n1 ,n2 ,n3 ,…以最小一个开始按次序排列。这个项由方程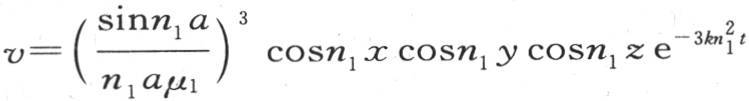 给出。所以,这就是这个温度系统不断趋于、并且在某个t值之后该温度系统与之重合而无明显误差的主状态。在这个状态下,每一点的温度与分数
给出。所以,这就是这个温度系统不断趋于、并且在某个t值之后该温度系统与之重合而无明显误差的主状态。在这个状态下,每一点的温度与分数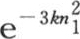 的幂成正比地降低;这时,各相继状态都是相似的,更准确地说,它们只是在温度的数值上不同,这些温度都随一个几何级数的项而减少,同时保持相同的比不变。由前面的方程我们不难得到这样一条规律:温度从一点到另一点沿立方体的对角线或者是边或者是最后在适当位置所给定的直线而降低。我们也可以确定决定薄层有相同温度的表面有什么样的性质。我们看到,在我们在此处所考虑的最后状态和稳定状态中,同一薄层的点总是保持相同的温度不变,这可能在初始状态和在紧随其后的那些状态中不成立。在终极状态的无限持续时间内,这一物体被划分成各点都有相同温度的无数薄层。
的幂成正比地降低;这时,各相继状态都是相似的,更准确地说,它们只是在温度的数值上不同,这些温度都随一个几何级数的项而减少,同时保持相同的比不变。由前面的方程我们不难得到这样一条规律:温度从一点到另一点沿立方体的对角线或者是边或者是最后在适当位置所给定的直线而降低。我们也可以确定决定薄层有相同温度的表面有什么样的性质。我们看到,在我们在此处所考虑的最后状态和稳定状态中,同一薄层的点总是保持相同的温度不变,这可能在初始状态和在紧随其后的那些状态中不成立。在终极状态的无限持续时间内,这一物体被划分成各点都有相同温度的无数薄层。
339 对于一个给定的时刻,不难确定这个物体的平均温度,即通过取每个分子的体积与它的温度的积的和,并且用整个体积除这个和所得到的温度。因此我们建立表达式 它是平均温度V的表达式。这个积分应当分别相对于x,y和z在区间a和-a之间取积分:由于v等于积XYZ,所以我们有V=∫Xdx∫Ydy∫Zdz; 【6】 由于这三个完全积分有相同的值,所以,平均温度是
它是平均温度V的表达式。这个积分应当分别相对于x,y和z在区间a和-a之间取积分:由于v等于积XYZ,所以我们有V=∫Xdx∫Ydy∫Zdz; 【6】 由于这三个完全积分有相同的值,所以,平均温度是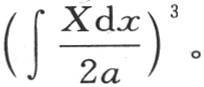 因此
因此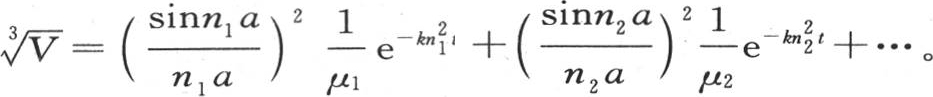
量na等于ε,它是方程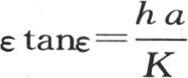 的一个根,μ等于
的一个根,μ等于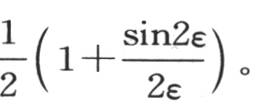 这样,用ε1 ,ε2 ,ε3 ,…表示这个方程不同的根,我们有
这样,用ε1 ,ε2 ,ε3 ,…表示这个方程不同的根,我们有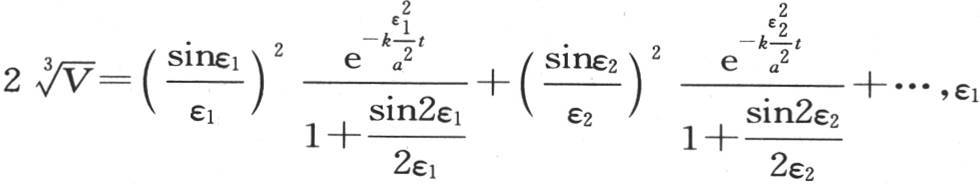 在0到
在0到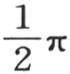 之间,ε2 在π到
之间,ε2 在π到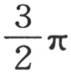 之间,ε3 在2π到
之间,ε3 在2π到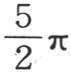 之间,根ε2 ,ε3 ,ε4 ,…愈来愈接近于下极限π,2π,3π,…,并且当下标i很大时,以与它们重合而结束。两倍的弧2ε1 ,2ε2 ,2ε3 ,…包含在0到π,2π到3π,4π到5π之间;由于这个原因,这些弧的正弦都为正:量
之间,根ε2 ,ε3 ,ε4 ,…愈来愈接近于下极限π,2π,3π,…,并且当下标i很大时,以与它们重合而结束。两倍的弧2ε1 ,2ε2 ,2ε3 ,…包含在0到π,2π到3π,4π到5π之间;由于这个原因,这些弧的正弦都为正:量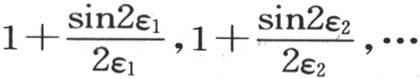 为正并且在1到2之间。由此得到,进入
为正并且在1到2之间。由此得到,进入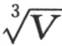 的值的所有项都是正的。
的值的所有项都是正的。
340 我们现在打算比较一下立方体中的冷却速度和我们所得到的球状物体的冷却速度。我们已经看到,对于这两个物体的任一个,温度系统都收敛于一个在一定时间之后所明显得到的永恒状态;这时,立方体不同点的温度一起降低,同时保持相同的比不变,某个这样的点的温度随一个几何级数的那些项而降低,它的比在两个物体中是不同的。从两个解得到,对于球,这个比是 对于立方体,它是
对于立方体,它是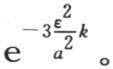 量n由方程
量n由方程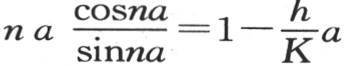 给出,a是球半径,量ε由方程
给出,a是球半径,量ε由方程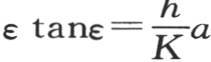 给出,a是立方体边长的一半。
给出,a是立方体边长的一半。
如此,让我们考虑两种不同的情况;在第一种情况中,球半径和立方体边长的一半都等于一个很小的量a;在第二种情况中,a的值很大。假定这两个物体的体积都很小,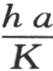 取很小的值,ε也如此,因此我们有
取很小的值,ε也如此,因此我们有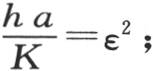 所以分数
所以分数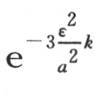 等于
等于 所以我们所观察到的终极温度被表示成
所以我们所观察到的终极温度被表示成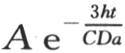 的形式。现在,如果在方程
的形式。现在,如果在方程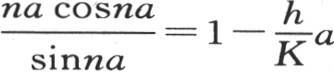 中我们假定右边与1相差无几,那么我们得到
中我们假定右边与1相差无几,那么我们得到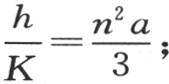 因此分数
因此分数 是
是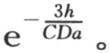
由此我们得到,如果球半径很小,那么这个物体和外切立方体的冷却速度相同,它们每一个都与半径成反比;也就是说,如果边长的一半为a的立方体的温度在时间t内从值A过渡到值B,那么半径为a的球在同一时间内也从温度A过渡到B。如果两个物体的量a发生变化,结果变成a′,那么从A到B的进程所需要的时间取另一个值t′,并且时间t和t′的比就是半边长a和a′的比。当半径a很大时情况则不同:这时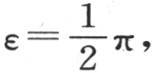 na的值是量π,2π,3π,4π,…。
na的值是量π,2π,3π,4π,…。
在这种情况下,我们不难得到分数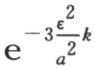 和
和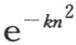 的值;它们是
的值;它们是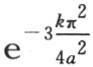 和
和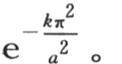
由此我们可以推出二个值得注意的结论:
第一,当两立方体有很大体积,并且a和a′是它们的半边长时;如果第一个在从温度A过渡到温度B时需要时间t,并且第二个对于这同一温差所需的时间是t′;那么时间t和t′与半边长的平方a2 和a′2 成正比。对于体积很大的球,我们得到一个类似的结果。
第二,如果立方体的半边长a是相当大的,球的半径有同一数值a,并且在时间t内立方体的温度从A下降到B,那么当球的温度从A降到B时,它将历经不同的时间t′,并且时间t和t′的比是4∶3。
因此,当立方体和内切球体积很小时,它们同样迅速地冷却;在这种情况下,每个物体的冷却时间都与它们的厚度成正比。如果立方体和内切球的体积很大,那么这两个固体的最后冷却时间不是一样的。立方体的这个时间比球的这个时间要大,其比为4∶3,这两个物体的冷却时间都分别随直径的平方而增加。
341 我们曾假定物体在温度恒定的空气中缓慢冷却。我们可以使表面受其他任何条件的作用。例如设想某种外因使它的所有点都保持固定温度0。进入余弦符号下的v值的量n,p,q应当在这种情况下使cosnx在x取完全值a时变成0,cospy和cosqz亦如此。如果立方体的边2a由π来表示,2π是半径为1的圆周;那么我们可以用下面的方程表示v的一个特殊值,这个方程同时满足热运动的一般方程和表面状态的一般方程,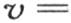

当或者是x或者是y或者是z得到其极值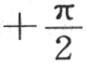 或者是
或者是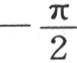 时,无论t如何,这个函数都为0:但是若不历经相当长的时间,温度的这个表达式就不可能有这种简单的形式,除非给定的初始状态本身就由cosx cosy cosz来表示。这就是我们在第一章第8节第100目中所假定的。前面的分析证明我们在刚才引述过的那一目中所运用过的这个方程成立。
时,无论t如何,这个函数都为0:但是若不历经相当长的时间,温度的这个表达式就不可能有这种简单的形式,除非给定的初始状态本身就由cosx cosy cosz来表示。这就是我们在第一章第8节第100目中所假定的。前面的分析证明我们在刚才引述过的那一目中所运用过的这个方程成立。
到目前为止,我们讨论了热的理论中的一些基本问题,并且考察了那种元素在一些主要物体中的作用。在我们所挑选出的这些问题中,每一个都有一个新的更大的困难。我们有意省略了许多中间问题,例如在两端保持固定温度或者是受空气作用的棱柱中的线性热运动问题。应当对在气体介质中冷却的立方体和矩形棱柱的变化的热运动的表达式进行概括,并假定任意的初始状态。这些研究只需本书所阐述过的那些原理就足够了。
傅立叶先生在巴黎1827年的《科学院研究报告》第7卷第605—624页中发表了的一篇题为“虚根的判别和由热理论所决定的超越方程的代数分析定理的应用”(Mémoire sur la distinction des racines imaginaires, et sur l'application des théorèmes d'analyse algébrique aux équations transcendantes qui dependent de la théorie de la chaleur)的研究报告。它包含热的理论中的两个命题的证明。如果有两个相类似的凸形固体,它们对应的基元有相同的密度、比热和热导率,并且有相同的初始温度分布,那么,第一,当表面的对应基元保持恒定温度时,或者第二,当表面的对应点的外部介质温度保持不变时,这两个物体的条件在经过像尺寸的平方这样的翻倍之后仍然相同。
因为沿经过对应棱柱基元端面积s、s′的那些热流线的流速是u-v∶u′-v′,此处(u,v),(u′,v′)是在s和s′的两对边(opposite sides)上在同一距离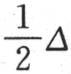 处的两对点(pairs of points)的温度;并且,如果n∶n′是量纲的比,则(u-v)∶(u′-v′)=n′∶n。此外,如果dt,dt′是对应的时间,则棱柱基元所得到的热量就是sk(u-v)dt∶s′k(u′-v′)dt′,或是n2 n′dt∶n′2 ndt′。但是由于体积是n3 ∶n′3 ,所以,如果温度的对应变化总是相等的,那么我们肯定有
处的两对点(pairs of points)的温度;并且,如果n∶n′是量纲的比,则(u-v)∶(u′-v′)=n′∶n。此外,如果dt,dt′是对应的时间,则棱柱基元所得到的热量就是sk(u-v)dt∶s′k(u′-v′)dt′,或是n2 n′dt∶n′2 ndt′。但是由于体积是n3 ∶n′3 ,所以,如果温度的对应变化总是相等的,那么我们肯定有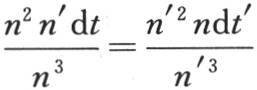 或者是
或者是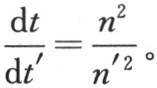 在第二种情况下,我们应当假定H∶H′=n∶n′。——A. F.
在第二种情况下,我们应当假定H∶H′=n∶n′。——A. F.

格勒诺布尔景
注释
【1】 M. 加斯东·达布在法文《文集》本中在此处加了一个如下的脚注:更准确地说,无论y和z怎样的,对于x=a,我们都有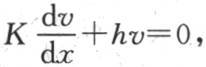 对于x=-a,我们有
对于x=-a,我们有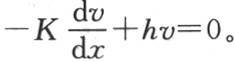 这个给定的条件自然适用于另外两个方程。——汉译者
这个给定的条件自然适用于另外两个方程。——汉译者
【2】 准确地说,a是边长的一半。——汉译者
【3】 M. 加斯东·达布在法文《全集》本中在此处有一个如下的脚注:这就是说,与这些符号相对应,如果我们取x=+a,那么方程就是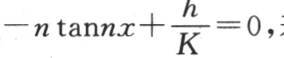 若取x=-a,则方程的符号相反。——汉译者
若取x=-a,则方程的符号相反。——汉译者
【4】 英译本中标明的是第321目,这显然不对。此处依法文《文集》本订正。——汉译者
【5】 法文《文集》本中这个方程右边的各项系数与英译本有出入。在那里,这个方程是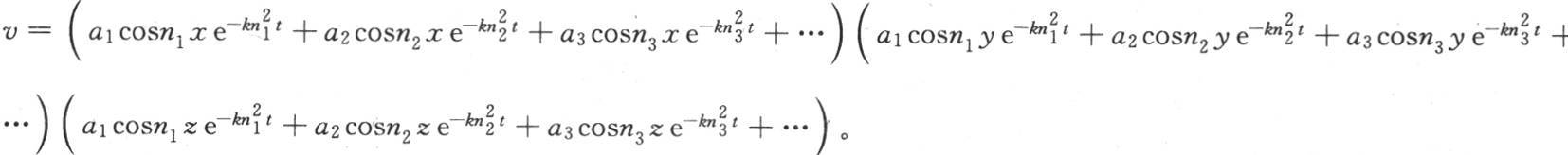
【6】 在法文《文集》本中,此式左边多一因子,即(2a)3 V=∫Xdx∫Ydy∫Zdz。——汉译者
