附录D

量子理论中的相干性与随机性

Appendix D

这个异乎寻常的发展带来了西方科学的基本概念和中国古典的自然观的更紧密的结合。正如李约瑟在他论述中国科学和文明的基本著作中经常强调的，经典的西方科学和中国的自然观长期以来是格格不入的。西方科学向来强调实体（如原子、分子、基本粒子、生物分子等），而中国的自然观则以“关系”为基础，因而是以关于物理世界的更为“有组织的”观点为基础的。

布鲁塞尔自由大学校景（彭丹歌摄）。

算符和超算符

在第9章中我们强调了不稳定性在统计物理学建立中所起的重要作用。附录A表明：从决定论的动力学出发，通过一个适当的非幺正的不丢失任何信息的“表象变换”，就有可能得到随机（马尔可夫）过程。只要系统的动力学有适当高度的不稳定性，就有可能去确定这个表象变换。这就证明，概率论的理论可以依然是“完备”的和“客观”的。

附录A中所采用的观点是：当一个（经典）动力学系统足够地不稳定时，我们就不能再谈轨道，我们就被迫采取一种根本不同的方法，去研究相空间中分布函数（或轨道束）的演化。在这样的条件下，不可能完成从分布函数到相空间中单个点的转变（见第9章“时间和变化”一节）。

在量子理论中，坐标和动量仍然有它们的意义，且测量可以在适当的相空间中划分出该系统所在的一个区域来。

于是，人们会问：是否存在另外一些（例如和量子理论的表述有关的）情形，在那里从相空间的分布函数到单个轨道的转变也是不可能的？

通常，我们采取另一种态度：到单个轨道的转变是在经典力学与量子力学两者间的关系问题尚未提出之前完成的。但是，经典的轨道概念与量子的波函数概念是如此不同，以至很难用一种有意义的方法对它们进行比较。

这里所遇到的这类问题，与在经典理论中遇到的完全不同。那里，我们处理的是不稳定的“无序”系统——实际上，它们是这样的无序，以致我们有可能去确定与熵密切相关的李雅普诺夫函数。相反，从经典力学到量子力学的过渡并没有影响经典动力学的基本可逆性（见第3章）。此处，如第3章“不稳定粒子的衰变”一节中所提到的，一切有限的量子力学系统都具有一个分立的能谱，因此有一个纯的周期运动。量子理论在这个意义上导致一种比经典理论更加“相干”的运动行为。这可以作为一种有力的物理论据，去反对任何要用“隐”变量或传统的随机模型来理解量子理论的企图。反之，这个增加的相干性似乎表明，量子理论应当对应于一种“超决定”的经典理论。换句话说，量子效应看来会导致相空间中相邻经典轨道之间的相关。这就是以一种直觉方式表达出来的古老的玻尔-索末菲的面积为h的相格概念。

为把这个概念用一种新的精确的方式表达出来^[1] ，我们必须重新引入算符与超算符之间的区别^[2] 。这种区别已在第8章“不可逆性以及经典力学和量子力学表述的扩展”一节中讨论过。我们还提到过（见方程3.35和附录C），刘维算符是一个可因式分解的超算符。按照定义，一个可因式分解的超算符F可以写作A₁ ×A₂ （见方程C.9）。其意义是

使用这个记法，对于刘维超算符，我们有：

量子超算符的可因式分解性是一个基本的性质，这一点不和经典超算符相类似。例如经典刘维算符L_e1 也是一个超算符，因为它作用在分布函数上（分布函数是两组变量q和p的函数，因此类似于一个连续矩阵）。但是，L_e1 是用一个泊松括号（见方程2.13）来表达的并且是不可因式分解的。

在经典超算符与量子超算符之间建立一个简单的对应关系将为洞察量子力学结构提供一个来源。

经典的对易规则

在只有一个自由度的经典系统中，可以引入四个基本算符（其中的两个是乘法超算符）：

使用大写字母是为了强调我们把它们看做是作用在分布函数上的超算符。乘以i是为了得到厄米超算符。

显然，这四个量满足两条独立的非对易规则：一个是关于P与i（∂/∂P）的，另一个是关于Q与-i（∂/∂Q）的（见第3章“算符及并协性”一节）。相反，经典轨道理论是完全用Q与P的函数建立起来的，不允许任何的非对易关系。

量子理论介于一个中间的位置，因为它导致量子力学算符Q_op 与P_op 之间单一的非对易关系。在这个意义上，量子力学含有的决定论甚于经典系综理论，而逊于经典轨道理论。

经典非对易规则的意义是什么呢？我和乔治最近的一篇文章^[1] 对这个问题作了详细的讨论。可以指望从与量子力学的类比中得到下面的对应关系：

因此，经典非对易规则有一个简单的意义：例如，一个分布函数不可能对应于一个完全确定的Q值而同时又与Q无关。这样一来，经典的测不准关系表达了一个“逻辑上”的矛盾。但是，任何东西也不能阻止我们有一个分布函数，它同时对应于P与Q的完全确定的值，因而对应于一条经典的轨道。

量子的对易规则

现在让我们对四个可因式分解的超算符引入量子机制。这些超算符是由算符q_op ，p_op 表达出来的，q_op 和p_op 满足海森伯测不准关系：

这四个超算符是：

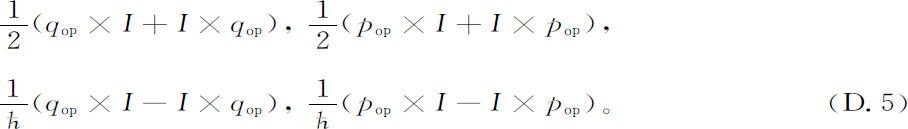
在经典超算符D.3与量子超算符D.5之间有着值得注意的同构。对易规则是相同的，而且我们可以写出下面的对应关系：

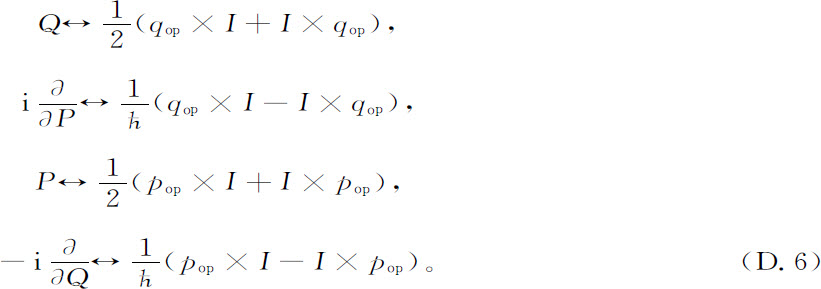
这个对应关系使我们能把“类似”的物理意义归属于这些量的集合。但这就意味着，利用线性组合和定义D.1，我们有下面的对应：

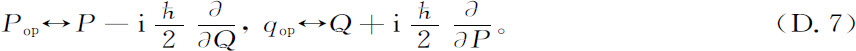
这个结果似乎是最使人感兴趣的。希尔伯特空间算符p_op ，q_op 不能用定义在一个轨道上的量P，Q来表达，它们还包含作用在分布函数上的超算符。现在我们清楚地看到为什么经典力学的纯态在希尔伯特空间不再能实现：经典超算符通过普适常数h的耦合阻止对应于完全确定的Q值和P值的本征系综的实现。

如果我们要努力从一个连续分布函数走向一个单个点（一个δ函数），那么表达式D.7中的导数就会趋于无穷，我们就会得到能量无穷大的态。这正表达出由h列出的相空间中相关的概念。

我们看到，过去常被提倡的系综观点说明了量子力学相对于经典理论的位置。量子力学的特点并不是出现了非对易的算符。这个特点总可以被纳入经典的系综理论。新的独特的特点是四个基本超算符（表达式D.5）用表达式D.7所给出的两个组合而进行的约化。只有当具有物理维数的一个作用量（动量×坐标）的普适常数存在时，这才是可能的。因此，希尔伯特空间中动量和坐标的概念不再是独立的，量子理论似乎是一种超决定的经典理论，在其中相邻点的运动不能被独立地预言。虽然永远也不会有一种量子力学的“经典”理论，但与这种物理情景非常类似的将会是一个弦的经典运动，在其中相邻点的运动同样不再能被独立地预言——如果我们真能这样做，这将会导致该弦的剧烈变形，以及导致能量可以任意大的态。

结　　语

如在本附录开头所提过的，我们也可以把非对易算符和一个经典并协性原理引入经典系综理论的框架之中。但是，这个原理具有平凡的意义：我们不能构造关于分布函数ρ的互相矛盾的说法。量子力学的新特点是可以构造出的系综的类型受到h的限制。此外，我们不再能限制单个轨道，因此并协性原理成为量子力学中的一个基本原理。

应当强调，在这种研究量子理论的方法中，无论在哪一点上，我们都不能消除来自观察者或是其他主观因素的涨落。

至于在统计力学中，从系综到轨道的转变被相空间结构的一种改变所阻止。在统计力学中，运动的不稳定性起着关键的作用（见第9章与附录A和C）。这里，描述量子系综的动态算符的结构导出一种既完备又是概率论的理论。

因此，在爱因斯坦-玻尔关于量子理论基础的著名辩论中（见文献［3］），处于核心的困难问题已开始采取新的形式：考虑完备而客观的概率论确实是可能的。概率的因素绝不是无知的表现，而可能是动态理论结构中新的基本特点的表现。

参考文献

［1］C. George and I. Prigogine，Physica 99A（1979）：369.

［2］I. Prigogine. Cl. George，F. Henin，and L. Rosenfeld，Chemica Scripta，4（1973）51.

［3］关于Wigner，Moyal，Bopp等工作的参考文献可见M. Jammer，The Philosophy of Quantum Mechanics（New York：Wiley 1974），其中有一个详尽的文献目录.