第五章

系统的音高或音阶的音、歌曲的种类、大调和小调均已在（相对于太阳上的观测者的）行星的视运动的比例中表现了出来 ⁽¹⁾

• Expressed the Pitches of the System •

为什么我要在措词上做文章呢？因为我曾拒绝并抛弃的大自然的真理，重新以另一种可以接受的方式，从后门悄悄地返回。也就是说，我没有考虑以前的方程，而只专注于对椭圆的研究，并确认它是一个完全不同的假说。然而，这两种假设实际上就是同一个，在下一章我将证明这一点。我不断地思考和探求着，直到我几乎发疯，所有这些对我来说只是为了找出一个合理的解释，为什么行星更偏爱椭圆轨道……噢，我曾经是多么的迟钝啊！

——开普勒

月面上清晰可见的开普勒环形山。

截至目前，我已经分别由得自天文学与和声学中的数值证明了，在围绕太阳旋转的六颗行星的12个端点或运动之间构成了和谐比例，或者仅与这些比例相差最小谐和音程的极小一部分。然而，正如在第三卷中，我们先是在第一章建立起单个的谐和音程，然后才在第二章把所有谐和音程——尽可能多地——合为一个共同的系统或音阶，或者说，是通过把包含了其余谐和音程在内的一个八度分成了许多音级或音高，从而得到了一个音阶一样；现在，在发现了上帝亲自在世界中赋予的和谐比例以后，我们接下来就要看看这些单个的和谐比例是分立存在的，以至于它们每一个都与其余的比例没有亲缘关系，还是彼此之间是相互一致的。然而，我们不用进一步探究就可以很容易地下结论说，那些和谐比例是以最高的技巧配合在一起的，以至于它们就好像在同一个框架内相互支持，而不会有一个与其他的相冲撞；因为我们的确看到，在这样一种对各项进行多重比较的时候，没有一处是不出现和谐比例的。因为如果所有谐和音程都不能很好地搭配成一个音阶，那么若干个不谐和音程是很容易产生的（只要可能，它们就会出现）。例如，如果有人在第一项和第二项之间建立了一个大六度，并且以独立于前者的方式在第二项和第三项之间建立了一个大三度，那么他就要承认，在第一项和第三项之间存在着一个不谐和音程12∶25。

现在，让我们看看我们在前面通过推理而得到的结果是否真的是实际存在的事实。不过我先要提出一些告诫，以免我们在前进过程中遇到过多阻力。首先，我们目前应当忽视那些小于一个半音的盈余或亏缺，因为我们以后将会看到什么是它们的原因；其次，通过连续对运动进行加倍或减半，我们将把所有音程都限制在一个八度的范围内，因为所有八度内的谐和音程都是一样的。

表示八度系统的所有音高或音的数值都列在第三卷第八章的一个图中， ⁽²⁾ 这些数值应被理解为许多对弦的长度。因此，运动的速度将与弦长成反比。 ⁽³⁾

现在，通过连续减半而对行星的运动进行相互比较，我们得到

水星在近日点的运动，第7次减半，或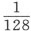 ，3′0″

在远日点的运动，第6次减半，或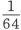 ，2′34″— ⁽⁴⁾

金星在近日点的运动，第5次减半，或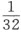 ，3′3″＋ ⁽⁵⁾

在远日点的运动，第5次减半，或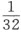 ，2′58″—

地球在近日点的运动，第5次减半，或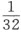 ，1′55″—

在远日点的运动，第5次减半，或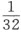 ，1′47″—

火星在近日点的运动，第4次减半，或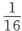 ，2′23″—

在远日点的运动，第3次减半，或 ，3′17″—

木星在近日点的运动，　　　减半，或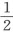 ，2′45″

在远日点的运动，　减半，或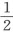 ，2′15″

土星在近日点的运动，　　　　　　　　　2′15″

在远日点的运动，　　　　　　　1′46″

设运动最慢的土星的远日运动，即最慢的运动，代表着系统中的最低音G，它的值是1′46″。于是地球的远日运动也代表着高出五个八度的同样的音高，因为它的值是1′47″；谁会愿意去为土星远日运动中的一秒而争论不休呢？不过，还是让我们考虑一下：这个差距将不会大于106∶107，它小于一个音差。如果你加上1′47″的四分之一即27″，那么得到的和将是2′14″，而土星的近日运动是2′15″； ⁽⁶⁾ 木星的远日运动也是类似的，只不过要高出一个八度。因此，这两个运动代表着b音或稍高一点。把1′47″的三分之一，即36″—，加到整个数值上，得到的和2′23″—代表c音；这就是具有同样数值的火星的近日运动所代表的音高，只不过要高出四个八度。 ⁽⁷⁾ 把1′47″加上它的一半，即54″—，得到的和2′41″—将代表d音；这就是木星的近日运动，只不过要高出一个八度，因为它的数值2′45″与此相当接近。如果把1′47″加上它的三分之二，即1′11″＋，那么得到的和将是2′58″＋。而金星的远日运动是2′58″—，因此它代表e音，不过要高出五个八度；水星的近日运动3′0″超过它不多，不过高出了七个八度。最后，把1′47″的2倍，即3′34″分成九份，把其中的一份24″从中减去，得到的差3′10″＋代表f音， ⁽⁸⁾ 而火星的远日运动3′17″与此接近，只不过高出了三个八度；不过实际数值要略大于正确的值，而接近于升f。 ⁽⁹⁾ 因为如果从3′34″中减去它的十六分之一13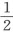 ″，那么剩下的3′20 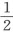″与3′17″相当接近。的确，正如我们在音乐中屡见不鲜的，f音经常用升f音来代替。

因此，大音阶（cantus duri）中的所有音（除了A音，它在第三卷的第二章中也没有被和谐分割表示）都被行星的所有极运动表示出来了，除了金星和地球的近日运动以及接近升c音的水星的远日运动2′34″。因为从d音2′41″中减去它的十六分之一10″＋，得到的差就是升c音2′30″。于是就像你在表中所看到的那样，只有金星和地球的远日运动不在这个音阶之内。

另一方面，如果把土星的远日运动2′15″作为这个音阶的开始，即代表G音，那么A音是2′32″—，它非常接近于水星的远日运动；根据八度的等价性，b音2′42″非常接近于木星的近日运动；C音是3′0″，非常接近于水星和金星的近日运动；d音是3′23″—，火星的远日运动3′17″并不比它低很多，所以这个数值少于它的音的量大约与前一次同一个值多于它的音的量相同。降e音3′36″大约是地球的远日运动；e音是3′50″，而地球的近日运动是3′49″；木星的远日运动则又一次占据了g音。这样，正如你在图中所见，除f音以外，小音阶的一个八度之内的所有音符都被行星的大多数远日运动和近日运动，特别是被以前漏掉的那些运动表示出来了。

前一次升f音表示出来了，A音却漏掉了；现在A音被表示出来了，升f音却被漏掉了，因为第二章中的和谐分割也漏掉了f音。

因此，一个具有所有音高的八度系统或音阶（在音乐中，自然歌曲 ⁽¹⁰⁾ 就是这样转调的）就在天上通过两种方式表示出来了，就好像歌曲的两种类型一样。唯一的区别是：在我们的和谐分割中，实际上两种方式都是从同一个端点G音开始的；但是对于行星的运动，以前的b音现在在小调中变成了G音。

天体运动的情况如下：

和谐分割的情况如下：

正如音乐中的比例是2160∶1800或6∶5，对应着天空系统的比例是1728∶1440，它也是6∶5；其他情况也是这样： ⁽¹¹⁾

2160∶1800∶1620∶1440∶1350∶1080 　　　

对应着　1728∶1440∶1296∶1152∶1080∶864

你现在将不会再怀疑，音乐系统或音阶中的声音或音级的极为漂亮的秩序已经被人建立起来了，因为你看到，他们这里所做的一切事情只不过是在模仿我们的造物主，就好像是表演了一场排列天体运动等级的特殊的戏剧。

实际上，这里还有另一种方法可以使我们理解天上的两种音阶，其中系统还是同一个，但却包含了两种调音（tensio），一种是根据金星的远日运动来调音的，另一种是根据金星的近日运动来调音的。因为这颗行星运动变化的量是最小的，它可以被包含在最小的协和音程第西斯之内。事实上，前面的远日调音已经给土星、地球、金星和（近似的）木星的远日运动定出了G音、e音和b音，给火星、（近似的）土星以及水星的近日运动定出了c音、e音和b音。 ⁽¹²⁾ 而另一方面，近日调音除了给木星、金星和（近似的）土星的近日运动，以及在某种程度上给地球，还有毫无疑问的水星的近日运动定出了音高，而且还给火星、水星和（近似的）木星的远日运动也定出了音高。让我们现在假定，不是金星的远日运动，而是其近日运动3′3″代表e音。根据本卷第四章的结尾，水星的近日运动3′0″在两个八度以上与此非常接近。如果从3′3″中减去这个近日运动的十分之一，即18″，那么余下的2′45″就是木星的近日运动，代表d音；如果加上它的十五分之一，即12″，得到的和为3′15″，大约为火星的近日运动，代表f音。对于b音，土星的近日运动和木星的远日运动大约代表同样的音高。如果把它的八分之一或23″乘以5，那么得到的1′55″就是地球的近日运动。 ⁽¹³⁾ 尽管在同一音阶里，这个音与前面所说的并不符合，因为它没有给出低于e音的5∶8这个音程或高于G音的24∶25这个音程。但是，如果现在金星的近日运动以及水星的远日运动 ⁽¹⁴⁾ 代表降e音而不是e音，那么地球的近日运动将代表G音，水星的远日运动就和谐了，因为如果把3′33的三分之一，即1′1″，乘以5，得到5′5″，它的一半2′32″＋大约就是水星的远日运动，它在这次特殊的排列中将定出c音。于是，所有这些运动彼此之间都位于同一调音系统内了。但是金星的近日运动 ⁽¹⁵⁾ 与前面三种（或五种）同处于一种调式的运动 ⁽¹⁶⁾ 对音阶的划分和它的远日运动即大调式（denere duro）不同；而且，金星的近日运动与后面的两种运动 ⁽¹⁷⁾ 划分同一音阶的方式也不同，即不是分成不同的谐和音程，而只是分成一种不同次序的谐和音程，即属于小调（generic mollis）的次序。

但是本章已经足以说清楚情况是怎么回事了，至于这些事物为什么分别是这种样子，以及为什么不仅有和谐，而且还有很小的不和谐，我们将在第九章用最为清晰的论证加以说明。

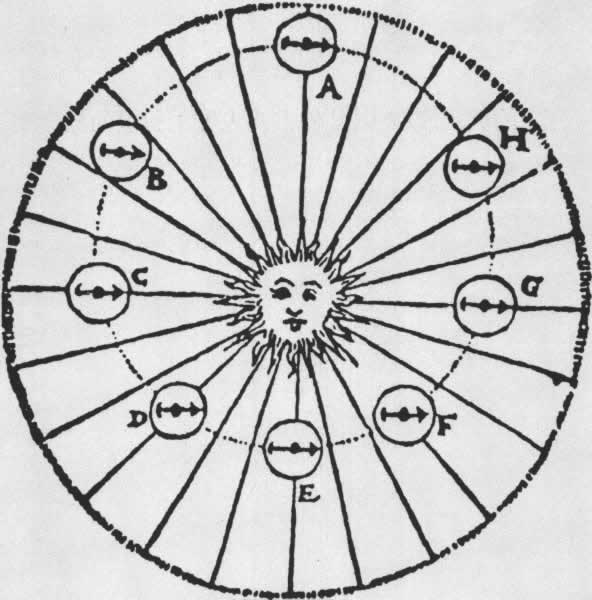
开普勒关于太阳如何影响一颗行星的解释

因为他发现行星是在以太阳为中心的椭圆轨道上运动。因此他不得不给出一个力来改变行星到太阳的距离。从磁的概念出发，他猜想太阳对行星轨道一部分进行吸引（A、B、C、D、E），而对其他的部分则进行排斥（E、F、G、H、A）。图中箭头表示磁力作用的方向。

————————————————————

(1) 参见前面对“距离与和谐比例的比较”的注释。——原注

(2) 此表如下：

——原注

(3) 运动之比之所以与弦长成反比，是因为较快的运动对应着较高的音调，于是也就对应着较短的弦。——中译者

(4) 减号表示实际数值达不到这个数。——中译者

(5) 加号表示实际数值超过了这个数。——中译者

(6) 加上四分之一等价于加上大三度4∶5的比例，所以如果较低的音取作G，那么较高的音将是h。土星的近日运动和木星的远日运动代表着一个比h音高134∶135的比例，它小于一个音差。——中译者

(7) 加上三分之一等价于加上四度3∶4的比例，由于较低的音取作G，所以较高的音就是c。——中译者

(8) f音比e音高出了半音，而e音与G音之间又相差大六度。于是，从G到f的音程就由3∶5和15∶16的乘积即9∶16表示。通过减法运算，开普勒得到了3′34″的8/9倍，这个值等于1′47″的16/9倍。因此，1′47″与3′10″的比例是9∶16。所以如果较慢的运动对应着G音，那么较快的运动就对应着f音。——中译者

(9) 火星的远日运动代表着一个高于f音约3个音差的音，而仅小于升f一个音差。——中译者

(10) 自然歌曲：无临时记号的基本的大调系统或小调系统的音乐。

——Elliott Carter，Jr．

(11) 这个关系对于这里没有列出的两种情况也是成立的，即2160∶1920＝1728∶1536和2160∶1215＝1728∶972。——中译者

(12) 对应关系如下：

——中译者

(13) 根据这里的计算，地球的远日运动代表一个比e音低小六度或比G音高一个第西斯的音。因为这些音程的和是G音和e音之间的大六度。但正如开普勒接着指出的，这样一个音并不属于他在前面所说的音阶。——中译者

(14) 开普勒本想说的是水星的近日运动。——中译者

(15) 这里应该是远日运动。——中译者

(16) 这里的三种（或五种）运动指的是土星的近日运动和远日运动、地球和木星的远日运动以及火星的近日运动，它们分别代表着G音、b音和c音。由于金星的远日运动对应着e音，它与G音之间构成一个大六度，所以所有的音都属于大音阶。——中译者

(17) 这里指的是地球的近日运动和水星的远日运动，分别对应着G音和c音。由于水星的近日运动对应着降e音，它与G音之间构成一个小六度，所以这种划分的所有音符都属于小音阶。——中译者