- 第3章 立体及超立体问题的作图
- 能用于所有问题的作图的曲线
- 求多比例中项的例证
- 方程的性质
- 方程能有几个根
- 何为假根
- 已知一个根时,如何将方程的次数降低
- 如何确定任一给定量是否是根
- 一个方程有多少真根
- 如何将假根变为真根,以及将真根变为假根
- 如何将方程的根变大或缩小
- 我们可通过增大真根来缩小假根;或者相反
- 如何消去方程中的第二项
- 如何使假根变为真根而不让真根变为假根
- 如何补足方程中的缺项
- 如何乘或除一个方程的根
- 如何消除方程中的分数
- 如何使方程任一项中的已知量等于任意给定的量
- 真根和假根都可能是实的或虚的
- 平面问题的三次方程的简约
- 用含有根的二项式除方程的方法
- 方程为三次的立体问题
- 平面问题的四次方程的简约,立体问题
- 利用简约手段的例证
- 简约四次以上方程的一般法则
- 所有简约为三或四次方程的立体问题的一般作图法则
- 对比例中项的求法
- 角的三等分
- 所有立体问题可约化为上述两种作图
- 表示三次方程的所有根的方法,此法可推广到所有四次方程的情形
- 为何立体问题的作图非要用圆锥截线,解更复杂的问题需要其他更复杂的曲线
- 需要不高于六次的方程的所有问题之作图的一般法则
第3章 立体及超立体问题的作图
On the Construction of Solid? and Supersolid Problems
我希望后世会给予我仁厚的评判,不单是因为我对许多事情作出的解释,而且也因为我有意省略了的内容——那是留给他人享受发明之愉悦的。
 笛卡儿著作中的插图
笛卡儿著作中的插图
能用于所有问题的作图的曲线
毫无疑问,凡能由一种连续的运动来描绘的曲线都应被接纳进几何,但这并不意味着我们将随机地使用在进行给定问题的作图时首先碰上的曲线。我们总是应该仔细地选择能用来解决问题的最简单的曲线。但应注意,“最简单的曲线”不只是指它最容易描绘,亦非指它能导致所论问题的最容易的论证或作图,而是指它应属于能用来确定所求量的最简单的曲线类之中。
求多比例中项的例证
例如,我相信在求任意数目的比例中项时,没有更容易的方法了,没有哪一种论证会比借助于利用前已解释过的工具XYZ 描绘的曲线所作的论证更清楚的了。所以,若想求YA 和YE 之间的两个比例中项,只需描绘一个圆,YE 为其直径并在D 点穿过曲线AD ;于是,YD 即是所求的一个比例中项。当对YD 使用此工具时,论证立即变得一目了然,因为YA (或YB )比YC 等于YC 比YD ,又等于YD 比YE 。
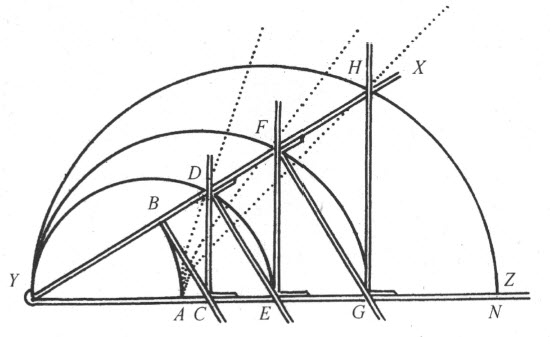
类似地,为求YA 和YG 之间的四个比例中项,或求YA 和YN 之间的六个比例中项,只需画一圆YEG ,它跟AF 的交点确定出直线段YF ,此即四个比例中项之一;或画图YHN ,它跟AH 的交点确定出直线段YH ,即六个比例中项之一;余者类推。
但曲线AD 属于第二类,而我们可以利用圆锥截线求两个比例中项,后者是第一类的曲线。再者,四个或六个比例中项可分别用比AF 和AH 更低类的曲线求得。因此,利用那些曲线可能在几何上是一种错误。另一方面,徒劳地企图用比问题的性质所限定的曲线类更简单的曲线类来解决作图问题,也将是一种大错。
方程的性质
在给出一些法则以避免这两种错误之前,我必须就方程的性质作些一般性的论述。一个方程总由若干项组成,有的为已知,有的为未知,其中的一些合在一起等于其余的;甚至可以让所有的项合在一起等于无;后者常常是进行讨论的最好形式。
方程能有几个根
每一个方程都有跟方程中未知量的次数 (1) 一样多的不同的根(未知量的值)。例如,设x =2,或x -2=0,又设x =3,或x -3=0。把x -2=0和x -3=0这两个方程相乘,我们有x 2 -5x +6=0或x 2 =5x -6。这是个方程,其中x 取值为2,同时,x 还取值为3。若我们接着取x -4=0,并用x 2 -5x +6=0乘之,我们得到另一个方程x 3 -9x 2 +26x -24=0,其中x 是三次的,因此有三个值,即2,3和4。
何为假根
然而,经常会出现一些根是假的、或者说比无更小的情形。于是,如果我们设x 表示量5这个假根,则我们有x +5=0,它用x 3 -9x 2 +26x -24=0乘之后变为x 4 -4x 3 -19x 2 +106x -120=0,这个方程有四个根,即三个真根2,3和4,一个假根5。
已知一个根时,如何将方程的次数降低
显然,由上述讨论可知,具有若干个根的方程的各项之和总能被这样的二项式除尽,它由未知量减去真根之一的值、或加上假根之一的值组成。据此,我们能使方程的次数降低。
如何确定任一给定量是否是根
另一方面,若方程各项的和不能被由未知量加或减某个别的量组成的二项式除尽,则这个“别的量”就不是该方程的根。于是,上述方程x 4 -4x 3 -19x 2 +106x -120=0可被x -2,x -3,x -4和x +5除尽,而不能被x 加或减其他任何一个量所除尽。因此,该方程仅有四个根2,3,4和5。
一个方程有多少真根
我们还能确定任一方程所能有的真根与假根的数目,办法如下:一个方程的真根数目跟它所含符号的变化、即从+到-或从-到+的多寡一致;而其假根的数目,跟连续找到两个+号或两个一号的次数一样。
于是,在最后一个方程中,因+x 4 之后是-4x 3 ,出现了从+到-的一次符号变化,-19x 2 之后是+106x ,+106x 之后是-120,又出现了两次变化,所以我们知道有三个真根;因-4x 3 之后是-19x 2 ,那么有一个假根。
如何将假根变为真根,以及将真根变为假根
我们还很容易将方程变形,使得它的所有假根都变为真根,所有真根都变为假根。办法是改变第二、第四、第六及所有偶数项的符号,保持第一、第三、第五及其他奇数项的符号不变。这样,若代替
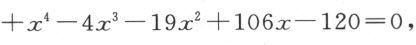
我们写出
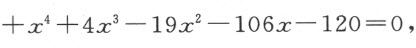
则我们得到的是具有一个真根5和三个假根2,3,4的方程。
如何将方程的根变大或缩小
当一个方程的根未知,而希望每一个根都增加或减去某个已知数时,我们必须把整个方程中的未知量用另一个量代替,它比原未知量大一个或小一个那个已知数。于是,若希望方程

的每个根的值增加3,那么用y 代替x ,并令y 比x 大3,即y -3=x 。此时,对于xz ,我们代之以y -3的平方或y 2 -6y +9;对于x 3 ,代之以它的立方,即y 3 -9y 2 +27y -27;对于x 4 ,代之以四次方,或y 4 -12y 3 +54y 2 -108y +81。在上述方程中代入这些值并进行归并,我们得到
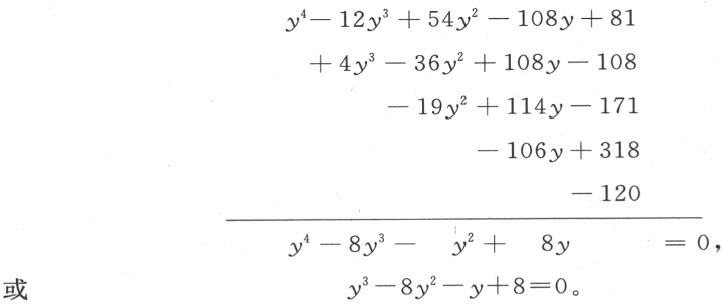
现在,它的真根是8而不是5,因为它已被增加了3。另一方面,若希望同一方程的根都减少3,我们必须令y +3=x ,y 2 +6y +9=x 2 等等,代替x 4 +4x 3 -19x 2 -106x -120=0,我们得到
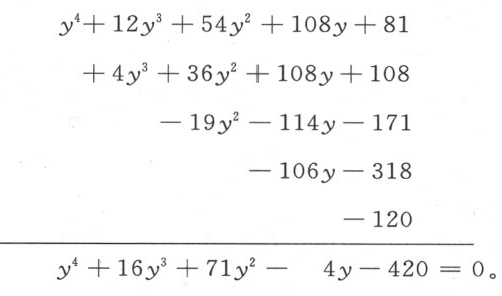
我们可通过增大真根来缩小假根;或者相反
应该注意,一个方程的真根的加大必使假根以同样的量减小;相反,真根的缩小会使假根增大;若以等于真根或假根的量来减小它们,则将使根变成零;以比根大的量来减小它,那么会使真根变假、假根变真。所以,给真根增加3,我们就使每个假根都变小了,原先是4的现只是1,原是3的根变成了零,原是2的现在成了真根,它等于1,因为-2+3=+1。这说明为什么方程y 3 -8y 4 -y +8-0仅有三个根,其中的两个1和8是真根,第三个也是1,但是假根;而另一个方程y 4 -16y 3 +71y 2 -4y -420=0仅有一个真根2(因为+5-3=+2),以及三个假根5,6和7。
如何消去方程中的第二项
于是,这种变换一个方程的根而无须先确定它们的值的方法,产生两个将被证明是有用的结论:第一,我们总能消去第二项。若方程第一和第二项的符号相反,只要使它的真根缩小一个量,该量由第二项中的已知量除以第一项的次数而得;或者,若它们具有相同的符号,可通过使它的根增加同样的量而达到目的。于是,为了消去方程y 4 +16y 3 +71y 2 -4y -420=0中的第二项,我用16除以4(即y 4 中y 的次数),商为4。我令z -4=y ,那么
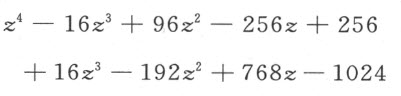
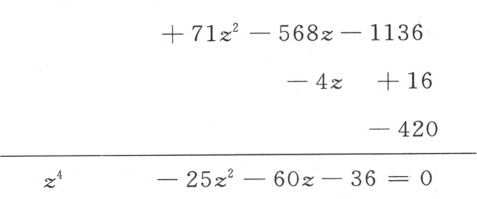
方程的真根原为2而现在是6,因为它已增加了4;而假根5,6,7成了1,2和3,因为每个根减小了4。类似地,我们可消去x 4 -2ax 3 +(2a 2 -c 2 )x 2 -2a 3 x +a 4 =0的第二项;因2a 除以4得 ,我们必须令
,我们必须令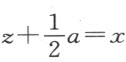 ,那么
,那么
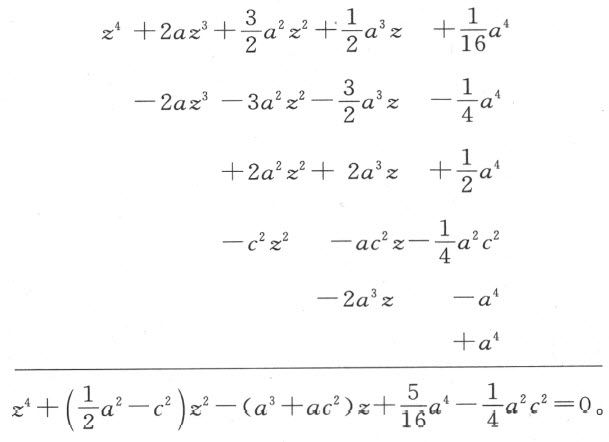
若能求出z 的值,则加上了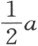 就得到x 的值。
就得到x 的值。
如何使假根变为真根而不让真根变为假根
第二,通过使每个根都增加一个比任何假根都大的量,我们可使所有的根都成为真根。实现这一点后就不会连续出现+或-的项了;进而,第三项中的已知量将大于第二项中已知量的一半的平方。这一点即使在假根是未知时也能办到,因为总能知道它们的近似值,从而可以让根增加一个量,该量应大到我们所需要的程度,更大些也无妨。于是,若给定
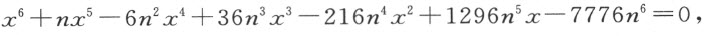
令y -6n =x ,我们便有
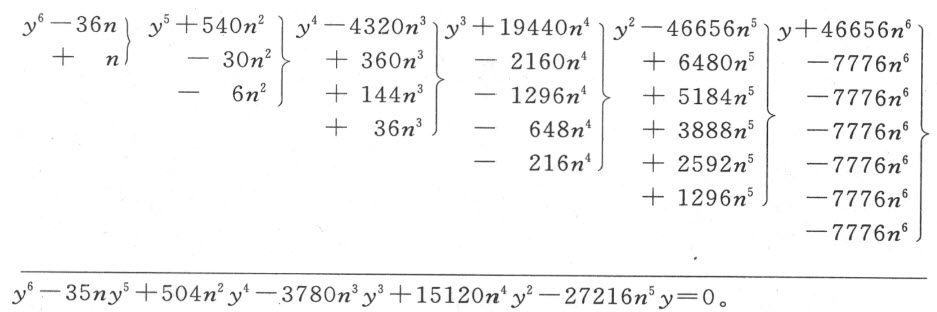
显然,第三项中的已知量504n 2 大于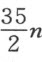 的平方,亦即大于第二项中已知量一半的平方;并且不会出现这种情形,为了假根变真根所需要增加的量,从它跟给定量的比的角度看,会超出上述情形所增加的量。
的平方,亦即大于第二项中已知量一半的平方;并且不会出现这种情形,为了假根变真根所需要增加的量,从它跟给定量的比的角度看,会超出上述情形所增加的量。
如何补足方程中的缺项
若我们不需要像上述情形那样让最后一项为零,为此目的就必须使根再增大一些。同样,若想提高一个方程的次数,又要让它的所有的项都出现,比如我们想要替代x 5 -b =0而得到一个没有一项为零的六次方程;那么,首先将x 5 -b =0写成x 6 -bx =0,并令y -a =x ,我们即可得到

显然,无论量a 多么小,这个方程的每一项都必定存在。
如何乘或除一个方程的根
我们也可以实现以一个给定的量来乘或除某个方程的所有的根,而不必事先确定出它们的值。为此,假设未知量用一个给定的数乘或除之后等于第二个未知量。然后,用这个给定的量乘或除第二项中的已知量,用这个给定量的平方乘或除第三项中的已知量,用它的立方乘或除第四项中的已知量,…,一直做到最后一项。
如何消除方程中的分数
这种手段对于把方程中的分数项改变成整数是有用的,对各个项的有理化也常常有用。于是,若给定 ,设存在符合要求的另一方程,其中所有的项皆以有理数表示。令
,设存在符合要求的另一方程,其中所有的项皆以有理数表示。令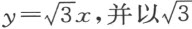 乘第二项,以3乘第三项,以
乘第二项,以3乘第三项,以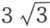 乘最后一项,所得方程为
乘最后一项,所得方程为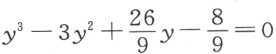 。接着,我们要求用已知量全以整数表示的另一方程来替代它。令z =3y ,以3乘3,9乘
。接着,我们要求用已知量全以整数表示的另一方程来替代它。令z =3y ,以3乘3,9乘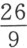 ,27乘
,27乘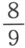 ,我们得到
,我们得到
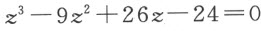
此方程的根是2,3和4;因此前一方程的根为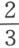 ,1和
,1和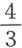 ,而第一个方程的根为
,而第一个方程的根为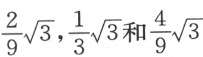 。
。
如何使方程任一项中的已知量等于任意给定的量
这种方法还能用于使任一项中的已知量等于某个给定的量。若给定方程

要求写出一个方程,使第三项的系数(即b 2 )由3a 2 来替代。令
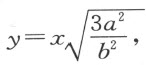
我们得到

真根和假根都可能是实的或虚的
无论是真根还是假根,它们并不总是实的;有时它们是虚的;于是,我们总可以想象,每一个方程都具有我已指出过的那样多的根,但并不总是存在确定的量跟所想象得到的每个根相对应。我们可以想象方程x 3 -6x 2 +13x -10=0有三个根,可是仅有一个实根2;对其余两个根,尽管我们可以按刚刚建立的法则使其增大、缩小或者倍增,但它们始终是虚的。
平面问题的三次方程的简约
当某个问题的作图蕴含了对一个方程的求解,该方程中未知量达到三次,则我们必须采取如下步骤:
首先,若该方程含有一些分数系数,则用上面解释过的方法将其变为整数;若它含有不尽方根,那么只要可能就将其变为有理数,或用乘法、或用其他容易找到的若干方法中的一种皆可。第二,依次检查最后一项的所有因子,以确定方程的左端部分,是否能被由未知量加或减这些因子中某个所构成的二项式除尽。若是,则该问题是平面问题,即它可用直尺和圆规完成作图;因为任一个二项式中的已知量都是所求的根,或者说,当方程的左端能被此二项式除尽,其商就是二次的了,从这个商出发,如在第1章中解释过的那样,即可求出根。
例如,给定y 6 -8y 4 -124y 2 -64=0。最后一项64可被1,2,4,8,16,32和64除尽;因此,我们必须弄清楚方程的左端是否能被y 2 -1,y 2 +1,y 2 -2,y 2 +2,y 2 -4等二项式除尽。由下式知方程可被y 2 -16除尽:
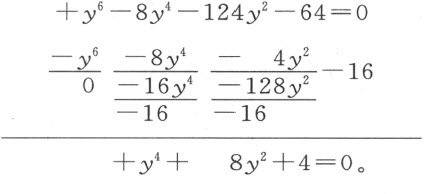
用含有根的二项式除方程的方法
从最后一项开始,我以-16除-64,得+4;把它写成商;以+y 2 乘+4,得+4y 2 ,并记成被除数(但必须永远采用由这种乘法所得符号之相反的符号)。将-124y 2 和-4y 2 相加,我得到-128y 2 。用-16来除它,我得到商+8y 2 ;再用y 2 来乘,我应得出-8y 4 ,将其加到相应的项-8y 4 上之后作为被除数,即-16y 4 ,它被-16除后的商为+y 4 ;再将-y 6 加到+y 6 上得到零,这表明这一除法除尽了。
然而,若有余数存在,或者说如果改变后的项不能正好被16除尽,那么很清楚,该二项式并不是一个因子。

其最后一项可被a ,a 2 ,a 2 +c 2 和a 3 +ac 2 等除尽,但仅需考虑其中的两个,即a 2 和a 2 +c 2 。其余的将导致比倒数第二项中已知量的次数更高或更低的商,使除法不可能进行。注意,此处我将把y 6 考虑成是三次的,因为不存在的y 5 ,y 3 或y 这样的项。试一下二项式
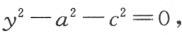
我们发现除法可按下式进行:
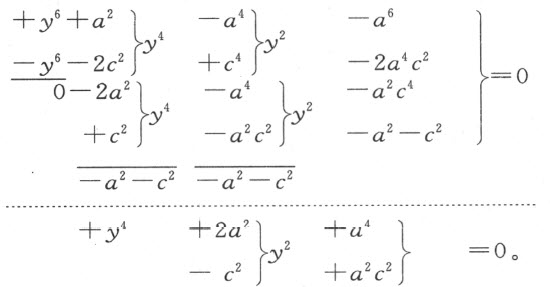
这说明,a 2 +c 2 是所求的根,这是容易用乘法加以验证的。
方程为三次的立体问题
当所讨论的方程找不到二项式因子时,依赖这一方程的原问题肯定是立体的。此时,再试图仅以圆和直线去实现问题的作图就是大错了,正如利用圆锥截线去完成仅需圆的作图问题一样;因为任何无知都可称为错误。
平面问题的四次方程的简约,立体问题
若给定一个方程,其中未知量是四次的,在除去了不尽方根和分数后,查看一下是否存在以表达式最后一项的因子为其一项的二项式,它能除尽左边的部分。如果能找到这种二项式,那么该二项式中的已知量即是所求的根,或者说,作除法之后所得的方程仅是三次的了;当然我们必须用上述同样的方法来处理。如果找不到这样的二项式,我们必须将根增大或缩小,以便消去第二项,其方法已在前面作过解释;然后,按下述方法将其化为另一个三次方程;替代

我们得到

对于双符号,若第一式中出现+p ,第二式中就取+2p ;若第一式中出现-p ,则第二式中应写-2p ;相反地,若第一式中为+r ,第二式中取-4r ,若为-r ,则取+4r 。但无论第一式中所含为+q 或-q ,在第二式中我们总是写-q 2 和+p 3 ,倘若x 4 和y 6 都取+号的话;否则我们写+q 2 和-p 2 。例如,给定
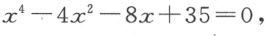
以下式替代它:
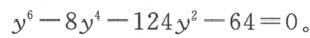
因为,当p =-4时,我们用-8y 4 替代2py 4 ;当r =35时,我们用(16-140)y 2 或-124y 2 替代(p 2 -4r )y 2 ;当q =8时,我们用-64替代-q 2 。类似地,替代
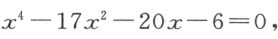
我们必须写下
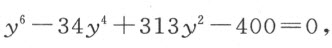
因为34是17的两倍,313是17的平方加6的四倍,400是20的平方。
使用同样的办法,替代

我们必须写出
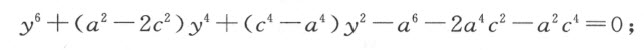
因为
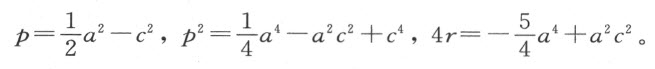
最后,

当方程已被约化为三次时,y 2 的值可以用已解释过的方法求得。若做不到这一点,我们便无需继续做下去,因为问题必然是立体的。若能求出y 2 的值,我们可以利用它把前面的方程分成另外两个方程,其中每个都是二次的,它们的根与原方程的根相同。替代+x 4 ±px 2 ±qx ±r =0,我们可写出两个方程:

对于双符号,当p 取加号时,在每个新方程中就取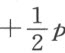 ;当p 取减号时,就取
;当p 取减号时,就取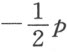 。若q 取加号,则当我们取-yx 时,相应地取
。若q 取加号,则当我们取-yx 时,相应地取 ,当取+yx 时,则用
,当取+yx 时,则用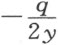 ;若q 取负号,情况正好相反。所以,我们容易确定所论方程的所有的根。接着,我们只要使用圆和直线即可完成与方程的解相关的问题的作图。例如,以y 6 -34y 4 +313y 2 -400=0替代x 4 -17x 2 -20x -6=0,我们可求出y 2 =16;于是替代+x 4 -17x 2 -20x -6=0的两个方程为+x 2 -4x -3=0和+x 2 +4x +2=0。因为y =4,
;若q 取负号,情况正好相反。所以,我们容易确定所论方程的所有的根。接着,我们只要使用圆和直线即可完成与方程的解相关的问题的作图。例如,以y 6 -34y 4 +313y 2 -400=0替代x 4 -17x 2 -20x -6=0,我们可求出y 2 =16;于是替代+x 4 -17x 2 -20x -6=0的两个方程为+x 2 -4x -3=0和+x 2 +4x +2=0。因为y =4,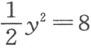 ,p =17,q =20,故有
,p =17,q =20,故有
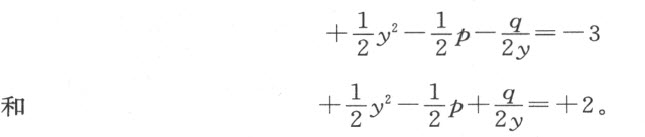
我们求出这两个方程的根,也就得到了含x 4 的那个方程的根,它们一个是真根 ,三个是假根
,三个是假根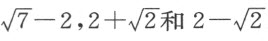 。当给定x 4 -4x 2 -8x +35=0,我们得到y 6 -8y 4 -124y 2 -64=0;因后一方程的根是16,我们必定可写出x 2 -4x +5=0和x 2 +4x +7=0。
。当给定x 4 -4x 2 -8x +35=0,我们得到y 6 -8y 4 -124y 2 -64=0;因后一方程的根是16,我们必定可写出x 2 -4x +5=0和x 2 +4x +7=0。
因为对于这一情形,
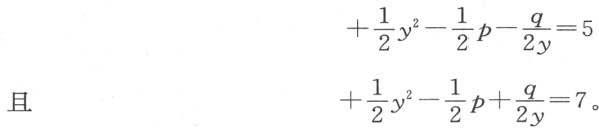
这两个方程即无真根亦无假根,由此可知,原方程的四个根都是虚的;跟方程的解相关的问题是平面问题,但其作图却是不可能的,因为那些给定的量不能协调一致。
类似地,对已给的
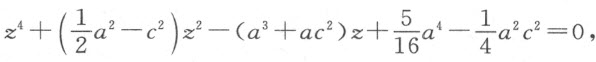
因我们得出了y 2 =a 2 +c 2 ,所以必定可写出
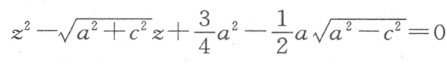
和

由于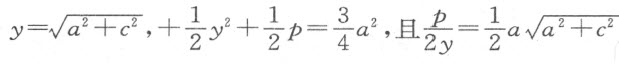 ,故我们有
,故我们有
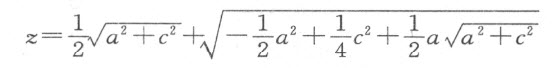
或

利用简约手段的例证
为了强调这条法则的价值,我将用它来解决一个问题。给定正方形AD 和直线段BN ,要求延长AC 边至E ,使得在EB 上以E 为始点标出的EF 等于NB 。
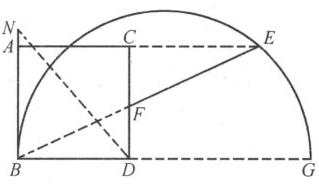
帕普斯指出,若BD 延长至G ,使得DG =DN ,并以BG 为直径在其上作一圆,则直线AC (延长后)与此圆的圆周的交点即为所求的点。
不熟悉此种作图的人可能不会发现它。如果他们运用此处提议的方法,他们绝不会想到取DG 为未知量,而会去取CF 或FD ,因为后两者中的任何一个都能更加容易地导出方程。他们会得到一个方程,但不借助于我刚刚解释过的法则,解起来不容易。
比如,令a 表示BD 或CD ,c 表示EF ,x 表示DF ,我们有CF =a -x ;又因CF 比FE 等于FD 比BF ,我们可写做
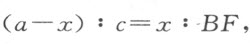
因此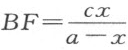 。在直角三角形BDF 中,其边为x 和a ,它们的平方和x 2 +a 2 等于斜边的平方,即
。在直角三角形BDF 中,其边为x 和a ,它们的平方和x 2 +a 2 等于斜边的平方,即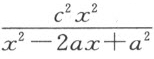 。两者同用x 2 -2ax +a 2 乘,我们得到方程
。两者同用x 2 -2ax +a 2 乘,我们得到方程

根据前述法则,我们便可知道其根,即直线段DF 的长度为
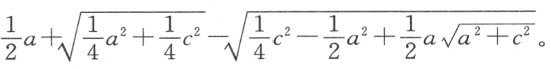
另一方面,若我们将BF 、CE 或BE 作为未知量,我们也会得到一个四次方程,但解起来比较容易,得到它也相当简单。
若利用DG ,则得出方程将相当困难,但解方程十分简单。我讲这些只是为了提醒你,当所提出的问题不是立体问题时,若用某种方法导出了非常复杂的方程,那么一般而论,必定存在其他的方法能找到更简单的方程。
我可以再讲几种不同的、用于解三次或四次方程的法则,不过它们也许是多余的,因为任何一个平面问题的作图都可用已给出的法则解决。
简约四次以上方程的一般法则
我倒想说说有关五次、六次或更高次的方程的法则,不过我喜欢把它们归总在一起考虑,并叙述下面这个一般法则:
首先,尽力把给定方程变成另一种形式,它的次数与原方程相同,但可由两个次数较低的方程相乘而得。假如为此所做的一切努力都不成功,那么可以肯定所给方程不能约化为更简单的方程;所以,若它是三或四次的,则依赖于该方程的问题就是立体问题;若它是五次或六次的,则问题的复杂性又增高一级,依此类推。我略去了大部分论述的论证,因为对于我来说太简单;如果你能不怕麻烦地对它们系统地进行检验,那么论证本身就会显现在你面前,就学习而论,这比起只是阅读更有价值。
所有简约为三或四次方程的立体问题的一般作图法则
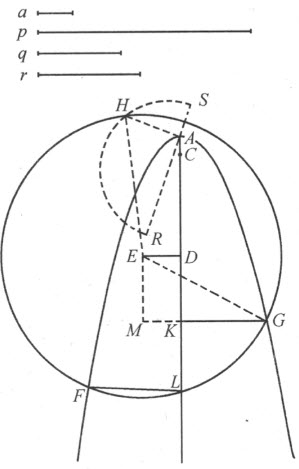
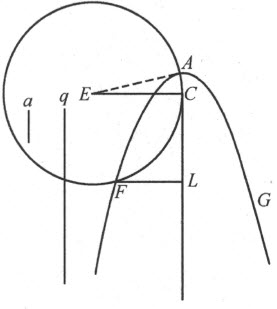
当确知所提出的是立体问题,那么无论问题所依赖的方程是四次的或仅是三次的,其根总可以依靠三种圆锥截线中的某一种求得,甚或靠它们中某一种的某个部分(无论多么小的一段)加上圆和直线求出。我将满足于在此给出靠抛物线就能将根全部求出的一般法则,因为从某种角度看,它是那些曲线中最简单的。
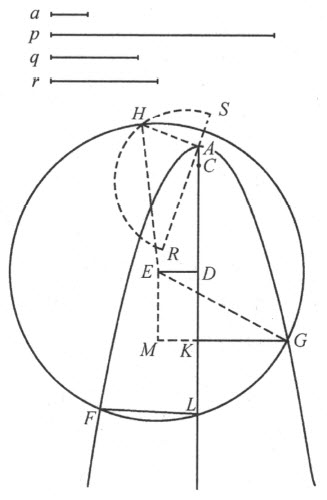
首先,当方程中的第二项不是零时,就将它消去。于是,若给定的方程是三次的,它可化为z 3 =±apz ±a 2 q 这种形式;若它是四次的,则可化为z 4 =±apz 2 ±a 2 qz ±a 3 r 。当选定a 作为单位,前者可写成z 3 =±pz ±q ,后者变为z 4 =±p z 2 ±qz ±r 。设抛物线FAG 已描绘好;并设ACDKL 为其轴,a 或1为其正焦弦,它等于2AC (C 在抛物线内),A 为其顶点。截取CD =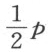 ,使得当方程含有+p 时,点D 和点A 落在C 的同一侧,而当方程含有-p 时,它们落在C 的两侧。然后,在点D (或当p =0时,在点C )处画DE 垂直于CD ,使得DE 等于
,使得当方程含有+p 时,点D 和点A 落在C 的同一侧,而当方程含有-p 时,它们落在C 的两侧。然后,在点D (或当p =0时,在点C )处画DE 垂直于CD ,使得DE 等于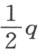 ;当给定方程是三次(即r 为零)时,以E 为心、AE 为半径作圆FG 。
;当给定方程是三次(即r 为零)时,以E 为心、AE 为半径作圆FG 。
 | 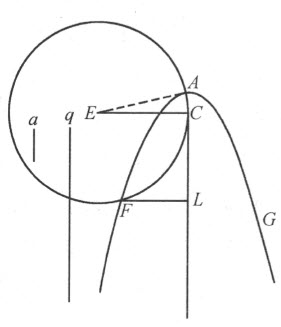 |
若方程含有+r ,那么,在延长了的AE 的一侧截取AR 等于r ,在另一侧截取AS 等于抛物线的正焦弦,即等于1;然后,以RS 为直径在其上作圆。于是,若画AH 垂直于AE ,它将与圆RHS 在点H 相交,另一圆FHG 必经过此点。
若方程含有-r ,以AE 为直径在其上作圆,在圆内嵌入一条等于AH 的线段AI ;那么,第一个圆必定经过点I 。
现在,圆FG 可能在1个,2个,3个或4个点处与抛物线相交或切触;如果从这些点向轴上引垂线,它们就代表了方程所有的根,或是真根、或是假根。若量q 为正,真根将是诸如跟圆心E 同在抛物线一侧的垂线FL ;而其余如GK 这样的将是假根。另一方面,若q 是负的,真根将是在另一侧的垂线,假根或者说负根 (2) 将跟圆心E 在同一侧面。若圆跟抛物线既不相交也不相切,这表明方程既无真根、亦无假根,此时所有的根都是虚的。
这条法则显然正是我们所能期待的、既具一般性又是很完全的法则,要论证它也十分容易。若以z 代表如上作出的直线段GK ,那么AK 为z 2 ,因为据抛物线的性质可知,GK 是AK 跟正焦弦(它等于1)之间的比例中项。所以,当从AK 中减去AC 或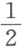 及CD 或
及CD 或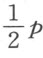 之后,所余的正是DK 或EM ,它等于
之后,所余的正是DK 或EM ,它等于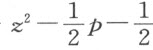 ,其平方为
,其平方为
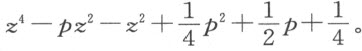
又因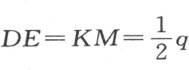 ,整条直线段
,整条直线段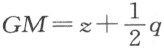 ,GM 的平方等于
,GM 的平方等于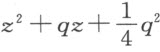 。将上述两个平方相加,我们得
。将上述两个平方相加,我们得 。此即GE 的平方,因GE 是直角三角形EMG 的斜边。
。此即GE 的平方,因GE 是直角三角形EMG 的斜边。
但GE 又是圆FG 的半径,因此可用另一种方式表示。因 ,ADE 是直角,我们可得
,ADE 是直角,我们可得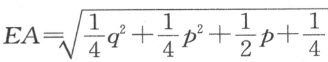 。
。
于是,由HA 是AS (或1)跟AR (或r )之间的比例中项,可得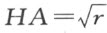 ;又因EAH 是直角,HE 或EG 的平方为
;又因EAH 是直角,HE 或EG 的平方为
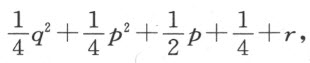
我们从这个表达式和已得到的那个式子可导出一个方程。该方程形如z 4 =pz 2 -qz +r ,从而证明了直线段GK 、或者说z 是这个方程的根。当你对所有其他的情形应用这种方法时,只需将符号作适当的变化,你会确信它的用途,因此,我无需再就这种方法多费笔墨。
对比例中项的求法
现在让我们利用此法求直线段a 和q 之间的两个比例中项。显然,若我们用z 表示两比例中项中的一个,则有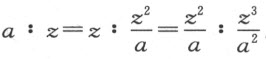 。我们由此得到q 和
。我们由此得到q 和 之间关系的方程,即z 3 =a 2 q 。
之间关系的方程,即z 3 =a 2 q 。
以AC 方向为轴描绘一条抛物线FAG ,AC 等于 ,即等于正焦弦的一半。然后,作CE 等于
,即等于正焦弦的一半。然后,作CE 等于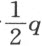 ,它在点C 与AC 垂直;并描绘以E 为心、通过A 的圆AF 。于是,FL 和LA 为所求的比例中项。
,它在点C 与AC 垂直;并描绘以E 为心、通过A 的圆AF 。于是,FL 和LA 为所求的比例中项。
角的三等分
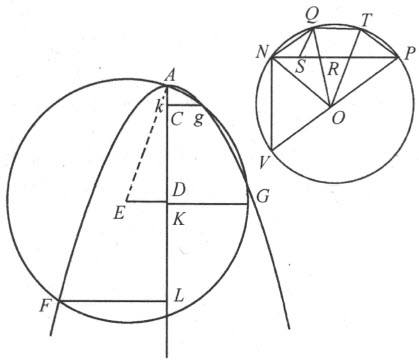
再举一例,设要求将角NOP ,或更贴切地说将圆弧NQTR 分成三等分。令NO =1为该圆的半径,NP =q 为给定弧所对的弦,NQ =z 为该弧的三分之一所对的弦,于是,方程应为z 3 =3z -q 。因为,联结NQ 、OQ 和OT ,并引QS 平行于TO ,显然可知NO 比NQ 等于NQ 比QR ,且等于QR 比RS 。又因NO =1,NQ =z ,故QR =z 2 ,RS =z 3 ;由于NP (或q )跟NQ (或z )的三倍相比只差RS (或z 3 ),我们立即得到q =3z -z 3 ,或z 3 =3z -q 。
描绘一条抛物线FAG ,使得正焦弦的二分之一CA 等于 ,垂线
,垂线 ;然后,以E 为心作过A 的圆FA gG 。该圆与抛物线除顶点A 外还交于三点F 、g和G 。这说明已得的方程有三个根,即两个真根GK 和gk ,一个假根FL 。两个根中的较小者gk 应取作所求直线段NQ 的长,因另一个根GK 等于NV ,而NV 弦所对的弧为VNP 弧的三分之一,弧VNP 跟弧NQP 合在一起组成一个圆;假根FL 等于QN 和NV 的和,这是容易证明的。
;然后,以E 为心作过A 的圆FA gG 。该圆与抛物线除顶点A 外还交于三点F 、g和G 。这说明已得的方程有三个根,即两个真根GK 和gk ,一个假根FL 。两个根中的较小者gk 应取作所求直线段NQ 的长,因另一个根GK 等于NV ,而NV 弦所对的弧为VNP 弧的三分之一,弧VNP 跟弧NQP 合在一起组成一个圆;假根FL 等于QN 和NV 的和,这是容易证明的。
所有立体问题可约化为上述两种作图
我不需要再举另外的例子,因为除了求两个比例中项和三等分一个角之外,所有立体问题的作图都不必用到这条法则。你只要注意以下几点,上述结论便一目了然:这些问题中之最困难者都可由三次或四次方程表示;所有四次方程又都能利用别的不超过三次的方程约简为二次方程;最后,那些三次方程中的第二项都可消去;故每一个方程可化为如下形式中的一种:
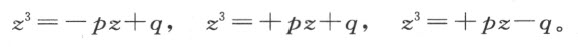
若我们得到的是z 3 =-pz +q ,根据被卡当(Cardan)归在西皮奥·费雷乌斯(S cipio Ferreus)名下的一条法则,我们可求出其根为
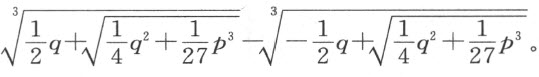
类似地,当我们得到z 3 =+pz +q ,其中最后一项的一半的平方大于倒数第二项中已知量的三分之一的立方,我们根据相当的法则求出的根为
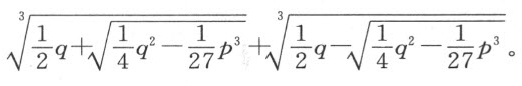
很清楚,所有能约简成这两种形式的方程中任一种的问题,除了对某些已知量开立方根之外,无需利用圆锥截线就能完成其作图,而开立方根等价于求该量跟单位之间的两个比例中项。若我们得到z 3 =+pz +q ,其中最后一项之半的平方不大于倒数第二项中已知量的三分之一的立方,则以等于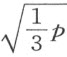 的NO 为半径作圆NQPV ,NO 即单位跟已知量p 的三分之一两者间的比例中项。然后,取
的NO 为半径作圆NQPV ,NO 即单位跟已知量p 的三分之一两者间的比例中项。然后,取 ,即让NP 与另一已知量q 的比等于1与
,即让NP 与另一已知量q 的比等于1与 的比,并使NP 内接于圆。将两段弧NQP 和NVP 各自分成三个相等的部分,所求的根即为NQ 与NV 之和,其中NQ 是第一段弧的三分之一所对的弦,NV 是第二段弧的三分之一所对的弦。
的比,并使NP 内接于圆。将两段弧NQP 和NVP 各自分成三个相等的部分,所求的根即为NQ 与NV 之和,其中NQ 是第一段弧的三分之一所对的弦,NV 是第二段弧的三分之一所对的弦。
最后,假设我们得到的是z 3 =pz -q 。作圆NQPV ,其半径NO 等于 ,令NP (它等于
,令NP (它等于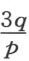 )内接于此圆;那么,弧NQP 的三分之一所对的弦NQ 将是第一个所求的根,而另一段弧的三分之一所对的弦NV 是第二个所求的根。我们必须考虑一种例外情形,即最后一项之半的平方大于倒数第二项中已知量的三分之一的立方;此时,直线段NP 无法嵌在圆内,因为它比直径还长。在这种情形,原是真根的那两个根成了虚根,而唯一的实根是先前的那个假根,据卡当的法则,它应为
)内接于此圆;那么,弧NQP 的三分之一所对的弦NQ 将是第一个所求的根,而另一段弧的三分之一所对的弦NV 是第二个所求的根。我们必须考虑一种例外情形,即最后一项之半的平方大于倒数第二项中已知量的三分之一的立方;此时,直线段NP 无法嵌在圆内,因为它比直径还长。在这种情形,原是真根的那两个根成了虚根,而唯一的实根是先前的那个假根,据卡当的法则,它应为
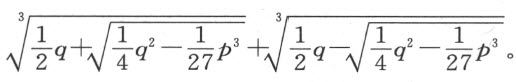
表示三次方程的所有根的方法,此法可推广到所有四次方程的情形
还应该说明,这种依据根与某些立方体(我们仅知道它的体积)的边的关系表示根的方法,绝不比另一种方法更清晰和简单,后者依据的是根与某些弧段(或者说圆上的某些部分)所对弦的关系,此时我们已知的是弧段的三倍长。那些无法用卡当的方法求出的三次方程的根,可用这里指出的方法表示得像任何其他方程的根一样清晰,甚至更加清晰。
例如,可以认为我们知道了方程z 3 =-qz +p 的一个根,因为我们知道它是两条直线段的和,其中之一是一个立方体的边,该立方体的体积为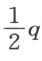 加上面积为
加上面积为 的正方形的边,另一条是另外一个立方体的边,此立方体的体积等于
的正方形的边,另一条是另外一个立方体的边,此立方体的体积等于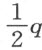 减去面积为
减去面积为 的正方形的边。这就是卡当的方法所提供的有关根的情况。无需怀疑,当方程z 3 =+qz -p 的根的值被看成是嵌在半径为
的正方形的边。这就是卡当的方法所提供的有关根的情况。无需怀疑,当方程z 3 =+qz -p 的根的值被看成是嵌在半径为 的圆上的弦的长度(该弦所对的弧为长度等于
的圆上的弦的长度(该弦所对的弧为长度等于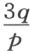 的弦所对的弧的三分之一)时,我们能更清楚地想象它、了解它。
的弦所对的弧的三分之一)时,我们能更清楚地想象它、了解它。
确实,这些术语比其他说法简单得多;当使用特殊符号来表示所论及的弦时,表述就更精炼了,正如使用符号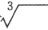 来表示立方体的边一样。
来表示立方体的边一样。
运用跟已解释过的方法类似的方法,我们能够表示任何四次方程的根,我觉得我无须在这方面作进一步的探究;由于其性质所定,我们已不可能用更简单的术语来表示这些根了,也不可能使用更简单同时又更具普遍性的作图法来确定它们。
为何立体问题的作图非要用圆锥截线,解更复杂的问题需要其他更复杂的曲线
我还一直没有说明为什么我敢于宣称什么是可能、什么是不可能的理由。但是,假如记住我所用的方法是把出现在几何学家面前的所有问题,都约化为单一的类型,即化为求方程的根的值的问题,那么,显然可以列出一张包括所有求根方法的一览表,从而很容易证明我们的方法最简单、最具普遍性。特别地,如我已说过的,立体问题非利用比圆更复杂的曲线不能完成其作图。由此事实立即可知,它们都可约化为两种作图,其一即求两条已知直线段之间的两个比例中项,另一种是求出将给定弧分成三个相等部分的两个点。因为圆的弯曲度仅依赖于圆心和圆周上所有点之间的简单关系,所以圆仅能用于确定两端点间的一个点,如像求两条给定直线段之间的一个比例中项或平分一段给定的弧;另一方面,圆锥截线的弯曲度要依赖两种不同的对象,因此可用于确定两个不同的点。
基于类似的理由,复杂程度超过立体问题的任何问题,包括求四个比例中项或是分一个角为五个相等的部分,都不可能利用圆锥截线中的一种完成其作图。
因此我相信,在我给出那种普遍的法则,即如前面已解释过的、利用抛物线和直线的交点所描绘的曲线来解决所给问题的作图之后,我实际上已能解决所有可能解决的问题;我确信,不存在性质更为简单的曲线能服务于这一目标,你也已经看到,在古人给予极大注意的那个问题中,这种曲线紧随在圆锥截线之后。在解决这类问题时顺次提出了所有应被接纳入几何的曲线。
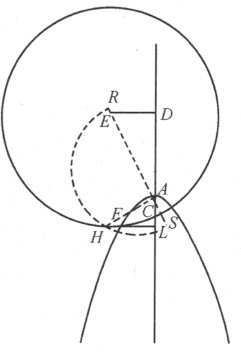
需要不高于六次的方程的所有问题之作图的一般法则
当你为完成这类问题的作图而寻找需要用到的量时,你已经知道该怎样办就必定能写出一个方程,它的次数不会超过5或6。你还知道如何使方程的根增大,从而使它们都成为真根,同时使第三项中的已知量大于第二项中的已知量之半的平方。还有,若方程不超过五次,它总能变为一个六次方程,并使得方程不缺项。
为了依靠上述单一的法则克服所有这些困难,我现在来考虑所有使用过的办法,将方程约化为如下形式:
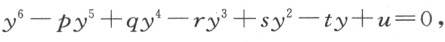
其中q 大于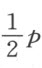 的平方。
的平方。
BK 沿两个方向随意延长,在点B 引AB 垂直于BK 、且等于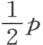 。在分开的平面上描绘抛物线CDF ,其主正焦弦为
。在分开的平面上描绘抛物线CDF ,其主正焦弦为
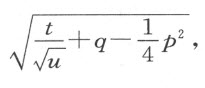
我们用n 代表它。
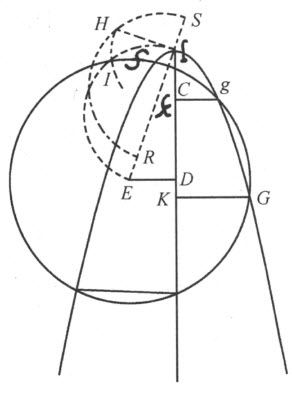
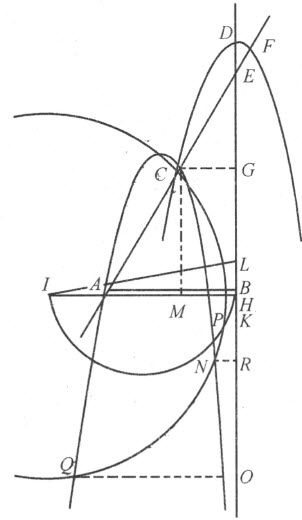
现在,把画有该抛物线的平面放到画有直线AB 和BK 的平面上,让抛物线的轴DE 落在直线BK 上。取点E ,使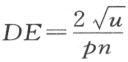 ,并放置一把直尺连接点E 和下层平面上的点A 。持着直尺使它总是连着这两个点,再上下拉动抛物线而令其轴不离开BK 。于是,抛物线与直线的交点C 将描绘出一条曲线ACN ,它可用于所提问题的作图。
,并放置一把直尺连接点E 和下层平面上的点A 。持着直尺使它总是连着这两个点,再上下拉动抛物线而令其轴不离开BK 。于是,抛物线与直线的交点C 将描绘出一条曲线ACN ,它可用于所提问题的作图。

描绘出这条曲线后,在抛物线凹的那边取定BK 上的一个点L ,使 ;然后,在BK 上朝B 的方向划出LH 等于
;然后,在BK 上朝B 的方向划出LH 等于 ,并从H 在曲线ACN 所在的那侧引HI 垂直于LH 。取HI 等于
,并从H 在曲线ACN 所在的那侧引HI 垂直于LH 。取HI 等于

为简洁起见,我们可令其为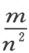 。我们再连接L 和I ,以LI 为直径并在其上描绘圆LPI ;然后,在该圆内嵌入等于
。我们再连接L 和I ,以LI 为直径并在其上描绘圆LPI ;然后,在该圆内嵌入等于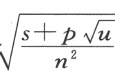 的直线段LP 。最后,以I 为心画过P 的圆PCN 。这个圆与曲线ACN 相交或相切触的点数跟方程具有的根的数目一样多;因此,由这些点引出的与BK 垂直的CG 、NR 、QO 等垂线段就是所求的根。这条法则绝不会失效,也不允许任何例外发生。
的直线段LP 。最后,以I 为心画过P 的圆PCN 。这个圆与曲线ACN 相交或相切触的点数跟方程具有的根的数目一样多;因此,由这些点引出的与BK 垂直的CG 、NR 、QO 等垂线段就是所求的根。这条法则绝不会失效,也不允许任何例外发生。

因为,若量S 与其他的量p 、q 、r 、t 、u 相比有如此之大,以至直线段LP 比圆LI 的直径还长,根本不可能嵌在圆内,那么,所论问题的每一个根将都是虚根;若圆IP 如此之小,以至跟曲线ACN 没有任何交点,方程的根也皆是虚根。一般而论,圆IP 将跟曲线ACN 交于六个不同的点,即方程可有六个不同的根。如果交点不足此数,说明某些根相等或有的是虚根。
当然,如果你觉得用移动抛物线描绘曲线ACN 的方法太麻烦,那么还有许多其他的办法。我们可以如前一样取定AB 和BL ,让BK 等于该抛物线的正焦弦;并描绘出半圆KST ,使其圆心在BK 上,与AB 交于某点S 。然后,从半圆的端点T 出发,向K 的方向取TV 等于BL ,再连接S 和V 。过A 引AC 平行于SV ,并过S 引SC 平行于BK ;那么,AC 和SC 的交点C 就是所求曲线上的一个点。用这种方法,我们可以如愿找出位于该曲线上的任意多个点。
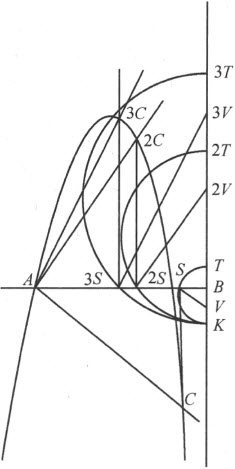
以上结论的证明是非常简单的。置直尺AE 和抛物线FD 双双经过点C 。这是总能办到的,因为C 落在曲线ACN 上,而后者是由该抛物线和直尺的交点描绘出来的。若我们令CG =y ,则GD 将等于 ,因为正焦弦n 与CG 的比等于CG 与GD 的比。于是,
,因为正焦弦n 与CG 的比等于CG 与GD 的比。于是,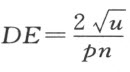 ,从GD 中减去DE ,我们得
,从GD 中减去DE ,我们得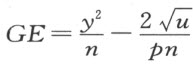 。因为AB 比BE 等于CG 比GE ,且AB 等于
。因为AB 比BE 等于CG 比GE ,且AB 等于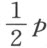 ,因此,
,因此,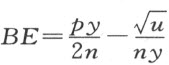 。现令C 为由直线SC (它平行于BK )和AC (它平行于SV )的交点所生成的曲线上的一个点。并令SB =CG =y ,抛物线的正焦弦BK =n 。那么,BT =
。现令C 为由直线SC (它平行于BK )和AC (它平行于SV )的交点所生成的曲线上的一个点。并令SB =CG =y ,抛物线的正焦弦BK =n 。那么,BT =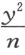 ,因为KB 比BS 等于BS 比BT ;又因TV =BL =
,因为KB 比BS 等于BS 比BT ;又因TV =BL =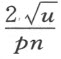 ,我们得
,我们得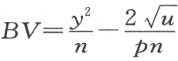 。同样,SB 比BV 等于AB 比BE ,其中BE 如前一样等于
。同样,SB 比BV 等于AB 比BE ,其中BE 如前一样等于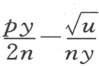 。显然,由这两种方法描绘出了同一条曲线。
。显然,由这两种方法描绘出了同一条曲线。
而且,BL =DE ,故DL =BE ;又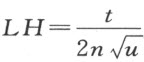 及
及
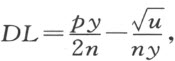
因此,
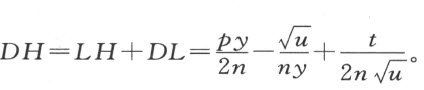
又因 ,故
,故
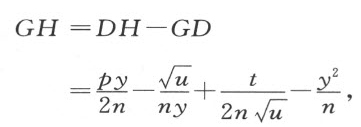
此式可写成
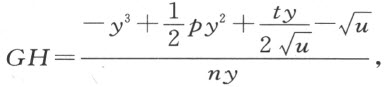
由此可得GH 的平方为
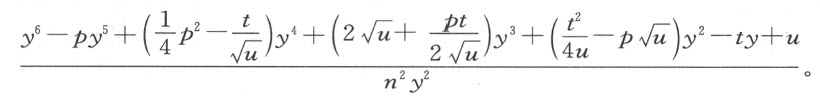
无论取曲线上的哪一点为C ,也不一论它接近N 或接近Q ,我们总是能够用上述同样的项和连接符号表示BH 之截段(即点H 与由C 向BH 所引垂线的垂足间的连线)的平方。
再者, ,由此可得
,由此可得
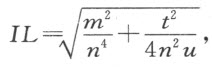
因为角IHL 是直角;又因
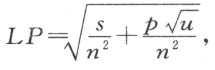
且角IPL 是直角,故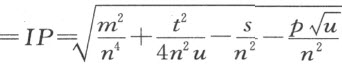 。现引CM 垂直于IH ,
。现引CM 垂直于IH ,
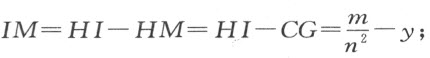
由此可得IM 的平方为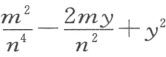 。
。
从IC 的平方中减去IM 的平方,所余的即为CM 的平方:
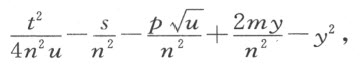
此式等于上面求得的GH 的平方。它可写成
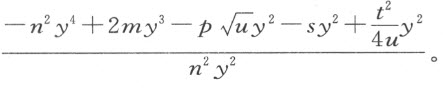
现在,式中的n 2 y 4 用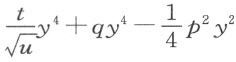 代替,2my 3 用
代替,2my 3 用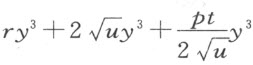 代替。在两个部分 (3) 皆以n 2 y 2 乘之后,我们得到
代替。在两个部分 (3) 皆以n 2 y 2 乘之后,我们得到

等于

即
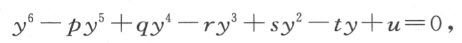
由此可见,直线段CG 、NR 、QO 等都是这个方程的根。
若我们想要找出直线段a 和b 之间的四比例中项,并令第一个比例中项为x ,则方程为x 5 -a 4 b =0或x 6 -a 4 bx =0。设y -a =x ,我们得
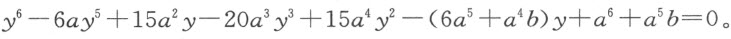
因此,我们必须取AB =3a ;抛物线的正焦弦BK 必须为
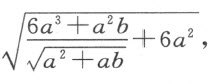
我称之为n 。DR 或BL 将为

然后,描绘出曲线ACN ,我们必定有
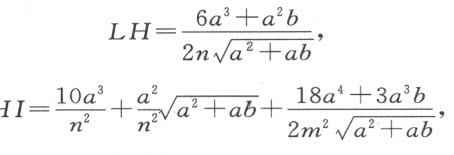
及
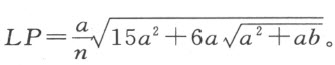
因为以I 为心的圆将通过如此找出的点P ,并跟曲线交于两点C 与N 。若我们引垂线NP 和CG ,从较长的CG 中减去较短的NR ,所余的部分将是x ,即我们希望得到的四比例中项中的第一个。
这种方法也可用于将一个角分成五个相等的部分,在圆内嵌入一正十一边形或正十三边形,以及无数其他的问题。不过,应该说明,在许多问题中,我们可能碰到圆与第二类抛物线斜交的情形而很难准确地定出交点。此时,这种作图法就失去了实际价值。克服这个困难并不难,只要搞出另一些与此类似的法则即可,而且有千百条不同的道路通向那些法则。
我的目标不是撰写一本大部头的书;我试图在少量的篇幅中蕴含丰富的内容。这一点你也许能从我的行文中加以推断:当我把同属一类的问题化归为单一的一种作图时,我同时就给出了把它们转化为其他无穷多种情形的方法,于是又给出了通过无穷多种途径解其中每个问题的方法;我利用直线与圆的相交完成了所有平面问题的作图,并利用抛物线和圆的相交完成了所有立体问题的作图;最后,我利用比抛物线高一次的曲线和圆的相交,完成了所有复杂程度高一层的问题。对于复杂程度越来越高的问题,我们只要遵循同样的、具有普遍性的方法,就能完成其作图;就数学的进步而言,只要给出前二、三种情形的做法,其余的就很容易解决。
我希望后世会给予我仁厚的评判,不单是因为我对许多事情作出的解释,而且也因为我有意省略了的内容——那是留给他人享受发明之愉悦的。
————————————————————
(1) 笛卡儿在描述方程的次数时,使用dimension这个词,在讨论几何对象的维数时,也用这同一个词。——译者
(2) 笛卡儿在这里首次直接使用“假根”的同义语“负根”,原文为“Les fausses ou moindres que rien”,直译为:假根或比无还小的根。——译者
(3) 指GH 的平方和CM 的平方。——译者
