第3章　论折射

采用磨光物体表面反射光波解释反射作用的同样方法，我们来解释透明性以及在透明体内光波传播的和穿过所引起的折射现象，这些透明体既可以是像玻璃那样的固体，也可以是像水、油等那样的液体。

在1671年绘制的一幅展示科学仪器的图画中，惠更斯制作的摆钟位于图画中心。

采用磨光物体表面反射光波解释反射作用的同样方法，我们来解释透明性以及在透明体内光波传播的和穿过所引起的折射现象，这些透明体既可以是像玻璃那样的固体，也可以是像水、油等那样的液体。不过，为了使波在这些物体中传播的假设不至于显得奇怪，我将首先说明，可以设想有可能不只一种模式。

首先，如果“以太”物质完全不能穿入透明体，则透明体的微粒就应该像“以太”微粒那样，能够连续地传播波的运动，只要假设它们像“以太”那样也具有起弹簧作用的性质。当考虑水和其他透明液体时，这一点很容易想象，因为它们的固性似乎不允许它们作除了它们同时以一个整体运动以外的其他运动。然而，这是可以避免的，因为这种固性不是我们看来的那种，说得确切些，这些物体根据它们凸凹不平的形状，不过是由一些相互靠得近的微粒构成的，这些微粒靠某种其他物质从外面加压结合在一起。主要是由于能简易地表现它们的稀薄性，磁旋物质在那里穿过，导致吸引力。而且不能认为这些物体有一种像海绵或软面包那样的结构，因为用火加热使它们变形，从而改变物体中微粒的位置。那么，正如已经讲过了的那样，物体是彼此邻接的微粒组成的复合物，而不是一个实心体。既然如此，这些微粒收受的运载光波的运动，只是由它们的某一部分传到另一部分，在这种情况下不需要微粒脱离其位置或者打乱，运动可以丝毫不损害复合物的表观固性而恰当地产生作用。

我所说的外压不应该理解为来自空气的压力，它是不够的，而应该理解为来自某种更精细的物质的压力。这一压力是很久以前我在实验中偶然发现的。在水里不含空气的情况下，虽然已经把空气从封闭管子的容器抽掉，压力继续存留在下端开口的这根管子中间。

那么可以用这种方式来想象固体的透明性，而无须设想传播光的“以太”物质能穿透固体或者在它里面找到进入的缝隙。但是，事实上“以太”物质不仅穿透了固体，而且还非常容易，前面提到的托里拆利实验就是一个证明。因为在玻璃管上部水银和水下落后留出的地方，由于光的穿透，显然立即被“以太”填满了。不过，这是检验透明体和其他各种物体中透明度的另一种论据。

光穿过一个四周封闭的空心玻璃球时，球内与球外一样充满着“以太”物质是肯定的。如上所述，这种“以太”物质由只是相互邻接的微粒组成。那么，假若“以太”像这样被关在球内而不能从玻璃的缝隙中出来，当球的位置改变时，“以太”就不得不随着球一起运动。因而，当把球置于一个水平面上时，要使球具有一定的速度所需要的力，几乎与它装满了水或者水银时一样。因为每一个物体对外加运动速度的抵抗，与所包含的随着运动的物质的量成正比。但是，正好相反，人们发现球对于运动效应的抵抗，只是正比于组成玻璃的物质量。由此可见，球内的“以太”物质肯定没有被关住，而是非常自由地流出来了。以后我们将证明，可以照此方法猜测有关不透明体的透明度。

接着来看解释透明性的第二种模式，似乎可能更合适些，即认为光波是由均匀地填充透明体间隙的“以太”物质传递的。由于光波连续自由地穿过透明体，所以透明体始终充满着“以太”。人们甚至可以证明，这些间隙比构成物体的相连接的微粒占据着更大的空间。因为，如果我们以上所说的是正确的，使物体具有一定水平速度所需要的力，正比于它包含的相连接的物质；并且如果力的比例遵守重力定律，就像实验所证实的那样，那么构成物体的量也遵守它们的重力比例。我们知道水只有同样体积水银的十四分之一重，于是水物质不是占据整体存在空间的十四分之一。它准是占据得还要少。由于水银还没有金重，而金物质也绝不是密实的，正如下述事实表明的那样，磁旋物质造成的吸引力非常随意地穿透它。

但在这里也许有人会问，如果水是如此稀薄的物体，并且它的微粒只占据了其表观体积中这么小的一部分，非常奇怪它还能如此强烈地抵抗压力而不让它本身被人们一向企图施加的各种力所压缩，在受到压力时甚至保持其整个的液性。

这个困难不小，但可以通过下述方法来解决。通过组成水的微粒的振动，覆盖水液体的精细物质的剧烈而快速的运动维持住这种液性，而不管谁曾有意给它施加过力。

既然透明体的稀薄性如上所述，就容易设想光波由填充微粒缝隙的“以太”物质传递。此外，也会相信光波在物体内部行进时应该稍微慢一些。因为微粒造成了一些小的迂回。我将要说明光速不同的物质中的折射。

在这么做以前，我简述一下关于透明性设想的第三个也是最后一个模式。假设光波的运动在占据物体缝隙的“以太”物质微粒中的传递，与在组成物体的微粒中的传递无关，使得运动在两种微粒中从一种向另一种传递。以后将看到，这个假设能用来很好地解释某种透明体的双折射。

假如有人以下述理由提出反对，即如果“以太”微粒比构成透明体的微粒小（因为“以太”微粒在透明体微粒的间隙中穿过），则它们可以传递运动，不过稍小些，可以作出的回答是，这些物体的微粒本身又是由更小的微粒组成的，可能正是这些次级微粒接受“以太”的运动。

另外，如果透明体的微粒比“以太”微粒的反冲稍微缓慢些，这不妨碍我们的假定，光波的行进在这些物体内比在这些物体外的“以太”物质中要慢。

所有这些就是我所发现的光波穿过透明体的最可能的模式。要作一点补充的是，这些物体与那些不透明体不一样，由于“以太”物质容易穿透它们，看起来似乎尤其如此，没有什么物体是不透明的。类比用以证实玻璃密度小以及容易为“以太”穿透的空心球的推理方法，也可以证明金属和其他种类的物体都具有同样的穿透性。譬如一个银制的球，球是封闭的，它无疑包含着传递光的“以太”物质，因为“以太”物质像在空气中一样存在于那里。还有，把球封闭起来置于一个水平面上，它只根据组成球的银物质量来抵抗施加给它的运动，因而必定得出同上的结论，封闭在球内的“以太”物质不随球运动；所以银跟玻璃一样很容易被这种物质穿透。于是，银和其他不透明体的微粒之间被大量的“以太”物质均匀地填满，又由于“以太”可以传递光，所以看起来这些物体都应该是透明的，然而实际情况并非如此。

于是人们就会问，它们为什么不透明？是否因为组成它们的微粒不硬？换句话说，由比它更小的微粒组成的微粒，在受到“以太”微粒的压力时，能否改变它们的形状并借此使运动衰竭从而阻碍光波持续？不是这样的。因为，如果金属的微粒不硬的话，擦亮的银和水银怎么会这样强有力地反射光呢？我在这里找到的最有可能的解释，就是认为金属作为几乎最合适的实在的不透明物体，在它们的硬微粒中混有一些不硬的微粒，使得一部分微粒反射而另一部分微粒阻碍穿透；另一方面，如上所说，透明体只包含具有反冲本领的硬微粒，同“以太”微粒一起传播光波。

我们现在转到关于折射效应的解释方面来，像前面所作的那样，假定光波在透明体内通过，而且在其中减慢速度。

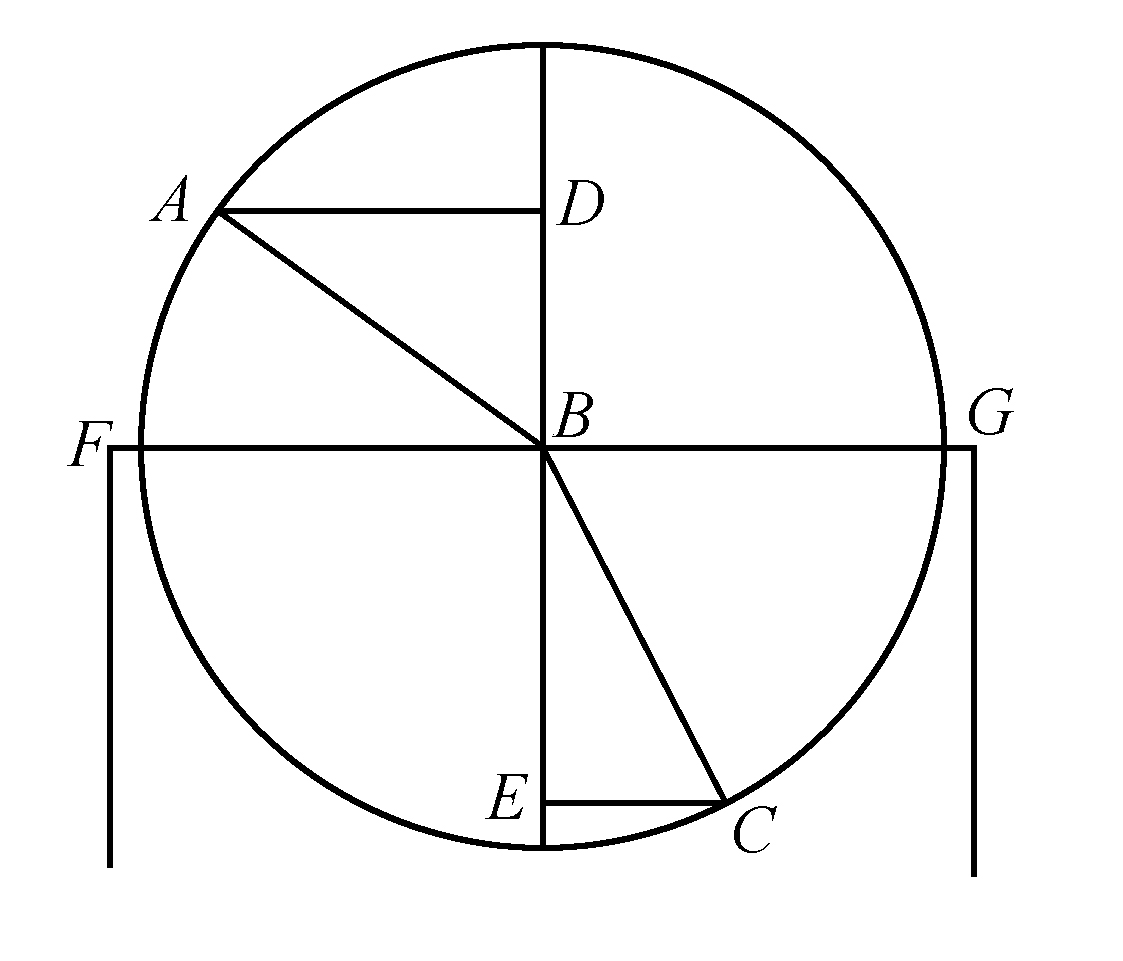图9

折射的主要性质是，在空气中的光线，譬如AB，倾斜地落在一个透明物体的擦亮的表面FG上，在入射点B处屈折，以垂直分割表面的直线DBE为界，使角度CBE小于角ABD，即在空气中与该垂线所夹的角（图9）。这些角的大小可以通过以B点为中心画出一个与半径AB、BC相截的圆得到。从交点向直线DE所作的垂线AD、CE，称为角ABD、CBE的正弦，它们之间有一个固定的比值，对于一个至少给定的透明体，入射光线的所有倾角，它们的比值是相同的。这一比值在玻璃中非常接近于3比2；在水中，非常接近于4比3；在其他透明体中，也同样有所不同。

与这一点类似的另一个性质是，折射对于进入和离开透明体的光线之间，是互换的。换句话说，如果进入透明体的光线AB被折射成BC，那么同样地，这个物体内的光线CB，在穿出时被折射成BA。

接着，为了用我们的原理来解释这些现象的原因，假设直线AB表示位于C方和N方的不同透明材料的分界平面（图10）。我这里所说的平面，并不意味着完全平坦，而像我们在研究反射时那样来理解，并且理由也是同样的。设直线AC代表光波的一部分，假定其中心离得非常远，使得这一部分可以被认为是一条直线。波AC上的点C在一定的时间间隔内将沿着直线CB推进到平面AB，可以被设想是从光亮中心出发，而且与AC正交。如果透明体物质与“以太”物质能同样快地传播波的运动，那么，在相同的时间间隔中，A点将沿着与CB平行而且相等的直线AG，到达G点；如果透明体的物质传送光波运动与“以太”物质一样快，波AC上的所有点应当到达GB。但是，我们假设透明体物质传送这种运动要慢些，例如，慢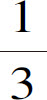 。于是，透明体中A点的运动像前面所说的那样产生自己的球面分波，将传播开等于 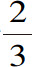CB的距离。这个分波用圆周SNR表示，它的中心为A，半径等于CB的 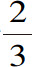。如果依次考虑波AC上的其他点H，就会发现，在C点到达B点的同时，它们不仅沿着与CB平行的直线HK到达了表面AB，而且还在透明材料中以K点为中心产生分波，在这里用一些半径等于 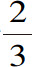的KM长度的圆周表示，这些半径也等于HK到直线BG的延长线的 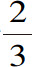；如果两种透明材料具有相同的穿透性，半径就将等于整个KM的长度。

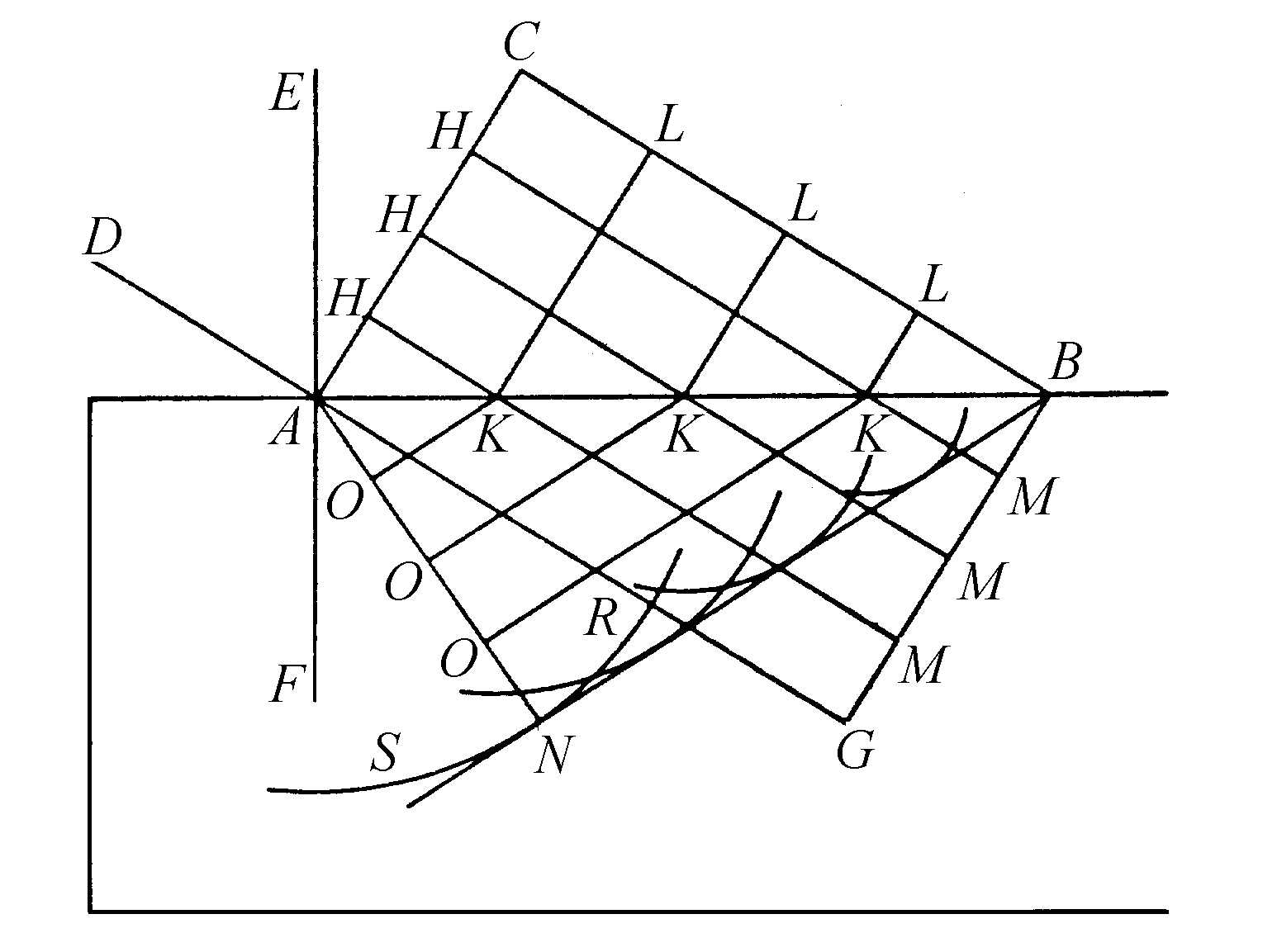图10

所有这些圆周有一条公切线BN，也就是我们先前考虑的从B点所作的与圆周SNR相切的那一条直线。因为容易看到，从B到AN落在BN上的垂足N，其他那些圆周都将与这同一条BN相切。

正是由这些圆周上的小弧线所组成的直线BN，使波AC在透明体内传播的运动终止，而且BN上的运动比其他地方更大。我们不止一次说过，由于这个原因，这条直线就是波AC在它的C点到达B点时的传播。因为平面AB下方的其他任何直线都不像BN那样，是所有这些分波的公切线。如果知道波AC是怎样逐渐到达BN的，需要做的只是在同一图形中画出所有平行于BN的直线KO以及平行于AC的直线KL。那就可以看到作为一条直线的波CA，各点接连地变成了曲折的LKO，在BN处再变成一条直线。这一点在前面的论述中已经很明显，没有必要作进一步解释。

在上述图形中，如果画出了与平面AB正交于点A的直线EAF，由于AD垂直于波AC，表示入射光线的应当是DA，而表示折射光线的是垂直于BN的AN，因为光线只不过是波的各个部分行进时沿着的直线。

由此容易识别折射的这种主要性质，即角DAE的正弦与角NAF的正弦之比总是为同一值，而不管光线DA的倾角如何。并且这一比值也是AE方向透明物质中的波速与AF方向透明物质中的波速之比。因为，假定AB为一个圆的半径，那么角BAC的正弦就是BC，角ABN的正弦就是AN。而角BAC又等于角DAE，因为它们加上角CAE后都是直角。角ABN又等于角NAF，因为它们加上角BAN后都是直角。因此，角DAF的正弦与角NAF的正弦之比，就等于BC比AN。而BC与AN之比又等于AE方向物质中的光速与AF方向物质中的光速之比；因此，角DAE的正弦与角NAF的正弦之比也就等于所说的光速之比。

所以，为了看一看当光波进入一种比它源出的那种物质中运动传播更快的物质中时（假定这一比为3比2）折射会是什么样子，只需要重复我们所采用过的解释与论证，仅仅各处用 来代替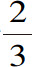 就行了。在图11中，通过同样的推理求得，当波AC上的C点到达表面AB上的B时，波AC上的各个部分行进到BN那样远，使得垂直于AC的BC与垂直于BN的AN之比等于2比3。最后，还有一个同样的比值，是角EAD的正弦与角FAN的正弦之比。

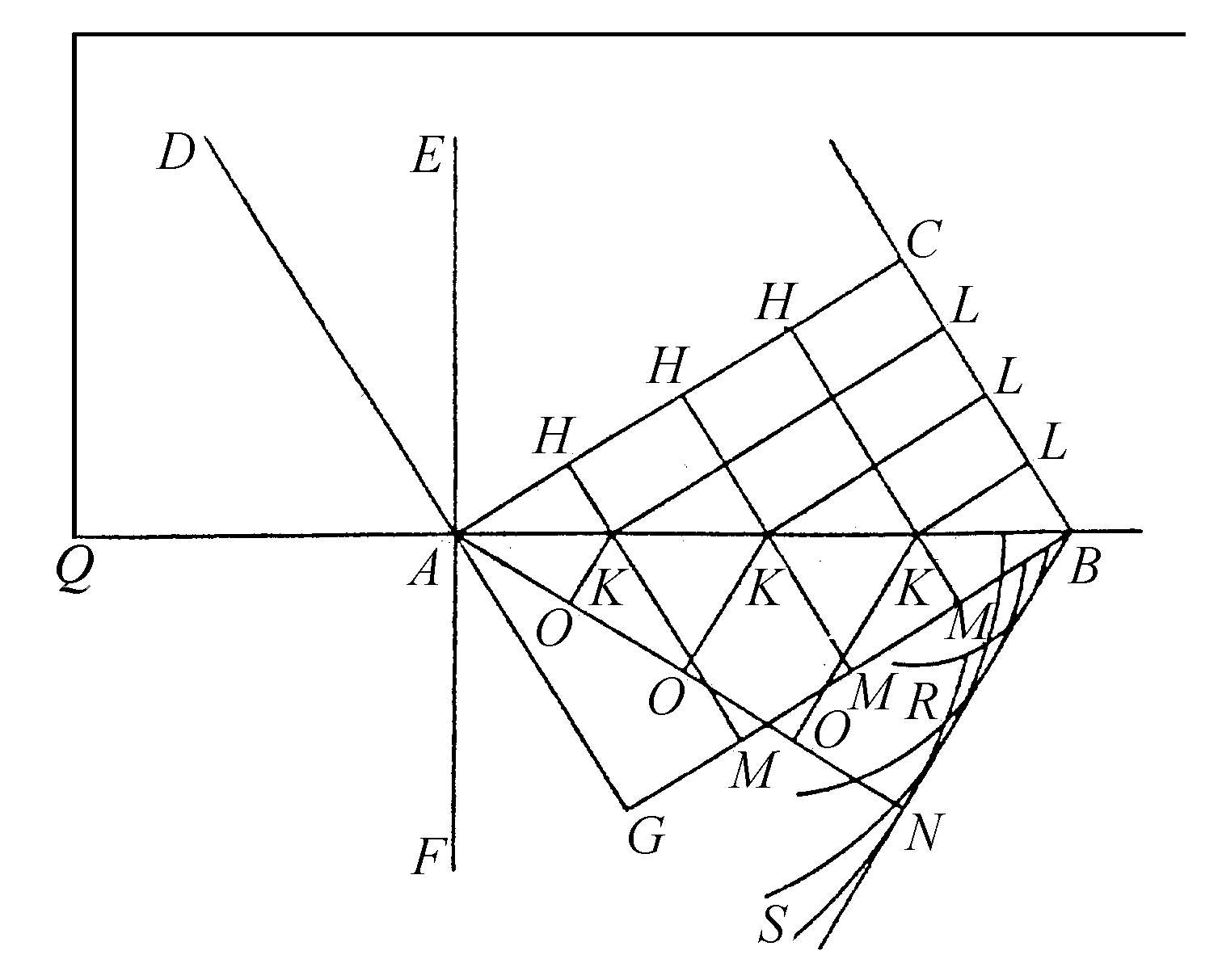图11

由此，可以看到光线进入和离开同一透明体的折射的互易关系，即如果落在表面AB上的光线NA被折射到AD方向，那么光线AD在离开透明体时将被折射到AN方向。

也可以看出这种折射中的一个值得注意的现象的原因：这一现象是这样的，超过某一个给定倾角的入射光线DA就开始不能进入另外的透明物质。如果角DAQ或者角CBA取这样的值，使得三角形ACB中的CB等于或者大于AB的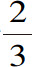 ，那么AN就不能构成三角形ANB的一条边，因为它等于或者大于AB。因此，任何地方都找不到波BN的部分，当然也就找不到属于它的垂线AN。因而入射光线DA不能进入表面AB。

当波速的比值像我们的例子中那样对于玻璃与空气为2比3时，要使光线DA能够折射穿透，角DAQ就必须大于48度11分，当速度比值十分接近于水与空气的3比4时，角DAQ就必须超过41度24分。这一点与实验完全一致。

在这里也许会问：既然波AC与表面AB的相遇应该在另一方的物质中产生运动，那么为什么在那里却没有光线穿过呢？如果还记得我们前面讲过的内容，那么对这个问题的回答就简单了。因为，尽管它在AB另一方的物质中产生了大量的分波，但是这些波在同一时刻没有一条公切线（直的或者弯曲的）；于是越过AB表面没有一条线终止波AC的运动，或者没有任何地方使运动聚集得足以产生光。容易看到这一说法的真实性，假定CB比AB的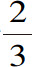 大，如果以K点为中心以LB的 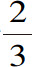长度为半径画出相应的圆，越过AB平面激发的这些波没有公切线。因为这些圆一个包一个并且都通过B点。

值得注意的是，从角DAQ小于允许折射光线DA进入另一种透明材料的角度起，就会发现表面AB上发生的内反射在亮度上大多了。通过三棱镜实验很容易实现这一点，而且我们的理论能够为此提供解释。如果角DAQ仍然大得足以使光线DA穿透，可以很明显地看到，由波的AC部分的出来光到达BN时，被汇聚到一个最小的空间中。随着角CBA或角DAQ的变小，波BN似乎更快地变小，直到角度减小到刚才所指出的极限时，波BN就汇聚成一点。换句话说，当波AC上的C点到达B时，波AC的传播BN将整个地缩小到同一点B上。同样，当H到达K时，AH也将整个地缩小到同一点K上。由此显而易见，根据前面已交代过的反射定律随着波AC到达AB表面，将产生大量的沿着那个表面的运动，这些运动也应当在透明体内传播，也应当有特别加强的子波在表面AB上产生内反射。

因为入射角DAQ减小一点就会使原先不小的BN缩小为零（当这个角在玻璃中为49度11分时，角BAN还有11度21分；而当这个角度只减小了1度时，角BAN就被减小到0度，于是BN就被缩小为一点），由此可见，当入射角的取值使光线不再去折射穿过，内反射会从模糊突然变得明亮起来。

现在来考虑通常的外反射，也就是入射角DAQ足够大，使得折射光线能穿透表面AB时所发生的反射。这种反射应当贴着在透明体外所连接的物质微粒发生。看来，反射是在空气或其他物质的微粒以及“以太”微粒之中产生的，而且大一些。另一方面，这些物体的外反射是在构成它们的微粒中发生的，这些微粒也比“以太”的微粒大，因为后者能在它们的缝隙中流动。事实上，在那些实验中还有一些反例，当把空气从容器和管子中抽掉，即使没有空气的微粒的贡献，内反射也能发生。

此外，经验告诉我们，这两种反射差不多一样强，在不同的透明物体中，这些物体的折射越大，反射就越强。于是可以明显看到，玻璃的反射比水强，钻石的反射比玻璃强。

我准备以一个值得注意的定理的论证来结束这个折射理论。该定理与折射理论有关，即位于不同介质中的两点，光线要从其中一点传播到另一点就得照这种方式折射，在连接这两种介质的平面上使光线花费最少的允许时间。在一个平面上的反射，发生的情况完全一样。费马（Fermat）先生第一个指出了折射的这种性质，他同我们一样与笛卡儿先生的观点正好相反，认为光在玻璃和水中比在空气中走得慢些。不过他还假定了一个我们刚才单靠速度的快慢而证明出的正弦的常数比值。更确切些来讲，他不仅假定速度不同而且还假定光线的传播所需的时间最小，并由此推导出正弦的常数比值。他的论证非常长，可以在他的已出版的著作中，以及在笛卡儿先生的通信集中看到。因此，我在这里给出另一个简易的证明。

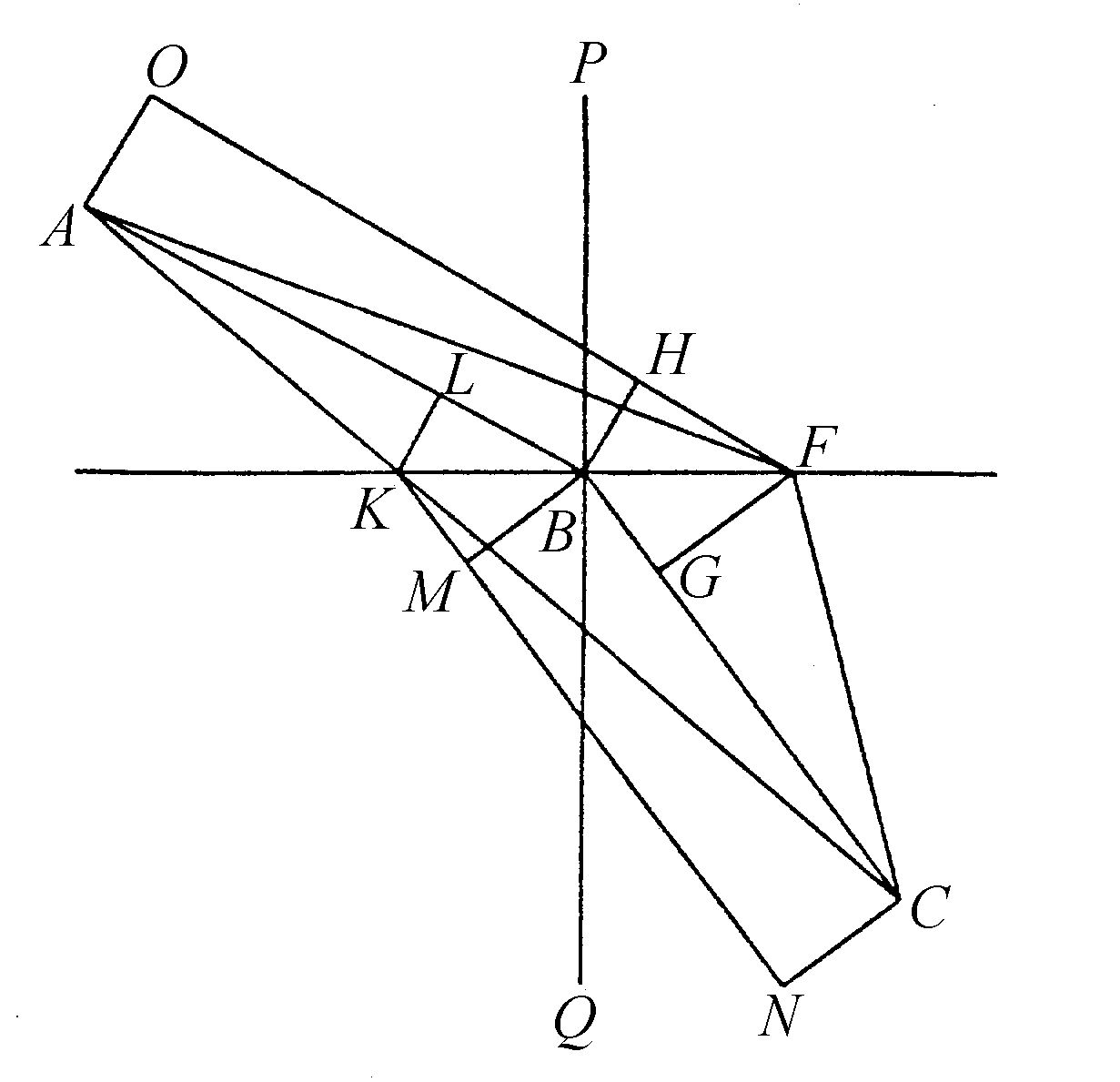图12

设KF为平面（图12）；A点在光容易传播的介质中，譬如空气，C点在另外一种很难穿透的介质，例如水中。再假定光线从A经过B到达C，在B点按照我们前不久证明的定理折射；也即是说，画出与平面正交的PBQ，使角ABP的正弦与角CBQ的正弦之比，等于A点所处介质中的光速与C点所处介质中的光速之比。要证明的是光沿AB和BC穿过所需要的时间，是各种可能值中最小的一个。首先不妨假定光可以沿其他路径传播，譬如沿AF和FC，折射点F与B点离A远一些；作AO垂直于AB，FO平行于AB；BH垂直于FO，FG垂直于BC。

那么，由于角HBF等于角PBA，角BFG等于角QBC，因而可以得到，角HBF的正弦与角BFG的正弦之比，等于介质A中的光速与介质C中的光速之比。而如果我们将BF看做圆的半径，那么这些正弦值就等于直线HF与BG的长度。于是直线HF与BG之比，就等于所说的速度比。因此，假定光线为OF，那么光沿HF传播的时间应当等于在介质C中沿BG传播的时间。而沿AB传播的时间又等于沿OH传播的时间；于是，沿OF传播的时间就等于沿AB和BG传播的时间。此外，沿FC传播的时间又大于沿GC传播的时间，因此沿OFC传播的时间将大于沿ABC传播的时间。同时AF又大于OF，于是沿AFC传播的时间将比沿ABC传播的时间更长。

现在，假定光线沿AK与KC从A点到达C点；其中折射点K比B点离A点近些，作CN为BC的垂线，KN平行于BC；BM垂直于KN，KL垂直于BA。

这里，BL和KM是角BKL和角KBM的正弦；也就是角PBA和角QBC的正弦。因此，它们之间的比值就等于介质A中的光速与介质C中的光速之比。于是沿LB传播的时间就等于沿KM传播的时间；又因为沿BC传播的时间等于沿MN传播的时间，所以沿LBC传播的时间就等于沿KMN传播的时间。而沿AK传播的时间又大于沿AL传播的时间，因此沿AKN传播的时间就大于沿ABC传播的时间。同时，KC又比KN长，于是沿AKC传播的时间将比沿ABC传播的时间更长。由此可见，沿ABC传播的时间是最短的可能值；这一点将会得到证实。