第1章　论沿直线传播的光线

正如在几何学被用于研究物质的所有学科中所遇到的那样，有关光学的论证都立足于从经验引出的事实上。

惠更斯手稿中的土星

正如在几何学被用于研究物质的所有学科中所遇到的那样，有关光学的论证都立足于从经验引出的事实上。这些事实是：光线沿直线传播，反射角与入射角相等以及光线折射时方向按正弦定律改变。后者现已为人们所熟悉，它和前面的两个定律一样准确可靠。

著文涉及光学不同领域的大多数人都以认定这些事实而感到满足。但一些更具好奇心的人们却渴望考察其起因与理由，认为这些事实本身是自然现象的奇异效应。在这方面他们提出了某些有创见的东西，然而还不足以使最有才智的人不去寻求更好、更满意的解释。所以在这里，我想抛砖引玉，对自然科学的这个领域贡献我力所能及的解释，而这个领域极有理由被认为是其中最困难的一个部分。我个人认为，应该非常感谢那些人们，是他们首先拨开了笼罩这些事实的迷雾，并且给了我们希望，有可能通过清晰的推理来说明它们。不过另一方面，也使我惊异的是，甚至在这一点上，这些人为了使人信服，总是乐于提出一些绝非结论性的推理。因为我还没有发现有人对光的第一个最值得注意的现象作出过较为合理的解释，即为什么它不以除了直线以外的方式传播，来自无数不同地方的可见光怎样彼此毫无妨碍地穿过。

因此，我将试图在这本书中依据已被当今哲学承认的原则，给出一些更为清晰并且更为合理的解释，首先是光以直线传播的性质，其次是光在遇到其他物体时被反射。接着，我将解释光线在穿过不同种类透明体时受到折射的现象；在这个部分，我还将解释由大气层不同密度而引起的空气的折射效应。

此后，我将考察一种取自冰岛的晶体具有奇异折射的原因。最后我还将论述由于透明体与反射体的种种形状而使得光线汇聚于一点或以不同方式偏离的问题。由此人们可以容易地看到，依照我们的新理论，我们求出的不仅有笛卡儿先生为此目的天才性地发明的椭圆、双曲线和其他曲线；而且还有玻璃透镜表面该具备的形状，这时它的另一个表面已被给定为球面、平面或别的任何可能的图形。

无法想象去怀疑光是某种物质的运动。因为，人们或者去考虑它的产生，会看到在地球上它主要由无疑含有快速运动物体的燃烧与火焰造成，而燃烧与火焰会溶解和熔化许多其他的甚至那些最坚硬的物体；或者去考虑它的效应，会看到当光被汇聚，如被凹面镜汇聚时，它具有像燃烧那样的起火性质，也就是说，它使物体微粒离开。这无疑是运动的标记，至少在采用机械运动来构思所有自然效应起因的实际哲学中是这样的。我认为我们必须这么考虑，不然就放弃了一贯领悟物理学一切现象的全部希望。

还因为依照这种哲学，只要人们确信视觉兴奋只是某种物质运动对我们眼后神经作用的感应，就更有理由相信光存在于我们与发光体之间的物质运动之中。

此外，当人们考虑到光向四面八方传播的极限速度时考虑到来自不同方位甚至正相对方位的光线又是怎样彼此不受干扰穿过时，或许会清楚地认识到，当我们看到一个发光体时，光线不可能像射弹或箭穿过空气那种方式由物质从发光体传运给我们；因为那必将严重地违背光的这两个性质，尤其是第二个性质。于是，光应以另外某种方式传播，而我们有关声音在空气中传播的知识可以给我们以启迪。

我们知道，借助于空气这种看不见摸不着的物体，声音通过连续不断地从空气的一部分传递到另一部分的运动由产生它的地方向周围传播；并且这种运动的传播在所有方向进行得同样的快因而应该形成一些不断扩大的并传入我们耳中的球面。现已毫无疑问，光从发光体来到我们的眼睛，也是通过施加在这之间物质上的运动；正如所看到的那样，因为光不可能被一个物体从一个地方运载到另一个地方。另外，如果光的传播需要时间——我们即将考察这一点——就可得知，施加在介质上的这种运动是连续的，因而它也应像声音那样以球面和波的形式传播：其所以称它们为波，是由于它们和看到石头扔入水中时所产生的情形类似，呈现出圆圈那样的连续分布，尽管它们的起因不同，而且仅在一个平面上。

为了弄清楚光的传播是否需要时间，让我们首先想一下是否有什么能使我们信服的相反的经验事实。至于那些在地球上可以取得的经验事实，尽管远处照光证实了光通过这些距离几乎不需要时间，人们还是可以有理由认为这些距离太小，由此能得到的唯一结论是光的传播极快。笛卡儿先生主张光瞬时传播，他不无理由地将其观点建立在从月食得出的一个较好的经验基础上；然而，正如我将要证明的，这也无法使人信服。为了使结论易懂，我将采用一种与他稍许不同的方式进行阐述。

设A为太阳的位置，BD为地球轨道或公转路径的一部分，ABC是一条直线，我假定它与月球的圆轨道CD相交于C点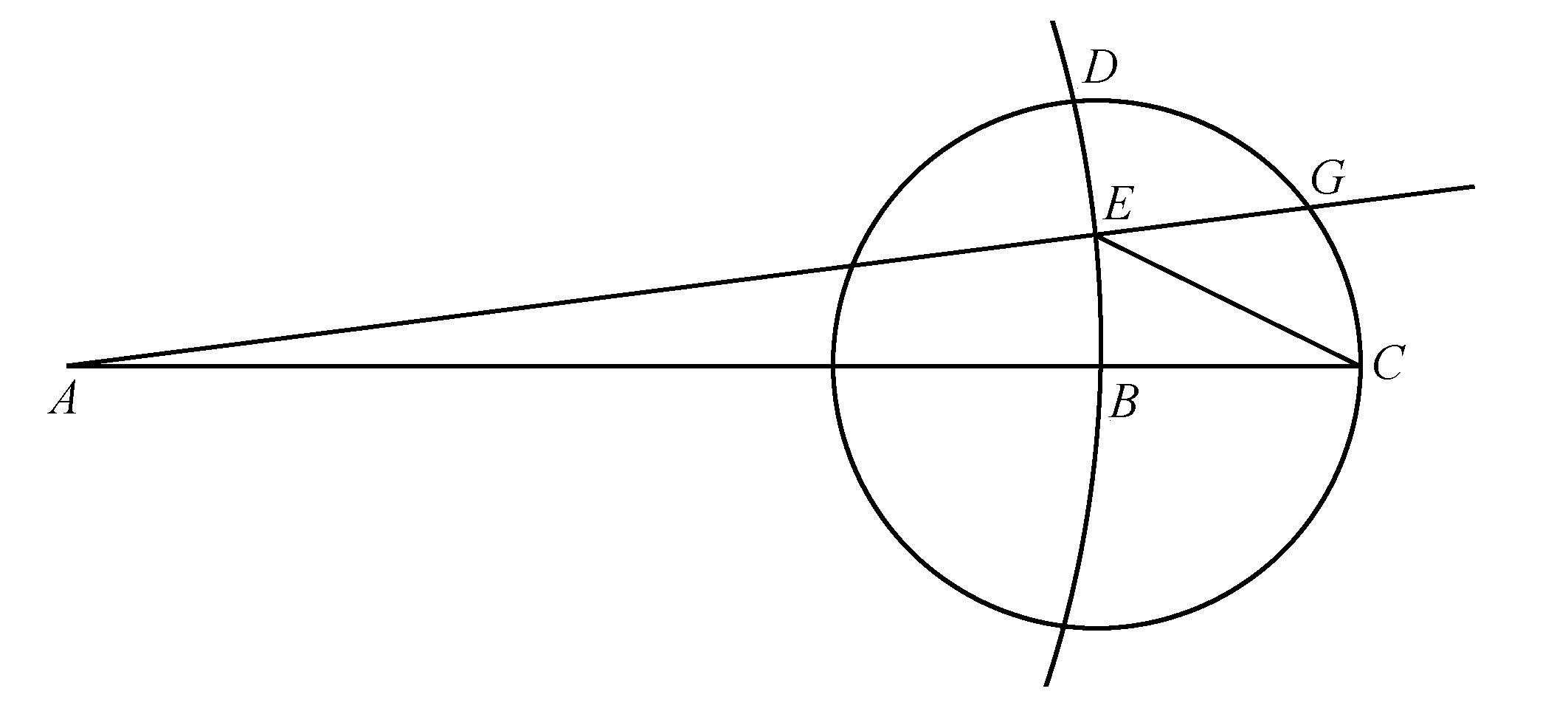（图1）。

图1

如果光需要时间，譬如一个小时穿过地球与月球之间的空间，那么当地球到达B点时，它投下的影子或亮光遮断就还不会到达C点，而将在一个小时后才到达那里。从地球到达B点的时刻算起，一小时后到达C点的月球将被遮暗：但是亮光遮断造成的昏暗不再经过一小时就到达不了地球。假定经过这两个小时地球到达了E点。那么在E点的地球将看到一小时前在C点被遮住的月球，与此同时还将看到位于A点的太阳。由于我依照哥白尼（Copernicus）那样假定太阳是静止的，而光又总是沿直线传播的，太阳总是在它那个地方出现。不过据说，人们一直观察到月食时的月球出现在正对太阳的黄道上那一点；然而眼下所考虑的，月球似乎在那点之后出现，相差角AEC的补角GEC那样大的角度。这一点无论如何正好同人们的经验相反，因为角GEC会很可观，大约为33度。那么，依据我们在有关土星现象起因的论文中给出的计算，地球到太阳的距离AB大约为地球直径的12000倍，也就比相当于30倍地球直径的到月球的距离BC要大400倍。于是，角ECB几乎比大小为五分的角BAE大400倍；即地球沿其轨道在二小时内穿过的行程，角BCE因而约为33度，角CEG也一样，只是大五分。

不过应当注意，这一论证中的光速被假定为它从这里到月球的行程需要耗费一个小时。倘若假定它只需要一分钟的时间，很显然角CEG仅有33分；而如果它只需要十秒钟时间，这个角就将小于6分。再者，人们既不容易由月食的观察中发觉什么；因而也不允许从中得出光的运动瞬时的结论。

确实，我们在这里假设了一个比音速快十万倍的怪速度。因为根据我所观测的结果，声音在一秒钟或者在大约一次脉搏的时间内约传递180突阿斯（toise）(1) 。但是，这个假设似乎应该被视为是有可能的；由于除了从某些物体向另外一些物体传递的连续运动的问题外，具有如此巨大速度的物体的传送倒并不是一个问题。鉴于以这种方式，光的所有现象都可以被解释，相反则所有的事情无法理解，我也就不反对去考虑这些事情，去假设需要时间来完成光的发射。因为在我一贯看来，即使是笛卡儿先生，他的研究曾清晰地论述了物理学的各种课题，他在这方面也的确比前人更加成功，但在处理光及其特性时，也说过一切都充满困难，乃至于难以相象。

我用来仅作为假设的东西，最近经过勒麦先生精巧的证明，仿佛成了既定的事实，虽然期待由他本人给出证实所必要的一切，我也打算在这里说一说。同先前的论证一样，也是由天体观测出发，不仅证明光的行程需要时间，而且给出需要多少时间，光速比我刚讲的至少还要大6倍。

图2

勒麦先生为此利用了绕木星旋转的众小星体造成的星食，这些现象经常使他困惑，期望得出其答案。如图2所示，设A为太阳，BCDE为地球的公转轨道，F为木星，GN为距离它最近的卫星的轨道。正是由于这个卫星旋转得快，而比其他三个卫星更适合于作此研究。假定这个卫星在G点进入木星的阴影部分，又在H点从阴影中出来。

再假设地球在下弦之前的某时刻到达B点，看见该卫星从阴影中出来；倘若地球留在原处不动，经过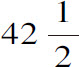 小时以后，必定会再看见它同样地出来，因为这恰好是卫星再跑到太阳对面绕其轨道一周所需的时间。如果这个卫星旋转了30次而地球始终在B点不动，就会每隔 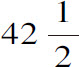小时看见卫星从阴影中出来30次。但是地球在这段时间内已跑到了C点，增加了它与木星间的距离，因而得出如果光的行程需要时间，它在C点就比在B点晚一些看到这个小星体的光亮，需要晚30个 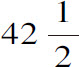小时，在这段时间里光走过MC这段空间，即CH与BH之差。类似地，在另一个弦内当地球从D点到E点逐渐接近木星时；在E点应当比地球在D点不动时早一些观察到卫星隐没到木星的阴影中。

在连续十年进行的大量星食观测中，已经发现这些差别非常明显，例如10分钟以上；光穿过公转轨道的直径KL，即地球到太阳距离的两倍，需要大约22分钟时间。

地球从B到C或者从D到E时木星在其轨道上的运动，已包括在这一计算中；因此，显然不能认为光程迟差或星食超前是小星体运动出现的紊乱或反常。

如果考虑到直径KL的巨大尺寸，据我看，大约为24000个地球直径，就会承认光的极限速度。如果假定KL不超过22000个地球直径，看来在22分钟内穿过它，要求光速为每分钟1000个地球直径，即每秒钟或每次脉搏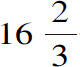 个地球直径，约一亿一千多万突阿斯。依据皮卡尔（Picard）先生1669年遵照国王的命令所作的精确测量，地球直径有2865里格（league）(2) ，估算误差程度25里格，每里格等于2282突阿斯。如前所述，在一秒钟的同样时间内声音仅穿过180突阿斯，因而光速比音速大六十多万倍。但是，这与瞬时远非同一回事，因为有限与无限完全不一样。用这种方法证实了光的连续运动后，如上所述，就可以得出光像声音的运动那样通过球面波来传播的结论。

如果说二者在这方面相似的话，那在其他方面就不同，也就是说，导致它们运动开始的原因不同；传播它们运动的介质不同；而且传播方式也不同。关于声音的产生的问题，人们知道，它是由物体整个或其中相当大的部分振动震击周围邻近的空气所引起的。但是，光的运动却必定由光亮物体上的每一点发源，不然的话，我们就分不出那个物体的各个不同部分。这一点在下文中会更明显。我相信没有什么别的方法能比下述假设更好地解释光的运动，即假设所有液态的光亮物体，例如火焰、太阳和星星的外表，是由漂浮在一种很难形容的介质中的微粒组成，这种介质能极快地震动这些微粒，并使它们撞击周围的比它们更细小的“以太”物质。不过我也认为，在固态的光亮物体，例如在火中，烧红了的木炭或者金属，金属或者木块微粒的激烈振动也会引起同样的光运动；固态光亮物体表面的微粒同样也会撞击“以太”物质。此外，产生光的微粒振动应该比产生声音的物体振动要更直接更迅速，因为我们看到，就像手在空气中的运动不能产生声音那样，产生声音的物体振动也不能产生光。

那么，如果询问被我称为“以太”的传递来自光亮物体运动的物质是什么，人们会看到，它与传播声音的物质不同。因为人们发现后者是我们可以真实感觉与呼吸的，当它从某个地方移开时，在那里仍然存在另一种能传送光的物质。这一点可以通过用抽气机抽出空气来密闭一个装在玻璃器皿内的发声体的方法来证明，这种抽气机是波义耳（Boyle）先生给我们的，他曾用它作过好多漂亮的实验。不过在做我所说的这个实验时，必须细心地将发声体用棉花或羽绒包住，以避免将其振动传递给装它的玻璃器皿或者传递给抽气机，这一预防措施向来被忽略了。这样一来，抽完所有的空气后，就听不到金属的声音了，尽管它仍被敲击着。

在这里，人们不仅看到，不能穿透玻璃的空气是传播声音的物质，而且看到，传播光的物质不是空气而是另一种物质，因为即使从器皿中抽掉了空气，光依旧穿过它。

最后这一点通过著名的托里拆利（Torricelli）实验能更清楚地得到证明。在这个实验中，水银下落留下的没有空气的玻璃管，能像有空气时那样传播光。这就证明了玻璃管内有一种不同于空气的物质，这种物质可以穿透玻璃或者水银，不过，不管是这还是那，空气都穿不透。在同样的实验中，如果在水银上先放一点水后再抽真空，一样可以得出结论，上述物质穿透玻璃或水，或者都穿透。

关于我所讲到的传送声音运动与光运动的不同方式，倘若考虑一下空气有一种能被压缩以至挤进此正常体积小得多的地方的性质时，就足以理解在声音情形下是如何进行的。空气按被压缩的比例尽量恢复其原状；这一特性连同其穿透性，即使在空气被压缩时也存在。这似乎表明，由更小部分构成的“以太”物质中，空气由被快速震动的到处飘浮的微粒组成。所以，声音传播的原因就是声波范围内的这些微粒稍微挤压在一起时，通过相互碰撞以恢复原状的结果。

然而光的极大速度以及它所具有的其他性质，不允许运动像这样传播。我准备在这里给出一个我以为光能够传播的方式。为此，有必要解释一下坚硬物体依次传递运动所应具有的性质。

把一些同样大小的由坚硬材料制成的球排成一条直线，并使它们彼此相切，再用一个同样的球撞击这些球中的头一个，我们发现，运动在一瞬间内就传到了它们的最后一个，并使它离开它们的行列，而我们并不觉察到其他球体曾经被撞动过，甚至于用来作撞击的那个球也同它们静止在一起了。由此可以看出，运动是以极快的速度传递的，做球的材料越坚硬，传递的速度越快。

不过有一点是确定无疑的，即运动的这个传递过程不是瞬时的，而是连续的，因而需要时间。因为如果你硬要这样说，假若运动或运动的序列不是连续地由这些球传送，则这些球就会同时获得运动，而一起往前跑；这种现象没有发生。只是最后一个球离开整个行列，获得了与撞击它们的球的速度一样的速度。此外，还有些实验表明，那些被我们当作最坚硬材料的物体，譬如硬化钢、玻璃以及玛瑙之类，不但在伸展为棒状时而且在制成球或其他形状时由于某种原因也会起到弹簧那样的作用而变形。换句话说，在它们被撞击的地方会凹进去一点儿，随即就恢复了它们原先的形状。因为我发现，在用一个玻璃或玛瑙球撞击由同样材料做成的大而相当厚并且表面平坦的物件时，先在物件上呵口气或用别的办法稍微弄点污，就会留下一些圆形的痕迹，痕迹的大小随撞击的强弱而定。显而易见，这些材料在被撞的地方凹进去，然后又弹回去：因此，必定需要时间。

现在把这种运动方式用来研究光的产生，就没有什么妨碍了。我们估计，“以太”微粒是由一种几乎达到理想硬度并具有可任意选择弹性度的材料构成的。没有必要在这里去考察这种硬度或弹性度的来源，那会使我们偏离了主题。不过，我还是要顺带提一下，我们可以设想“以太”微粒，尽管它们很小，同样也是由其他组分构成的，它们的弹性度取决于一种到处充满着的微妙物质的极快运动，使它们的结构不得不呈现为像液态物质那样极为明显和容易流过的形式。这一点与笛卡儿关于弹性的解释相符，不过我不像他那样以为孔就是圆形的空心管子。不要以为这里面有什么是荒谬或不可能的，其实恰好相反，正是这种无穷的大小不同、速度不同的微粒才使自然界出现这么多千奇百怪的效应。

虽然我们将不管弹性的实际起因，但我们仍然看到许多物体都具有这个性质，因而假定像“以太”微粒这样的微小不可见的物体也具有这一性质，也不值得奇怪。除此以外，如果企图另外寻找任何一种光连续传播的运动方式，会发现没有哪种方式，在似乎是必须均匀行进方面，比弹性方式更合适。因为，假如光运动随着参与传送的物质越多，成比例地变得越慢，光在离开光源后就不可能经过遥远距离而保持其巨大的速度。除非假设“以太”物质的弹性，它的微粒才会具有一样迅速恢复原状的性质，而不论它们是否或强或弱地被推开。因此，光将总是依照同一速度传播。

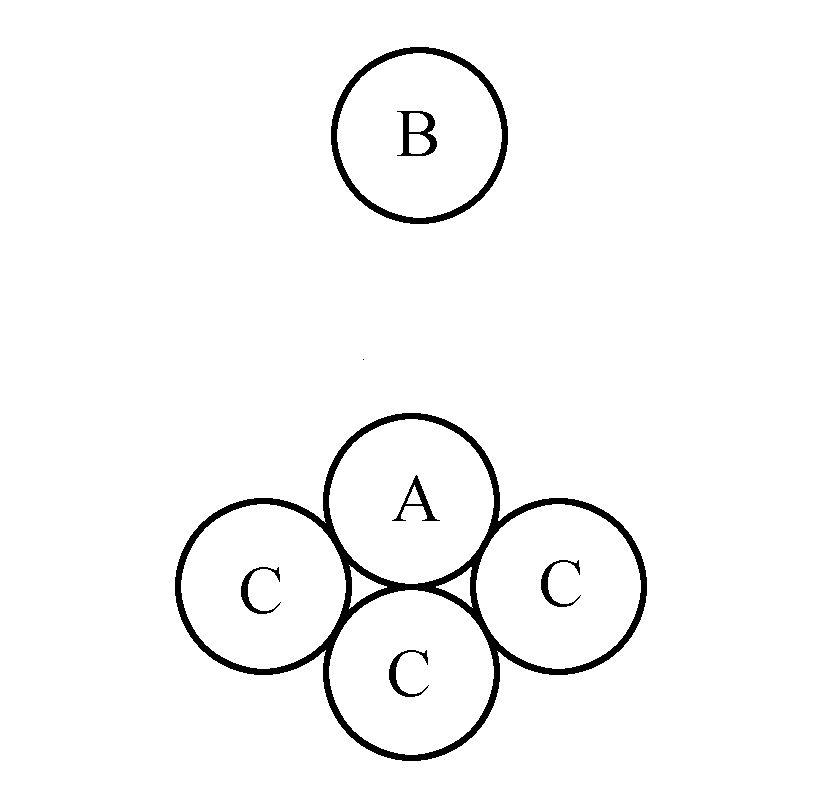图3

必须知道，尽管“以太”微粒不是排成一条直线，像我们举例中的那样，而是混乱的，因而它们中的任何一个都与另外几个相切。这不影响“以太”微粒发送和向前传播它们的运动。关于这方面，有必要值得再提一下一个经过实验证实了的可用于这种传播的运动定律。这个定律是，当一个球，譬如这里的A，与其他几个相同的球CCC相切时，如果它被另一个球B撞击，使它给所有与之相切的球CCC都施加一个推力，把它的运动整个都发送给了它们，而后就像B球那样不动了（图3）。即使不假设“以太”微粒是球形的（在我看来，其实也用不着这么假设），也能很好地了解传递推力的这种性能不会不对上述的运动传播起作用。

大小相同似乎更加必要，否则根据我几年前发表的《碰撞定律》（Laws of Percussion），当运动从一个较小微粒向一个较大微粒传递时，应该存在运动的某种反冲。

无论如何，以后将会看到，对于光的传播，即要使传播更轻易和更有效，我们甚至也没有一点必要去作出大小相同这种假设。虽然在像光传播这样重要的问题中，作出“以太”微粒大小相同的假设，并没超出可能的范围，至少在大气层外似乎只传送太阳光和星光的浩瀚空间中是这样。

我在某种程度上已经指出，可以设想光以球面波连续传播，这一传播伴随一种在实验与天体观测中所要求的巨大速度。在这里，或许要进一步指出，尽管假定了微粒作连续运动（关于这一点有很多理由），并不妨碍波的连续传播；因为传播并不在于那些微粒的传送，而只在于一种不可避免向它们周围传递的小的扰动，不管施加在它们上面引起位置改变的是什么运动。

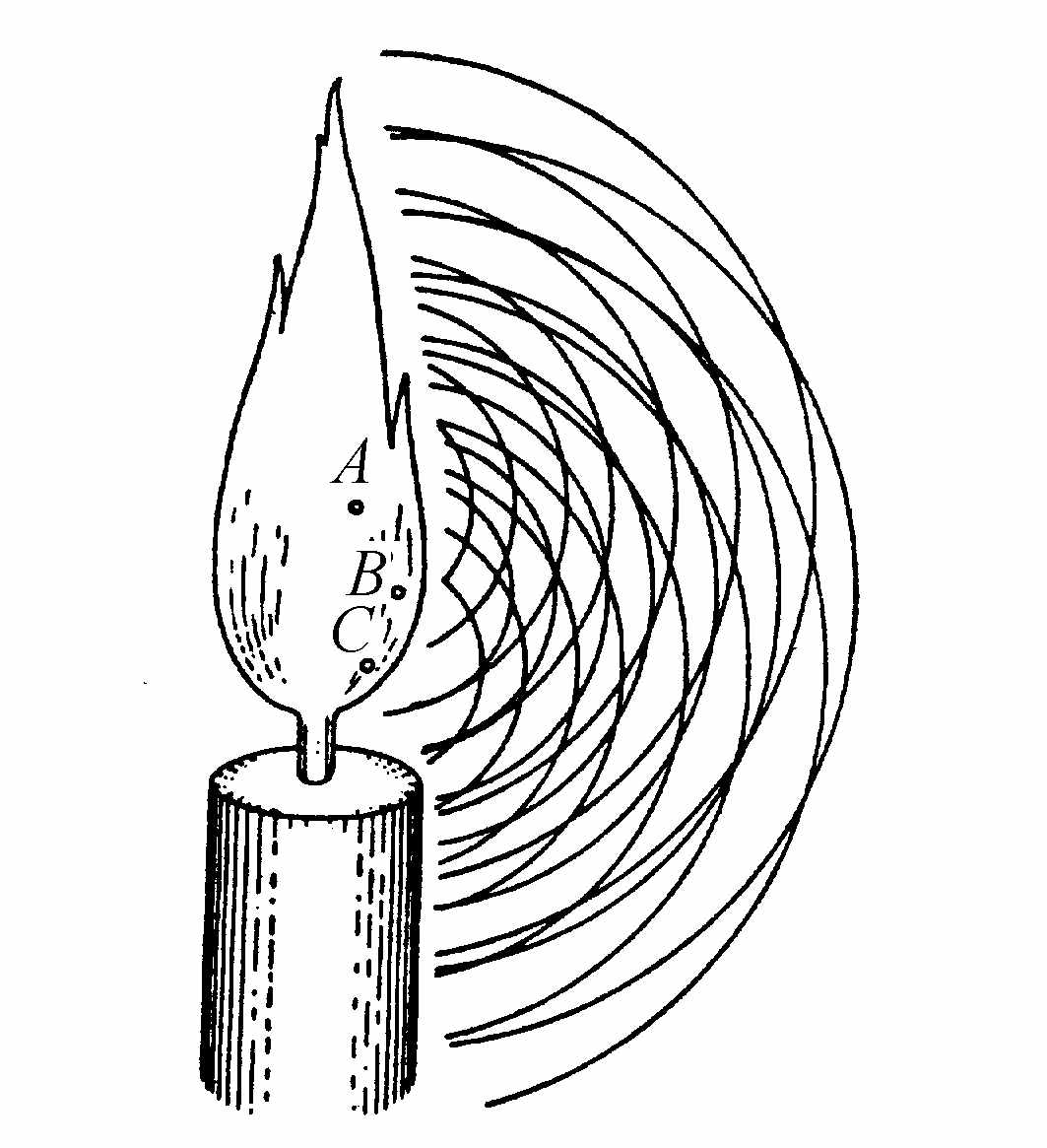图4

但是，我们还是有必要更具体地研究这些波的起源，以及它们的传播方式。首先，依据我们刚刚所作的有关光产生的论述，太阳、蜡烛或燃烧的煤这样的光亮物体上面每一个小区域，都能以该区域为中心产生其本身的波。于是，在蜡烛的火焰中标出了点A、B、C，分别以这些点为中心作出的同心圆就表示来自它们的波。并且，对于火焰表面以及内部的每一点，都必须这样来设想（图4）。

不过由于这些波的中心的振动不具有规则的次序，所以不能假定这些波本身以相等的距离一个接一个；假若距离像图中所标出的那样，与其用以表示来自同一中心的几个波，不如表示在相等的时间间隔同一个波的行进。

终归不必认为这种互不干扰互不抵消的数量巨大的波不可想象，同一种物质微粒可以适用于来自不同方向，甚至相反方向的许多波是确定无疑的，不仅在它被一次紧接着一次的撞击时是这样，而且对于同时施加在它上面的撞击也是这样。之所以能这样是因为运动的传播是连续的。这一点可以参照上述的一列相同的硬球来证明。如果在同一时刻，从相反的两边朝这列球撞来两个一样的球A和D，将会看到，它们中的每一个都以在撞击时同样的速度反弹回来，但整列球依然保持在原来位置上，尽管运动已经沿着它们传递了两次。如果这两个相反的运动正好在中间的球B或者另外某一个球C上相遇，这个球的两边将像弹簧一样伸缩，并由此在同一时刻内传递这两种运动（图5）。

图5

但是，一开始就显得十分奇怪甚至不可相信的一点是，由如此小的运动和微粒产生的波动竟能传播如此无限遥远，例如从太阳或星星到我们这里这么远。因为这些波的强度必定随着离开其波源而成比例地减弱，以至于每个波的作用将无疑不能单个使我们的视觉觉察到。不过考虑一下由遥远的光亮物体发出的无穷多个波是怎样组合得看起来仅为一个波，尽管它们来自这个物体上的不同点，这个波当然就有足够的强度能观察得到，就不会再感到奇怪了。于是，这些在同一时刻一个大得像太阳一样的固定的星体产生的无穷多个波，实际上构成一个单一的波，可能有足够的强度对我们的眼睛产生影响。此外，在可以想象的最小时间内，每个亮点通过撞击“以太”的那些微粒的频繁振动发出成千的波，这使它们的效应更加明显。

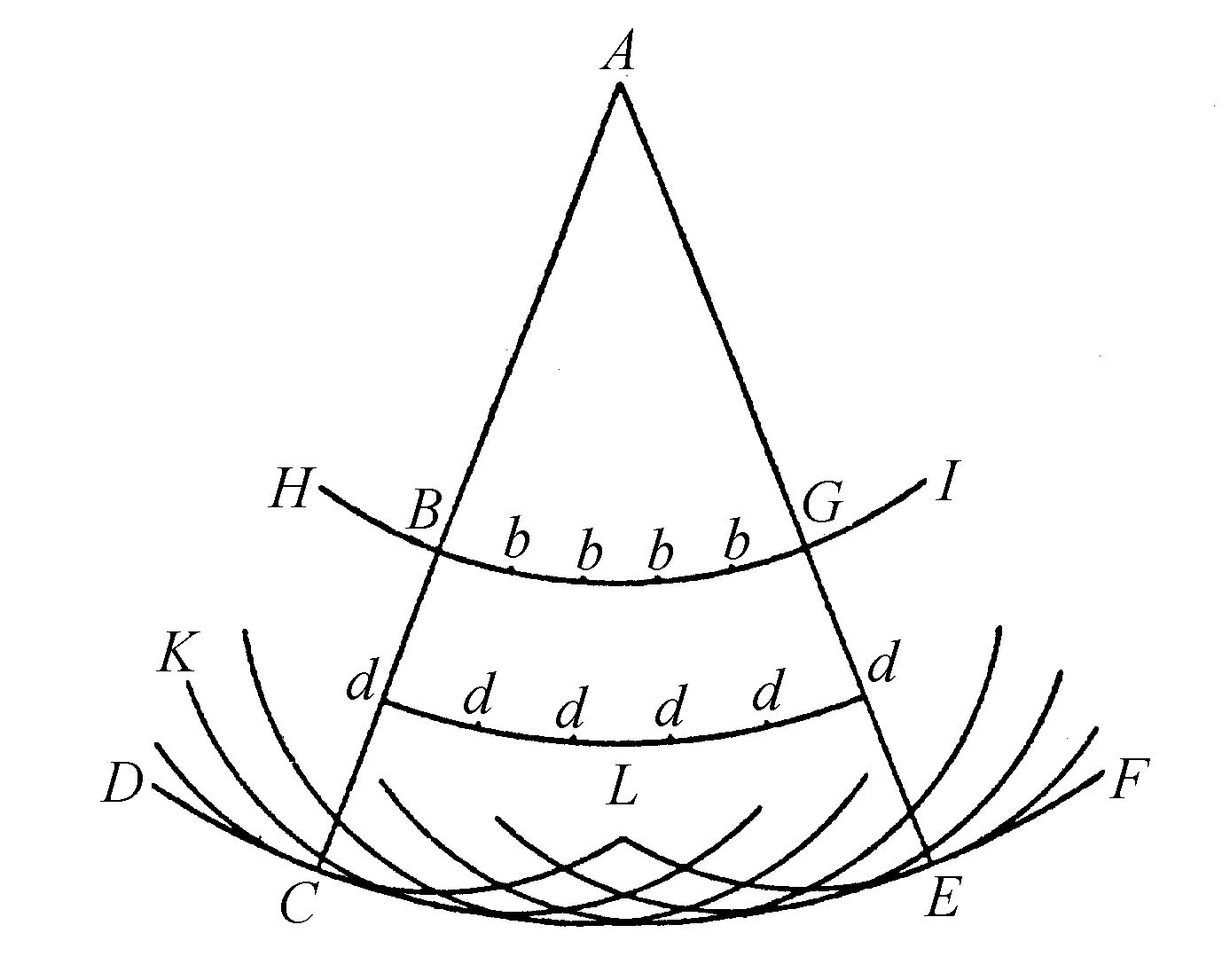图6

关于这些波的发射还有另外一种见解，传播波的物质的每一个微粒，应当不仅朝沿亮点出发的直线上的下一个微粒传递其运动，而且必定朝所有与它相邻和背向运动的微粒传递。因此可以得出，围绕每一个微粒，都有一个以该微粒为中心的波产生。如图6所示，若DCF是以亮点A为中心发出的波，在球DCF内的微粒B发出其分波为KCL，它将在由A发出的主波到达DCF的同时，与波DCF在C点相遇。显然，波KCL上的只有区域C才与波DCF相遇，即只在AB的联线上相遇。同样，球DCF内的其他微粒，譬如bb、dd等，也会产生它们自己的波。不过这些波中的每一个单独与波DCF相比起来，可能是极其微弱的，波DCF是由所有那些波的离中心A点最远的表面部分组成的。另外看到，波DCF决定于由A点出发的运动在一定的时间间隔内所通过的距离，虽然在它包围的空间中存在有不与球DCF相邻的那些分波部分，DCF这个波之外却没有运动。所有这一切似乎不应当伴随过于细致或微妙的差别，因为在后面我们将看到，光的性质及其反射与折射所具有的一切属性，原则上都能通过这一方法作出解释。对于至今已着手研究光波的那些人而言，这一切都是鲜为人知的。他们当中有胡克（Hooke）先生，在他的《显微术》（Micrangraphia）中作了研究，还有法迪斯（Fardies）神父，他在一篇论文中已经试图利用这些波来证实反射和折射的效应。他曾让我阅读过这篇论文的一部分，由于他不久后去世而没有完成这篇论文。不过我刚才所作论述的要点，在他的论证中是没有的；而且他对其他问题的观点也与我非常不同，如果他的文章被保存下来，将来有一天会看到这一点。

我们接着讨论光的性质。我们首先注意到。波的每一个部分都应当这样传播，使其末端总是落在由亮点出发的两条直线之间。于是，以亮点A为中心的波的BG部分，将传播到由直线ABC和AGE所夹的弧CE上。因为，尽管包含在CAE范围内的微粒所产生的分波也能传播到这个范围之外，像它们正好都传播到其公切圆周CE上那样，它们也不会同一时刻凑合成运动被限制的一个波。

因此人们明白，至少在光线不被反射或屈折时，光为什么只沿直线传播，结果除非在从光源到物体的路径畅通之外，光就照不到该物体。例如，如果有一个被不透明物体BH和GI限制的开口BG，正如以上所揭示的那样，由A点出发的光波将总是被直线AC与AE所限制；而传播到ACE范围之外的分波微弱到以至于不能在那里发亮。

无论我们把开口BG做得多么小，总有同样的理由使得那里的光在直线之间穿过，因为这个开口总是大得足以包含大量由难以想象小的“以太”物质微粒，所以看起来光波的每一个小部分必定沿着从亮点出发的直线行进。那么，这样一来，我们可以把光线当做直线。

此外，通过以上有关分波微弱的讨论，可以看出“以太”微粒不必要一样大，尽管一样大小更方便于运动的传播。事实上，在与较大的微粒撞击时，不一样大的微粒随着它的一部分运动而反弹，但这只是产生了一些背向亮点的不能发光的某些分波，而不是像CE那样由许多波组合而成的一个波。

光波的另外一个性质，也是最不可思议的性质，是来自不同的或者甚至相对方向的光波，能够毫无阻碍地相互穿过。由此也可以得出，一群旁观者可以在同一时刻通过同一开口看到不同的物体。而且两个人可以同时看到对方的眼睛。依据对光的作用所作的解释，光在相互穿过时是怎样不相互破坏或者不相互干扰，这些我已经提到过的效应就很容易想象了。依我看来，如果遵循笛卡儿的观点，认为光只是达到运动的连续压力，这些效应就完全不容易解释。因为这个压力不可能同时从两个相反方向，对两个没有互相接近趋向的物体施加作用。因而，就不可能理解我刚才所说的现象，即两个人能互相看到对方的眼睛，或者两个火把能互相照亮对方。

————————————————————

(1) 法国旧制长度单位，1突阿斯相当于1.949米。——编者

(2) 长度单位，1里格约合3海里。——编者