附录Ⅱ 等腰三角形底角相等的定理
这篇附录是我的论文“等腰三角形底角相等的定理 ”(Über den Satz von der Gleich-heit der Basiswinkel im gleichschenkligen Dreieck) (1) 的修正稿,它说明这个定理在平面欧几里得几何 中的作用。
这里假设下面的公理:
Ⅰ.平面关联公理,即公理Ⅰ1~3 ;
Ⅱ.顺序公理;
Ⅲ.下述的合同公理:
未改变形式的公理Ⅲ1~4 ,较狭形式的三角形合同公理Ⅲ5 ,即只需要具有相同周向 的三角形的情况。在本书,依平面几何中三角形的周向的规定系在它们间根据“右 ”和“左 ”来区分。从一直线的右侧和左侧的定义,立即说明任何角可以用唯一的方法来确定它的一条边作为右侧边,另一边则为左侧边,亦即:按照位置与方向,角的右侧边系指位于角的另一边所在直线的右侧,角之左侧边系指位于角的另一边所在直线的左侧。两角的右侧边称为关于这两个角具有相同位置 ,关于两角的左侧边也是同样的。
三角形合同公理的较狭形式可叙述如下:
 如果在两个三角形ABC 和A ′B ′C ′中,合同式AB ≡A ′B ′,AC ≡A ′C′及
如果在两个三角形ABC 和A ′B ′C ′中,合同式AB ≡A ′B ′,AC ≡A ′C′及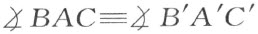 成立,则合同式
成立,则合同式
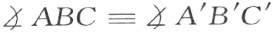
也成立,假如AB 及A ′B ′分别是两角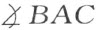 及
及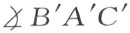 具有相同位置的边。
具有相同位置的边。
从较广形式的公理Ⅲ5 及公理Ⅲ4 的第二部分可立即得出“底角定理”。反过来,较广形式的公理Ⅲ3 可以借用上面所提到的公理Ⅰ,Ⅱ,Ⅲ1~4 ,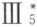 ,底角定理和下面的两公理来证明:
,底角定理和下面的两公理来证明:
Ⅲ6 . 如果角 和角
和角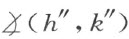 均合同于角
均合同于角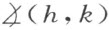 ,则角
,则角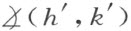 也合同于角
也合同于角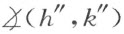 ,
,
这个公理的陈述借助于较广形式的公理Ⅲ5 ,在本书上作为定理19已经证明。
Ⅲ7 . 自角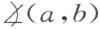 的顶点引二射线c 和d 均位于这个角的内部,则角
的顶点引二射线c 和d 均位于这个角的内部,则角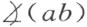 将不合同于
将不合同于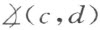 。
。
借用上述公理以及底角定理。关于公理Ⅲ5 的证明这里从略 (2) 。
Ⅳ.平行公理这里可采取较弱形式Ⅳ。
Ⅴ.下面的连续公理:
Ⅴ1 .阿基米德公理Ⅴ1 。
(Ⅴ2 。此处不用完备性公理Ⅴ2 。)
Ⅴ3 .(邻域公理)已知任意线段AB ,则存在一个三角形,于其内部不可能找出一线段与AB 合同。
这个公理可用较广形式的三角形合同公理Ⅲ5 来证明。这个证明建立在从定理11及定理23所导出的定理“三角形两边之和大于第三边”之上。
下面的结果是正确的,其证明从略 (3) 。
从前面所引入的公理Ⅰ~Ⅴ可以证明底角定理(定理11),因之也可以证明较广形式的三角形的合同公理。
于是就出现下面的问题,从较狭形式的三角形的合同公理不用连续公理Ⅴ1 和Ⅴ3 是否也能证明较广形式的三角形的合同公理。下面的研究将指出阿基米德公理不能去掉,甚至在比例论的定理成立下,邻域公理也不能去掉。 依我看来,在我随后所建立的种种几何学里将阐明新的见解,就是关于等腰三角形的定理和平面几何的其他初等定理,特别是和面积论中定理的逻辑联系。
如果t 是参数,α 是任一个具有有限项或无限项的表示式,
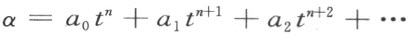
其中a 0 (≠0),a 1 ,a 2 ,…表示任意实数,又n 为任意整有理数 。今就形如α 的表示式的全体连同0在内加以考虑。当它们适合下列公约后即可作为§13意义上的一个复数系T 。也就是在数系T 里的任何数相加、相减、相乘和相除与在通常绝对收敛幂级数里一样,而这个幂级数是按照变量t 的升幂排列的。所得的和、差、积、商结果仍是形如α 的表示式,因而仍是复数系T 中的数。根据T 中α 表示式的首系数a 0 <0或>0而分别将α 称为<0或>0。已知复数系T 中任意两数α ,β ,则依据α -β <0或>0而分别称为α <β 或α >β 。据此,显然可见§13中的规律1~16均成立,然而对数系T 作§13中的第17条阿基米德公理并不成立。这是因为不管正实数A 选的如何大,总有A t <1。故复数系T 是非阿基米德数系。
。今就形如α 的表示式的全体连同0在内加以考虑。当它们适合下列公约后即可作为§13意义上的一个复数系T 。也就是在数系T 里的任何数相加、相减、相乘和相除与在通常绝对收敛幂级数里一样,而这个幂级数是按照变量t 的升幂排列的。所得的和、差、积、商结果仍是形如α 的表示式,因而仍是复数系T 中的数。根据T 中α 表示式的首系数a 0 <0或>0而分别将α 称为<0或>0。已知复数系T 中任意两数α ,β ,则依据α -β <0或>0而分别称为α <β 或α >β 。据此,显然可见§13中的规律1~16均成立,然而对数系T 作§13中的第17条阿基米德公理并不成立。这是因为不管正实数A 选的如何大,总有A t <1。故复数系T 是非阿基米德数系。
如果τ 是形如
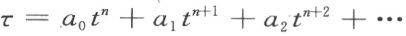
的一个表示式,其中a 0 (≠0),a 1 ,a 2 ,…是任意实数,且指数n 是t 的最低次正幂,则τ 称为复数系T 的一个无限小数。
任意形如
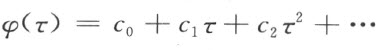
的幂级数,其中c 0 ,c 1 ,c 2 ,…是任意实数且τ 是数系T 的无限小数,仍是数系T 中的一个数。诚然,它可以按照参数t 的增幂排列,其中每一个系数可由实数经过有限次运算而得出。
再者,设α 和β 是数系T 中任意两数,则
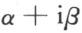
叫做复数系T 中的一个虚数,其中i是虚单位,亦即i2 =1,且α +iβ =α ′+iβ ′系指α =α ′,β=β ′。
如果无限小数τ 的函数sinτ ,cosτ ,e τ ,e iτ 是由幂级数来规定的,则函数值分别是数系T 中的数或是这系中的虚数。现在设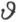 是一个实数,则T 中的
是一个实数,则T 中的
 能够用下面的公式来规定:
能够用下面的公式来规定:

从这些定义,我们将得到熟知的关系
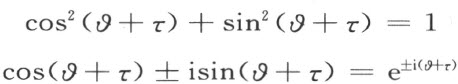
现在可以借助复数系T 建立一种几何学如下:
将数系T 中一对数(x ,y )作为一点,并且T 中任意三数比(u :v :w )作为一条直线,其中u ,v 不同时是零。而且令方程

表示点(x ,y )在直线(u :v :w )上。
在复数系里按照已知的方法所建立的平面几何适合§13的1—16规律,则如同§9所指出的也必适合公理Ⅰ1~3 和Ⅳ。
容易看出,一直线也可以由它上面的一点(x 0 ,y 0 )和两个均不是零的数α ,β 的比来确定。方程
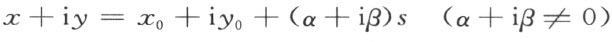
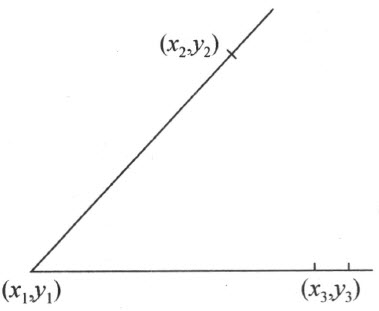
其中s 是数系T 中任意数,它将表示点(x ,y )与已知直线相结合的特征。设直线上的点按参数s 的大小排列,则从已知直线上的点(x 0 ,y 0 )所引的两条半线将分别由辅助条件s >0或s <0来决定。设参数值s a 和s b (>s a )对应着一直线上的两点A 和B ,则线段AB 可由这直线的方程和辅助条件s a ≤s ≤s b 来表示。此时公理Ⅱ1—3 成立。为了使公理Ⅱ4 也成立,我们给出下面的公约:点(x 3 ,y 3 )位于两点(x 1 ,y 1 )和(x 2 ,y 2 )所定直线的一侧或另一侧,系依行列式
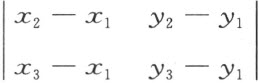
的符号分别为正或负而定。容易使人确信,对于上面所规定的关于在一直线侧的定义并不依赖于两点(x 1 ,y 1 )和(x 2 ,y 2 )的选择,并且它与前面所给关于侧的定义是一致的。
关于合同的定义,取变换
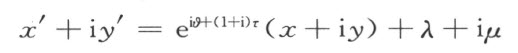
可以简单地写成下列形式
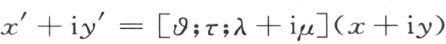
其中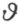 是任意实数,τ 是数系T 中任意无限小数,又λ ,μ 表示数系T 中任意两数。这个形式的变换叫做合同映射,λ ,μ 均是零的合同映射叫做关于(0,0)的一个旋转。
是任意实数,τ 是数系T 中任意无限小数,又λ ,μ 表示数系T 中任意两数。这个形式的变换叫做合同映射,λ ,μ 均是零的合同映射叫做关于(0,0)的一个旋转。
这些合同映射的集合形成一群,亦即具有下面的四条性质:
1.存在一个合同映射 [0,0;0]使所有点不动 ,即
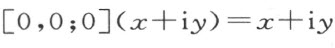
2.陆续施行两个合同映射 ,则其结果仍是一个合同映射 。

对每个合同映射存在它的一个反逆:

这个性质是性质1,2,4,5的推论。
合同映射这一运算适合结合律 ,亦即 ,给定三个合同映射 K 1 ,K 2 ,K 3 ,且按照 2,陆续施行 K 1 ,K 2 所得的合同映射用 K 2 K 1 来表示 ,则
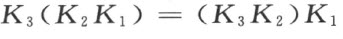
永成立 。
除此以外,下面再指出合同映射的一些性质:
3.一个点还能映射成这种几何的一个点 。
数系T 中的一个数偶x ,y 经过合同映射仍映射成数系T 中的一个数偶x ′,y ′。
4.一直线仍映射成一直线 ,且其上点的顺序不变 。
我们容易推出下列关系

其中由于指数函数永不为零,自α +iβ ≠0总有 。
。
作为直接结果:两个不同的点仍映射成两个不同点。
5.恰有一个合同映射使已知射线 h 映射成已知射线 h ′。
如果h 的方程是

h ′的方程是
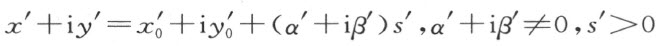
将h 映射成h ′的一个合同映射 首先要使h 的射出点x 0 +iy 0 映射成h ′的射出点
首先要使h 的射出点x 0 +iy 0 映射成h ′的射出点
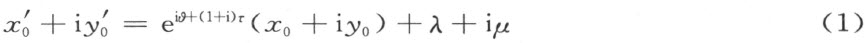
再者,对s 的每一个正值,必须给出s ′的一个正值,而使
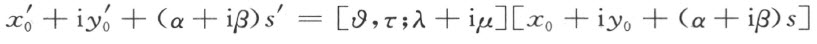
因此有
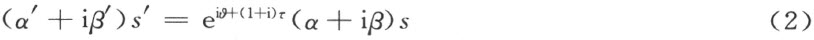
反过来,适合方程(1)和(2)的每个合同映射必将h 映射成h ′。
将方程(2)用其共轭式来除即得

设
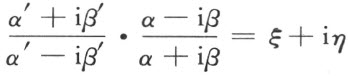
我们得到
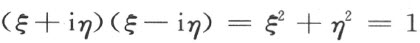
其中ξ 和η 都是数系T 中的数,它们均是参数t 的幂级数。由比较系数得知后一方程没有参数t 的负幂项。而且它们可以写作
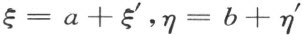
其中a ,b 是普通实数,且ξ ′,η ′表示T 中无限小数,并且具有关系

由方程(3)得
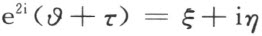
借用所给三角函数的定义可得下述形式:
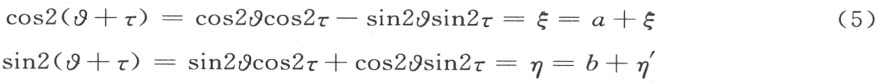
在这两等式中当τ 有相同的幂时,则将系数看做是相同的,因此可得等式
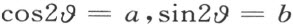
以方程a 2 +b 2 =1为基础,实数 在π的整倍数范围内唯一确定。将
在π的整倍数范围内唯一确定。将 代入方程(5)得到关系式
代入方程(5)得到关系式

因为由方程组(4)两式右端的平方和等于1,所以无限小数τ 唯一确定。从比较后两方程中之一的系数即可计算。
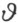 既然在π 的整倍数范围内来确定,于是因数
既然在π 的整倍数范围内来确定,于是因数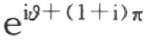 仅在正负两个符号内确定。容易看出,仅对两个符号中之一,在方程(2)中一个正的s 就得出一个正的s ′。因此实数
仅在正负两个符号内确定。容易看出,仅对两个符号中之一,在方程(2)中一个正的s 就得出一个正的s ′。因此实数 在2π的整倍数范围内来确定。将
在2π的整倍数范围内来确定。将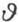 ,τ 的一对值代入方程(1)也唯一确定T 中的一对数λ 和μ ,最后,自方程(1)和(3),及所求出的值
,τ 的一对值代入方程(1)也唯一确定T 中的一对数λ 和μ ,最后,自方程(1)和(3),及所求出的值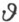 ,τ ,λ ,μ 可以看出与半线h 及h ′的表示形式无关。
,τ ,λ ,μ 可以看出与半线h 及h ′的表示形式无关。
6.任意两点 A 和 B ,永有一合同映射使 A 映射成 B ,B 映射成 A 。
如果两点A 和B 的坐标分别是x 1 ,y 1 和x 2 ,y 2 ,则合同映射
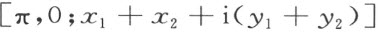
即为所求。
7.如果一个合同映射将半线 h 映射成 h ′,而且将 h 右侧或左侧的一点 P 映射成点 P ′,则 P ′也将分别在 h ′的右侧或左侧 。简言之 ,P 和 P ′分别关于 h 和 h ′具有相同位置 。
其次将证明两个行列式
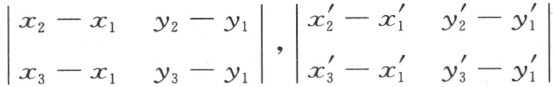
具有相同符号,当且仅当点(x 3 ,y 3 )和(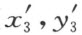 )分别关于(x 1 ,y 1 )和(x 2 ,y 2 )以及(
)分别关于(x 1 ,y 1 )和(x 2 ,y 2 )以及(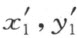 )和(
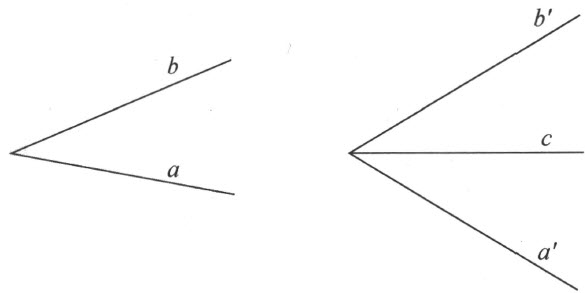
)和( )所决定的有向直线具有相同位置。其次,所给“右”和“左”的定义可以得出点(x 3 ,y 3 )和(x 2 ,y 2 )将分别关于(x 1 ,y 1 )和(x 2 ,y 2 )以及(x 1 ,y 1 )和(x 3 ,y 3 )所决定的有向直线不具有相同位置(附图2)。事实上,所相应的行列式仅有符号之差。这个断言由下列事实得出:即一直线侧的定义借助于已知行列式的符号适合于前面所给出的关于直线侧的性质。
)所决定的有向直线具有相同位置。其次,所给“右”和“左”的定义可以得出点(x 3 ,y 3 )和(x 2 ,y 2 )将分别关于(x 1 ,y 1 )和(x 2 ,y 2 )以及(x 1 ,y 1 )和(x 3 ,y 3 )所决定的有向直线不具有相同位置(附图2)。事实上,所相应的行列式仅有符号之差。这个断言由下列事实得出:即一直线侧的定义借助于已知行列式的符号适合于前面所给出的关于直线侧的性质。
附图 2
假如行列式
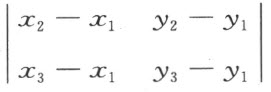
的符号经过合同映射不变,则性质7立即证明。由于这个行列式仅与商

的虚部相差一个正因子,故直接看出这个商在合同映射下不变。
现在已知:一个线段与另一个线段合同,当而且仅当存在一个合同映射使第一个映射成第二个,又一个角与另一个角合同,当而且仅当存在一个合同映射使第一个映射成第二个。
下面将要证明:
若所假设的合同映射具有性质 1~7,则上面关于线段与角的合同定义 ,满足公理 Ⅲ1~6 。
公理Ⅲ1 是性质5的直接推论。
公理Ⅲ2 的正确性可用下列方式来证明:设合同映射K 1 和K 2 将线段A ′B ′和A ″B ″分别映射成AB 。自性质1,2,4,5推出合同映射K 2 存在一个逆合同映射 。由性质2存在合同映射
。由性质2存在合同映射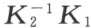 使线段A ′B ′映射成A ″B ″。
使线段A ′B ′映射成A ″B ″。
公理Ⅲ6 的正确性可用类似的方法来证明。
现在将要证明:如果线段AB 与线段A ′B ′合同,则合同映射K 将使半线AB 映射成半线A ′B ′且使B 映射成B ′,设线段AB 和A ′B ′的合同由合同映射K 1 所建立。在K 1 将A 映射成A ′的情况下,则由性质4合同映射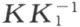 将半线A ′B ′映射到它自身,再由性质1和5可知它必是恒同映射。但在K 1 将A 映射成B ′的情况下,由性质6,存在映射K 2 使A 映射成B ,B 映射成A 。合同映射
将半线A ′B ′映射到它自身,再由性质1和5可知它必是恒同映射。但在K 1 将A 映射成B ′的情况下,由性质6,存在映射K 2 使A 映射成B ,B 映射成A 。合同映射 将使半线A ′B ′映射到它自身,因而是恒同映射。
将使半线A ′B ′映射到它自身,因而是恒同映射。
从这里所证的结果以及性质4和5立即推出公理Ⅲ3 的正确性,并且从这些结果以及性质4,5和7也立即可以推出公理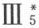 的正确性。
的正确性。
最后,公理Ⅲ4 的正确性可作如下证明:如果给出一个角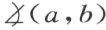 及一半线c ,则由性质5恰存在合同映射K 1 及K 2 分别使a 映射成c ,b 映射成c 。考虑合同映射
及一半线c ,则由性质5恰存在合同映射K 1 及K 2 分别使a 映射成c ,b 映射成c 。考虑合同映射 ,由性质4可以看出K 1 将b 映射成与c 不同的半线b ′,同理K 2 将半线a 映射成与c 不同的半线a ′。合同映射
,由性质4可以看出K 1 将b 映射成与c 不同的半线b ′,同理K 2 将半线a 映射成与c 不同的半线a ′。合同映射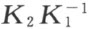 将使c 映射成a ′,b ′映射成c 。由性质7,a ′和b ′将位于c 的异侧。于是公理Ⅲ4 的第一部分得以证明。第二部分则是性质1的直接推论。
将使c 映射成a ′,b ′映射成c 。由性质7,a ′和b ′将位于c 的异侧。于是公理Ⅲ4 的第一部分得以证明。第二部分则是性质1的直接推论。
从下面的考虑,公理Ⅲ7 的正确性是显然的。从O (0,0)点所射出的半线可以由形如
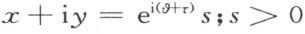
附图 3
的方程来表示,且它可由正x 轴旋转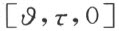 而得到。自O 向上半平面所射出的两半线中,我们可以看出,具有较小和
而得到。自O 向上半平面所射出的两半线中,我们可以看出,具有较小和 的一条半线将位于另一条半线及正x 轴之间。
的一条半线将位于另一条半线及正x 轴之间。
如果一个角的右侧边h 与正x 轴重合,其左侧边k 的方程是
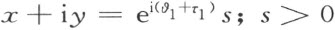
在此角的内部,自O ′作半线h ′,于是恰好存在一个合同映射使h 映射成h ′,此即一个旋转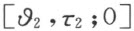 。它将k 映射成半线k ′,它的方程是
。它将k 映射成半线k ′,它的方程是
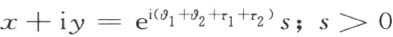
因为

k ′将不在 的内部。
的内部。
邻域公理Ⅴ3 的正确性可用下列方式证明。利用第二合同定理及公理Ⅳ容易证明:对三角形内部的每一个线段可以找到自一个顶点射出的一个合同线段,它或者在三角形的一边上或者在其内部。
自公理Ⅲ1 ,对一已知线段AB 恰存在一个自O 射出的一个线段OB ′,它具有正x 轴的方向,且与AB 合同。令B ′的横坐标β 表示线段AB 的长度,即
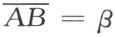
今考虑以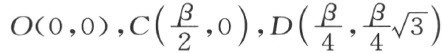 为顶点的三角形。它必是等边三角形且其内角相等,这可以由合同映射
为顶点的三角形。它必是等边三角形且其内角相等,这可以由合同映射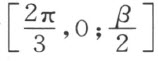 将O 映射成C ,C 映射成D ,D 映射成O 来证明。自O 射出自由端点为F 的一个线段,它位于
将O 映射成C ,C 映射成D ,D 映射成O 来证明。自O 射出自由端点为F 的一个线段,它位于 的一边上或其内部且与AB 合同,此点可用
的一边上或其内部且与AB 合同,此点可用

来表示。然而,因此形式所表示的所有点将位于不含O 点的直线C 的一侧,这可将O 及F 的坐标代入CD 所表示的行列式
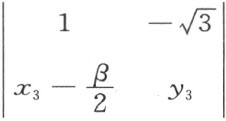
看出。这样就证明了在三角形OCD 中不存在与AB 合同的线段。
这些可归纳于下:
在所给的几何里 ,前面所给的关于通常平面几何的全部公理除阿基米德公理Ⅴ 1 以外 ,均属正确 ;此时合同公理必须采取较狭形式的 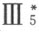 。
。
再者,下面定理成立:
每个角能够平分,且直角存在。
证明自O 射出的每个角,能够平分便足够了。设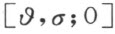 为使角的右边映射到左边的旋转。旋转
为使角的右边映射到左边的旋转。旋转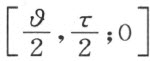 将使角的右边映射到它的角平分线上。
将使角的右边映射到它的角平分线上。
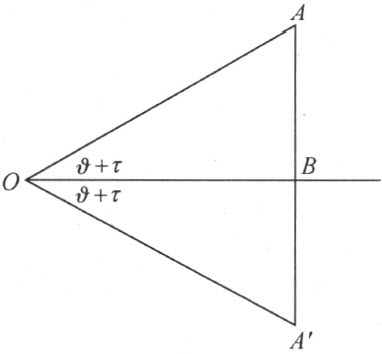
考虑旋转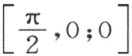 ,即可得知直角的存在。现在我们用下列方法引出关于直线a 的反射的概念。自任一点A 到任一直线a 作垂线(附图4),垂足是B ,且延长到点A ′使线段BA ′合同于AB ,则点A ′称为点A 的象点。首先将坐标为α >0,β >0的点A 关于正x 轴作反射。设半线OA 和正x 轴间的角
,即可得知直角的存在。现在我们用下列方法引出关于直线a 的反射的概念。自任一点A 到任一直线a 作垂线(附图4),垂足是B ,且延长到点A ′使线段BA ′合同于AB ,则点A ′称为点A 的象点。首先将坐标为α >0,β >0的点A 关于正x 轴作反射。设半线OA 和正x 轴间的角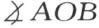 等于
等于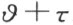 。再者位于x 轴上的一点x =γ 经旋转角为
。再者位于x 轴上的一点x =γ 经旋转角为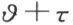 +τ 的旋转映射到A ,则有
+τ 的旋转映射到A ,则有
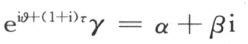
附图 4
点A 关于x 轴的反射点A ′的坐标是α ,-β 。若旋转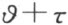 ,将点A ′映射到一点,以复数表示为
,将点A ′映射到一点,以复数表示为

即此点位于正x 轴上。因此角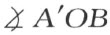 等于
等于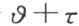 ,也就是等于角
,也就是等于角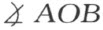 。这个结果可叙述如下:
。这个结果可叙述如下:
如果在两个有对称位置的直角三角形中两条直角边对应相等,则它们所对斜边上的一对对应角亦必相等。
同时我们得到更普遍的定理:
在一个图形的反射图形中的角和原图形的对应角相等。
在所给的几何里,规定直线用一次方程来表示则不难导出比例论的基本定理(定理42)和巴斯噶定理(定理40)。自此得出:
在所给的几何里,比例论是正确的,并且仿射几何中的所有定理也都正确(参看§35)。
由于公理Ⅲ7 的正确性,能够证明所给几何中的角可以用唯一的方法按照其数值 来比较。
利用这个结果,能够证明三角形的外角定理(定理22),这是因为在所给的几何里,对顶角永远相等,本书的证明可以移放到这里。从这个结果,在我们的几何里,两角之和可以唯一规定,借公理Ⅳ,我们即得关于三角形的角和定理(定理31)。
现在我们将接近于基本问题:即在给定的几何里,等腰三角形底角相等的定理能否成立(定理11)。
从这个定理以及外角定理可得关于底角定理的逆命题的一个间接证法,并借助于所熟知的欧几里得定理:在每个三角形中,两边之和大于第三边。然而在所给的几何中这两个定理均不成立,因而同时将证明底角定理是不成立的。
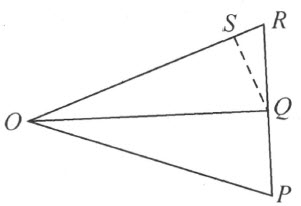
考虑三角形OQP (附图5),其顶点具有坐标0,0;cost ,0;cost ,-sint ,分别利用合同映射[0,t ;0]和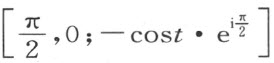 可得线段OP 与QP 的长度。
可得线段OP 与QP 的长度。
附图 5
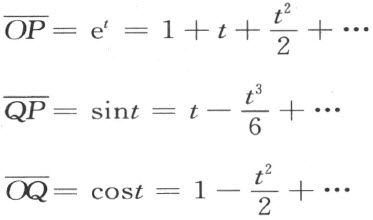
从数系T 中顺序的定义可以看出

于是任意三角形两边之和大于第三边的定理在我们的几何里不成立 。
从这里看出这个定理基本地依赖于广义的三角形合同公理。
利用这个结果同时得出:
在所给的几何里,关于等腰三角形的定理不成立,因之广义的三角形合同公理也就不能成立。
同时关于等腰三角形底角定理的逆命题也不成立,这可由三角形OPR (附图5)的例子直接得出。三角形OPR 的顶点R 是点P 关于直线OQ 的反射象,即点R 具有坐标cost ,sint 。那么由前面所证明的定理,

尽管如此,边OP 和OR 却不能互相合同。经过旋转[0,-t ;0],线段OR 的长度由计算得
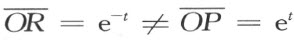
由此我们看出:具有对称位置和一公共直角边的两个直角三角形,一般说来,其斜边是不同的。因此,关于直线的反射来说,一线段的象并不必须等于原图形上的原线段。
正如罗赛曼 (4) (W. Rosemann)曾经证明过的:在所给的几何里,关于合同三角形的第三个定理(定理18)甚至对具有相同位置的三角形在狭义形式下也不能成立。 为了证明这个结论,首先取点 所形成的等边三角形,其次考虑点(附图6)
所形成的等边三角形,其次考虑点(附图6)


附图 6
因为合同映射[0,t ;t ]将点D 映射到自身,而将点A 映射到点B 。这就看出了AD ≡BD ,并能确认点A 和B 在直线CD 的同侧。由此首先得出三角形ACD 和BCD ,对应边均相等,且占有相同位置,其次它们的对应角则均不能相等。
下面将讨论我们几何中多边形面积的欧几里得理论。这个理论建立在§20三角形面积 的度量概念上。三角形面积的度量等于底和高的乘积之半,而不依赖于它所采用三角形的哪一个边作为底边,它的证明,曾借助于将三角形合同公理应用到具有对称位置的三角形上。从本书的例中可以看出不用这公理的广义形式就不能证明这个问题。在三角形OQR 中,QR 是边OQ 上的高。利用合同映射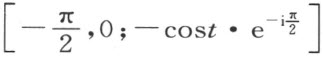 即得长度
即得长度
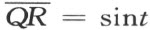
因为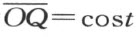 ,一方面就可得出面积数量是
,一方面就可得出面积数量是
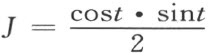
另一方面,计算Q 到OR 上的垂足S 而得
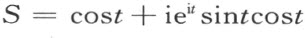
再利用合同映射
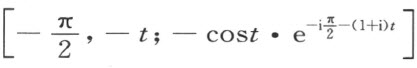
即得长度
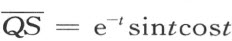
因为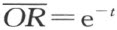 ,故又得面积
,故又得面积
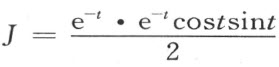
它确小于
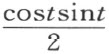
此时在没有广义形式的三角形合同公理Ⅲ5 下,面积的度量概念失去了意义,然而多角形剖分相等和多角形拼补相等 的概念恰如§18所定义的。于是可得恰如§19的定理46,两个等底和等高的三角形拼补相等 。
再者,可以看出于较狭义形式公理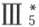 (5) 下,在每一线段上可作一正方形,即具有等边的长方形。于是在所给几何里 ,毕达哥拉斯定理也成立 ,这就是在任意直角三角形两直角边上 所作正方形的和与斜边上正方形拼补相等 ,这是由于在毕达哥拉斯定理的欧几里得的全部证明中只用到具有相同位置的三角形的合同性,因此只需要狭义形式的合同公理 (6) 。
(5) 下,在每一线段上可作一正方形,即具有等边的长方形。于是在所给几何里 ,毕达哥拉斯定理也成立 ,这就是在任意直角三角形两直角边上 所作正方形的和与斜边上正方形拼补相等 ,这是由于在毕达哥拉斯定理的欧几里得的全部证明中只用到具有相同位置的三角形的合同性,因此只需要狭义形式的合同公理 (6) 。
今将毕达哥拉斯定理用于的三角形OQP 和三角形OQR 上,借助定理43,我们得到在线段OP 和OQ 上所作的正方形拼补相等 ,然而这两线段 由上面的计算彼此并不相等 (附图7)。

附图 7
将这种情况和定理52相联系可以得出:两个等底的拼补三角形具有等高的欧几里得基本定理在我们的几何里也不成立 。
事实上,定理48在§20~§21中利用面积的概念在本质上已经证明了。
于是在所给的几何里得出如下结果:
甚至于假定比例论是正确的,而以较狭义的三角形合同公理作为欧几里得面积论的基础是不可能的。
因为在所给几何里,对熟知的直角三角形的直角边和斜边的关系,即普通几何里的毕达哥拉斯定理,都不成立。故这种几何称为非毕达哥拉斯几何 。
非毕达哥拉斯几何的主要结果可归纳如下:
如果采取狭义形式的三角形合同公理,及连续公理中仅邻域公理成立,甚至在假设比例论成立的情况下,等腰三角形底角相等的定理不能予以证明,欧几里得面积论也不能得出,甚至于三角形两边之和大于第三边的定理以及具有相同位置的两个三角形的第三合同公理都不是所给假定的必然结论。
现在我们建立另外一种非毕达哥拉斯几何 ,它与上面主要的不同是:阿基米德公理Ⅴ1 成立,但是邻域公理Ⅴ3 不成立。
这种几何系建立在实数所成的子域Q 上,这个子域是由数1及τ =tan1经过有限次加法ω 1 +ω 2 ,减法ω 1 -ω 2 ,乘法ω 1 ·ω 2 ,除法ω 1 :ω 2 (其中ω 2 ≠0)以及乘方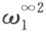 (7) 诸运算产生的。这里ω 1 和ω 2 表示由数1及τ 经过指出的五种运算所得到的数。为了从1和τ 得到数ω ,设将第一种运算作了n 1 次,第二种运算作了n 2 次,…,第五种运算作了n 5 次。于是域Q 的数ω 可用递增的和n 1 +n 2 +…+n 5 来表出。
(7) 诸运算产生的。这里ω 1 和ω 2 表示由数1及τ 经过指出的五种运算所得到的数。为了从1和τ 得到数ω ,设将第一种运算作了n 1 次,第二种运算作了n 2 次,…,第五种运算作了n 5 次。于是域Q 的数ω 可用递增的和n 1 +n 2 +…+n 5 来表出。
在这个数系上如同本书在数系T 上建立第一种非毕达哥拉斯几何的同样规约来建立一种平面几何。恰如那里,公理Ⅰ1~3 ,Ⅱ,Ⅳ的正确性在所给的几何里可由以下事实看出,于自然确定的顺序下,§13的所有运算1~16在Q 内成立。
在增加数∞所扩充的域Q 中的每个数ω ,存在无穷个数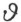 适合
适合
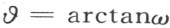
适合这个方程的数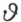 的全体形成一个域Θ ,它与Q 虽不完全相同,但与Q 同样是可数的。取Θ 的任一个可数子集,在其中存在第一个数,它不是π 的倍数,用
的全体形成一个域Θ ,它与Q 虽不完全相同,但与Q 同样是可数的。取Θ 的任一个可数子集,在其中存在第一个数,它不是π 的倍数,用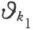 来表示。设Θ 中第一个数不能表示成
来表示。设Θ 中第一个数不能表示成

其中r ,r 1 是任意有理数。如果这样的数全然存在则用 来表示,以此类推,设Θ 中第一个数不能表示成
来表示,以此类推,设Θ 中第一个数不能表示成
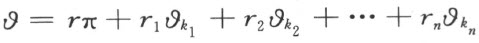
如果这样的数全然存在,则用 来表示。这样所定义的数列
来表示。这样所定义的数列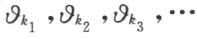 一定包含一项或者无限项。Θ 中每个数
一定包含一项或者无限项。Θ 中每个数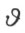 能唯一地 表示成
能唯一地 表示成
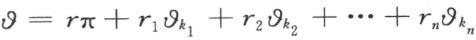
其中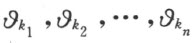 是上面所规定数列的首n 项,且
是上面所规定数列的首n 项,且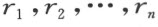 是任意有理数。
是任意有理数。
利用合同映射 ,正如本书第一种非毕达哥拉斯几何那样,我们规定线段与角的合同性,这里用形如
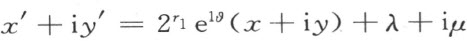
的每个变换表示合同映射,其中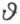 是Θ 中的一个数,在
是Θ 中的一个数,在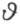 的表示式中,所出现的r 1 是一个有理数,并且λ ,μ 是Q 中任意数。
的表示式中,所出现的r 1 是一个有理数,并且λ ,μ 是Q 中任意数。
我们容易看出合同映射形成一个群。它具有本书所引入的性质1和2,性质3可由下列事实得出,即数
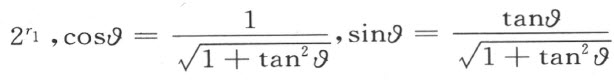
是域Q 中的数。性质5可由下面的方法得到:
这个证明类似于本书所作,将简化为从方程
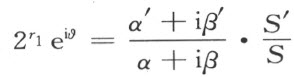
在2π的整倍数内确定Θ 中唯一的一个 。
。
将虚部以实部去除

从这个方程可以确定π的整倍数内数系Θ 中的数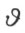 。如同第一种非毕氏几何,这种确定在2π整倍数内,性质4,6和7的推证恰如那里所证的一样。
。如同第一种非毕氏几何,这种确定在2π整倍数内,性质4,6和7的推证恰如那里所证的一样。
从已经证明的合同映射的七条性质,利用在本书所给的一般证明可以得到在所给几何中公理Ⅲ1~6 成立,与第一种非毕达哥拉斯几何方法类似,公理Ⅲ7 也成立。
借助顺序与合同的定义,由域Q 是实数域的子域的事实可推出阿基米德公理Ⅴ1 的正确性。
至于邻域公理Ⅴ3 不成立可由下面的方法来证明:对于每个三角形能够找到一个合同的三角形OAB ,它的顶点是O =(0,0),A =(α ,0),B =(β ,γ ),其中α 及γ 是正数。于是证明一个单位线段,能位于这样的三角形内就足够了。不论β 是否为零射线,OB 可以表示成下列形式:
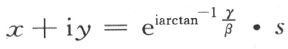
其中s 表示Q 中的一个正参数。因为αγ 与︱α -β ︱+γ 都是正的,可能找到一个整数γ 1 ,它不必须是正数,而适合不等式

就已知数 一定存在两个整数a 及b 适合不等式
一定存在两个整数a 及b 适合不等式
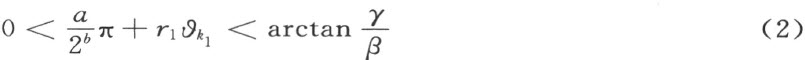
从公式
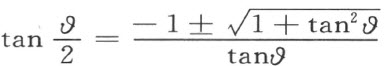
可知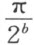 以及正切函数加法公式可知
以及正切函数加法公式可知
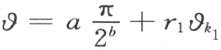
均是数域Θ 中的数。自不等式(2)可得出半线

位于角 的内部。自O 点射出的射线上一个单位线段的自由端点C (附图8)可表示成
的内部。自O 点射出的射线上一个单位线段的自由端点C (附图8)可表示成
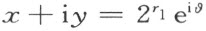
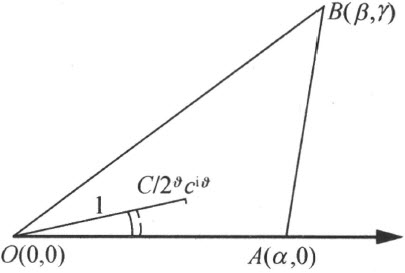
附图 8
点O 和点C 位于直线AB 的同侧,这是因为两个行列式
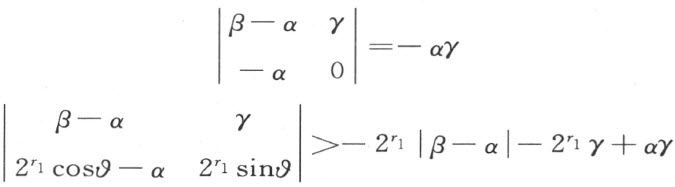
均为正,后一个利用了不等式(1)。故C 位于三角形OAB 的内部;亦即在三角形内部存在一个单位线段。
一角平分的可能性以及直角的存在恰如第一种非毕达哥拉斯几何那样能得到证明。在本书所引入的反射映象的定理以及比例论和仿射几何中的所有定理也同样能够证明均为正确。这种几何的所有角也在欧几里得几何里出现,并且量的顺序是同样的。从此也可推出外角定理(定理22)和三角形角和定理(定理31)的正确性。然而,等腰三角形底角相等的定理是不成立的。从这个定理并借助外角定理,如同上面所说明的,可以立即得出它的逆命题。但在这种几何里,逆命题并不成立,这可由下例看出。就三角形OPR 加以考虑,其中 ,它在P 与R 处有等角,但是边长
,它在P 与R 处有等角,但是边长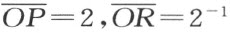 不等。
不等。
欧几里得面积论也不成立。同样,三角形两边和大于第三边的定理也不成立。因为从这个定理可立即推出位于三角形内部的每一线段小于其周界,这样邻域公理Ⅴ3 必成立。
从非毕达哥拉斯几何的研究得到下面的结果:
为了证明等腰三角形底角相等定理,即不能去掉阿基米德公理Ⅴ1 又不能去掉邻域公理Ⅴ3 。
关于这个附录的一些补充见后面的补篇Ⅴ1 和Ⅴ2 。
————————————————————
(1) Proceedings of the London Math. Soc. Vol. XXXV。(原文刊载于第七版以前的《几何基础》书内作为附录Ⅱ。从第7版起由希尔伯特本人重行改写,去掉原发表杂志的名称,直到第十二版未曾变动。——译者注)
(2) 这个证明原来是由查贝尔(W. Zabel)利用一个较广泛的公理来给出的。现在用公理Ⅲ,来代替是足够的。这个注记是由贝尔耐斯所给出的。参看本书的脚注。
(3) 这个证明是由斯米特(Arnold Schmidt)在他的文章“从平面运动导入反射”(Die Herleitung der Spiegelung aus der ebenen Bewegung, Math, Ann., Bd. 109, 1934)给出的。
(4) 见“不用对称公理,平面几何的建立”(Der Aufbau der ebenen Geometrio ohne das Symmetrieaxiom, Dissertation Göttingen, 1922, Math. Ann. Bd. 90)。在这里首先证明关于合同映射的若干性质成立的相关性。
(5) 这里需要平行公理以及直角的存在性。
(6) 参看补篇Ⅴ1 。
(7) 乘方仅对正ω 1 来进行,也可用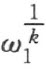 (k 表自然数)来代替
(k 表自然数)来代替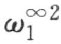 。
。
