补篇Ⅴ

1．附录Ⅱ中模型的剖分相等

在附录Ⅱ中已经指出，假如三角形的合同公理Ⅲ₅ ，用限制在同周向的对应三角形的情况下较狭义的合同公理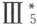 来代替，则不用阿基米德公理而用第四章（§18～§21）的方法，面积论的发展已不再可能。甚至将（借用Ⅲ₅ 能证明的）关于角合同的Ⅲ₆ 和Ⅲ₇ 的断言（参看79页）作为公理并附加所需要的直角存在性也是不可能的。将这解释予以扩展从而更将突出这个结果。

附录Ⅱ讨论到依共同原理所构造的两个平面几何模型，每个都是包含在一种解析几何里，其中的数集具有有序数域的所有性质，但并不是实数集。在一种情况里是由参数t 所产生的非阿基米德数集，它起着“无限小数”的作用，另一种情况则是实数集的一个可数子集。结合、顺序以及平行等的定义和通常所用的一样，仅旋转的定义含有异常的情况，这是由于将一向量旋转角α 将产生一个依赖于α 的正因子。两个图形（线段、角、多角形）称为合同，假如它们经过旋转和平移可以互相得到。

在这些模型中，除去论证直角的存在性外，可以证明公理Ⅰ_1～3 ，Ⅱ，Ⅲ_{1～4，5^* ，6～7} ，Ⅳ均成立。于是，有关合同理论的定理在具有同周向（即在“右”及“左”的情况下）的对应图形的范围内必成立。角可以比较，凡直角均相等成立，且三角形的角和定理也是正确的。

甚至一些定理可用不同周向的合同定理证明，又三角形的三边中垂线，三内角平分线分别交于一点的定理也均成立。这些可以由下面的反射定理得到，它是由反射的解析表示直接推出的。关于具有方向角α ₁ ，α ₂ ，α ₃ 且过一公共点S的三直线的三个反射的组合，产生一个关于方向角为α ₁ －α ₂ ＋α ₃ 且过S 的一直线的反射。

圆的理论也可以借助于前述的定理导出，由规定“在线段AB 上的圆”作为点C 的几何轨迹而使ACB 为一直角。于是也可以证明一圆上同弧的圆周角均相等，并且获得所有的工具。按照第三章或补篇Ⅱ的方法展开比例论的研究。

在希尔伯特的前几版书中，所考虑的两个模型里，比例论成立的证明方法确实能用一个比较直接的证法来代替 ^（1） ，即在这两个模型里，下面的解析几何定理成立：如果分别具有坐标x ₁ ，y ₁ 和x ₂ ，y ₂ 的两点P ₁ 和P ₂ 均在具有坐标x ₀ ，y ₀ 的P ₀ 点所射出的半线上，则线段P ₀ P ₁ 与P ₀ P ₂ 的比等于横标差x ₁ －x ₀ 与x ₂ －x ₀ 的比，假如它们均不是零，同时也等于纵标的差y ₁ －y ₀ 与y ₂ －y ₀ 之比，假如这些也均不是零。

这两种几何与普通欧几里得几何之间的差别特别表现在附图5中两个直角三角形OQP 和OQR 互为镜象反射，且选取角QOP 使得OR 之长小于OP 甚至小于OQ 。（在第一种非阿基米德模型里，长度之差仅是“无限小”，而在第二种模型里，它能够任意大。）

长度测量的基本原则在这里并不成立，这是因为线段长度的测量是由它在X 轴及Y 轴上的射影来决定，即毕达哥拉斯定理作为关于直角三角形中线段长度的定理。这样就促动希尔伯特将它叫做“非毕达哥拉斯几何”。另一方面，希尔伯特却证明了在所建立的几何中毕达哥拉斯定理作为拼补相等的定理 是正确的，即在直角三角形斜边上所作正方形与两个直角边上所作的正方形拼补相等也是成立的。

事实上，欧几里得关于拼补相等的证明仅用到同周向对应图形的合同。对这种几何，如以前所提到的，借合同映射（参看82页）来定义多角形的合同，即利用合同映射如果两个多角形可以互相得到，则说它们合同，并且如前规定它们的剖分相等和拼补相等。于是欧几里得的论断仍可适用。（特别注意必须应用补篇Ⅲ所给的方法对拼补相等传递性的证明在较狭义的合同定义下仍然成立。）

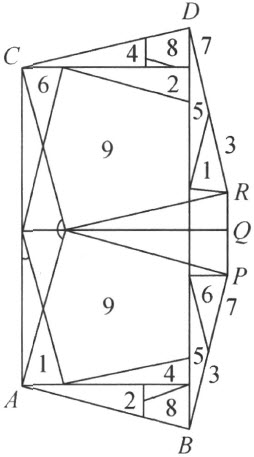
对已知图形（补图6）OPQR 可特别推出OP 上所作的正方形与OR 上所作的正方形拼补相等。虽然线段OR 较OP 短些，因而OP 上所作正方形却能与安装在它内部的正方形拼补相等。

补图　6

这个结果现在还可以深入，因为人们知道，在直角三角形斜边上的正方形不仅能证明与两个直角边上的正方形拼补相等而且也能证明剖分相等。据此，具有同向的对应三角形及四角形甚至可用平行位移相联系 ^（2） 。于是由剖分相等的传递性可得，在所考虑的图形OPQR 中，线段OP 上的正方形与线段OR上的正方形剖分相等 。

补图　7

最后，剖分相等也可由补图6直接看出，其中每个正方形OABP 及OCDR 都剖分成九个多角形，即七个三角形，一个四角形和一个五角形。在每个正方形中用相同数字所表示的对应多角形可以由平行位移互相得到。

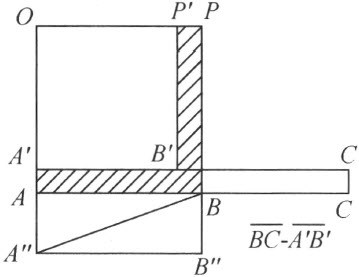
如果在OP 上O 到P′ 作较短的线段OR ，则在OP′ 所作能安装在OP 上的正方形内部的正方形OP′B′A′ 与它剖分相等。

下面的论证也可以用到这种情况。于补图7中，六角形AA′B′P′PB 的边AB 及BP 的长分别是OP 与A′B′ ，且B′P′ 之长是OR ，它与长方形ACC′A′ 剖分相等，其中点C 在自B 所作AB 的延长线上，且与B 的距离等于A′B′ ，并且C′ 是C 到直线A′B′ 的垂足。这个矩形与三角形AA″B 剖分相等，其中A″ 是从A 点所作OA 的延长线上的一点。这可以用初等方法由AC 长度小于AB 长度的二倍的事实来说明。

今将正方形OABP 用T表示，OA′B′P′ 用T′ 表示，六角形AA′B′P′PB 用W 来表示，且三角形AA″B 用Δ 表示，于是T 和T′ ，Δ 和W 均剖分相等，因而T ＋Δ 和T′ ＋W ，亦即和T 也剖分相等。

今再自B 延长线段PB 到B″ 使它与AA″ 合同，于是三角形A″B″B ，用Δ ′表示，将与三角形Δ 合同（连同周向）。故T ＋Δ ＋Δ ′与T ＋Δ 剖分相等。但是，T ＋Δ ＋Δ ′是长方形OA″B″P ，并且T ＋Δ 是由这长方形去掉Δ ′而得。在这种几何中定理52中的一个反例已经如此得出。

补图　8

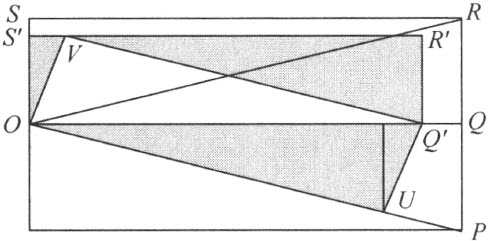
最后仍从图形OPQR 开始，能够得到彼此构型一样且剖分相等的两个长方形的一个方法，此法比考虑作OP 和OR 上的正方形较为简单。旋转长方形OQRS ，这里S 在过O 点所作OQ 的垂线上，且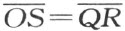 ，经过角QOP 依反方向旋转即得长方形OUQ′V ，其中U 和Q′ 分别在线段OP 和OQ 上。这个长方形，用简便的方法可以看出，它与长方形OQ′R′S′ 剖分相等，其中R′ 及S′ 位于过V 与OQ 平行的直线上，且S′ 位于OS 上，则长方形OQ′R′S′ 安装在长方形OQRS 内部且与之剖分相等。

2．希尔伯特的嵌入公理

在以前的各版里，与面积理论相联系的附录Ⅱ，采用与定理52等价的嵌入公理，得到一个能从较狭义的合同公理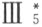 导出开始的较广义的合同公理Ⅲ₅ 的证明。这里所给出的是少量无足轻重的变动，为使它能适应这个新版。

前面已经指出（参看79页）合同公理Ⅲ₅ 以及较广形式图形的合同必须从较狭形式的三角形合同公理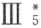 以及前面的公理一起连同Ⅲ₆ 和Ⅲ₇ 推出，但要在假定等腰三角形底角相等的定理成立 ^（3） 的情况下。特别值得注意的是较狭义形式的合同公理 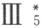也可用十分不同的方法来形成，即用一个很直观的要求，它的内容本质上与定理52（47页）由我在几何基础里证明的相同，且另一方面如同附录Ⅱ（88页）所指明的它不是较狭义的合同公理的一个推论。

设多角形“剖分相等”和“拼补相等”的概念如§18所定义的，再设“组合”及“合成多角形”的“剖分相等”的概念如补篇Ⅲ所给出的。然而，合同则理解为较狭意义 下的概念。因此以后永远采用较狭形式的三角形合同公理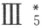 并且将用到以前的公理Ⅰ_1～3 ，Ⅱ，Ⅲ_1～4 以及平行公理Ⅳ。

问题中需要作如下的一个推广：

嵌入公理 　一个多角形永远不能与另一个多角形剖分相等，它的边界包含第一个多角形的内点，但不包含其外点，即它是嵌入在第一个的内部。

从这个公理首先导出下面定理：

一个多角形永不能与嵌入它内部的另一个多角形拼补 相等。

事实上，一个多角形P 与它内部的一个多角形Q 如果拼补相等，则必存在每个剖分相等的合成多角形P′ 和Q′ 而使P ＋P′ 与Q ＋Q′ 成为剖分相等的多角形。P′ 和Q 必不相交，且由剖分相等的可加性，Q ＋P′ 与Q ＋Q′ 也剖分相等，并且由剖分相等的传递性P ＋P′ 与Q ＋P′ 也必剖分相等。另一方面，因为Q 在P 的内部，存在一个组合P ＝Q ＋R ，其中R 是一个合成多角形。按照补篇Ⅲ的引理（参看138页），靠近P ＋P′ 能有一多角形P″ ，它与R 剖分相等且使P ＋P′ ＋P″ 是一多角形。由于P ＋P′ 和Q ＋P′ 以及P″ 和R 均剖分相等，连同剖分相等的可加性就可推得P ＋P′ ＋P″ 和Q ＋P′ ＋R 亦即和P ＋P′ 剖分相等。然而，这与嵌入公理相矛盾。

现在将证明下面的定理：

如果三角形ABC 的两个角A 和B 相等，则它们的对边也永远相等。

为了证明，在AB 上确定两点E 和D 而使AD ＝BC 且BE ＝AC ，利用较狭形式的第一三角形合同公理可得三角形DAC 和CBE 合同；这两个三角形也拼补相等。于是可知底AD 和BE 也必相等。假如不是这种情形，取AD′ ＝BE （补图9），则由熟知的欧几里得方法（参看43页）必将得出两个三角形AD ′C 和BEC 拼补相等。因之三角形ADC 和AD ′C 也将拼补相等，这将与嵌入公理所推出的前面定理相矛盾。由线段AD 和BE 的相等立即得出所要求的结论。

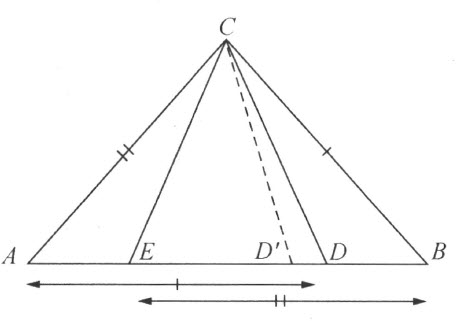
补图　9

如果三角形ABC 的两条边AC 和BC 相等，则它们所对的角也相等。

为了证明，假定结论不成立，且设 大于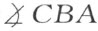 （补图10）。在直线AB 上确定两点A′ 和B′ 而使

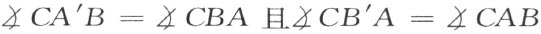
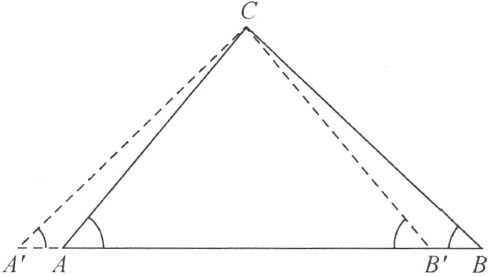
补图　10

于是由前面所证明的定理

CA′ ＝CB 且CB′ ＝CA

利用假设故可得

对三角形ACA′ 和BCB′ ，利用三角形外角定理得

和

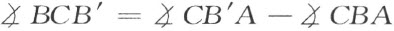
因之

公式（1 ）和（2 ）连同假设证明三角形ACA′ 与三角形BCB′ 是在较狭意义下合同。于是推出

这个结论是谬误的，因为这两个角分别是三角形A′B′C 的内角和不相邻的外角。

所述的定理即得以证明。同时可以看出假如借助上面直观的关于剖分相等的嵌入公理，较广义的合同定理将是较狭义形式的合同公理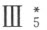 的一个推论。

从这个证明同时显见对目前的应用嵌入公理可以用下面较简单的公理来代替：

如果在三角形 ABC 中点 D 位于 AB 边上且在点 A 与点 B 之间 ，则三角形 ABC 和 ADC 不可能拼补相等 ^（4） 。

————————————————————

（1） 由于这个原因，在所提到的关于反射定理的讨论及其推论在第七版的附录中都被去掉。

（2） 就补图7，“新娘的席位”这一名词是9世纪由印度人传下来的。阿尔乃芮基（Alnarizi）是阿拉伯关于欧几里得原本的注释者，也曾建立了剖分相等。

（3） 关于一个更精确的说明参看贝尔耐斯的论文“几何基础的注记”（Bemer Kungen zu den Grundlagen der Geometrie, Courant Anniversery Volume, 1948, 29—44）。如何将包含阿基米德公理及平行公理底角定理的假定能够用不同方法由不含对称公理的特征的要求来代替，即同向三角形第三合同公理的要求。这个证明见斯米特的论文“从平面的运动引出反射”（Die Herleitung der Spiegelung aus der ebenen Bewegung, Math. Ann., 109（1934）,538—571）。

（4） 我的一篇文章“论多角形面积在平面几何公理法的反射公理的运用中所处的地位”（Über die Verwendung der Polygon inhalte an Stelle eines Spiegelungsaxioms in der Axiomatik der Planimetrie，Elem. d. Math.，8（1953），102—107），我曾用到与此结果的论证相类似的论证。当准备这篇文章时，我并未用到附录Ⅱ中前面的几段。在所引文章的结尾，我也并未给出适当的参考文献。

（关于附录，正如苏联著名几何学家拉舍夫斯基在德文第七版俄译本序言中所指出的，附录的文章具有非常专门的主题，而且程度高深，叙述上也颇具特色。现将这部分内容补译整理出来，仅供专门读者参考。因限于水平，不妥之处敬请指正。—译者注）