第三编

磁　学

·Part III Magnetism·

我们实验室的主要工作是熟悉各式各样的科学方法，并对它们进行比较，以对它们的价值作出估计。这是我们大学值得做的工作，在这里更可能好地完成任务。通过对不同科学程序相对价值的讨论，我们就可以成功地对某一学派进行科学的批评，这有助于方法学的发展。

——麦克斯韦（周兆平译）

静电电流被用作恶作剧，电成了上流社会的玩物。来自旋转球体的电流通过一个男人（做了认真的绝缘）和他的剑将酒精点燃。

第二十六章　磁学的初等理论

371．〕　人们发现，某些物体，例如被称为磁石的一种铁矿石、地球本身以及经过某种处理的钢铁，具有下述的性质，并称为“磁体”。

如果一个磁体在地球表面附近除地磁极以外的任何地方被悬挂起来，使得它可以绕一个竖直轴而自由转动，则一般说来它将倾向于使自己沿着一个确定的方位，而如果从该方位上被扰动，它就将在该方位附近进行振动。一个没被磁化的物体并不具备这样的倾向，而是在任何方位上都同样处于平衡。

372．〕　经发现，作用在磁体上的力，倾向于使磁体中叫做“磁体轴线”的一条确定的线和空间中一条叫做“磁力的方向”的定线相平行。

让我们假设，磁体被悬挂得可以绕一个固定点而向一切方向自由转动。为了消除重力的影响，我们可以假设这个点就是它的重心。设磁体达到了一个平衡位置。在磁体上标出两个点，并记下它们在空间中的位置。然后，让磁体达到一个新的平衡位置，并注意磁体上两个标志点在空间中的位置。

既然在两个位置上磁体的轴线都和磁力的方向相重合，我们就必须找出在运动前后在空间中占据相同位置的那条线。由不变形物体的运动理论可知，这样一条线总是存在的，而和实际运动相等价的一种运动可以通过绕该线的简单转动来实现。

为了求得这条线，把每一标志点的起始位置和终末位置连接起来，并作这些连线的垂直平分面。二平面的交线就将是所求的线，它指示着磁体轴线的方向和磁力在空间中的方向。

上述这种方法在确定这些方向时是不方便的。当处理磁学测量时，我们还将回到这一课题上来。

经发现，在地面上的不同部分，磁力的方向是不同的，如果注意磁体轴线指向北方的一端，就会发现磁轴所沿的方向通常是从真实经线偏开一个一定的角度的，而两标志端点的整体则在北半球向下倾斜，而在南半球向上倾斜。

磁力方向从真正北方向西的偏转，叫做“磁偏角”。磁力方向和水平面之间的夹角，叫做“磁倾角”。这两个角度确定了磁力的方向，而当磁力强度也为已知时，磁力就是完全确定的了。地面不同部分的这三个要素之值的测量，它们按照观测地点和观测时间的变化方式的讨论，以及磁力及其变化的原因的考察，就构成“地磁”科学。

373．〕　现在让我们假设，若干个磁体的轴线已经确定，而每一磁体指向北方的一端也已标出。这时，如果其中一个磁体是自由悬挂的，而另一个磁体被带到了它的附近，那就会发现，两个标志端互相推斥，一个标志端和一个未标志端互相吸引，而两个未标志端也互相推斥。

如果磁体是长棒形或长线形的，而且是沿着纵向而均匀磁化的（参阅第284节），那就会发现，当一个磁体的一端和另一磁体的一端相距很近时，力就显示得最为强烈；而这种现象就可以通过一种假设来加以说明，即假设各磁体的相似端互相推斥，其不相似端互相吸引，而各磁体的中间部分则没有显著的相互作用。

一个细长磁体的两端，通常叫做它的“极”。在沿长度均匀磁化的无限细磁体的事例中，两个端点就起着力心的作用，而磁体的其余部分则没有磁作用。在所有实际的磁体中，磁化都不是绝对地均匀，从而没有任何单个的点可以被看成磁极。然而，通过应用仔细磁化的细长棒，库仑却做到了两个相似磁极之间的力定律的建立（磁极间的媒质为空气） ^〔1〕 。

二相同磁极之间的推斥力沿二极之连线，其数值等于二极强度的乘积除以极间距离的平方。

374．〕　这一定律，当然假设每一磁极的强度是用某种单位来量度的，该单位的大小可由定律的叙述推知。

单位磁极是一个指北的极，而且当在空气中和另一个单位磁极相距为一个单位时，它就会以单位的力推斥那个磁极，此处单位力的定义和第6节中的定义相同。一个指南的磁极被看成负的。

如果m₁ 和m₂ 是两个磁极的强度，l是二者之间的距离，而f是推斥力，各量都以数字来表示，则有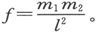

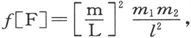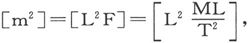但是，如果［m］、［L］和［F］是磁极、长度和力的具体单位，则有 由此即得 或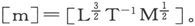 因此，单位磁极的量纲就是长度的 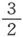次方、时间的（-1）次方和质量的 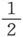次方。这种量纲是和在第41、42节中用完全相同的方法确定的电荷静电单位的量纲相同的。

375．〕　这一定律的精确性，可以认为已由库仑的扭秤实验所确立，并已由高斯和韦伯的实验以及许多磁观测站的所有观测员的实验所证实。那些观测员们每天都在进行着磁学量的测量，而假如力定律是错的，他们就会得出互相矛盾的结果。这一定律也通过它和电磁现象的定律的一致性而得到了更多的支持。

376．〕　我们一直称之为磁极强度的这个量，也可以叫做“磁量”，如果我们除了在磁极方面观察到的那些性质以外并不给“磁”指定别的性质的话。

既然“磁量”之间的力定律和数值相同的“电量”之间的力定律具有相同的数学形式，关于磁的许多数学处理就必然和关于电的处理相类似。然而也存在磁体的另外一些性质，它们是必须牢记的和可能在物体的电学性质方面提供某些启示的。

一个磁体的磁极之间的关系

377．〕　磁体一极的磁量和另一极的磁量等值而异号，或者，说得更普遍一些就是：

在每一个磁体中，总的磁量（代数地算起来）是零。

因此，在一个在磁体所占之空间中是均匀而平行的力场中，作用在磁体的标志端上的力，就和作用在未标志端上的力恰好相等、反向而平行，从而二力之和就是一个静力矩，它倾向于使磁体的轴线转到一个确定的方向上，但是并不会沿任何方向而推动整个的磁体。

这一点，可以很容易地通过把磁体放入一个小容器并把容器浮在水面上来加以证明。容器将转到某一方向，以便磁体轴线尽可能地和地球磁力的方向相接近，但是却不存在整个容器沿任何方向的运动，因此就并不存在北向力对南向力的超额，也不存在相反的超额。根据一个事实也可以证明，一块钢铁的磁化并不会改变它的重心，并不会在一些纬度上使重心沿着轴线向北偏移。由转动现象确定的质心是保持不变的。

378．〕　如果对一个细长磁体的中部进行检验，就会发现那里并不具备任何磁性。但是如何在该点把磁体打断，则会发现两段物体在断点处各有一个磁极，而且这个新磁极是和该段原有的另一磁极正好相等而相反的。不论是通过磁化，或是通过打断磁体，或是通过任何别的办法，都是不可能得到一个具有不相等的磁极的磁体的。

如果把一个细长磁体打成若干短段，我们就将得到一系列短磁体，其中每一磁体的各极都和原始长磁体的各极具有接近相同的强度。这种磁极的增多不一定是能量的增大，因为我们必须记得，由于它们的互相吸引，我们在打断磁体以后必须做功才能使各段分开。

379．〕　现在，让我们把磁体的各段像从前那样摆在一起。在每一个接头处，将有两个正好相等而反号的磁极互相接触着，从而它们对任一其他磁极的合作用都将为零。因此，这样重新组合起来以后，磁体就将和以前具有相同的性质，就是说，它在两端各有一极，二者相等而异号，而其二极之间的部分则不显示任何磁作用。

既然在这一事例中我们知道长磁体是由一些小的短磁体组成的，而且现象又和在未打断磁体时的情况相同，那么我们就可以认为，甚至在未被打断以前。磁体也是由一些小的粒子组成的，其中每一粒子都有两个相等而异号的极。如果我们假设所有的磁体都是由这样的粒子组成的，那就显而易见，既然每一个粒子中的磁量代数和为零，整个磁体的总磁量也必为零，或者换句话说，它的磁极将具有相等的强度和相反的种类。

“磁质”学说

380．〕　既然磁作用的定律和电作用的定律具有完全相同的形式，赋予电现象以单“流体”或二“流体”之作用的那些相同的理由，就可以用来论证一种或两种“磁质”的存在，它可能是也可能不是“流体”。事实上，若只在纯数学的意义下来运用，一种磁质学说是不会无法解释现象的，如果新的规律被自由地引用来说明各个实际事实的话。

这些新规律之一必须是，磁流体不能从磁体的一个分子或粒子转移到它的另一个分子或粒子，而磁化过程则只是每一粒子中两种流体在某种程度上互相分离，这就使得一种流体在粒子的一端更加集中，而另一种流体则在粒子的另一端更加集中。这就是泊松的学说。

按照这种学说，一种可磁化物体的一个粒子，和一个已绝缘的不带电荷的小导体相仿佛；按照二流体学说，这种导体含有无限而正好相等的两种电的数量。当有一个电动势作用在这个导体上时，它就造成两种电的分离，而使它们在导体的对面两侧显示出来。按照这种学说，磁化力将以相仿的方式使起初处于中和状态的两种磁质互相分开，并使它们出现在被磁化粒子的面对面的两侧。

在某些物质中，例如在软铁或其他那些不可能被永久磁化的磁性物质中，当施感力消失时，这种磁状态将像导体的起电那样随之而消失 ^〔2〕 。在另一些物质中，例如在硬钢中，这种磁状态不易发生，而一旦发生，它在施感力被取消时也还会存留下来。

这种情况是用下列说法来表达的：在后一事例中，存在一种“顽滞力”（coercive force），它倾向于阻止磁化的改变，而要增强或减弱一个磁体的性能，必先克服这个顽滞力。在起电物体的事例中，这种顽滞力将对应于一种电阻，而这种电阻和在金属中观察到的电阻不同，它在低于某值的电动势下将和完全的绝缘相等价。

这种关于磁的学说，正如关于电的对应学说一样，显然对于事实来说是太宽松的，它需要用一些人为的条件来加以限制。因为，它不仅没有给出任何理由来说明何以一个物体不会因为含有更多的两种流体而不同于另一物体，而且它还使我们能够说出含有过多的一种流体的一个物体将有什么样的性质。确实，关于这样的一个物体何以不能存在，倒是提出了一种理由的，但是这种理由只是作为一种事后的想法而被引用了来解释这一特定事实的。它并不是从这一学说中自动生长出来的。

381．〕　因此，我们必须寻求一种表达模式，它不会表达得太多，而且也将为由新事实发展而成的新想法的引用留下余地。我想，如果我们从认为一个磁体的粒子是“极化的”来开始，我们就将得到这样的表达模式。

“极化”一词的意义

如果一个物体的粒子具有一些和物体中某一直线或方向有关的性质，而且当物体保持着这些性质而被转动，以使这一方向反向时，如果粒子的这些性质相对于其他物体也反向，则按照这些性质来说，粒子就叫做极化的，而这些性质就叫做构成一种特定的极化。

例如，我们可以说物体绕一条轴线的转动就构成一种极化。因为，如果在转动继续进行中轴线方向被颠倒过来，则物体对空间来说将是向反方向转动的。

通有电流的一个导电粒子可以说是极化的，因为，如果把粒子倒过来，而粒子中的电流则相对于粒子来说仍沿相同的方向在流动，则电流在空间中的方向将是反了向的。

简短地说，如果任何一个数学量或物理量具有在第11节中定义了的那种矢量的性质，则这种有向量所属于的任何一个物体或粒子就可以被说成是“极化的” ^〔3〕 ，因为在有向量的两个方向或两个极上，它是具有相反的性质的。

例如，地球的两极是和它的转动有关的，从而各极就具有不同的名称。

“磁极化”一词的意义

382．〕　当把一个物体的各粒子的状态说成磁极化时，我们的意思就是，一个磁体所能分成的那些最小部分中的每一个部分，都具有某些和通过粒子的一个确定方向有关的性质，该方向叫做粒子的“磁化轴”，而且，和这个轴的一端有关的那些性质，是与和另一端有关的那些性质相反的。

指定给粒子的那些性质，是和我们在整个磁体中观察到的那些性质同一种类的，而在假设各粒子具有这些性质时，我们所肯定的只是我们可以通过把磁体打成小块来证明的情况，因为我们发现其中每一小块都是一个磁体。

一个磁化粒子的性质

383．〕　设体积元dxdydz是磁体的一个粒子。让我们假设，粒子的性质就是一个磁体的性质，该磁体的正极强度是m，而它的长度是ds。于是，设P是空间中的任意点，它离正极的距离是r而离负极的距离是r′，则由正极在P点引起的磁势将是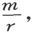 而由负极在P点引起的磁势将是 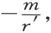或者写成　　

如果二极之间的距离ds很小，我们就可以令

式中ε是从磁体画到P点的矢量和磁体轴线之间的夹角 ^〔4〕 ，或者，在这种极限下就有

磁　　矩

384．〕　均匀纵向磁化的棒形磁体的长度和它的正极强度的乘积，叫做它的“磁矩”。

磁化强度

一个磁性粒子的磁化强度，就是它的磁矩和体积之比。我们将用I来代表它。

磁体任一点处的磁化，可以用磁化强度和磁化方向来定义。该方向可以用它的方向余弦λ、μ、v来定义。

磁化分量

磁体一点处的磁化（作为一个矢量或有向量），可以用它相对于各坐标轴的三个分量表示出来。把这些分量写成A、B、C，就有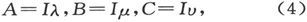　　

而I的数值就由方程　　

来给出。

385．〕　如果我们所考虑的磁体部分是微分体积元dxdydz，而I代表这一体积元的磁化强度，则它的磁矩是Idxdydz。将方程（3）中的mds代成比式，并记得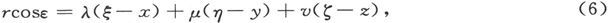

式中ξ、η、ζ是从点（x，y，z）画起的矢量r的端点坐标，我们就得到由点（x，y，z）上的磁化体积元在点（ξ、η、ζ）上引起的势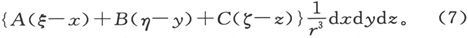　　

为了求出由一个有限大小的磁体在点（ξ，η，ζ）上引起的势，我们必须对包含在磁体所占空间中的各个体积元求这个表示式的积分，或者说，

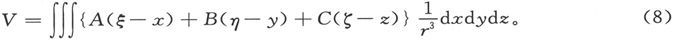
分部积分，比式就变成

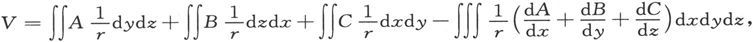
式中前三项的双重积分是在磁体的表面上求的，而第四项的三重积分则是在表面内的空间中求的。

如果l、m、n代表从面积元ds向外画的法线的方向余弦，我们就可以像在第21节中那样把前三项的和式写成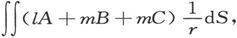

式中的积分遍及于磁体的整个表面。

如果现在我们引用由方程组σ＝lA＋mB＋nC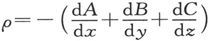， 来定义的两个新符号σ和ρ，则势的表示式可以写成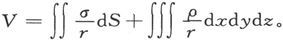

386．〕　这一表示式和由一个物体所引起的电势的表示式完全相同；在该物体的表面上，有一个面密度为σ的面电荷，而在它的整个体积中则有一个体密度为ρ的体电荷。因此，如果我们假设σ和ρ就是我们曾经称之为“磁质”的那种假想物质分布的面密度和体密度，由这一假想分布所引起的势就将和由磁体之每一体积元的实际磁化所引起的势完全相同。

面密度σ就是磁化强度I在面积的外向法线方向上的分量，而体密度ρ就是磁体中给定点上的磁化强度的“敛度”（参阅第25节）。

这种把一个磁体的作用表示成由一种“磁质”分布所引起的作用的方法，是很方便的，但是我们必须永远记得，这只是一种表示一组极化粒子之作用的人为方法。

关于一个磁体性粒子对另一磁性粒子的作用

387．〕　如果我们像在关于球谐函数的一章的第129b节中那样令

式中l、m、n是轴线h的方向余弦，则由原点上磁轴平行于h₁ 而磁矩为m₁ 的一个磁性分子所引的势应是　　

式中λ₁ 是h₁ 和r之间的夹角的余弦。

其次，如果在矢径r的端点上放上第二个磁性分子，其磁矩为m₂ 而其磁轴平行于h₂ ，则由一个分子对另一个分子的作用而引起的势能将是

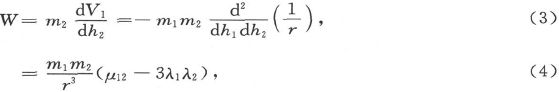
式中μ₁₂ 是二轴线所夹之角的余弦，而λ₁ 、λ₂ 是各轴线和r所夹之角的余弦。

其次让我们确定第一个磁体倾向于使第二个磁体绕其中心而转动的那一力偶的矩。

让我们假设，第二个磁体在垂直于某一第三个轴线h₃ 的平面内转过了一个角度dφ，则反抗磁力所做的功将是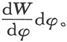 而作用在磁体上的各力在这一平面上的力矩将是

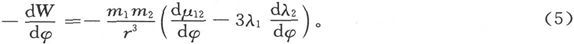
因此，作用在第二个磁体上的实际力矩可以看成两个力偶矩之和，其中一个力偶在平行于二磁体之轴线的平面内起作用，并以一力偶矩　　

而倾向于使二轴线之间的夹角增大，而第二个力偶则在通过r和第二个磁体的轴线的平面内起作用，并倾向于使这些方向之间的夹角减小，其力偶矩是

式中（rh₁ ）、（rh₂ ）、（h₁ h₂ ）表示各线r、h₁ 、h₂ 之间的夹角 ^〔5〕 。

为了确定沿着平行于一条线h₃ 的方向而作用在第二个磁体上的力，我们必须计算

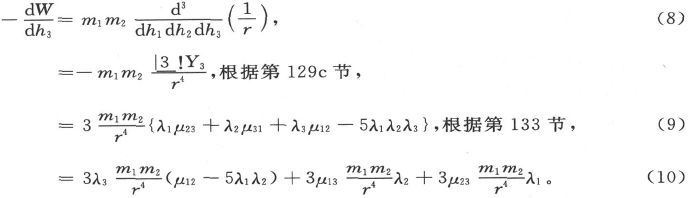
如果我们假设实际的力是由三个分别沿r、h₁ 和h₂ 方向的力R、H₁ 和H₂ 合成的，则沿h₃ 方向的力是　　

既然h₃ 的方向是任意的，我们就应该有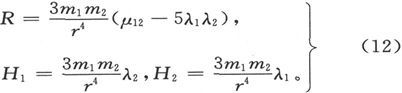

力R是一个倾向于使r增大的推斥力；H₁ 和H₂ 分别沿着第一个和第二个磁体的轴线而作用在第二个磁体上。

这种关于两个小磁体之间的作用力的分析，是由泰特教授在1860年1月份的Quarterly Math. Journ. 上利用四元数分析而最初给出的。并请参阅他关于四元数的著作第二版的第442～443节。

特殊位置

388．〕　（1）如果λ₁ 和λ₂ 各等于1，也就是说，如果两个磁体的轴线位于同一直线上而且方向相同，则μ₁₂ ＝1，而两磁体之间的力是一个推斥力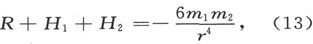

负号表示它实际上是一个吸引力。

（2）如果λ₁ 和λ₂ 是零，而μ₁₂ 是1，则二磁体的轴线互相平行而垂直于r，而力则是一个推斥力　　

在这两种事例中，任何力偶都是不存在的。

（3）如果λ₁ ＝1而λ₂ ＝0则

作用在第二个磁体上的力将是 沿着它的轴线的方向；力矩将是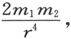 并倾向于把它转得和第一个磁体相平行。这就和单独一个力 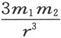相等价，该力沿着平行于第二个磁体轴线的方向而起作用，并和r相交于从m₂ 算起的2/3的长度处 ^〔6〕 。

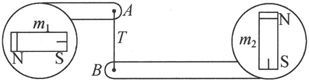
图40

例如，在图40中，两个磁体被浮在水面上，m₂ 位于m₁ 的轴线方向上，但是它自己的轴线却垂直于m₁ 的轴线。如果把两个分别和m₁ 及m₂ 刚性连接着的点A、B用一个弹簧T连接起来，则体系将处于平衡，如果T和直线m₁ m₂ 在从m₁ 到m₂ 的1/3距离处垂直相交的话。

（4）如果我们让第二个磁体绕着它的中心而自由转动，直到它达到一个稳定平衡位置时为止，则W对h₂ 而言将是一个极小值，从而由m₂ 引起的沿h₁ 方向的分力将是一个极大值。因此，如果我们希望利用中心位置给定的一些磁体来在给定点上沿给定方向产生尽可能大的磁力，则为了确定这些磁体的轴线的适当方向来产生这一效应，我们只需把一个磁体沿着给定的方向而放在给定点上，并观察当第二个磁体的中心位于另一给定点上时它的轴线的稳定平衡方向。于是，各磁体就必须摆得使它们的轴线沿着第二个磁体的轴线所指示的那些方向了。

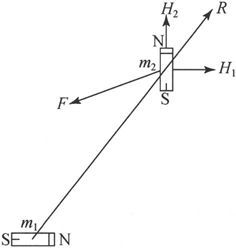
图41

设第二个磁体位于一个对它的方向而言为稳定的平衡位置上，那么，既然作用在它上面的力偶为零，第二个磁体的轴线就必然和第一个磁体的轴线位于同一平面上。由此就有　　

而既然力偶是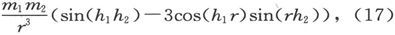

则当此力偶为零时我们就有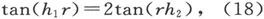

或者写作

当这一位置已经被第二个磁体所占据时，W的值就变成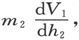 式中h₂ 是由m₁ 在m₂ 处引起的力线的方向。由此即得

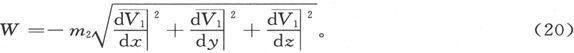
因此，第二个磁体将倾向于向着合力更大的地方运动。

作用在第二个磁体上的力，可以分解成力R和力H₁ 。在这一事例中，R永远是指向第一磁体的一个吸引力；力H₁ 是平行第一磁体的轴线的。我们有

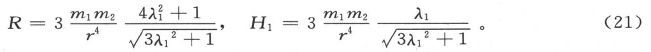
在本卷后面所附的图版14中，画出了二维空间中的力线和等势面。引起这些力线和等势面的磁体被假设为两个长的圆棒，其截面由图中的两个空白圆面积来代表；这些圆棒是沿着箭头的方向而横向磁化的。

如果我们记得沿着力线是有一种张力的，那就很容易看到，每一个磁体都将倾向于按顺时针的方向而转动。

作为一个整体，位于右方的那个磁体也将倾向于向纸面上方运动，而位于左方的那个磁体则将倾向于向纸面下方运动。

放在磁场中的一个磁体的势能

389．〕　设V是由对所考虑的那个磁体起着作用的任一磁体系引起的磁势。我们将把V叫做外磁力的势。如果有一个强度为m而长度为ds的小磁体被摆得正极位于势为V的一点而负极位于势为V′的一点，则这个磁体的势能将是m（V－V′），或者，如果ds是从负极向正极测量的，则势能是　　

如果I是极化强度，而λ、μ、v是它的方向余弦，我们就可以写出　mds＝Idxdydz，和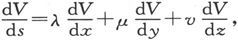 最后，如果A，B，C是极化分量，就有A＝λI，B＝μI，C＝vI，于是磁体元的势能表示式（1）就变成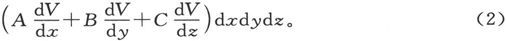

为了求出一个有限大小的磁体的势能，我们必须针对每一个磁体元求这一表示式的积分。于是我们就得到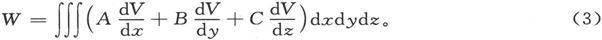

这就是磁体相对于它所在的磁场而言的势能的值。

在这儿，势能是用磁化分量和由外因引起的磁力的分量表示出来的。

通过分部积分，我们可以用磁质的分布和磁势来表示它，于是就有

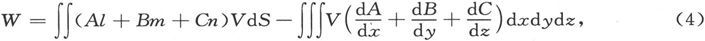
式中l、m、n是面积元dS上的法线的方向余弦。如果我们把在第365节中给出的磁质的面密度和体密度的表示式代入这一方程中，则势能表示式变为

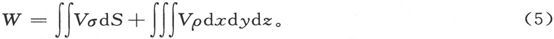
我们可以把（3）式写成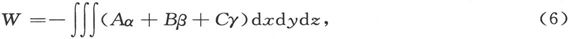

式中α、β和γ是外磁力的分量。

论一个磁体的磁矩和轴线

390．〕　如果外磁场在磁体所占据的空间中到处都在方向和大小上是均匀的，则各分量α、β、γ将是常量，而如果我们写出

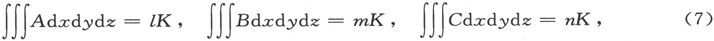
式中的积分遍及磁体的全部物质，则W的值可以写成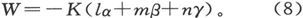

在这一表示式中，l、m、n是磁体轴线的方向余弦，而K是磁体的磁矩。如果ε是磁体轴线和磁力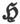 的方向所夹的角，则W的值可以写成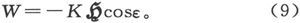

如果磁体是悬挂着并可以绕着一条竖直轴线而转动的，就如在一个普通指南针的事例中那样，那就可以用φ来表示磁体轴线的方位角，而用θ来表示轴线对水平面的倾角。

设地磁力的方向有一个方位角δ和一个倾角ξ，则有

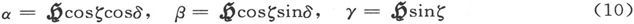
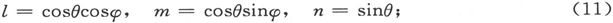
由此即得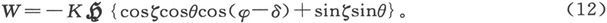　　

倾向于使磁体绕竖直轴线转动而增大其φ角的力矩是

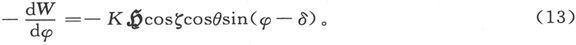
磁体的势的体谐函数展式

391．〕　设V是由位于点（ξ，η，ζ）上的一个单位磁极所引起的势。在点（x，y，z）上，V的值是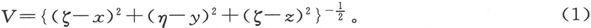　　

这一表示式可以按中心位于坐标原点上的球谐函数展开。于是我们就有

式中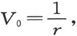

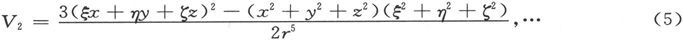
为了确定当磁体位于用这个势来表示的力场中时的势能值，我们必须在第389节方程（3）的W表示式中对x，y，z求积分而把ξ，η，ζ和r看成常量。

如果我们只考虑由V₀ 、V₁ 和V₂ 所引入的各项，则结果将依赖于下列这些体积分，

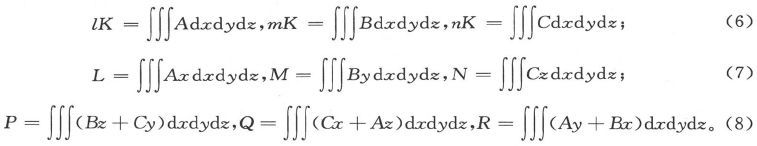
于是我们就得到一个磁体受到位于点（ξ，η，ζ）上的单位磁极的作用时的势能的值

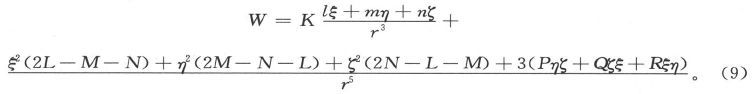
这一表示式也可以看成一个单位磁极受到一个磁体的作用时的势能，或者简单地看成磁体在点（ξ，η，ζ）上引起的势。

一个磁体的中心及其主轴线和副轴线

392．〕　这一表示式可以通过改变坐标轴的方向和坐标原点的位置来加以简化。首先，我们将使x轴的方向平行于磁体的轴线。这就等于令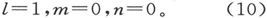

如果我们保持各轴的方向不变而把坐标原点移到点（x′，y′，z′）上，则各体积分lK、mK和nK将保持不变，而其他的积分则将变化如下：

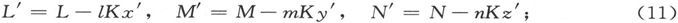
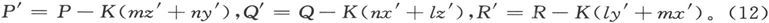
现在，如果我们令z轴平行于磁体轴线，并令

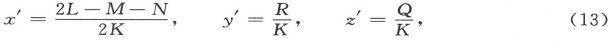
则对于新坐标轴来说，M和N的值都保持不变在而L′的值则变成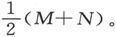 P保持不变，而Q和R则变为零。因此我们就可以把势写成

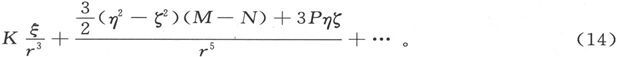
于是我们就找到了一个相对于磁体为固定的点，而当取这个点作为坐标原点时，势函数的第二项将取最简单的形式。因此我们就把这个点定义为磁体的中心，而通过中心沿着以前称之为磁体轴线的那个方向画出的轴，则可以定义为磁体的主轴。

通过使y轴和z轴绕着x轴而转过一个角度，该角度等于其正切为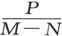 的那个角度的二分之一，我们就可以进一步简化结果。这将使P变为零，而势函数的最后形式就可以写成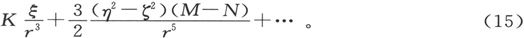　　

这就是一个磁体的势函数中头两项的最简单形式。当y轴和z轴取这种位置时，它们就可以叫做磁体的副轴。

我们也可以通过找到坐标原点的一个位置来确定磁体的中心，对于那个位置来说，在一个单位半径的球面上求出的势函数第二项的平方的面积分是一个极小值。

按照第141节，必须取极小值的那个量就是

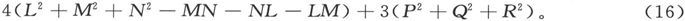
由于原点位置的改变而引起的这个量的值的改变，可以由方程（11）和（12）推出。因此极小值的条件就是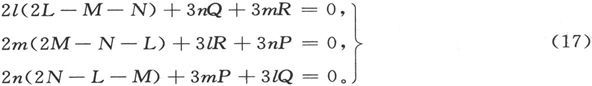　　

如果我们令l＝1，m＝0，n＝0，这些条件就变成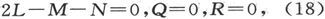

这就是在前面的探讨中利用了的条件。

这种探讨可以和把由一个有重物质体系引起的势展开的那种探讨相对比。在后一事例中，最适宜取作原点的一点就是体系的重心，而最方便的坐标轴就是通过该点的几个惯量主轴。

在磁体的事例中，和重心相对应的一点位于磁轴上的无限远处，而我们称之为磁体中心的那个点是和重心性质不同的一个点。量L、M、N对应于一个物质体的惯量矩，而P、Q、R则对应于惯量积，只不过L、M和N不一定是正量。

当把磁体的中心取作原点时，第二阶球谐函数具有瓣谐形式，其轴线和磁体轴线相重合，而这一情况对于任何其他的点都是不成立的。

当磁体在这一轴线的所有各侧都为对称时，例如在一个旋成图形的事例中，包括二阶谐函数的那一项就根本不出现。

393．〕　在地球表面的所有各部分，除了两极附近的某些部分以外，一个磁体的一端总是指向北方，或者说至少是指向偏北的方向的，而其另一端则总是指向偏南的方向的。在谈到磁体的各端时，我们将采用流行的办法，即指北的一端叫做磁体的北端，而把指南的一端叫做它的南端。然而，当我们用磁质学说的语言来叙述问题时，我们将利用“玄武”（Boreal）和“朱雀”（Austral）二词。玄磁性是一种假想的物质，被假设为在地球的北半部最为丰富；而朱磁性则是在地球的南半部更丰富的那种假想磁质。一个磁体的北端的磁性是朱磁性，而其南端的磁性是玄磁性。因此，当我们谈到一个磁体的北端和南端时，我们并不是把那个磁体和看成一个大磁体的地球相比拟，而只是表达当磁体可以自由活动时它所力图采取的位置而已。另一方面，当我们想要比较假想的磁流体在磁体中和在地球中的分布时，我们就将利用“玄磁性”和“朱磁性”这些更加夸饰的名词。

394．〕　在谈到一个磁力场时，我们将用“磁北方”一词来表示当一个磁针被放在力场中时它的北端所指的方向。

在谈到磁力线时，我们将永远假设它是从磁南方画向磁北方的，而且我们将把这一方向称为正方向。同样，一个磁体的磁化方向，用从磁体的南端画向北端的一条线来表示，而磁体指北的一端被算作正端。

我们将把朱磁性即磁体指北的一端上的磁性叫做正磁性。如果我们用m来代表它的数值，则磁势是 而磁力的正方向就是V减小的方向。

第二十七章　磁力和磁感

395．〕　我们已经确定了由一个磁体在一个给定点上引起的磁势（第385节），该磁体的磁化在它的物质的每一点上都是已给定的。我们已经指明，数学结果可以用磁体中每一个体积元的实际磁化表示出来，或是用一种假想的“磁质”分布表示出来；那种磁质的一部分集中在磁体的表面上，而其另一部分则散布在它的整个体积中。

这样定义的磁势，不论所给之点是在磁体之外或之内，都是用相同的数学过程来求出的。作用在位于磁体之外任一点上的一个单位磁极上的力，像在对应的电学问题中一样用相同的微分过程来从势函数求出。如果这个力的分量是α、β、γ，则有

为了用实验来测定磁体内部一点上的磁力，我们首先必须把一部分磁化了的物质弄走，以形成一个空腔，而在这个空腔中我们将放进〔测量用的〕磁极。一般说来，作用在磁极上的力将依赖于这一空腔的形状，并依赖于各个腔壁和磁化方向所成的角。因此，在谈到磁体内部的磁力时，为了避免混淆，就有必要指定测量磁力时所在的空腔的形状和位置。很明显，当空腔的形状和位置已经指定时，空腔中放上磁极的那个点就必须被认为不再是位于磁体物质之内的，从而测定力的普通方法也就立刻成为可用的了。

396．〕　现在让我们考虑一个磁体的一部分，假设在磁体内部磁化的方向和强度都是均匀的。在磁体的这一部分中，设有一个柱状空腔被挖出，空腔的轴线平行于磁化的方向。另外，设有一个单位强度的磁极被放在了轴线的中点上。

既然这一柱体的母线是沿着磁化方向的，在弯曲的柱面上就不会有磁质的表面分布，而既然柱体的圆形端面是垂直于磁化方向的，那里就会有一种均匀的表面分布，其面密度在负端为I而在正端为-I。

设柱体轴线的长度为2b，而柱体的半径为a。于是由表面分布引起的作用在位于轴线中点上的一个磁极上的力，就是来自正端圆盘的吸引力和来自负端圆盘的推斥力。这两个力是相等而同向的，而其合力就是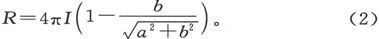　　

由这一表示式可以看出，力并不依赖于空腔的绝对尺寸而是依赖于柱体的长度和直径之比。因此，不论我们把空腔弄得多小，由腔壁上的表面分布所引起的力一般都将保持为有限。

397．〕　迄今为止，我们一直假设在挖出空腔的那一磁体部分中磁化是均匀的和到处方向相同的。当磁化并不是如此限定时，一般说来就有假想磁质的一种分布存在于整个磁体的物质中。柱体的挖除将带走这种分布的一个部分。但是，既然相似图形中各对应点上的力正比于图形的线度，由磁质体密度而来的作用在磁极上的力的改变量〔即由挖出空腔而造成的改变量〕，就将随着空腔尺寸的减小而无限地减小，而由腔壁上的面密度引起的效应则一般将会保持有限。

因此，如果我们假设柱体的尺寸足够小，以致被挖走的部分的磁化可以看成到处都平行于柱体轴线并具有常值大小I，则作用在位于柱状空腔的轴线中点上的一个磁极上的力将由两个力合成。其中第一个力就是由磁体外表面上的磁质分布以及除所挖空腔以外整个磁体内部的磁质分布所引起的力。这个力的分量，就是按照方程（1）而由势函数导出的α、β和γ。第二个力就是沿着柱体的轴线而作用的力R，其方向是磁化的方向。这个力的值依赖于柱状空腔的长度和直径之比。

398．〕　事例Ⅰ。设这一比值很大，或者说，设柱体的直径比它的长度小得多。把R的表示式按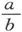 的幂次展开，我们就有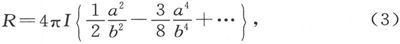　　

这是当令b和a之比趋于无限大时就会变为零的一个量。因此，当空腔是轴线平行于磁化方向的一个很细的柱体时，空腔中的磁力就不会受到柱体两端的表面分布的影响，从而这个力的分量就简单地是α、β、γ而此处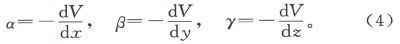　　

我们将把这种形状的空腔中的力定义为磁体内部的磁力。威廉·汤姆孙爵士曾把这种定义称为磁力的“极定义”（Polar definition）。当我们有机会把这个力看成一个矢量时，我们将用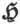 来代表它。

399．〕　事例Ⅱ。设柱体的长度比它的直径小得多，以致柱体变成一个很薄的圆盘。把R的表示式按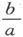 的幂次展开，它就变成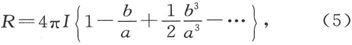　　

当把a和b的比值取为无限大时，这个表示式的最终值就是4πI。

因此，当空腔的形状是其平面垂直于磁化方向的一个薄圆盘时，放在轴线中点上的一个单位磁极就受到起源于盘子的圆形表面上的表面磁性的一个沿磁化方向的力4πI ^〔7〕 。

既然I的分量是A、B和C，这个力的分量就是4πA、4πB和4πC。这个力必须和分量为α、β、γ的那个力合成在一起。

400．〕　设用矢量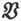 代表作用在单位磁极上的实际力，用a、b和c代表它的分量，则有　　

我们将把其平面垂直于磁化方向的一个中空圆盘中的力定义为磁体中的“磁感”。威廉·汤姆孙爵士曾把这一定义叫做磁力的“电磁定义”。

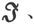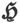磁化 磁力 和磁感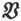 这三个矢量，是用矢量方程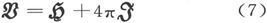　　

来互相联系的。

磁力的线积分

401．〕　既然在第398节中定义的磁力是由磁体的表面上的和整个体积中的自由磁质引起的，而且是不受空腔之表面磁质的影响的，它就可以由磁体之势的普遍表示式直接推得，而从点A到点B沿任意曲线计算的磁力的线积分就是

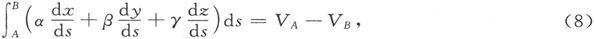
式中V_A 和V_B 分别代表A点和B点的势。

磁感的面积分

402．〕　通过曲面S的磁感〔通量〕，定义为下列积分的值：　　

式中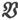 代表面积元dS上的磁感的量值，ε代表磁感方向和面积元法线之间的夹角，而积分应遍及整个的曲面，该曲面可以是闭合的，也可以是以一条闭合曲线为其边界的。

如果a、b、c代表磁感的分量，而l、m、n代表法线的方向余弦，则面积分可以写成

如果把磁感的各个分量代换成第400节中给出的用磁力分量和磁化分量表示出来的那些值，我们就得到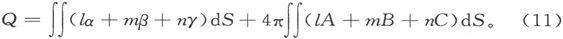　　

现在我们将假设求积分时所在的曲面是一个闭合曲面，并考察等式右端两项的值。

既然磁力和自由磁质之间的关系与电力和自由电荷之间的关系具有相同的数学形式，我们就可以把在第77节中给出的结果应用于Q值中的第一项。为此，我们用磁力分量α、β、γ来代替在第77节中给出的电力分量X、Y、Z，并用闭合曲面中自由磁质的代数和M来代替自由电荷的代数和e。

于是我们就得到一个方程　　

既然每一个磁粒子都有两个数值相等而符号相反的极，粒子的磁质的代数和就是零。因此，完全位于闭合曲面S之内的那些粒子就不会对S内的磁质代数和有任何贡献。因此M的值就只依赖于被曲面S所交截的那些磁粒子。

试考虑磁体的一个体积元，设其长度为s，截面积为k² ，并沿着它的长度而被磁化，使得它的磁极强度为m。这一体积元的磁矩将是ms，而既然磁化强度I等于磁矩和体积之比，我们就有　　

设这个小磁体被曲面S所交截，而其磁化方向和曲面之外向法线的夹角为ε′，则有

此处dS代表交截面积。这一磁体的负极-m位于曲面S内部。

因此，如果我们用dM来代表这一小磁体对S内部自由磁质的那一部分贡献，就有

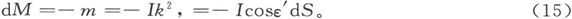
为了求出闭合曲面S内部自由磁质的代数和M，我们必须在该闭合曲面上求这一表示式的积分，于是就有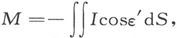 或者，用A、B、C代表磁化分量，用l、m、n代表外向法线的方向余弦，就得到

这就给出了方程（11）右端第二项中的积分的值。因此，该方程中的Q的值就可以由方程（12）和（16）求出，　　

或者说，通过任一闭合曲面的磁感的面积分都是零。

403．〕　如果把微分体积元dxdydz的表面取成所涉及的闭合曲面，我们就得到一个方程　　

这就是磁感分量永远满足的管状条件。

既然磁感的分布是管状的，通过以一条闭合曲线为边的任意曲面的磁感就只依赖于曲线的形状和位置，而不依赖于曲面本身的形状和位置。

404．〕　每一点都满足条件　　

的曲面，叫做无磁感面，而两个这种曲面的交线叫做无磁感曲线。因此，一条曲线s可以是无磁感曲线的条件就是　　

通过一条闭合曲线上每一点的一族磁感线，形成一个管状的曲面，叫做一个“磁感管”。

通过一根管子的任一截面的磁感都是相同的。如果磁感为1，则此管叫做“单位磁感管”。

如果按照磁感线和磁感管来理解，则法拉第 ^〔8〕 关于磁力线和磁力管的一切议论都是数学地正确的。

磁力和磁感在磁体外面是等同的，但是在磁体物质的内部，它们却必须仔细地加以区分。

在一个均匀磁化的直棒磁体中，由磁体本身引起的磁力在磁体内部和外面的空间中都是从我们称之为正极的指北极到负极即指南极的。

另一方面，磁感却在磁体外面从正极到负极，而在磁体内部从负极到正极，从而磁感线和磁感管都是一些回头的或循环的图形。

磁感作为一个物理量的重要性，我们当学到电磁现象时就会更清楚地看出。当磁场是用一条运动导线来加以探测，就如在法拉第的Exp. Res. 3076中那样时，直接被测的就是磁感而不是磁力。

磁感的矢势

405．〕　既然正如我们已经在第403节中指明了的那样，通过以一条闭合曲线为边的曲面的磁感是依赖于该闭合曲线而不依赖于闭合曲线所限定的曲面的，那就必然能够利用一种只依赖于该曲线而不涉及形成曲线之罩膜的一个曲面之画法的过程，来确定通过闭合曲线的磁感。

这一点可以通过求出和磁感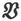 相联系着的一个矢量 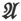来达成，这时 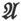沿闭合曲线的线积分应该等于 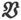在以闭合曲线为边的一个曲面上的面积分。

如果在第24节中把F、G、H看成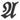 的分量而把a、b、c看成 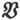的分量，我们就得到这些分量之间的关系式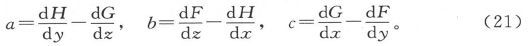　　

其分量为F、G、H的矢量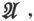 叫做磁感的矢势。

如果有一个磁矩为m而其磁化轴线的方向为（λ，μ，v）的磁分子位于坐标原点上，则由第387节可知，距原点为r的一个点（x，y，z）上的势是

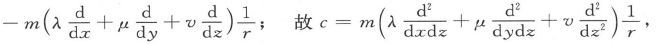
利用拉普拉斯方程，此式可以写成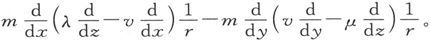

a、b各量也可以按同样方式来处理。

由此即得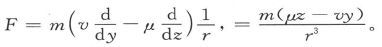

利用对称性，由此式也可求出G和H。于是我们就看到，由一个位于原点上的磁化粒子在一个给定点上引起的矢势，在数值上等于粒子的磁矩除以矢径的平方并乘以磁化轴线和矢径之夹角的正弦，而矢势的方向则垂直于磁化轴线和矢径的平面，而且对于一个沿磁化轴线的正方向看过去的眼睛来说，矢径是沿着顺时针的方向画出的。

由此可见，对于任意形状的磁体来说，若在点（x，y，z）处的磁化分量是A、B、C，则点（ξ，η，ζ）上的矢势分量是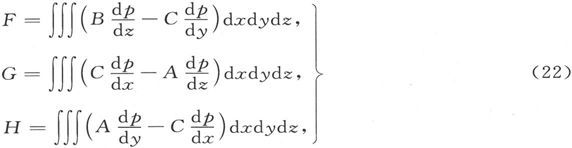　　

式中为了方便，用p代表了点（ξ，η，ζ）和点（x，y，z）之间的距离的倒数，而积分则遍及于磁体所占的空间。

406．〕　第385节中磁力的标势或普通的势，当用同样的符号表示出来时就是

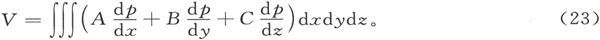
记得 并记得积分　　

当点（ξ，η，ζ）位于积分域内时的值是-4π（A），而当它不位于积分域内时的值是零，此处（A）是A在点（ξ，η，ζ）上的值，我们就得到磁感之x分量的表示式如下：

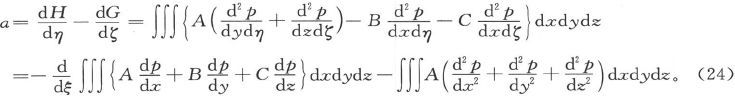
此式的第一项，显然就是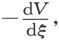 或者说是磁力的分量α。

第二项中的被积分式对每一体积元都为零，只有包含点（ξ，η，ζ）的体积元例外。如果A在点（ξ，η，ζ）上的值是（A），则很容易证明第二项的值是4π（A），此处（A）在磁体外面的所有各点上显然都是零。

现在我们可以把磁感的x分量写成　　

这是和第400节中给出的那些方程的第一个方程相等同的一个方程。关于b和c的方程也将和第400节中的方程相一致。

我们已经看到，磁力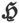 是通过哈密顿算符∇的应用而从标量磁势V推出的，从而我们可以像在第17节中一样地写出　　

而且这个方程是在磁体之外或之内都成立的。

由现在的考察可以看出，磁感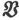 是通过同一算符的应用而从矢势 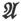导出的，而且结果是在磁体之内和之外都能成立的。

这一算符对一个矢量函数的应用，通常将给出一个标量和一个矢量。然而，我们曾称之为矢量函数之敛度的那个标量部分，当矢量函数满足管状条件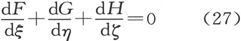

时将等于零。通过求方程组（22）中F、G、H的表示式的导数，我们发现各该量是满足这一条件的。

因此我们可以写出磁感和它的矢势之间的关系式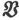 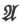＝∇ ，这可以用文字表示出来，即磁感等于矢势的旋度。参阅第25节。

第二十八章　磁管和磁壳 ^〔9〕

论特殊形式的磁体

407．〕　如果形如导线的一种磁性物质的细长丝到处沿纵向而被磁化，则细丝的任一截面和该截面上平均磁化强度的乘积，叫做磁体在该截面上的强度。如果细丝在截面处被切成两段而不改变其磁化，则两个表面在分开以后将被发现具有相等而异号的表面磁量，其中每一磁量都在数值上等于磁体在该截面处的强度。

一条磁性物质细丝，如果磁化得在每一截面上都具有相同强度而不论截面取在沿轴线的何处，就叫做一条“磁管”。如果m是磁管的强度，ds是它的一个长度元，而s是从磁体的负极向正极测量的，设r是这一长度元到一个给定点的距离，而ε是r和长度元的磁化轴线之间的夹角，则由这一长度元在所给点上引起的势是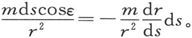

把这一表示式对s求积分，以照顾到磁管的所有各长度元，就得到磁管的势函数 式中r₁ 是磁管的正极到测量磁势所在之点的距离，而r₂ 是磁管的负极到该点的距离。

因此，由一条磁管引起的势，从而还有它的一切磁效应，都只依赖于磁管的强度及其两个端点的位置，而完全不依赖于它在二点之间的形状，不依赖于它是直的还是弯的。

因此，一条磁管的两个端点，就可以在一种直接的意义下被称为它的两个极。

如果磁管形成一条闭合的曲线，则由它引起的势在每一点上都为零，因此这样一条磁管不能产生任何的磁作用，而且，不在某一点上把它切断并将断点分开，它的磁化也就不可能被发现。

如果一个磁体可以划分为若干磁管，而且各磁管不是形成闭合曲线就是在磁体的外表面上有其端点，则磁体的磁化叫做管状的，而且，既然磁体的作用完全取决于各磁管端点的作用，假想磁质的分布就将是完全的面分布。

因此，磁化为管状的条件就是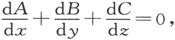 式中A、B、C是磁体任一点上的磁化分量。

408．〕　一条纵向磁化的、其强度沿长度而变化的细丝，可以设想为由一束不同长度的磁管构成，所有通过一个给定截面的磁管的强度之和，就是细丝在该截面上的磁性强度。因此，任何一条纵向磁化的丝，可以叫做一条“复杂磁管”。

如果一条复杂磁管在任一截面上的强度是m，则由它的作用而引起的势

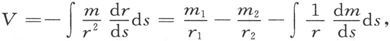
式中m为变量，这就表明，除了在这一事例中强度可以不相等的二端点的作用以外，还存在一种由假想磁质沿丝长的分布所引起的作用，而这种分布的线密度是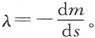

磁　　壳

409．〕　如果磁性物质的一个薄壳是沿着到处和表面相垂直的方向而被磁化的，则任一点上的磁化强度乘以该点的薄壳厚度，就叫做磁壳在该点的“强度”。

如果一个磁壳的强度到处相同，它就叫做一个“简单磁壳”；如果强度逐点变化，磁壳就可以被设想为由若干个简单磁壳叠加在一起而构成。因此它就叫做一个“复杂磁壳”。

设dS是磁壳上一点Q处的一个面积元，而Φ是磁壳强度，则由这一磁壳元在任意点P处引起的势是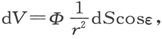 式中ε是矢量QP或r和磁壳正表面上的外向法线之间的夹角。

但是，如果dω是dS在P点所张的立体角，r² dω＝dScosε，则有dV＝Φdω，从而在简单磁壳的事例中就有V＝Φω，或者说，由一个磁壳在任一点上引起的势，等于它的强度和它的边界在所给点所张立体角的乘积 ^〔10〕 。

410．〕　同样的结果可以用另一种办法求得，那就是假设磁壳被放在任何一个磁力场中，并确定由于磁壳的放入而引起的势能。

如果V是面积元dS处的势，则由这一面积元引起的能量是

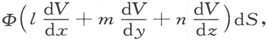
或者说，能量就是磁壳强度乘以由磁壳元dS引起的dV/dv的那一部分面积分。

因此，按所有这样的磁壳元求积分，由磁壳在场中的位置而引起的能量，就是磁壳强度和磁感在磁壳面积上的积分的乘积。

既然这一面积分对任何两个具有相同的边界线而在二者之间并不包含任何力心的曲面来说是相同的，磁壳的作用就只依赖于它的边界线。

现在假设力场是由强度为m的一个磁极引起的。我们已经看到（第76节的引理），在边界线给定的一个曲面上求的面积分，等于磁极强度和边界线在磁极那儿所张立体角的乘积。因此，由磁极和磁壳的相互作用而引起的能量就是Φmω，而由格林定理可知，这个量就等于磁极强度和磁壳在磁极那儿引起的势的乘积。因此磁壳引起的势就是Φω。

411．〕　如果一个磁极m从一个磁壳的负侧的任一点开始，并沿着空间中的一条任意路径绕过边界线而运动到磁壳正侧和起始点很靠近的一点，则立体角将连续变化，并在过程中增大4π。磁极所做的功将是4πΦm，从而磁壳正侧任一点上的势，将比负侧一个邻近点上的势大4πΦ。

如果一个磁壳形成一个闭合曲面，则磁壳外面的势到处为零，而磁壳内部空间中的势则到处是4πΦ；它是正的，若磁壳的正面是朝里的。因此，这样一个磁壳就对放在壳外或壳内的任何磁体都不作用任何力。

412．〕　如果一个磁体可以划分为一些简单磁壳，而各该磁壳不是闭合的就是其边界线位于磁体的表面上，则磁性的分布叫做“层状”分布。如果φ是一个点当从一个给定位置沿着磁体内部的一条路线而运动到一个点（x，y，z）时所穿过的所有各磁壳的强度之和，则层状磁化的条件是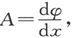

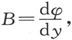
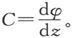
这样地完全确定着任一点上的磁化的这个量φ，可以叫做“磁化势”。它必须被认真地和“磁势”区分开来。

413．〕　一个可以分成复杂磁壳的磁体，叫做具有磁性的一种复杂层状分布。这样一种分布的条件是，磁化线的分布必须使得有可能画出一组和它们正交的曲面。这一条件由众所周知的方程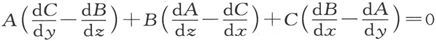 来表示。

管状和层状磁体的势函数形式

414．〕　一个磁体的标势的普遍表示式是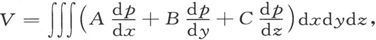 式中p代表由位于（ξ，η，ζ）处的一个单位磁极在点（x，y，z）上引起的势，或者换句话说，它代表从测量磁势之点（ξ，η，ζ）到引起磁势的磁体元所在之点（x，y，z）的距离的倒数。

这个量可以分部求积分，正如在第96、386节中那样

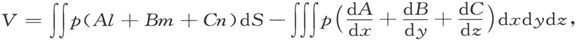
式中l、m、n代表磁体表面的一个面积元dS上的外向法线的方向余弦。

当磁体是管状的时，第二项中的被积函数在磁体内部的每一点上都为零，从而三重积分为零，从而在磁体之内或之外的任一点上，磁势都由第一项中的面积分来给出。

因此，当磁体表面的每一点上的磁化法向分量为已知时，一个管状磁体的标势就是完全确定的，而且它是和磁体内部的磁管形状无关的。

415．〕　在一个层状磁体的事例中，磁化由磁化势φ来确定，即有

因此V的表示式就可以写成　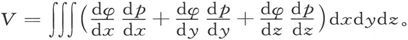　 把这一表示式分部求积分，就得到

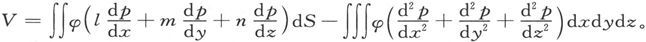
第二项为零，除非点（ξ，η，ζ）被包含在磁体内部；在那种事例中，该项变为4π（φ），此处（φ）是φ在点（ξ，η，ζ）上的值。面积分可以用从（x，y，z）到（ξ，η，ζ)的直线r以及该直线和dS上的外向法线之间的夹角θ表示出来，于是势函数就可以写成

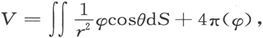
式中的第二项，当点(ξ，η，ζ)并不位于磁体物质内时当然等于零。

由这一方程来表示的势V，甚至在φ突然变为零的磁体表面上也是连续的。因为，如果我们写出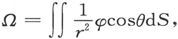 而且Ω₁ 是Ω在刚刚位于表面内部的一个点上的值，而Ω₂ 是它在刚刚位于表面外面并和前面那个点很靠近的一个点上的值，就有Ω₂ ＝Ω₁ ＋4π（φ），或者说V₂ ＝V₁ 。因此Ω这个量在磁体的表面上是连续的。

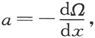
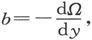
磁感分量和Ω的联系由方程组 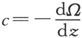来表示。

416．〕　在层状磁性分布的事例中，我们也能简化磁感的矢势。

它的x分量可以写成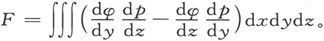

通过分部求积分，我们可以把这个量写成面积分的形式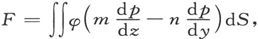 或者写成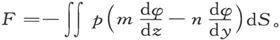

矢势的其他分量，也可以通过适当的代换而据这一表示式写出。

论立体角

417．〕　我们已经证明，在任一点上，由一个磁壳引起的势等于由磁壳边界线所张的立体角乘以磁壳的强度。由于我们在电流理论中将有机会涉及立体角，现在我们将解释一下立体角是怎样量度的。

定义　一条闭合曲线在一个给定点上所张的立体角，由一个球面上的一块面积来量度；球面的中心位于所给之点，球面的半径为一个单位，而所取的面积则由当矢径描绘该闭合曲线时它和曲面的交点的运动轨迹来限定。这一面积的是正是负，按照从所给点看来该面积是位于矢径路径的左侧或右侧来决定 ^〔11〕 。

设（ξ，η，ζ）是所给的点，而（x，y，z）是闭合曲线上的一个点。坐标x，y，z是s的函数，s即从一个给定点算起的曲线长度。这些坐标是s的周期函数；每当s增加一个等于闭合曲线全长度的量时，正数就重复一次。

我们可以根据这样的定义来直接计算立体角ω。利用以（ξ，η，ζ）为中心的球坐标，并令x－ξ＝rsinθcosφ，y－η＝rsinθsinφ，z－ζ＝rcosθ，我们通过积分就能求出球面上任意曲线的面积ω＝∫（1－cosθ）dφ，或者，利用直角坐标，就有

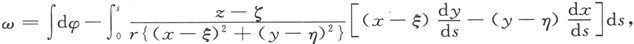
积分是沿曲线s计算的。

如果z轴穿过闭合曲线一次，则第一项为2π。如果z轴并不穿过闭合曲线，则此项为零。

418．〕　这种计算立体角的方法涉及坐标轴的在某种程度上带有任意性的一种选择，从而它并不是只依赖于闭合曲线的。因此，为了几何学上的适当性，可以谈谈下面这种并不涉及任何曲面画法的方法。

当从一个给定点画起的矢径描绘出一条闭合曲线时，设有一个通过所给点的平面在闭合曲线上滚动，以致这个平面逐次成为曲线上每一点的切面。设从所给点开始画一条单位长度的直线使它垂直于这个平面。当平面沿闭合曲线滚动时，这条垂线的端点将描绘出第二条闭合曲线。设第二条闭合曲线的长度为σ，则第一条闭合曲线所张的立体角是ω＝2π－σ。

这一结果可以从一条众所周知的定理推出。那定理就是，单位半径的球面上一条闭合曲线所限定的面积，以及这一极坐标曲线的周长，在数值上等于球面上一个大圆的周长。

这种想法有时在求一个直线图形所张的立体角时是方便的。我们的目的是要形成物理现象的一种清晰的概念。对于这种目的来说，下述的办法是更合用的，因为它并不会用到问题之物理数据以外的任何构想。

419．〕　设在空间中给定了一条闭合曲线s，而我们必须求出s在一个给定点P上所张的立体角。

如果我们把这个立体角看成边界线和闭合曲线相重的一个单位强度的磁壳所引起的势，我们就必须把它定义为一个单位磁极在从无限远处运动到点P时反抗磁力而做的功。因此，如果σ是磁极向P点运动过来时所沿的路径，则磁势必然是沿这一路径的一个线积分的结果。它也必将是沿闭合曲线s的一个线积分的结果。因此，立体角表示式的正确形式，必将是按两条曲线s和σ来计算的一个二重积分。

当P位于无限远处时，立体角显然是零。当P逐步靠近时，从运动点看来的闭合曲线就显得是逐渐张开的，从而整个的立体角就可以设想为是当运动点靠近过来时由闭合曲线上不同线段元的表观运动来生成的。

当P点径由线段元dσ从P运动到P′时，我们用ds来代表的闭合曲线之线段元QQ′将相对于P而改变其位置，而单位球上和QQ′相对应的直线则将在球面上扫过一个面积，我们可以把这个面积写成

为了求出Π，让我们假设P为固定而闭合曲线却平行于自身而移动了一段等于PP′但方向相反的距离dσ。P点的相对运动将和实际事例中相同。

在这种运动过程中，线段元QQ′将生成一个平行四边形的面积，其二边分别平行于并等于QQ′和PP′。如果我们以这个平行四边形为底而以P为顶点来画出一个角锥体，则这个角锥体的立体角就将是我们正在寻求的增量dω。

图42

为了确定这一立体角的值，设Q和Q′分别是ds及dσ和PQ之间的夹角，并设φ是这两个角度的平面之间的夹角，于是平行四边形dsdσ的PQ或r的垂面上的投射面积就将是dsdσsinθsinθ′sinφ，而既然这一面积等于r² dω，我们就有

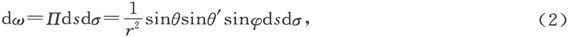
由此即得　　

420．〕　我们可以用r及其对s和σ的微分系数来把角θ、θ′和φ表示出来，因为

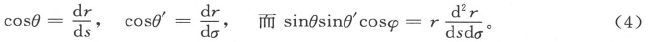
于是我们就求得Π² 的值如下：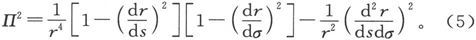

用直角坐标来表示的第三个Π表示式可以由下述考虑来得出：立体角为dω而边长为r的那个角锥体的体积是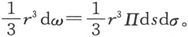

但是这个角锥体的体积也可以用r、ds和dσ在x轴、y轴和z轴上的投影来表示成这九个投影的行列式，而我们则必须取这个行列式的第三个部分。于是，作为Π的值，我们就得到 ^〔12〕

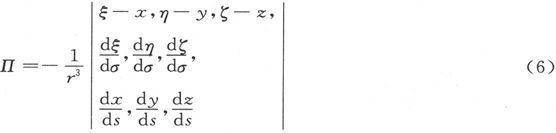
这一表示式给出Π的值，而不带方程（5）所引入的正负号方面的含糊性。

421．〕　现在，闭合曲线在P点所张立体角ω的值就可以写成

式中对s的积分是沿着整个闭合曲线计算的，而对σ的积分则从曲线上的一个固定点A计算到点P。常数ω₀ 就是立体角在点A上的值。如果A位于离闭合曲线的无限远处，则ω₀ 为零。

ω在任一点P上的值和A、P之间的曲线形状无关，如果该曲线并不穿过磁壳本身的话。如果磁壳是无限薄的，而P和P′是相距很近的两个点，但是P位于磁壳的正表面上而P′位于它的负表面上，则曲线AP和AP′必然位于磁壳边界相反的两侧，于是PAP′就是一条曲线，它和无限短的线段P′P一起形成绕过边界线的一条闭合曲线。ω在P点的值比在P′点的值大4π，这也就是一个单位半径的球面的面积。

因此，如果画一条闭合曲线使它穿过磁壳一次，或者换句话说，如果它和磁壳的边界线互相穿套一次，则在这两条曲线上计算的积分∬Πdsdσ的值将是4π。

因此，当看成只依赖于闭合曲线s和任意曲线AP时，这个积分就是一个多值函数的实例。因为，如果我们沿着不同的路径从A移动到P，则积分将有不同的值，全看曲线AP穿过曲线s的次数而定。

如果A和P之间曲线的一种形状可以不经过和曲线s相交的连续变动而变换成另一种形状，则积分在这两条曲线上将有相同的值，但是，如果它在变动中和闭合曲线相交n次，则积分值将相差4πn。

设s和σ是空间中任意两条闭合曲线，如果它们并不互相穿套，则在两条曲线上各计算一次的积分是零。

如果它们沿同一方向互相穿套n次，则积分的值为4πn。然而，也可能有两条曲线沿相反的方向而交替穿套，以致它们不可分离地互相扭结在一起，尽管积分的值是零。见图43。

图43

这个积分表示着一个磁极当在一个闭合电流的附近描绘一条闭合曲线时外界对它做的功，它也指示着两条闭合曲线之间的几何学联系；正是由于高斯发现了这个积分，才使他因为自从莱布尼兹、欧勒和范德蒙德以来“位置几何学”的进步之慢而深感遗憾。然而我们现在却有些进步可以报告，这主要归功于黎曼、亥姆霍兹和李斯廷。

422．〕　现在让我们考察沿闭合曲线对s求积分的结果。方程（7）中Π的一项是

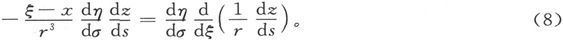
如果我们为了简单而写出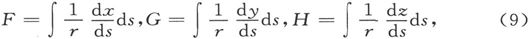　　

式中的积分沿着闭合曲线s计算一周，则Π的这一项可以写成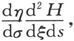 而∫Πds中的对应项则为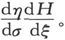

现在，把Π的各项归并起来，我们就可以写出

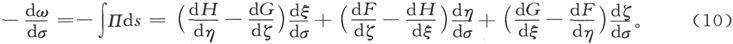
这个量显然就是ω的减少率，即磁势沿曲线σ绕行时的减少率；或者换句话说，它就是dσ方向上的磁力。

通过逐次假设dσ和x、y及z轴方向一致，我们就得到磁力分量的值

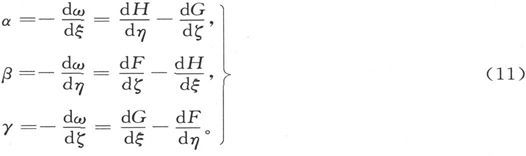
各量F、G、H是一个磁壳的矢势分量，该磁壳的强度为1而其边界线是s。它们并不像标势ω那样是一些有着一系列值的函数，而在空间的每一点上都完全确定。

由以一条闭合曲线为边界的一个磁壳在一点P上引起的矢势，可以用下述的几何作图方法求得。

设一点Q沿闭合曲线而运动，其速度在数值上等于该点到P的距离；再设第二个点R从一个固定点A开始，其运动速度的方向永远平行于Q的速度，但其速度的数值等于1，当Q已经沿闭合曲线运行了一周时，作连线AR，于是线段AR就在方向上和量值上表示由闭合曲线在P点引起的矢势。

放在磁场中的一个磁壳的势能

423．〕　我们在第410节中已经证明，放在势为V的磁场中的一个强度为φ的磁壳的势能是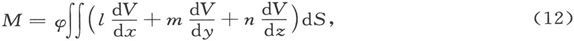　　

式中l、m、n是磁壳正侧的外向法线的方向余弦，而积分遍布于磁壳的面积上。

现在，借助于磁场的矢势，可以把这个面积分变换成一个线积分，而且我们可以写出

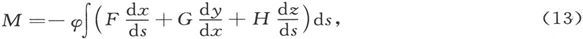
式中的积分应沿形成磁壳之边界的闭合曲线s计算一周，而从磁壳的正侧看去ds的方向应是逆时针的。

如果现在我们假设磁场是由强度为φ′的第二个磁壳引起的，我们就可以由第416节或第405节的结果直接定出F的值。如果l′、m′、m′是第二个磁壳的面积元ds′上的外向法线的方向余弦，我们就有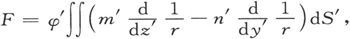 式中r是面积元dS′和第一磁壳边界线上一点之间的距离。

现在，这个面积分可以变换成一个沿第二磁壳边界线的线积分，那就是

同样即得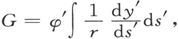

把这些值代入M的表示式中，我们得到

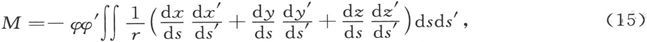
式中的积分沿s计算一周并沿s′计算一周。这一表示式给出由两个磁壳的相互作用而来的势能，而且正如理所当然的那样当把s和s′互换时表示式是不变的。这在电流理论中是一个很重要的物理量。如果我们用ε来代表线段元ds和ds′的方向之间的夹角，则s和s′的势可以写成　　　

这显然是一个具有长度量纲的量。

第二十九章　感生磁化

424．〕　迄今为止，我们一直把磁体中的磁性分布看成一种明确给出的研究数据。除了在曾经设想磁体被打成小块或是一些小块被从磁体取走而并不改变任何部分的磁化的那些推理段落以外，我们对磁化是永久的或暂时的问题并未作出任何假设。

现在我们必须参照磁化所能被产生或被改变的方式来考虑物体的磁化。经发现，保持在平行于地球磁力的方向上的一根铁棒，会变成有磁性，其二极和地球的各极相反，或者说它是采取罗盘指针处于稳定平衡时的位置。

放在磁场中的任何一块软铁，都被发现为显示磁性。如果它被放在场中磁力较大的部分，例如放在一个蹄形磁铁的两极之间，则软铁的磁性变强。如果铁块被从磁场中取出，则它的磁性大大减弱或完全消失。如果铁的磁性完全依赖于它所在的场中的磁力，而当从场中取出时磁性就消失，则它叫做“软铁”。在词的意义上是软的铁。它很容易被弄弯并得到永久的变形，而且很不容易被弄断。

当从磁场中被取出时仍保持其磁性的铁，叫做“硬铁”。这样的铁不像软铁那样容易达成其磁状态。锤击手续或任何其他种类的振动，能使硬铁在磁力的影响下更容易达成磁状态，并使它当磁化力被取消时更容易离开磁状态 ^〔13〕 。磁性上硬的铁也更难弯曲而更易于折断。

锻造、轧制、拉丝和突然冷却等过程倾向于使铁变硬，而退火过程则倾向于使铁变软。

硬钢和软钢之间的磁性差别，也像它们的机械差别一样，是比硬铁和软铁之间的差别大得多的。软钢几乎像铁一样容易被磁化和被去磁，而最硬的钢则是制造我们希望长久使用的磁体的最好材料。

铸铁虽然比钢含有更多的碳，但是却不像钢那样易于保持磁性。

假如一个磁体可以磁化得使它的磁化分布不会被它能受到的任何磁力所改变，它就将可以称为一个刚性磁化的物体。唯一已知的满足这种条件的物体就是里边通有恒定电流的一个传导电路。

这样一个电路显示磁学性质，从而可以叫做一个电磁体，但是它的磁学性质却不受其他场中的磁力的影响。我们将在第四编中回到这一课题上来。

一切实际的磁体，不论是用硬化的钢做成还是用磁石做成的，都被发现为会受到外来作用的任何磁力的影响。

为了科学的目的，区分永久磁化和暂时磁化是方便的；这时把永久磁化定义为不依赖于磁力而存在的磁化，把暂时磁化定义为依赖于磁力而存在的磁化。然而我们必须注意，这种区分并不是建筑在一种有关可磁化物质之内在本性的知识上的，它只是一种为了使计算和现象发生关系而引入的一个假说的表达方法而已。在第五章中，我们将回到物理的磁化理论上来。

425．〕　在目前，我们将考察暂时磁化，所依据的假设是，物质中任一粒子的磁化，只依赖于作用在该粒子上的磁力。这个磁力可以部分地起源于外界的原因，并部分地起源于附近各粒子的暂时磁化。

借助于磁力的作用而这样磁化了的一个物体，叫做被感应磁化了，而其磁化则叫做由磁化力所感生的。

由一个给定磁力所感生的磁化，在不同的物质中是不同的。在最纯的和最软的铁中，感生磁化最大，这时磁化和磁力之比可以达到32，甚至达到45 ^〔14〕 。

其他的物质，例如金属镍和金属钴，可以达到一种较低的磁化程度，而且人们发现，当受到足够强的磁力作用时，所有的物质都会显示极性。

当磁化和磁力方向相同，就像在铁、镍、钴等等中那样时，物质就叫做“顺磁性的”、“铁磁性的”或简称为“磁性的”物质。当感生磁化和磁力方向相反，就像在铋等等中那样时，物质就被说成是“抗磁性的”。

在所有的这些抗磁性物质中，磁化和产生磁化的磁力之比都是非常小的，在铋中仅为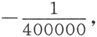 而铋是已知的最高度抗磁性的物质。

在结晶的、形变的和组织化的物质中，磁化的方向并不总是和引起磁化的磁力的方向相一致。相对于固定在物体内的坐标轴来说，磁化分量和磁力分量之间的关系，可以用一组三个线性方程来表示。我们即将证明，在这些方程所包含的九个系数中，只有六个是独立的。有关这一类物体的现象，叫做“磁晶现象”。

当放在一个磁力场中时，晶体倾向于转入适当的取向，以使最大顺磁感应或最小抗磁感应的轴线和磁力线相平行。见第436节。

在软铁中，磁化的方向和该点磁力的方向相重合，而且对于小值的磁力来说磁化近似地正比于磁力 ^〔15〕 。然而，当磁力较大时，磁化却增加得较慢一些，而且由第六章中所描述的那些实验将可看出，存在一个磁化的极限值，而不论磁力的值是什么，磁化都不能超过这个值。

在下面的简略感生磁理论中，我们将从一种假设开始，那就是，磁化正比于磁力，并且和磁力共线。

感生磁化系数的定义

426．〕　设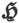 是在物体中任意点上像在第398节中那样定义的磁力，而 是该点的磁化，则 和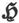 之比叫做“感生磁化系数”。

用κ代表这个系数，则感生磁的基本方程是　　

系数κ对铁磁性和顺磁性物质来说是正的，对铋及其他抗磁性物质来说是负的。它在铁中可高达｛1600｝，而且在镍和钴的事例中也被说成是大的，但在所有其他的事例中它都是一个很小的量，不超过0.00001。

磁力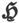 部分地起源于被感生磁化的物体外部的那些磁体，部分地起源于物体本身的感生磁化。这两部分都满足有势条件。

427．〕　设V是由物体外面的磁体所引起的势，而Ω是由感生磁化所引起的势，那么，如果U是由这两种原因所引起的实际的势，则有　　

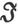设磁力 沿x、y、z方向的分量是α、β、γ，而磁化 的分量是A、B、C，则由方程（1）得到

将这些方程分别乘以dx、dy、dz并相加，我们就得到

Adx＋Bdy＋Cdz＝κ（αdx＋βdy＋γdz）。

但是，既然α、β和γ是由势U推得的，我们就可以把右端写成-κdU。

因此，如果κ在物质中到处为常量，则上式的左端也必然是x、y和z的一个函数的全微分。用φ代表这个函数，则上式变成　　

式中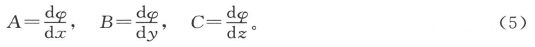　　

因此，磁化是层状的，正如在第412节中定义的那样。

在第385节中已经证明，如果ρ是自由磁量的体密度，则有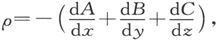　　

由于存在方程（3），上式变为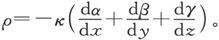

但是，由第77节就有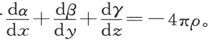 因此得到（1＋4πκ）ρ＝0由此即得，在整块物质中应有　　

从而磁化既是层状的，也是管状的。

因此，除了在物体的边界面上以外，不存在任何自由磁量。如果v是表面的内向法线，则磁量的面密度是　　

因此，由这一磁化在任意一点上引起的势Ω，可以由下列的面积分求得：

Ω的值将到处是有限的和连续的，而且在表面的内外都将满足拉普拉斯方程。如果我们用一个撇号来区分表面外部的Ω值，而且，如果v′是外向法线，则我们在表面上得到

因此我们可以写出第二个表面条件式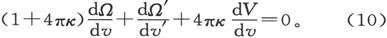　　

由此可见，在一个以曲面S为边界并受到其势为V的磁力的作用的均匀各向同性的特体中，感性磁量的确定可以归结为下列的数学问题。

我们必须求出满足下列条件的两个函数Ω和Ω′：

在曲面S内部，Ω必须是有限和连续的，而且必须满足拉普拉斯方程。

在曲面S的外面，Ω′必须是有限和连续的，它在无限远处必须变为零，而且它必须满足拉普拉斯方程。

在曲面本身的每一点上，Ω＝Ω′，而且Ω、Ω′和V沿法线求的方向导数必须满足方程（10）。

这种处理感生磁量问题的方法，是由泊松提出的。他在自己的论著中使用的一个量k和这里的κ并不相同，而是和它有下列的关系：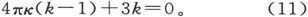　　

我们在这里采用的k这个系数，是由F. E. 诺依曼引入的。

428．〕　感生磁的问题，也可以通过像法拉第那样引入我们称之为“磁感”的那个量来用另一种办法处理。

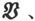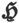磁感 磁力 和磁化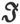 之间的关系，由方程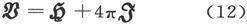 　　

来表示。

用磁力来表示感生磁化的方程是　　

因此，消去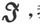 我们就得到其磁化由磁力感生而成的物质中的磁感和磁力之间的关系式如下：　　

在最普遍的事例中，κ可以不仅是物质中各点位置的函数，而且是矢量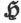 的方向的函数。但是在我们现在考虑的事例中，κ却是一个数字量。

如果写出　　

我们就可以把μ定义成磁感和磁力之比，而且我们可以把这一比值叫做物质的磁感本领，以别于感生磁化系数κ。

如果用U来代表由外界原因所引起的势V和感生磁化所引起的势Ω合成的总磁势，我们就可以表示磁感分量a、b、c和磁力分量α、β、γ如下：

各分量a、b、c满足管状条件　　

由此可见，势U必须在μ为常量处的每一点上满足拉普拉斯方程

也就是必须在均匀物质或真空中的每一点上满足该方程。

在表面本身上，设v是指向物质内部的法线而v′是外向法线，如果物质外部各量的符号用一个撇号来区分，则磁感的连续性条件是

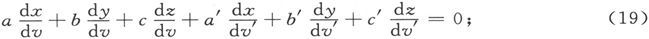
或者，由方程（16）就得，　　

磁体外面的磁感系数μ′将是1，除非周围的媒质是磁性的或抗磁性的。

如果把U的值用V和Ω表示出来，并把μ的值用κ表示出来，我们就得到以前用泊松法求得的同一方程（10）。

当从磁感和磁力的关系方面来看它时，感生磁的问题是和在第310节中给出的那种各向异性媒质中的传导电流的问题确切对应的。

磁力从磁势中导出，恰恰和电力从电势中导出完全一样。

磁感是一个具有流量本性的量，而且像电流一样满足同样的连续性条件。

在各向同性媒质中，磁感依赖于磁力的方式，恰恰和电流依赖于电动势的方式相对应。

一个问题中的磁比感本领，对应于另一问题中的电导率。因此汤姆孙在他的Theory of Induced Magnetism (Reprint, 1872, p. 484）［《感生磁理论》］中曾称这个量为媒质的“磁导率”。

现在我们做好准备来从我所认为的法拉第观点考虑感生磁的理论了。

当磁力作用在任何一种媒质上时，不论媒质是磁性的、抗磁性的还是中性的，它都会在媒质中引起一种叫做“磁感应”的现象。

磁感是一种具有流量本性的有向量，而且像电流及其他流量那样地满足相同的连续性条件。

在各向同性媒质中，磁力和磁感方向相同，而且磁感是磁力和我们曾用μ来代表之的一个叫做磁感系数的量的乘积。

在真空中，磁感系数是1。在可以受到感生磁化的物体中，磁感系数是1＋4πκ＝μ，式中κ是已经定义为感生磁化系数的那个量。

429．〕　设μ、μ′是两种媒质的分界面两侧的μ值，如果V、V′是两种媒质中的势，则两种媒质中指向分界面的磁力是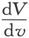 和

通过面积元dS的磁感通量，沿指向dS的方向计算，在两种媒质中分别是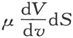 和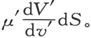

既然流向dS的总通量为零，就有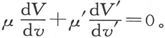 但是，由关于密度为σ的表面附近的势的理论可知， 由此即得，

如果κ₁ 是系数为μ的媒质中表面磁化和法向力之比，我们就有

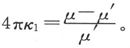
由此可见，按照μ是大于或小于μ′，κ₁ 将是正的或负的。如果我们令μ＝4πκ＋1和dμ′＝4πκ′＋1，就有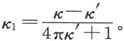

在这一表示式中，κ和κ′是由在空气中进行的实验推得的第一种和第二种媒质的感生磁化系数，而κ是当被第二种媒质所包围时第一种媒质的感生磁化系数。

如果κ′大于κ，则κ₁ 是负的，或者说第一种媒质的表观磁化是和磁化力方向相反的。

例如，如果一个充有顺磁性铁盐之稀水溶液的容器被挂在同种盐类的较浓溶液中并受到一个磁体的作用，则容器将运动，就像是沿着和当一个磁体被悬在同一地点时所将采取的方向相反的方向而被磁化了那样。

这一点可以用一条假说来加以解释；其假说就是，容器中的溶液确实是沿着磁力的方向而被磁化的，但是容器周围的溶液却是更强地沿着同一方向而被磁化的。因此，容器就像是放在两个强磁体之间的一个弱磁体，三者都沿着相同的方向而被磁化，从而相反的极互相接触。弱磁体的北极指向强磁体北极所指的同一方向，但是，既然它是和较强磁体的南极接触着的，在它的北极附近就有一些多余的南磁量，这就使得弱磁体显得像是沿相反的方向而被磁化了一样。

然而，在某些物质中，即使当它们被悬挂在所谓的真空中时，它们的表观磁化也是负的。

如果我们假设真空的κ＝0，则这些物质的κ将是负的。然而却从来不曾发现任何具有数值上大于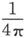 的负κ的物质，因此一切已知物质的μ都是正的。

κ为负从而μ小于1的物质，叫做“抗磁性物质”。κ为正而μ大于1的物质叫做“顺磁性物质”或“铁磁性物质”，或者简称为“磁性物质”。

当我们在第832—845节中讨论到电磁现象时，我们将考虑抗磁性质和顺磁性质的物理理论。

430．〕　磁感应的数学理论是由泊松 ^〔16〕 最初提出的。他的理论所依据的，是二磁流体假说，这是和二电流体学说有着相同的数学优点和物理困难的一个假说。然而，为了解释为什么一块软铁可以通过感应来被磁化，而却不能充以数量不相等的两种磁质，泊松就假设了一般的物质是磁流体的非导体，而且只有物质的某些小部分才含有处于自由状态从而可以服从所受作用力而运动的磁流体。物质中的这些小的磁性元，每个都含有数量恰好相等的两种磁流体，而且在每一磁性元的内部，磁流体是可以完全自由地运动的，但是磁流体却绝不能从一个磁性元转入另一个磁性元中。

因此，问题就和关于若干个小的导电物体的问题属于同一类型，那些小导体是散布在一种介电绝缘的媒质中的。这些导体可以具有任意的形状，如果它们是小的并且互不接触的话。

如果它们是一些沿着同一公共方向排列的长形物体，或者，如果它们在一个方向上比在另一个方向上更加密集，则正如泊松本人已经证明的那样，媒质将不是各向同性的。因此，为了避免无用的复杂性，泊松就考虑了这样一种事例：每一个磁性元都是球形的，而且它们的分布并不偏向于任何轴线。他假设了，物质的单位体积中所含各磁性元的总体积是k。

我们在第314节中已经考虑了一种媒质的电导率，在那种媒质中，分布得有一些另一种媒质的小球。

如果媒质的电导率是μ₁ 而小球的电导率是μ₂ ，则我们已经求得复合体系的电导率是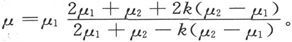 令μ₁ ＝1而μ₂ ＝∞，此式就变为 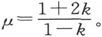这个量μ就是由一些理想导电的小球分布在一种电导率为1的媒质中而形成的复合媒质的电导率，单位媒质体积中小球的总体积为k。μ这个符号也代表一种媒质的磁感系数，该媒质包括一些磁导率为无限大的小球，分布在一种磁导率为1的媒质中。我们将称之为“泊松磁系数”的k这个符号，代表的是各磁性元的和物质的总体积之比。κ这个符号被称为“诺依曼磁感系数”。它比泊松的系数更适用。我们将把符号μ叫做“磁感系数”。它的优点在于能使我们很容易地把磁的问题翻译成有关电和热的问题。

这三个符号的关系如下：

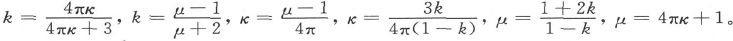
如果我们按照塔伦 ^〔17〕 有关软铁的实验令κ＝32，就会得到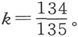 按照泊松的理论，这就是磁分子的总体积和铁的总体积之比。在一个空间中堆满相等的小球，是不可能做到使它们的体积和空间总体积之比如此接近于1的，而且也很难想象铁的这么大一部分体积都被刚性的分子所占满，不论这些分子是什么形状。这是我们之所以必须放弃泊松假说的理由之一。其他的理由将在第六章中加以论述。当然，泊松的数学探讨的价值并不会减小，因为这种探讨不是建筑在他的假说上，而是建筑在感生磁化的实验事实上的。

第三十章　磁感应的特殊问题

中空球壳

431．〕　一个磁感问题的完备解的第一个例子，是由泊松针对一个受到任意磁力作用的中空球壳而给出的。为了简单，我们将假设磁力的源位于球壳外面的空间中。

如果用V代表由外部磁体系引起的势，我们就可以把V展成体谐函数的级数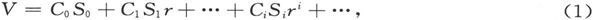

式中r是从球壳中心量起的距离，S_i 是i阶的面谐函数，而C_i 是一个系数。

设球壳的外半径为a₂ 而内半径为a₁ ，并设由球壳的感生磁量所引起的势是Ω。函数Ω的形式，通常在球内空间、球壳物质和球外空间中是不同的。如果把这些函数展成球谐函数的级数并只注意包含面谐函数S_i 的各项，我们就会发现，如果Ω₁ 是对应于球壳内部的空间的函数，则Ω₁ 的展式必然是由形如A₁ S₀ rⁱ 的正的谐函数构成的，因为势一定不能在半径为a₁ 的球内变为无限大。

在r介于a₁ 和a₂ 之间的球壳物质中，级数可以既包含r的正次幂也包含r的负次幂而形如A₂ S_i rⁱ ＋B₂ S_i r^-（i＋1） 。

在球壳外面，r大于a₂ ，既然不论r多大级数也必须收敛，我们就必将只有r的负次幂，形如B₃ S_i r^-（i＋1） 。

函数Ω所必须满足的条件是：它必须是1°有限的，2°连续的，3°在无限远处变为零，4°到处满足拉普拉斯方程。

由1°，就有B₁ ＝0。

由2°，当r＝a₁ 时应有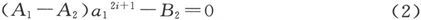　　

而当r＝a₂ 时应有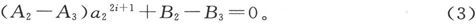　　

由3°就有A₃ ＝0，而条件4°是到处满足的，因为各函数是一些谐函数。

但是，除了这些条件以外，由于有第427节中的方程（10），还有另外一些条件必须在内表面和外表面上得到满足。

在r＝a₁ 的内表面上，有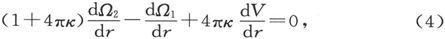　　

而在r＝a₂ 的外表面上则有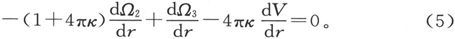　　

由这些条件，我们得到两个方程

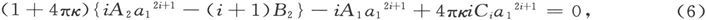
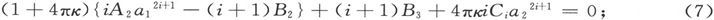
而且，如果令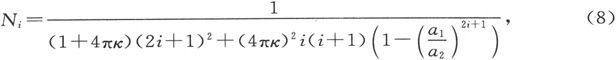　　

我们就得到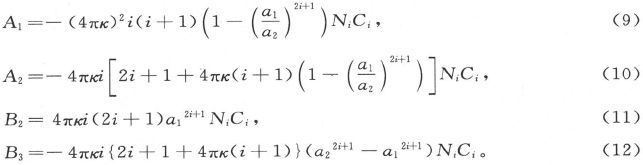　　

把这些量代入谐函数展式中，就得到由球壳的磁化所引起的那一部分磁势。量N_i 永远是正的，因为1＋4πκ不可能为负。由此可知A₁ 永远为负，或者换句话说，磁化球壳在壳内一点上的作用永远和外磁力的作用相反，不论球壳是顺磁性的还是抗磁性的。球壳内部的合磁势的实际值是（C_i ＋A₁ ）S_i rⁱ ，或者写作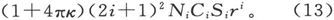

432．〕　当像在软铁的事例中一样κ是一个大数时，球壳内的磁力只是外磁力的一个很小的分数，除非球壳十分的薄。

用这种办法，W. 汤姆孙爵士曾经通过把他的海上电流计封装在一个软铁管中，来使该电流计不致受外磁力的影响。

433．〕　具有最大的实用重要性的事例就是i＝1的事例。这时就有：

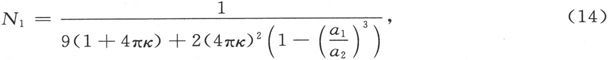
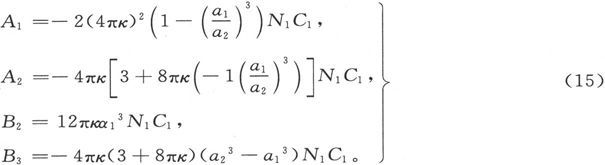
在这一事例中，空壳内部的磁力是均匀的，其量值等于

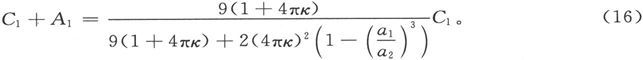
如果我们希望通过测量一个空壳中的磁力并把它和外磁力相比较而来确定κ，则球壳厚度的最佳值可由下列方程求得：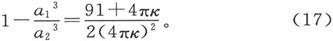　　

这个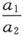 值使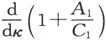 成为一个最大值，因此，当 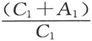的误差给定时，κ的对应误差是尽可能地小的。这时，壳内的磁力是壳外的磁力的二分之一。

既然在铁的事例中κ是一个介于20和30之间的数，球壳的厚度就应该大约是它的半径的百分之二。这种方法只有当κ较大时才是可用的。当它很小时，A₁ 的值就变得微乎其微了，因为它是依赖于κ的平方的。

对于一个具有很小球形空腔的几乎是实心的球来说，我们有

全部的这种探索，也可以从第312节中所给出的关于球壳导电的探索直接推得，只要在那儿所给出的表示式中令k₁ ＝（1＋4πκ）k₂ ，并记得导电问题中的A₁ 和A₂ 等价于磁感应问题中的C₁ ＋A₁ 和C₁ ＋A₂ 就行了。

434．〕　二维空间中的对应解，图解式地表示在本书末尾的图版15上。在离开中心有一个距离处，磁感线接近水平；图中表示的是磁感线受到一个圆柱的干扰时的情况，圆柱被横向磁化，并放在它的稳定平衡位置上。和这组曲线相正交的曲线代表等势面，其中一个是圆柱面。大的虚线圆代表一个顺磁性物质圆柱的截面，圆内那些作为外部磁感线之延长线的水平虚线代表物质内部的磁感线。竖直的虚直线代表内部的等势面，它们和外部的一组等势面也是相接连的。可以看到，磁感线在物质内部被画得较密，而等势面则被顺磁性圆柱隔开得较远一些，而按照法拉第的说法就是，顺磁性圆柱能够比周围的媒质更好地传导磁感线。

如果把竖直的直线族看成磁感线而把水平的直线族看成等势面，我们首先就得到一个在力线中位于其不稳定平衡位置上的横向磁化的圆柱的事例，这时圆柱会使力线散开。其次，把大的虚线圆看成一个抗磁性圆柱的截面，圆内的虚直线和外面的曲线一起，就代表一种抗磁性物质把磁感线排开和把等势面拉近的效应，而这种物质是比周围媒质更差地传导磁感线的。

磁化系数在不同方向上有不同值的一个球的事例

435．〕　设α、β、γ是任意点上的磁力分量，A、B、C是磁化分量，则这些量之间的最普遍的线性关系由下列方程组给出：

式中的系数r、p、q是九个磁化系数。

现在让我们假设，这就是一个半径为a的球的内部的磁化情况，而且物质内的每一点上的磁化都是均匀的和同方向的，其分量为A、B、C。

让我们再假设，外部的磁化力也是均匀的和平行于一个方向的，而且它的分量是X、Y、Z。

因此，V的值就是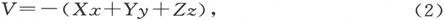　　

而由第391节可知，磁化球外面的势Ω′的值就是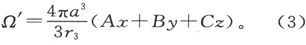　　

磁化球内部的势Ω的值是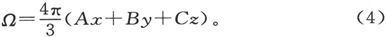　　

球内的实际势是V＋Ω，因此，关于球内的磁力分量，我们将有

由此即得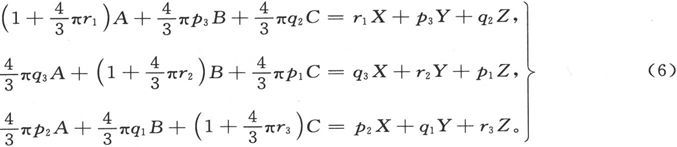　　

求解这些方程，我们得到　　

式中　　

此处D是方程组（6）右端的系数行列式，而D′是其左端的系数行列式。

只有当系数组p、q、r是对称的，即当p式的系数等于对应的q式的系数时，新的系数组p′、q′、r′才是对称的。

436．〕　倾向于使球体绕着x轴从y轴转向z轴的力偶矩 ^〔18〕 ，通过考虑由一个元体积引起的力偶并对球体求力偶矩之和来得出。结果就是

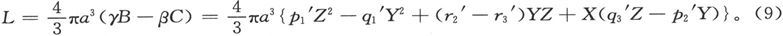
如果我们令X＝0，Y＝Fcosθ，Z＝Fsinθ，这就对应于一个位于yz平面上并和y轴成一个角度θ的磁力F。如果在这个力保持恒定时使球转动，则每转一周力对球做的功将是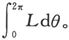 但是这个功等于

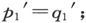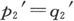由此可见，为使转动的球不致变成取之不尽的能源，应有 同理应有 和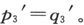

这些条件表明，在原有的方程组中，第三个方程中B的系数等于第二个方程中C的系数，余类推。因此，方程组是对称的，而当相对于磁化主轴写出时，各方程就变成

倾向于使球体绕x轴而转动的力偶矩是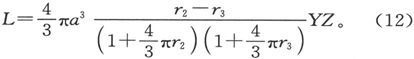

在多数事例中，不同方向上的磁化系数之差是很小的，因此，如果r代表系数平均值，我们就可以令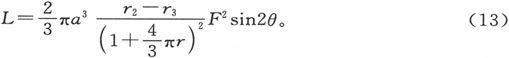　　

这就是倾向于使一个晶体球绕着x轴而从y轴转向z轴的力［力矩］。它永远倾向于使最大磁系数轴（或最小抗磁系数轴）转得和磁力线相平行。

二维空间中的对应事例已表示在图版16上。

如果我们假设该图的上方是向北的，此图就代表受到一个圆柱的干扰的力线和等势面，该圆柱是横向磁化的，其北极一面向着东方。合力倾向于使圆柱从东向北转动。大的虚线圆代表一个结晶物质的柱体的截面，该柱体沿着从东北到西南的一条轴线的磁感系数大于它沿着从西北到东南的轴线的磁感系数。圆内的虚线代表磁感线和等势面，二者在这一事例中并不是互相正交的。作用在柱体上的合力显然倾向于使柱体从东向北转动。

437．〕　放在均匀而平行的磁力场中的一个椭球体的事例，是由泊松用一种很巧妙的方式求了解的。

如果V是一个任意形状的具有均匀密度ρ的物体在点（x，y，z）上引起的引力势，则 应是由同一物体的磁量所引起的势，如果物体被沿着x方向而均匀磁化到强度为I＝ρ的话。

因为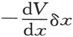， 在任意点上的值，就是物体的势V对另一值V′的超额，此处V′就是当物体沿着x方向运动了一段距离-δx时的势的值。

如果我们假设物体移动了一个距离-δx，而且它的密度从ρ变成了-ρ（就是说，它不再是由引力物质构成的而是由斥力物质构成的了），则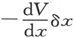 将是由这样两个物体所引起的势。

现在考虑物体的任意一个元部分，设其体积为δυ。它的质量是ρδv，而与此对应，就有一个移动后的物体元，其质量为-ρδv，并位于距离-δx处。这两个物体元的效应是和一个强度为ρδυ而长度为δx的磁体的效应相等价的。磁化强度通过把物体元的磁矩除以它的体积来求得。结果就是ρδx。

因此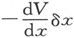， 就是一个沿x方向而磁化到强度ρδx的物体的磁势，而 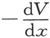就是磁化到强度ρ的物体的磁势。

这个势也可以从另一角度来加以考虑。物体被移动了一个距离-δx并由密度为-ρ的物质所构成。在物体在其两个位置上所共同占据的整个空间区域中，密度到处为零，因为，就其引力而言，两个相等而异号的密度将互相抵消。因此，剩下来的只是一个壳，一边是正物质另一边是负物质，从而我们可以认为合势就是由这物质引起的。在外向法线和x轴的夹角为ε的地方，壳的厚度是δxcosε而其密度为ρ。因此面密度就是ρδxcosε，而在势为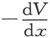 的事例中则面密度为ρcosε。

用这种办法，我们可以求出沿给定方向而均匀磁化的任意物体的磁势。现在，如果这种均匀磁化起源于磁感应，则物体内部所有各点上的磁化力也必须是均匀而平行的。

这个力包括两部分，一部分由外界原因引起，另一部分由物体磁化引起。因此，如果外磁力是均匀而平行的，则由磁化所引起的磁力在物体内部的所有各点上也必将是均匀而平行的。

因此，为了使这一方法可以导致磁感问题的一个解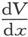， 就必须在物体内部是坐标x、y、z的一个线性函数，从而V就必须是坐标的二次函数。

现在，我们所熟知的V在物体内部是坐标的二次函数的事例，只有那些物体的边界面是某些完全的二次曲面的事例，而其中这样一个物体为有限大小的唯一事例就是当物体为一椭球体时的事例。因此我们将对椭球体的事例应用这一方法。

设椭球的方程是　　

而Φ₀ 代表定积分　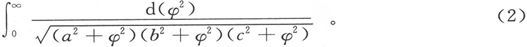　 ^〔19〕

于是，如果我们令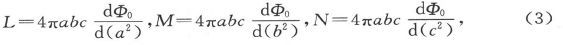　　

则势在椭球内的值将是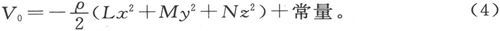　　

如果椭球是沿着其方向余弦为l、m、n的方向而磁化到均匀强度I的，则磁化分量是

A＝Il，B＝Im，C＝In，

而由这一磁化在椭球内部引起的势则是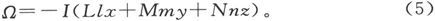

如果外磁化力是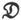 而其分量为X、Y、Z，则它的势将是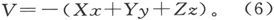

因此，物体内部任一点上的实际磁化力的分量就是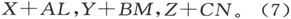

磁化和磁化力之间的最普遍的关系，由包含着九个系数的三个线性方程来给出。然而，为了满足能量守恒的条件，在磁感应的事例中这九个系数中的三个系数必须等于另外三个系数，从而我们就应该有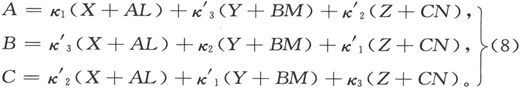

根据这些方程，我们可以由X、Y、Z求出A、B和C，而这就将给出问题的最普遍的解。

这时，椭球外面的势就将是由椭球的磁化所引起的势再加上由外磁力所引起的势。

438．〕　唯一具有实际重要性的事例就是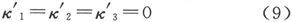　　

的事例。

这时我们就有　　

如果椭球有两个轴是相等的，而且它的形状属于扁平型，则有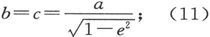　　

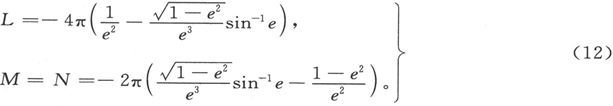
如果它的形状属于细长型，则有

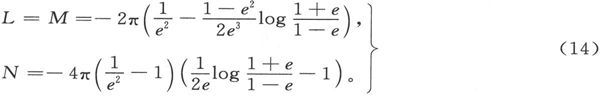
在球的事例中，e＝0，故有　　

在平板式的椭球的事例中，L的值在极限下等于-4π，而M和N变为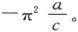

在细长卵形的椭球的事例中，L和M趋近于一个值-2π，而N趋近于一个形式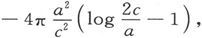

并当e＝1时变为零。

由这些结果可以看出：

（1）当磁化系数κ很小时，不论它为正为负，感生磁化将近似地等于磁化力乘以κ，而几乎和物体的形状无关。

（2）当κ是一个很大的量时，磁化主要依赖于物体的形状而几乎和κ的确切值无关，只除了作用在一个细长椭球上的纵向力的事例以外，该椭球是如此的细长，以致尽管κ很大而Nκ却是一个小量。

（3）假如κ的值可以为负而等于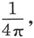 我们在垂直作用在一个平盘上的磁化力的事例中就将得到无限大的磁化。这一结果的荒谬性，就证实了我们在第428节中给出的结论。

由此可见，只要κ很小，就可以利用任意形状的物体来做测定κ值的实验，例如在一切抗磁性物体以及除铁、镍、钴以外的一切磁性物体的事例中就是这种情况。

然而，如果像在铁的事例中那样κ是一个大数，则利用球形或扁平形的物体来做实验就是不适于测定κ的；例如，在球体的事例中，如果像在某些种类的铁中那样κ＝30，则磁化和磁化力之比将等于1比4.22，而假如κ为无限大，则这一比值将等于1比4.19，因此，磁化测定中的很小误差将导致κ值中的很大误差。

但是，如果我们使用一块很长的卵形铁，只要Nκ和一相比还有中等的大小，我们就可以由磁化的测定来推知κ的值，而N值越小则κ值将越准确。

事实上，如果Nκ被弄得足够小，则N本身方面的一个小误差将不会引入多大误差，因此我们可以使用任意形状的长物体，例如长丝或长棒，而不一定使用卵形体 ^〔20〕 。

然而我们必须记得，只有当Nκ还远小于1时这种代换才是允许的。事实上，平头长柱上的磁量分布是和长卵形体上的分布并不相像的，因为在柱端附近自由磁是很集中的，而在卵形体的事例中自由磁的密度却和到赤道的距离成正比。

然而，圆柱上的电的分布，却确实可以和卵形体上的分布相比拟，正如我们已经在第152节中看到的那样。

这些结果也使我们能够理解，当一个永磁体具有细长形状时，为什么它的磁矩可以达到大得多的值。假若我们必须垂直于盘面的方向来把一个圆盘磁化到强度I，然后就把它放置不管，则内部各粒子将受到一个等于4πI的恒定的去磁力，而这个去磁力即使还不足以破坏一部分磁化，它也会很快地做到这一点，如果受到一些振动或温度变化的促进的话 ^〔21〕 。

假如我们要横向地磁化一个柱体，则去磁力将只是2πI。

假如磁体是一个球，则去磁力将是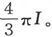

在一个横向磁化的圆盘中，去磁力是 而在一个纵向磁化的长卵形体中，去磁力是最小的，它等于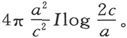

因此，一个细长的磁体，比一个粗短的磁体更不容易失去其磁性。

作用在沿三个轴线具有不同磁系数的一个椭球上并倾向于使它绕x轴转动的力矩是

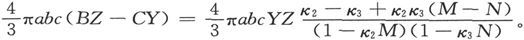
因此，如果κ₂ 和κ₃ 很小，这个力就将主要依赖于物体的结晶品质而不依赖于它的形状，如果它的各方线度相差并不悬殊的话；但是，如果κ₂ 和κ₃ 相当大，就像在铁的事例中那样，力就会显著地依赖于物体的形状，而物体就会转动得使自己的长轴平行于力线。

假如可以得到一个足够强的然而却是均匀的磁力场，则一个细长的各向同性的抗磁性物体也会转动，以使自己的最长的线度和磁力线相平行 ^〔22〕 。

439．〕　一个旋转型椭球在任意磁力作用下的磁化分布问题，曾由J. 诺依曼 ^〔23〕 研究过。基尔霍夫 ^〔24〕 把这种方法推广到了任意力作用下的无限长圆柱的事例。

在他的著作的第17节中，格林曾对受到平行于柱轴的均匀外力X作用的一个有限长圆柱中的磁量分布作出了探讨。尽管这种探讨中的某些步骤并不是很严格，所得结果却很可能大致代表了这一最重要事例中的实际磁化。它肯定很好地表示了从κ很大的柱体事例到κ很小的柱体事例的过渡，但是它在抗磁性物质那样的κ为负数的事例中却是完全失效的。

格林发现，在一个半径为a而长度为2l的圆柱上，距柱体中点为x距离处的自由磁量线密度是 式中p是应由下列方程中求出的一个数字：0.231863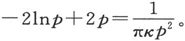

下面是p和κ的一些对应值。

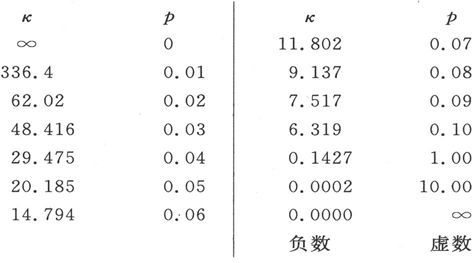
当圆柱的长度远大于它的半径时，柱体中点每一侧的总的自由磁量就理所当然地是

M＝πa² κX。

在这些磁量中，一个量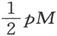 是位于柱体的端平面上的 ^〔25〕 ，而从总量M的重心到柱端的距离是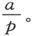

当κ很小时p就很大，从而几乎所有的自由磁都位于柱体的两端。当κ增大时p就减小，而自由磁就分散在离柱端较大的距离处。当κ是无限大时，柱体任意点上的自由磁将简单地正比于从该点到中点的距离，这种分布和均匀力场中的一个导体柱上的电荷分布相仿。

440．〕　在除了铁、镍、钴以外的所有物质中，磁化系数都很小，以致物体的感生磁化只引起磁场中的力的很小变化。因此，作为初级近似，我们可以假设物体内部的实际磁力和物体不存在时的磁力相同。因此，作为初级近似，物体的表面磁化就是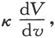 此处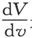 是由外部磁体引起的磁势在表面的内向法线方向上的增加率。现在如果算出由这一表面磁化所引起的势，我们就可以用它来得到第二级近似。

为了在这种初级近似下求出由磁量分布所引起的机械能量，我们必须求出在物体的整个表面上计算的面积分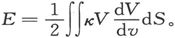 现在，我们在第100节中已经证明，这一积分等于在物体所占的整个空间中计算的体积分 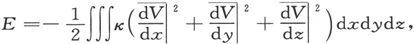或者，如果R是合磁力，则有 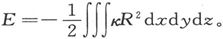现在，既然在一个位移δx上磁力对物体所做的功是Xδx，此处X是x方向上的机械力，而且，既然∫Xδx＋E＝常量，就有 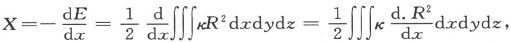而这就表明，作用在物体上的力，就仿佛使物体的每一部分都从R² 较小的地方运动到R² 较大的地方一样，而作用在单位体积上的力则是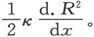

如果像在抗磁性物体中那样κ是负的，则正如法拉第所首次证明的那样，这个力是从磁场的较强部分指向它的较弱部分的。在抗磁性物体的事例中观察到的多数作用，都取决于这一性质。

船舶的磁学

441．〕　差不多磁科学的每一个部分，都在航海中有其用处。地磁对罗盘指针的定向作用，是在太阳和星星都隐没时确定船舶航程的唯一方法。指针对直实子午线的偏角，起初似乎是罗盘在航海方面的应用的一种障碍，但是，当这一困难通过磁力海图的绘制而被克服以后，看来磁偏角本身就很可能会帮助海员确定他的船的位置了。

航海中的最大困难，一直是经度的确定；但是，既然磁偏角在同一经度平行线的不同点上是不同的，一种磁偏角的观测和有关纬度的知识一起，就将使海员能够在磁力海图上定出自己的位置了。

但是，近年来，人们在造船中大量地使用了钢铁，以致不照顾到船舶本身作为一个磁性物体而对指针发生的作用，罗盘的使用就是不可能的了。

正如我们已经看到的那样，确定一块任意形状的铁在地球磁力的影响下的磁量分布，即使铁块没有受到机械胁变或其他干扰的影响也是一个很困难的问题。

然而，在现在这一事例中，问题却通过下面的考虑而得到了简化。

罗盘被假设为放在船上，其中心位于船上的一个固定点，而且离任何的铁质都很远，以致指针的磁性并不在船上感生任何可觉察的磁性。罗盘指针的体积被假设为很小，以致我们可以认为指针每一点上的磁力都是相同的。

船上的铁被假设为只有两种。

（1）按恒定方式被磁化了的硬铁。

（2）其磁化由地球或其他磁体所感生的软铁。

严格说来我们必须承认，最硬的铁也不仅能够受到感应而且会以各种方式损失其一部分所谓的永久磁化。

最软的铁也能够保持其所谓的剩磁化。铁的实际性质并不能通过它由以上定义的硬铁和软铁所合成来准确地加以表示。但是已经发现，当一只船受到地球磁力的作用而没有受到气候的任何反常作用的影响时，可以假设船的磁性部分地起源于永久磁化而部分地起源于感应，而当把这种假设应用于罗盘的改正时是可以得出足够准确的结果的。

作为罗盘变化理论之基础的那些方程，是由泊松在第五卷Mémoires de l'Institut, p. 533（1824）上给出的。

包含在这些方程中的唯一和感生磁性有关的假设就是，如果起源于外界磁性的一个磁力X在船舶的铁中引起一种感生磁化，而这种感生磁化对罗盘指针作用一个其分量为X′、Y′、Z′的干扰力，那么，如果外磁力按一个给定的比例而发生了变化，则干扰力的分量将按相同的比例而发生变化。

确实，当作用在铁上的磁力很大时，感生磁化就不再和外磁力成正比了，但是对于由地球所引起的那样大小的磁力来说，这种比例性的欠缺却是不可觉察的。

因此在实践中我们就可以假设，如果一个其值为1的磁力通过船上铁器的媒介而对罗盘指针作用一个x分量为a、其y分量为d而其z分量为g的干扰力，则由一个沿x方向的力X所引起的干扰力的分量将是aX、dX和gX。

因此，如果我们假设把坐标轴固定在船上，使得x轴指向船头，y轴指向右舷，而z轴指向龙骨，如果X、Y、Z代表地球磁力在这些方向上的分量，而X′、Y′、Z′代表地球和船作用在罗盘指针上的合磁力的分量，则有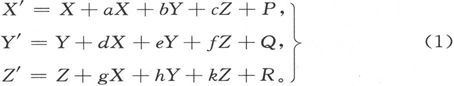

在这些方程中，a、b、c、d、e、f、g、h、k是依赖于船上软铁的数量、布置及其感应性能的九个常系数。

P、Q、R是依赖于船只的永久磁化的常量。

很显然，如果磁感是磁力的线性函数，则这些方程是充分普遍的，因为它们不多不少，恰恰是一个矢量作为另一矢量之线性函数的最普遍的表示式。

也可以证明，它们并不是太普遍的，因为，通过铁的一种适当布置，任何一个系数都可以被弄得独立于其他系数而变。

例如，一根细长的铁棒在纵向磁力的作用下会获得磁极，其中每一磁极的强度在数值上等于棒的截面乘以磁化力再乘以感生磁化系数。一个对棒为横向的磁力会产生弱得多的磁化，其效应在几倍直径的距离处就几乎是觉察不到的。

如果在罗盘指针的前方在向船头方向量去的x距离处放一根长铁棒，那么，设棒的截面是A而它的磁化系数是κ，则磁极强度将是AκX，而如果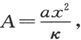 则这个磁极对罗盘指针作用的力将是aX。可以假设棒很长，以致另一个磁极对罗盘的效应可以忽略不计。

这样，我们就得到了使系数a具有任何需要的值的办法。

如果我们把截面为B的另一根棒放得有一个端点位于同一点上，即位于向船头量去的x距离处，而棒的长度则伸向右舷，且其远处的一极对罗盘并不发生可觉察的效应，则由这个棒引起的干扰力将是沿着x方向的，而且是等于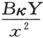 的，或者，如果 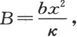则力将是bY。

因此这个棒就将引入系数b。

从同一点伸向下方的第三根棒将引入系数c。

系数d、e、f可以用从罗盘右侧的一点伸向船头、右舷和下方的三根棒来引入，而g、h、k则由从罗盘下面的一点沿上述三个方向摆放的三根棒来引入。

由此可见，九个系数中的每一个系数，都可以通过适当摆放的铁棒来分别地加以改变。

各量P、Q、R不过是作用在罗盘上的力的分量，该力起源于船的永久磁化以及由这种永久磁化所引起的那一部分感生磁化。

方程组（1）的一种全面讨论，以及船的真实磁学航向和罗盘所示航向之间的关系的全面讨论，已由阿乞巴耳德·斯密茨先生在海军部的《罗盘偏差手册》（Manual of the Deviation of the Compass）中给出。

那里给出了一种研究问题的很有价值的图解方法。取一个固定点作为原点，从该点开始作一直线，其方向和大小代表着作用在罗盘指针上的实际磁力的水平部分。在船只转来转去而使它的船头逐次采取不同的方位时，这条直线的端点就描绘出一条曲线，曲线上的每一点都对应于一个特定的方位。

这样一条曲线叫做“磁迹图”（dygogram），利用这种图，可以按照船只的磁学航向来给出作用在罗盘上的力的方向和大小。

磁迹图有两种形式。在第一种形式中，曲线画在一个平面上，而该平面在船只转动时是固定在空间中的。在第二种形式中，曲线是画在相对于船为固定的平面上的。

第一种磁迹图是帕斯卡蚶线，第二种磁迹图是椭圆。关于这些曲线的作图和使用，以及许多在数学家看来很有兴趣而在航海家看来也很重要的定理，请读者参阅海军部的《罗盘偏差手册》。

第三十一章　感生磁的韦伯理论

442．〕　我们已经看到，泊松假设了铁的磁化就在于每一磁分子内部的两种磁流体的分离。如果我们希望避免关于存在磁流体的假设，我们也可以用另一种形式来叙述同一理论；我们可以说，当磁化力作用在铁的分子上时，每一个分子都会变成一个磁体。

韦伯的理论与此不同。他假设，即使在加上磁化力以前，铁分子也永远是一些磁体，但是，在普通的铁中，各分子的磁轴是不偏不倚地指向各个方向的，从而整块的铁就不会显示任何磁性。

当一个磁力作用在铁上时，它就倾向于把分子的轴都转到同一个方向，这样就会使整块的铁变成一个磁体。

假如所有分子的磁轴都已摆得互相平行，铁就会显示它所能获得的最大磁化强度。因此，韦伯的理论就蕴涵了一个极限磁化强度的存在，从而关于存在这样一个极限的实验证据就是这种理论所必需的。显示着对一个磁化极限值的趋近的实验，曾由焦耳 ^〔26〕 J. 密勒 ^〔27〕 以及厄翁和娄 ^〔28〕 作出。

比兹 ^〔29〕 关于在磁力的作用下沉积出来的电解铁（electrotypeiron）的实验，提供了有关这一极限的最全面的证据。

一条银导线涂了漆，在漆层上划开一条很细的纵向开口，以露出很细的一条金属。然后把这条导线浸入一种铁盐的溶液中，并放入磁场中，使开口沿着一条磁力线的方向。用这根导线作为通过溶液的一个电流的阴极，铁就会一个分子一个分子地沉积在导线的很窄地暴露部分上。然后就对这样形成的一个铁的细丝进行磁的检验。经发现，对于如此小的一部分铁来说，它的磁矩是很大的，而当使一个强大的磁力沿相同方向作用上去时，却发现暂时磁化的增量很小，而永久磁化则并不改变。沿相反方向而作用的一个磁力将立刻使细丝回到按普通方式而被磁化的铁的状况。

韦伯理论认为，在这一事例中，磁化力在每一分子的沉积时刻就把它的磁轴摆到了相同的方向上；这种理论是和观察到的现象符合得很好的。

比兹发现，当电解在磁化力的作用下继续进行时，后来沉积下来的铁的磁化强度就将较小。当各个分子肩并肩地被排在早先已经沉积下来的那些分子旁边时，它们的磁轴或许会偏离磁力线的方向，因此只有在很细的铁条纹的事例中才能得到近似的平行性。

如果像韦伯所假设的那样，铁分子本来就已经是一些磁体，则在它们的电沉积过程中足以使它们的磁轴平行排列的任何磁力，都将足以在沉积丝中产生最高的磁化强度。

另一方面，如果铁分子并不是磁体而只是能够受到磁化，则沉积丝的磁化将依赖于磁化力，其方式和一般软铁依赖于磁化力的方式相同。比兹的实验没有为后一假说留下任何余地。

443．〕　现在我们将像韦伯那样假设，在铁的每单位体积中共有n个磁性分子，而每个磁性分子的磁矩是m。假如所有分子的磁轴都已摆得相互平行，则单位体积的磁矩将是M＝nm，而且这就将是铁所能得到的最大磁化强度。

韦伯假设，在普通铁的非磁化状态中，各分子的磁轴是杂乱无章地沿各个方向摆放的。

为了表示这一点，我们可以假设画出了一个球，而且从球心画一些半径，分别和n个分子中的每一个分子的磁轴方向相平行。这些半径的端点的分布，将代表各分子的磁轴的分布。在普通铁的事例中，这n个点是均匀地分布在球面的各个部分上的，因此，其磁轴和x轴的夹角小于α的分子的数目就是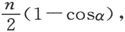 而其磁轴和x轴的夹角介于α和α＋dα之间的分子的数目就是 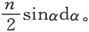这就是一块从来未被磁化的铁中的分子分布。

现在让我们假设，使一个磁力X沿着x轴的方向而作用在铁上，并考虑其磁轴起先和x轴成α角的一个分子。

如果这个分子是可以完全自由地转动的，它就会把自己转到磁轴平行于x轴的位置，而假如所有的分子都是这样的，则我们将发现最小的磁化力都将足以引发最高的极化程度。然而事实却不是这样的。

各分子并不把它们的磁轴转得平行于x轴，而这不是因为每一个分子都受到一个倾向于保持其原始方向的力的作用，就是因为整个分子体系的相互作用引起了一种与此等价的效应。

韦伯作为最简单的假设而采用了前一种假设。它假设，当受到偏转时，每一个分子都倾向于以一个力而返回其原始位置；这个力和一个沿原始磁轴方向作用的磁力D所将产生的力相同。

因此，磁轴所实际采取的位置，就是沿着X和D的合力方向的。

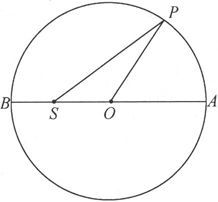
图44

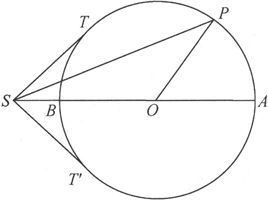
图45

设APB代表一个球的截面，球的半径以一定的比例代表着力D。

设半径OP平行于某一特定分子在其原始位置上的磁轴。

设SO按相同的比例代表被假设为从S向O而起作用的磁化力X。这样，如果分子受到一个沿SO方向的力X和一个平行于分子磁轴之原始方向OP的力D的作用，则其磁轴将转到SP的方向，也就是X和D的合力的方向。

既然各分子的磁轴起初是沿着一切方向的，P就可以是球面上随便哪一个点。在X小于D的图44中，磁轴的末位置SP可以取任意方向，但却不是完全随便的，因为磁轴转向A的分子将比磁轴转向B的分子更多。在X大于D的图45中，分子的磁轴将全都包括在和球面相切的锥面TST′中。

因此，按照X是小于还是大于D，就有两种不同的事例。

设α＝AOP，即分子磁轴对x轴的初倾角。

θ＝ASP，即磁轴在受到力X的倾转时的倾角。

β＝SPO，即偏转角。

SO＝X，即磁化力 ^〔30〕 。

OP＝D，即倾向于回返初位置的力。

SP＝R，即X和D的合力。

m＝分子的磁矩。

于是，倾向于使角θ减小的由X引起的力偶矩就是mL＝mXsinθ，而倾向于使θ增大的由D引起的力偶矩就是mL＝mDsinβ。

令这些值相等并记得β＝α－θ，我们就得到　　

以确定偏转后的磁轴方向。

其次我们应该求出力X在物体中引起的磁化的强度，而为此目的，我们必须把每一个分子的磁矩投影到x轴上，然后把所有这些分量加起来。

分子磁矩沿x轴方向的分量是mcosθ。其磁矩之初倾角介于α和α＋dα之间的分子数是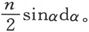

因此我们必须记得θ是α的函数并计算积分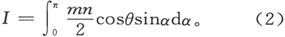　　

我们可以把θ和α都用R表示出来，于是被积分式就变成

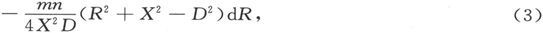
它的不定积分是　　

在第一种事例中，即当X小于D时，积分限是从R＝D＋X到R＝D－X。在第二种事例中，即当X大于D时，积分限是从R＝X＋D到R＝X－D。

当X小于D时，有　　

当X等于D时，有　　

当X大于D时，有　　

而当X变为无限大时则有

按照韦伯 ^〔31〕 所采用的这种理论的形式，当磁化力从0增大到D时，磁化就按相同的比例而增大。当磁化力达到D这个值时，磁化是极限值的三分之二。当磁化力进一步增大时，磁化不是无限地增大而是趋于一个有限的极限。

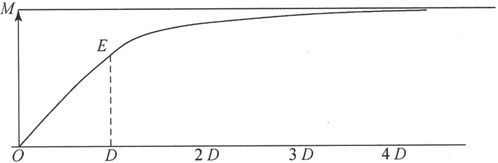
图46

磁化的规律如图46所示。图中的磁化力是从0向右算起的，而磁化则用纵坐标来代表。韦伯自己的实验给出了和这一规律符合得令人满意的结果。然而，也可能D值并不是对同一块铁中的所有分子都相同，从而从由0至E的直线到E以后的曲线的过渡也可能并不像图中所示的那样突然。

444．〕　这种形式的理论并不能对剩磁化作出任何说明，而人们发现，当磁化力被取消以后，剩磁化是存在的。因此我曾经想到，有必要检查再作出一条假设的后果，这条假设牵涉到分子的平衡位置可以永久性地改变的条件。

让我们假设，如果被偏转了任意一个小于β₀ 的角度β，磁性分子的轴线在致偏力被取消时将返回其原始位置，但是，如果偏转角β超过β₀ ，则当致偏力被取消时磁轴并不会回返到原始位置，而是将永久性地偏转一个角度β－β₀ ，这个角度可以叫做分子的永久取向 ^〔32〕 。

这条关于分子偏转规律的假设，并不能认为是建筑在任何有关物体之内部结构的确切知识上的，这只不过是我们由于对事情的真实情况全无所知而采取的一种追随韦伯所提示的猜想的想象方式而已。

设　　

那么，如果作用在一个分子上的力偶矩小于mL，就不会有任何永久偏转；但是，如果力偶矩超过了L，那就会出现平衡位置的永久改变了。

为了追索这一假设的后果，设作中心在O点而半径为OL＝L的一个球。

只要X还小于L，一切情况就将和以前考虑过的事例中的情况相同；但是，一旦X超过了L，它就将开始引起某些分子的永久偏转。

让我们考虑图47中的事例，这时X大于L而小于D。以S为顶点作一个双锥面和球L相切。设这个锥面和球D交于P及Q。那么，如果一个分子的磁轴在它的初位置上是位于OA和OP之间或OB和OQ之间的，则它将偏过一个小于β₀ 的角度，从而就不会有永久偏转。但是，如果分子的磁轴起初位于OP和OQ之间，则将有一个力矩大于L的力偶作用在分子上并使它偏转到位置SP上，而当力X停止作用时，分子并不会回返原来的取向而是采取永久偏转的方向OP

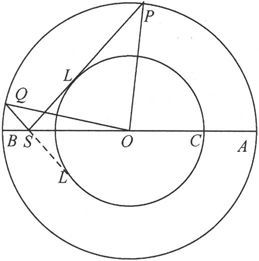
图47

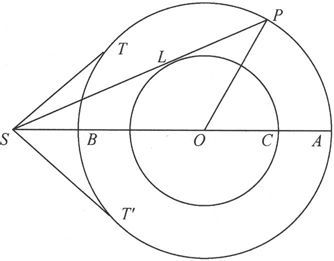
图48

让我们令L＝Xsinθ₀ ，式中θ₀ ＝PSA或QSB，于是，按照以前的假说其磁轴将具有介于θ₀ 和π－θ₀ 之间的θ值的所有那些分子，在力X的作用过程中都将被弄得具有θ₀ 这个值。

因此，在力X的作用过程中，那些在偏转以后磁轴位于半顶角为θ₀ 的双锥面的任一片内的分子，都将像在以前的事例中一样地排列，但是，那些按照以前的理论其磁轴将位于两片锥面之外的分子却将永久性地受到偏转，使得它们的磁轴将在锥面指向A的那一片附近形成一种密集带。

随着X的增大，属于B点周围那一锥面的分子数就持续减小，而当X变为等于D时，所有的分子就都已被迫离开了它们从前的平衡位置，而转到A点周围的锥面一带了；因此，当X变得大于D时，所有的分子就将形成锥面的一部分或密集在锥面附近了。

当力X被撤销时，在X小于L的事例中一切情况就都会返回原始的状态。当X介于L和D之间时，将有一个围绕A点的而其半顶角为AOP＝θ₀ ＋β₀ 的锥面，和一个围绕B点的而其半顶角为BOQ＝θ₀ －β₀ 的锥面。在这些锥面内部，分子的磁轴是均匀分布的。但是，其磁轴的原始方向位于这两个锥面之外的所有分子，却都已经被驱离了它们的原始位置而在A点周围的锥面附近形成了密集带。

如果X大于D，则B点周围的圆锥将完全分散，而起先形成这一圆锥的所有分子将被转化成A点周围的密集带，而其倾角则是θ_ω ＋β₀ 。

445．〕　用和以前相同的办法处理这一事例 ^〔33〕 ，我们就能求得在力X作用期间的暂时磁化强度，此处的X是被假设为作用在以前从示被磁化过的铁上的。

当X小于L时，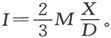

当X等于L时，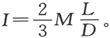

当X介于L和D之间时，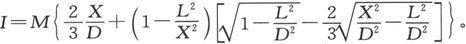

当X等于D时，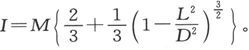

当X大于D时，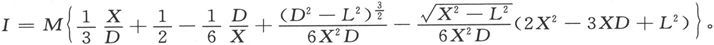

当X为无限大时，I＝M。

当X小于L时，磁化服从以前的规律，而且是和磁化力成正比的。一旦X超过了L，磁化就会有一个更快的增加率，因为这时有些分子开始被从一个圆锥转送到另一个圆锥。然而，随着形成负圆锥的分子数的减少，这种迅速的增大很快就会停止，而最后磁化就会达到极限值M。

假若我们必须假设不同的分子具有不同的L值和D值，我们就会得到不同的磁化阶段区别得并非如此明显的一种结果。

由磁化力X引起而当该力已被撤销时才能观察到的剩磁化I′如下所述：

当X小于L时，没有剩磁化。

当X介于L和D之间时，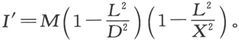

当X等于D时，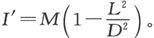

当X大于D时，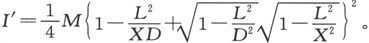

当X为无限大时，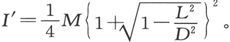

如果令M＝1000，L＝3，D＝5，我们就得到下列的暂时磁化和剩磁化的值

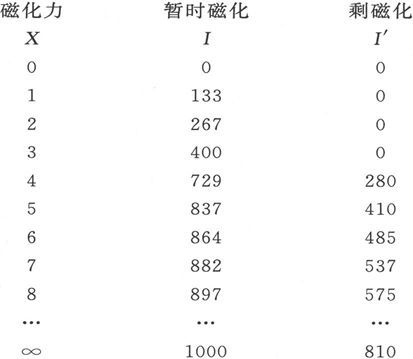
这些结果表示在图49中。

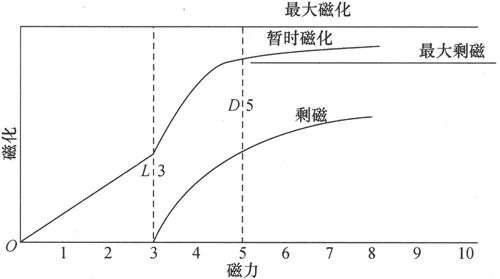
图49

剩磁化曲线在X＝L时开始，并趋近于一条渐近线，其纵坐标＝0.81M。

必须记得，这样求得的剩磁对应于一种情况，即当外力被撤销时并不存在任何起源于物体本身之磁性分布的去磁力。因此，这种计算只适用于很长的纵向磁化的物体。在短粗物体的事例中，剩磁将由于自由磁的反作用而有所减小，其方式正如有一个反向的外磁化力作用在物体上一样 ^〔34〕 。

446．〕　在这种理论中我们作出了如此多的假设和引用了如此多的调节常量；这样一种理论的科学价值，并不能单纯地根据它和某一组实验的数值符合来加以评估。如果它还有任何价值，那就是因为它使我们能够对一块铁中在磁化过程中出现的变化得到一种思维形象。为了检验理论，我们必须把它应用于这样一个事例：一块铁在受到一个磁化力X₀ 的作用以后又受到一个磁化力X₁ 的作用。

如果新力X₁ 是沿着和X₀ 的作用方向相同的方向（我们将称之为正方向）而作用的，那么，如果X₁ 小于X₀ ，则它将不会引起分子的任何永久取向，从而当X₁ 被撤销以后，剩磁化将和由X₀ 所引起的相同。如果X₁ 大于X₀ ，则它所引起的效应将和X₀ 不曾起过作用时的效应完全相同。

但是，让我们假设X₁ 是沿负方向而作用的，并且让我们假设

X₀ ＝Lcscθ₀ ，而X₁ ＝-Lcscθ₁ 。

当X₁ 在数值上增大时，θ₁ 就减小。X₁ 将引起其永久偏转的第一批分子，就是形成A点周围的锥面之密集带的那些分子 ^〔35〕 ，以及当未受偏转时有一个倾角θ₀ ＋β₀ 的那些分子。

一旦θ₁ －β₀ 变到小于θ₀ ＋β₀ ，去磁过程就将开始。既然这时θ₁ ＝θ₀ ＋2β，去磁开始时所要求的力X₁ 就将小于引起磁化的力X₀ 。

假如D值及L值对所有的分子来说都是相同的，则X₁ 的很小增量就将把所有磁轴倾角为θ₀ ＋β₀ 的分子都转到一个磁轴对负轴OB的倾角为θ₁ ＋β₀ 的位置上去。

虽然去磁并不是按一种如此突然的方式发生的，但是它却发生得相当迅速，以致给过程的这种解释模式提供了某种支持。

现在让我们假设，通过取一个反向力X₁ 的适当值，我们在撤销X₁ 后恰好使铁块完全去了磁。

现在，各分子的磁轴将不会像在一块从来未被磁化的铁中那样完全随便地分布在一切方向上，而是将形成三组。

（1）在一个围绕正极而半顶角为θ₁ －θ₀ 的锥面内，分子的磁轴保持在它们的原始位置上。

（2）在一个围绕负极而半顶角为θ₀ －β₀ 的锥面内，情况也如此。

（3）所有其他分子的磁轴方向形成一个围绕负极的锥面，而其倾角为θ₁ ＋β₀ 。

当X₀ 大于D时，第二组是不存在的。当X₁ 大于D时，第一组也不存在。

因此，尽管在外观上去了磁，铁的状态却是和一块从来未经磁化的铁的状态不同的。

为了证明这一点，让我们考虑一个沿正方向或负方向而作用的磁化力X₂ 的效应。这样一个力的第一种永久效应将发生在磁轴和负方向成角θ₁ ＋β₀ 的第三组分子上。

如果X₂ 是沿负方向作用的，则一旦θ₂ ＋β₀ 变成小于θ₁ ＋β₀ ，也就是说一旦X₂ 变成大于X₁ ，它就将开始产生永久性的效应。但是，如果X₂ 是沿正方向作用的，则一旦θ₂ －β₀ 变成小于θ₁ ＋β₀ ，也就是说当θ₂ ＝θ₁ ＋2β₀ 即当X₂ 还比X₁ 小得多时，X₂ 就将开始再引起铁的磁化。

因此，由我们的假说可以看出：

当一块铁受到一个力X₀ 的磁化时，不加上一个大于X₀ 的力就不能使它的剩磁有所增加。一个小于X₀ 的反向力就足以使它的剩磁有所减少。

如果铁被一个反向力所完全去磁，不加上一个大于X₁ 的力就不能沿反方向把它磁化，但是一个小于X₁ 的正向力却足以开始沿原有的方向而把它再磁化。

这些结果是和瑞奇 ^〔36〕 、雅考比 ^〔37〕 、马瑞安尼尼 ^〔38〕 以及焦耳 ^〔39〕 所实际观察到的结果相一致的。

关于铁及钢的磁化和磁力的及机械胁变的关系的一种很全面的论述，已由魏德曼在他的《动电》一书中给出。他 通过磁化的效应和扭变的效应的一种仔细比较已经证明，我们通过有关线材之暂时扭变和永久扭变的实验而导出的关于弹性和塑性的概念，可以同等适当地应用于铁及钢的暂时磁化和永久磁化。

447．〕　马吐西 ^〔40〕 发现，一个硬铁棒在受到磁化力时的拉伸，会增大其暂时磁化 ^〔41〕 。这一点曾由外尔泰姆加以证实。在软铁棒的事例中，磁性会因拉伸而减小。

一根铁棒的永久磁性当棒被拉伸时就增大，当它被压缩时就减小。

因此，如果一块铁首先沿着一个方向被磁化然后沿着另一方向被拉伸，则磁化的方向将倾向于趋近拉伸的方向。如果它被压缩，则磁化的方向将倾向于变得和压缩方向相垂直。

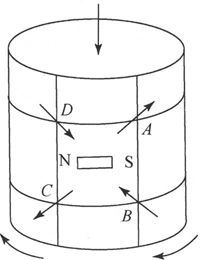
图50

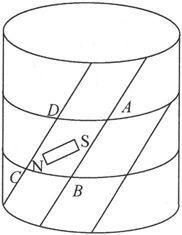
图51

这就解释了魏德曼的一个实验的结果。在一条竖直的导线中由上向下通一个电流。如果在电流正在通过或在它已经停止以后，把导线按右手螺旋方向加以扭转，则导线的下端变成一个北极。

在这儿，向下的电流对导线的每一部分沿切线方向进行磁化，正如字母NS所指示的那样。

沿右手螺旋方向对导线的扭转，使得ABCD这一部分沿对角线AC而被拉伸，并沿对角线BD而被压缩。因此，磁化方向就倾向于趋近AC而背离BD，于是下端就变成北极而上端就变成南极。

磁化对磁体尺寸的影响

448．〕　焦耳 ^〔42〕 在1842年发现，当一根铁棒被围绕它的一个线圈中的电流所磁化时，它就会变长。后来他 ^〔43〕 又通过把铁棒放在一个玻璃管里的水中来证明了，铁的体积并不会因为磁化而变大，从而他就得出结论说，它的横向线度缩小了。

最后，他使一个电流通过一根铁管的轴线并由管外返回，这样就使铁管变成了一条闭合的磁管。经发现，铁管的轴线在这一事例中是缩短了的。

他发现，在纵向压力下，一根铁棒当被磁化时也会伸长。然而，当铁棒受到相当大的纵向拉力时，磁化的效应却是使它缩短。

在一根硬钢丝的事例中，磁化力的效应却总是使钢丝缩短，不论钢丝是处于拉力还是处于压力作用之下。长度的改变只有当磁化力还在起作用时才是存在的，没有观察到由钢的永久磁化而引起的任何长度变化。

焦耳发现，铁导线的伸长近似地正比于实际磁化的平方，从而一个去磁电流的最初效应就是使导线缩短 ^〔44〕 。

另一方面，他发现，对拉力作用下的铁导线和对钢来说，缩短效应是正比于磁化强度和磁化电流的乘积而变的。

魏德曼发现，如果一根竖直导线被磁化得上端成为南极，并且由上向下在导线中通一个电流，如果导线的下端是自由的，则从上向下看去时，导线的下端是按顺时针的方向而扭转的；或者换句话说，导线将像一个右手螺旋那样地发生扭转，如果纵向电流和磁化电流之间的关系是右手关系的话。

在这一事例中，电流的作用和由早先存在的磁化而造成的合磁化，是沿着右手螺旋的方向而围绕导线的。因此，这种扭转就似乎表明，当铁受到磁化时，它就沿着磁化的方向而膨胀并沿着垂直于磁化的方向而收缩。这是和焦耳的结果相一致的。

关于磁化理论的进一步发展，请参阅第832～845节。

第三十二章　磁学测量

449．〕　主要的磁学测量就是一个磁体的磁轴和磁矩的测定，以及一个给定位置上的磁力的方向和强度的测定。

既然这些测量是在地面附近进行的，磁体就总是既受到地磁的作用又受到重力的作用的，而且，既然各个磁体是用钢做成的，它们的磁性就部分地是永久磁性而部分地是感生磁性。永久磁性会被温度的变化、被强烈感应和被激烈的敲打所改变；感生磁性会随着外磁力的每一次变化而变化。

观察作用在一个磁体上的力的最方便办法就是使磁体可以绕着一条竖直轴线而自由转动。在普通的罗盘中，这是通过把磁体平衡地支放在一个支轴上来做到的。支轴的尖端越细，干扰磁力作用的摩擦力矩就越小。为了更精密的观察，磁体是用无扭转的丝线悬挂起来的；这种悬线是一根单丝或几根丝合并成的一条线，每根丝互相平行，各自负担尽可能相等的部分重量。这样一根线的扭力比同样强度的金属线的扭力要小得多，而且可以借助于磁体的方位而计算出来，而由支轴的摩擦所引起的力则不是这样的。

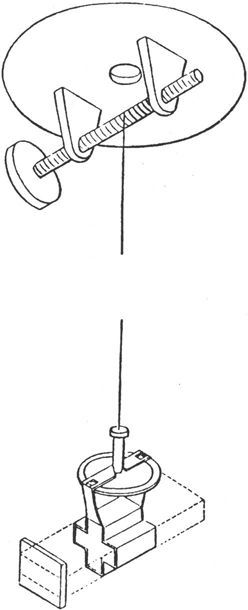
图52

通过转动装在固定螺母中的螺丝，悬线可以升高或降低。悬线是绕在螺丝的螺纹上的，因此当螺丝转动时悬线永远沿同一竖直线悬挂着。

悬线下面挂着一个水平的圆圈，上有刻度，叫做“扭转圆”；另外还挂着一个附有指针的镫形器，可以任意调节，以使指针和扭转圆上的任一刻度相重合。镫形器的造型使得磁棒可以放在上面，使其轴线水平，其四个侧面中的任一侧面都可以朝上。

为了保证零扭转，把一个和磁体重量相同的非磁性物体放在镫形器上，并定出平衡时的扭转圆位置。

磁体本身是一块硬淬火的钢。按照高斯和韦伯的研究，它的长度至少要是它的最大横向线度的八倍。当磁体内部的磁轴方向之永久性是最首要的考虑时，这一点是必要的。当所要求的是运动的及时性时，磁体就应该短一些，而当观察磁力的突然变化时，甚至宜于使用一根横向磁化的棒，并把它挂得最长的线度位于竖直方向 ^〔45〕 。

450．〕　磁体上附有测定其角位置的装置。为了普通的目的，磁体的两端做成两个尖，而在它的下面装一个刻度图；利用这个刻度图，就可以用肉眼读出两个尖端的位置，这时人眼应位于通过悬线和磁针尖端的平面上。

为了更精确的观察，一个平面镜被固定在磁体上，使得镜面的法线尽可能接近地和磁化轴相重合。这就是高斯和韦伯所采用的方法。

另一种方法是在磁体的一端装一个透镜，而在其另一端装一个用玻璃制成的标尺，透镜和标尺之间的距离等于透镜的主焦距。标尺零点和透镜光心的连线应该尽可能接近地和磁轴相重合。

因为这些确定悬挂仪器之角位置的光学方法在许多物理研究中是有很大重要性的，我们将在这里一劳永逸地考虑考虑它们的数学理论。

镜尺法的理论

我们将假设，要测定其角位置的那件仪器是可以绕着一个竖直轴转动的。这个轴通常是悬挂仪器的一根悬丝或金属线。镜面必须真正是平面，这样，一个毫米标尺就可以通过反射而在离镜面数米处被看到。

镜面中点上的法线应该通过悬挂轴线，而且应该是严格水平的。我们将把这一法线称为仪器的准直线（line of collimation）。

大致地确定了准直线在所要进行的实验过程中的平均方向以后，在镜面前面的一个适当距离上，在略高于镜面的水平面的地方架起一个望远镜来。

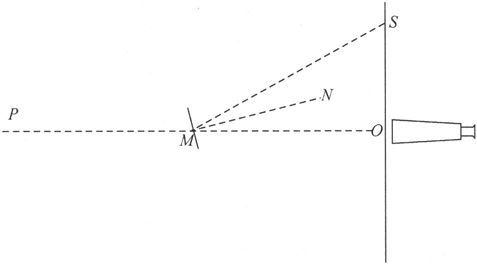
图53

这个望远镜可以在竖直平面内运动，它指向悬丝上略高于镜面的地方，另外再在视线上设立一个固定的标记，标记到物镜的距离等于镜面到物镜的距离的两倍。如果可能的话，仪器应该安装得使这个标记是在一面墙上或在其他固定物体上。为了同时在望远镜中看到标记和悬丝，可以在物镜上加一个盖子，盖子上沿着竖直的直径开一细缝。在进行别的观察时应把这个盖子取掉。然后调节望远镜，使得标记可被清楚地看到和望远镜焦点上竖丝相重合。然后把一根铅垂线调节得切近地通过物镜光心的前面并位于望远镜的下方。在望远镜下方恰好在铅垂线之后的位置上装一个具有相等刻度的标尺，使它被通过标记、悬丝和铅垂线的平面所垂直平分。标尺和物镜的离地高度之和应该等于镜面的离地高度的两倍。现在，望远镜既已指向镜面，观察者就将在望远镜中看到标尺的反射像。如果标尺上被铅垂线穿越的那一部分显得是和望远镜的竖丝相重合的，镜面的准直线就是和标记及物镜光心的平面相重合的。如果竖丝和标尺上的任何其他刻度相重合，准直线的角位置就应如下求出：

设纸面是水平的，而不同的点就投影在这一平面上。设O为望远镜物镜的中心，P为固定标记：P和望远镜竖丝相对于物镜来说是共轭焦点。设M是OP和镜面的交点。设MN是镜面的法线，则OMN＝θ是准直线和固定平面所夹的角。设MS是OM和MN的平面上的一条满足NMS＝OMN的直线，则S是通过反射将被看到和望远镜竖丝相重合的那一部分标尺。现在，既然MN是水平的，投影在图上的角度OMN和NMS就是相等的，从而OMS＝2θ。由此即得OS＝OMtan2θ。

因此我们必须按标尺的刻度来量度OM；然后，如果s₀ 是标尺上和铅垂线相重合的度数，而s是观察到的度数，则有s－s₀ ＝OMtan2θ，由此就可以求出θ。我们在量度OM时必须记得，如果镜子是由背面镀银的玻璃构成的，则竖直反射面是在玻璃前表面后边一段距离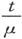 处，此处t是玻璃的厚度而μ是折射率。

我们也必须记得，如果悬线并不通过反射点，则M的位置将随θ而变。因此，如果可能，最好使镜子的中心和悬线相重合。

也值得建议把标尺作成以悬线为轴的凹圆柱面的形状，特别是当有必要观察大的角度变化时。这样，角度就立即是按圆周测量的，用不着查正切表。标尺应该仔细调节，使得柱轴和悬丝相重合。标尺上的数字应该永远沿同一方向从一端排到另一端，以避免负读数。图54代表必须和镜面及倒向望远镜一起应用的一个标尺的中间部分。

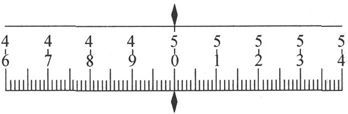
图54

当运动较慢时，这种观察方法是最好的。观察者坐在望远镜旁，并看到标尺的像运动着向右或向左而通过望远镜的竖丝。利用他旁边的一个时钟，他可以记下标尺上一个给定的刻度通过竖丝的时刻，或是记下在给定秒数通过竖丝的标尺刻度，而且他也可以记录每一次振动的两端界限。

当运动更快时，就将不可能读出标尺刻度，只除了在振动极限的静止时刻以外。可以在标尺的一个已知的刻度上作一个明显记号，并注意这个记号的通过时刻。

当仪器很轻而力又是变化的时，运动就会如此的灵活而迅速，以致通过一个望远镜来进行的观察将成为无用的。在这一事例中，观察者可以直接注视标尺，并观察由一个灯投射到标尺上的竖丝像的运动。

很显然，既然经过镜面反射和物镜折射而成的标尺像是和竖丝相重合的，那么，如果充分照明，竖丝的像就将和标尺相重合。为了观察这一点，房间必须遮暗，并使一个灯的会聚光线向着物镜而射在竖丝上。在标尺上，就看到一片光亮上面竖立着竖丝的暗影。它的运动可用眼睛追踪，而它停在那儿的那个标尺刻度就可以经过注视而定下来，并且被从容不迫地读出。如果想要注意光点通过标尺上一个给定地点的时刻，可以在那儿放一根针或一根光亮的金属丝，这样当光点通过时就会看到闪光。

通过用薄膜上的小孔来代替叉丝，像就变成一个在标尺上左右运动的小光点；而通过把标尺换成一个用时钟装置使之绕水平轴面转动的上面卷有作图纸的圆筒，光点就在上面描出一条曲线，而这条曲线可以在事后被弄成可见的。这条曲线的每一个横坐标对应于一个特定的时刻，而其纵坐标则指示镜子在该时刻的角位置。按照这种方法，已经在丘市观测站和其他观测站上建立了连续记录地磁之所有要素的自动系统。

在某些事例中，望远镜被略去，而一根竖丝则被放在它后面的一个灯所照亮，而镜面则是一个凹面镜，它在标尺上造成竖丝的像，那是一个光斑上的一道黑线。

451．〕　在丘市的可携式仪器中，磁体被做成了一根管子，一端装有透镜，而另一端则装有标尺，经过调节，标尺位于透镜的主焦面上。光由标尺后面射入，通过透镜以后用一个望远镜来加以观察。

既然标尺是位于透镜的主焦面上的，来自任一标尺刻度处的光就都会从透镜平行射出，而如果望远镜是聚焦在无限远处的，它就会使标尺的像和望远镜的叉丝相重合。如果一个给定的标尺刻度和叉丝交点相重合，则该刻度和透镜光心的连线必然平行于望远镜的准直线。通过固定磁体而移动望远镜，我们可以确定标尺刻度的角度值；然后，当磁体被挂起而望远镜的位置为已知时，我们就能通过读出和叉丝相重合的标尺刻度来测定磁体在任一时刻的位置。

望远镜架在一个臂上，这个臂的中心位于悬丝的直线上，而望远镜的位置则通过仪器方位圆上的游标来读出。

这种安排对于一个小的可携式磁强计是合用的；在那种磁强计中，整个仪器都装在同一个三脚架上，而且由偶然干扰所造成的振动将很快地衰减掉。

磁体轴线方向的确定和地磁方向的确定

452．〕　设在一个磁体内画一个坐标系；假设磁体是一个长方体，坐标系的z轴沿磁体长度的方向，而x轴和y轴垂直于其他侧表面。

设l、m、n和λ、μ、ν分别是磁轴及准直线和这些坐标轴之间的夹角。

设M是磁体的磁短，H是地磁的水平分量，Z是竖直分量，而δ是H的从北向西计算的方位角。

设ζ是观察到的准直线的方位角，α是镫形器的方位角，而β是扭转圆上的指针读数，于是α－β就是悬丝下端的方位角。

设γ是当没有扭力时的α－β的值，则倾向于使α减小的扭力矩就将是τ（α－β－γ），式中τ是依赖于悬丝本性的扭转系数。

为了确定x轴和准直线在xz平面上的夹角λ_x ，固定镫形器，使得y轴竖直向上，z轴指北而x轴指西，然后观察准直线的方位角ζ。然后取下磁体，把它绕z轴转一个π角再放在这个反了个儿的位置上，然后观察当y轴向下而x轴指西时的准直线方位角ζ′，

由此即得　　

其次，把镫形器挂在悬丝上并把磁体放上去，仔细地调节它以做到y轴竖向上，于是倾向于使α增大的力矩就是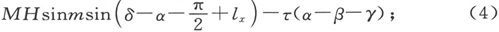　　

式中l_x 是x轴和磁轴在xz平面上的投影之间的夹角。

但是，如果ζ是观察到的准直线的方位角，则有　　

于是力［矩］就可以写成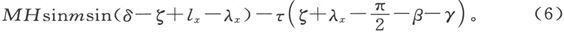　　

当仪器处于平衡时，这个量对一个特定的ζ值变为零。

当仪器永不停止而必须在一种振动状态下来加以观察时，对应于平衡位置的ζ值可以用一种即将在第735节中加以描述的方法来进行计算。

当扭力矩远小于磁力矩时，我们可以用δ－ζ＋l_x －λ_x 来代替它的正弦。

如果我们使扭转圆的读数β取两个值β₁ 和β₂ ，而ζ₁ 和ζ₂ 是对应的ζ值，则有

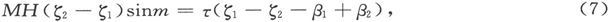
或者，如果我们令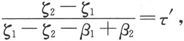 则有　　

而方程（6）除以MHsinm后就变成　　

如果我们现在把磁体翻过来，使得y轴向下，并调节仪器直到y轴确切竖直，而如果这时ζ′是方位角的新值，而δ′是对应的倾角，则

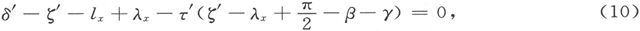
由此即得　　

现在必须调节扭转圆，使得τ′的系数尽可能接近于零。为此目的，我们必须确定当没有扭力时的α－β的值γ。此点可以这样做到：放上一个和磁体等重的非磁性棒，并在平衡状态下测定α－β。既然τ′很小，测定时并不要求多大的精确度。另一种方法是利用一个和磁体等重的扭转棒，里边含有一个很小的磁体，其磁矩是主磁体之磁矩的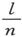 倍。既然τ并不改变，τ′就将变成nτ′，而如果ζ₁ 和ζ₁ ′是利用扭转棒求得的ζ值，就有

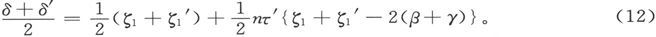
从（11）中减去此式，即得

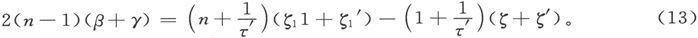
既经用这种办法求出了β＋γ的值，就应该改变扭转圆的读数，直到在仪器的普通位置下尽可能近似地做到　　

这时，既然τ′是一个很小的数，而且它的系数也很小，τ′值和γ值的微小误差就不会引起δ表示式中第二项的值的多大变化，而τ′和γ正是我们知道最不准确的两个量。

磁倾角δ的值可以用这种办法相当精确地求出，如果它在实验过程中保持不变，从而我们可求假设δ′＝δ的话。

当要求很大的精确度时，必须照顾到δ在实验时间内的变化。为此目的，必须在观察ζ值的各个相同时刻对另一个悬挂着的磁体进行观察。如果η、η′是观察到的对应于ζ和ζ′的第二个磁体的方位角，而δ和δ′是对应的δ值，则有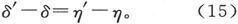　　

由此可见，为了求出δ值，我们必须在（11）式中加一个改正量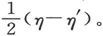

因此，第一次观察时的倾角就是

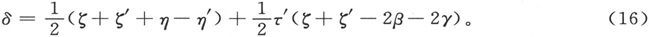
为了求出磁体内部的磁轴方向，从（9）减去（10）并加上（15），即得

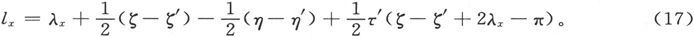
使棒的两面分别朝下来重复进行实验，即令x轴竖直向上和竖直向下，我们就可以求出m。如果准直线是可以调节的，它就必须被调得尽可能近似地重合，这样由于磁体并不是正好翻转而引起的误差就可以尽可能地小 ^〔46〕 。

关于磁力的测量

453．〕　最重要的磁力测量就是确定一个磁体的磁矩M和确定地磁水平分量强度的那些测量。通常这是通过结合运用两个实验的结果来进行的，一个实验确定这两个量的比值，而另一个实验则确定它们的乘积。

由一个磁矩为M的无限小的磁体在磁轴正方向的延线上离磁体中心为r处一点引起的磁力强度是　　

而且是沿r方向的。如果磁体具有有限的大小，但却是球形的，而且是沿着轴线方向均匀磁化的，则上述的力值仍是准确的。如果磁体是一个长度为2L的圆柱形磁棒，则

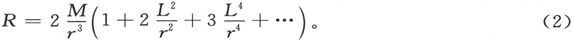
如果磁体是任意种类的，只要它的一切线度都远小于r，则有

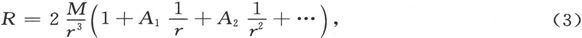
式中A₁ 、A₂ 等等是一些依赖于磁棒之磁化分布的系数。

设H是任意地方的地磁水平分量的强度。H是指向磁北方的。设r是向磁西方量度的，则r终点上的力将是向北的H和向西的R。合力将和磁子午面夹一个角度，设向西量度为θ，而且　　　

因此，为了测定 我们可以进行如下：

既经确定了磁北的方向，把一个尺寸不应该太大的磁体像在前面的实验中那样悬挂起来，而致偏磁体M则摆在悬挂磁体的正磁东方，在同一水平面内，从它的中心到悬挂磁体中心的距离为r。

M的磁轴要仔细地调到水平，并指向r的方向。

在拿过M来以前和在把它摆好以后，对悬挂磁体进行观察。设θ是观察到的偏角，如果应用近似公式（1），我们就有　　

或者，如果我们应用公式（3），就有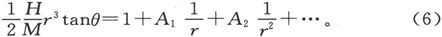　　

这儿我们必须记得，尽管偏角θ可以观察得很精确，磁体中心之间的距离r却是一个不容易准确测定的量，除非两个磁体都是固定的，而且它们的中心是用记号标明了的。

这种困难可以克服如下：

磁体M放在一个刻了度的标尺上，标尺沿东西方向伸向悬挂磁体的两侧。M两端之间的中点被认为是磁体的中心。这个点可以在磁体上标出，它的位置可以在标尺上观测，或者也可以观测其两端的位置并取算术平均值。设这个平均值为s₁ ，并设悬挂磁体的悬丝延线和标尺相交于s₀ ，就有r₁ ＝s₁ －s₀ ，式中s₁ 为精确地已知而s₀ 为近似地已知。设θ是当M在这一位置上时观察到的偏角。

现在把M反向，就是说，把它两端颠倒过来摆在标尺上，这时r₁ 将相同，但是M和A₁ 、A₂ 等等则将变号，因此，如果Q₂ 是向西的偏角，则有

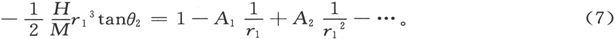
取（6）和（7）的算术平均值，即得

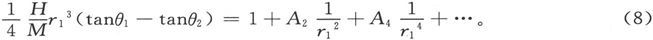
现在把M移到悬挂磁体的西边，并把它的中心放在标尺上刻度为2s₀ －s₁ 的地方。设当轴线位于第一位置上时的偏角是θ₃ ，而当位于第二位置上时的偏角是θ₄ ，则有

以及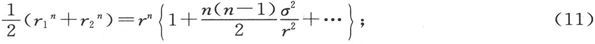　　

而且，当测量作得很小心时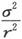， 是可以忽略不计的，因此我们确信可以取 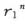和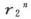 的算术平均值作为rⁿ 。

因此，取（8）和（9）的算术平均值，即得

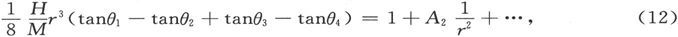
或者，利用　　

即得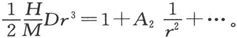

454．〕　现在我们可以认为D和r是能够被准确测定的。量A₂ 在任何情况下都不会超过2L² ，此处L是磁体长度的一半，因此，当r比L大得多时，我们就可以略去含A₂ 的一项并立即定出H和M之比。然而我们却不能假设A₂ 等于2L² ，因为它可以较小，而且对于其最大线度和磁轴横交的磁体来说A₂ 甚至可以是负的。含A₄ 的项和所有更高次的项，可以毫无问题地忽略不计。

为了消失A₂ ，利用距离r₁ 、r₂ 、r₃ 等等来重作实验，设D₁ 、D₂ 、D₃ 等等是D的值，则有

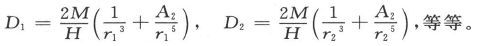
如果我们假设这些方程的可几误差是相同的（而它们也将是相同的，只要它们仅仅依赖于D的测定），另外，如果不存在关于r的不确定性，那么，根据当每一方程的可几误差被假设为相同时不准测量之组合理论的普遍规则，用r^-3 乘每一个方程并把结果加起来，我们就得到一个方程；而用r^-5 乘每一个方程并把结果加起来，我们就得到另一个方程。

对于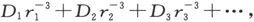 让我们写出∑（Dr^-3 ）并利用关于其他符号组之和的类似表示式，则两个结果方程可以写成

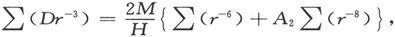
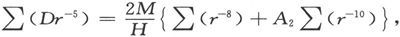
由此即得

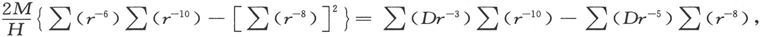
以及

A₂ ｛∑（Dr^-3 ）∑（r^-10 ）－∑（Dr^-5 ）∑（r^-8 ）｝＝∑（Dr^-5 ）∑（r^-6 ）－∑（Dr^-3 ）∑（r^-8 ）。

由这些方程推得的A₂ 应该小于磁体M的长度平方的一半。如果它不是这样的，我们就可以推想观测中有些不对头的地方。这种观测和化简的方法，是由高斯在《磁学协会的第一份报告》（First Report of the Magnetic Association）中给出的。

当观察者只能在距离r₁ 和r₂ 处进行两组实验时，由这些实验导出的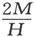 值和A₂ 值就是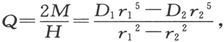　　

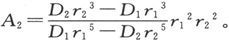
如果δD₁ 和δD₂ 是观察到的偏角D₁ 和D₂ 的实际误差，则计算结果Q的实际误差将是

如果我们假设误差δD₁ 和δD₂ 是独立的，而且其中每一个的可几误差是δD，则Q的计算值中的误差的可几值将是δQ，此处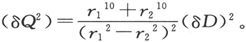

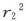如果我们假设，其中一个距离已经给定，譬如说较小的那个距离已经给定，则较大的那个距离的值可以适当确定以使δQ取最小值。这一条件导致一个 的五次方程，它只有一个大于 的实根，由此得到r₁ 的值是 ^〔47〕 r₁ ＝1.3189r₂ 。

如果只进行一次观测，则最佳条件出现在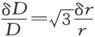 时 ^〔48〕 ，式中δD是一次偏角测量中的可几误差，而δr是一次距离测量中的可几误差。

正　弦　法

455．〕　我们刚才描述了的方法可以叫做“正切法”，因为偏角的正切是磁力的一种量度。

如果线段r₁ 不是沿东西方向测量而是被调节得垂直于偏转以后的磁体的轴，则R仍和以前相同，但是，为了使悬挂的磁体可以垂直于r，力H在r方向上的分量必须和R相等而反向。因此，如果θ是偏角，则有R＝Hsinθ。

这种方法叫做“正弦法”。只有当R小于H时这种方法才是可以应用的。

丘市可携式的仪器就是采用的这种方法。悬挂的磁体挂在仪器的一个部件上，那个部件和望远镜及装有致偏磁体的臂一起转动，而整体的转动就在方位圆上被测量。

仪器首先被调节，使得望远镜的轴线和磁体在未受扰状态中的准直线的平均位置相重合。如果磁体是振动的，则通过观察透明标尺的振动极限并对方位圆读数进行适当的改正来求出磁北方的真实方位。

然后，致偏磁体就被放在一个直杆上，该直杆通过仪器的转动轴而和望远镜的轴线相垂直，而且调节得使致偏磁体的轴线位于一条通过悬挂磁体之中心的直线上。

然后整个的转动仪器被调节，直到悬挂磁体的准直线再次和望远镜的轴线相重合，而如果有必要，新方位就要借助于振动极限上的刻度读数来加以改正。

改正后的方位角之差就给出偏角。在此以后，我们就像在正切法中那样地操作，只除了在D的表示式中要用sinθ来代替tanθ。

在这种方法中，用不着有关悬丝扭力的改正，因为悬丝、望远镜和磁体的相对位置在每一次观察中都是相同的。

在这种方法中，两个磁体的轴永远互相垂直，因此长度的改正可以作得更正确。

456．〕　即已这样测量了致偏磁体的磁矩和地磁水平分量之比，其次我们就必须通过确定当同一磁体偏离磁子午面时地磁倾向于使它转动的那一力偶矩来求出上述二量的乘积。

进行这种测量的方法有二：动态法和静态法。在动态法中，观察的是磁体在地磁作用下的振动时间；在静态法中，磁体在一个可测量的静力偶和磁力［偶］之间保持平衡。

动态法要求的仪器比较简单，而且在绝对测量方面也比较精确，但是却要用颇长的时间。静态法几乎可以进行瞬时的测量，从而在追踪磁力强度的变化中是有用的，但是它却要求更精密的仪器，而且在绝对测量方面也不是那么精确。

振　动　法

磁体被适当悬挂，使它的磁轴为水平，并使它沿很小的弧而发生振动。振动用已经描述的任何方法来进行观察。

在标尺上选定一个点，和振动弧的中点相对应。把沿正方向而通过标尺上这个点的时刻观测出来。如果在磁体回到同一点以前还有足够的时间，则把沿负方向通过这一点的时刻也观测出来。继续进行这种工作，直到观测了n＋1次正向通过和n次负向通过时为止。如果振动太快而无法逐次观测，则每振动三次或五次观测一次，但要注意使观测到的通过是正负交替的。

设观测到的时间是T₁ 、T₂ 、T_2n＋1 ，如果我们令

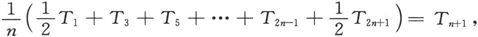
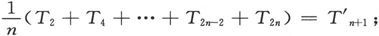
则正通过的平均时间T_n＋1 应该和负通过的平均时间T′_n＋1 相符合，如果点选得适当的话。这些结果的平均值被取为中点通过的平均时间。

在多次振动已经发生之后，但是在振动不再是清楚而规则的以前，观测者应进行另一系列的观测，由此他就可以推出第二系列的中点通过的平均时间。

根据第一或第二观测系列来计算振动周期，观测者应该能够确定在一系列的中点通过时间之间的时间阶段中已经发生过的振动次数。用这一振动数去除两个系列的中点通过之平均时间之间的时间阶段，就得到平均振动时间。

然后，利用和在摆观测中所用的同一种公式，观测到的振动时间可以折算成无限小振幅的振动时间，而且，如果发现振动的振幅是迅速递减的，就还要有一种关于阻力的改正，见第740节。然而，当磁体是用悬丝挂着的而振动弧又只有几度时，这些改正都是很小的。

磁体的运动方程是　　

式中θ是磁轴和力H的方向之间的夹角，A是磁体和悬置装置的惯量矩，M是磁体的磁矩，H是水平磁力的强度，MHτ′是扭转系数：τ′像在第452节中那样地确定，而且是一个很小的量。平衡时的θ值是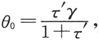　　

这是一个很小的角，对很小的振幅值来说，方程的解是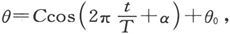　　

式中T是周期，α是一个常数，C是振幅，而且 由此我们就得到MH的值，

这里的T是由观测定出的一次完全振动所需的时间。惯量矩M是针对磁体而一劳永逸地求出的；如果它有一种规则的外形，就可以通过称重和量度来求出，或是通过和一个惯量矩已知的物体相对应的动力学手续来求出。

把这种MH值和以前求得的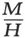 值结合起来，我们就得到 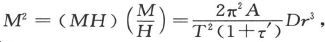以及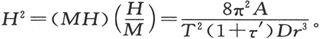

457．〕　我们曾经假设，H和M在两个实验系列中保持恒定，H的涨落可以通过即将描述的双线磁强计的同时观察来确定，另外，如果磁体已经使用颇久，而且在实验过程中并未受到什么温度变化或撞击的影响，则依赖于永久磁性的那一部分M可被假设为常量。然而，所有的钢质磁体都能够获得依赖于外磁力的感生磁性。

现在，当应用于偏角实验时，磁体是被放成磁轴取东西方向的，因此地磁是沿横向而作用在磁体上，从而并不倾向于增大或减小M，当磁体是在振动中使用时，它的磁轴是南北向的，于是地磁的作用就倾向于在轴的方向上对它进行磁化，并从而使它的磁矩增加一个量kH，此处k是一个必须通过对磁体进行实验来求出的系数。

有两种方法可以避免这种误差来源而不必计算k，即适当安排实验，使得磁体在用来使另一磁体发生偏转时和在自己摆动时都处于相同的条件之下。

我们可以把致偏磁体摆得磁轴指北，到悬挂磁体中心的距离为r，而且直线r和磁子午面之间有一个余弦为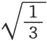 的夹角。于是，致偏磁体对悬挂磁体的作用就将垂直它自己的方向，而且等于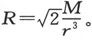

在这儿，M是当磁轴正如在振动实验中那样指北时的磁矩，因此用不着关于感应的任何改正。

然而，这种方法是极其困难的，因为致偏磁体的微小位移将引起很大的误差，而且，由于用翻转致偏磁体的办法来进行改正在这儿是不适用的，因此这种方法一般不被采用，除非目的在于确定感应系数。

在下述方法中，磁体在振动中不会受到地磁的感应；这种方法起源于J. P. 焦耳博士 ^〔49〕 。

制备两个磁体，使它们的磁矩尽可能近似地相等。在偏角实验中，这些磁体被分别地使用，或者，它们也可以同时摆在悬挂磁体的两侧以引起较大的偏角。在这些实验中，地磁的感应力是垂直于磁轴的。

设把其中一个磁体挂起来，而把另一个磁体摆得和前一磁体相平行，其中心位于悬挂磁体的中心的正下方，其磁轴指向相同的方向。固定磁体作用在悬挂磁体上的力是和地磁作用力方向相反的。如果使固定磁体慢慢向悬挂磁体靠拢，振动时间就会增加，直到在某一点上平衡不再稳定时为止，而越过了这一点，悬挂磁体将在反向位置附近进行振动。通过按这种方式进行实验，就能找出固定磁体的一个位置；在该位置上，固定磁体将恰好中和地磁对悬挂磁体的影响。两个磁体被联成一体，以便互相平行，它们的磁轴指向相同的方向，二者之间的距离就是刚刚通过实验求得的那个距离。然后它们就被用通常的方式挂起来，并沿着很小的圆弧一起振动。

下面的磁体恰能中和地磁对上面磁体的影响，而既然两磁体具有相等的磁矩，上面的磁体也将中和地球对下面磁体的感应作用。

因此，M值在振动实验中和在偏角实验中是相同的，从而任何关于感应的改正都是不必要的。

458．〕　确定水平磁力强度的最精确的方法，就是我们刚刚描述过的方法。然而，整个系列的实验并不能在比一小时短得多的时间内足够精确地完成，因此，发生在几分钟的时间之内的强度变化都将观察不到。因此就需要一种不同的方法来观察磁力在任一时刻的强度。

静态方法就在于用一个在水平面上起作用的静力偶来使磁体发生偏转。如果L是这个力偶的矩，M是磁体的磁矩，H是地磁的水平分量，而θ是偏角，则有MHsinθ＝L。由此可见，如果L作为θ的函数为已知，则MH可以求得。

力偶L可以用两种方法得到，像在普通扭秤中那样利用一条悬线的扭变弹性来得到，或是像在双线悬置中那样利用被悬挂的仪器的重量来得到。

在扭秤中，磁体固定在一根竖直金属丝的下端，其上端可以转动，而它的转动可以利用一个扭转圆来加以量度。

于是我们就有L＝τ（α－α₀ －θ）＝MHsinθ，此处α₀ 是当磁体的轴和磁子午线相重合时的扭转圆读数，而α是实际的读数。如果扭转圆被转动，使得磁体几乎垂直于磁子午面，从而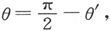 那就会有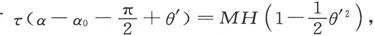 或者写作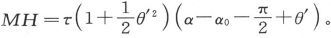

通过观察磁体在平衡时的偏角θ′，我们可以在τ为已知时算出MH。

如果我们只想知道H在不同时刻的相对值，那就既不必知道M也不必知道τ。

通过在同一金属丝上挂一个非磁性物体并观察其振动时间，我们就很容易用绝对单位来测量τ。这时，如果A是物体的惯量矩而T是一次完整振动的时间，则有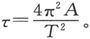

对应用扭秤的主要反对意见就在于，零读数α₀ 肯定是要变化的。在由磁体转向指北的倾向所引起的恒定扭力作用之下，金属丝将逐渐获得一种永久性的扭变，因此就有必要每过一段时间就重新测定扭转圆的零读数。

双线悬置

459．〕　用两根金属丝或纤维来悬挂磁体的方法，是由高斯和韦伯引入的。由于双线悬置在许多电学仪器中都会被用到，我们将比较仔细地考察考察它。这种悬置的一般外貌如图55所示，而图56则代表各悬丝在一个水平面上的投影。

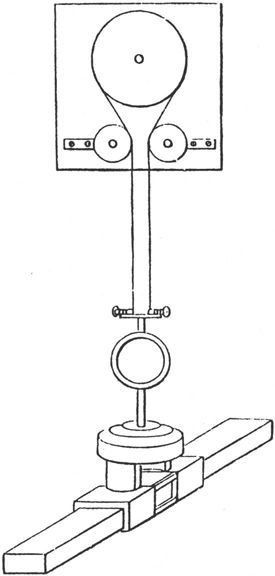
图55

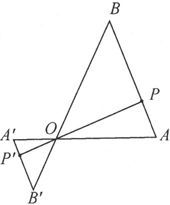
图56

AB和A′B′是两条悬丝的投影。AA′和BB′是两条悬丝的上端连线的和下端连线。a和b是线段AA′和BB′的长度。α和β是它们的方位角。W和W′是悬丝张力的竖直分量。Q和Q′是它们的水平分量。h是AA′和BB′之间的竖直距离。

作用在磁体上的力是：它的重量，由地磁引起的力偶，悬丝的扭力（如果有的话）和它们的张力。在这些力中，地磁和张力的效应具有力偶的性质。由此可见，张力的合力必然包括一个等于磁体重量的竖直力和一个力偶。因此，张力的竖直分量之和是沿着其投影为O点的那条直线的；该点就是AA′和BB′的交点，而其中每一条线段都是按照W′和W之比在O点被分割的。

张力的水平分量形成一个力偶，从而它们是量值相等而方向［反］平行的。用Q代表其中一个力，它们所形成的力偶的矩就是　　

式中PP′是平行线AB和A′B′之间的距离。

为了求得L的值，我们有力矩方程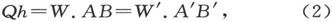　　

和几何方程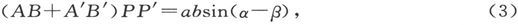　　

由此即得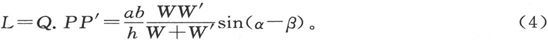　　

如果m是悬挂着的仪器的质量，g是重力强度，则有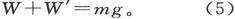

如果也写出　　

我们就有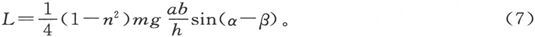　　

因此，当n为零时，也就是当所悬物体的重量由两条悬丝平均负担时，L的值就相对于n来说是一个最大值。

为了把悬丝的张力调成相等，我们可以观察振动时间并把它调到最小值，或者，我们也可以像在图55中那样把悬丝的上端接在一个滑轮上，滑轮绕轴旋转直到张力相等时为止，这样我们就得到一种自动调节的装置。

两根悬丝的上端之间的距离用另外两个滑轮来控制。悬丝下端之间的距离也是可以调节的。

通过这种张力调节，由悬丝张力所引起的力偶就变成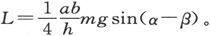

由悬丝张力引起的力偶矩具有如下形式：τ（γ－β），式中τ是二悬丝的扭转系数之和。

当α＝β时各悬丝应该没有扭转，因此我们可以取γ＝α。

由水平磁力引起的力偶矩具有形式MHsin（δ－θ），式中δ是磁偏角，而θ是磁体轴线的方位角。如果我们假设磁体轴线平行于BB′，或者说假设β＝θ，我们就可以既避免引用不必要的符号而又不会牺牲普遍性。

于是，运动方程就变成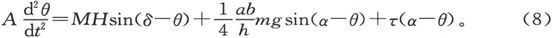　　

这种仪器的主要位置有三。

（1）当α近似地等于δ时。如果T₁ 是这一位置上一次完整振动的时间，则有

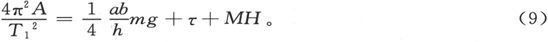
（2）当α近似地等于δ＋π时。如果T₂ 是这一位置上一次完整振动的时间，现在磁体的北端转得指向南方了，于是就有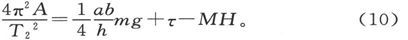　　

这一方程右端的量，可以通过减小a或b而弄得要多小就有多小，但是它不能被弄成负值，不然磁体的平衡就会变成非稳定的了。在这一位置上，磁体就形成一种仪器，可以用来使磁力方向的微小变化成为可觉察的。

因为，当θ－δ非常近似地等于π时，sin（δ－θ）就近似地等于θ－δ－π，从而我们就得到

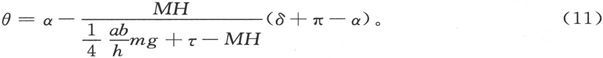
通过减小最后一个分式中的分母，我们可以把θ的改变量弄得远远大于δ的改变量。必须注意，这一表示式中的δ的系数是负的，因此，当磁力向一边转动时，磁体就向另一边转动。

（3）在第三种位置上，悬置装置的上部被转动，直到磁体的轴线近似垂直于磁子午面时为止。

如果我们令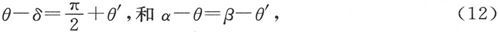　　

则运动方程可以写成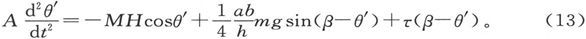　　

如果当H＝H₀ 而θ′＝0时达到平衡，则有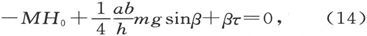　　

而如果H是和一个小角θ′相对应的水平力的值，则有

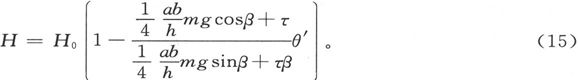
为了使磁体能够处于稳定平衡，第二项中分式的分子必须为正，但是，它越接近于零，仪器在指示地球水平分量的强度值变化方面将越灵敏。

估计力之强度的静态方法依赖于一种仪器的作用，该仪器本身对不同的力值将有不同的平衡位置。因此，在磁体上加一个小镜子，使它把一个光点投射在用时钟装置带动的一个感光表面上，就可以画出一条曲线，而由这条曲线，就可以按照我们暂时假设其为任意的一种标度来确定力在任意时刻的强度。

460．〕　在一个观测站中，人们利用肉眼观察或利用自动摄影法来保持一种偏角和强度的连续记录制度。在这种观测站中，偏角和强度的绝对值，以及一个磁体之磁轴的位置和磁矩，都可以在很大的精确度下被测定。

因为，磁偏计在每一时刻给出受到一个恒定误差影响的偏角，而双线磁强计则给出乘以一个恒定系数的每一时刻的强度。在实验中，我们用δ′＋δ₀ 来代替δ，式中δ′是磁偏计在所给时刻的读数而δ₀ 是未知然而恒定的误差，从而δ′＋δ₀ 就是该时刻的真实偏角。

同样，我们用CH′来代替H，此处H′是磁强计按任意标度的读数，而C是把这种读数换算到绝对单位的一个未知而恒定的因子，从而CH′就是该时刻的水平力。

测定各量之绝对值的那些实验，必须在离磁偏计和磁强计足够远的地方进行，以便不同的磁体不会明显地互相影响。必须记下每一次观测的时刻，并把对应的δ′值和H′代进去。然后处理各方程，以求得磁偏计的恒定误差δ₀ 和必须乘在磁强计读数上的系数C。求得了这些量，两种仪器上的读数就都可以用绝对单位表示出来了。然而，绝对测量必须时常重作，以照顾到可能发生在各磁体之磁轴和磁矩方面的那些变化。

461．〕　测定地磁竖直分量的方法不曾发展到同样的准确程度。竖直力必须作用在一个绕水平轴而转动的磁体上。喏，一个绕水平轴而转动的物体的不能被弄得和一个用悬丝挂起并绕竖直轴而转动的物体一样对小力的作用十分敏感。此外，磁体的重量比作用在它上面的磁力要大得多，以致由于不对称的膨胀等等所造成的一个微小的质心位移将比磁力的颇大变化对磁体的位置发生更大的影响。

因此，竖直力的测量，或者说竖直力和水平力的比较，就是磁测制度中最不完善的部分。

磁力的竖直部分通常是通过总力方向的测定而从水平力导出的。

如果i是总力和它的水平分量之间的夹角，它就叫做磁倾角；另外，如果H是已经求得的水平力，则竖直力是Htani而总力是Hseci。

磁倾角用一个“倾角针”来求得。

理论的磁倾针是一个磁体，它有一个通过其质心并垂直于其磁轴的转轴。转轴的两端作成很细的圆柱状，圆柱的中轴和通过质心的直线相重合。这两个柱状的轴端放在两个水平的平面上，可以在上面自由滚动。

当转轴取磁的东西向时，指针就可以在磁子午面内自由转动，而如果仪器调节得很完善，磁轴就将使自己沿着总磁力的方向。

然而，实际上并不能把一个倾角针调节得使它的重量不会影响它的平衡位置，因为，即使它的质心起初是位于转轴之柱状端的中心线上的，当针被稍稍弯曲或发生不对称的膨胀时，质心也会不再位于这一直线上的。另外，由于磁力和重力之间的互相干扰，一个磁体的质心的测定也是一种很困难的手续。

让我们假设针的一端和支轴的一端都被标记了出来。设在针上画了一条实在的或假想的线，我们将称之为准直线。这条线的位置在一个竖直的圆上读出。设θ是这条线和零刻度半径之间的夹角，在此我们将假设零刻度半径是水平的。设λ是磁轴和准直线之间的夹角，因此，当针在它的位置上时，磁轴和水平面之间的夹角就是θ＋λ。

设p是从质心到转轴在上面滚动的那个平面的垂线，则不论滚动表面的形状如何，p都将是θ的一个函数。如果转轴两端的滚动部分都是圆的，我们就有一个形如

的方程，式中a是质心到滚动部分之中心连线的距离，而α是这一连线和准直线之间的夹角。

如果M是磁体的磁矩，m是它的质量，g是重力［强度］，I是总磁力，而i是倾角，则由能量的守恒可知，当存在一种稳定平衡时，量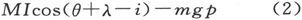　　

必须对θ来说有一个极大值，或者说，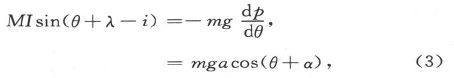

如果转轴的两端呈圆柱状的话。

另外，如果T是在平衡位置附近振动的周期，则有

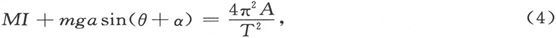
式中A是针对转轴而言的惯量矩，而θ由（3）来确定。

在测定倾角时，用一个位于磁子午面内和向西刻度的倾角圆取一个读数。

设θ₁ 是这个读数，于是我们就有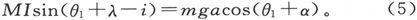　　

现在把仪器绕竖直轴转过180°，使得刻度变成向东，而如果现在读数为θ₂ ，则有

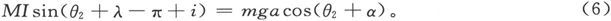
从（5）中减去（6），并记得θ₁ 近似地等于i，θ₂ 近似地等于π－i，而λ是一个小角，从而和MI相比mgaλ可以忽略不计，于是就有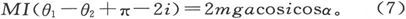　　

现在把磁体从它的支架上取下并把它放在第453节中的磁偏角仪器上，以利用一个悬挂磁体的偏角来指示它自己的磁矩，于是就有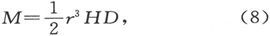　　

式中D是偏角的正切。

其次把针的磁性颠倒过来并通过观察其正切为D′的一个新偏角来测定其新磁矩M′，而距离则和以前相同，于是　　

式中　　

然后再把它放在支架上并取两个读数θ₃ 和θ₄ ，其中θ₃ 近似于π＋i而θ₄ 近似于-i，于是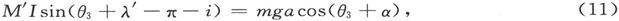　　

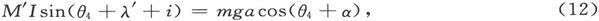
由此就像以前一样得到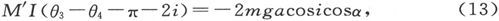　　

和（7）相加，就得到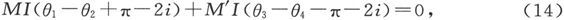　　

或者写成　　

由此我们就得到倾角，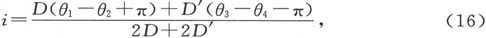　　

式中D和D′是由磁针分别在第一磁化和第二磁化中所引起的偏角的正切。

在利用倾角针来进行观测时，竖直轴应调节得使磁体转轴所在的那个平面在每一方位角上都为水平。磁体被磁化得A端下倾。把磁体放好，其转轴位于支撑平面上，而当圆的平面位于磁子午面内和圆的刻度面向东时取观测值。磁体的每一端都借助于读数显微镜来进行观察；显微镜装在一个臂杆上，并沿着倾角圆的同心圆而运动。使显微镜的叉丝和磁体上一个记号的像相重合，然后臂杆的位置就借助于一个游标来在倾角圆上读出。

于是我们就在刻度向东时得到A端的一个观测值和B端的一个观测值。必须观测两端，为的是消除由于磁体的转轴和倾角圆并不同心而引起的任何误差。

然后把刻度转成向西，并进行更多的两次观测。

然后把磁体翻转，使它的转轴反向，并注视着磁体的另一面来再进行四次观测。

然后把磁体的磁化倒转，使得B端下倾，测定其磁矩并在这一状态下取八个观测值，而这十六个观测值结合起来，就给出真实的倾角。

462．〕　曾经发现，尽管作得极其细心，由用一个倾角圆求得的观测值导出倾角，仍和由用另一个倾角圆在同一地点求得的观测值导出倾角颇不相同。布劳恩先生曾经指出了由于转轴的椭圆性而引起的效应，并指出了怎样通过用磁化到不同强度的磁体取得观测值来进行改正。

这种方法的原理可以叙述如下。我们将假设，任何一次观测的误差都是一个不超过一度的小量。我们也将假设，有一未知的然而却是规则的力作用在磁体上，把它干扰得离开其正确位置。

如果L是这个力的力矩，θ₀ 是真实倾角，而θ是观测到的倾角，则有

式中θ－θ₀ 是小量。

显然，M变得越大，磁针就越接近于它的正确位置。现在，设测定倾角的手续进行两次，第一次使磁化等于磁针可能达到的最大磁化M₁ ，第二次使磁化等于M₂ ，这是一个小得多的值，但仍能使读数清晰可辨而误差也还不致很大。设θ₁ 和θ₂ 是从这两组观测值推得的倾角，而L是对每次测定中的八个位置而言的未知干扰力［矩］的平均值——我们将假设这个平均值在两次测定中是相同的。于是就有

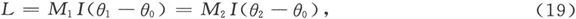
由此即得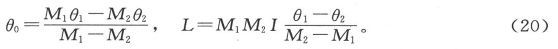　　

如果我们发现若干次实验给出近似相等的L值，我们就可以认为θ₀ 必然是和倾角的真实值很相近的。

463．〕　焦耳博士近来制造了一个倾角圆。在这种倾角圆中，磁针的转轴不是在水平的玛瑙平面上滚动而是套在两根丝线或蛛丝上。悬丝的两端固定在一个灵敏天平的两臂上。于是磁针的转轴就在悬丝的两个套儿上滚动，而焦耳博士发现，它的运动自由性是比在玛瑙平面上滚动时大得多的。

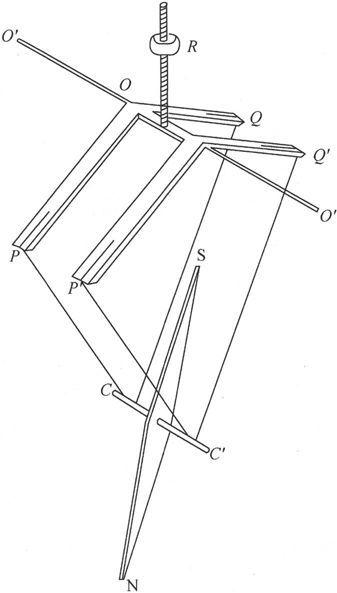
图57

在图57中，NS是磁针；CC′是转轴，这是一条直的柱状金属丝；而PCQ和P′C′Q′是转轴在上面滚动的悬丝。PCQ是天平，由支持在一根金属丝O′O′上的一个双重的弯杠杆构成；O′O′架在一个叉状架的尖齿上，成水平方向；另外天平还有一个用螺丝上下调节的平衡器，以使天平位于O′O′周围的一个随遇平衡的位置上。

为了使磁针当在悬丝上滚动时处于随遇平衡，重心必须既不升高也不降低。因此，在磁针的滚动中，距离OC必须保持不变。这一条件将得到满足，如果天平的两臂OP和OQ是相等的，而且悬丝是垂直于两臂的。

焦耳博士发现，磁针不应该长过五英寸。当它长达八英寸时，针的弯曲就倾向于使表观倾角减小一分的一个分数。磁针的转轴起初是一段钢丝，通过在一个砝码的拉伸下烧到赤热而被拉直，但是焦耳博士却发现，有了新的悬置，就不必再用钢丝了，因为铂乃至标准金就是够硬的了。

天平连接在一根金属丝O′O′上；O′O′长约一英尺，水平地张在一个叉子的两齿之间。这个叉子通过支撑整个仪器的三脚架上的一个圆来转动其方位。一小时可以进行六次完整的倾角观测，而单独一次观测的平均误差是一分角度的一个分数。

曾经建议，剑桥物理实验室中的倾角针应该借助于一个双像仪器来进行观察。这种仪器包括两个全反射棱镜，像在图58中那样装在一个竖直的刻度圆上，从而反射面可以绕着一个水平轴而转动，该水平轴近似地和悬挂着的倾角针的转轴延线相重合。磁针借助于放在棱镜后面的一个望远镜来观察，从而针的两端就可以同时被看到，如图59所示。通过绕着竖直圆的中轴转动棱镜，可以使画在针上的两条直线的像互相重合。于是针的倾角就可以根据竖直圆的读数来确定。

图58

图59

沿着倾角直线的磁力的总强度I可以根据在已经描述过的四个位置上的振动时间T₁ 、T₂ 、T₃ 、T₄ 来推出如下：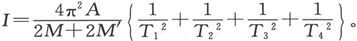

M和M′的值必须用以上描述的偏转和振动的方法来求出，而A是磁针绕其转轴的惯量矩。

利用悬挂磁体来进行的观测是更加精确得多的，因此通常是借助于方程I＝Hsecθ来根据水平力推求总力，式中I是总力，H是水平力，而θ是倾角。

464．〕　测定倾角的手续是很麻烦的，它不适于用来确定磁力的连续变化。用于连续观测的最方便的仪器是竖直力磁强计。这简单的就是平衡在刀口上而其磁轴近似水平地处于稳定平衡的一个磁体。

如果Z是磁力的竖直分量，M是磁矩，而θ是磁矩和水平面之间的小夹角，则有MZcosθ＝mgacos（α－θ），式中m是磁体的质量，g是重力［强度］，a是从重心到悬置轴线的距离，而α是通过轴及重心的平面和磁轴之间的夹角。

由此可见，对于竖直力的微小改变量δZ来说，既然θ很小，将有磁体之角位置的一个改变量δθ，使得MδZ＝mgasin（α－θ）δθ。

在实践中，这种仪器并不是用来测定竖直力的绝对值，而是用来记录其微小的变化。为此目的，只要知道当θ＝0时的z的绝对值以及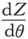 的值就够了。当水平力和倾角为已知时，Z的值由方程Z＝Htanθ₀ 求得，式中θ是倾角而H是水平力。

为了求出由Z的一个给定改变量所引起的偏转，取一个磁体把它放在轴线为东西向的位置上，并使它的中心在磁偏计之东或之西的r₁ 距置处，正如在偏角实验中那样。设偏角的正切为D₁ 。

然后把它放得轴线沿竖直方向，而其中心在竖直力磁强计之上或之下的r₂ 距离处，并设在磁强计中引起的偏角的正切为D₂ 。那么，如果致偏磁体的磁矩是M′，则有

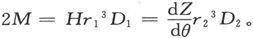
由此即得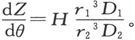

竖直力在任意时刻的实际值是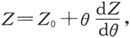 式中Z₀ 是当θ＝0时的Z值。

为了在一个固定观测站上对磁力的变化进行连续的观测，单线磁偏计、双线水平力磁强计和天平竖直力磁强计是最方便的仪器。

在一些观测站上，现在已在用钟表装置带动的专用纸上描绘摄影曲线，以便在任何时刻都对三种仪器上的指示形成一种连续的纪录。这些曲线表示着力的三个垂直分量对它们的标准值的改变量。磁偏计给出指向平均磁西方的力，双线磁强计给出指向磁北方的力的改变量，而天平磁强计则给出竖直力的改变量。这些力的标准值，或者说这些力在各仪器示数为零时的值，是通过对绝对偏角、水平力和倾角的频繁观测来推得的。

第三十三章　关于地磁

465．〕　我们关于地磁的知识，是由对于磁力在任一时刻在地面上的分布的研究以及对于这一分布在不同时刻的变化的研究导出的。

任一地点和任一时刻的磁力，当它的三个坐标为已知时，就是已知的。这三个坐标可以在力的偏角或方位角、对水平面的倾角和总强度的形式下被给出。

然而，考察磁力在地面上的普遍分布的最方便的方法，就在于考虑力的三个分量的量值，即　　

式中H代表水平力，δ代表偏角，而θ代表倾角。

如果V是地面上的磁势而我们把地球看成一个半径为a的球，则有

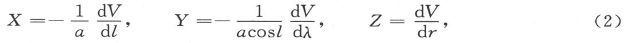
式中l是纬度，λ是经度，而r是从地心算起的距离。

关于地面上的V的一种知识，可以只依赖于有关水平力的观测而得出如下。

设V₀ 是真实北极上的V值，那么，沿任一子午线求线积分，我们就得到

这就是该子午线上纬度为l处的势的值。

于是，如果我们知道每一点上的指北分量X的值，又知道北极上的V值V₀ ，就可以求出地面上每一点的势。

既然力并不依赖于V的绝对值而是依赖于V的导数，那也就没有必要指定任何特定的V₀ 了。

任意点上的V值可被定出，如果我们知道沿任意子午线的X值和整个地面上的Y值的话。

令　　

式中的积分沿所给的子午线从极点计算到纬度l，于是就有

式中的积分沿l纬度线从已给的经度λ₀ 计算到所要考虑的点。

这种方法意味着，必须在地面上进行完备的磁勘测，以便在给定的时期知道地面上每一点的X值、Y值或X和Y的值。我们实际上知道的是若干观测站上的磁力分量。在地球上的各个开化部分，这样的观测站是比较多的；在其他的部分，却有大片的地面是我们并不掌握其数据的。

磁　勘　测 ^〔50〕

466．〕　让我们假设，在最大线度为几百英里的一个中等大小的国家中，在适当分布在全国各地的相当多的观测站上已经作出了关于偏角和水平力的观测。

在这一区域内，我们可以假设V的值能够足够精确地用公式

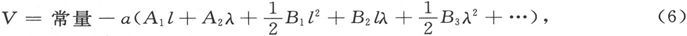
来表示，由此即得　　

设共有n个站，它们的纬度是l₁ 、l₂ 等等而它们的经度是λ₁ 、λ₂ 等等，并设每一个站上的X和Y都已测出。

令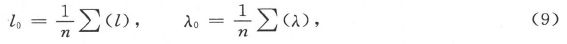　　

l₀ 和λ₀ 可以叫做中心站的纬度和经度。令

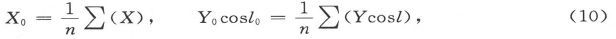
于是X₀ 和Y₀ 就是假想的中心站上的X值和Y值，于是就有

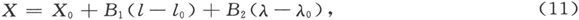
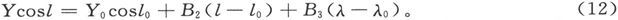
我们有n个形如（11）的方程和n个形如（12）的方程。如果我们用ζ来代表测定X时的可几误差，而用η来代表测定Ycosl时的可几误差，我们就可以假设二者起源于H和δ的观测误差，并根据这一假设来计算ζ和η。

设H的可几误差是h而δ的可几误差是∆，既然　　　　dX＝cosδ. dH－Hsinδ. dδ，

就有　　　　ξ² ＝h² cos² δ＋∆² H² sin² δ。

同理可得　　　　η² ＝h² sin² δ＋∆² H³ cos² δ。

如果X和Y对由形如（11）和（12）的方程给出的值而言的改变量远远超过观测的可几误差，我们就可以断定这些改变量是由地域性的吸引力引起的，而这时我们就没有任何理由不认为ζ和η之比等于1。

按照最小二乘式法，我们把形如（11）的方程乘以η而把形如（12）的方程乘以ζ，以便它们的可几误差相同。然后我们把每一个方程乘以B₁ 、B₂ 或B₃ 中一个未知量的系数并把结果加起来，这样就得到可以求出B₁ 、B₂ 、B₃ 的三个方程，即P₁ ＝B₁ b₁ ＋B₂ b₂ ，η² P₂ ＋ξ² Q₁ ＝B₁ η² b₂ ＋B₂ （ξ² b₁ ＋η² b₃ ）＋B₃ ξ² b₂ ，Q₂ ＝B₂ b₂ ＋B₃ b₃ ；在这些方程中，我们为了方便使用了下列符号：

b₁ ＝∑（l² 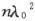）－ ，b₂ ＝∑（lλ）－nl₀ λ₀ ，b₃ ＝∑（λ² ）－ ，

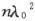P₁ ＝∑（lX）－nl₀ X₀ ，　Q₁ ＝∑（lYcosl）－nl₀ Y₀ cosl₀ ，

P₂ ＝∑（λX）－nλ₀ X₀ ，　Q₂ ＝∑（λYcosl）－nλ₀ Y₀ cosl₀ 。

通过计算B₁ 、B₂ 和B₃ 并代入方程（11）和（12）中，我们可以求出勘测界限以内任一点上的X值和Y值而不受地区性干扰的影响；经发现，当观测站附近存在像大多数火成岩那样的磁性岩石时，地区性干扰就是存在的。

只有在磁学仪器可以运往各地并在许多观测站上安装起来的那种国家，这种勘测才可以做到。对于世界上的其他部分来说，我们必须满足于利用在相距很远的较少观测站的数据之间进行内插的办法来求出地磁要素的分布。

467．〕　现在让我们假设，通过这种手续，或是通过等价地绘制各磁性要素之等值线图的作图手续，X和Y的值，从而还有势V的值，在整个的地球表面上都是已知的。下一步就是要把V展成球谐函数的级数了。

假如地球在它的全部体积内都是沿同一方向而均匀磁化的，V就将是一个一阶的谐函数，磁子午线将是通过两个对面磁极的大圆，磁赤道将是一个大圆，磁赤道的所有各点上的水平力将相等，而如果H₀ 是这个常量，则任一其他点上的值将是H＝H₀ cosl′，式中l′是磁纬度。竖直力将是z＝2H₀ sinl′，而如果θ是倾角，则tanθ将等于2tanl′。

在地球的事例中，磁赤道被定义为无倾角的曲线。它并不是球体的大圆。

磁极被定义为没有水平的点，或者说是倾角为90°的点。共有两个这样的点，一个在北半球，一个在南半球，但它们却并不是正好对面，而且它们的连线并不平行于地球的磁轴。

468．〕　磁极就是地面上V值为极大值或极小值，或为稳定值的那些点。

在势为极小值的任一点上，倾角针的北端将竖直向下，而如果把一个罗盘指针放在该点附近的任何地方，则其北端将指向该点。

在势为极大值的点上，倾角针的南端将指向下方，而在该点附近，罗盘指针的南端将指向该点。

如果在地球的表面上有p个V的极小值，那就必然有p－1个另外的点，在那儿，倾角针的北端是指向下方的，但是当使罗盘指针沿圆周绕该点运动一周时，指针的转动却并不是使北端永远指向该点，而是有时北端指向该点，而有时南端指向该点。

如果我们把势为极小值的各点叫做真北极，则这些另外的点可以叫做赝北极，因为罗盘指针对它们并不忠实。如果共有p个真北极，那就必有p－1个赝北极；同样，如果共有q个真南极，那就必有q－1个赝南极。同名磁极的数目必须是奇数，因此曾经流行一时的认为共有两个北极和两个南极的观念是不对的。按照高斯的意见，地球表面上事实上只有一个真北极和一个真南北，从而没有任何赝极。这两个极的连线并不是地球的直径，而且它也并不平行于地球的磁轴。

469．〕　大多数关于地磁本性的早期探索，都力图把它表示成一个或多个磁棒的作用结果，而磁棒各极的位置则是有待确定的。高斯是第一个通过把势函数展成体谐函数的级数来用一种完全普遍的方式表示了地磁分布的人，他定出了前四阶体谐函数的系数。这些系数共有24个；3个属于一阶函数，5个属于二阶函数，7个属于三阶函数，而9个属于四阶函数。经发现，为了对地磁的实际状态作出一种尚称精确的表示，所有这些项都是必要的。

试图定出观测到的磁力的哪一部分起源于外因和哪一部分起源于内因

470．〕　现在让我们假设，我们已经得到了地球磁势的一种球谐函数的展式，和地球表面每一点上水平力的方向及量值相容，这样，高斯就已经指明，如何根据观测到的竖直力来确定磁力是地球内部的磁化和电流之类的原因引起的呢，还是有某一部分是由地球表面以外的原因所直接引起的。

设V是展成球谐函数之双级数的实际磁势。

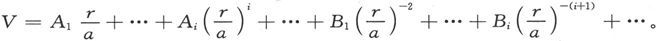
第一个级数代表由地球外部的原因所引起的那一部分势，而第二个级数则代表由地球内部的原因所引起的那一部分势。

水平力的观测向我们提供的是当r＝a＝地球的半径时这两个级数之和。其i次项是V_i ＝A_i ＋B_i 。

竖直力的观测给我们以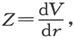 而其aZ的i次项是aZ_i ＝iA_i －（i＋1）B_i ，由此即得，

由外因引起的部分是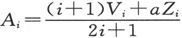 而由内因引起的部分是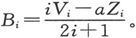

V的展式迄今只是针对在或接近某一年代的V的平均值算出的。看来这一平均值并没有任何部分是由地球以外的原因所引起的。

471．〕　关于V的改变量展式的日因部分和月因部分的形式，我们知道得不够清楚，不足以利用这种方法来确定这些改变量是否有任何部分起源于从外界作用过来的磁力。然而可以肯定，正如斯通内先生和钱伯斯先生已经证明的那样，假设太阳和月亮是一些磁体，这些改变量的主要部分也不可能起源于太阳和月亮的任何直接的磁作用 ^〔51〕 。

472．〕　曾经注意到的磁力的主要变化如下。

Ⅰ．较规则的变化

（1）日因变化，依赖于一天内的钟点和一年内的时序。

（2）月因变化，依赖于月球的时间角以及它的其他位置要素。

（3）这些变化并不在不同的年份中重复出现，而是受到一种周期更长的即约为十一年的变化的影响。

（4）除此以外，地磁的状态还有一种久期变化，它自从有地磁勘测以来就一直在进行着，而且正在引起各地磁要素的变化，其量值远大于任何小周期变化的量值。

Ⅱ．干扰

473．〕　除了较规则的变化以外，各地磁要素还会受到或大或小的突然干扰的影响。曾经发现，这些干扰在一段时间之内会比在别的时期更强，而且在干扰较大的时期内规则变化的规律会受到掩盖，尽管那些规律在干扰较小的时期内是很清楚的。因此，曾对这些干扰给予了很大的注意，而且曾经发现，特定种类的干扰在一天的某些时候以及在某些季节和时期更容易发生，尽管每一次干扰是十分无规则地出现的。除了这些更加普通的干扰以外，还偶然有些大干扰的时期，在那种时期内，地磁会在一两天内受到很强的干扰。这叫做“磁暴”。个体的干扰有时会在相距很远的观测站上同时被观测到。

艾瑞先生曾经发现，格林尼治的干扰的一个很大的部分，和安装在附近的土内的电极所收集到的电流相对应，而且是电流将对磁体直接产生的一种干扰，如果地电流保持其实际的方向而通过放在磁体下面的一根导线的话。

曾经发现，每十一年就有一个最大干扰时期，而且这个时期看来是和太阳黑子数目最多的时期相对应的。

474．〕　我们被地磁的研究所带入的探索领域是既深且广的。

我们知道，太阳和月亮都对地磁有影响。曾经证明，这种作用并不能通过假设太阳和月亮是磁体来加以解释。因此作用是间接的。

在太阳的事例中，部分的影响可能是热作用，但是在月亮的事例中我们却不能把作用归之于这种原因。也有可能，这些物体的吸引力通过在地球内部发生胁变而引起地球内部早已存在的磁性的一些变化（第447节），并从而通过一种潮汐作用而造成一些半昼夜的变化吧？

但是，和地磁的很大的久期变化相比，所有这些变化的数量都是很小的。

什么原因，地球外部的或其内部深处的原因，引起地磁的如此巨大的变化，以致磁极会慢慢地从大地的一部分移动到另一部分呢？当我们考虑到大地球的磁化强度完全可以和我们克服了许多困难才在我们的钢铁磁体中造成的磁化强度相比时，如此巨大的一个物体中的这些巨大变化，就迫使我们作出结论说，我们还不熟悉自然界中最强有力的作用之一，它的活动场所位于地球内部的深处，而要获得有关那种地方的知识，我们可用的手段是很少的。 ^〔52〕

泰勒斯（Thalȇs，约前624年—前546年）。泰勒斯曾用磁石和琥珀做实验，发现这两种物体对其他物体有吸引力。

吉尔伯特（William Gilbert, 1540—1605）正在锤打一根热铁条，以便制作出一根磁铁。吉尔伯特在物理学中的贡献是开创了电学和磁学的近代研究。1600年他发表了一部巨著《论磁》，系统地总结和阐述了他对磁的研究成果。他还发明了第一只验电器。

莱顿瓶是在18世纪时科学家们用来储存电量的一种电容器。其实，它就是一个玻璃瓶，只不过在这个玻璃瓶的内外壁都涂有一层金属箔，并且在瓶子的中间插有一根电极。在当时，科学家们把几个玻璃瓶排在一起，然后用金属挂钩连接每个瓶子的电极以获得更强大的电流输出。

富兰克林（Benjamin Franklin, 1706－1790）。富兰克林证明，闪电是一种放电，并且他阐述了高大的建筑物如何通过把电荷导向地面而免受雷击。

富兰克林早期的避雷装置之一。1754年用避雷针来防护建筑物免遭雷击，首先由狄维施（Procopius Divisch, 1698—1765）实现，这是迄今所知的电的第一个实际应用。

在18世纪的一次沙龙上，参加派对的人在做性质不明但显然很有趣味的电实验取乐。

18世纪的一个有关电的恶作剧：一个带电的男孩被吊在天棚上，右侧那位妇女从他的鼻子上提取火花。~TZ1

1794年2月27日，在法国加莱进行的电流通过一片水面上空的实验。

奥斯特（Hans Christian Oersted, 1777—1851）用一种仪器发现了电和磁之间的联系，即当电流在罗盘的指针周围流过时，罗盘的指针发生偏转。

库仑（Charlse-Augustin de Coulomb, 1736—1806年）。1785年，库仑设计了精巧的扭秤实验，直接测定了两个静止的同种点电荷之间的斥力与它们之间距离的平方成反比，与它们的电量乘积成正比。经过不断的探索，他又用电扭摆实验对吸引力测出了相同的结果。至此，库仑定律得到了世界公认，从而开辟了近代电磁理论研究的新纪元。

1773年，卡文迪什用数学方法得出了类似库仑定律的关系，但他的成果未公开发表，一直到1879年，才由麦克斯韦整理，注释出版了这些手稿。

安培（André-Marie Ampère, 1775—1836）。1820年安培发现了电流的磁效应（电产生磁）。

伏打电堆是第一个现代的化学电池，能提供较长时间的电流。它是在1800年由伏打（Alessandro Vlota, 1745—1827）发明的。

欧姆（Georg Simon Ohm, 1787—1854年）。1826年他建立了欧姆定律。

法拉第（Michael Faraday, 1791—1867）在19世纪20年代制造的一个早期的电磁体。1831年法拉第发现电磁感应现象（磁产生电）。

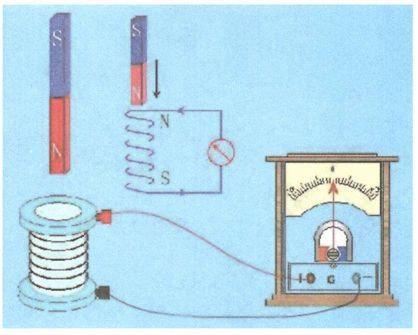
楞次定律实验演示仪器。1834年楞次（Heinrich Friedrich Emil Lenz, 1804—1865）建立楞次定律。

麦克斯韦和赫兹（Heinrich Rudolf Hertz, 1857—1894）的肖像一起出现在这张墨西哥发行的电信纪念票中。1888年赫兹用实验证明了电磁波的存在，麦克斯韦的电磁理论才得到人们确信，麦克斯韦被公认为“牛顿以后世界上最伟大的数学物理学家”。

1873年出版的《电磁通论》（第一版）的扉页。麦克斯韦第一次成功地将电和磁这两个不同的自然现象统一起来。

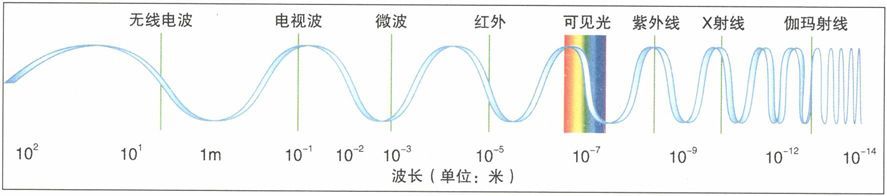
麦克斯韦首先认识到电场的表现是和光完全一样的高速波。科学家后来确认了电磁辐射谱的存在，在这个谱中，可见光只不过是一小部分。

麦克斯韦创立电磁理论用过的实验仪器。

麦克斯韦方程组。这些方程被誉为改变世界的最伟大的方程。

关于《电磁通论》的漫画。

麦克斯韦的老师开尔文爵士。正是开尔文卓有成效地运用类比的方法使麦克斯韦深受启示，在他的电磁场理论的论文中多次使用了类比研究方法，寻找到了不同现象之间的联系，建立了统一的电磁场理论。

麦克斯韦在《电磁场的动力理论》一书中预言了电磁波的存在，赫兹通过实验发现了在空中传播的电磁波。图为马可尼（Guglielmo Marchese Marconi, 1874—1937）在两者基础上，于1901年首次成功实现了横跨大西洋的无线电通信。

在当时的百科全书中看到的电报机。电报引领了通信的现代革命。

爱迪生（Thomas Alva Edison, 1847—1931）自己设计的电灯依然照亮蒙罗园主楼楼上的大实验室，这里是电话送话器、留声机和电灯泡的诞生地。

1904年的巴黎电话总局。电话接线员主要由妇女组成。对她们来说，这项发明提供了干净、令人尊敬、报酬相对较高的工作机会。早期的电话如果传送较高的频率，效果似乎好些，所以女子的声音听起来较清楚。

麦克斯韦还热衷研究颜色的组成，他手里正拿着他的色陀螺（1855年摄于剑桥）。

麦克斯韦的色陀螺。这是根据麦克斯韦的老师福布斯（James David Forbes, 1809—1868）在1849年发明的色陀螺发展起来的，它有两套着色纸，排列成可调整的扇形，当陀螺旋转时，这些颜色就在眼睛里混合起来，通过各种颜色显露的角度，一个色方程就构成了。

1861年在伦敦通过三个不同的滤镜（红、蓝、绿）向公众演示由三张反转片叠加而成的彩图。

这架诞生于1900年前后的三色投影仪是根据麦克斯韦“所有颜色都源自三种基本色彩（红、蓝、绿）的理论研制的。

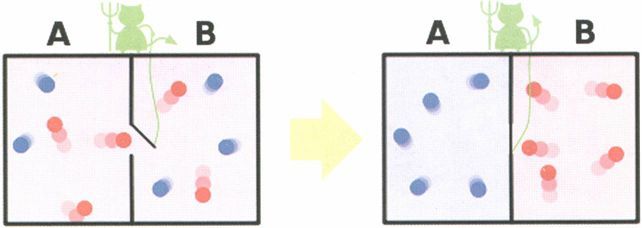
麦克斯韦妖示意图

麦克斯韦使用过的实验仪器

用偏振光研究光弹性

土星光环模型

可调陀螺

旋转线圈

对库仑定律的验证

电量单位比实验

注　释

〔1〕 　Coulomb, Mém. de l'Acad. 1785, p. 603，并见Biot's Truité de Physique, tome iii.

〔2〕 　参阅第56页的脚注。

〔3〕 　“极化”（polarizatisn，偏振）一词在光学中曾按和此处不一致的意义而被应用。在光学中，当一条光线具有一些和光线的侧向有关的性质，而这些性质在光线的对面两侧是相同的，则光线被说成是polarized（偏振的）。这种polarization涉及另一种有向量，可以叫做“偶极量”，而以前那种有向量则可以叫做“单极量”。

当一个偶极量被反向时，它将和以前保持相同。固体中的张力和压强，伸长、压缩和畸变，以及结晶物体的大多数光学的、电学的和磁学的性质，都是偶极量。

磁性在透明物体中引起的使入射光的偏振面发生旋转的那种性质，正如磁性本身一样，是单极的性质。在第303节中提到过的那种旋转性，也是单极的。

〔4〕 　这一轴线的正方向是从负极指向正极的。

〔5〕 　如果θ₁ 、θ₂ 是各磁体轴线和r之间的夹角， 是分别包含第一个和第二个磁体的轴线及r的平面之间的夹角，则有μ₁₂ －3λ₁ λ₂ ＝-2cosθ₁ cosθ₂ ＋sinθ₁ sinθ₂ cos 。

于是作用在第二个磁体上的力偶，就和两个力偶相等价，其中一个力偶的轴线是r，而且倾向于使 增大的力偶矩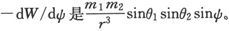 另一个力偶位于r和第二个磁体之轴线的平面内，其倾向于使θ₂ 增大的方偶矩-dW/dθ₂ 是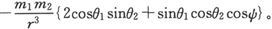

这些力偶是和由（6）和（7）给出的力偶相等价的。

〔6〕 　在事例（3）中，第一磁体叫做“正指”第二磁体，而第二磁体则为“侧向”第一磁体。我们很容易利用公式（6）和（7）证明，假如第一磁体是“侧向”第二磁体的，则作用在第二磁体上的力偶将是m₁ m₂ /r³ 。因此，当致偏磁体“正指”时，力偶将是当它为“侧向”时的二倍。高斯曾经证明，假如力定律是和极间距离的p次方成反比的，则致偏磁体为“正指”时的力偶将是它为“侧向”时的p倍。通过比较这些情况下的力偶，我们可以比利用扭秤更精确地检证平方反比定律。

〔7〕 　关于其他形状的空腔中的力。

1．任意窄缝——起源于表面磁化的力是4πlcosε，并着裂缝平面的法线方向ε，此处ε是该法线和磁化方向之间的夹角。当裂缝平行于磁化方向时，力就是磁力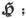 当裂缝垂直于磁化方向时，力就是磁感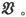

2．在其轴线和磁化方向成一角度ε的一个无限拉长的柱体中，由表面磁性引起的力是2πlsinε，并在包含轴线和磁化方向的平面内垂直于轴线。

3．在一个球中，由表面磁性引起的力是 并沿着磁化的方向。

〔8〕 　Exp. Res. series. xxviii.

〔9〕 　见Sir. W. Thnomson's 'Mathematical Theory of Magnetism,' Phil. Trans., June 1849和June 1850. 或Reprint of Papers on Electrostatics and Magnetism. p. 310.

〔10〕 　这一定理归功于高斯，General Theory of Terrestrial Magnetism, § 38.

〔11〕 　当要确定一条已给闭合曲线对它所张立体角的那个点是运动的时，如果我们假设矢径沿曲线的运动方向永远相同，则球上的面积可以看成正的，若当从球心看过去时该面积是位于球的一侧，即矢径端点的运动显得是顺时针进行的那一侧：它是负的，如果情况相反的话。

〔12〕 　Π的正负号可以通过考虑一个简单事例来最容易地得出；为此目的，一个垂直于盘面而被磁化的圆盘的事例是很合用的。

〔13〕 　厄翁（Phil. Trans., Part ii. 1885）曾经证明，当不受到振动和去磁力的影响时，软铁可以比最硬的钢保持其更大的磁性。

〔14〕 　Thalén, Nova Acta, Reg. Soc. Sc., Upsal, 1863。厄翁（见前引文献）已经证明，这个比值可以高达279，而且，如果铁丝在受到磁力作用时经过摇动，则比值甚至可以达到1600。

〔15〕 　瑞利勋爵（Phil. Mag. 23, p. 225. 1887）曾经证明，当磁化力小于地球水平磁力的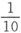 时，磁化是正比于磁化力的，而当磁力较大时二者就不再成正比了。

〔16〕 　Mémoires de l'lnstitut, 1824, p. 247.

〔17〕 　Recherches sur les proprietés magnétiques du fer, Nova Acta, Upsal, 1863.

〔18〕 　系数p和q的相等可以证明如下：设作用在球上的力使它绕着一个方向余弦为λ、μ、ν的直径转了一个角δθ，若用W代表球的能量，则由第436节得到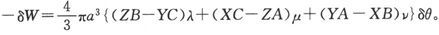 但是，如果坐标轴是固定在球中的，则转动的结果将导致δX＝（Yν－Zμ）δθ，…。

因此我们可以令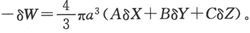 既然转动的球不能变成一种能源，上式右端的表示式就必须是一个全微分。于是，既然A、B、C是X、Y、Z的线性函数，W就必然是X、Y、Z的二次函数，由此立刻得到所要的结果。

并请参阅Sir W. Thomson's Reprint of Papers on Electrostatics and Magnetism, pp. 480～481.

〔19〕 　参阅Thomson and Tait's Natural Philosophy, § 525, 2nd Edition。

〔20〕 　如果使用长丝，它们的长度至少应为直径的300倍。

〔21〕 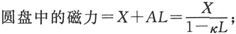　 而既然在这一事例中L＝-4π，磁力就是 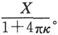于是通过圆盘的磁感就是X，这也就是当圆盘被拿开时磁感所将有的值。

〔22〕 　这种效应依赖于κ的平方，将在第440节中研究的力依赖于κ的一次方；因此，既然抗磁性物体的κ是很小的，后一种力就将胜过本节所讨论的这种倾向，只有特例除外。

〔23〕 　Crelle, bd. xxxvii (1848).

〔24〕 　Crelle, bd. xlviii (1854).

〔25〕 　柱体正端的圆柱面上的自由磁量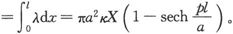 假设端平面上的密度和x＝l时的圆柱面上的密度相同，则端平面上的磁量是 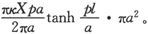于是总的自由磁量就是 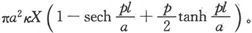当pl/a很大时，这个量就等于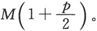

〔26〕 　Annals of Electricity, iv. p. 131, 1839; Phil. Mag. [4] iii. p. 32.

〔27〕 　Pogg. Ann. lxxix. p. 337, 1850.

〔28〕 　Phil. Trans. 1889. A. p. 221.

〔29〕 　Pogg. cxi. 1860.

〔30〕 　作用在磁体内部一个磁极上的力是不确定的，它依赖于磁极所在的空腔的形状。例如力X是不确定的，因为，既然我们关于分子磁体的形状及布置一无所知，那也就没有任何理由假设力是一种形状的空腔中的那个力而不是另一种形状的空腔中的那个力。于是，看样子，除非作出别的假设，我们似乎应该令X＝X₀ ＋pI，式中X₀ 是外磁力而p是我们只知道它介于0和4π之间的一个常数。在铁中，I比X₀ 大得多；由于有这种事实，这里的不确定性就更加讨厌，因为包含不确定性的那一项可以是两项之中更加重要得多的一项。

〔31〕 　韦伯在Abhandlungen der Kg. Sächs-Gesellschaft der Wissens. i. p. 572（1852）或Pogg., Ann., lxxxvii. p. 167（1852）上给出的公式中有些错误，他没有给出计算步骤而只给出了这一积分的结果。他的公式是

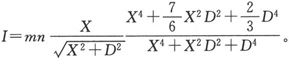
〔32〕 　麦克斯韦所真正作出的，似乎并不是本节叙述的这条假设，而是在第445节的脚注中论述的那种假设。

〔33〕 　正文中给出的结果，除了一点小小的例外，都可以按照下述的手续得出。第444节中的修订理论的叙述如下：一个磁性分子的磁轴，如果偏转了一个小于β₀ 的角β，则当致偏力被撤销时将返回其原始位置；但是，当偏转超过了β₀ 时，倾向于反抗偏转的力就会垮掉而允许分子偏转到和其偏转为β₀ 的分子相同的方向，而当致偏力被撤销时，分子就将采取一个方向，平行于其偏转本为β₀ 的那种分子的方向。这个方向可以叫做分子的永久取向。

在X＞L＜D的事例中，磁矩的表示式I包括两个部分。第一部分是由锥面AOP和BOQ中的分子引起的，可以按照和第443节中的方法完全相同的方法来求出，只要适当注意到积分限就行了。参照图8，我们按照以上的理论叙述就能求得表示式的第二部分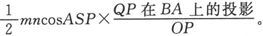 经过化简，这两部分就共同给出正文中的结果。

当X＞D时，积分又是包括两部分，其中一部分正如在第443节中那样应在圆锥AOP上计算。第二部分是（见图49）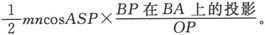

经过化简以后，这一事例中的I的值和正文中所给的值在第三项上有所不同，就是说我们有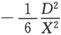 而不是 这种改变对正文中所给数值表的影响就是，当X＝6、7、8时，对应的l值将是887、917、936。这些变化并不会改变图10中所给的暂时磁化曲线的一般特点。

图47的事例中的I′值是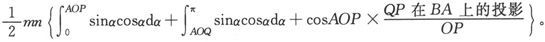

图48的事例中的I′值可按类似的方式求出。

〔34〕 　试考虑这样一个事例：一块铁沿正方向受到一个磁力的作用，该磁力从零增加到一个足以产生永久磁化的值X₀ ，然后又减小到零。很显然，按照上述的理论，由于给予了某些分子磁体以永久性的取向，对于磁化力的一个给定值来说，磁化强度在磁化力减小时将比在磁化力增加时为大。因此，铁在磁场中的行为将依赖于他的以前处理。这一效应被厄翁称为“磁滞”，他充分地研究了这种效应（见Phil. Trans. Part Ⅱ, 1885）。然而，第445节中给出的理论却并不能解释厄翁所发现的现象的全部。因为，如果我们在上一事例中在减小了磁力之后又增大它，则针对一个值X₁ ＜X₀ 来说，磁化强度的值应该和磁力第一次减小到X₁ 时相同。然而厄翁的研究却表明情况不是这样。这些研究以及类似的研究的一种简短介绍，将在本书的补遗卷中给出。

〔35〕 　这里假设，在图47和图58中，P点是位于C点的右方的。

〔36〕 　Phil. Mag. 3, 1833.

〔37〕 　Pogg., Ann., 31, 367, 1834.

〔38〕 　Ann. de Chimie et de Physique, 16, pp. 436 and 448, 1846.

〔39〕 　Phil. Trans., 1856, p. 287.

〔40〕 　Ann. de Chimie et de Physigue, 53. p. 385. 1858.

〔41〕 威拉利曾经证明，只有当磁化力小于某一临界值时，这种结论才是对的，但是当磁化力超过临界值时，拉伸却会引起磁化强度的减小；Pogg. Ann., 126, p. 87. 1865．正文中关于软铁棒之行为的论述，对于小胁变和弱磁场是不成立的。

〔42〕 　Sturgeon's Annals of Electricity, vol. viii. p. 219.

〔43〕 　Phil. Mag., xxx. 1847.

〔44〕 　｛歇耳福·比德外耳曾经证明，当磁化力很大时，磁体的长度是随磁化力的增大而减小的。Proc. Roy. Soc. xl. p. 109.｝

〔45〕 　Joule, Proc. Phil. Soc., Manchester., Nov. 29, 1864.

〔46〕 　参阅论文‘Imperfect Inrersion,' by W. Swan. Trans. R. S. Edin., vol. xxi (1855), p. 349.

〔47〕 　见Airy's Magnetism.

〔48〕 　在这一事例中，忽略含A₂ 的项，我们就有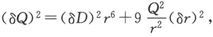 而当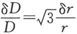 时此式即取最小值。

〔49〕 　Proc. Phil. S., Manchester, March 19, 1867.

〔50〕 　读者应参阅Rücker and Thorpe的论文‘A Magnetic Survey of the British Isles,' Phil. Trans., 1890, A, pp. 53～328.

〔51〕 　布拉格的赫尔施坦教授曾经发现了各磁要素的一种周期变化，其周期为26.33天，几乎正好等于太阳的朔望转动，正如由太阳赤道附近的黑子的观测所推知的那样。这种根据它对磁针的效应来发现太阳的未被看到的整体转动时间的方法，是地磁学对天文学的借贷偿还的第一次支付。请参阅Anzeiger der k. Akad., Wien, june 15, 1871．见Proc. R. S., Nov. 16, 1871.

〔52〕 　巴耳福·斯提瓦特曾经建议，周日变化是由大气上层区域的稀薄空气中的感生电流引起的，当这种空气扫过地球的磁力线而运动时，这种电流就会出现。舒斯特近来在Phil. Trans. A, 1889, p. 467上通过格林方法的应用已经证明，这些干扰的较大部分是在地球表面的上方有其起源的。