- 第2章 曲线的性质
- 哪些曲线可被纳入几何学
- 区分所有曲线的类别,以及掌握它们与直线上点的关系的方法
- 对上篇提到的帕普斯问题的解释
- 仅有三线或四线时该问题的解
- 对该解的论证
- 平面与立体轨迹,以及求解它们的方法
- 对五线情形解这一古代问题所需曲线中最基本、最简单的曲线
- 经由找出其上若干点而描绘的几何曲线
- 可利用细绳描绘的曲线
- 为了解曲线的性质,必须知道其上的点与直线上点的关系;在各点引与该曲线成直角的曲线的方法
- 求一直线与给定曲线相交并成直角的一般方法
- 对蚌线完成这一问题作图的例证
- 对用于光学的四类新的卵形线的说明
- 所论卵形线具有的反射与折射性质
- 对这些性质的论证
- 如何按我们的要求制作一透镜,使从某一给定点发出的所有光线经透镜的一个表面后会聚于一给定点
- 如何制作有如上功能的透镜,而又使一个表面的凸度跟另一表面的凸度或凹度形成给定的比
- 如何将涉及平面上的曲线的那些讨论应用于三维空间或曲面上的曲线
第2章 曲线的性质
On the Nature of Curved Lines
为了讨论本书引进的所有曲线,我想只需引入一条必要的假设,即两条或两条以上的线可以一条随一条地移动,并由它们的交点确定出其他曲线。
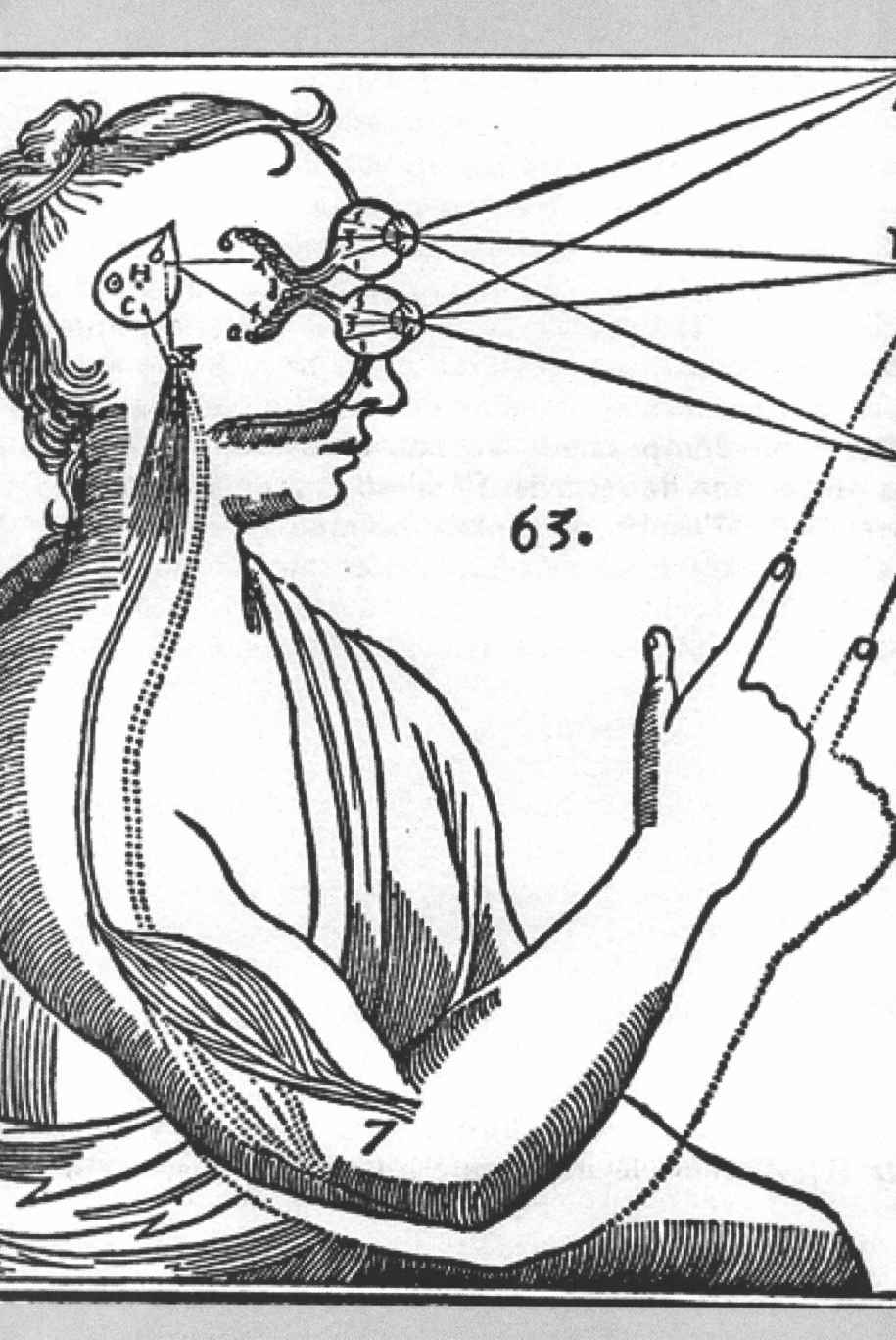 笛卡儿关于人的感知系统与手臂的运动关系示意图
笛卡儿关于人的感知系统与手臂的运动关系示意图
哪些曲线可被纳入几何学
古代人熟悉以下事实,几何问题可分成三类,即平面的、立体的和线的问题。这相当于说,某些问题的作图只需要用到圆和直线,另一些需要圆锥截线,再有一些需要更复杂的曲线。然而,令我感到吃惊的是他们没有再继续向前,没有按不同的次数去区分那些更复杂的曲线;我也实在不能理解他们为什么把最后一类曲线称做机械的而不称做几何的。如果我们说,他们是因为必须用某种工具才能描绘出这种曲线而称其为机械的,那么为了协调一致,我们也必须拒绝圆和直线了,因为它们非用圆规和直尺才能在纸上画出来,而圆规、直尺也可以称做是工具。我们也不能说因为其他工具比直尺和圆规复杂故而不精密;若这样认为,它们就该被排除出机械学领域,作图的精密性在那里甚至比在几何中更重要。在几何中,我们只追求推理的准确性,讨论这种曲线就像讨论更简单的曲线一样,都肯定是绝对严格的。我也不能相信是因为他们不愿意超越那两个公设,即:(1)两点间可作一直线,(2)绕给定的中心可作一圆过一给定的点。他们在讨论圆锥截线时,就毫不犹豫地引进了这样的假设:任一给定的圆锥可用给定的平面去截。现在,为了讨论本书引进的所有曲线,我想只需引入一条必要的假设,即两条或两条以上的线可以一条随一条地移动,并由它们的交点确定出其他曲线。这在我看来决不会更困难。
真的,圆锥截线被接纳进古代的几何,恐怕绝非易事,我也不关心去改变由习惯所认定的事物的名称;无论如何,我非常清楚地知道,若我们一般地假定几何是精密和准确的,那么机械学则不然;若我们视几何为科学,它提供关于所有物体的一般的度量知识;那么,我们没有权力只保留简单的曲线而排除复杂的曲线,倘若它们能被想象成由一个或几个连续的运动所描绘,后者中的每一个运动完全由其前面的运动所决定——通过这种途径,总可以得到涉及每一个运动的量的精确知识。
也许,古代几何学拒绝接受比圆锥截线更复杂的曲线的真正理由在于,首先引起他们注意的第一批这类曲线碰巧是螺线、割圆曲线以及类似的曲线,它们确实只归属于机械学,而不属于我在这里考虑的曲线之列,因为它们必须被想象成由两种互相独立的运动所描绘,而且这两种运动的关系无法被精确地确定。尽管他们后来考查过蚌线、蔓叶线和其他几种应该能被接受的曲线;但由于对它们的性质知之不多,他们并没有比之其他曲线给予更多的思考。另一方面,他们可能对圆锥截线所知不多,也不了解直尺和圆规的许多可能的作图,因此还不敢去做更困难的事情。我希望从今以后,凡能巧妙地使用这里提到的几何方法的人,不会在应用它们解决平面或立体问题时遇到大的困难。因此,我认为提出这一内容更加广泛的研究方向是适宜的,它将为实践活动提供充分的机会。
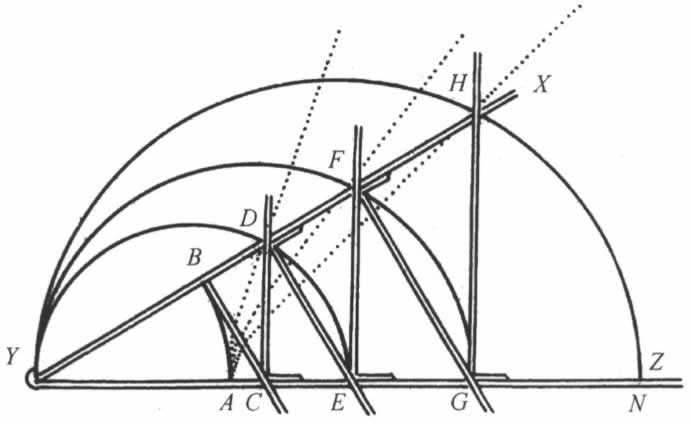
考虑直线AB ,AD ,AF ,等等,我们假设它们可由工具YZ 所描绘。该工具由几把直尺按下述方式绞接在一起组合而成:沿直线AN 放置YZ ,角XYZ 的大小可增可减,当它的边集拢后,点B ,C ,D ,E ,F ,G ,H 全跟A 重合;而当角的尺寸增加时,跟XY 在点B 固定成直角的直尺BC ,将直尺CD 向Z 推进,CD 沿YZ 滑动时始终与它保持成直角。类似地,CD 推动DE ,后者沿XY 滑动时始终与BC 平行;DE 推动EF ;EF 推动FG ;FG 推动GH ,等等。于是,我们可以想象有无穷多把尺子,一个推动另一个,其中有一半跟XY 保持相等的角度,其余的跟YZ 保持等角。
当角XYZ 增加时,点B 描绘出曲线AB ,它是圆;其他直尺的交点,即点D ,F ,H 描绘出另外的曲线AD ,AF ,AH ,其中后两条比第一条复杂,第一条比圆复杂。无论如何,我没有理由说明为什么不能像想象圆的描绘那样,清晰明了地想象那第一条曲线,或者,至少它能像圆锥截线一样明白无误;同样,为什么这样描绘出的第二条、第三条,以至其他任何一条曲线不能如想象第一条那样清楚呢;因此,我没有理由在解几何问题时不一视同仁地使用它们。
区分所有曲线的类别,以及掌握它们与直线上点的关系的方法
我可以在这里给出其他几种描绘和想象一系列曲线的方法,其中每一条曲线都比它前面的任一条复杂,但是我想,认清如下事实是将所有这些曲线归并在一起并依次分类的最好办法:这些曲线——我们可以称之为“几何的”,即它们可以精确地度量——上的所有的点,必定跟直线上的所有的点具有一种确定的关系,而且这种关系必须用单个的方程来表示。若这个方程不包含次数高于两个未知量所成的矩形或一个未知量的平方的项,则曲线属于第一类,即最简单的类,它只包括圆、抛物线、双曲线和椭圆;当该方程包含一项或多项两个未知量中的一个或两个的三次或四次的项,(因方程需要两个未知量来表示两点间的关系),则曲线属于第二类;当方程包含未知量中的一个或两个的五次或六次的项,则曲线属于第三类,依此类推。
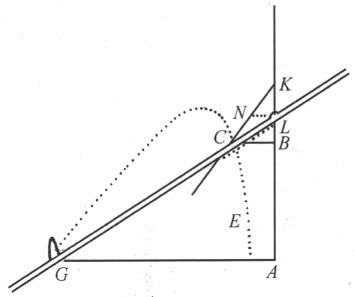
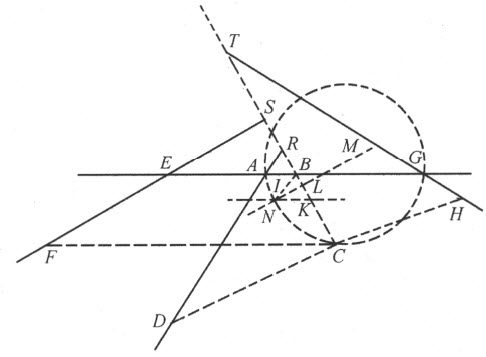
设EC 是由直尺GL 和平面直线图形CNKL 的交点所描绘出的曲线;直线图形的边KN 可朝C 的方向任意延长,图形本身以如下方式在同一平面内移动:其边KL 永远跟直线BA (朝两个方向延长)的某个部分相重,并使直尺GL 产生绕G 的转动(该直尺与图形CNKL 在L 处铰接)。当我想弄清楚这条曲线属于哪一类时,我要选定一条直线,比如AB ,作为曲线上所有点的一个参照物;并在AB 上选定一个点A ,由此出发开始研究。我在这里可以说“选定这个选定那个”,因为我们有随意选择的自由;若为了使所得到的方程尽可能地短小和简单,我们在作选择时必须小心从事,但不论我选哪条线来代替AB ,可以证明所得曲线永远属于同一类,而且证明并不困难。
然后,我在曲线上任取一点,比如C ,我们假设用以描绘曲线的工具经过这个点。我过C 画直线CB 平行于GA 。因CB 和BA 是未知的和不确定的量,我称其中之一为y ,另一个为x 。为了得到这些量之间的关系,我还必须考虑用以决定该曲线作图的一些已知量,比如GA ,我称之为a ;KL ,我称之为b ;平行于GA 的NL ,我称之为c 。于是,我说NL 比LK (即c 比b )等于CB (即y )比BK ,因此BK 等于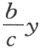 。故BL 等于
。故BL 等于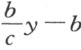 ,AL 等于
,AL 等于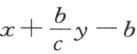 。进而,CB 比LB (即y 比
。进而,CB 比LB (即y 比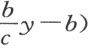 等于AG (或a )比LA
等于AG (或a )比LA 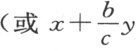 -b )。用第三项乘第二项,我们得
-b )。用第三项乘第二项,我们得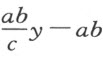 ,它等于
,它等于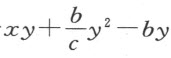 ,后者由最后一项乘第一项而得。所以,所求方程为
,后者由最后一项乘第一项而得。所以,所求方程为
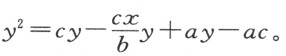
根据这个方程,我们知曲线EC 属于第一类,事实上它是双曲线。
若将上述描绘曲线的工具中的直线图形CNK 用位于平面CNKL 的双曲线或其他第一类曲线替代,则该曲线与直尺GL 的交点描绘出的将不是双曲线EC ,而是另一种属于第二类的曲线。
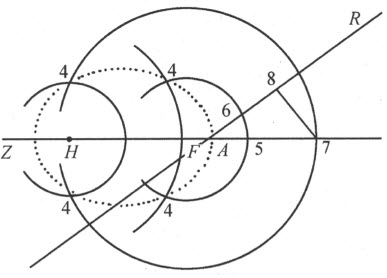
于是,若CNK 是中心在L 的圆,我们将描绘出古人可知的第一条蚌线;若利用以KB 为轴的抛物线,我们将描绘出我已提到过的最主要的也是最简单的曲线,它们属于帕普斯问题所求的解,即当给定五条位置确定的直线时的解。
若利用一条位于平面CNKL 上的第二类曲线来代替上述第一类曲线,我们将描绘出一条第三类曲线;而要是利用一条第三类曲线,则将得到一条第四类曲线,依此类推,直至无穷。上述论断不难通过具体计算加以证明。
无论如何,我们可以想象已经描绘出一条曲线,它是我称之为几何曲线中的一条;用这种方法,我们总能找到足以决定曲线上所有点的一个方程。现在,我要把其方程为四次的曲线跟其方程为三次的曲线归在同一类中;把其方程为六次的跟其方程为五次的曲线归在一类,余者类推。这种分类基于以下事实:存在一种一般的法则,可将任一个四次方程化为三次的,任一六次方程化为五次方程,所以,无需对每一情形中的前者作比后者更繁复的考虑。
然而,应该注意到,对任何一类曲线,虽然它们中有许多具有同等的复杂性,故可用来确定同样的点,解决同样的问题,可是也存在某些更简单的曲线,它们的使用范围也更有限。在第一类曲线中,除了具有同等复杂性的椭圆、双曲线和抛物线,还有圆——它显然是较为简单的曲线;在第二类曲线中,我们有普通的蚌线,它是由圆和另外一些曲线描绘的,它尽管比第二类中的许多曲线简单,但并不能归入第一类。
对上篇提到的帕普斯问题的解释
在对一般的曲线分类之后,我很容易来论证我所给出的帕普斯问题的解。因为,首先我已证明当仅有三条或四条直线时,用于确定所求点的方程是二次的。由此可知,包含这些点的曲线必属于第一类,其理由是这样的方程表示第一类曲线上的所有点和一条固定直线上的所有点之间的关系。当给定直线不超过八条时,方程至多是四次的,因此所得曲线属于第二类或第一类。当给定直线不超过十二条时,方程是六次或更低次的,因此所求曲线属于第三类或更低的类。其他情形可依此类推。
另一方面,就每一条给定直线而言,它可以占据任一处可能想象得到的位置,又因为一条直线位置的改变会相应地改变那些已知量的值及方程中的符号+与-,所以很清楚,没有一条第一类曲线不是四线问题的解,没有一条第二类曲线不是八线问题的解,没有一条第三类曲线不是十二线问题的解,等等。由此可知,凡能得到其方程的所有几何曲线,无一不能作为跟若干条直线相联系的问题的解。
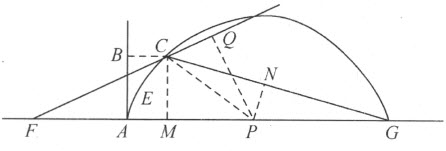
仅有三线或四线时该问题的解
现在需要针对只有三条或四条给定直线的情形作更具体的讨论,对每个特殊问题给出用于寻找所求曲线的方法。这一研究将表明,第一类曲线仅包含圆和三种圆锥截线。
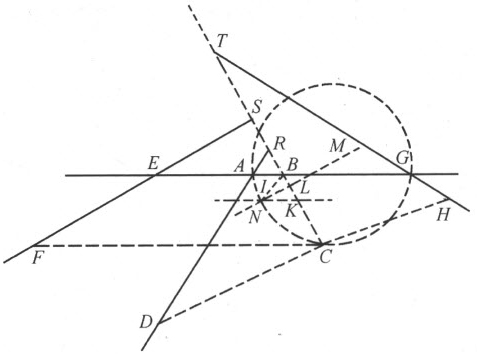
再次考虑如前给定的四条直线AB ,AD ,EF 和GH ,求点C 描出的轨迹,使得当过点C 的四条线段CB ,CD ,CF 和CH 与给定直线成定角时,CB 和CF 的积等于CD 和CH 的积。这相当于说:若
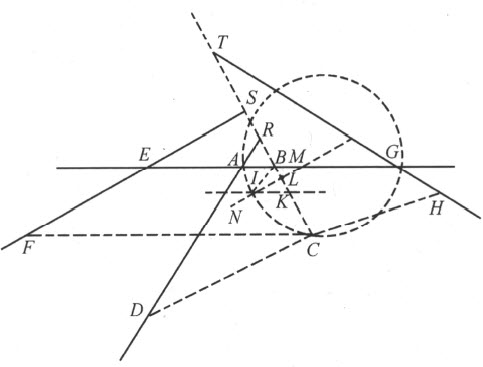

于是,方程为
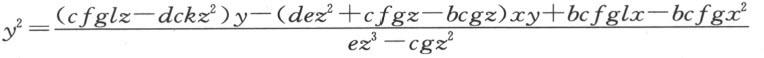
此处假定ez 大于cg ;否则所有的符号+和-都必须掉换。在这个方程中,若y 为零或比虚无还小 (1) ,并假定点C 落在角DAG 的内部,那么为导出这一结论,必须假定C 落在角DAE 、EAR 或RAG 中的某一个之内,且要将符号改变。若对这四种位置中的每一个,y 都等于零,则问题在所指明的情形下无解。
让我们假定解可以得到;为了简化推导,让我们以2m 代替 。于是,我们有
。于是,我们有
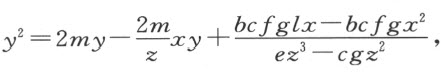
其根为
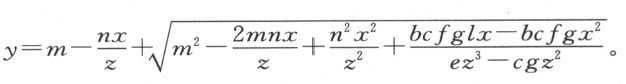
还是为了简洁,记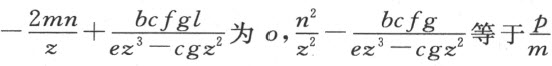 ;对于这些已给定的量,我们可随意按某一种记号来表示它们。于是,我们有
;对于这些已给定的量,我们可随意按某一种记号来表示它们。于是,我们有
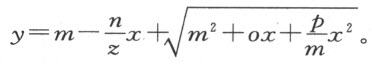
这就给出了线段BC 的长度,剩下AB 或x 是尚未确定的。因为现在的问题仅涉及三条或四条直线,显然,我们总可得到这样的一些项,尽管其中某些可能变成零,或者符号可能完全变了。
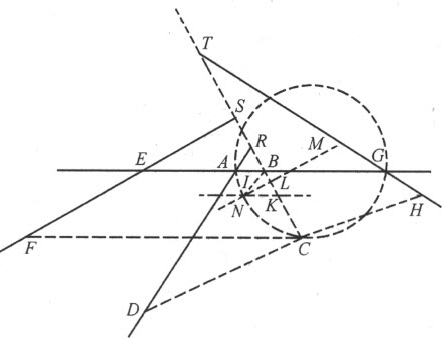
接着,我作KI 平行且等于BA ,在BC 上截取一段BK 等于m (因BC 的表示式含+m ;若它是-m ,我将在AB 的另一边作IK ;而当m 是零时,我就根本不去画出IK )。我再作IL ,使得IK :KL =z :n ;即,使得当IK 等于x 时,KL 等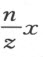 。用同样的方法,我可以知道KL 对IL 的比,称为n :a,所以,若KL 一等于
。用同样的方法,我可以知道KL 对IL 的比,称为n :a,所以,若KL 一等于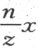 ,则IL 等
,则IL 等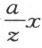 。因为该方程含有
。因为该方程含有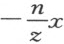 ,我可在L 和C 之间取点K ;若方程所含为
,我可在L 和C 之间取点K ;若方程所含为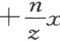 ,我就应该在K 和C 之间取L ;而当
,我就应该在K 和C 之间取L ;而当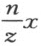 等于零时,我就不画IL 了。
等于零时,我就不画IL 了。
做完上述工作,我就得到表达式
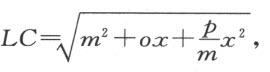
据此可画出LC 。很清楚,若此式为零,点C 将落在直线IL 上;若它是个完全平方,即当m 2 和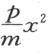 两者皆为+而o 2 等于4pm ,或者m 2 和ox (或ox 和
两者皆为+而o 2 等于4pm ,或者m 2 和ox (或ox 和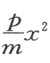 )皆为零,则点C 落在另一直线上,该直线的位置像IL 一样容易确定。
)皆为零,则点C 落在另一直线上,该直线的位置像IL 一样容易确定。
若无这些例外情形发生,点C 总是或者落在三种圆锥截线的一种之上,或是落在某个圆上,该圆的直径在直线IL 上,并有直线段LC 齐整地附在这条直径上 (2) ,另一方面,直线段LC 与一条直径平行,而IL 齐整地附在它上面。
特别地,若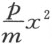 这项为零,圆锥截线应是抛物线;若它前面是加号,则得双曲线;最后,若它前面是减号,则得一个椭圆。当a 2 m 等于pz 2 而角ILC 是直角时出现例外情形,此时我们得到一个圆而非椭圆。
这项为零,圆锥截线应是抛物线;若它前面是加号,则得双曲线;最后,若它前面是减号,则得一个椭圆。当a 2 m 等于pz 2 而角ILC 是直角时出现例外情形,此时我们得到一个圆而非椭圆。
当圆锥截线是抛物线时,其正焦弦 (3) 等于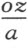 ,其直径总是落在直线IL 上。为了找出它的顶点N ,作IN 等于
,其直径总是落在直线IL 上。为了找出它的顶点N ,作IN 等于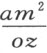 ,使得m 为正并且ox 亦为正时,点I 落在L 和N 之间;而当m 为正并且ox 为负时,L 落在I 和N 之间;而当m 2 为负并且ox 为正时,N 落在I 和L 之间。可是,当各个项像上面那样安排时,m 2 不可能为负。最后,若m 2 等于零,点N 和I 必定相重。所以,根据阿波罗奥斯著作的第一篇中的第一个问题,很容易确定这是抛物线。
,使得m 为正并且ox 亦为正时,点I 落在L 和N 之间;而当m 为正并且ox 为负时,L 落在I 和N 之间;而当m 2 为负并且ox 为正时,N 落在I 和L 之间。可是,当各个项像上面那样安排时,m 2 不可能为负。最后,若m 2 等于零,点N 和I 必定相重。所以,根据阿波罗奥斯著作的第一篇中的第一个问题,很容易确定这是抛物线。
然而,当所求轨迹是圆、椭圆或双曲线时,必须首先找出图形的中心,点M 。它总是落在直线IL 上,可以取IM 等于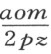 而求得。若o 等于零,则M 和I 相重。当所求轨迹是圆或椭圆时,若ox 项为正,则M 和L 必落在I 的同侧,而若ox 为负,则它们必落在异侧。另一方面,对于双曲线的情形,若ox 为负,则M 和L 落在I 的同侧。若ox 为正,则它们落在异侧。
而求得。若o 等于零,则M 和I 相重。当所求轨迹是圆或椭圆时,若ox 项为正,则M 和L 必落在I 的同侧,而若ox 为负,则它们必落在异侧。另一方面,对于双曲线的情形,若ox 为负,则M 和L 落在I 的同侧。若ox 为正,则它们落在异侧。
当m 2 为正、轨迹是圆或椭圆,或者m 2 为负而轨迹是双曲线时,图形的正焦弦必定为
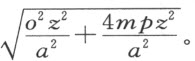
而当所求轨迹是圆或椭圆、m 2 为负时,或者轨迹是双曲线、o 2 大于4mp 、且m 2 为正时,它必定为
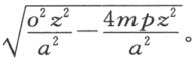
但是,若m 2 等于零,则正焦弦为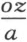 ;又若oz 等于零,则它为
;又若oz 等于零,则它为
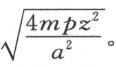
为得到相应的直径,必须找出跟正焦弦之比为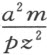 的直线;即,若正焦弦为
的直线;即,若正焦弦为
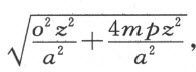
直径应为
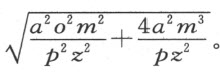
无论哪一种情形,该圆锥截线的直径都落在IM 上,LC 是齐整地附于其上的线段之一。可见,取MN 等于直径的一半,并取N 和L 在M 的同侧,则点N 将是这条直径的端点。所以,根据阿波罗尼奥斯著作第一篇中的第二和第三个问题,确定这条曲线是轻而易举的事。
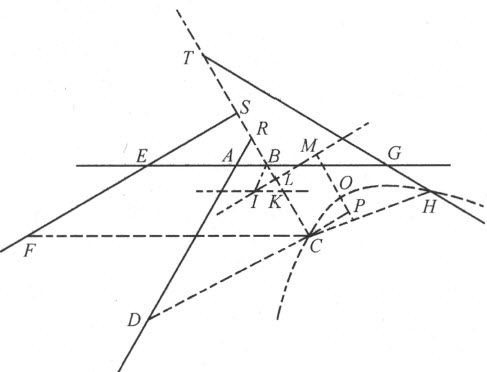
若轨迹是双曲线且m 2 为正,则当o 2 等于零或小于4pm 时,我们必须从中心M 引平行于LC 的直线MOP 及平行于LM 的CP ,并取MO 等于
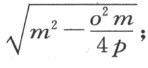
而当ox 等于零时,必须取MO 等于m 。考虑O 为这条双曲线的顶点,直径是OP ,齐整地附于其上的线段是CP ,其正焦弦为
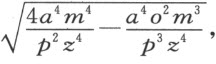
其直径为
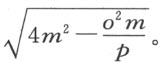
我们必须考虑ox 等于零这种例外情形,此时正焦弦为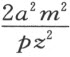 ,直径为2m 。从这些数据出发,根据阿波罗尼奥斯著作的第一篇中的第三个问题,可以确定这条曲线。
,直径为2m 。从这些数据出发,根据阿波罗尼奥斯著作的第一篇中的第三个问题,可以确定这条曲线。
对该解的论证
以上陈述的证明都十分简单。因为,像正焦弦、直径、直径NL 或OP 上的截段这些上面给出的量,使用阿波罗尼奥斯第一篇中的定理11、12和13就能作出它们的乘积,所得结果将正好包含这样一些项,它们表示直线段CP 的平方或者说CL ,那是直径的纵标线 (4) 。
在这种情形下,我们应从NM 或者说从跟它相等的量

中除去IM ,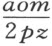 。在余下的IN 上加IL ,或者说加
。在余下的IN 上加IL ,或者说加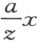 ,我们得
,我们得
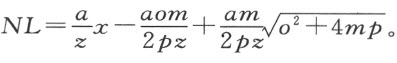
以该曲线的正焦弦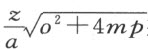 乘上式,我们得一矩形的值
乘上式,我们得一矩形的值
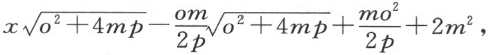
并从中减去一个矩形,该矩形与NL 的平方之比等于正焦弦与直径之比。NL 的平方为
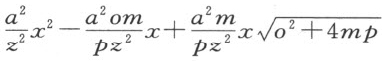
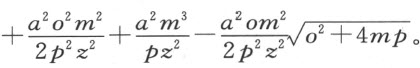
因为这些项表示直径与正焦弦之比,我们可用a 2 m除上式,并以pz 2 乘所得的商,结果为
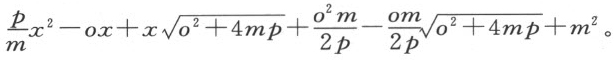
我们再从上面所得的矩形中减去此量,于是CL 的平方等于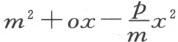 。由此可得,CL 是附于直径的截段NL 上的椭圆或圆的纵标线。
。由此可得,CL 是附于直径的截段NL 上的椭圆或圆的纵标线。
设所有给定的量都以数值表示,如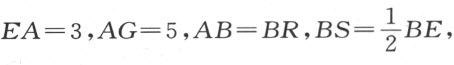
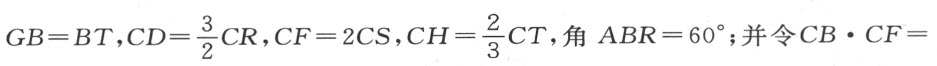
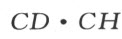 。如果要使问题完全确定,所有这些量都必须是已知的。现令AB =x ,CB =y 。用面给出的方法,我们将得到
。如果要使问题完全确定,所有这些量都必须是已知的。现令AB =x ,CB =y 。用面给出的方法,我们将得到
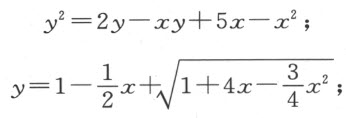
此时BK 必须等于1,KL 必须等于KI 的二分之一;因为角IKL 和ABR 都是60°,而角KIL (它等于角KIB 或IKL 的一半)是30°,故角ILK 是直角。因为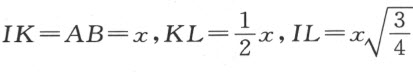 ,上面以z表示的量为1,我们得a =
,上面以z表示的量为1,我们得a =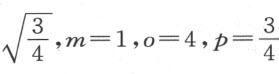 ,由此可知
,由此可知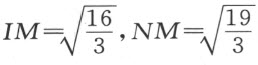 ;又因
;又因 等于pz 2 ,角ILC 是直角,由此导出曲线NC 是圆。对其他任何一种情形的兰讨论,不会产生困难。
等于pz 2 ,角ILC 是直角,由此导出曲线NC 是圆。对其他任何一种情形的兰讨论,不会产生困难。
平面与立体轨迹,以及求解它们的方法
由于所有不高于二次的方程都已包括在上述讨论之中,所以,我们不仅完全解决了古代人有关三线与四线的问题,而且也完全解决了他们所谓的立体轨迹的作图问题;这自然又解决了平面轨迹的作图,因为后者包含在立体轨迹之中。解任何这类轨迹问题,无非是去找出一种状态所要求的一个完全确定的点,整条线上所有的点满足其他状态所提出的要求(正如已举的例子所表明的那样)。如果这条线是直线或圆,就说它是平面轨迹;但如果它是抛物线、双曲线或椭圆,就称它是立体轨迹。对于每一种情形,我们都能得到包含两个未知量的一个方程,它完全跟上面找出的方程类似。若所求的点位于其上的曲线比圆锥截线的次数高,我们同样可称之为超立体轨迹,余者类推。如果在确定那个点时缺少两个条件,那么点的轨迹是一张面,它可能是平面、球面或更复杂的曲面。古人的努力没有超越立体轨迹的作图;看来,阿波罗尼奥斯写他的圆锥截线论著的唯一目的是解立体轨迹问题。
我已进一步地说明了,我称做第一类曲线的只包括圆、抛物线、双曲线和椭圆。这就是我所论证的内容。
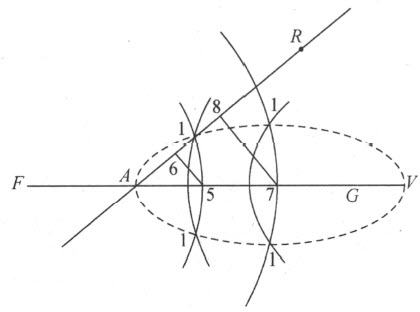
对五线情形解这一古代问题所需曲线中最基本、最简单的曲线
若古人所提出的问题涉及五条直线,而且它们全都平行,那么很显然,所求的点将永远落在一条直线上。假设所提问题涉及五条直线,而且要求满足如下条件:
(1)这些直线中的四条平行,第五条跟其余各条垂直;
(2)从所求点引出的直线与给定的直线成直角;
(3)由所引的与三条平行直线相交的三条线段作成的平行六面体必须等于另三条线段作成的平行六面体,它们是所引的与第四条平行线相交的线段、所引的与垂直直线相交的线段,以及某条给定的线段。
除了前面指出的例外情况,这就是最简单的可能情形了。所求的点将落在由抛物线以下述方式运动所描出的曲线上:
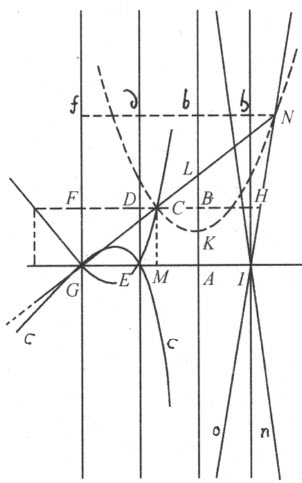
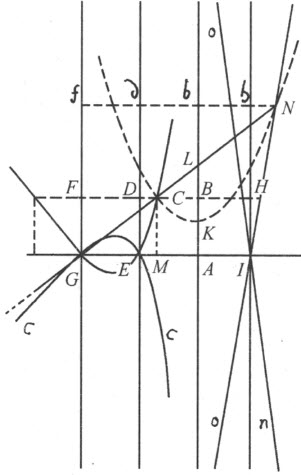
令所给直线为AB ,IH ,ED ,GF 和GA 。设所要找的点为C ,使得当所引的CB ,CF ,CD ,CH 和CM 分别垂直于给定直线时,三条线段CF ,CD 和CH 作成的平行六面体应等于另两条线段CB 、CM 跟第三条线段AI 所作成的平行六面体。令CB =y ,CM =x ,AI 及AE 及GE =a ;因此,当C 位于AB 和DE 之间时,我们有CF =2a-y ,CD =a-y ,CH =y +a 。将三者相乘,我们得到y 3 -2ay 2 -a 2 y +2a 3 等于其余三条线段的积,即等于axy 。
接着,我将考虑曲线CEG 。我想象它是由抛物线CKN (让它运动但使其直径KL 总落在直线AB 上)和直尺GL (它绕点G 旋转,但始终过点L 保持在抛物线所在的平面内 (5) )的交点所描绘出的。我取KL 等于a ,令主正焦弦——对应于所给抛物线的轴的正焦弦——也等于a ,并令GA =2a ,CB 或MA =y ,CM 或AB =x 。因三角形GMC 和CBL 相似,GM (或2a -y )比MC (或x )等于CB (或y )比BL ,因此BL 等于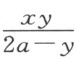 。因KL 为a ,故BK 为
。因KL 为a ,故BK 为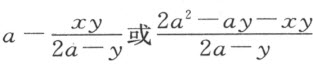 。最后,因这同一个BK 又是抛物线直径上的截段,BK 比BC (它的纵标线)等于BC 比a (即正焦弦)。由此,我们得到y 3 -2a y2 -a 2 y +2a 3 =axy ,故C 即所求的点。
。最后,因这同一个BK 又是抛物线直径上的截段,BK 比BC (它的纵标线)等于BC 比a (即正焦弦)。由此,我们得到y 3 -2a y2 -a 2 y +2a 3 =axy ,故C 即所求的点。
点C 可以在曲线CEG ,或它的伴随曲线cEGc 的任何部分之上取定;后一曲线的描绘方式,除了令抛物线的顶点转到相反的方向之外,其余都和前者相同;点C 也可以落在它们的配对物NIo 和nIO 上,NI 和nIO 由直线GL 和抛物线KN 的另一支的交点所生成。
其次,设给定的平行线AB 、IH 、ED 和GF 彼此之间的距离互不相等,且不与GA 垂直,而过C 的直线段与给定直线亦不成直角。在这种情形下,点C 将不会永远落在恰好具有同样性质的曲线上。甚至对于没有两条给定直线是平行的情形,也可能导致这种后果。
再其次,设我们有四条平行直线,第五条直线与它们相交,过点C 引出的三条线段(一条引向第五条直线,两条引向平行线中的两条)所作成的平行六面体等于另一平行六面体,后者由过C 所引的分别到达另两条平行线的两条线段和另一条给定线段作成。这种情形,所求点C 将落在一条具有不同性质的曲线上,即所有到其直径的纵标线等于一条圆锥截线的纵标线,直径上在顶点与纵标线之间的线段跟某给定线段之比等于该线段跟圆锥截线的直径上具有相同纵标线的那一段的比。
我不能说,这条曲线比前述的曲线复杂;确实,我总觉得前者应首先考虑,因为它的描绘及其方程的确定多少要容易些。
我不再仔细讨论相应于其他情形的曲线,因为我一直没有对这课题进行完全的论述。由于已经解释过确定落在任一曲线上的无穷多个点的方法,我想我已提供了描绘这些曲线的方法。
经由找出其上若干点而描绘的几何曲线
值得一提的是,这种由求出曲线上若干点而描出曲线的方法,跟用来描绘螺线及其类似曲线的方法有极大差异;对于后者,并不是所求曲线上面的任何一点都能随意求得的,可求出的只是这样一些点,它们能由比作出整条曲线所需的办法更简单的方法所确定。因此,严格地说,我不可能求出曲线上的任何一个点;亦即所有要找的点中没有一个是曲线上的特殊点,它能不借助曲线本身而求得。另一方面,这些曲线上不存在这样的点,它能为无法使用我已给出的方法解决的问题提供解答。
可利用细绳描绘的曲线
但是,通过任意地取定曲线上的一些点而描出曲线的方法,只适用于有规则的和连续的运动所生成的曲线,这一事实并不能成为把它们排除出几何的正当理由。我们也不应该拒绝这样的方法,即,使用细绳或绳环以比较从所求曲线上的一些点到另外一些点间所引的两条或多条直线段是否相等,或用于跟其他直线作成固定大小的角。在《折光》一文中,我在讨论椭圆和双曲线时已使用了这种方法。
另一方面,几何不应包括像细绳那样有时直有时弯的线;由于我们并不知道直线与曲线之间的比,而且我相信这种比是人的智力所无法发现的,因此,不可能基于这类比而得出严格和精确的结论。无论如何,因为细绳还能用于仅需确定其长度为已知的线段的作图,所以不应被完全排除。
为了解曲线的性质,必须知道其上的点与直线上点的关系;在各点引与该曲线成直角的曲线的方法
当一条曲线上的所有点和一条直线上的所有点之间的关系已知时,用我解释过的方法,我们很容易求得该曲线上的点和其他所有给定的点和线的关系,并从这些关系求出它的直径、轴、中心和其他对该曲线有特殊重要性的线或点;然后再想出各种描绘该曲线的途径,并采用其中最容易的一种。
仅仅依靠这种方法,我们就可求得凡能确定的、有关它们的面积大小的量;对此,我没有必要作进一步的解释。
最后,曲线的所有其他的性质,仅依赖于所论曲线跟其他线相交而成的角。而两条相交曲线所成的角将像两条直线间的夹角一样容易度量,倘若可以引一条直线,使它与两曲线中的一条在两曲线交点处成直角的话。这就有理由使我相信,只要我给出一种一般的方法,能在曲线上任意选定的点引直线与曲线交成直角,我对曲线的研究就完全了。我敢说,这不仅是我所了解的几何中最有用的和最一般的问题,而且更是我一直祈求知道的问题。
求一直线与给定曲线相交并成直角的一般方法
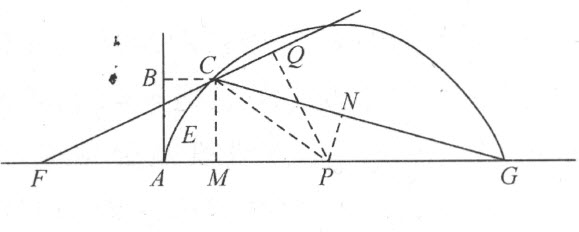
设CE 是给定的曲线,要求过点C 引一直线与CE 成直角。假设问题已经解决,并设所求直线为CP 。延长CP 至直线GA ,使CE 上的点和GA 上的点发生联系。然后,令MA =CB =y ;CM =BA =x 。我们必须找到一个方程来表示x 和y 的关系。我令PC =s 、PA =v ,因此PM =v -y 。因PMC 是直角,我们便知斜边的平方s 2 等于两直角边的平方和x 2 +v 2 -2vy +y2 。即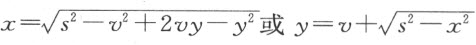 。依据最后两个方程,我可以从表示曲线CE 上的点跟直线GA 上的点之间关系的方程中,消去x 和y 这两个量中的一个。若要消去x 很容易,只要在出现x 的地方用
。依据最后两个方程,我可以从表示曲线CE 上的点跟直线GA 上的点之间关系的方程中,消去x 和y 这两个量中的一个。若要消去x 很容易,只要在出现x 的地方用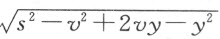 代替,x 2 用此式的平方代替,x 3 用它的立方代替,…,而若要消去y ,必须用
代替,x 2 用此式的平方代替,x 3 用它的立方代替,…,而若要消去y ,必须用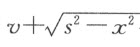 代替y ,y 2 ,y3 ,则用此式的平方、立方代替,…。结果将得到仅含一个未知量x 或y 的方程。
代替y ,y 2 ,y3 ,则用此式的平方、立方代替,…。结果将得到仅含一个未知量x 或y 的方程。
例如,若CE 是个椭圆,MA 是其直径上的截段,CM 是其纵标线,r 是它的正焦弦,q 是它的贯轴,那么,据阿波罗尼奥斯的第一篇中的定理13,我们有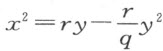 。消去x 2 ,所得方程为
。消去x 2 ,所得方程为
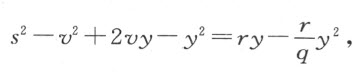
或
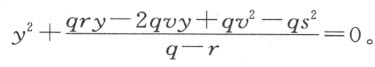
在这一情形,最好把整个式子看成是单一的表达式,而不要看成由两个相等的部分所组成。
若CE 是由已讨论过的由抛物线的运动所生成的曲线,当我们用b 代表GA 、c 代表KL 、d 代表抛物线的直径KL 的正焦弦时,表示x 和y 之间关系的方程为y 3 -by 2 -cdy +bcd +dxy =0。消去x ,我们得
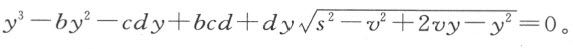
将该式平方,各项按y 的次数排列,上式变为
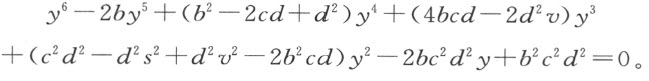
其他情形可类推。若所论曲线上的点不是按已解释过的方式跟一条直线上的点相联系,而是按其他某种方式相联系,那么也同样能找出一个方程。
令CE 是按如下方式与点F 、G 和A 相联系的曲线:从其上任一点(比如C )引出的至F 的直线段超出线段FA 的量,与GA 超出由C 引至G 的线段的量,形成一个给定的比。令GA =b ,AF =c ;现在任取曲线上一点C ,令CF 超出FA 的量跟GA 超出GC 的量之比为d 比e 。于是,当我们用z 表示尚未确定的量,那么,FC =c +z 且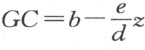 。令MA =y ,则GM =b -y ,FM =c +y 。因CMG 是直角三角形,从GC 的平方中减去GM 的平方,我们得到余下的CM 的平方,或
。令MA =y ,则GM =b -y ,FM =c +y 。因CMG 是直角三角形,从GC 的平方中减去GM 的平方,我们得到余下的CM 的平方,或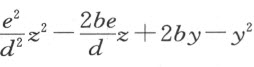 。其次,从FC 的平方中减去FM 的平方,我们得到另一种方式表示的CM 的平方,即z 2 +2cz -2cy -y 2 。这两个表达式相等,由此导出y 或MA 的值,它为
。其次,从FC 的平方中减去FM 的平方,我们得到另一种方式表示的CM 的平方,即z 2 +2cz -2cy -y 2 。这两个表达式相等,由此导出y 或MA 的值,它为
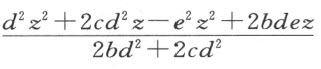
利用此值代替表示CM 平方的式子中的y ,我们得
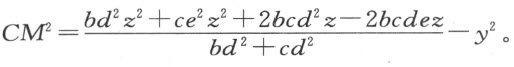
如果我们现在设直线PC 在点C 与曲线交成直角,并像以前一样,令PC =s 、PA =v ,则PM 等于v -y ;又因PCM 是直角三角形,我们知CM 的平方为s 2 -v 2 +2vy -y 2 。让表示CM 平方的两个值相等,并以y 的值代入,我们便得所求的方程为
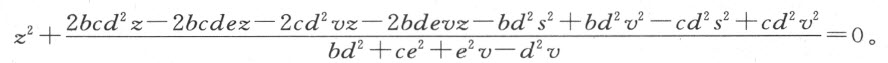
已经找出的这个方程,其用处不是确定x ,y 或z ,它们是已知的,因为点C 是取定了的;我们用它来求v 或s ,以确定所求的点P 。为此目的,请注意当点P 满足所要求的条件时,以P 为心并经过点C 的圆将与曲线CE 相切触而不穿过它;但只要点P 离开它应在的位置而稍微靠近或远离A ,该圆必定穿过这条曲线,其交点不仅有C ,而且还有另一个点。所以,当这个圆穿过CE ,含有作为未知量的x 和y 的方程(设PA 和PC 为已知)必有两个不等的根。例如,假设该圆在点C 和点E 处穿过曲线。引EQ 平行于CM 。然后,可用x 和y 分别表示EQ 和QA ,正如它们曾被用来表示CM 和MA 一样;因为PE 等于PC (同一个圆的半径),当我们寻求EQ 和QA (假设PE 和PA 是给定的)时,我们应得到跟寻求CM 和MA (假设PC 和PA 是给定的)时所得到的同样的方程。由此可知,x 的值,或y 的值,或任何其他一个这种量的值,在这个方程中都取双值,即,方程将有两个不相等的根。若求x 的值,这两个根中的一个将是CM ,另一个是EQ ;而求y 的值时,一个根将是MA ,另一个是QA 。肯定,当E 不像C 那样跟曲线在同一侧,它们之中便只有一个是真根,另一个将画在相反的方向上,或者说它比虚无还小。然而,当点C 和点E 更靠近时,两根的差也就更小;当两个点重合时,两个根恰好相等,也就是说,过C 的圆将在点C 与曲线相切而不穿过它。
进而可知,当方程有两个相等的根时,方程的左端在形式上必定类似于这样的式子,即当已知量等于未知量时,它取未知量与已知量的差自乘的形式;那么,若最终所得的式子的次数达不到最初那个方程的次数,就可以用另一个式子来乘它,使之达到相同的次数。这最后一步使得两个表达式得以一项一项地对应起来。

例如,我可以说,目前的讨论中找出的第一个方程,即
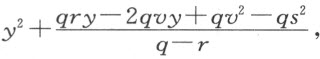
它必定跟如下方式得到的式子具有相同的形式:取e =y ,令(y -e)自乘,即y 2 -2ey +e 2 。然后,我们可以逐项比较这两个表达式:因为各式中的第一项y 2 相同,第一式中的第二项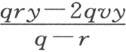 等于第二式中的第二项-2ey ;由此可解出v 或PA ,我们得
等于第二式中的第二项-2ey ;由此可解出v 或PA ,我们得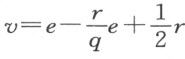 ;或者,因为我们已假定e 等于y ,故v =
;或者,因为我们已假定e 等于y ,故v =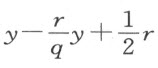 。用同样的方法,我们可以从第三项
。用同样的方法,我们可以从第三项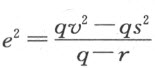 来求s;因为v 完全确定了P ,这就是所要求的一切,因此无需再往下讨论。
来求s;因为v 完全确定了P ,这就是所要求的一切,因此无需再往下讨论。
同样,对于上面求得的第二个方程 (6) ,即
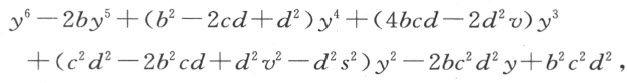
它必定跟用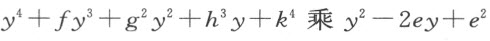 所得的式子具有相同的形式,后者形如
所得的式子具有相同的形式,后者形如
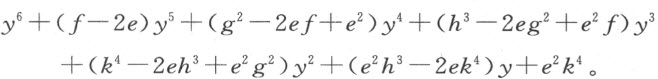
从这两个方程出发可得到另外六个方程,用于确定六个量f ,g ,h ,k ,v 和s 。容易看出,无论给定的曲线可能属于哪一类,这种方法总能提供跟所需考虑的未知量的数目一样多的方程。为了解这些方程,并最终求出我们真正想要得到的唯一的量v 的值(其余的仅是求v 的中间媒介),我们首先从第二项确定上述式中的第一个未知量f ,可得f =2e -2b 。然后,我们依据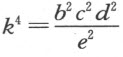 ,可求得同一式中的最后一个未知量k 。从第三项,我们得到第二个量
,可求得同一式中的最后一个未知量k 。从第三项,我们得到第二个量
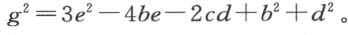
由倒数第二项,我们得出倒数第二个量h ,它是
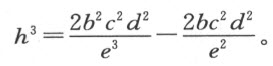
同样,我们可循这样的次序做下去,直到求得最后一个量。
那么,我们从相应的一项(这里指第四项)可求得v ,我们有
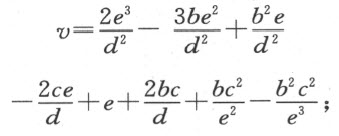
或者用等于e 的y 代入,我们得AP 的长度为
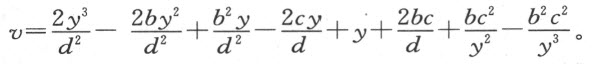
其次,第三个方程

由此可得

因此,当我们取AP 等于上述的v 值,其中所有的项都是已知的,并将由其确定的点P 跟C 相联,这条联线跟曲线交成直角,这正是所要求的。我有充分的理由说,这样的解法适用于可应用几何方法求解的所有曲线。
应该注意,任意选定的、用来将最初的乘积达到所需次数的式子,如我们刚才取的式子
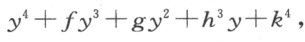
其中的符号+和-可以随意选定,而不会导致v 值或AP 的差异。这一结论很容易发现,不过,若要我来证明我使用的每一个定理,那需要写一本大部头的书,而这是我所不希望的。我宁愿顺便告诉你,你已经看到了有关这种方法的一个例子,它让两个方程具有相同的形式,以便逐项进行比较,从中又得到若干个方程。这种方法适用于无数其他的问题,是我的一般方法所具有的并非无足轻重的特征。
我将不给出与刚刚解释过的方法相关的、我们想得到的切线和法线的作图法,因为这是很容易的,尽管常常需要某种技巧才能找出简洁的作图方法。
对蚌线完成这一问题作图的例证
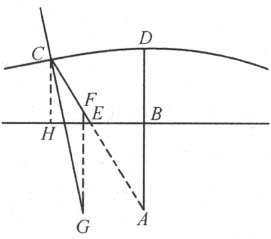
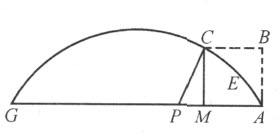
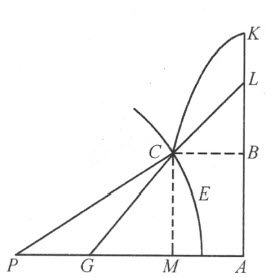
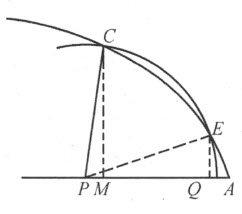
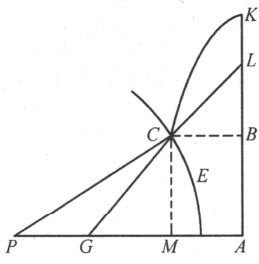
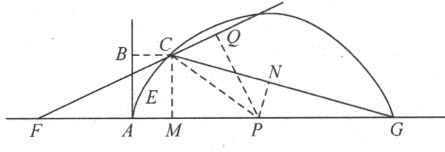
例如,给定CD 为古人所知的第一条蚌线。令A 是它的极点,BH 是直尺,使得像CE 和DB 这种相交于A 并含于曲线CD 和直线BH 间的直线段皆相等。我们希望找一条直线CG ,它在点C 与曲线正交。在试图寻找CG 必须经过的、又位于BH 上的点时(使用刚才解释过的方法),我们会陷入像刚才给出的计算那样冗长或者更长的计算,而最终的作图可能非常简单。因为我们仅需在CA 上取CF 等于BH 上的垂线CH ;然后,过F 引FG 平行于BA 、且等于EA ,于是就定出了点G ,所要找的直线CG 必定通过它。
对用于光学的四类新的卵形线的说明
为了说明研究这些曲线是有用的,以及它们的各种性质跟圆锥截线的同样重要,我将再来讨论某种卵形线;你们会发现,它们在反射光学和折光学的理论中非常有用,可以用下述方式描绘:引两条直线FA 和AR ,它们以任一交角相会于A ,我在其中的一条上任选一点F (它离A 的远近依所作卵形线的大小而定)。我以F 为心作圆,它跟FA 在稍微超过A 处穿过FA ,如在点5处。然后,我引直线56,它在6处穿过AR ,使得A 6小于A 5,且A 6比A 5等于任意给定的比值,例如在折光学中应用卵形线时,该比值度量的是折射的程度。做完这些之后,我在直线FA 上任取一点G ,它与点5在同一侧,使得AF 比GA 为那个任意给定的比值。其次,我沿直线A 6划出RA 等于GA ,并以G 为心、等于R 6的线段为半径画圆。该圆将在两个点1,1处穿过第一个圆,所求的卵形线中的第一个必定通过这两个点。
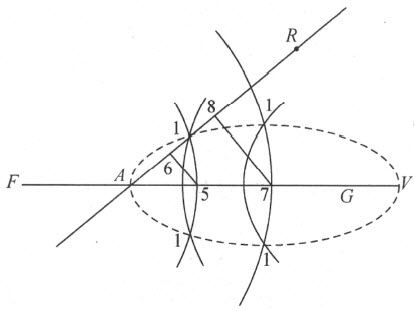
接着,我以F 为心画圆,它在比点5离A 稍近或稍远处穿过FA ,例如在点7处。然后,我引78平行于56,并以G 为心、等于R 8的线段为半径画另一个圆。此圆将在点1,1处穿过点7在其上的圆,这两个点也是同一条卵形线上的点。于是,我们通过引平行于78的直线和画出以F 和G 为心的圆,就能找到所要求的那许多点。
在作第二条卵形线时,仅有的差别是我们必须在A 的另一侧取AS 等于AG ,用以代替AR ;并且,以G 为心、穿过以F 为心且过5的圆的那个圆的半径,必须等于直线段S 6;或者当它穿过7在其上的圆时,半径必须等于S 8,如此等等。这样,这些圆在点2,2处相交,它们即是第二条卵形线A 2X 上的点。
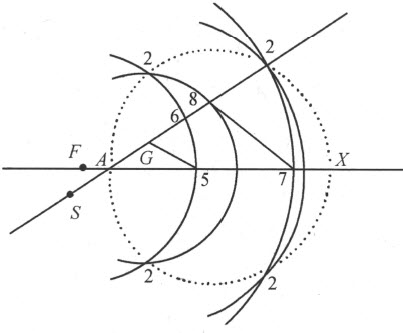
为了作出第三条和第四条卵形线,我们在A 的另一侧,即F 所在的同一边,取AH 以代替AG 。应该注意,这条直线段AH 必须比AF 长;在所有这些卵形线中,AF 甚至可以为零,即F 和A 相重。然后,取AR 和AS ,让它们都等于AH 。在画第三条卵形线A 3Y 时,我以H 为心,等于S 6的线段为半径画圆。它在点3处穿过以F 为心过5的圆,另一个圆的半径等于S 8,也在标3的点处穿过7在其上的圆,如此等等。
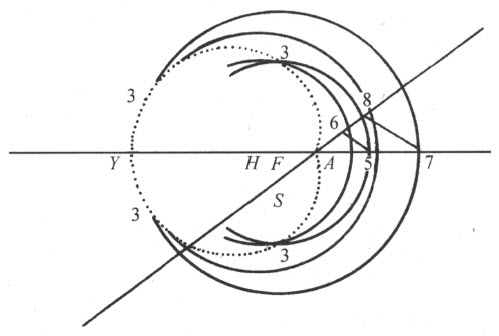
最后,对于第四条卵形线,我以H 为心,等于R 6、R 8的线段为半径画同,它们在标有4的点处穿过另外的圆。
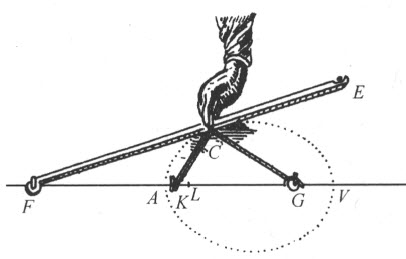
为了作出同样的这几条卵形线,还有其他许多办法。例如,第一种卵形线AV (如果我们假定FA 和AG 相等),可以用下述方法描绘:将直线段FG 在L 处分为两部分,使得FL :LG =A 5:A 6,即对应于折射率的比。然后,平分AL 于K ,令直尺FE 绕点F 转动,用手指将细绳EC 在C 点压住,此绳系在直尺的端点E 处,经过C 拉到K ,返回C 后再拉到G ,绳的另一端就系牢在这里。于是,整条绳的长度为GA +AL +FE -AF ,点C 就描绘出第一种卵形线,这跟《折光》中描绘椭圆和双曲线的方式类似。但我不能更多地关注这个主题。
虽然这些卵形线的性质看起来几乎相同,但无论如何属于四种不同的类型,每一种又包含无穷多的子类,而每个子类又像每一类椭圆和双曲线那样包含许多不同的类型;子类的划分依赖于A 5对A 6的比的值。于是,当AF 对AG 的比、或AF 对AH 的比改变时,每一个子类中的卵形线也改变类型,而AG 或AH 的长度确定了卵形线的大小。
若A 5等于A 6,第一和第三类卵形线变为直线;在第二类卵形线中,我们能得到所有可能的双曲线,而第四类卵形线包含了所有可能的椭圆。
所论卵形线具有的反射与折射性质
就每一种卵形线而言,有必要进一步考虑它的具有不同性质的两个部分。在第一类卵形线中,朝向A 的部分使得从F 出发穿过空气的光线、遇到透镜的凸圆状表面1A 1后向G 会聚,根据折光学可知,该透镜的折射率决定了象A 5对A 6这样的比,卵形线正是依据这个比描绘的。
而朝向V 的部分,使从G 出发的所有光线到达形如1V 1的凹形镜面后向F 会聚,镜子的质料按A 5对A 6的比值降低了光线的速度,因为折光学已证明,此种情形下的各个反射角将不会相等,折射角亦然,它们可用相同的方法度量。
现在考虑第二种卵形线。当2A 2这个部分作反射用时,同样可假定各反射角不相等。因为若这种形状的镜子采用讨论第一种卵形线时指出的同一种质料制成,那么它将把从G 出发的所有光线都反射回去,就好像它们是从F 发出似的。
还要注意,如果直线段AG 比AF 长许多,此时镜子的中心(向A )凸,两端则是凹的;因为这样的曲线不再是卵形而是心形的了。另一部分X 2对制作折射透镜有用;通过空气射向F 的光线被具有这种形状的表面透镜所折射。
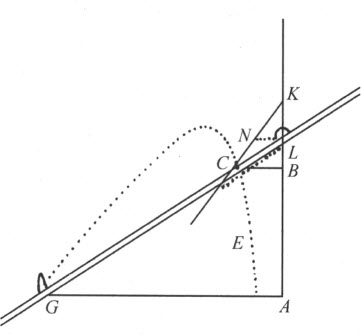
第三类卵形线仅用于折射,使通过空气射向F 的光线穿过形如A 3Y 3的表面之后在玻璃体内射向H ;此处A 3YA 除稍向A 凹之外,其余部分全是凸的,因此这条曲线也是心形的。这种卵形线的两个部分的差别在于,一部分靠近F 远离H ,另一部分靠近H 而远离F 。 (7)
类似地,这些卵形线中的最后一种只用于反射的情形。它的作用是使来自H 的所有光线、当遇到用前面提到过的同种质料制成的形如A 4Z 4凹状曲面时,经反射皆向F 会聚。
点F ,G 和H 可称为这些卵形线的“燃火点”,相应于椭圆和双曲线的燃火点,在折光学中就是这样定名的。
我没有提及能由这些卵形线引起的其他几种反射和折射;因为它们只是些相反的或逆的效应,很容易推演出来。
对这些性质的论证
然而,我必须证明已做出的结论。为此目的,在第一种卵形线的第一部分上任取一点C ,并引直线CP 跟曲线在C 处成直角。这可用上面给出的方法实现,做法如下:
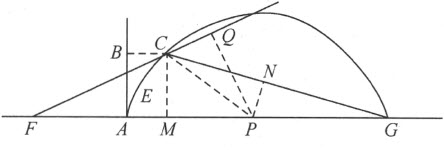
令AG =b ,AF =c ,FC =c +z 。以d 对e 的比——我总是用它度量所讨论的透镜的折射能力——表示A 5对A 6的比,或用于表示能描述该卵形线的类似的直线段之间的比。于是,

由此可知
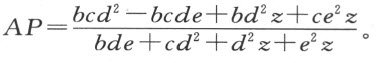
我们从P 引PQ 垂直于FC ,引PN 垂直于GC 。现若有PQ :PN =d :e ,即,如果PQ :PN 等于用来度量凸玻璃体AC 的折射状况的直线段之间的比,那么过F 射向C 的光线,必被折射进入玻璃体而且射向G 。这由折光学立即可知。
现在,假如PQ :PN =d :e 真的成立,让我们用计算来证实结论。直角三角形PQF 和CMF 相似,由此可得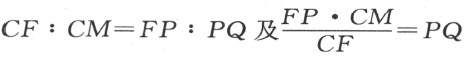 。此外,直角三角形PNG和CMG相似,因此
。此外,直角三角形PNG和CMG相似,因此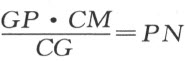 。由于用同一个数乘或除一个比中的两项并不改变这个比,又若
。由于用同一个数乘或除一个比中的两项并不改变这个比,又若 ,那么用CM 除第一个比中的每项,再用CF 及CG 乘每项,我们得到FP •CG :GP •CF =d :e 。根据作图可知
,那么用CM 除第一个比中的每项,再用CF 及CG 乘每项,我们得到FP •CG :GP •CF =d :e 。根据作图可知
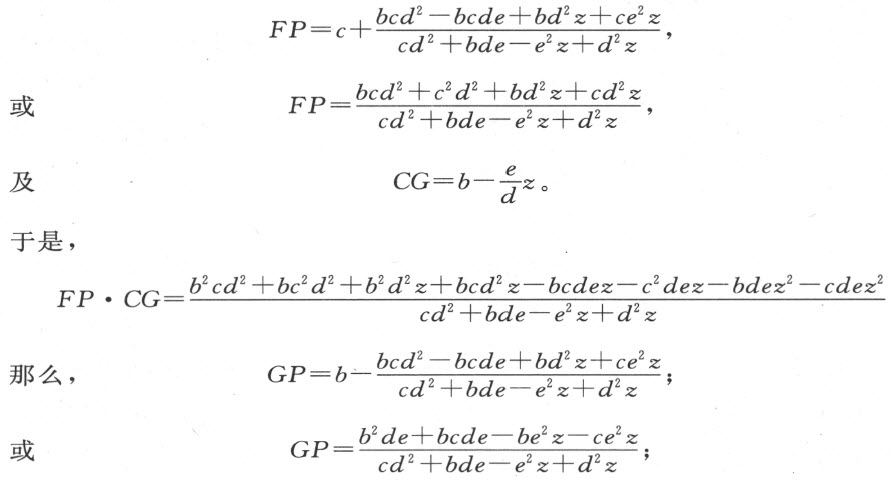
以及CF =c +z 。故
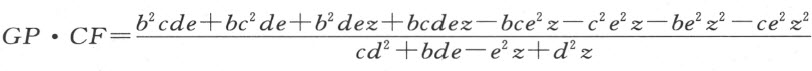
上述第一个乘积用d 除后,等于第二个用e 除,由此可得PQ •PN =FP •CG :GP •CF =d :e ,这就是所要证明的。这个证明经正负号的适当变更,便可用来证明这些卵形线中任一种具有的反射和折射性质;读者可逐个去研究,我不需要在此作进一步的讨论。
这里,我倒有必要对我在《折光》中的陈述作些补充,大意如下:各种形式的透镜都能同样使来自同一点的光线,经由它们向另一点会聚;这些透镜中,一面凸另一面凹的比起两面皆凸的,是性能更好的燃火镜;另一方面,后者能作成更好的望远镜。我将只描述和解释那些我认为是最具实用价值的透镜,考虑琢磨时的难点。为了完成有关这个主题的理论,我必须再次描绘这种透镜的形状:它的一个面具有随意确定的凸度或凹度,能使所有平行的或来自单个点的光线,在穿过它们之后向一处会聚;还要描绘另一种透镜的形状:它具有同样的效用,但它的两个面是等凸的,或者,它的一个表面的凸度与另一表面的凸度形成给定的比。
如何按我们的要求制作一透镜,使从某一给定点发出的所有光线经透镜的一个表面后会聚于一给定点
第一步,设G 、Y 、C 和F 是给定的点,使得来自G 或平行于GA 的光线穿过一凹状透镜后在F 处会聚。令Y 是该透镜内表面的中心,C 是其边缘,并设弦CMC 已给定,弧CYC 的高亦已知。首先我们必须确定那些卵形线中的哪一个可用来做此透镜,使得穿过它而朝向H (尚未确定的一个点)的光线,在离开透镜后向F 会聚。
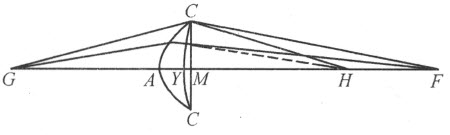
在这些卵形线中,至少有一种不会让光线经其反射或折射而仍不改变方向的;容易看出,为得到上述特殊结果,可利用第三种卵形线上标为3A 3或3Y 3的任何一段,或者利用第二种卵形线上标为2X 2的部分。由于各种情形都可用同一种方法处理,所以无论对哪种情形,我们可以取Y 为顶点,C 为曲线上的一点,F 为燃火点之一。于是尚待确定的只是另一个燃火点H 了。为此,考虑FY 和FC 的差比HY 和HC 的差为d 比e ,即度量透镜折射能力的两直线段中较长者跟较短者之比,这样做的理由从描绘卵形线的方法中是显而易见的。
因为直线段FY 和FC 是给定的,我们可以知道它们的差;又因为知道那两个差的比,故我们能知道HY 和HC 的差。
又因YM 为已知,我们便知MH 和HC 的差,也就得到了CM ,尚需求出的是直角三角形CMH 的一边MH 。该三角形的另一边CM 已经知道,斜边CH 和所求边MH 的差也已知。因此,我们能容易地确定MH ,具体过程如下:
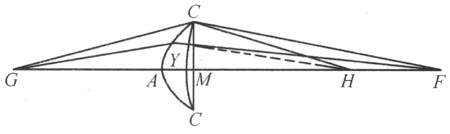
令k =CH -MH ,n =CM ;那么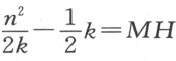 ,它确定了点H 的位置。
,它确定了点H 的位置。
若HY 比HF 长,曲线CY 必须取为第三类卵形线的第一部分,它已标记为3A 3。
要是假定HY 比FY 短,会出现两种情形:第一种,HY 超出HF 的量达到这种程度,使它们的差跟整条线段FY 的比,大于表示折射能力的直线段中较小的e 跟较大的d 之比;即令HF =c ,HY =c +h ,那么dh 大于2ce +eh。在这种情况,CY 必须取为第三类中同一卵形线的第二部分3Y 3。
在第二种情形,dh 小于或等于2ce +eh ,CY 取为第二类卵形线的第二部分2X 2。
最后,若点H 和点F 相重,FY =FC ,那么曲线YC 是个圆。
我们还需要确定透镜的另一个表面CAC 。若我们设落在它上面的光线平行,它应是以H 为其一个燃火点的椭圆,其形状容易确定。然而,当我们设光线来自点G ,则透镜必须具有第一类卵形线的第一部分的形状,该卵形线经过点C ,它的两个燃火点是G 和H 。点A 看来是它的顶点,依据是:GC 超出GA 的部分比HA 超出HC 的部分等于d 比e 。因为若令k 表示CH 和HM 的差,x 表示AM ,那么x -k 表示AH 和CH 的差;若令g 表示皆为已知的GC 和GM 的差,那么g +x 表示GC 和GA 的差;由于g +x :x -k =d :e ,我们知 它使我们得以确定所求的点A 。
它使我们得以确定所求的点A 。
如何制作有如上功能的透镜,而又使一个表面的凸度跟另一表面的凸度或凹度形成给定的比
其次,假设只给定了点G 、C 和F ,以及AM 对YM 的比;要求确定透镜ACY 的形状,使得所有来自点G 的光线都向F 会聚。
在这种情况下,我们可以利用两种卵形线AC 和YC ,它们的燃火点分别是G 、H 和F 、H 。为了确定它们,让我们首先假设两者共同的燃火点H 为已知。于是,AM 可由三个点G 、C 和H 以刚刚解释过的方法确定;即,若k 表示CH 和HM 的差,g 表示GC 和GM 的差,又若AC 是第一类卵形线的第一部分,则我们得到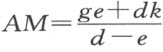 。
。
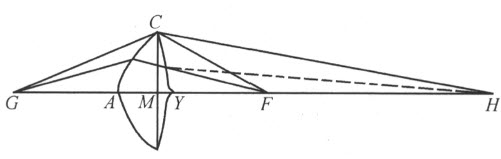
于是,我们可依据三个点F 、C 和H 求得MY 。若CY 是第三类的一条卵形线的第一部分,我们取y 代表MY ,f 代表CF 和FM 的差,那么CF 和FY 的差等于f +y ;再令CH 和HM 的差等于k ,则CH 和HY 的差等于k +y 。那么(k +y ):(f +y )=e :d ,因为该卵形线是第三类的,因此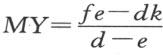 。所以
。所以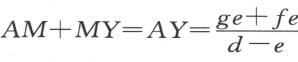 ,由此可得,无论点H 可能落在哪一边,直线段AY 对GC +CF 超出GF 的部分的比,总等于表示玻璃体折射能力的两条直线段中较短的e 对两直线段之差d -e 的比,这给出了一条非常有趣的定理。
,由此可得,无论点H 可能落在哪一边,直线段AY 对GC +CF 超出GF 的部分的比,总等于表示玻璃体折射能力的两条直线段中较短的e 对两直线段之差d -e 的比,这给出了一条非常有趣的定理。
正在寻找的直线段AY ,必须按适当的比例分成AM 和MY ,因为M 是已知的,所以点A ,Y ,最后还有点H ,都可依据前述问题求得。首先,我们必须知道这样求得的直线段AM 是大于、等于或小于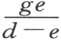 。当出现大于的情形,AC 必须取为已考虑过的第三类中的某条卵形线的第一部分。当出现小于的情形,CY 必须为某个第一类卵形线的第一部分,AC 为某个第三类卵形线的第一部分。最后,当AM 等于
。当出现大于的情形,AC 必须取为已考虑过的第三类中的某条卵形线的第一部分。当出现小于的情形,CY 必须为某个第一类卵形线的第一部分,AC 为某个第三类卵形线的第一部分。最后,当AM 等于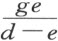 时,曲线AC 和CY 必须双双皆为双曲线。
时,曲线AC 和CY 必须双双皆为双曲线。
上述两个问题的讨论可以推广到其他无穷多种情形,我们将不在这里推演,因为它们对折光学没有实用价值。
我本可以进一步讨论并说明,当透镜的一个表面是给定的,它既非完全平直、亦非由圆锥截线或圆所构成,此时如何确定另一个表面,使得把来自一个给定点的所有光线传送到另一个也是给定的点。这项工作并不比我刚刚解释过的问题更困难;确实,它甚至更容易,因为方法已经公开;然而,我乐于把它留给别人去完成,那样,他们也许会更好地了解和欣赏这里所论证的那些发现,虽然他们自己会遇到某些困难。
如何将涉及平面上的曲线的那些讨论应用于三维空间或曲面上的曲线
在所有的讨论中,我只考虑了可在平面上描绘的曲线,但是我论述的要点很容易应用于所有那样的曲线,它们可被想象为某个物体上的点在三维空间中作规则的运动所生成。具体做法是从所考虑的这种曲线上的每个点,向两个交成直角的平面引垂线段,垂线段的端点将描绘出另两条曲线;对于这两个平面中的每一个上面的这种曲线,它的所有点都可用已经解释过的办法确定,所有这些点又都可以跟这两个平面所共有的那条直线上的点建立起联系;由此,三维曲线上的点就完全确定了。
我们甚至可以在这种曲线的给定点引一条直线跟该曲线成直角,办法很简单,在每个平面内由三维曲线上给定点引出的垂线的垂足处,分别作直线与各自平面内的那条曲线垂直,再过每一条直线作出另外两个平面,分别与含有它们的平面垂直,这样作出的两个平面的交线即是所求的垂直直线。
至此,我认为我在理解曲线方面再没有遗漏什么本质的东西了。
————————————————————
(1) 笛卡儿在此处的用词是“moindre que rien”,意为“比虚无还小”,即现代术语“负的”意思。——译者
(2) 原文称LC “appliquee par order a ce diametre”,英译本注说这表示LC是“A ordinate”,意即纵标。——译者
(3) 笛卡儿所用的词是costé droi,英译本译作latus rectum.——译者
(4) 笛卡儿原著中未用“纵标”这个词:而使用“appliguee par order…”形容具有此性质的线段。英译本从此处起将此种线段意译为“纵标”,我们则译为“纵标线”。——译者
(5) 注意,点L 将随抛物线的运动而变换位置。——译者
(6) 笛卡儿常把方程写为一含未知量的多项式等于零的形式。此时:他会称等号左端的部分为“方程”。——译者
(7) 以上两段对应的图为本书34页的第2个图。——译者
 笛卡儿的手稿
笛卡儿的手稿
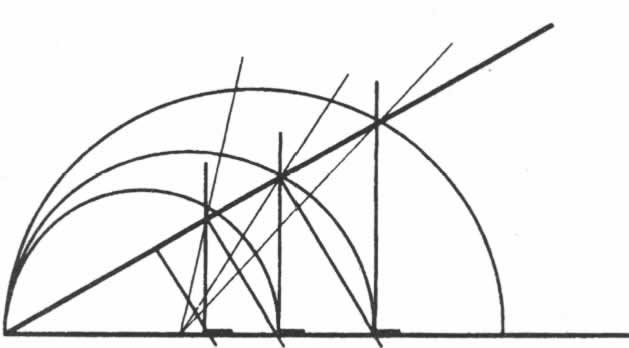 笛卡儿发明的圆规
笛卡儿发明的圆规
