绪　论

量的测量

·Preliminary on the Measurzement of Quantities·

我希望你们不要只死记结果，适用于特殊例子的公式，你们要好好研究这些公式与原则赖以成立的条件，没有事实作根据，公式只不过是精神垃圾。我了解人的精神倾向是活动胜于思考，但精神上的劳作并不是思想，只有那些付出了巨大劳动的人们，才会获得运用的习惯。发现理解一个原则要比写出一个公式难得多。

——麦克斯韦（周兆平译）

1880年，经麦克斯韦扩建后的格伦莱尔庄园。

1．〕一个量的每一种表示式都包括两个因子或成分。其中一个成分就是作为参照标准来表示该量的某一已知同类量的名称。另一个成分就是形成所求之量对应该采取的标准量的倍数。标准量在技术上称为该量的单位，而倍数则称为该量的数值。

有多少不同的要测的量，就必须有多少不同的单位，但是在所有的动力科学中却可能用长度、时间和质量这三个基本单位来定义这许多单位。例如，面积和体积的单位就分别定义为一个正方形和一个立方体，它们的边长是一个长度单位。

然而，有时我们也见到同一类量的若干种建立在独立的考虑上的不同单位。例如加仑即十磅水的体积被用作容积的单位，正如立方英尺被用作这种单位一样。在某些情况下加仑可以是一种方便的单位，但它不是一个系统的单位，因为它对立方英尺而言的数值不是一个确切的整数。

2．〕在构成一个数学体系时，我们假设长度、时间和质量的基本单位已经给定，并根据这些单位而通过尽可能简单的定义来推出所有的导出单位。

我们所求得的公式必须是这样的：任何国籍的一个人，通过把式中的不同符号代成用他自己国家的单位测量的各量的数值，就将得到一个真确的结果。

因此，在一切的科学研究中，最重要的就是要应用属于一个适当定义的单位制的单位，并且要知道这些单位和基本单位的关系，以便我们可以立刻把我们的结果从一个单位制换算到另一个单位制。

此事可以通过确定用三个基本单位表示的每一个单位的量纲来最方便地做到。当一个给定的单位随三个单位中一个单位的n次方而变化，它就叫做相对于该单位有n个量纲。

例如，科学上的体积单位总是其边为单位长度的一个立方体。如果长度单位改变了，体积单位就将按长度的三次方而变化，于是体积单位就叫做相对于长度单位有三个量纲。

关于单位量纲的知识提供一种检验，它应该应用于由任何冗长的研究所得到的方程。这样一个方程中的每一项相对于三个基本单位中每一个单位而言的量纲，必须是相同的。如果不相同，方程就是无意义的，从而它必然含有某种差错，因为按照我们采用的任意单位制之不同，它的诠释将是不同的 ^〔1〕 。

三个基本单位

3．〕（1）长度　在我国〔指英国〕，适用于科学目的的长度标准是一英尺，它是保存在财政部（Exchequer Chambers）中的标准码的三分之一。

在法国和采用了米制的其他各国，长度单位是米。在理论上，一米就是从一极量到赤道的一条地球子午线的千万分之一；但是在实用上，它是保存在巴黎的一个原器的长度，该原器是由鲍尔达制成的，它在融冰的温度下对应于戴兰伯所测定的上述长度。米并不曾改变以适应于对地球的新的和更准确的测量结果，而子午线的弧长却用原始的米来进行了估量。

在天文学中，从太阳到地球的平均距离有时被取作长度的单位。

在目前的科学状况下，我们所愿意采取的最普适的长度单位就是某种特定的光在真空中的波长，那种光是由钠之类的高度分散的物质所发射的，它在该物质的光谱中有很确定的波长。这样一个标准将和地球尺寸的任何变化都无关，从而应该被那些指望自己的著作比地球更能持久的人们所采用。

在处理单位的量纲时，我们将把长度的单位叫做［L］。如果l是一个长度的数值，它就被理解为是用具体的单位［L］来表示的，于是实际的长度就将是由l［L］来充分表示的。

4．〕（2）时间 在所有的文明国家中，时间的标准单位都是由地球绕轴自转的时间得出的。恒星日，或地球的真实自转周期，可以通过天文学家们的普通观察结果而很精确地定出；而且平均太阳日可以根据我们关于一年的长度的知识而由恒星日推出。

一切物理研究中所采用的时间单位是平均太阳时的一秒。

在天文学中，一年有时被用作时间的单位。一个更加普适的时间单位可以通过采用某种特定光的振动周期来求得，该种光的波长是长度的单位。

我们将把具体的时间单位称为［T］，而时间的数值则是t。

5．〕（3）质量 在我国，质量的标准单位是保存在财政部中的常衡磅。常常取作单位的格令定义为这种磅的七千分之一。

在米制中，质量单位是克。克在理论上是标准温度和标准压强下一立方厘米的蒸馏水的质量，而在实用上则是保存在巴黎的一个千克原器的一千分之一。

通过称量可以比较的物体质量的精确度，远大于迄今在长度的测量中所达到的精确度，因此，如果可能，一切的质量都应该和标准单位直接比较，而不是从关于水的实验来推出。

在描述天文学中，太阳的质量或地球的质量有时被取作单位，但是在天文学的动力学理论中，质量的单位却是结合万有引力的事实而从时间和长度的单位导出的。天文学的质量单位是那样一个质量，它吸引放在单位距离处的另一物质而使之得到单位加速度。

在制定一个普适的单位制时，我们可以按这种办法从已经定义的长度单位和时间单位来导出质量的单位，而在目前的科学状况下，我们可以在一种粗略的近似下做到这一点。或者，如果我们指望 ^〔2〕 很快就能确定一种标准物质的单一分子的质量，我们也可以等待这种确定的结果而暂不规定一个普适的质量单位。

在处理其他单位的量纲时，我们将用符号［M］来表示具体的质量单位。质量单位将被看成三个基本单位之一。当像在法国制中那样把一种特定物质即水取作密度的标准时，质量的单位就不再是独立的而是按体积单位即按［L³ ］而变的了。

如果像在天文单位制中那样质量的单位是相对于引力本领而定义的，则〔M〕的量纲是〔L³ T^-2 〕。

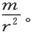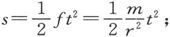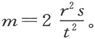因为，由一个质量m在一个距离r处引起的加速度由牛顿定律给出为 假设这种外力在一段小时间t中作用在一个起初为静止的物体上并使它移动一个距离s，则由伽利略公式可得 由此即得 既然r和s都是距离而t是时间，这个方程就不可能成立，除非m的量纲是〔L³ T^-2 〕。针对任何一个在某些项中而不是在一切项中含有一个物体质量的天文学方程，也可以证明相同的结果 ^〔3〕 。

导出单位

6．〕速度的单位就是在单位时间内走过单位距离的那个速度。它的量纲是［LT^-1 ］。

如果我们采用从光的振动导出的长度和时间的单位，则速度的单位就是光速。

加速度的单位就是速度在单位时间内增加1的那个加速度。它的量纲是［LT^-2 ］。

密度的单位是在单位体积内含有单位质量的一种物质的密度。它的量纲是［ML^-3 ］。

动量的单位就是以单位速度运动着的单位质量的动量。它的量纲是［MLT^-1 ］。

力的单位就是在单位时间内产生单位动量的力。它的量纲是［MLT^-2 ］。

这是力的绝对单位，而且这一定义是暗含在动力学的每一个方程中的。不过，在载有这些方程的许多书中，却采用了另一种力的单位，那就是质量的国家单位的重量。于是，为了满足方程，质量的国家单位本身就被放弃而改用了一个动力学单位，该单位等于国家单位除以当地的重力强度的值。按照这种方法，力的单位和质量的单位就都被弄得依赖于随地点而不同的重力强度的值了，因此，涉及这些量的那些说法就是不完全的。

对于一切科学目的来说，这种量度力的方法的废除主要是由于高斯引用了一种在重力强度不同的各国进行磁力观测的普遍制度。现在所有这样的力都是按照一种从我们的定义推得的严格动力学的方法来量度的，从而其数值不论在什么国家做实验都是相同的。

功的单位就是单位力通过沿其本身方向测量的单位距离时所做的功。它的量纲是［ML² T^-2 ］。

作为体系做功本领的体系能量，通过体系耗尽全部能量所能做的功来量度。

其他量的定义，以及它们所涉及的单位，将在我们用到它们时再行给出。

在把用一种单位测定的物理量的值换算成用种类相同的任何其他单位来表示时，我们只需记得一点，即量的每一个表示式都包含两个因子，即单位和表示应取多少个单位的那个数字。由此可知，数字部分是反比于单位的大小而变化的，也就是反比于导出单位之量纲所指示的各基本单位之不同幂次而变化的。

物理的连续性和不连续性

7．〕一个量被说成是连续变化的，如果当从一个值变到另一个值时它将采取一切中间值。

我们可以从一个质点在时间和空间中的连续存在的考虑得到关于连续性的观念。这样一个质点不能从一个位置过渡到另一个位置而并不在空间中描绘一条连续的线，从而它的位置的坐标必然是时间的连续函数。

在有关水力学的论著中给出的所谓“连续性方程”中，所表示的事实就是：物质不能在一个体积元中出现或消失而并不通过体积元的各边进入或逸出。

一个量被说成是它的各变量的连续函数，如果当各变量连续变化时该量本身也连续地进行变化。

例如，如果u是x的一个函数，而且当x从x₀ 连续地变到x₁ 时，u从u₀ 连续地变到u₁ ，但是当x从x₁ 变到x₂ 时，u却从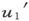 变到u₂ ，而 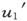不等于u₁ ，这时u就被说成在x＝x₁ 值处对它对x而言的变化中有一种不连续性，因为当x连续地通过x₁ 时，u却突然地从u₁ 变到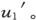

如果我们把u在值x＝x₁ 处对x而言的微分系数看成令x₂ 和x₀ 都无限趋近于x₁ 时的分数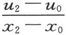 的极限，那么，如果x₀ 和x₂ 永远位于x₁ 的两侧，则分子的最终值将是 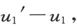而分母的最终值将是零。如果u是一个物理上连续的量，则不连续性只能针对变量x的个别值而存在。在这种情况下我们必须承认，当x＝x₁ 时，u有一个无限大的微分系数。如果u并不是物理上连续的，则它是完全不可微的。

在物理问题中，有可能消除不连续性这一概念而不致很显著地改变事例的条件。如果x₀ 只比x₁ 小一点点而x₂ 只比x大一点点，则u₀ 将很近似地等于u₁ 而u₂ 将很近似地等于u₁ ′。现在我们就可以假设u在界限x₀ 和x₂ 之间以一种任意的然而却是连续的方式从u₀ 变到u₂ 。在许多物理问题中，我们可以从这样的一种假设开始，然后再研究当令x₀ 和x₂ 的值都趋近于x₁ 的值并终于达到该值时的结果如何。如果结果不依赖于我们所设的u在二界限间的任意变化方式，则可以假设当u为不连续时结果也是真确的。

多变数函数的不连续性

8．〕如果我们假设除x以外所有变数的值都是恒定的，则函数的不连续性可以相对于x的特殊值而出现，而且这些特殊值是通过一个方程来和其他各变数的值相联系的；我们可以把这个方程写成φ＝φ（x，y，z，…）＝0。不连续性将在φ＝0时出现。当φ为正时，函数将具有F₂ （x，y，z，…）的形式。当φ为负时，函数将具有F₁ （x，y，z，…）的形式。形式F₁ 和F₂ 之间不一定有什么必要的关系。

为了用一种数学形式来表示不连续性，设其中一个变数例如x被表示成φ和其他变数的函数，并设F₁ 和F₂ 被表示成x、y、z等等的函数。现在我们可以用任何一个公式来表示函数的普遍形式，只要那个公式当φ为正时明显地等于F₂ ，而当φ为负时明显地等于F₁ 。这样一个公式如下：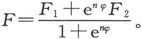

只要n是一个有限的量，不论它多么大，F都将是一个连续函数。但是如果我们令n变为无限大，则当φ为正时F将等于F₂ 而当φ为负时F将等于F₁ 。

连续函数的导数的不连续性

一个连续函数的一阶导数可以是不连续的。设出现导数之不连续的各变数之值由方程φ＝φ（x，y，z，…）＝0来联系，并设F₁ 和F₂ 用φ和n－1个其他变数例如（x，z，…）表示出来。

于是，当φ为负对，应取F₁ ，而当φ为正时，应取F₂ ；而且，既然F本身是连续的，当φ为零时就有F₁ ＝F₂ 。

因此，当φ为零时，导数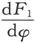 和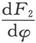 可能不相同，但是对其他变数的导数，例如 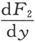和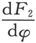 却必然相同。因此，不连续性只限制在对φ的导数上，而所有其他的导数都是连续的。

周期函数和多重函数

9．〕如果u是x的一个函数，而且它的值在x、x＋a、x＋na以及一切相差为a的x值处都相同，u就叫做x的一个周期函数，而a就叫做它的周期。

如果x被看成u的一个函数，则对于一个给定的u值，必有彼此相差为a的倍数的一系列无限多个a值。在此情况下，x就叫做u的一个多重函数，而a就叫做它的循环常数。

对应于一个给定的u值，微分系数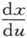 只有一系列有限个值。

物理量和空间方向的关系

10．〕在区分物理量的种类时，很重要的就是要知道各物理量和我们通常用来定义物体之位置的那些坐标轴的方向是如何联系的。笛卡儿在几何学中引用坐标轴，是数学进步中最大的步伐之一，因为这就把几何学的方法简化成了关于数字量的计算。一个点的位置被弄成了依赖于永远沿确定方向画出的三条线的长度，而两点之间的连线也类似地被看成了三条线段的合成量。

但是，对于物理推理的许多目的来说，不同于计算，却很有必要避免明白地引入笛卡儿坐标，并把思想一举而固定在一个空间点上而不是它的三个坐标上，固定在一个力的大小和方向上而不是它的三个分量上。这种考虑几何量和物理量的模式是比另一种模式更加原始和更加自然的，尽管和它相联系着的那些概念直到哈密顿通过发明他的四元数算法 ^〔4〕 而在处理空间方面迈出又一大步时才算得到了充分的发展。

因为笛卡儿方法仍是学习科学的人们所最熟悉的方法，也因为这种方法对计算的目的来说确实是最有用的，所以我们将在笛卡儿的形式下表述我们所有的结果。然而我却确信，关于四元数的概念而不是它的运算及方法的引入，在我们的课题之一切部分的研究中都将是大有用处的；尤其是在电动力学中，我们在那里将必须对付若干物理量，而它们彼此之间的关系可以用哈密顿的少数几个表示式来表示，比用普通的方程要简单得多。

11．〕哈密顿方法的最重要特色之一，就在于把各个量区分为标量和矢量。

一个标量可以通过单独一个数字的指定来完全地定义。它的数值并不以任何方式依赖于我们所取的各坐标轴的方向。

一个矢量或有向量要求用三个数字的指定来定义它，而这些数字可以最简单地理解为参照了各坐标轴的方向。

标量不涉及方向。一个几何图形的体积、一个物质体的质量和能量、流体中一点处的流体静力学压强，以及空间中一点处的势，就是一些标量的例子。

一个矢量既有量值又有方向，而且当它的方向反转时它的正负号也反转。一个点的位移用从初位置到末位置一段直线来代表。这就可以看成典型的矢量，而事实上矢量一词正是由此得来的。

一个物体的速度、它的动量、作用在它上的力、一个电流、一个铁粒子的磁化强度，就是矢量的一些例子。

还有另一种物理量，它们是和空间中的方向有关的，但它们不是矢量。固体中的胁强和胁变就是这种量的例子，在弹性理论和双折射理论中考虑到的物体的某些性质也是这种量的例子。这一类量要用九个数字的指定来定义。它们在四元数的语言中是用一个矢量的线性矢量方程来表示的。

一个矢量和另一个同类矢量的相加，按照静力学中所给出的力的合成法则来进行。事实上，泊松所给出的关于“力的平行四边形”的证明是适用于任何那种方向的反转就相当于变号的量的。

当我们想要用单独一个符号来代表一个矢量并使人们注意到它是一个矢量从而我们必须既考虑它的量值又考虑它的方向这一事实时，我们将用一个德文大楷字母来代表它，例如 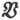， ，等等。

在四元数算法中，一个点在空间中的位置用一个矢量来定义，该矢量从一个叫做原点的定点画到该点。如果我们必须考虑其值依赖于点的位置的任一物理量，那个量就被看成从原点画起的那个矢量的一个函数。函数本身可以是标量也可以是矢量。一个物体的密度、它的温度、它的流体静力学压强、一个点上的势，就是标量函数的例子。一个点上的合力、流体中一点上的速度、流体的一个体积元的转动速度以及引起转动的力偶矩，就是矢量函数的例子。

12．〕物理矢量可以分成两类。一类矢量是参照一条直线来定义的，而另一类矢量是参照一个面积来定义的。

例如，一种吸引力在任一方向上的合力通过求得它在一个物体沿该方向移动一小段距时对物体所做的功并除以该段距离来加以量度。在这里，吸引力就是参照一条直线来定义的。

另一方面，固体中任一点上沿任一方向的热通量可以通过求得流过垂直于该方向的一个小面积的热量并除以该面积和时间来加以量度。在这里，通量就是参照一个面积来定义的。

也有某些情况，一个量既可以参照一个面积又可以参照一条直线来加以量度。

例如，在处理弹性固体的位移时，我们可以把自己的注意力集中到一个质点的原始位置和实际位置上。在这种情况下，质点的位移就是由第一个位置画到第二个位置的直线来量度的。或者，我们也可以考虑固定在空间中的一个小面积，并确定在位移过程中有多大数量的固体物质通过了那个面积。

同样，一种流体的速度可以参照着各个质点的实际速度来加以研究，也可以参照着通过任一固定面积的流体数量来加以研究。

但是，在这些情况下，我们要求分别地既知道位移或速度又知道物体的密度，以便应用第一种方法，而一旦我们企图形成一种分子理论，我就必须应用第二种方法了。

在电的流动事例中，我们根本不知道有关导体中的电密度或电速度的任何东西，我们只知道按照流体理论将对应于密度和速度之乘积的那个值。因此，在所有的这种事例中，我们必须应用测量通过面积之通量的那种更普遍的方法。

在电科学中，电动强度和磁强度属于第一类，它们是参照直线来定义的。当我们想要指明这一事实时，我们可以把它们叫做“强度”。

另一方面，电感和磁感，以及电流，却属于第二类，它们是参照面积来定义的。当我们想要指明这一事实时，我们将称它们为“通量”。

这些强度中的每一种强度，都可以被认为可以产生或倾向于产生它的对应通量。例如，电动强度在导体中产生电流，而在电介质中则倾向于产生电流。它在电介质中产生电感，而且或许在导体中也产生电感。在同样的意义上，磁强度产生磁感。

13．〕在某些事例中，通量简单地正比于强度并和强度同向，但是在另一些事例中我们只能断定通量的方向和量值是强度的方向和量值的函数。

通量的分量是强度分量的线性函数的事例将在关于传导方程的一章的第297节中加以讨论。一般共有九个系数，确定着强度和通量之间的关系。在某些事例中，我们有理由相信其中六个系数形成三对相等的量。在这样的事例中，强度的方向直线和通量的垂直平面之间的关系属于椭球体的半直径和它的共轭径平面之间的关系那一类。在四元数的语言中，一个矢量被说成是另一矢量的线性矢量函数，而当存在三对相等的系数时，该函数就被说成是自轭的。

在铁中的磁感事例中，通量（铁的磁化）不是磁强度的线性函数。然而，在任何情况下，强度和通量在其方向上的分量的乘积都给出一个很有科学重要性的结果，而且这个乘积永远是一个标量。

14．〕有两种适用于这两类矢量或向量的常常出现的数学运算。

在强度的事例中，我们必须沿着一条线计算线元和强度在线元方向上的分量的乘积的积分。这种运算的结果叫做强度的线积分。它代表沿该线对物体做的功。在某些事例中，线积分不依赖于线的形状而只依赖于它的两个端点的位置，这种线积分叫做势。

在通量的事例中，我们必须在一个曲面上计算通过每一面积元的通量的积分。这种运算的结果叫做通量的面积分。它代表通过曲面的量。

有些曲面上没有通量。如果两个这样的曲面相交，则它们的交线是一条通量线。在通量和力同向的那些事例中，这样一种线常常被称为力线。然而，更正确的办法是在静电学和磁学中把它们叫做感应线，而在动电学中把它们叫做流线。

15．〕还有另一种不同种类的有向量之间的区别；这种区别虽然从物理观点看来是很重要的，但是对数学方法的目的来说却是不必考虑的。这就是纵向性质和旋转性质之间的区别。

一个量的方向和量值可以依赖于完全沿着某一条线而出现的某种作用或效应，或者，它可以依赖于其本性为以该线为轴的转动的某种东西。不论有向量是纵向的还是旋转的，它们的合成定律都是相同的，因此在这两类量的数学处理方面并没什么不同，但是却可能有一些物理情况指示着我们必须把一种特定的现象归入哪一类中。例如，电解就是某些物质沿着一条线向一个方向传递，而另一些物质则向相反的方向传递。这显然是一种纵向现象，而且不存在关于绕着力的方向的任何转动效应的证据。因此我们就推测，引起或伴随着电解现象的电流，是一种纵向的而不是旋转的现象。

另一方面，一个磁体的南极和北极，并不像在电解过程中出现在对面位置上的氧气和氢气那样地彼此不同，因此我们并没有磁性是一种纵向现象的证据，而磁性使平面偏振光的偏振面发生转动的效应却清楚地表明磁性是一种旋转现象 ^〔5〕 。

关于线积分

16．〕一个矢量沿一条线的分量的积分，这种运算在物理科学中是普遍重要的，从而应该清楚地加以理解。

设x、y、z是一条线上一点P的坐标，而从某点A量起的线的长度是s。这些坐标将是单一变数s的函数。

设R是一个矢量在P点上的数值，并设P点处曲线的切线和R的方向成一个角度ε，则Rcosε就是R沿曲线的分量，而积分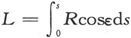 就叫做R沿曲线s的线积分。

我们可以把这一表示式写成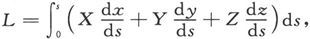 式中X、Y、Z分别是R平行于x、y、z的分量。

一般说来，这个量对于在A、P之间画出的不同曲线来说是不同的。然而，当在某一区域内量Xdx＋Ydy＋Zdz＝-DΨ时，也就是说当它在该区域中是一个全微分时，L的值就变为L＝Ψ_A －Ψ_P ，而且对A和P之间的路径的任何两种形式来说都是相同的，如果一种形式可以通过连续的运动来变成另一种形式而不必越出这一区域的话。

关　于　势

量Ψ是点的位置的一个标量函数，从而是不依赖于各参照方向的。它叫做势函数，而分量为X、Y、Z的矢量被说成具有一个势Ψ，如果

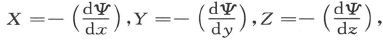
当存在一个势时，势为常数的那种曲面就叫做等势面。在这种面上的任一点上，R的方向和该面的法线相重合，而如果n是P点上的一条法线，则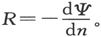

把一个矢量的各分量看成某一坐标函数对这些坐标的一阶导数的方法，是由拉普拉斯在他关于引力理论的论著中发明的 ^〔6〕 。势这个名称是首先由格林赋予这个函数的 ^〔7〕 ，他把这个函数当成了处理电学问题的基础。格林的著作直到1846年都没有受到数学家们的重视，而在1846年以前，大多数他的重要定理都已经被高斯、查斯耳斯、斯图尔姆和汤姆孙 ^〔8〕 所重新发现了。

在引力理论中，势和此处所用的函数异号，从而任意方向上的合力就是由势函数沿该方向的增加率来量度的。在电和磁的研究中，势被定义得使任意方向上的合力由势在该方向上的减少率来量度。这种使用表示式的办法使它可以和势能的正负号相适应，因为当物体沿着作用在它上面的力的方向运动时势能总是减小的。

17．〕势和由它如此导出的矢量之间的关系的几何学本性，通过哈密顿发现算符形式而得到了很大的澄清；利用这种算符，可以由势导出矢量。

正如我们已经看到的那样，矢量沿任何方向的分量，就是势对沿该方向画出的一个坐标的一阶导数并变号。

现在，如果i、j、k是互相垂直的三个单位矢量，而X、Y、Z是矢量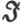 平行于这些矢量的分量，就有　　

而按照我们以上的说法，如果Ψ是势，就有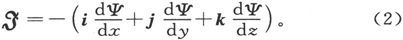　　

现在，如果我们用∇代表下列算符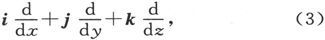　　

就有　　

算符∇可以诠释为指示我们，沿着三个正交的方向测量Ψ的增加率，然后把这样求得的各量看成矢量，并把它们合成起来成为一个量。这就是表示式（3）指示我们所要作的。但是我们也可以认为它是指示我们首先找出Ψ在哪个方向上增加得最快，然后沿着那个方向画出一个矢量来表示这一增加率。

拉梅先生在他的《论反函数》（Traité des Fonction Inverses）一书中用了微分参数一词来代表这个最大增加率的量值，但是不论这一名词还是拉梅应用它的方式都不曾指示这个量既有大小又有方向。在少数情况下我将必须把这一关系说成纯几何的关系，那时我将把矢量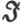 叫做标量函数Ψ的空间改变量，用这种说法来既指示Ψ的最快增加率的大小，又指示其最快增加的方向。

18．〕然而，在某些事例中，Xdx＋Ydy＋Zdz是一个全微分的条件

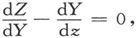
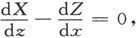以及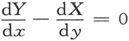

在某一个空间域中到处都能满足，但是在两条线上从A到P的线积分却可以不同，而其中每一条线又完全位于该域之内。如果域呈环形，而从A到P的两条线通过了环的对面段，那就会是这种情况。在这种情况下，一条路径并不能通过不越出域外的连续运动而转变成另一条路径。

在这儿，我们被引导到了属于“位置几何学”的考虑；这一课题的重要性虽已由莱布尼兹指出并由高斯例示，但是该课题还几乎没被研究过。这一课题的最完全的处理已由J. B. 李斯廷给出 ^〔9〕 。

设空间中有p个点，并设画了l条任意形状的连接着这些点的线，使得没有任何两条线相交，而且没有一个点被孤立地留下来。我们将由一些线这样构成的图形叫做一个“图式”（Diagram）。在这些线中，p—1条线已经足以把p个点连成一个连接体系了。每一条新线都完成一条圈线或闭合路径，或者，我们将把它叫做回路。因此，图式中的回路数目就是k＝l－p＋1。

沿着图式中的那些线画出的任何闭合路径，都是由这些独立的回路构成的，其中每一回路都可以被走过任何多次，而且是沿任何方向。

回路的存在叫做“环流性”，而图式中的回路的数目则叫做“接圆数”。

曲面上和空间域中的环流性

曲面或完全或有界。完全曲面或无限或闭合。有界曲面是以一个或多个闭合曲线为边界的，而闭合曲线在极限情况下可以变成有限的双线或变成点。

一个有限的空间域是以一个或多个闭合曲面为边界的。其中一个是外表面，其余各曲面都被表面所包围而且互不相交，它们被称为内表面。

如果域只有一个边界面，我们就可以假设那个表面向内收缩而不打破其连续性或和自己相交。如果域是一个简单连续域，例如一个球，这一过程就可以继续进行直到域收缩成一个点。但是，如果域是多连通的，则收缩的结果将是一个曲线图式，而图式的接环数也就是域的接环数。域外的空间和域本身具有相同的接环数。因此，如果域是既由外表面又由内表面所限定的，则它的接环数就是所有各表面的接环数之和。

当一个域的本身中包括了其他的域时，它就叫做一个“回绕域”（Periphractic region）。

一个域的内表面的数目，叫做它的回绕数。一个闭合曲面也是回绕的，它的回绕数为1。

一个闭合曲面的接环数是它所包含的各域中的任一域的接环数的二倍。为了求得一个有界曲面的接环数，设想一切边界线都向内收缩而不打破其连续性，直到收缩得相遇为止。这时，在非循环曲面的事例中曲面收缩成一个点，而在循环曲面的事例中它则变成一个曲线图式。

图式的接环数就是曲面的接环数。

19．〕定理一　如果在一个非循环域中到处都有　Xdx＋Ydy＋Zdz＝-DΨ，则沿着域内任一路径所取的从点A到点P的线积分之值都相同

我们首先将证明，沿着域内任一闭合路径所求的线积分为零。

设各等势面已被画出。它们全都不是闭合曲面就是完全被域的表面所限定的，因此，如果域内的一条闭合曲线在它的行程的任何部分和任何等势面相交，则它必将在行程的某一其他部分沿相反的方向和同一等势面相交，而既然线积分的对应部分相等而异号，总的值就是零。

于是，如果AQP和AQ′P是从A到P的两条路径，则沿AQ′P的线积分就是沿AQP的和沿闭合路径AQ′PQA的线积分之和。但是沿闭合路径的线积分是零，从而沿两条路径的线积分就是相等的。

20．〕 定理二 如果在一个循环域中方程　Xdx＋Ydy＋Zdz＝-DΨ到处得到满足，则沿着在域内画出一条曲线从A到P的线积分一般并不是确定的，除非A和P之间的交通渠道已经指定。

设N是域的接环数，则我们可以用一些称之为屏障的曲面将域分成N部分，以封住N条交通渠道并把域简化到非循环的情况而不破坏它的连续性。

根据上述定理，沿着一条并不和任何这些屏障相交的曲线计算的从A到任一点P的线积分将有定值。

现在设A和P被取得彼此无限靠近但却位于一个屏障的两侧，并设K是从A到P的线积分。

设A′和P′是位于同一屏障两侧的彼此无限靠近的另外两个点，并设K′是从A′到P′的线积分。于是就有K′＝K。

因此，如果我们画出接近重合的然而却位于屏障两侧的AA′和PP′，则沿着这两条线的线积分将相等 ^〔10〕 。设每一线积分等于L，则沿A′P′的线积分K′等于沿A′A＋AP＋PP′的线积分，即等于-L＋K＋L＝K＝沿AP的线积分。

因此，沿着一条按给定方向通过体系的一个屏障的闭合曲线的线积分是一个常量K。这个量叫做对应于所给回路的循环常量。

设在域内画一条任意的闭合曲线，使它沿着正方向通过p次第一回路的屏障，并沿着负方向通过p′次。设p－p′＝n₁ 。于是沿这条闭合曲线的线积分就将是n₁ p₁ 。

同理，任意闭合曲线上的线积分将是n₁ K₁ ＋n₂ K₂ ＋…＋n_s K_s ，式中n_s 代表曲线沿正方向通过回路S的屏障的次数减去它沿负方向通过该屏障的次数而得的余额。

设有两条曲线。若其中一条可以通过连续的运动且在任何时候都不通过势的存在条件不成立的任何空间部分而转换成另一条，则这两条曲线叫做“可调和的”曲线。不能实现这样的转换的曲线叫做“不可调和的”曲线 ^〔11〕 。

Xdx＋Ydy＋Zdz在某一域的所有各点上都是某一函数Ψ的全微分的条件，在若干物理研究中是出现的。在那些研究中，有向量和势具有各种不同的物理诠释。

在纯运动学中，我们可以假设X、Y、Z是一个连续物体中某一点的位移分量，该点的原始坐标为x、y、z。于是，上述条件就表明这些位移构成一种非转动的胁变 ^〔12〕 。

如果X、Y、Z代表一种流体在点x、y、z上的速度分量，则上述条件表明流体的运动是非转动性的。

如果X、Y、Z代表点x、y、z上的分力，则上述条件表示：当一个质点从一点运动到另一点时，力对该质点做的功是这两点上的势差，而且这一势差的值对两点之间一切可调和的路径来说都是相同的。

关于面积分

21．〕设dS是一个曲面上的面积元，而ε是向曲面的正方向画出的一条法线和矢量R之间的夹角，则∬RcosεdS叫做R在曲面S上的面积分 ^〔13〕 。

定理三　通量指向一个闭合曲面内部的面积分，可以表示成在曲面内部所求敛度的体积分。（见第25节。）

设X、Y、Z是R的分量，并设l、m、n是S的外向法线的方向余弦，则R在S上的面积分是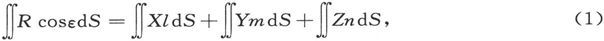　　

式中X、Y、Z的值是在曲面上一个点上的值，而积分则遍及整个曲面。

如果曲面是闭合的，则当y和z为给定时坐标x必有偶数个值，因为平行于x的一条线必将以相等的次数进入和离开所包围的空间，如果它和曲面相交的话。

在每一个进入点上，有ldS＝-dydz，而在每一个离开点上，则有ldS＝dydz。

设有一点从x＝-∞运动到x＝+∞，第一次当x＝x₁ 时进入此空间，而当x＝x₂ 时离开此空间，余以此类推。再设X在这些点上的值是X₁ 、X₂ 等等，则有

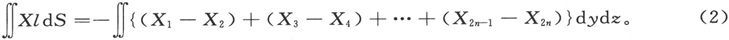
如果X是一个连续的量，而且在x₁ 和x₂ 之间没有无限大的值，则有

式中的积分从第一个交点算到第二个交点，也就是沿着位于闭合曲面内部的那一段x计算。把所有位于闭合曲面内部的线段都考虑在内，我们就得到

这里的双重积分限制在闭合曲面上，但是三重积分则遍及整个被包围的空间。因此，如果X、Y、Z在一个闭合曲面S的内部是连续的和有限的，则R在该曲面上的总的面积分将是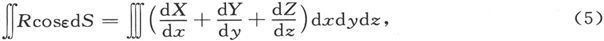　　

式中的三重积分遍及S内部的整个空间。

其次让我们假设X、Y、Z在闭合曲面内部是连续的，然而在某一个曲面F（x，y，z）＝0上，X、Y、Z的值却从反面的X、Y、Z突然变成正面的X′、Y′、Z′。

如果这种不连续性出现在例如x₁ 和x₂ 之间，则X₂ －X₁ 的值将是

此处在积分号下的表示式中只计及X的导数的有限值。

因此，在这一事例中，R在闭合曲面上的总面积分将是

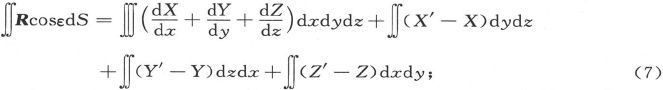
或者，如果l′、m′、n′是不连续性曲面的法线的方向余弦，而dS′是曲面的面积元，则有

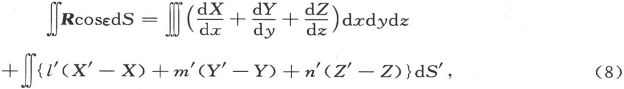
式中最后一项的积分是在不连续性曲面上计算的。

如果在X、Y、Z为连续的每一点上都有　　

而且在它们为不连续的每一个曲面上都有

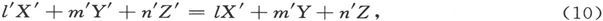
则每一个闭合曲面上的面积分都为零，而矢量的分布就被说成是“管状的”。

我们将把方程（9）叫做“普遍管状条件”，而把方程（10）叫做“表面管状条件”。

22．〕现在让我们考虑在曲面S内部的每一点上方程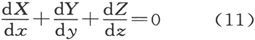　　

都得到满足的那种事例。作为这一点的后果，我们有每一个闭合曲面上的面积分都为零。

现在设闭合曲面S由三个部分S₁ 、S₀ 和S₂ 组成。设S₁ 是由一条闭合曲线L₁ 包围着一个任意形状的曲面。设S₀ 是通过从L₁ 的每一点上画出永远和R方向一致的线而形成的曲面。如果l、m、n是曲面S₀ 的任一点上的法线的方向余弦，我们就有

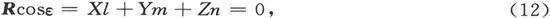
因此曲面的这一部分对面积分的值并无任何贡献。

设S₂ 是由闭合曲线L₂ 包围着的另一个任意形状的曲面，而L₂ 是S₂ 和S₀ 的交线。

设Q₁ 、Q₀ 、Q₂ 是曲面S₁ 、S₀ 、S₂ 上的面积分，而Q是闭合曲面S上的面积分。于是

而我们知道　　

从而就有　　

换句话说，曲面S₂ 上的面积分和S₁ 上的面积分相等而异号，不论S₁ 的形状和位置如何，只要中间曲面S₀ 是到处和R相切的就行。

如果我们假设L₁ 是一个面积很小的闭合曲线，S₀ 就将是一个管状的曲面，而且它具有这样的性质：管子的每一个完全截面上的面积分都相同。

既然如果　　

则整个空间都可以划分成一些这样的管子，和这一方程相容的一种矢量分布就叫做“管状分布”。

关于流管和流线

如果空间被分成一些管子，而每一个管子的面积分都为1，则各管称为“单位管”，而由一条闭合曲线L所包围的任一有限曲面S上的面积分就等于沿正方向通过S的这种管子的数目，或者换句话说，就等于穿过闭合曲线L的这种管子的数目。

因此，S上的面积分只依赖于S的边界L的形状，而不依赖于边界所围成的曲面的形状。

关于回绕域

如果在外面由单独一个闭合曲面S所包围的整个域中，管状条件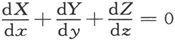 到处都是满足的，则在域内画出的任何闭合曲面上，面积分都将是零，而一个有界曲面上的面积分则只取决于形成该面积之边界的那条闭合曲线的形状。

然而，如果管状条件在其中为满足的那个域不是由单独一个曲面所包围的，则通常并不能得到同样的结果。

因为，如果它是由多于一个连续曲面包围而成的，则其中一个曲面是外表面，而其余的都是内表面，从而域就是回绕的，在它内部有另一些域被它所完全包含在内。

在其中一个这种被包含的域中，例如在由闭合曲面S₁ 所包围的域中，如果管状条件并不满足，则可以令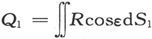 等于包围这个域的曲面上的面积分，并令Q₁ 、Q₂ 等等等于其他被包含域的曲面S₁ 、S₂ 等等上的对应量。

于是，如果在S内部画一个闭合曲面S′，则只有当S′不包含任何被包含域S₁ 、S₂ 等等时，S′上的面积分的值才将是零。如果它包含了任何的这种域，则面积分是位于它内部的不同被包含域上的面积分之和。

同理，在以一条闭合曲线为边的曲面上计算的面积分，也只有在那样一些曲面上才是相同的，那些曲面以该曲线为边，而且通过在域S内的连续运动可以和所给的曲面相调和。

当我们必须处理回绕域时，首先要做的就是通过画一些把内表面S₁ 、S₂ 等等和外表面S连接起来的线L₁ 、L₂ 等等来把该域简化为非回绕域。其中的每一条线，如果并不是连接了本来已经连续接触着的曲面的话，都将使回绕数减少1，从而为了消除回绕性而必须画的线数就等于回绕数，或者说等于内表面的数目。在画这些线时我们必须记得，任何连接着已经连接起来的曲面的线并不能减少回绕数而却只引入循环性。当这些线已经画好时我们就可以断定，如果管状条件在域S中是满足的，则完全在S内部画出且不和任何一条这种线相交的任一曲面都将有等于零的面积分。如果它和任何一条线例如L₁ 相交一次或任何偶数次，它就包含曲面S₁ ，从而它的面积分就是Q₁ 。

管状条件在其中为满足的最习见的回绕域的例子就是一个物体周围的域，该物体是反比于距离平方的力吸引或推斥其他物体的。

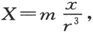
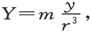
在斥力的事例中，我们有 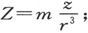式中m是假设为位于坐标原点上的物体质量。

在r为有限的任一点上，有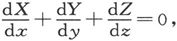 但是在原点上这些量却变为无限大。对于不包含原点的任一闭合曲面来说，面积分是零。如果一个闭合曲面包含了原点，则其面积分是4πm。

如果由于任何原因，我们愿意把m周围的域看得就像它不是一个非回绕域那样，我们就必须从m到无限远画一条线，而当计算面积分时我们就必须记得，每当这条线从反面向正面通过曲面时，面积分中就必须增加4πm。

关于空间中的右手关系和左手关系

23．〕在本论著中，沿任一轴线的前进平动和绕该轴的转动，将被认为当它们的方向对应于一个常见的或右手的螺旋的前进方向和转动方向时就具有相同的正负号 ^〔14〕 。

例如，如果地球从西向东的实际转动被取为正的，则从南到北的地轴将被取为正，从而如果一个人沿正方向前进，则正向转动是合适的，头为右旋而脚为左旋。

如果我们把自己放在一个曲面的正面一边，则它的边界线的正向将和表面朝向我们的一个表上的指针转动方向相反。

这就是在汤姆孙和泰特的《自然哲学》（Natural Philosophy）以及泰特的《四元数》（Quaternians）中采用了的右手制。相反的左手制在哈密顿的《四元数》中被采用（Lecture, p. 76; Elements, p. 108及p. 117的小注）。从一种体制到另一种体制的变换被李斯廷称为“反转”（Perversion）。

一个物体在镜中的反射像，是物体的一个反转了的像。

当我们应用笛卡儿坐标x、y、z时，我们应该把它们画得使有关各符号之轮换次序的通常惯例导致空间中的一种右手制的方向。例如，如果x是向东画而y是向北画的，则z必须向上画 ^〔15〕 。

当求积分的次序和各符号的轮换次序一致时，曲面的面积将被认为是正的。例如，xy平面上的一个闭合曲线的面积可以写成∫xdy或-∫ydx；求积分的次序在第一式中是x、y，而在第二式中则是y、x。

两个乘积dxdy和dydx之间的这种关系，可以和四元数方法中两个垂直矢量之积的法则相对比，该矢量积的正负号取决于乘法的次序；而且也可以和当一个行列式中的两行或两列互换时行列式的变号相对比。

同理，当积分次序是变数x、y、z的轮换次序时，一个体积分就被认为是正的，当轮换次序倒转时则积分被认为是负的。

现在我们来证明一条定理。在建立一个有限曲面上的面积分和沿曲面边界的线积分之间的联系方面，这条定理是有用的。

24．〕定理四　沿一条闭合曲线计算的一个线积分，可以用以该曲线为边的一个曲面上的面积分表示出来。

设X、Y、Z是一个矢量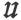 的分量，该矢量的线积分应沿一条闭合曲线s来计算。

设S是完全由闭合曲线s围成的任一连续的有限曲面，并设ξ，η，ζ是另一矢量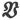 的分量，它们和X、Y、Z的关系由下列方程来确定：

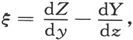
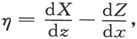
于是在曲面S上求的 的面积分就等于沿曲线s求的 的线积分。很显然，ξ，η，ζ本身是满足管状条件的：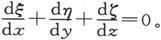

设l、m、n是曲面的一个面积元dS上法线的方向余弦，dS按正方向计算。于是， 的面积分的值就可以写成　　

为了对面积元dS的意义形成一个确切的概念，我们将假设曲面上每一点的坐标x、y、z是作为两个独立变数α和β的函数而被给出的。如果β不变而α变化，则点（x，y，z）将在曲面上描出一条曲线，而如果赋予β以一系列值，则将有一系列这样的曲线被画出，它们全都位于曲面S上。同样，通过赋予α以一系列恒定的值，第二系列曲线就可以被画出；它们和第一系列曲线相交，而把整个曲面分成元部分，其中每一个部分都可以被看成面积元dS。

按照常用的公式，这一面积元在yz平面上的投影是

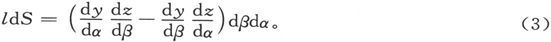
适用于mdS和ndS的表示式通过按轮换次序将x、y、z代入上式来得出。

我们所要求的面积分是　　

或者，将ξ、η、ζ按照X、Y、Z表示出来，就得到

此式中依赖于X的部分可以写成

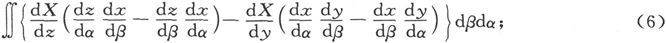
加上并减去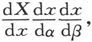 就变成

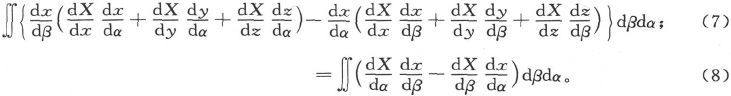
现在让我们假设α为恒定的那些曲线形成一系列闭合曲线，包围着曲面上一个α具有极小值α₀ 的点，并设最后一条曲线，α＝α₁ 的那条曲线，和闭合曲线s相重合。

让我们再假设β为恒定的那些曲线形成一系列从α＝α₀ 的点画到闭合曲线s的线，而且第一条β₀ 和最后一条β₁ 相重合。

对（8）分部求积分，第一项对α而第二项对β求积分，各双重积分就互相消除，而表示式就变成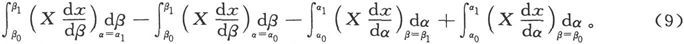　　

既然点（α，β₁ ）和点（α，β₀ ）完全相同，第三项就和第四项相消；而且，既然在α＝α₀ 的点上只有一个x值，第二项就等于零，而表示式就简化成了第一项。

既然曲线α＝α₁ 和闭合曲线s相重合，我们就可以把表示式写成下式：

式中的积分是沿着曲线s求的。我们可以用同样的办法处理面积分中依赖于Y和依赖于Z的部分，因此我们最后就得到

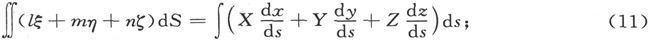
式中的第一个积分是在曲面S上计算的，而第二个积分是沿边界线s计算的 ^〔16〕 。

关于算符∇对一个矢量函数的作用

25．〕我们已经看到，用∇来代表的算符就是用来从矢量的势求出该矢量的那个算符。然而，同一个算符，当应用到一个矢量函数上时就得到包括在我们刚刚证明了的两条定理（定理三和定理四）中的一些结果。这一算符在一个矢量位移上的推广应用，以及大部分进一步的发展，都是由泰特教授作出的 ^〔17〕 。

设σ是变点矢径ρ的一个矢量函数。让我们像通常一样假设ρ＝ix＋jy＋kz而σ＝iX＋jY＋kZ；式中X、Y、Z是σ沿各轴的分量。

我们必须把算符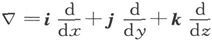 作用在σ上。完成这一运算并记得i、j、k的乘法规则，我们就发现∇σ包括两个部分，一个部分是标量而另一个部分是矢量。

标量部分是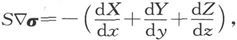 见定理三，而矢量部分是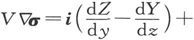

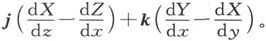
如果X、Y、Z和ξ、η、ζ之间的关系是由上一定理中的方程（1）给出的，我们就可以写出V∇σ＝iξ＋jη＋kζ。见定理四。

由此可见，出现在两条定理中的那些X、Y、Z的函数都可以通过对分量为X、Y、Z的矢量进行∇运算来得到。定理本身可以写成

式中ds是体积元，ds是面积元，dρ是线元，而Uv是一个沿着法线方向的单位矢量。

为了理解一个矢量的这些函数的意义，让我们假设σ₀ 是σ在点P上的值，并让我们在P点的邻域中考查σ－σ₀ 的值。如果我们围绕着P点画一个闭合曲面，那么，如果σ在这曲面上的面积分是指向内部的，则S∇σ将为正，而P点附近矢量在总的看来将是指向P的，如图1所示。

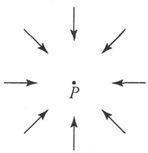
图1

因此我建议把∇σ的标量部分称为σ在P点的敛度。

为了诠释矢量部分，设其分量为ξ、η、ζ的那个矢量是从纸面垂直向上的，并且让我们在P点附近考查矢量σ－σ₀ 。它将显现得如图2所示，这个矢量在总的看来是按照反时针的方向而和纸面相切的。

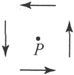
图2

我（很无把握地）建议把∇σ的矢量部分称为σ在P点的旋度。

在图3中，我们有一个旋度和敛度相结合的图示。

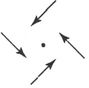
图3

现在让我们考虑V∇σ＝0这一个方程的意义。它意味着∇σ是一个标量，或者说矢量σ是某一标量函数的空间变化率。

26．〕算符∇最引人注目的性质之一就是，当运用两次时，它就变成

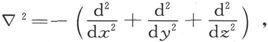
这是在物理学的所有各部分都会出现的一个算符，我们可以称之为拉普拉斯算符。

这个算符本身，在本质上是一个标量算符。当它作用在一个标量函数上时，结果是标量；当它作用在一个矢量函数上时，结果是矢量。

如果我们以任一点P为中心画一个半径为r的小球，那么，如果q₀ 是q在球心上的值而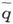 是q在球内各点上的平均值，就有 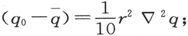因此，按照∇² q的为正或为负，球心上的值将大于或小于平均值。

因此我建议把∇² q称为q在P点上的浓度，因为它指示的是q在该点上的值比它在该点邻域中的平均值大多少。

如果q是一个标量函数，则求它的平均值的方法是众所周知的。如果它是一个矢量函数，我们就必须通过求矢量函数之积分的法则来求它的平均值。求得的结果当然是一个矢量。

注　释

〔1〕 　量纲的理论最初是由傅立叶提出的，见Théorie de Chaleur, §160．

〔2〕 　参阅Prof. J. Loschmidt, "Zur Grösse der Luftmolecule," Academy of Vienna, Oct, 12, 1865; G. J. Stoney, "The Internal Motion of Gases," Phil. Mag. Aug., 1868；以及Sir W. Thomson, "The Size of Atoms," Nature, March 31, 1870.

并参阅Sir W. Thomson, "The size of Atoms," Nature, V. 28, pp. 203, 250, 274.

〔3〕 　如果取厘米和秒作为单位，则按照白利重作的卡文迪什实验，质量的天文单位约是1.537×10⁷ 克，或15.37吨。白利按照他的所有实验的平均结果，把地球的平均密度取作了5.6604，而联系到所用的地球尺寸和地面上的引力强度，就作为实验的直接结果而得到了上述的值。

科纽重新计算了白利的结果，得到的地球平均密度是5.55，从而质量的天文单位是1.50×10⁷ 克；而科纽本人的实验则给出地球的平均密度5.50，质量的天文单位为1.49×10⁷ 克。

〔4〕 　关于四元数的初等论述，读者可以参阅Kelland and Tait的“Introduction to Quaternians”，Tait的“Elementary Treatise on Quaternians”，以及Hamilton的“Elements of Quaternians”．

〔5〕 　一定不要以为这就意味着，在假设电现象和磁现象是由一种媒质的运动所引起的任何一种理论中，电流就必然起源于平移运动而磁力必然起源于旋转运动。例如，也有一些旋转效应是和电流联系着的，例如，一个磁极会绕着它转动，而且也很可能的是，如果静电现象在其中有其根源的那种媒质在它的内部各处有一个分量为f、g、h的电位移并且是以速度u、v、w而转动的，它就将是一个磁力的根源，其分量分别是4π（wg－vh）、4π（uh－wf）、4π（vf－ug）；于是，在这一事例中，一种平移运动就能产生一个磁场。Phil Mag. July, 1889．

〔6〕 　Méc. Céleste, liv. iii.

〔7〕 　Essay on the Application of Mathematical Analysis to the Theories of Electrioitv and Magnetism, Nottingham, 1828。重印于Crelle's Journal，并重印于Mr. Ferrers'edition of Green's Works.

〔8〕 　Thomson and Tait, Natural Philosophy, §483.

〔9〕 　Der Census Raümlicher Complere, Gött. Abh., Bd. x. S. 97 (1861). 关于对物理目的来说是必要的那些多连通空间的性质的一种初等论述，见Lamb, Treatise on the Motion of Fluids, p. 47．

〔10〕 　因为X、Y、Z是连续的。

〔11〕 　见Sir W. Thomson, "On Vortex Motion", Trans. R. S. Edin., 1867～1868.

〔12〕 　见Thomson and Tait, "Natural Philosophy", §190(i).

〔13〕 　在以下的研究中，法线的正方向指向曲面的外面。

〔14〕 　当我们把右手的上沿向外转，而同时把手伸向前方时，手臂肌肉的联合作用将比任何的文字定义更加牢固地在我们的记忆中留下印象。

W. H. 密勒教授曾向我指出，常春藤的卷须是右旋的，而啤酒花的卷须是左旋的，从而空间中的两种关系体制可以分别称为常春藤制和啤酒花制。

我们所采用的常春藤制是林诺乌斯的体制，也是除日本以外一切文明国家中螺旋制造者们的体制。德·堪道里是把啤酒花卷须说成“右旋”的第一个人，李斯廷学了他的样，而且论述光的圆偏振的多数作者也学了他的样。啤酒花式的螺旋是被做出来用以连接铁路车辆的，也用于把普通车辆的轮子安装在左侧，但是这种螺旋被它们的使用者叫做左手螺旋。

〔15〕 　就像在这个图中那样：

〔16〕 　这一定理是由斯托克斯教授给出的，见Smith's prize Examination, 1854，问题8。在Thomson and Tait的Natural Philosophy, §190(j)中，对定理进行了证明。

〔17〕 　见Proc. R. S. Edin, April 28, 1862, 'On Green'g and other siliea Theorems, Trans. R. S. Edin., 1869～1870, 这是一篇很有价值的论文；并见'On some Quaternion Integrals,' Proc. R. S. Edin., 1870～1871.