补篇Ⅰ

1．关于§3和§4的一些注记

在第一章§3的末尾，我们已经注意到下面的事实：即一条直线a 不能与三角形ABC 的三条边同时相交，这是一个能证明的定理，由定理4按照下列方法就可得到它的证明，如果直线a 与三线段BC ，CA ，AB 分别交于D ，E ，F ，则这三个点将是不同的。由定理4，它们中的一个将位于其他两者之间。

如果D 位于E 和F 之间，则对三角形AEF 和直线BC ，利用公理Ⅱ₄ 可知这直线必将经过线段AE 或AF 的一点。在这两种情况下，均将引出与Ⅱ₃ 或Ⅰ₂ 的一个矛盾结果。

范·德瓦尔登曾考虑到帕士公理Ⅱ₄ 可以用下述的空间顺序公理来代替。

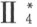．设A ，B ，C 是三个不共线点，且α 是不含这三个点的平面；若平面α 通过线段AB 的一点，则它也通过线段AC 或线段BC 的一点。

利用这个替换，不仅Ⅱ₄ 变为可以证明的定理，而且关联公理Ⅰ₇ 也是这样。关于这个问题可以参看范·德瓦尔登的“欧几里得几何的逻辑基础”（De Logische Grondslagen der Euklidische Meetkunde）一文，此此文刊载于Zeitschrift Christian Huygens卷13～14（1934—1936），§3。

对于用公理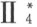 来证明Ⅰ₇ 的论断可如下进行考虑。范·德瓦尔登在他的证明里，用到每个平面含有三个不共线点这个公理。此公理曾出现在希尔伯特《几何基础》的前几版里，现已被较弱要求的公理Ⅰ₃ 和Ⅰ₄ 所代替（参看§2）。即“存在不全属于一直线上的三点”和“每一个平面至少存在一点”。选择这两个公理，由 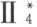即可证明Ⅰ₇ 。首先由 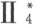证明下面有限制的定理“如果含有三个不共线点的平面β 与一平面α 有一公共点，则α 和β 必有其他公共点”。于是借助这个定理以及关联公理Ⅰ_1～6 和Ⅰ₈ 即可证明：每个平面含有三个不共线点。据此，对平面β 的限制条件即可去掉。

公理Ⅰ₇ 的论断可以从 来证明，这一事实表达这空间最多是三维的类比于公理Ⅱ₄ ，当直线a 位于平面ABC 的条件去掉时，维数则限制到二的情况。

关于§4的定理9，费格尔（G. Feigel）曾在他的文章“关于初等几何的顺序公理”（Über die elementaren Anordnungssätze der Geometrie）中给出一个较详细的证明。此文载于Jahresbericht der Deutschen Math. Vereinigung. Bd. 33（1924），§4。

2．关于§13的一些注记

在§13里所叙述的关于实数的公理系统，实质上是从希尔伯特的一篇文章“关于数的概念”（Über den Zahlbegriff, Jahrb, d. Deutsch. Math. Ver. 8（1900））里抽出来的。在§13里列举为定理，而在文章里，则是作为公理的。在这里我们从他的那篇文章引进下面的注记：

1．数0的存在（定理3）是定理1、定理2和加法结合律的一个推论。

2．数1的存在（定理6）是定理4、定理5和乘法结合律的一个推论。

3．加法交换律（定理8）是定理1～6、加法结合律和两个分配律的一个推论，即

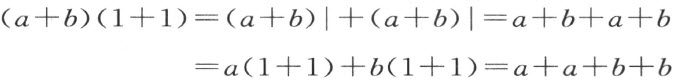
由此

从而根据定理2

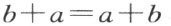
乘法交换律（定理12）可以从定理1～11、13～16和17（阿基米德定理）推出，但是不能不用定理17，这一点是在§32～§33中所明确的。