第1章　仅使用直线和圆的作图问题

Problems the Construction of … and Circles

在《几何》中，笛卡儿分析了几何学与代数学的优缺点：西腊人的几何过于抽象，而且过多地依赖于图形，总是要寻求一些奇妙的想法；代数却完全受法则和公式的控制，以致阻碍了自由的思想和创造。他同时看到了几何的直观与推理的优势和代数机械化运算的力量。于是他着手解决这个问题，并由此创立了解析几何。

笛卡儿《哲学原理》中的插图

任何一个几何问题都很容易化归为用一些术语来表示，使得只要知道直线段的长度的有关知识，就足以完成它的作图。

如何将算术运算转为几何的运算

算术仅有四或五种运算组成，即加、减、乘、除和开根，后者可认为是一种除法；在几何中，为得到所要求的线段，只需对其他一些线段加加减减；不然的话，我可以取一个线段，称之为单位，目的是把它同数尽可能紧密地联系起来，而它的选择一般是任意的；当再给定其他两条线段，则可求第四条线段，使它与给定线段之一的比等于另一给定线段与单位线段的比（这跟乘法一致）；或者，可求第四条线段，使它与给定线段之一的比等于单位线段与另一线段之比（这等价于除法）；最后，可在单位线段和另一线段之间求一个、两个或多个比例中项（这相当于求给定线段的平方根、立方根，等等）。为了更加清晰明了，我将毫不犹豫地将这些算术的术语引入几何。

如何在几何中进行乘、除和开平方根

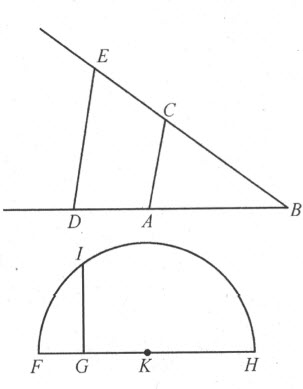
例如，令AB 为单位线段，求BC 乘BD 。我只要联结点A 与点C ，引DE 平行CA ；则BE 即是BD 和BC 的乘积。

若求BD 除BE ，我联结E 和D ，引AC 平行DE ；则BC 即为除得的结果。

若想求GH 的平方根，我沿该直线加上一段等于单位长的线段FG ；然后平分FH 于K ；我再以K 为心作圆FIH ，并从G 引垂线延至I 。那么，GI 即所求的平方根。我在这里不讲立方根或其他根的求法，因为在后面讲起来更方便。

我们如何在几何中使用算术符号

通常，我们并不需要在纸上画出这些线，而只要用单个字母来标记每一条线段就够了。所以，为了作线段BD 和GH 的加法，我记其中的一条为a ，另一条为b ，并写下a ＋b 。同样，a －b 将表示从a 中减去b ；ab 表示b 乘a 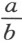； 表示b 除a ；aa 或a 2 表示a 自乘；a 3 表示自乘所得的结果再乘a ，并依此类推。类似地，若求a 2 ＋b 2 的平方根，我记作 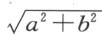；若求a 3 －b 3 ＋ab 2 的立方根，我写成 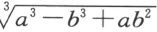，依此可写出其他的根。必须注意，对于a 2 ，b 3 及类似的记号，我通常用来表示单一的一条线段，只是称之为平方、立方等等而已，这样，我就可以利用代数中使用的术语了。

还应该注意，当所讨论的问题未确定单位时，每条线段的所有部分都应该用相同的维数来表示。a 3 所含的维数跟ab 2 或b 3 一样，我都称之为线段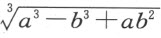 的组成部分。然而，对单位已确定的情形就另当别论了，因为不论维数的高低，对单位而言总不会出现理解上的困难；此时，若求a 2 b 2 －b 的立方根，我们必须认为a 2 b 2 这个量被单位量除过一次，而B 这个量被单位量乘过2次。

最后，为了确保能记住线段的名称，我们在给它们指定名称或改变名称时，总要单独列出名录。例如，我们可以写AB ＝1，即AB 等于1；GH ＝a ，BD ＝b ，等等。

我们如何利用方程来解各种问题

于是，当要解决某一问题时，我们首先假定解已经得到，并给为了作出此解而似乎要用到的所有线段指定名称，不论它们是已知的还是未知的。然后，在不对已知和未知线段作区分的情况下，利用这些线段间最自然的关系，将难点化解，直至找到这样一种可能，即用两种方式表示同一个量。这将引出一个方程，因为这两个表达式之一的各项合在一起等于另一个的各项。

我们必须找出跟假定为未知线段的数目一样多的方程；但是，若在考虑了每一个有关因素之后仍得不到那样多的方程，那么，显然该问题不是完全确定的。一旦出现这种情况，我们可以为每一条缺少方程与之对应的未知线段，任意确定一个长度。

当得到了若干个方程，我们必须有条不紊地利用其中的每一个，或是单独加以考虑，或是将它与其他的相比较，以使得到每一个未知线段的值；为此，我们必须先统一地进行考察，直到只留下一条未知线段，它等于某条已知线段；或者是未知线段的平方、立方、四次方、五次方、六次方等中的任一个，等于两个或多个量的和或差，这些量中的一个是已知的，另一些由单位跟这些平方、或立方、或四次方得出的比例中项乘以其他已知线段组成。我用下列式子来说明：

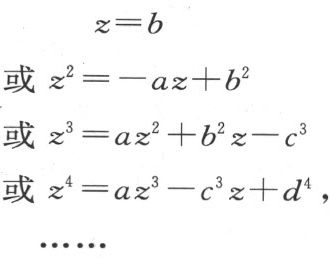
即，z 等于B ，这里的z 我用以表示未知量；或z 的平方等于B 的平方减z 乘a ；或z 的立方等于：z 的平方乘以a 后加z 乘以B 的平方，再减C 的立方，其余类推。

这样，所有的未知量都可用单一的量来表示，无论问题是能用圆和直线作图的，或是能用圆锥截线作图的，甚或是能用次数不高于三或四次的曲线作图的。

我在这里不作更详细的解释，否则我会剥夺你靠自己的努力去理解时所能享受的愉悦；同时，通过推演导出结论，对于训练你的思维有益，依我之见，这是从这门科学中所能获得的最主要的好处。这样做的另一个理由是，我知道对于任何熟悉普通的几何和代数的人而言，只要他们仔细地思考这篇论著中出现的问题，就不会碰到无法克服的困难。

因此，我很满意如下的说法：对于一名学生来说，如果他在解这些方程时一有机会就能利用除法，那么他肯定能将问题约化到最简单的情形。

平面问题及其解

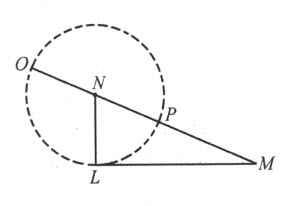
如果所论问题可用通常的几何来解决，即只使用平面上的直线和圆的轨迹，此时，最后的方程要能够完全解出，其中至多只能保留有一个未知量的平方，它等于某个已知量与该未知量的积，再加上或减去另一个已知量。于是，这个根或者说这条未知线段能容易地求得。例如，若我得到z 2 ＝az ＋b 2 ，我便作一个直角三角形NLM ，其一边为LM ，它等于b ，即已知量b 2 的平方根；另一边LN ，它等于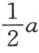 ，即另一个已知量——跟我假定为未知线段的z 相乘的那个量——的一半。于是，延长MN ，整个线段OM 即所求的线段z 。它可用如下方式表示：

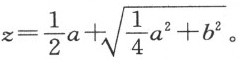
但是，若我得到y 2 ＝－ay ＋b 2 ，其中y 是我们想要求其值的量，此时我作同样的直角三角形NLM ，在斜边上划出NP 等于NL ，剩下的PM 即是所求的根y。我们写作

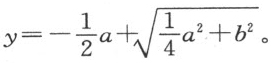
同样地，若我得到

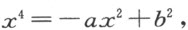
此时PM 即是x 2 ，我将得出

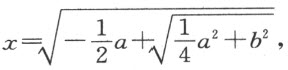
其余情形类推。

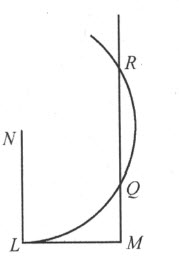
最后，若得到的是z 2 ＝az －b 2 ，我如前作NL 等于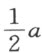 ，LM 等于b ；然后，我不去联结点M 和N ，而引MQR 平行于LN ，并以N 为心画过L 的圆，交MQ R于点Q 和R ；那么，所求线段z 或为MQ ，或为MR ，因为此时有两种表达方式，

即：

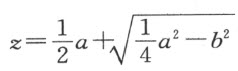
和

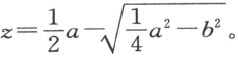
当以N 为心过L 的圆跟直线MQR 既不相交也不相切，则方程无根，此时我们可以说这个问题所要求的作图是不可能的。

还有许多其他的方法可用来求出上述同样的根，我已给出的那些非常简单的方法说明，利用我解释过的那四种图形的作法，就可能对通常的几何中的所有问题进行作图。我相信，古代数学家没有注意到这一点，否则他们不会花费那么多的劳动去写那么多的书；正是这些书中的那些命题告诉我们，他们并没有一种求解所有问题的可靠方法，而只是把偶然碰到的命题汇集在一起罢了。

帕普斯的例子

帕普斯在他的第7卷书的开头所写的内容也证明了这一点。在那里，他先用相当多的篇幅列出了他的前辈撰写的大量几何著作；最后才提到一个问题，他说那既非欧几里得，亦非阿波罗尼奥斯或其他人所能完全解决的；他是这样写的：

此外，他（阿波罗尼奥斯）说与三线或四线相关的轨迹问题，欧几里得并未完全解决，他本人和其他任何人也没能够完全解决。他们根本没有利用在欧几里得之前已论证过的圆锥截线，来为欧几里得所写下的内容添加任何东西。

在稍后的地方，帕普斯叙述了这个问题：

他（阿波罗尼奥斯）对与三线或四线相关的轨迹问题引以为豪，对其前辈作者的工作则不置一词。问题的性质如下：若给定了三条直线的位置，并且从某一点引出的三条直线段分别和三条给定直线相交成给定的角；若所引的直线段中的两条所作成的矩形与另一条的平方相比等于给定的比，则具有上述性质的点落在一条位置确定的立体轨迹上，即落在三种圆锥截线的一种上。

同样，若所引直线段与位置确定的四条直线相交成给定的角，并且所引直线段中两条所作成的矩形与另两条作成的矩形相比等于给定的比；那么，同样地，点将落在一条位置确定的圆锥截线上。业已证明，对于只有二线的情形，对应的轨迹是一种平面轨迹。当给定的直线的数目超过四条时，至今并不知道所描绘出的是什么轨迹（即不可能用普通的方法来确定），而只能称它做‘线’。不清楚它们是什么东西，或者说不知其性质。它们中有一条轨迹已被考查过，它不是最重要的而是最容易了解的，这项工作已被证明是有益的。这里要讨论的是与它们有关的命题。

若从某一点所引的直线段与五条位置确定的直线相交成固定的角，并且所引直线段中的三条所作成的直角六面体与另两条跟一任意给定线段作成的直角六面体相比等于给定比，则点将落在一条位置确定的“线”上。同样，若有六条直线，所引直线段中的三条所作成的立体与另三条作成的立体的比为给定的比，则点也将落在某条位置确定的“线”上。但是当超过六条直线时，我们不能再说由四条直线段所作成的某物与其余直线段作成的某物是否构成一个比，因为不存在超过三维的图形。

这里，我请你顺便注意一下，迫使古代作者在几何中使用算术术语的种种考虑，未能使他们逾越鸿沟而看清这两门学科间的关系，因而在他们试图作解释时，引起了众多的含糊和令人费解的说法。

帕普斯这样写道：

对于这一点，过去解释过这些事情（一个图形的维数不能超过3）的人的意见是一致的。他们坚持认为，由这些直线段所作成的图形，无论如何都是无法理解的。然而，一般地使用这种类型的比来描述和论证却是允许的，叙述的方式如下：若从任一点引出若干直线段，与位置确定的一些直线相交成给定的角；若存在一个由它们组合而成的确定的比，这个比是指所引直线段中的一个与一个的比，第二个与某第二个的比，第三个与某第三个的比，等等。如果有七条直线，就会出现跟一条给定直线段的比的情形，如果有八条直线，即出现最后一条与另外最后某条直线段的比；点将落在位置确定的线上。类似地，无论是奇数还是偶数的情形，正如我已说过的，它们在位置上对应四条直线；所以说，他们没有提出任何方法使得可以得出一条线。 ⁽¹⁾

这个问题始于欧几里得，由阿波罗尼奥斯加以推进，但没有哪一位得以完全解决。问题是这样的：

有三条、四条或更多条位置给定的直线，首先要求找出一个点，从它可引出另外同样多条直线段，每一条与给定直线中的某条相交成给定的角，使得由所引直线段中的两条作成的矩形，与第三条直线段（若仅有三条的话）形成给定的比；或与另两条直线段（若有四条的话）所作成的矩形形成给定的比；或者，由三条直线段所作成的平行六面体与另两条跟任一给定直线段（若有五条的话）所作成的平行六面体形成给定的比，或与另三条直线段（若有六条的话）所作成的平行六面体；或者（若有七条的话）其中四条相乘所得的积与另三条的积形成给定的比，或（若有八条的话）其中四条的积与另外四条的积形成给定的比。于是，问题可以推广到有任意多条直线的情形。

因为总有无穷多个不同的点满足这些要求，所以需要发现和描绘出含有所有这些点的曲线。帕普斯说，当仅给定三或四条直线时，该曲线是三种圆锥截线中的一种；但是当问题涉及更多条直线时，他并未着手去确定、描述或解释所求的线的性质。他只是进而说，古代人了解它们之中的一种，他们曾说明它是有用的，似乎是最简单的，可是并不是最重要的。这一说法促使我来作一番尝试，看能否用我自己的方法达到他们曾达到过的境界。

解帕普斯问题

首先，我发现如果问题只考虑三、四或五条直线，那么为了找出所求的点，利用初等几何就够了，即只需要使用直尺和圆规，并应用我已解释过的那些原理；当然五条线皆平行的情形除外。对于这个例外，以及对于给定了六、七、八或九条直线的情形，总可以利用有关立体轨迹的几何来找出所求的点，这是指利用三种圆锥截线中的某一种；同样，此时也有例外，即九条直线皆平行的情形。对此例外及给定十、十一、十二或十三条直线的情形，依靠次数仅比圆锥截线高的曲线便可找出所求的点。当然，十三条线皆平行的情形必须除外，对于它以及十四、十五、十六和十七条直线的情形，必须利用次数比刚提到的曲线高一次的曲线；余者可依此无限类推。

其次，我发现当给定的直线只有三条或四条时，所求的点不仅会出现全体都落在一条圆锥截线上的情形，而且有时会落在一个圆的圆周上，甚或落在一条直线上。

当有五、六、七或八条直线时，所求的点落在次数仅比圆锥截线高一次的曲线上，我们能够想象这种满足问题条件的曲线；当然，所求的点也可能落在一条圆锥截线上、一个圆上或一条直线上。如果有九、十、十一或十二条直线，所求曲线又比前述曲线高一次，正是这种曲线可能符合要求。余者可依此无限类推。

最后，紧接在圆锥截线之后的最简单的曲线是由双曲线和直线以下面将描述的方式相交而生成的。

我相信，通过上述办法，我已完全实现了帕普斯告诉我们的、古代人所追求的目标。我将试图用几句话加以论证，耗费过多的笔墨已使我厌烦了。

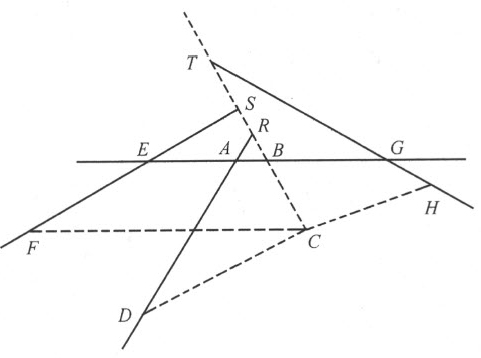
令AB ，AD ，EF ，GH ……是任意多条位置确定的直线，求点C ，使得由它引出的直线段CB ，CD ，CF ，CH ……与给定直线分别成给定的角CBA ，CDA ，CFE ，CHG ……并且，它们中的某几条的乘积等于其余几条的乘积，或至少使这两个乘积形成一给定的比，这后一个条件并不增加问题的难度。

我们应如何选择适当的项以得出该问题的方程

首先，我假设事情已经做完；但因直线太多会引起混乱，我可以先把事情简化，即考虑给定直线中的一条和所引直线段中的一条（例如AB 和BC ）作为主线，对其余各线我将参考它们去做。称直线AB 在A 和B 之间的线段为x ，称BC 为y 。倘若给定的直线都不跟主线平行，则将它们延长以与两条主线（如需要也应延长）相交。于是，从图上可见，给定的直线跟AB 交于点A 、E 、G ，跟BC 交于点R 、S 、T 。

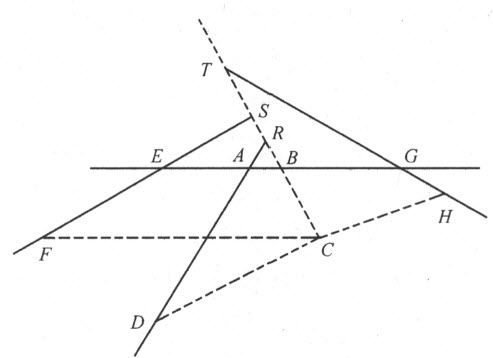
因三角形ARB 的所有角都是已知的，故边AB 和BR 的比也可知。若我们令AB ：BR ＝z ：b 因AB ＝x ，我们有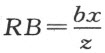 ；又因B 位于C 和R 之间，我们有 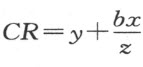。（当R 位于C 和B 之间时，CR 等于 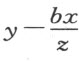；当C 位于B 和R 之间时，CR 等于 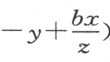。又，三角形DRC 的三个角是已知的，因此可以确定边CR 和CD 的比，记这个比为z ：c ，因 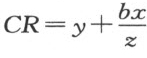，我们有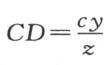 。那么，由于直线AB ，AD 和EF 的位置是确定的，故从A 到E 的距离已知。若我们称这段距离为k，那么EB ＝k＋x ；虽然当B 位于E 和A 之间时EB ＝k-x ，而当E 位于A 和B 之间时EB ＝－k＋x 。现在，三角形ESB 的各角已知，BE 和BS 的比也可知，我们称这个比为z ：d 。于是BS 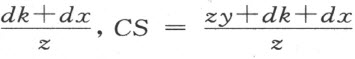＝ 。而当S 位于B 和C 之间时，我们有 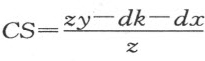，而当C 位于B 和S 之间时，我们有 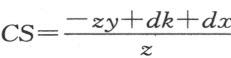。三角形FSC 的各角已知，因此，CS 对CF 的比也可知，记作z ：e 。于是， 。同样地，AG 或l 为已知，BG ＝l －x 。在三角形BGT 中，BG 对BT 的比，或者说z ：f 为已知。因此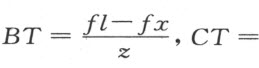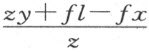， 。在三角形TCH 中，TC 对CH 的比，或者说z ：g 也可知，故 。

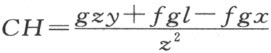于是，你们看到，无论给定多少条位置确定的直线，过点C 与这些直线相交成给定角的任何直线段的长度，总可以用三个项来表示。其一由某个已知量乘或除未知量y 所组成；另一项由另外某个已知量乘或除未知量x 所组成；第三项由已知量组成。我们必须注意例外，即，给定的直线跟AB 平行（此时含x 的项消失），或跟CB 平行（此时含y 的项消失）的情形。这种例外情形十分简单，无须进一步解释。在每一种可以想象到的组合中，这些项的符号或是＋或是－。

你还能看出，在由那些线段中的几条作出的乘积中，任一含x 或y 的项的次数不会比被求积的线段（由x 和y 表示）的数目大。所以，若两条线段相乘，没有一项的次数会高于2；若有三条线段，其次数不会高于3，依此类推，无一例外。

当给定的直线不超过五条时，我们如何知道相应的问题是平面问题

进而，为确定点C ，只需一个条件，即某些线段的积与其他某些线段的积，或者相等或者（也是相当简单的）它们的比为一给定的值。由于这个条件可以用含有两个未知量的一个方程表示，所以我们可以随意给x 或y 指定一个值，再由这个方程求出另一个的值。显然，当给定的直线不多于五条时，量x ——它不用来表示问题中原有的那些直线段——的次数绝不会高于2。

给y 指定一个值，我们得x 2 ＝±ax ±b 2 ，因此x 可以借助直尺和圆规，按照已经解释过的方法作出。那么，当我们接连取无穷多个不同的线段y 的值，我们将得到无穷多个线段x 的值，因此就有了无穷多个不同的点C ，所求曲线便可依此画出。

这个方法也适用于涉及六条或更多直线的问题，如果其中某些直线跟AB 或BC 中的任一条平行的话；此时，或者x 、或者y 的次数在方程中只是2，所以点C 可用直尺和圆规作出。

另一方面，若给定的直线都平行，即使问题仅涉及五条直线，点C 也不可能用这种办法求得。因为，由于量x 根本不在方程中出现，所以不再允许给y 指定已知的值，而必须去求出y 的值。又因为此时y 的项是三次的，其值只需求解一个三次方程的根便可得到，三次方程的根一般不用某种圆锥截线是不能求得的。

进而，若给定的直线不超过几条，它们不是彼此平行的，那么方程总能写成次数不高于4的形式。这样的方程也总能够利用圆锥截线，并按照我将要解释的方法去求解。

若直线的数目不超过13，则可利用次数不超过6的方程，它的求解可依靠只比圆锥截线的次数高一次的曲线，并按照将要解释的方法去做。

至此，我已完成了二必须论证的第一部分内容，但在进入第二部分之前，还必须一般性地阐述一下曲线的性质。

————————————————————

(1) 笛卡儿所引帕普斯的这段话含义不清，我们只能从上下文来理解它。——译者

笛卡儿在工作