第3章
物体受部分正比于速度部分正比于速度平方的阻力的运动
命题11 定理8
如果物体受到部分正比于其速度部分正比于其速度的平方的阻力,在均匀的介质中只受到惯性力的推动而运动;而且把时间按算术级数划分:则反比于速度的量,在增加某个给定量后,变为几何级数。
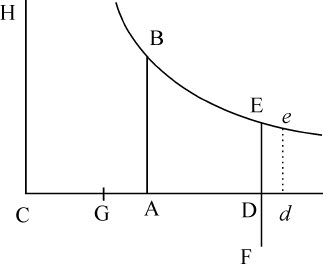
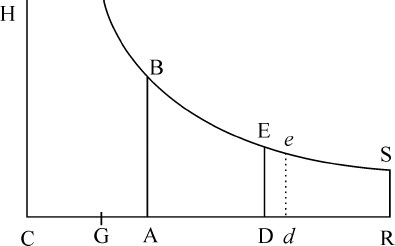
以C为中心,CADd 和CH为直角渐近线画双曲线BEe ,令AB,DE,de 平行于渐近线CH。在渐近线CD上令A,G为已知点;如果由双曲线面积ABED表示的时间均匀增加,则以GD为其倒数的长度DF与给定直线CG所共同组成的长度CD所表示的速度按几何级数增加。
因为,令小面积DEed 为时间的最小增量,则Dd 反比于DE,因而正比于CD。所以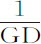 的减量
的减量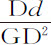 (由第二编引理2),也正比于
(由第二编引理2),也正比于 或
或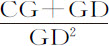 ,即正比于
,即正比于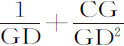 。所以,当时间ABED均匀地增加给定间隔EDde 时,
。所以,当时间ABED均匀地增加给定间隔EDde 时,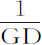 以与速度相同的比率减小。因为速度的减量正比于阻力,即(由题设),正比于两个量的和,其中之一正比于速度,另一个正比于速度的平方;而
以与速度相同的比率减小。因为速度的减量正比于阻力,即(由题设),正比于两个量的和,其中之一正比于速度,另一个正比于速度的平方;而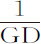 的减量正比于量
的减量正比于量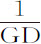 和
和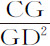 ,其中第一项是
,其中第一项是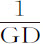 本身,后一项
本身,后一项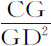 正比于
正比于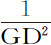 :所以
:所以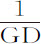 正比于速度,二者的减量是类似的。如果量GD反比于
正比于速度,二者的减量是类似的。如果量GD反比于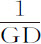 ,并增加给定量CG;则当时间ABED均匀增加时,其和CD按几何级数增加。
,并增加给定量CG;则当时间ABED均匀增加时,其和CD按几何级数增加。
证毕。
推论Ⅰ.如果点A和G已知,双曲线面积ABED表示时间,则速度由GD的倒数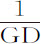 表示。
表示。
推论Ⅱ.取GA比GD等于任意时间ABED开始时速度的倒数比该时间结束时速度的倒数,则可以求出点G。求出该点后,则可由任意给定的其他时间求出速度。
命题12 定理9
在相同条件下,如果将掠过的距离分为算术级数,则速度在增加一个给定量后变为几何级数。
设在渐近线CD上已知点R,作垂线RS与双曲线相交于S,令掠过的距离以双曲线面积RSED表示;则速度正比于长度GD,该长度与给定线CG组成的长度CD,当距离RSED按算术级数增加时,按几何级数减小。
因为,空间增量EDde 为给定量,GD的减量短线Dd 反比于ED,因而正比于CD;即正比于同一个CD与给定长度CG的和。而在掠过给定空间间隔Dde E所需的正比于速度的时间中,速度的减量正比于阻力乘以时间,即正比于两个量的和,反比于速度,这两个量中之一正比于速度,另一个正比于速度的平方;因而正比于两个量的和,其中一个是给定的,另一个正比于速度。所以,速度以及直线GD二者的减量正比于给定量与一个减小量的乘积;而因为两个减量相似,两个减小的量,即速度与线段GD,也总是相似的。
证毕。
推论Ⅰ.如果以长度GD表示速度,则掠过的距离正比于双曲线面积DESR。
推论Ⅱ.如果任意设定点R,则通过取GR比GD等于开始时的速度比掠过距离RSED后的速度,则可以求出点G。求出点G后,即可由给定速度求出距离;反之亦然。
推论Ⅲ.由于由给定时间(通过命题11)可以求出速度,而(由本命题)距离又可以由给定速度推出,所以由给定时间可以求出距离;反之亦然。
命题13 定理10
设一物体受竖直向下的均匀重力作用沿一直线上升或下落;受到的阻力同样部分正比于其速度,部分正比于其平方:如果作几条平行于圆和双曲线直径且通过其共轭直径端点的直线,而且速度正比于平行线上始自一给定点的线段,则时间正比于由圆心向线段端所作直线截取的扇形面积;反之亦然。
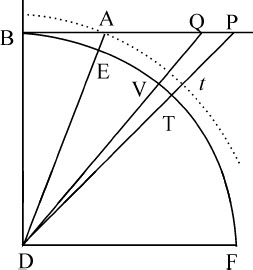
情形1.首先设物体上升,以D为圆心,以任意半径DB画圆的四分之一BETF,通过半径DB的端点B作不定直线BAP平行于半径DF。在该直线上设有已知点A,取线段AP正比于速度。由于阻力的一部分正比于速度,另一部分正比于速度的平方,令整个阻力正比于AP2 +2BA·AP。连接DA,DP,与圆相交于E和T,令DA2 表示重力,使得重力比P处的阻力等于DA2 比AP2 +2BA·AP;则整个上升时间正比于圆的扇形EDT。
作DVQ,分割出速度AP的变化率PQ,以及对应于给定时间变化率的扇形DET的变化率DTV;则速度的减量PQ正比于重力DA2 与阻力AP2 +2BA·AP的和;即(由欧几里得《几何原本》第二卷命题12),正比于DP2 。而正比于PQ的面积DPQ正比于DP2 ,面积DTV比面积DPQ等于DT2 比DP2 ,因而DTV正比于给定量DT2 。所以,面积EDT减去给定间隔DTV后,均匀地随着未来时间的比率减小,因而正比于整个上升时间。
情形2.如果物体的上升速度像前一情形那样以长度AP表示,则阻力正比于AP2 +2BA·AP;而如果重力小得不足以用DA2 表示,则可以这样取BD的长度,使AB2 -BD2 正比于重力,再令DF垂直且等于DB,通过顶点F画出双曲线FTVE,其共轭半径为DB和DF,曲线与DA相交于E,与DP,DQ相交于T和V;则整个上升时间正比于双曲线扇形TDE。

因为在已知时间间隔中产生的速度减量PQ正比于阻力AP2 +2BA·AP与重力AB2 -BD2 的和,即正比于BP2 -BD2 ,但面积DTV比面积DPQ等于DT2 比DP2 ;所以,如果作GT垂直于DF,则上述比等于GT2 或者GD2 -DF2 比BD2 ,也等于GD2 比BP2 ,由相减法知,等于DF2 比BP2 -BD2 。所以,由于面积DPQ正比于PQ,即,正比于BP2 -BD2 ,因而面积DTV正比于给定量DF2 。所以,面积EDT在每一个相等的时间间隔内,通过减去同样多的间隔DTV,将均匀减小,因而正比于时间。
证毕。
情形3.令AP为下落物体的速度,AP2 +2BA·AP为阻力,BD2 -AB2 为重力,角DBA为直角。如果以D为中心,B为顶点,作直角双曲线BETV与DA,DP和DQ的延长线相交于E,T,V;则该双曲线的扇形DET正比于整个下落时间。
因为速度的增量PQ,以及正比于它的面积DPQ,正比于重力减去阻力的剩余,即正比于
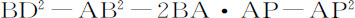
或BD2 -BP2 。而面积DTV比面积DPQ等于DT2 比DP2 ;所以等于GT2 或GD2 -BD2 比BP2 ;也等于GD2 -BD2 ,由相减法,等于BD2 比BD2 -BP2 。所以,由于面积DPQ正比于BD2 -BP2 ,面积DTV正比于给定量BD2 。所以面积EDT在若干相等的时间间隔内,加上同样多的间隔DTV后,将均匀增加,因而正比于下落时间。
证毕。

推论.如果以D为中心,以DA为半径,通过顶点A作一个弧At 与弧ET相似,其对角也是ADT,则速度AP比物体在时间EDT内在无阻力空间由于上升所失去或由于下落所获得的速度,等于三角形DAP的面积比扇形DAt 的面积;因而该速度可以由已知的时间求出。因为在无阻力的介质中速度正比于时间,所以也正比于这个扇形;在有阻力介质中,它正比于该三角形;而在这二种介质中,当它很小时,趋于相等,扇形与三角形也是如此。
附注
还可以证明这种情形,物体上升时,重力小得不足以用DA2 或AB2 +BD2 表示,但又大于以AB2 -DB2 来表示,因而只能用AB2 表示。不过我在此拟讨论其他问题。
命题14 定理11
在相同条件下,如果按几何级数取阻力与重力的合力,则物体上升或下落所掠过的距离,正比于表示时间的面积与另一个按算术级数增减的面积的差。
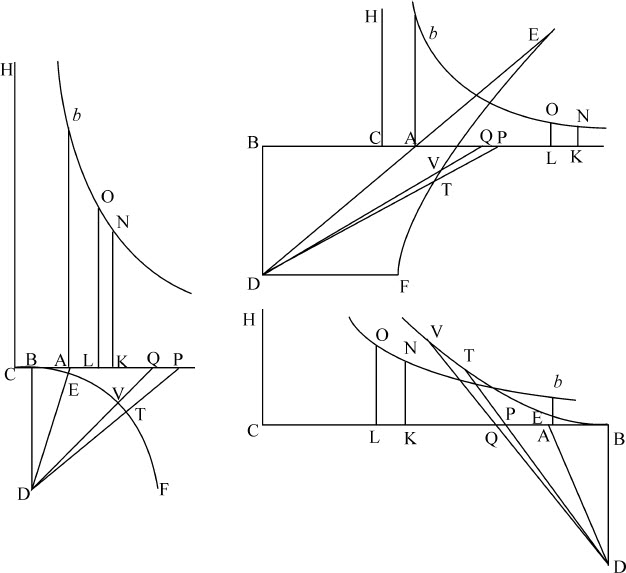
取AC(在三个图中)正比于重力,AK正比于阻力;如果物体上升,这二者取在点A的同侧,如果物体下落,则取在两侧。作垂线Ab ,使它比DB等于DB2 比4BA·CA;以CK,CH为直角渐近线作双曲线b N;再作KN垂直于CK,则面积Ab NK在力CK按几何级数取值时按算术级数增减,所以,物体到其最大高度的距离正比于面积Ab NK减去面积DET的差。
因为AK正比于阻力,即,正比于AP2 ·2BA·AP;设任意给定量Z,取AK等于 ;则(由本编引理2)AK的瞬KL等于
;则(由本编引理2)AK的瞬KL等于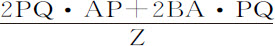 或者
或者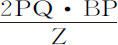 ,而面积Ab NK的瞬等于
,而面积Ab NK的瞬等于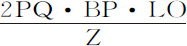 或者
或者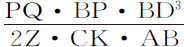 。
。
情形1.如果物体上升,重力正比于AB2 +BD2 ,BET是一个圆,则正比于重力的直线AC等于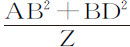 ,而DP2 或AP2 +2BA·AP+AB2 +BD2 等于AK·Z+AC·Z或CK·Z;所以面积DTV比面积DPQ等于DT2 或DB2 比CK·Z。
,而DP2 或AP2 +2BA·AP+AB2 +BD2 等于AK·Z+AC·Z或CK·Z;所以面积DTV比面积DPQ等于DT2 或DB2 比CK·Z。
情形2.如果物体上升,重力正比于AB2 -BD2 ,则直线AC等于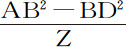 ,而DT2 比DP2 等于DF2 或DB2 比BP2 -BD2 或AP2 +2BA·AP+AB2 -BD2 ,即,比AK·Z+AC·Z或CK·Z。所以面积DTV比面积DPQ等于DB2 比CK·Z。
,而DT2 比DP2 等于DF2 或DB2 比BP2 -BD2 或AP2 +2BA·AP+AB2 -BD2 ,即,比AK·Z+AC·Z或CK·Z。所以面积DTV比面积DPQ等于DB2 比CK·Z。
情形3.由相同理由,如果物体下落,因而重力正比于BD2 -AB2 ,直线AC等于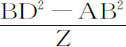 ;则面积DTV比面积DPQ等于DB2 比CK·Z,与前述相同。
;则面积DTV比面积DPQ等于DB2 比CK·Z,与前述相同。
所以,由于这些面积总是取这同一个比值,如果不用不变的面积DTV表示时间的瞬,而代之以任意确定的矩形BD·m ,则面积DPQ,即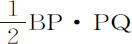 比BD·m 等于CK·Z比BD2 ,因而PQ·BD3 等于2BD·m ·CK·Z,而以前求出的面积Ab NK的瞬KLON变成
比BD·m 等于CK·Z比BD2 ,因而PQ·BD3 等于2BD·m ·CK·Z,而以前求出的面积Ab NK的瞬KLON变成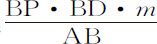 。由面积DET减去它的瞬DTV或BD·m ,则余下
。由面积DET减去它的瞬DTV或BD·m ,则余下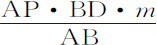 。所以,瞬的差,即面积的差的瞬,等于
。所以,瞬的差,即面积的差的瞬,等于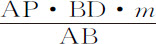 ;所以(因为
;所以(因为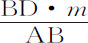 是给定量)正比于速度AP;即正比于物体在上升或下落中掠过距离的瞬。所以,二面积的差,与正比于瞬,且与之同时开始又同时消失的距离的增减,是成正比的。
是给定量)正比于速度AP;即正比于物体在上升或下落中掠过距离的瞬。所以,二面积的差,与正比于瞬,且与之同时开始又同时消失的距离的增减,是成正比的。
证毕。
推论.如果以M表示面积DET除以直线BD所得到的长度;再取一个长度V,使它比长度M等于线段DA比线段DE;则物体在有阻力介质中上升或下落的总距离,比在无阻力介质中相同时间内由静止开始下落的距离,等于上述面积差比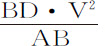 ;因而可以由给定时间求出。因为在无阻力介质中距离正比于时间的平方,或正比于V2 ;又因为BD与AB是已知的,也即正比于
;因而可以由给定时间求出。因为在无阻力介质中距离正比于时间的平方,或正比于V2 ;又因为BD与AB是已知的,也即正比于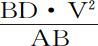 。该面积等于面积
。该面积等于面积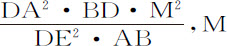 的瞬是m ;所以该面积的瞬是
的瞬是m ;所以该面积的瞬是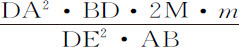 。而该瞬比上述二面积DET与Ab NK的差的瞬,即比
。而该瞬比上述二面积DET与Ab NK的差的瞬,即比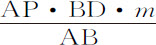 ,等于
,等于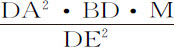 比
比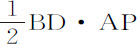 ,或等于
,或等于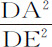 乘以DET比DAP;所以,当面积DET与DAP极小时,比值为1。所以,当所有这些面积都极小时,面积
乘以DET比DAP;所以,当面积DET与DAP极小时,比值为1。所以,当所有这些面积都极小时,面积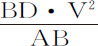 以及面积DET与Ab NK的差,有相等的瞬;所以二者相等,由于在下落开始与上升终了时的速度,因而在两种介质中所掠过的距离,是趋于相等的,所以二者相比等于面积
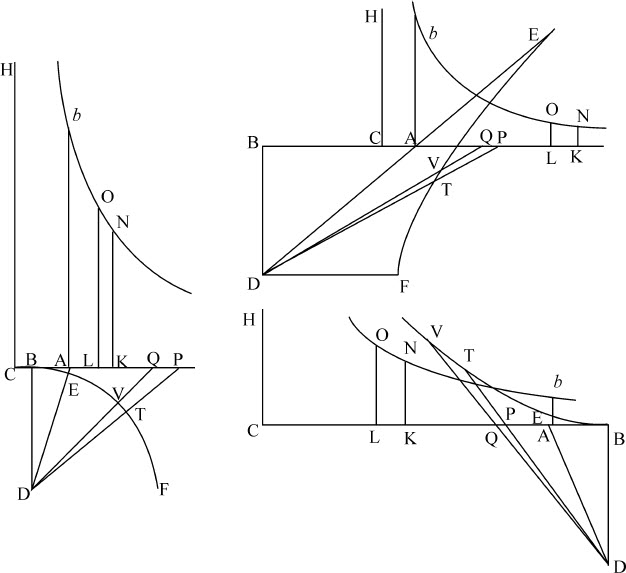
以及面积DET与Ab NK的差,有相等的瞬;所以二者相等,由于在下落开始与上升终了时的速度,因而在两种介质中所掠过的距离,是趋于相等的,所以二者相比等于面积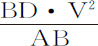 比面积DET与Ab NK的差;而且,由于在无阻力介质中距离连续正比于
比面积DET与Ab NK的差;而且,由于在无阻力介质中距离连续正比于 ,而在有阻力介质中,距离连续正比于面积DET与Ab NK的差;由此必然推导出在二种介质中,相同时间内所掠过的距离的比,等于面积
,而在有阻力介质中,距离连续正比于面积DET与Ab NK的差;由此必然推导出在二种介质中,相同时间内所掠过的距离的比,等于面积 比面积DET与Ab NK的差。
比面积DET与Ab NK的差。
证毕。
附注
球体在流体中受到的阻力部分来自粘滞性,部分来自摩擦,部分来自介质密度。其中来自流体密度的那部分阻力,我已讨论过,是正比于速度的平方的;另一部分来自流体的粘滞性,它是均匀的,或正比于时间的瞬;因此,我们现在可以进而讨论这种物体运动,它受到的阻力部分来自一个均匀的力,或正比于时间的瞬,部分正比于速度的平方。不过早在前面的命题8和9及其推论中,就已经为解决这种问题彻底扫清了道路。因为在这些命题中,可以将上升物体的重力所带来的均匀阻力,代之以介质的粘滞性所产生的均匀阻力,前提是物体只受惯性力的推动;而当物体沿直线上升时,可把均匀力叠加在重力上,当物体沿直径下落时,则从中减去。还可以进而讨论受到部分是均匀的,部分正比于速度,部分正比于同一速度的平方的阻力的物体的运动。而我在前述的命题13和14中为此铺平了道路,其中,只要用介质粘滞性产生的均匀阻力代替重力,或者像以前那样,代之以二者的合力。我们还有其他问题要讨论。
