补篇Ⅲ　平面面积理论的注记

在§18中关于剖分相等和拼补相等的定义以及其后的定理，这里将给出有关它们的一些更清楚和更深入的注释。又“多角形”这一名词此处常指“简单多角形”而言。

首先，要注意到将一个多角形P “剖分”成两个多角形P ₁ ，P ₂ 的精确含义必须与剖分成几个多角形的定义相吻合。

与§18剖分相等和拼补相等直接有关的推论一般是成立的，假如对“结合”与“移去”这两个概念是在有限制的情况下来理解。如果不打算在所说的方面加以限制，就必须引进多角形概念外的另一个普遍的概念——“合成多角形”。从这点出发就能运用定理：每个简单多角形能够剖分成三角形。

为了按照多角形边数用归纳法证明这个定理，只要证明边数n >3的多角形P 能够剖分成两个边数较少的多角形就够了。

设A ₁ ，…，A _n 为一多角形P 的相邻顶点。今考虑自A ₁ 向多角形内部所射出的半线。如果此半线首次再遇此多角形于B （这半线可以如此选取使得B 不在直线A ₁ A ₂ 或A ₁ A _n 上）。当B 是多角形P 的一个顶点，则线段A ₁ B 立即将P 剖分成边数较少的两个多角形，否则当B 位于多角形的边A _i A _i＋1 上，其中2≤i ≤n －1，且相等符号最多仅能出现一次。如果2<i <n －1，则线段A _i B 仍产生一个所要求类型的剖分。至少i ＝n －1及i ＝2的情形仍然用同样的方法来处理。如果i ＝2，则线段A ₁ B 剖分多角形P 成三角形A ₁ A ₂ B 及n 角形A ₁ BA ₃ …A _n ，今将后者用P ′表示，线段A ₁ A ₃ 将P ′剖分成一个三角形及一个（n －i ）角形，或者P′ 位于三角形A ₁ BA ₃ 的内部（在每种情况下均含有P′ 的内点），或至少一个顶点A _j ，其中j >3，位于三角形的边A ₁ A ₃ 上。在第一种情况下，即得出所要求的剖分。否则，从A ₁ 射出且过顶点A _j 中的一个所作的半线中取出一条，它与直线BA ₃ 的交点是与B 最靠近的，并且在此半线上取P′ 中与A ₁ 最靠近的一个顶点，设此顶点是A _k ，如果k ≠n ，则线段A ₁ A _k 将多角形P′ 剖分成边数较少的两个多角形。如果k ＝n ，线段BA _k 即产生这样一个剖分 ^（1） 。

将一多角形剖分成三角形产生不相交 的情况，即没有两个三角形有公共的一个内点。当必须时，由附加划分也可能更适合三角形剖分的条件 ；每对三角形或者不交，或仅有一公共顶点，或者有一边然而却没有其他公共点。

平面内具有 ^（2） 三角形剖分条件的有限个三角形的集合并不需要形成一个多角形剖分为三角形。用这样的三角形的集合可以三角剖分的图形具有一般的特性，设将它们叫做合成多角形 。

为了从三角形集合得到能三角剖分的合成多角形的图形，首先必须去掉两个三角形的公共边。于是其余的折线段可能形成一个简单多角形，其中两个或多个三角形的相邻边在同一直线上，它形成多角形的一个边。或者将折线段剖分（按照已给形成法）成几个简单多角形。这些多角形的边也叫合成多角形的边。平面内不属于多角形的点划分为合成多角形的“外点”和“内点”，它们可如下法形成：三角形的有限集合可以被一个多角形甚至于一个三角形所包围，在包围合成多角形的多角形外部的点叫合成多角形的外点。另外，内点和外点可以由下列事实来区分。穿过合成多角形的每一边（或）由外点进入内点或由内点到外点。因之人们可这样考虑外点是所有那些位于三角形集合外部的点，而内点则是位于这些三角形中一个的内部或在这些三角形的一条边上但不在合成多角形边上的那些点。

这样，每个不相交 三角形的有限集合决定一个合成多角形。由它利用一个适当划分可得到一个三角形的集合，它具有三角剖分的性质且结果所得的合成多角形与各种不同划分的选择无关。另言之，对于每两个划分，常可确定一个第三者，它是另两个划分中的某一个划分。通过划分从一个合成多角形的三角剖分所得的三角形集合仍产生同一合成多角形，这是因为在划分中三角形加入的边在较狭义的三角剖分下常出现两次。

从两个不相交的合成多角形P ，Q 能够得到一个新的合成多角形，它是利用P 及Q 的三角形剖分中的两个三角形集合里不相交的三角形的集合所形成。如此所得的合成多角形与P 及Q 的某种特殊的三角形剖分无关，这可从前面关于划分的注记得出，因此它由P 及Q 唯一确定，而称为P 与Q 的一个组合 ，或者说自P 通过Q 的添加 ，并且“P ＋Q ”来表示。

这种组合的方法可以推广到几个成对的不相交的合成多角形。并且这种组合具有结合及可换的性质，这是因为成对的不相交的三角形集合的并具有这些性质。

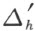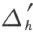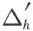今设P 及Q 为剖分成三角形的三角形集合Δ1 ，…，Δ _k 和 所给出的两个任意合成多角形。于是对每一个三角形Δ _i 能够确定一个剖分为三角形的划分 ，使得没有Δ _ij 是与 的一边相交，并且每个Δ _ij 或者完全位于 内或与它没有公共内点。这样，我们可得到P 的一个三角形的剖分，使得其中每个三角形或者全部是 中的某一个或者与这些三角形的任一个没有公共内点。第一类三角形产生合成多角形T ₁ 的一个三角形剖分，第二类则产生合成多角形T ₂ 的一个三角形剖分，且P ＝T ₁ ＋T ₂ 。如果在 中将T ₁ 的三角形剖分的三角形从 中分出，余下的图形能够剖分为三角形并能看做是一个合成多角形R _h 。于是两两不相交的合成多角形R ₁ ，…，R _ι 的组合产生一个合成多角形T ₃ 且Q ＝T ₁ ＋T ₃ 。这样合成多角形T ₁ ，T ₂ ，T ₃ 是两两不交的。它们的组合T ₁ ＋T ₂ ＋T ₃ 规定为P 与Q 的并 ，T ₁ 则叫做P 与Q 的交 。

对于这个分析较精确的论述必须用到下面的情况：如果三角形某一边上的一点或顶点在一个合成多角形的内部，则这三角形的一个内点也将位于这合成多角形的内部。因此得出：如果在两个三角剖分的合成多角形P 与Q 中，P 的三角剖分中的一个三角形如果与Q 的三角剖分中的一个三角形无公共内点，则P 与Q 是不相交的。

作为最后讨论的一个结果，要注意到：对任意两个合成多角形P ，Q 常存在一个并V 及一个交D 而具有下述特性：V 与D 是合成多角形，能够确定合成多角形P′ 及Q′ 而使P′ ，Q′ ，D 两两不交，且

P ＝D ＋P′ ，Q ＝D ＋Q′ ，V ＝D ＋P′ ＋Q′

并且也有

V ＝P ＋Q′ ，V ＝Q ＋P′

现在给出关于合成多角形的剖分相等和拼补相等的一般定义。

定义 　两个合成多角形P ，Q 称为剖分相等，假如能够确定P 的一个三角形剖分Δ ₁ ，…，Δ _n 和Q 的一个三角形剖分 而使Δ _i 及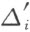 ：是合同三角形。两个合成多角形P ，Q 称为拼补相等如果能够对P 添加一个合成多角形P′ ，对Q 添加一个合成多角形Q′ 而使P′ 与Q′ 剖分相等，且P ＋P′ 与Q ＋Q′ 剖分相等。

为了说明这些定义的正确，必须证明它们与以前所提到的多角形的剖分相等和拼补相等的定义（§18）是一致的。

就剖分相等来讲，立即看出关于多角形的新定义与以前所述者有相同的意义。

至于剖分相等的传递性 ，即两个合成多角形分别与第三者剖分相等，则这两个也必剖分相等的定理，它可用与以前多角形十分类似的方法来证明。在没有更多的注释下我们也可得到剖分相等的可加性的定理 。如果一个合成多角形P 由两个合成多角形P ₁ 及P ₂ 组成，类似地合成多角形Q 由两个合成多角形Q ₁ 及Q ₂ 组成。且如果P ₁ 与Q ₁ ，P ₂ 与Q ₂ 分别剖分相等，则P 与Q 剖分相等。

为了证明合成多角形拼补相等的定义与以前关于多角形P ，Q 的定义相同，必须建立下面的引理 ：如果P 是一个多角形，K 是一个合成多角形，于是在P 上可添加与K 剖分相等的多角形H ，因此P ＋H 是一多角形，简言之P 可由添加与K 剖分相等的多角形H 而扩展成一个多角形。

为了证明，首先考虑下面的情况，即多角形P 的一边a 位于一直线g 上，并使多角形的所有顶点，除掉a 的端点外，均位于g 的同侧，合成多角形K被剖分成三角形Δ ₁ ，…，Δ _k 。现在每个三角形与一个长方形剖分相等。这可从下面的方法看出：设ABC 是一个三角形，它的A 角和B 角都是锐角。又设CA 与CB 中点的联线是p ，且F 与G 是由A 与B 分别到p 所作垂线的垂足，于是长方形ABGF 与三角形ABC 剖分相等，这可由C 到FG 作垂线看出（参看本书为证明定理39的图）。

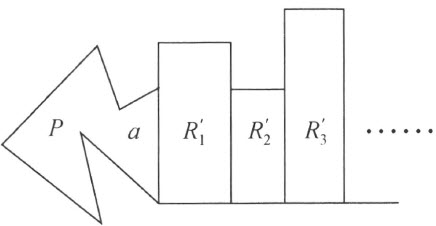
补图　4

这样一个长方形R _i 与每个三角形Δ _i （i ＝1，…，k ）剖分相等，于是将长方形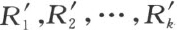 连续附加在多角形P 上而使 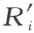与R _i 合同这是可能的。 连同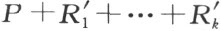 ，同为多角形。于是多角形 与合成多角形K 剖分相等，在这种情况下，断言得以证明。

对普遍情况可依下法化成上面的特殊情况。经过多角形P 的一个顶点作一直线q 不含有p 的其他顶点且不平行于连接p 的两顶点的直线。过p 的所有顶点作q 的平行线q ₁ ，…q _i 且与直线c 相交。在这些交点中有两个是最外面的。设q _i 是直线q ₁ ，…，q _r 中过最外面的交点的一条。于是仅有P 的一个顶点E _i 在q _i 上，并且P 的所有其他顶点均位于q _i 的同侧。今对多角形添加以E _i 为顶点的一个三角形Δ ，而使P ＋Δ 仍是一个多角形，且Δ 的一边位于直线q _i 上，而Δ 的该边的对顶位于P 的终止在E _i 的一条边上，这将是可能的，同时还可选择Δ 如此小使得K 的剖分具有形式K ＝Δ ′＋K ′，其中Δ 与Δ ′是合同的关于上面特殊情况的条件，现对P ＋Δ 及K′ 都满足。按照已经证明的情况，可对P ＋Δ 确定一个多角形H ，它与K′ 剖分相等而使P ＋Δ ＋H 是一多角形。故由上面的论证Δ ＋H 也是一个多角形。再者Δ ＋H 与Δ ＋K ′剖分相等，因之与K 也是这样，故论断即得以证明。

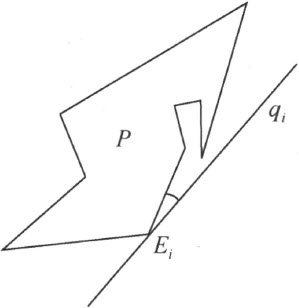
补图　5

设P 与Q 是按照合成多角形拼补相等定义下的两个拼补相等的多角形。于是存在剖分相等的合成多角形P ′，Q ′而使P ＋P ′，Q ＋Q ′仍是剖分相等的合成多角形。按照这个引理，能够确定一个多角形P″ ，它与P′ 剖分相等，同时确定一多角形Q″ ，它与Q′ 剖分相等，因而P ＋P″ 及Q ＋Q″ 是多角形。这样P ＋P′ 及Q ＋Q′ 将分别与P ＋P″ 及Q ＋Q″ 剖分相等。由剖分相等的传递性从这些剖分相等可以推出：P″ 与Q″ 剖分相等且P ＋P″ 与Q ＋Q″ 也剖分相等。于是按照§18所定义拼补相等的条件将适合。反之。按照这个定义两个多角形拼补相等而在两个合成多角形拼补相等定义的意义下，也拼补相等。这将是很明显的，不需要更多注释。因此将两个合成多角形拼补相等的定义应用到多角形上与前面所提到的定义有相同的意义。

同时由这个证明可得下面的定理：如果P ，Q 是两个拼补相等的多角形，则能够就P 和Q 分别添加一个多角形P′ 和Q′ ，而P′ 与Q′ 剖分相等因而P ＋P′ 及Q ＋Q′ 是剖分相等的多角形 ^（3） 。

将拼补相等的概念推广到合成多角形上现在将可以证明两个多角形均与第三个拼补相等，则它们彼此拼补相等。

如果两个多角形P 和Q 均与多角形R 拼补相等，则存在合成多角形P′ ，Q′ ，S ，T 具有以下性质P′ 与S 剖分相等，Q′ 与T 剖分相等，并且P ＋P′ 与R ＋S 连同Q ＋Q′ 与R ＋T 均是剖分相等的合成多角形。这同时说明P 与P′ 连同Q 与Q′ 都是可交的。并且R 与S 连同R 与T 也是这样，故R 与S 及T 并也是不交的。这个并如同前面所指出的一方面可以表作S ＋T′ ，而另一方面又可表作T ＋S′ ，其中T′ 与S′ 都是合成多角形。

现在可以确定合成多角形P ＋P′ ，它能被一个三角形所包围，与T′ 剖分相等的一个合成多角形P″ 完全在P ＋P′ 的外部，并且就Q ＋Q′ 确定一个与S′ 剖分相等的合成多角形Q″ ，完全在Q ＋Q′ 的外部。利用剖分相等的可加性可知P′ ＋P″ 与S ＋T′ ，Q′ ＋Q″ 与T ＋S′ ，P ＋P′ ＋P″ 与R ＋S ＋T′ ，Q ＋Q′ ＋Q″ 与R ＋T ＋S′ 之间都剖分相等。而且S ＋T′ ＝T ＋S′ 。故得P′ ＋P″ 与Q′ ＋Q″ 剖分相等且P ＋P′ ＋P″ 与Q ＋Q′ ＋Q″ 剖分相等，因而P 与Q 拼补相等。

在证明中引理是不需要的。更重要的是下述事实：对每个合成多角形，能够确定与它剖分相等的另一个合成多角形，完全在已知多角形的外部，并且每个合成多角形能用一个多角形（三角形）所包围。除去这些，也用到合成多角形的剖分相等的传递性和可加性。

利用这些结果也能够推出拼补相等的可加性。设P ，Q ，S ，T 是合成多角形，而且P ，Q 以及S ，T 都是不交的。如果P 与S 以及Q 与T 都拼补相等，进一步可以证明P ＋Q 与S ＋T 也拼补相等。

由假设存在着合成多角形P′ ，Q′ ，S′ ，T′ 而使P 与P′ ，Q 与Q′ ，S 与S′ 以及T 与T′ 之间均可交，并且P′ 与S′ ，Q′ 与T′ 连同P ＋P′ 与S ＋S′ 以及Q ＋Q′ 与T ＋T′ 均剖分相等。

现在能够确定一个合成多角形P ，它与位于合成多角形P ＋Q 外部的P′ 剖分相等，同时还确定一个合成多角形Q ，它与位于P ＋Q ＋P 外部的Q′ 剖分相等。同时也能够确定合成多角形S 及T ，而使S′ 与S ，T′ 与T 剖分相等，且使S 位于S ＋T 外部，T 位于S ＋T ＋S 外部。

利用剖分相等的假设以及剖分相等的传递性和可加性得出P 与S ，Q 与T ，P ＋P 与S ＋S ，Q ＋Q 与T ＋T 均剖分相等。因之P ＋Q 与S ＋T 以及P ＋Q ＋P ＋Q 与S ＋T ＋S ＋T 剖分相等。故得P ＋Q 与S ＋T 拼补相等。

————————————————————

（1） 将一个简单多角形能剖分成三角形的一个不同论证可从补篇Ⅰ₁ 所引范·德瓦尔登的文章中得到，参看§5，定理24。

（2） 在拓扑学里，这样的集合叫做有限平面三角复形。

（3） 在前几版里，关于P 和Q 的这个条件是取作规定拼补相等的性质。