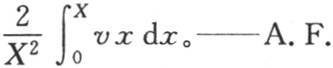第六章 实圆柱中的热运动
·Chapter VI Of the Movement of Heat in A Solid Cylinder·
傅立叶的物理思想是深刻的。他对力学理论的完美性非常赞赏,但他明确表示:“力学理论不能应用于热效应”。这比持相反观点的泊松要有远见得多。他指出,“热的理论在今后将构成普通物理学的最重要的分支之一”,这同样是有远见的。他对热理论的广阔运用前景也有非常清醒的认识。

法国科学院Roosevelt广场
306 无穷长实圆柱体中的热运动由方程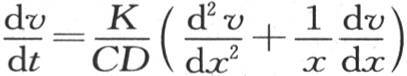 和
和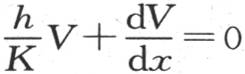 来表示,我们在第118、119和120目中叙述过这两个方程。为了求这两个方程的积分,我们对v给定由方程v=ue-mt 所表示的简单的特殊值;m是任一数,u是x的一个函数。我们用k表示进入第一个方程的系数
来表示,我们在第118、119和120目中叙述过这两个方程。为了求这两个方程的积分,我们对v给定由方程v=ue-mt 所表示的简单的特殊值;m是任一数,u是x的一个函数。我们用k表示进入第一个方程的系数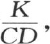 用h表示进入第二个方程的系数
用h表示进入第二个方程的系数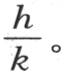 代入对v所规定的值,我们得到下述条件
代入对v所规定的值,我们得到下述条件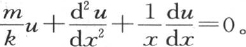 接下来我们为u选择一个满足该微分方程的x的函数。不难看到,这个函数可以用下述级数
接下来我们为u选择一个满足该微分方程的x的函数。不难看到,这个函数可以用下述级数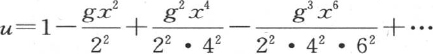 来表示,g表示常数
来表示,g表示常数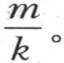 我们在后面将更详细地考察导出这个级数的微分方程;这里,我们把函数u看做是已知的,把ue-gkt 作为v的特殊值。
我们在后面将更详细地考察导出这个级数的微分方程;这里,我们把函数u看做是已知的,把ue-gkt 作为v的特殊值。
圆柱体凸面的状态服从于由定义方程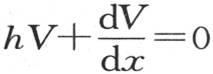 所表示的条件,当半径x取其总值X时,它肯定被满足。因此我们得到定义方程
所表示的条件,当半径x取其总值X时,它肯定被满足。因此我们得到定义方程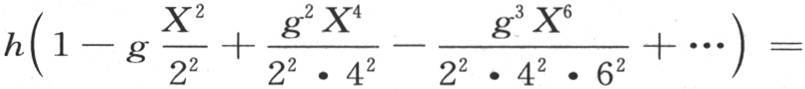
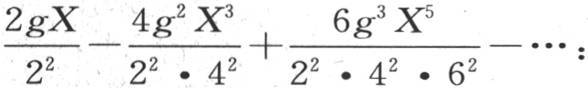 因此,进入特殊值ue-gkt 的数g不是任意的。这个数必然满足前面的方程,该方程含g和X。
因此,进入特殊值ue-gkt 的数g不是任意的。这个数必然满足前面的方程,该方程含g和X。
我们要证明g的这个方程有无数个根,h和X在该方程中为已知数,并要证明所有这些根均为实根。由此得到,我们可以赋予变量v无数形如ue-gkt 的特殊值,这些值的差别只在于指数g的不同。用来解所提出的这个方程的积分在它的所有范围内都由下述方程v=a1 u1 e-g1 kt +a2 u2 e-g2 kt +a3 u3 e-g3 kt +…所给出,g1 ,g2 ,g3 ,…表示满足定义方程的所有g值;u1 ,u2 ,u3 ,…表示对应于这些不同根的u值;a1 ,a2 ,a3 ,…是只能由固体的初始状态所确定的任意系数。
307 现在我们必须考察给出g值的定义方程的性质,并证明这个方程的所有根都是实根,这是需要仔细考察的一项研究。
在表示当x=X时u所得到的值的级数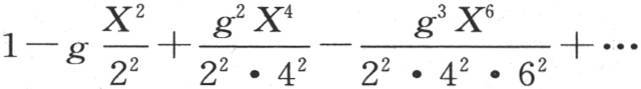 中,我们用量θ取代
中,我们用量θ取代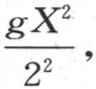 用f(θ)或者是y表示θ的这个函数,我们有
用f(θ)或者是y表示θ的这个函数,我们有
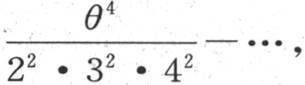 定义方程变成
定义方程变成 或者是
或者是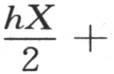
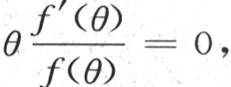 f′(θ)表示函数
f′(θ)表示函数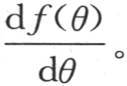
θ的每一个值都由方程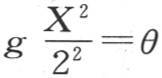 来提供一个g的值,因此我们得到量g1 ,g2 ,g3 ,…,这些数目无穷的量进入所需要的解。
来提供一个g的值,因此我们得到量g1 ,g2 ,g3 ,…,这些数目无穷的量进入所需要的解。
这样,问题就是要证明方程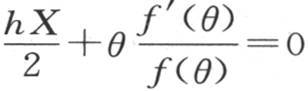 的所有根都是实根。我们事实上将证明方程f(θ)=0的所有根都是实根,因此方程f′(θ)=0的根亦如此,并由此得到方程
的所有根都是实根。我们事实上将证明方程f(θ)=0的所有根都是实根,因此方程f′(θ)=0的根亦如此,并由此得到方程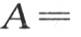
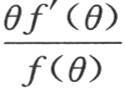 的所有根也是实根,A表示已知数
的所有根也是实根,A表示已知数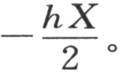
308 方程 只要微分两次,就给出下述关系
只要微分两次,就给出下述关系
我们记这个方程和所有那些可通过对它微分所能得到的方程如下:
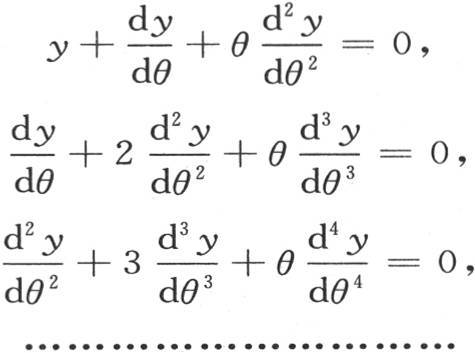
一般地,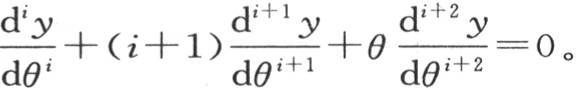 现在,如果我们把代数方程X=0和所有那些通过对它微分所能得到的方程按下述顺序写出,
现在,如果我们把代数方程X=0和所有那些通过对它微分所能得到的方程按下述顺序写出,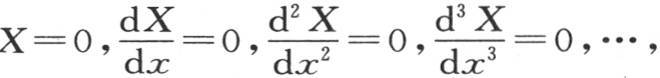 如果我们假定,任一个这样的方程的每一个实根只要被代进它前面和它后面的方程中,它都给出两个反号结果;那么可以肯定,所提出的方程X=0的所有根都是实根,因此,所有从属方程
如果我们假定,任一个这样的方程的每一个实根只要被代进它前面和它后面的方程中,它都给出两个反号结果;那么可以肯定,所提出的方程X=0的所有根都是实根,因此,所有从属方程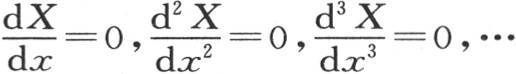 亦如此。
亦如此。
这些命题建立在代数方程的理论之上,并早已被证明。现在只要证明方程y=0,
 满足前面的条件就够了。这可以通过一般方程
满足前面的条件就够了。这可以通过一般方程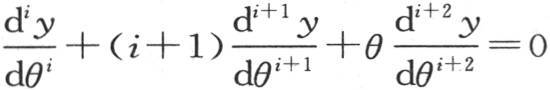 而得到:因为,如果我们对θ给定一个使流数
而得到:因为,如果我们对θ给定一个使流数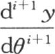 为0的正值,那么其他两项
为0的正值,那么其他两项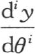 和
和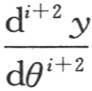 就得到反号值。关于θ的负值,由函数f(θ)的性质显然可知,代入θ的负值不可能把那个函数或者是对那个函数微分所得到的其他任一函数变为0:因为任一负值的代换都对所有项给出相同的符号。因此我们确信方程y=0的所有根都是正实根。
就得到反号值。关于θ的负值,由函数f(θ)的性质显然可知,代入θ的负值不可能把那个函数或者是对那个函数微分所得到的其他任一函数变为0:因为任一负值的代换都对所有项给出相同的符号。因此我们确信方程y=0的所有根都是正实根。
309 由此得到,方程f′(θ)=0或者是y′=0的所有根也是实根;根据代数学原理,这是已知的结论。现在让我们考察当我们对θ给定从θ=0连续增到θ=∞的值时,项θ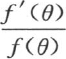 或
或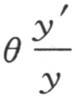 所得到的逐个值是怎样的。如果θ的一个值使y′为0,那么量
所得到的逐个值是怎样的。如果θ的一个值使y′为0,那么量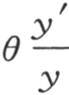 也变成0;当θ使y为0时,它则变得无穷大。现在由方程理论得到,在所说的情况下,y′=0的每个根都处在y=0的两个相邻的根之间,反之亦然。因此,若用θ1 和θ3 表示方程y′=0的两个相邻的根,用θ2 表示方程y=0在θ1 和θ3 之间的那个根,则包含在θ1 和θ2 之间的每个θ值对y所给出的符号,都与函数y在θ有一个包含在θ2 和θ3 之间的值时所得到的那个符号不同。因此,当θ=θ1 时,量
也变成0;当θ使y为0时,它则变得无穷大。现在由方程理论得到,在所说的情况下,y′=0的每个根都处在y=0的两个相邻的根之间,反之亦然。因此,若用θ1 和θ3 表示方程y′=0的两个相邻的根,用θ2 表示方程y=0在θ1 和θ3 之间的那个根,则包含在θ1 和θ2 之间的每个θ值对y所给出的符号,都与函数y在θ有一个包含在θ2 和θ3 之间的值时所得到的那个符号不同。因此,当θ=θ1 时,量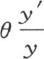 为0;当θ=θ2 时,它是无穷大,当θ=θ3 时,它为0。因此量
为0;当θ=θ2 时,它是无穷大,当θ=θ3 时,它为0。因此量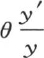 在从θ到θ2 的区间内必然取从θ到无穷大的所有可能的值。并且在从θ2 到θ3 的区间内也一定取从无穷大到0的所有可能的反号值。这样,方程
在从θ到θ2 的区间内必然取从θ到无穷大的所有可能的值。并且在从θ2 到θ3 的区间内也一定取从无穷大到0的所有可能的反号值。这样,方程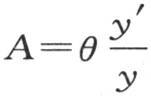 必然在θ1 和θ3 之间有一个实根,并且,由于方程y′=0的根是数目无穷的实根,由此得到,方程
必然在θ1 和θ3 之间有一个实根,并且,由于方程y′=0的根是数目无穷的实根,由此得到,方程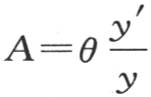 有同样的性质。如此,我们完成了定义方程
有同样的性质。如此,我们完成了定义方程 的所有根都是正实根的证明,方程中的未知数是g。我们现在继而开始对函数u和它所满足的微分方程进行研究。
的所有根都是正实根的证明,方程中的未知数是g。我们现在继而开始对函数u和它所满足的微分方程进行研究。
310 由方程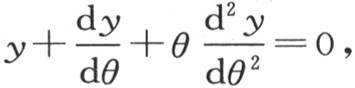 >我们得到一般方程
>我们得到一般方程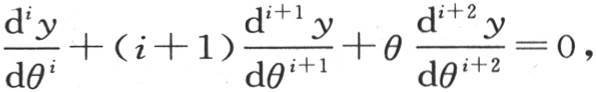 如果我们假定θ=0,则我们有方程
如果我们假定θ=0,则我们有方程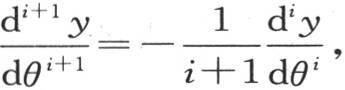 它用来确定函数f(θ)的展开式的各个项的系数,因为这些系数依赖于这些微分系数在它们之中的变量变为0时所得到的值。假定第一项已知并且等于1,则我们有级数
它用来确定函数f(θ)的展开式的各个项的系数,因为这些系数依赖于这些微分系数在它们之中的变量变为0时所得到的值。假定第一项已知并且等于1,则我们有级数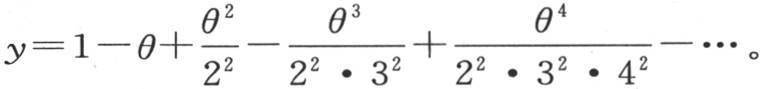 如果我们现在所提出的方程
如果我们现在所提出的方程 中使
中使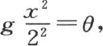 并寻找u和θ的新方程,那么当我们把u看做是θ的函数时,我们有
并寻找u和θ的新方程,那么当我们把u看做是θ的函数时,我们有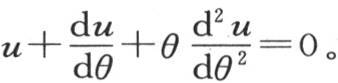 因此我们得到
因此我们得到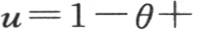
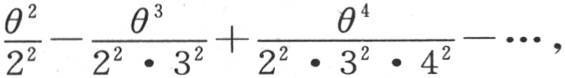 或者是
或者是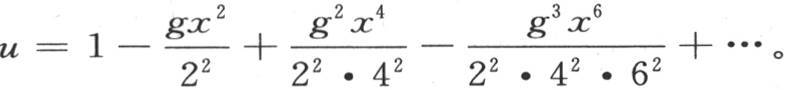
不难表示这个级数的和。为了得到这个结果,以多重弧的余弦展开函数cos(αsinx)如下。由已知的一些变换,我们有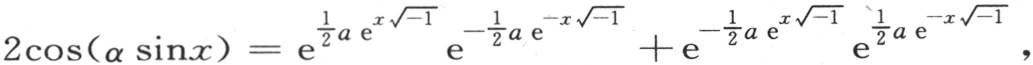 用ω表示
用ω表示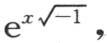 则
则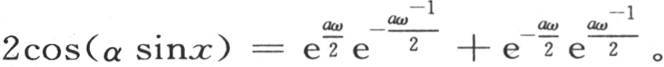 根据ω的幂展开右边,我们得到在2cos(αsinx)的展开式中不含ω的项是
根据ω的幂展开右边,我们得到在2cos(αsinx)的展开式中不含ω的项是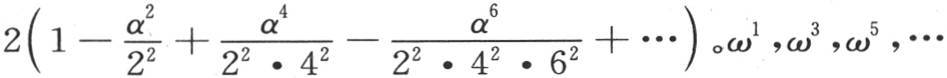 的系数是0,含ω-1 ,ω-3 ,ω-5 ,…的项的系数亦如此;ω-2 的系数和ω2 的系数相同;ω4 的系数是
的系数是0,含ω-1 ,ω-3 ,ω-5 ,…的项的系数亦如此;ω-2 的系数和ω2 的系数相同;ω4 的系数是 的系数与ω4 的系数相同。不难表示这些系数前后相继的规律;我们不陈述它,而用2cos2x代替(ω2 +ω-2 ),或者是用2cos4x代替(ω4 +ω-4 ),…。因此量2cos(αsinx)不难以形如A+B cos2x+C cos4x+D cos6x+…的级数展开,第一个系数A等于
的系数与ω4 的系数相同。不难表示这些系数前后相继的规律;我们不陈述它,而用2cos2x代替(ω2 +ω-2 ),或者是用2cos4x代替(ω4 +ω-4 ),…。因此量2cos(αsinx)不难以形如A+B cos2x+C cos4x+D cos6x+…的级数展开,第一个系数A等于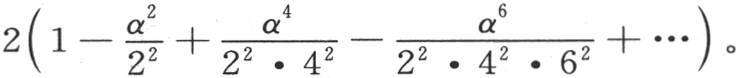 如果我们现在比较我们在前面所给出的方程
如果我们现在比较我们在前面所给出的方程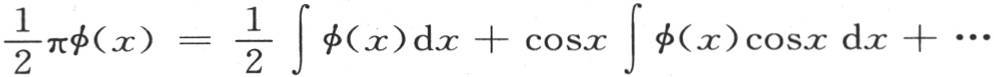 和方程2cos(αsinx)=A+B cos2x+C cos4x+…,那么我们会得到由定积分所表示的系数A,B,C的值。这里只需求出第一个系数A的值就够了。于是我们有
和方程2cos(αsinx)=A+B cos2x+C cos4x+…,那么我们会得到由定积分所表示的系数A,B,C的值。这里只需求出第一个系数A的值就够了。于是我们有 积分应当从x=0取到x=π。因此,级数
积分应当从x=0取到x=π。因此,级数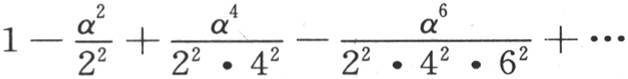 的值是定积分
的值是定积分 的值。通过两个方程的比较,我们同样可以得到逐个系数B,C,…的值;我们指明这些结果是因为它们在依赖于同一理论的其他研究中是有用的。由此得到,满足方程
的值。通过两个方程的比较,我们同样可以得到逐个系数B,C,…的值;我们指明这些结果是因为它们在依赖于同一理论的其他研究中是有用的。由此得到,满足方程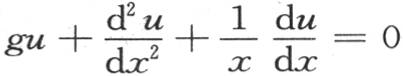 的u的特殊值是
的u的特殊值是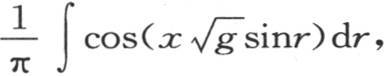 积分从r=0取到r=π。用q表示u的这个值,并使u=qS,则我们得到
积分从r=0取到r=π。用q表示u的这个值,并使u=qS,则我们得到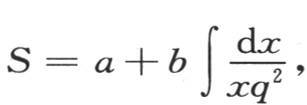 并且,作为方程
并且,作为方程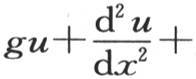
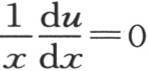 的完全积分,我们有
的完全积分,我们有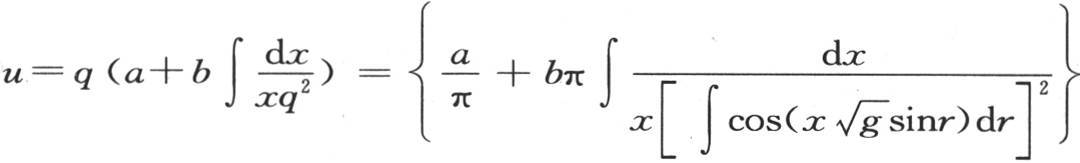
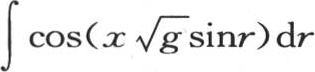 。 【1】 a和b是任意常数。如果我们假定b=0,那么和前面一样,我们有
。 【1】 a和b是任意常数。如果我们假定b=0,那么和前面一样,我们有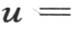
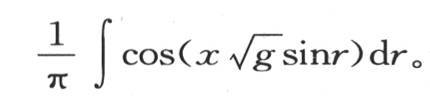 对于这个表达式,我们增加下面的注记。
对于这个表达式,我们增加下面的注记。
311 方程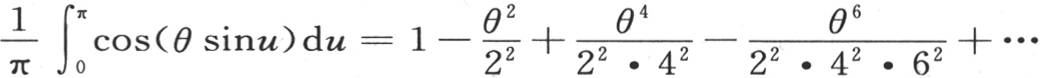 本身是可以检验的。事实上,我们有
本身是可以检验的。事实上,我们有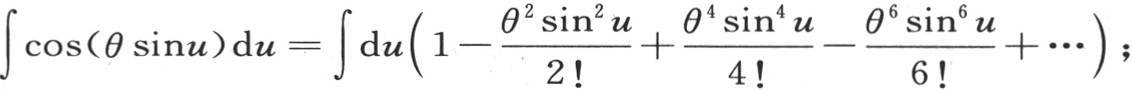 若从u=0到u=π取积分,用S2 ,S4 ,S6 ,…表示定积分∫sin2 udu,∫sin4 udu,∫sin6 udu,…,则我们们有
若从u=0到u=π取积分,用S2 ,S4 ,S6 ,…表示定积分∫sin2 udu,∫sin4 udu,∫sin6 udu,…,则我们们有 剩下的只是确定S2 ,S4 ,S6 ,…。由于项sinn u中的n是偶数,所以它可以展开成sinn u=An +Bn cos2u+Cn cos4u+…,乘以du,并在u=0和u=π的界限内积分,我们直接有
剩下的只是确定S2 ,S4 ,S6 ,…。由于项sinn u中的n是偶数,所以它可以展开成sinn u=An +Bn cos2u+Cn cos4u+…,乘以du,并在u=0和u=π的界限内积分,我们直接有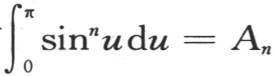 π,其他项变为0。根据正弦整数幂展开式的已知公式,我们有
π,其他项变为0。根据正弦整数幂展开式的已知公式,我们有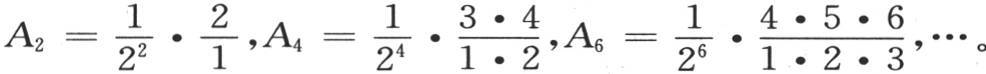 把这些值代入S2 ,S4 ,S6 ,…中,我们得到
把这些值代入S2 ,S4 ,S6 ,…中,我们得到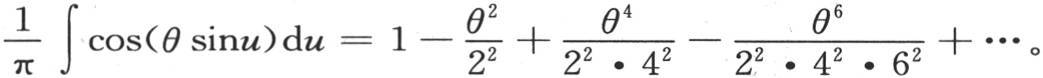
不用cos(t sinu),而代之以取t sinu的任一函数φ,我们可以使这个结果更一般化。
假定我们有一个函数φ(z),因而它可以展开成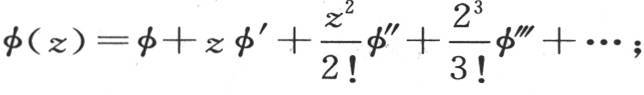 则我们有
则我们有
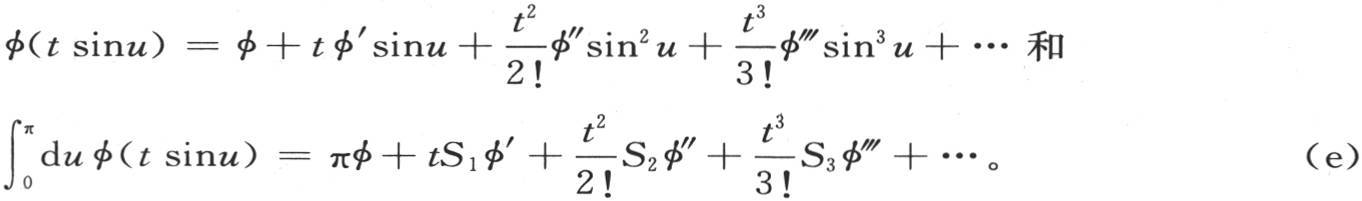
现在容易看到,S1 ,S3 ,S5 ,…为0。至于S2 ,S4 ,S6 ,…,它们的值是我们在前面用πA2 ,πA4 ,πA6 ,…所表示的量。由此,把这些值代入方程(e)中,无论函数φ怎样,我们都一般有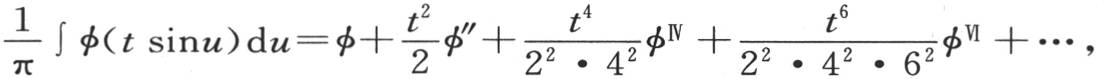 在所说的情况下,函数φ(z)表示cosz,我们有φ=1,φ″=-1,φIV =-1,φVI =-1,等等。
在所说的情况下,函数φ(z)表示cosz,我们有φ=1,φ″=-1,φIV =-1,φVI =-1,等等。
312 为了完全确定函数f(θ)和给出g值的方程的性质,有必要考虑其方程是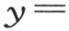
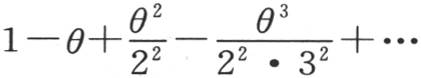 的曲线的形式,该曲线与横轴一起组成交替为正和负的面积,这些面积相互抵消;我们还可以通过定积分使前面这些关于级数值的表达式的注记更一般化。当变量x的函数依x的幂而展开时,如果用cosx,cos2x,cos3x,…代替幂x,x2 ,x3 ,…,那么不难推出表示同一级数的函数。运用这种简化和第235目第二段所使用过的过程,我们得到与已知级数等价的一些定积分;但是为了不至于离我们的主要目的太远,我们不打算讨论这一研究。
的曲线的形式,该曲线与横轴一起组成交替为正和负的面积,这些面积相互抵消;我们还可以通过定积分使前面这些关于级数值的表达式的注记更一般化。当变量x的函数依x的幂而展开时,如果用cosx,cos2x,cos3x,…代替幂x,x2 ,x3 ,…,那么不难推出表示同一级数的函数。运用这种简化和第235目第二段所使用过的过程,我们得到与已知级数等价的一些定积分;但是为了不至于离我们的主要目的太远,我们不打算讨论这一研究。
指明能使我们用定积分来表示级数的值的方法就够了。
我们只补充带有连分式的量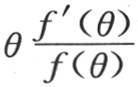 的展开式。
的展开式。
313 待定的y或者是f(θ)满足方程 因此,用y′,y″,
因此,用y′,y″, ,…表示函数
,…表示函数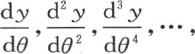 则我们有
则我们有
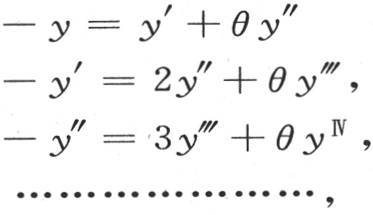
或者是
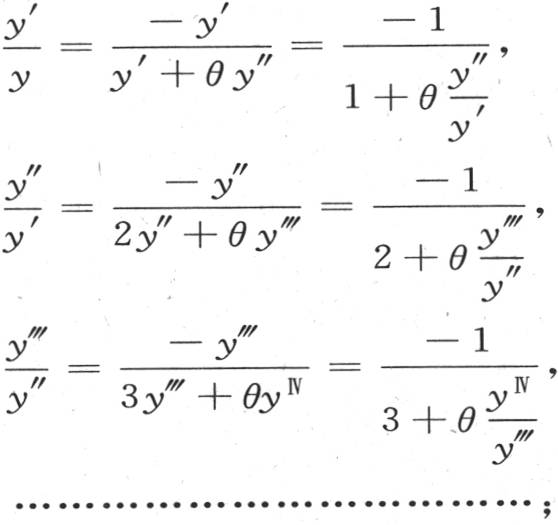
因此我们得到
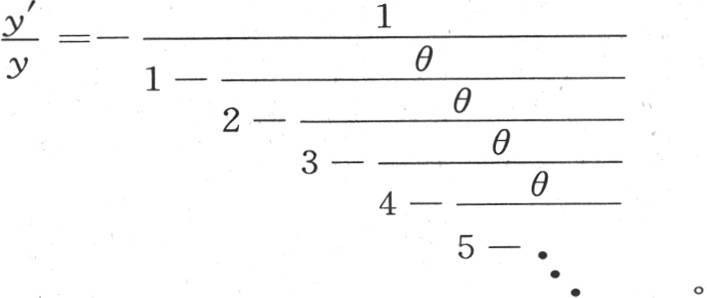
所以,进入定义方程的函数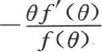 在表示成一个无穷连分式时,就是
在表示成一个无穷连分式时,就是
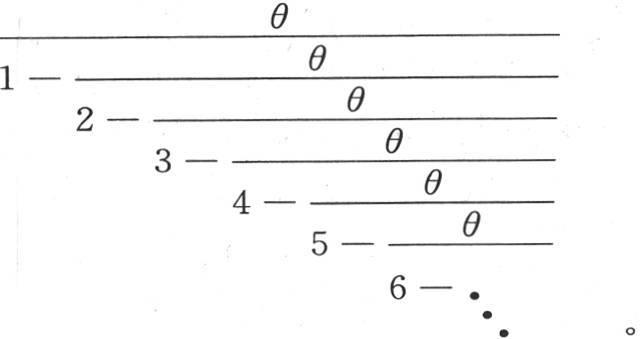
314 我们现在陈述我们直到现在才得到的这些结果。
如果用x表示圆柱体薄层的可变半径,用x和时间t的函数v来表示这个薄层的温度;那么所求函数v应当满足偏微分方程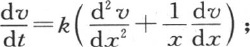 我们可以为v假定下面的值v=ue-mt ;u是x的一个函数,它满足方程
我们可以为v假定下面的值v=ue-mt ;u是x的一个函数,它满足方程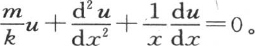
如果我们使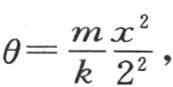 并把u看做是x的一个函数,那么我们有
并把u看做是x的一个函数,那么我们有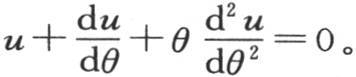 下面的值
下面的值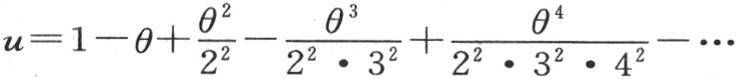 满足u和θ的这个方程。因此,我们假定用x所表示的u值是
满足u和θ的这个方程。因此,我们假定用x所表示的u值是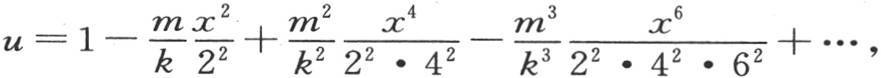 这个级数的和是
这个级数的和是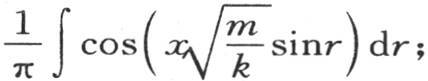 积分从r=0取到r=π。由x和m所表示的这个u值满足微分方程,当x为0时,它保持一个有限值不变。此外,当x等于圆柱体的半径X时,方程
积分从r=0取到r=π。由x和m所表示的这个u值满足微分方程,当x为0时,它保持一个有限值不变。此外,当x等于圆柱体的半径X时,方程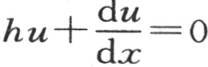 肯定被满足。如果我们赋予量m以任一值,则这个条件不成立;我们必然有方程
肯定被满足。如果我们赋予量m以任一值,则这个条件不成立;我们必然有方程
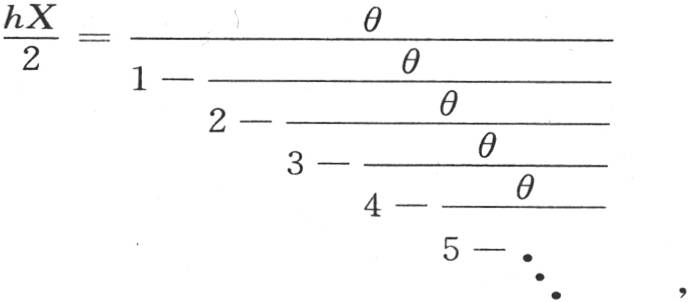
其中θ表示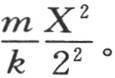
这个定义方程等价于下述方程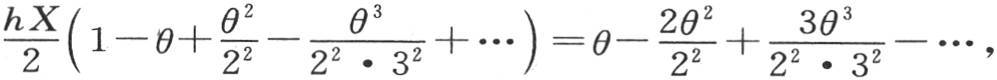 它对θ给出由θ1 ,θ2 ,θ3 ,…所表示的无数实数值;m的对应值是
它对θ给出由θ1 ,θ2 ,θ3 ,…所表示的无数实数值;m的对应值是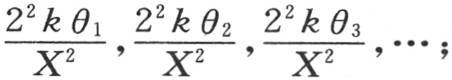 因此v的一个特殊值由
因此v的一个特殊值由 来表示。
来表示。
我们可以用根θ1 ,θ2 ,θ3 ,…中的某一个来代替θ1 ,并且用它们组成一个更一般的值,这个一般值由方程
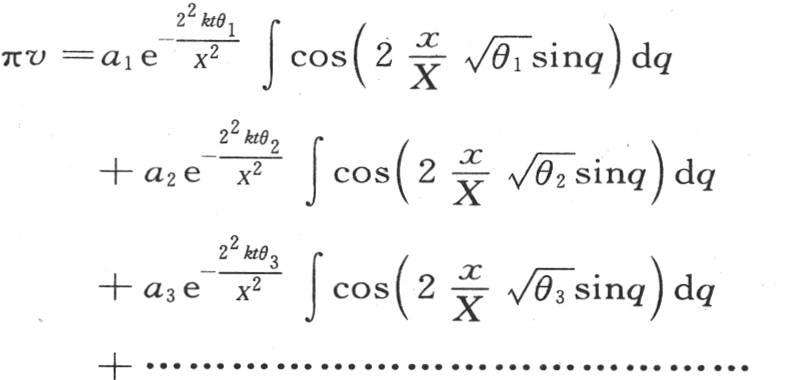
来表示。a1 ,a2 ,a3 ,…是任意系数:在从q=0到q=π取这些积分之后,变量q被消掉。
315 为了证明这个v值满足问题的所有条件,并且包含通解。需要做的事情只是根据初始状态确定系数a1 ,a2 ,a3 ,…。取方程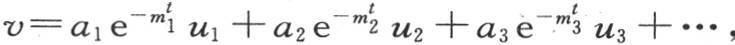 其中u1 ,u2 ,u3 ,…是由函数u或者是
其中u1 ,u2 ,u3 ,…是由函数u或者是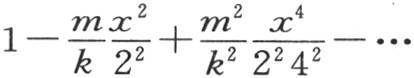 在用g1 ,g2 ,g3 ,…依次取代
在用g1 ,g2 ,g3 ,…依次取代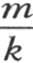 时所呈现的不同的值。在它之中令t=0,我们有方程V=a1 u1 +a2 u2 +a3 u3 +…,其中V是x的已知函数。设这个函数是φ(x);如果我们用
时所呈现的不同的值。在它之中令t=0,我们有方程V=a1 u1 +a2 u2 +a3 u3 +…,其中V是x的已知函数。设这个函数是φ(x);如果我们用 表示下标是i的函数ui ,那么我们有
表示下标是i的函数ui ,那么我们有
为了确定第一个系数,用σ1 dx乘方程两边,σ1 是x的函数,并且从x=0到x=X取积分。然后我们确定函数σ1 ,以便积分后右边可以简化得只剩第一项,并且可以得到系数a1 ,其他所有积分取0值。同样,为了确定第二个系数a2 ,我们用另一个因子σ2 dx乘方程φ(x)=a1 u1 +a2 u2 +a3 u3 +…的两边,并且从x=0到x=X取积分。因子σ2 应当是这样的:它使得除某一项,即受系数a2 作用的那一项外,右边所有积分都变成0。一般地,我们运用由σ1 ,σ2 ,σ3 ,…所表示的一系列x的函数,σ1 ,σ2 ,σ3 ,…对应于函数u1 ,u2 ,u3 ,…;每个因子σ都有这样的性质:它使得包含定积分的所有项除某一项外都在积分中消去;如此,我们得到每个系数a1 ,a2 ,a3 ,…的值。我们现在应当考察什么样的函数具有所说的这种性质。
316 方程右边的每一项是一个形如a∫σudx的定积分;u是x的一个函数,它满足方程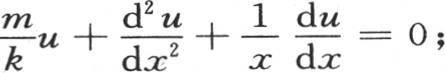 因此我们有
因此我们有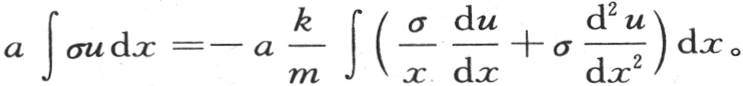 用分部积分的方法展开项
用分部积分的方法展开项 和
和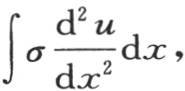 我们有
我们有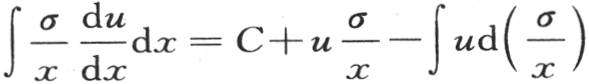
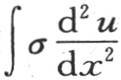 和
和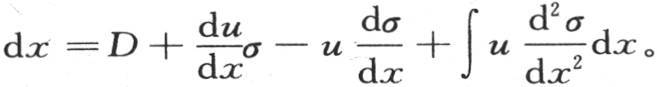
这些积分应当在x=0到x=X的区间内来取,我们由这个条件确定进入展开式并且不在这些积分号内的那些量。为了指明我们在哪个x的表达式中假定x=0,我们对那个表达式增加下标α;为了指明当我们对变量x给定其最后的值X时x的函数所取的值,我们对它给定下标ω。
在前面两个方程中假定x=0,我们有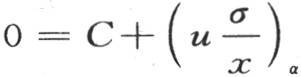 和
和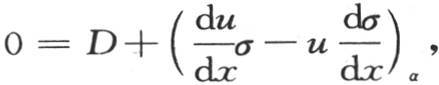 因此我们确定系数C和D。然后在这同样两个方程中取x=X,并假定积分从x=0取到x=X,则我们有
因此我们确定系数C和D。然后在这同样两个方程中取x=X,并假定积分从x=0取到x=X,则我们有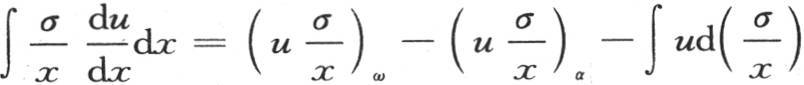 和
和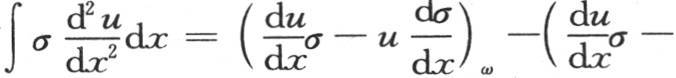
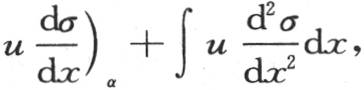 因此我们得到方程
因此我们得到方程
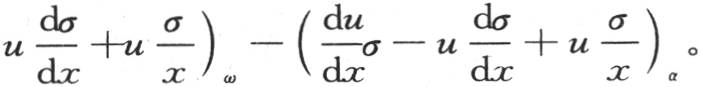
317 如果右边积分号下乘u的量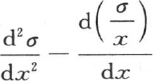 等于σ与一个常数的积,那么项
等于σ与一个常数的积,那么项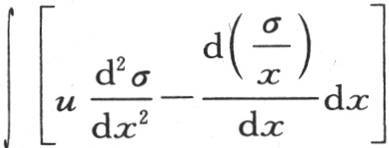 和∫σu dx就合并成一项,对于待求的积分∫σu dx,我们得到只含一些不带积分符号的确定量的一个值。要做的只是使那个值等于0。
和∫σu dx就合并成一项,对于待求的积分∫σu dx,我们得到只含一些不带积分符号的确定量的一个值。要做的只是使那个值等于0。
这样,像函数u满足方程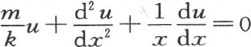 那样,假定因子σ满足二阶微分方程
那样,假定因子σ满足二阶微分方程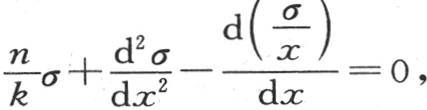 m和n是常系数,我们有
m和n是常系数,我们有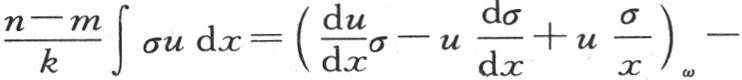
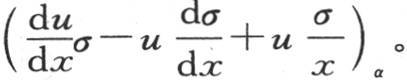
在u和σ之间有一个很简单的关系,当我们在方程 中假定σ=xs时可以发现这种关系;作为这个代换的结果,我们有方程
中假定σ=xs时可以发现这种关系;作为这个代换的结果,我们有方程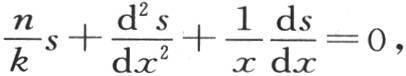 它表明函数s依赖于由方程
它表明函数s依赖于由方程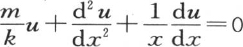 所给定的函数u。为了求出s,只需在u的值中把m变成n就够了;u的值已由
所给定的函数u。为了求出s,只需在u的值中把m变成n就够了;u的值已由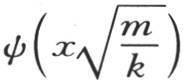 表示,因此σ的值是
表示,因此σ的值是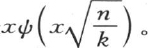
这样我们有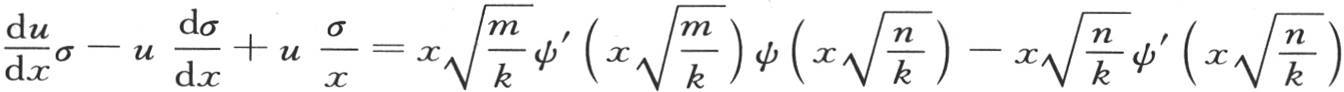
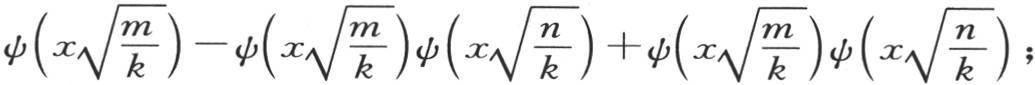 后两项相互抵消,由此得到,只要使x=0,它对应于下标α,那么右边就完全变成0。我们由此得到下述方程
后两项相互抵消,由此得到,只要使x=0,它对应于下标α,那么右边就完全变成0。我们由此得到下述方程
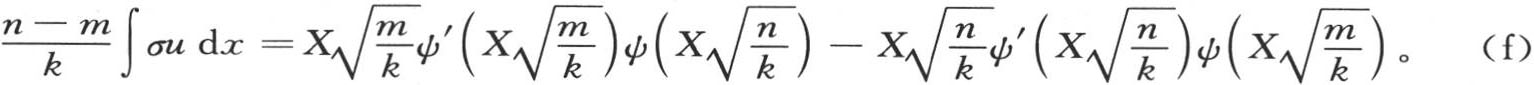
不难看到,当量m和n是从我们在前面用m1 ,m2 ,m3 ,…所表示的那些量中挑选出来时,这个方程的右边就总是为0。
事实上,我们有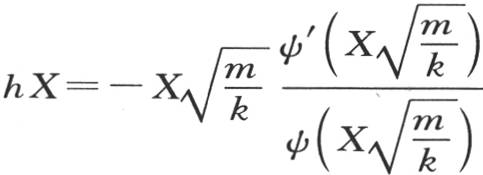 和
和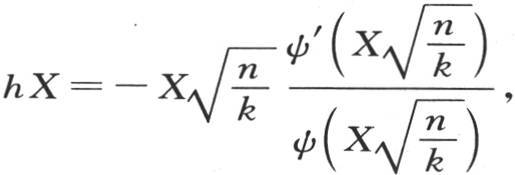 比较hX的这两个值,我们看到方程(f)的右边为0。
比较hX的这两个值,我们看到方程(f)的右边为0。
由此得到,在我们用σdx乘方程φ(x)=a1 u1 +a2 u2 +a3 u3 +…的两边 【2】 并对两边从x=0到x=X取积分后,为了使右边每一项变成0,只需把σ取作量xu或者是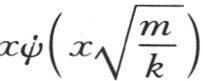 就够了。
就够了。
当从方程(f)所导出的∫σu dx的值化为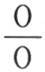 的形式并且由已知规则确定时,我们应当唯一除开n=m的情况。
的形式并且由已知规则确定时,我们应当唯一除开n=m的情况。
318 如果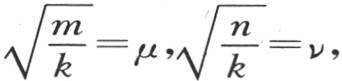 那么我们有
那么我们有
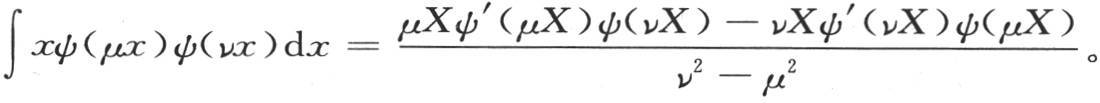
如果使右边的分子分母分别对ν微分,那么只要μ=ν,这个因子就变成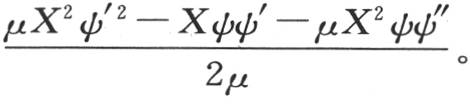 ψ,ψ′,ψ″表示ψ(μX),ψ′(μX),ψ″(μX)。 【3】 另一方面,我们有方程
ψ,ψ′,ψ″表示ψ(μX),ψ′(μX),ψ″(μX)。 【3】 另一方面,我们有方程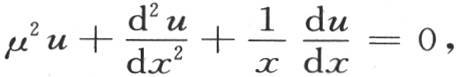 或者是
或者是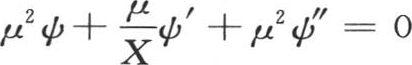 , 【4】 还有hxψ+μxψ′=0,或者是hψ+μψ′=0;所以我们有
, 【4】 还有hxψ+μxψ′=0,或者是hψ+μψ′=0;所以我们有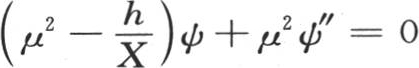 , 【5】 因此,我们可以从需要求其值的积分中消去量ψ′和ψ″,通过前面这些方程,我们有
, 【5】 因此,我们可以从需要求其值的积分中消去量ψ′和ψ″,通过前面这些方程,我们有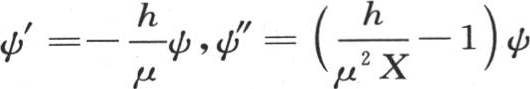 ; 【6】 作为这个所求积分的值,我们得到
; 【6】 作为这个所求积分的值,我们得到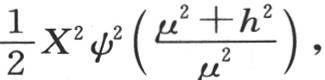 或者,用μ的值代替μ,用Ui 表示函数u或者是
或者,用μ的值代替μ,用Ui 表示函数u或者是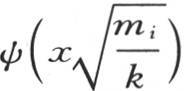 在我们假定x=X时所取的值,则我们有
在我们假定x=X时所取的值,则我们有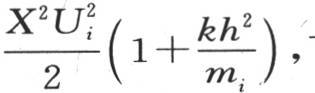 下标i表示给出无数m值的定义方程的根m的序号。如果我们在
下标i表示给出无数m值的定义方程的根m的序号。如果我们在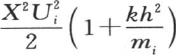 中代入mi 或者是
中代入mi 或者是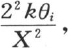 那么我们有
那么我们有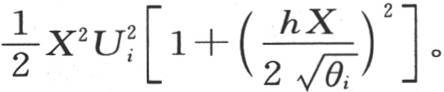
319 由前面的分析可知,我们有两个方程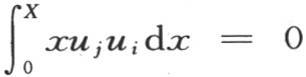 和
和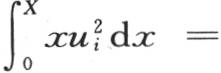
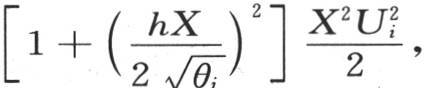 第一个在i和j互异时总是成立,第二个在它们相等时成立。
第一个在i和j互异时总是成立,第二个在它们相等时成立。
这时,取方程φ(x)=a1 u1 +a2 u2 +a3 u3 +…,其中,系数a1 ,a2 ,a3 ,…是待定的,用xui dx乘方程两边,并从x=0到x=X取积分,我们得到由ai 所表示的系数,右边由这个积分简化得只剩一项,我们有方程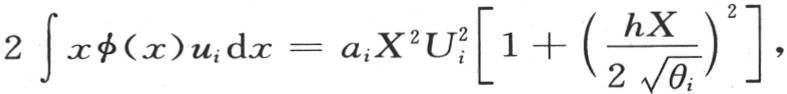 它给出ai 的值,由于系数a1 ,a2 ,a3 ,…,ai 被确定,所以,与由方程φ(x)=a1 u1 +a2 u2 +a3 u3 +…所表示的初始状态有关的条件被满足。
它给出ai 的值,由于系数a1 ,a2 ,a3 ,…,ai 被确定,所以,与由方程φ(x)=a1 u1 +a2 u2 +a3 u3 +…所表示的初始状态有关的条件被满足。
现在我们可以给出所提出的问题的完全解了;它由下述方程表示: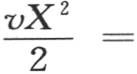
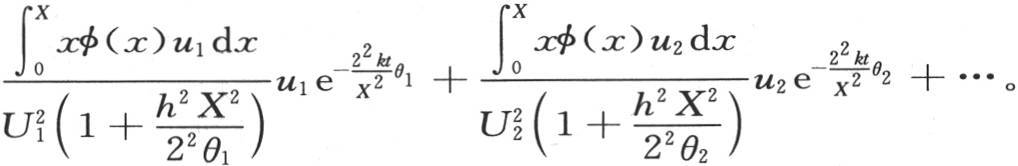
在上面的方程中,由u所表示的x的函数由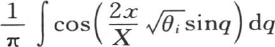 来表示。所有相对于x的积分应当从x=0取到x=X,为了得到函数u,我们应当从q=0到q=π取积分;φ(x)是在圆柱体内在与轴相距x处所取的温度的初始值,这个函数是任意的,θ1 ,θ2 ,θ3 ,…是方程
来表示。所有相对于x的积分应当从x=0取到x=X,为了得到函数u,我们应当从q=0到q=π取积分;φ(x)是在圆柱体内在与轴相距x处所取的温度的初始值,这个函数是任意的,θ1 ,θ2 ,θ3 ,…是方程
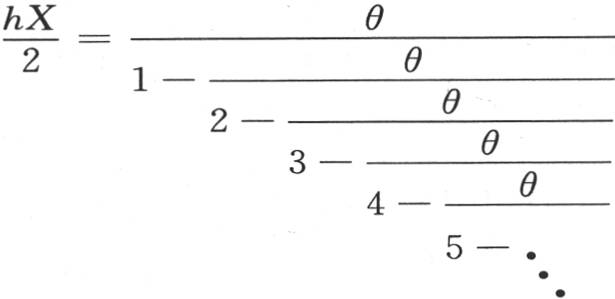
的正实根。
320 如果我们假定圆柱体在保持恒温的液体中已经浸泡了无穷时间,整个物体已经变成等加热的物体,代表初始状态的函数φ(x)由1来表示。在这个代换之后,一般方程严格表示渐进冷却过程。
如果历经时间无穷,那么右边只含有一项,即包含了所有的根θ1 ,θ2 ,θ3 ,…中最小的一个的那一项;由此,假定这些根依它们的数值而排列,并且θ1 是最小的,则这个固体的终极状态由方程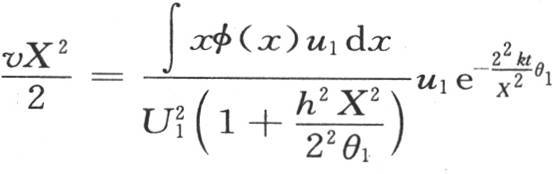 来表示。
来表示。
根据这个通解,我们可以推出和球体中的热运动所提供的相类似的结论。我们首先注意到存在无数特殊状态,在每一个这样的状态中,初始温度之间所建立的比一直保持到冷却结束时为止。当初始状态与某个这样的简单状态不一致时,它总是由它们中的几个组成,并且温度的比随时间的增加而连续变化。一般地,这个固体很快达到不同薄层的温度以保持相同比值而连续降低的状态。在半径X很小时 【7】 ,我们发现温度与分数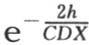 成正比地降低。
成正比地降低。
如果反过来,半径X很大 【8】 ,那么在表示终极温度系统的项中e的指数包含整个半径的平方。我们由此看到这个固体的体积对最后的冷却速度产生什么样的影响。如果半径为X的圆柱体的温度 【9】 在时间T内从值A过渡到值B,那么,半径等于X′的第二个圆柱体的温度在不同的时间T′内从A过渡至B。如果两者都很细,那么时间T和T′的比是两个直径的比。相反,如果这两个圆柱体的直径很大,那么时间T和T′的比就是直径的平方的比。
注释
【1】 在英译本中,此式是: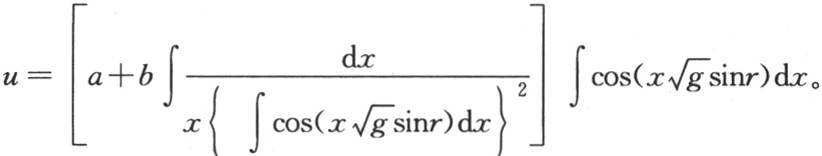 虽然,由于a和b是任意常数,因此上述式子仍然不错,但法文《文集》本中此式的表述更明确。为便于理解,此处在后一个版本订正。——汉译者
虽然,由于a和b是任意常数,因此上述式子仍然不错,但法文《文集》本中此式的表述更明确。为便于理解,此处在后一个版本订正。——汉译者
【2】 在英文版和法文《文集》版中都是说“两项”,然而这里虽然应当是乘方程的“两边”。如此看来,这个笔误出在1822年的版本中。——汉译者
【3】 这句话依据法文《文集》本所加。——汉译者
【4】 这里,式中的“X”,在英译本中是“x”,现依法文《文集》本订正。——汉译者
【5】 这里,式中的“X”,在英译本中是“x”,现依法文《文集》本订正。——汉译者
【6】 这两个式子及其相应文字是根据法文《文集》本加的。——汉译者
【7】 当X很小时,由第314目的方程,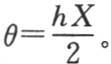 因此
因此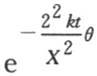 变成
变成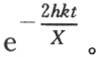
在本书中,h是表面热导率。
【8】 当X很大时,与二次方程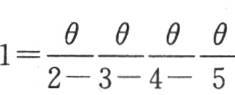 的某个根近似相等的一个θ值使第314目中的连分式取其特征量。因此,θ近似地等于1.446,并且
的某个根近似相等的一个θ值使第314目中的连分式取其特征量。因此,θ近似地等于1.446,并且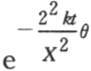 变成
变成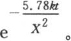 略去θ4 之后的项,f(θ)的最小的根是1.4467。——A. F.
略去θ4 之后的项,f(θ)的最小的根是1.4467。——A. F.
【9】 所指的温度是平均温度,它等于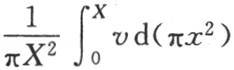 或者是
或者是