附录A

面包师变换的时间算符和熵算符

Appendix A

普里戈金花费了他一生的大部分精力，试图把生物学和物理学重新装到一起，把必然性和偶然性重新装到一起，把自然科学和人文科学重新装到一起。

布鲁塞尔自由大学校景（彭丹歌摄）。

第8章已经引入了面包师变换，现在我们将更详细地叙述我们如何把这个变换和时间算符T（式8.22）以及微观熵算符M相连结起来。

在这里给出的结果是近期米斯拉、普里戈金和库巴奇文章^[1] 的总结，在那里，可以找到全部证明及其结果向其他系统的种种推广。与面包师变换有关而在此不作论述的其他概念可以在莱博维茨，奥恩斯坦以及其他作者的重要文章^[2～6] 中找到。

相空间Ω是在平面上的单位正方形。正如我们在第8章（参见图8.11）中看到的，面包师变换B把Ω的点ω＝（p，q）转移到Bω，具有

变换B描述一种在固定的时间间隔中发生的分立过程，这种过程趋向于把一个任意给定的表面元逐渐地分裂成碎片。作为一个例子，让我们应用面包师变换B到半个正方形0≤q≤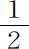 之上，这结果再现于图A.1中。

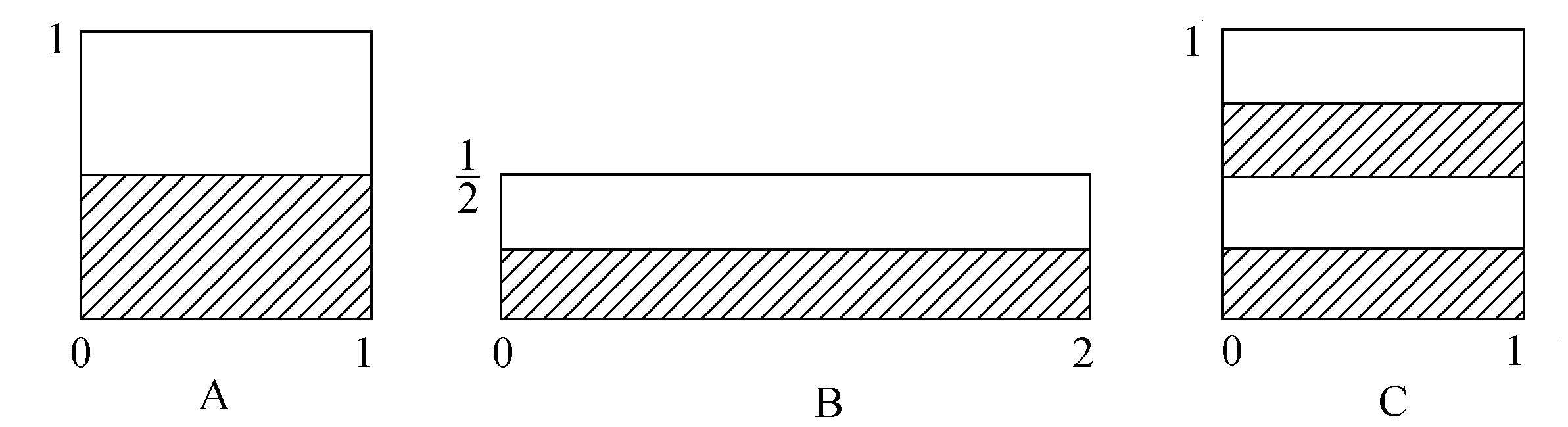
图A.1　面包师变换应用于半正方形

当面包师变换B重复进行了若干次，开始的半个正方形被分裂成为图A.2所示的小而又小的长方形。

图A.2　在半正方形上逐次实行面包师变换的效果

这个面包师变换容许一种叫做“伯努利移动”的不平常表象。为了了解这个关系，我们以一个二进制的小数展开写出坐标p和q：

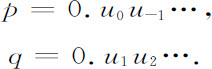
这个记法意味着

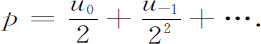
对于q有类似的表达式，在此u_i 取值0或1。

因此，Ω中的一点ω由双序列{u_i }来表示，其中i＝0，±1，±2，…。用一些具体的例子，可以容易地验证，这里与Bω对应的是序列{u′_i }，其中u′_i ＝u_i-1 ，我们很清楚地看出，面包师变换引起序列的一个移动，这是人们谈及“伯努利移动”的主要理由^[6] 。

现在我们考虑在“相空间”上所有的平方可积函数的一个简单的正交基。设X是在（0，1）上由

定义的函数，对于每一个整数n，在Ω上由

定义一个函数X_n （ω）。因此，在Ω的每一点上X_n （ω）的值唯一地依赖于坐标p、q的二进制展开中的第n位。

此外，我们对于每一有限的整数组（n_n ，n₂ ，…，n_N ）＝n定义乘积函数X_n （ω）：

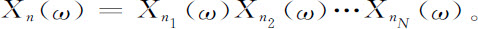
我们采用记法

其中，X_φ （ω）对应于微正则系综，我们可以证实这函数组确实形成一套正交基。正如现今在量子力学中使用的那样（见第3章“量子化规则”一节），这意味着

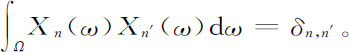
在此δ_n，n′ 当n＝n′（即 ）时等于1，否则等于零。例如使用式A.3，很容易验证（同样可见图A.3和图A.6）：

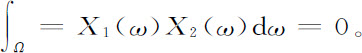
还有，函数X_n （ω）与X_φ 一起形成一完备组：在Ω上的每一个（平方可积）函数都能通过这些函数的适当的线性组合来展开。

在下面我们将使用两个平方可积函数f₁ ，f₂ 的标积，这标积定义为

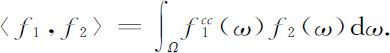
面包师变换也能依据作用在函数φ（ω）上的算符U来表示（正如在教科书中解释的，U是一个幺正算符，见文献［5］）：

使用式A.3，作为一个结果我们有

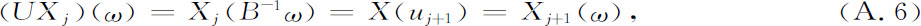
简言之

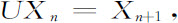
式中n+1是整数组（n₁ +1，n₂ +1，…，n_N +1）。因此，面包师变换导致基函数的一个简单的移动。现在我们引入在Ω中区域Δ的一个特征函数，φΔ；这函数在Δ上取值为1，在Ω中的其余的地方等于零。我们能通过已经引入的基函数X_n 来表达这样的特征函数。

其中面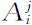 是u_i ＝j这样的点ω的集合，而 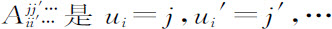这样的点ω的集合，此外，我们已给出在这些面上X_i （ω）的值（i＝0，1，2）以及它们的特征函数 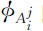的值。

作为一个例子，让我们考虑X₁ （ω），依照定义X₁ （ω）＝X（u₁ ）是一个函数，当u₁ ＝0（即对于0≤p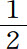＜ 时）取值为-1，以及当u₁ ＝1（即对于 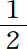≤p＜1）时取值为+1。因此X₁ （ω）在正方形的下半边 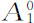取值为-1，和在正方形的上半边 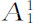取值为+1。要写出正方形的分块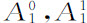（ ）“原子”的特征函数现在是很容易的事，特征函数的表达式表述在图A.3上。对于相应于固定分块的特征函数来说，类似的表达式是正确的。

图A.3　表示面 和它们的交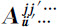 的形状的若干例子

现在我们将研究Ω中一个任意区域的演化以及把这一演化与在这本书中一再讨论过的“弱稳定性”的思想联系起来。（见第2章“弱稳定性”一节）。我们可以从式A.5得到变换后的区域B¹ Δ的特征函数，为此，接连使用如下定义：

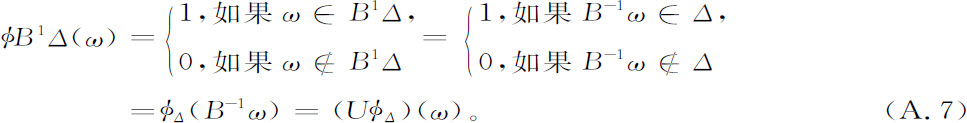
因而我们有

例如，在n次应用B¹ 之后，区域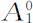 变换成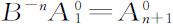 （参见图A.3中这些区域的形状以及通过基X_i 给出的它们的特征函数）。

在一般情形中，我们可以考虑Ω的一个任意小的“原子”，其特征函数是：

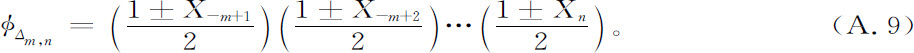
靠增加n和m的值，这样的“原子”能选择得我们想要的那样小。令人感兴趣的是在第（m+1）次应用变换B^-1 之后，Δm，n分裂成两个原子。

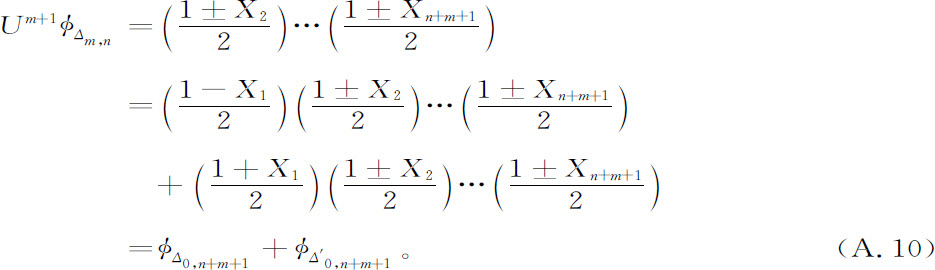
这样得到的两个“原子”是对称的且被2^n+m 个子块所分离。

因此，我们看出，即使初始时刻系统是处在相空间中某个任意小的区域中，随着时间的推移，系统也将演化到相空间中分离开的不同的区域中去。并且我们只能估计在这些不同的区域中发现系统的概率。换句话说，每一个区域（不管多么小）包含引导到各式各样的区域中去的不同形式的“轨道”，这正是弱稳定性的真正定义。

在这些初步的考虑之后，现在让我们引入基本的算符T，这算符T对应于“年龄”或对应于一个“内部”时间，按照定义，它满足（对于连续变换来说）关系式10.15或（用离散的时间）

在面包师变换的情形，要构成T的明显的表达式是容易的（至于更加详细的材料，可参见文献［1］）。我们已看出，当U应用于基函数{X_n }的时候，使X_n 移动到X_n+1 。

因此，X_n 是共轭算符T的本征矢量并不令人惊奇。此外，对于每一个X_n ，相应的本征值是n_i 中的最大值（n是n₁ ，n₂ ，…，n_N 的有限集合）。例如，与X_n 对应的本征值是n，与X₀ X₁ X₂ 对应的本征值是2，等等。结果，T的谱形式如下：

在这里E_n 是在由函数X_n ：X_i X_n （i＜n），X_i X_j X_n （i，j＜n），等等产生的微正则系综的正交补中的子空间上的投影，我们可以证实.

这里正好得出关系式A.11。T的本征值（年龄算符的数值）是从-∞到+∞的全部整数，这有一简明的物理意义，举例来说，如果我们考虑对应于年龄2的本征函数如X₂ ，使用U变换使X₂ 进到对应于年龄3的本征函数X₃ ，如此等等。注意：第一个不等式10.28从Λ保持为正的要求中直接得到。这一点可以容易地用表达下式的正定来验证：

式中φ_Δ 和φ_Δ′ 是对应于类Δ和Δ′的特征函数^[1] 。戈尔茨坦、米斯拉和库巴奇^[8] 已经给出了一个简洁的推导。类似地，第二个不等式10.35得自下式的恒正性：

这导出第二个条件（式10.35）。

参考文献

［1］B. Misra，I. Prigogine，and M. Courbage，Proceedings of the National Academy of Sciences，U. S. A.76（1979）：3607；Physica 98A（1979）：1.

［2］J. L. Lebowitz，Proceedings of I. U. P. A. P. Conference on Statistical Mechanics（Chicago，1971）.

［3］D. S. Ornstein，Advances in Mathematics，4（1970）：337.

［4］J. G. Sinai，Theory of Dynamical Systems，vol. 1（Denmark：Aarhus University，1970）.

［5］V. I. Arnold，and A. Avez，Ergodic Problems of Classical Mechanics（New York：Benjamin，1968）.

［6］P. Shields，The Theory of Bernouilli Shifts（Chicago：University of Chicago Press，1973）.

［7］B. Misra and I. Prigogine，in Long-Time Prediction in Dynamics，edited by C. M. Horton，Jr.，L. E. Reichl，and V. G. Szebeley（New York：John Wiley & Sons，1983）.

［8］S. Goldstein，B. Misra and Courbage，J. Stat. Phys. 25（1982）：111.