第二章

论和谐比例与五种正立体形之间的关系

• Kinship Between the Harmonic Ratios and the Five Regular Figures •

我永远无法用语言来描述我从自己的发现中获得的快乐。现在我再也不惋惜失去的时间，再也不厌倦工作，无论有多大困难，我也不回避计算。日日夜夜我不停地从事计算，直到我看见用公式的语言表达的句子与哥白尼的轨道完全吻合，直到我的欢乐被风吹走。

——开普勒

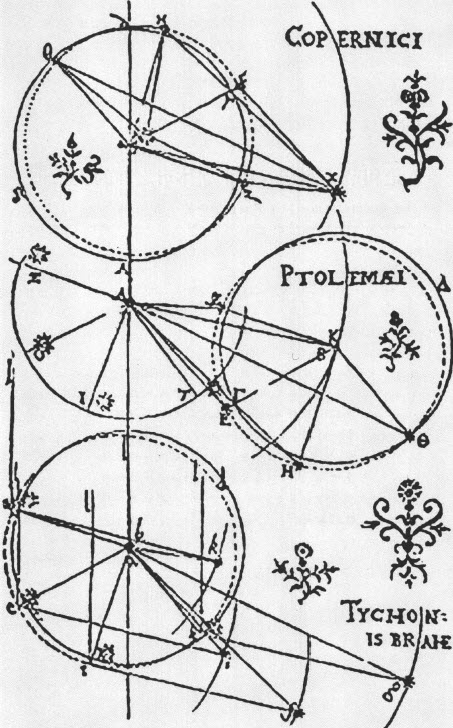
在开普勒之前，三种行星运动模式的示意图。

这些关系 ⁽¹⁾ 不仅多种多样，而且层次也不尽相同，我们可以由此把它们分为四种类型：它或者仅来源于立体形的外在形状；或者在构造棱边时产生了和谐比例；或者来源于已经构造出来的立体形，无论是单个的还是组合的；或者等于或接近于立体形的内切球与外接球之比。

对于第一种类型的关系，如果比例的特征项或大项为3，则它们就与四面体、八面体和二十面体的三角形面有关系；如果大项是4，则与立方体的正方形面有关系；如果大项是5，则与十二面体的五边形面有关系。这种面相似性也可以拓展到比例中的小项，于是，只要3是连续双倍比例中的一项，则该比例就必定与前三个立体形有关系，比如1∶3、2∶3、4∶3和8∶3等等；如果这一项是5，则这个比例就必定与十二面体的结合有关系，比如2∶5、4∶5和8∶5。类似的，3∶5、3∶10、6∶5、12∶5和24∶5也都属于这些比例。但如果表示这种相似性的是两比例项之和，那么这种关系存在的可能性就较小了。比如在2∶3中，两比例项加起来等于5，于是2∶3近似与十二面体有关系。因立体角的外在形式而具有的关系与此类似：在初级立体形中，立体角是三线的，在八面体中是四线的，在二十面体中是五线的。因此，如果比例中的一项是3，则该比例将与初级立体形有关系；如果是4，则与八面体有关系；如果是5，则与二十面体有关系。对于雌性立体形，这种关系就更为明显了，因为潜藏于其内部的特征图形具有与角同样的形式：八面体中是正方形，二十面体中是五边形。 ⁽²⁾ 所以3∶5有两个理由属于二十面体。

对于第二种起源类型的关系，可做如下考虑：首先，有些整数之间的和谐比例与某种结合或家庭有关系，或者说，完美比例只与立方体家庭有关系；而另一方面，也有一些比例无法用整数来表示，而只能通过一长串整数逐渐逼近。如果这一比例是完美的，它就被称为神圣的，并且自始至终都以各种方式规定着十二面体的结合。因此，以下这些和谐比例1∶2、2∶3、3∶5、5∶8是导向这一比例的开始。如果比例总是和谐的，因1∶2最不完美，5∶8稍完美一些，我们把5加上8得到13，并且在13前面添上8，那么得出的比例就更完美了。 ⁽³⁾

此外，为了构造立体形的棱边，（外接）球的直径必须被切分。八面体需要直径分为两半，立方体和四面体需要分为3份，十二面体的结合需要分为5份。因此，立体形之间的比例是根据表达比例的这些数字而分配的。直径的平方也要切分，或者说立体形棱边的平方由直径的某一固定部分形成。然后，把棱边的平方与直径的平方相比，于是就构成了如下比例：正方体是1∶3，四面体是2∶3，八面体是1∶2。如果把两个比例复合在一起，则正方体和四面体给出的复合比例是1∶2，立方体和八面体是2∶3，八面体和四面体是3∶4，十二面体的结合的各边是无理的。

第三，由已经构造出来的立体形可以根据各种不同方式产生和谐比例。我们或者把每一面的边数与整个立体形的棱数相比，得到如下比例：正方体是4∶12或1∶3，四面体是3∶6或1∶2，八面体是3∶12或1∶4，十二面体是5∶30或1∶6，二十面体是3∶30或1∶10；或者把每一面的边数与面数相比，得到以下比例：正方体是4∶6或2∶3，四面体是3∶4，八面体是3∶8，十二面体是5∶12，二十面体是3∶20；或者把每一面的边数或角数与立体角的数目相比，得到以下比例：正方体是4∶8或1∶2，四面体是3∶4，八面体是3∶6或1∶2，十二面体的结合是5∶20或3∶12（即1∶4）；或者把面数与立体角的数目相比，得到以下比例：立方体是6∶8或3∶4，四面体是1∶1，十二面体是12∶20或3∶5；或者把全部边数与立体角的数目相比，得到以下比例：立方体是8∶12或2∶3，四面体是4∶6或2∶3，八面体是6∶12或1∶2，十二面体是20∶30或2∶3，二十面体是12∶30或2∶5。

这些立体形彼此之间也可以相比。如果通过几何上的内嵌，把四面体嵌入立方体，把八面体嵌入四面体和立方体，则四面体等于立方体的三分之一，八面体等于四面体的二分之一和立方体的六分之一，所以内接于球的八面体等于外切于球的立方体的六分之一。其余立体形之间的比例都是无理的。

对于我们的研究来说，第四类或第四种程度的关系是更为适当的，因为我们所寻求的是立体形的内切球与外接球之比，计算的是与此接近的和谐比例。只有在四面体中，内切球的直径才是有理的，即等于外接球的三分之一。但在立方体的结合中，这唯一的比例只有在相应线段平方之后才是有理的，因为内切球的直径与外接球的直径之比为1∶3的平方根。如果把这些比例相互比较，则四面体的两球之比 ⁽⁴⁾ 将等于立方体两球之比的平方。在十二面体的结合中，两球之比仍然只有一个值，不过是无理的，稍大于4∶5。因此，与立方体和八面体的两球之比相接近的和谐比例分别是稍大的1∶2和稍小的3∶5；而与十二面体的两球之比相接近的和谐比例分别是稍小的4∶5和5∶6，以及稍大的3∶4和5∶8。

然而，如果由于某种原因，1∶2和1∶3被归于立方体， ⁽⁵⁾ 而且确实就用这个比例，则立方体的两球之比与四面体的两球之比之间的比例，将等于已被归于立方体的和谐比例1∶2和1∶3与将被归于四面体的和谐比例1∶4和1∶9之比，这是因为这些比例（即四面体的比例）等于前面那些和谐比例（即立方体的和谐比例）的平方。对于四面体而言，由于1∶9不是和谐比例，所以它只能被1∶8这一与它最接近的和谐比例所代替。根据这个比例，属于十二面体的结合的比例将约为4∶5和3∶4。因为立方体的两球之比近似等于十二面体的两球之比的立方，所以立方体的和谐比例1∶2和1∶3将近似等于和谐比例4∶5和3∶4的立方。4∶5的立方是64∶125，1∶2即为64∶128；3∶4的立方是27∶64，1∶3即为27∶81。

伽利略（1575—1642）（素描画）。

————————————————————

(1) 开普勒所使用的原拉丁文词为cognatio，表示一种内在固有的亲缘关系。为了表述的方便，这里姑且译为“关系”。——中译者

(2) 即八面体的四线立体角和二十面体的五线立体角分别与八面体中的正方形和二十面体中的五边形具有相同的形式。——中译者

(3) 开普勒这里引用的比例是菲波那契（Fibonacci）数列的连续几项。如果无限发展下去，它的比值就将接近黄金分割，即十二面体结合的神圣比例。——中译者

(4) 即内切球与外接球的直径或半径之比，下同。——中译者

(5) 这里没有说明为什么要把1∶3归于立方体而非四面体，其原因要到第九章的“8．命题”才能说明。——中译者