第7章
物体的直线上升或下降
命题32 问题24
设向心力反比于处所到中心的距离的平方;求物体在给定时间内沿直线下落的距离。
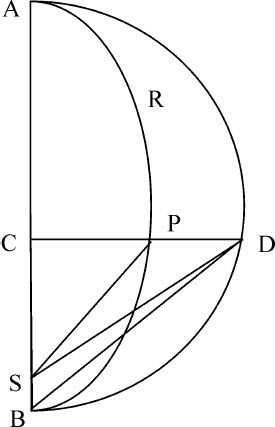
情形1.如果物体不是垂直下落,它将(根据命题13,推论I)掠过一焦点在力的中心的圆锥曲线。设该圆锥曲线为ARPB,焦点为S。首先,如果轨迹是椭圆,在长轴AB上作半圆ADB,令直线DPC通过下落物体,与主轴成直角;再作DS,PS,则面积ASD将正比于面积ASP,所以也正比于时间。保持主轴AB不变,令椭圆的宽度连续缩小,面积ASD总是正比于时间。设宽度无限缩小;此时轨道APB与主轴AB重合,焦点S与主轴顶点B重合,则物体沿直线AC下落,面积ABD也将正比于时间。所以,如果取面积ABD正比于时间,并由点D作直线DC垂直落向直线AB,则物体在给定时间内由处所A垂直下落所掠过的距离可以求出。
完毕。
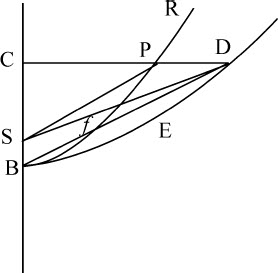
情形2.如果图形RPB是双曲线,在同一主轴AB上作直角双曲线BED;因为在几块面积与高度CP和CD之间有如下关系存在:CSP:CSD=CBf D:CBED=SPf B:SDEB=CP:CD,以及面积SPf B正比于物体P通过弧Pf B所用的时间而变化,面积SDEB也将正比于时间变化。令双曲线RPB的通径无限缩小,同时横轴保持不变,则弧PB将与直线CB重合,焦点S与顶点B重合,而直线SD与直线BD重合。所以面积BDEB将正比于物体C沿直线CB垂直下落所用时间而变化。
完毕。
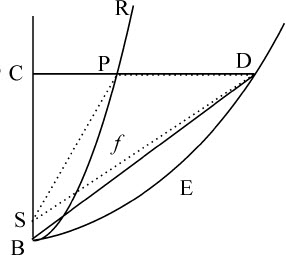
情形3.由相似理由,如果图形RPB是抛物线,以同一顶点B作另一条抛物线BED,并使之保持不变,同时物体P沿其边缘运动的前一条抛物线随着其通径缩小并变为零而与直线CB重合,则抛物线截面BDED将正比于物体P或C落向中心S或C所用的时间而变化。
完毕。
命题33 定理9
在上述假设中,落体在任意处所C的速度与它环绕以B为中心,BC为半径的圆运动的速度的比,等于物体到该圆或直角双曲线的远顶点A的距离与该图形的主半径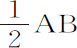 的比值的平方根。
的比值的平方根。
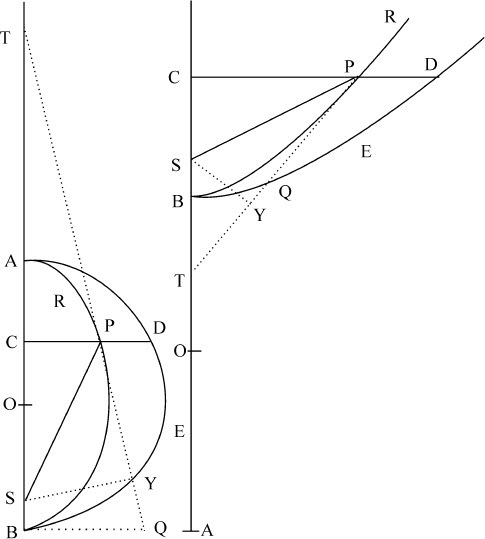
令两个图形RPB,DEB的公共直径AB在O点被等分;作直线PT与图形RPB相切于P,并与公共直径AB(必要时作延长)相交于T;令SY垂直于该直线,BQ垂直于直径,设图形RPB的通径为L。由命题16推论IX知,物体沿关于中心S的曲线RPB运动时在任意处所P的速度,比它沿关于同一中心,半径为SP的圆运动的速度,等于乘积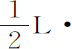 SP与SY2 的比值的平方根。因为由圆锥曲线的性质,AC·CB比CP2 等于2AO比L,所以
SP与SY2 的比值的平方根。因为由圆锥曲线的性质,AC·CB比CP2 等于2AO比L,所以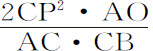 等于L。所以这些速度相互间的比等于
等于L。所以这些速度相互间的比等于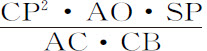 与SY2 的比值的平方根。又根据圆锥曲线的性质。
与SY2 的比值的平方根。又根据圆锥曲线的性质。
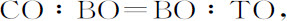
所以,

而且,

由此,

而且,
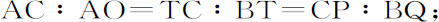
由于,
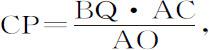
即得到,
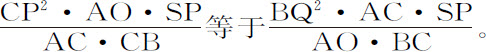
现在设图形RPB的宽CP无限缩小,使点P与点C重合,点S与点B重合,直线SP与直线BC重合,直线SY与直线BQ重合;则物体沿直线CB垂直下落的速度比它沿以B为中心,BC为半径的圆运动的速度,等于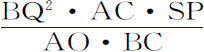 与SY2 的比值的平方根,即(消去相等的比值SP比BC,以及BQ2 比SY2 )等于AC与AO或
与SY2 的比值的平方根,即(消去相等的比值SP比BC,以及BQ2 比SY2 )等于AC与AO或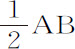 的比值的平方根。
的比值的平方根。
证毕。
推论Ⅰ.当点B与S重合时,TC比TS将等于AC比AO。
推论Ⅱ.以给定距离绕中心做圆周运动的物体,当其运动变为竖直向上时,可上升到距中心二倍的高度。
命题34 定理10
如果图形BED是抛物线,则落体在任意处所C的速度等于物体以间隔BC的一半关于中心B做匀速圆运动的速度。
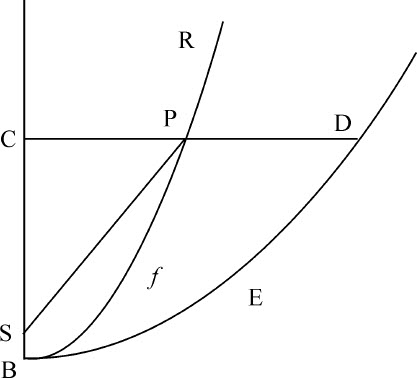
因为(由命题16,推论Ⅶ)物体沿关于中心S的抛物线RPB运动时,在任意处所P的速度,等于物体在间隔SP的一半处关于同一中心做匀速圆运动的速度,令抛物线宽CP无限缩小,使抛物线弧Pf B与直线CB重合,中心S与顶点B重合,间隔SP与间隔BC重合,命题得证。
证毕。
命题35 定理11
在相同假设下,不定半径SD所掠过的图形的面积DES,等于物体以图形DES的通径的一半为半径关于中心S做匀速圆运动在相同时间里所掠过的面积。
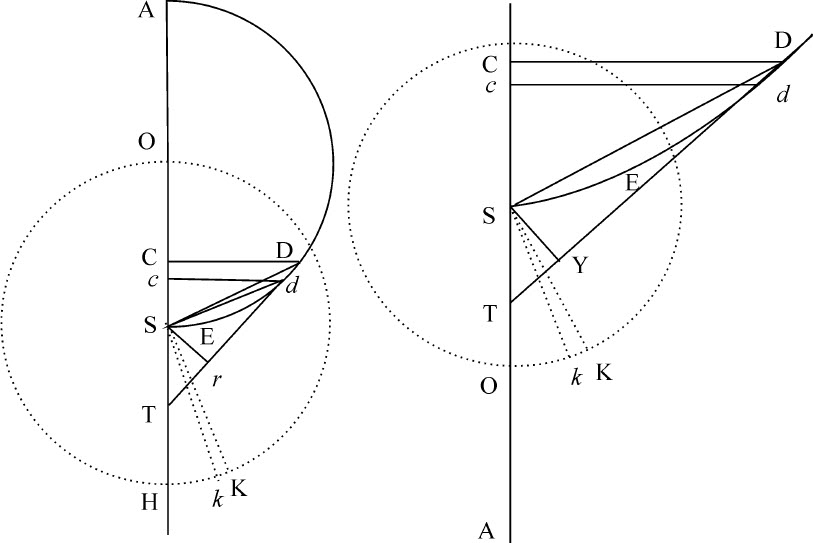
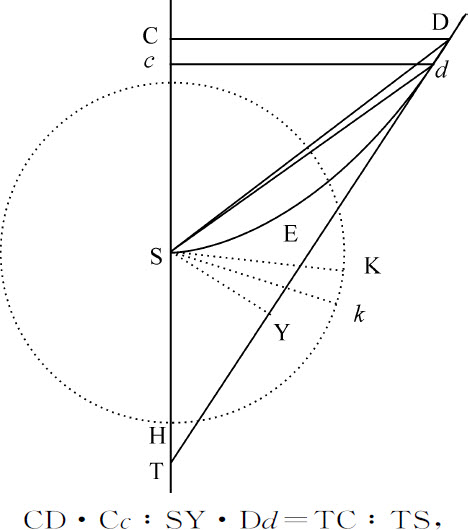
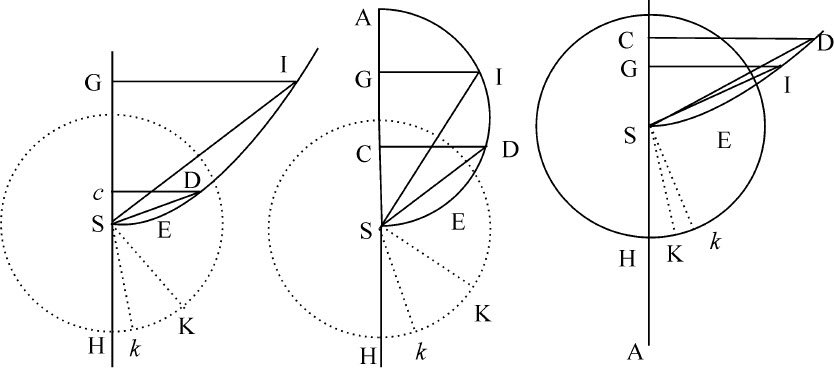
设物体C在最小时间间隔里下落一个不定小线段Cc ,同时另一物体K关于中心S沿圆周OKk 作匀速运动,掠过弧Kk 。作垂线CD,cd 与图形DES相交于D,d 。连接SD,Sd ,SK,Sk ,作Dd 与轴AS交于T,并在其上作垂线SY。
情形1.如果图形DES是圆,或直角双曲线,在O点等分其横向直径AS,则SO为其半通径。而因为

以及

即得到
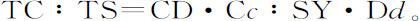
但(由命题33,推论Ⅰ)
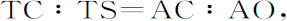
即,如果点D,d 合并,取线段的最后比值。所以,

而且,落体在C的速度比物体以间隔SC关于中心S作圆运动的速度,等于AC与AO或SK的比值的平方根(由命题33);而该速度比物体沿圆OKk 运动的速度等于SK与SC的比值的平方根(由命题4,推论Ⅵ);因而,第一个速度比最后一个速度,即小线段Cc 比弧Kk ,等于AC与SC的比值的平方根,即等于AC与CD的比值。
所以,
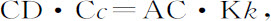
因而,

而且
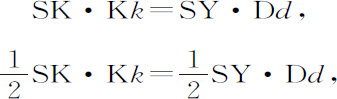
即面积KSk 等于面积SDd 。所以,在每一个时间间隔中,都产生出两个相等的面积元KSk 和SDd ,如果它们在大小趋于零,而数目无限增多,则(由引理Ⅳ的推论)得到二者同时产生的整个面积总是相等的。
证毕。
情形2.如果图形DES是抛物线,与上述情形相同,也有
即=2:1,所以,
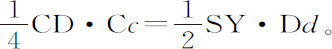
但落体在C点的速度等于在间隔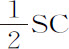 处作匀速圆周运动的速度(由命题34)。而该速度比沿以半径SK作圆运动的速度,即小线段Cc 比弧Kk ,(由命题4,推论Ⅵ)等于SK与
处作匀速圆周运动的速度(由命题34)。而该速度比沿以半径SK作圆运动的速度,即小线段Cc 比弧Kk ,(由命题4,推论Ⅵ)等于SK与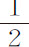 SC的比值的平方根;即等于SK比
SC的比值的平方根;即等于SK比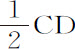 。所以
。所以 等于
等于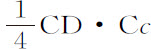 ,所以等于
,所以等于 SY·Dd ;即面积KSK等于面积SDd ,与上述情形相同。
SY·Dd ;即面积KSK等于面积SDd ,与上述情形相同。
证毕。
命题36 问题25
求物体自给定处所A下落的时间。

在直径AS上,以开始下落时物体到中心距离为半径作半圆ADS,再以为中心作一相同的半圆OKH。由物体的任意处所C作纵坐标CD。连接SD,取扇形OSK等于面积ASD。显然(由命题35)在落体掠过距离AC的同时,另一关于中心S作匀速圆运动的物体将掠过弧OK。
完毕。
命题37 问题26
求由给定处所上抛或下抛物体所用的上升或下降的时间。
设物体以任意速度沿直线GS离开给定处所G,取GA比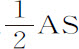 等于该速度与该物体以给定间隔SG关于中心S作匀速圆运动的速度的比值平方。如果该比值等于2比1,则点A在无限远处;此时应像命题34所说画一抛物线,其通径是任意的,顶点为S,主轴为SG;但如果该比值小于或大于2比1,则根据命题33,应在直径SA上,前一情形画一个圆,后一情形画一直角双曲线。然后关于中心S,以半通径为半径画一个圆Hk K;再在物体开始上升或下降的处所G,以及其任意处所C,作垂直线GI,CD,与圆锥曲线或圆交于I和D。连接SI,SD,令扇形HSK,HSk 等于弓形SEIS,SEDS,则在(由命题35)物体G掠过距离GC的同时,物体K掠过弧Kk 。
等于该速度与该物体以给定间隔SG关于中心S作匀速圆运动的速度的比值平方。如果该比值等于2比1,则点A在无限远处;此时应像命题34所说画一抛物线,其通径是任意的,顶点为S,主轴为SG;但如果该比值小于或大于2比1,则根据命题33,应在直径SA上,前一情形画一个圆,后一情形画一直角双曲线。然后关于中心S,以半通径为半径画一个圆Hk K;再在物体开始上升或下降的处所G,以及其任意处所C,作垂直线GI,CD,与圆锥曲线或圆交于I和D。连接SI,SD,令扇形HSK,HSk 等于弓形SEIS,SEDS,则在(由命题35)物体G掠过距离GC的同时,物体K掠过弧Kk 。
完毕。
命题38 定理12
设向心力正比于物体的处所到中心的高度或距离,则物体下落的时间和速度,以及所掠过的距离,将分别正比于弧,弧的正弦和正矢。
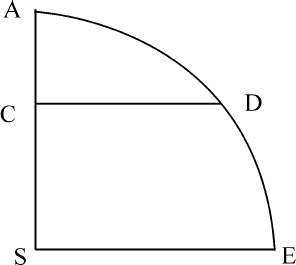
设物体由任意处所A沿直线AS下落;关于力的中心S,以AS为半径作四分之一圆AE;令CD为任意弧AD的正弦,则物体A将在时间AD内下落掠过距离AC,并在处所C获得速度CD。
此定理证法与命题10相同,一如命题32由命题11得证。
推论Ⅰ.物体由处所A到达中心S所用时间,与另一物体掠过四分之一圆弧ADE所用时间相等。
推论Ⅱ.所以物体由任意处所到达中心的时间都相等。因为(由命题4,推论Ⅲ)所有环绕物体的周期都相等。
命题39 问题27
设已知任意种类的向心力,以及曲线图形的面积:求沿一直线上升或下落的物体在它所通过的不同处所的速度,以及它到达任一处所所用的时间;或反过来由速度或时间求出处所。

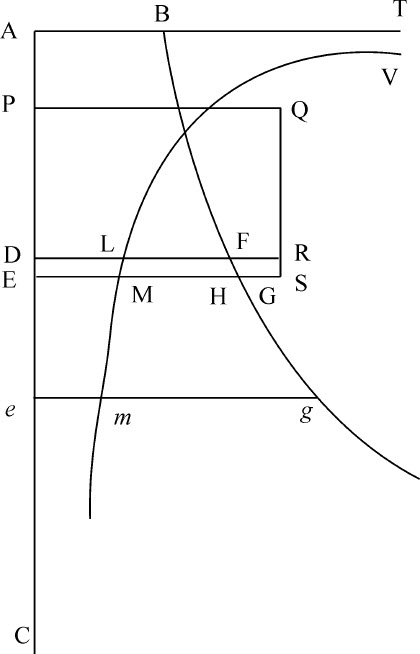
设物体E由任意处所A沿直线ADEC下落;在处所E设想一垂线EG总是正比于在该点指向中心C的向心力;令BFG为一曲线,是点G的轨迹。在开始运动处设EG与垂线AB重合;则在任意处所E物体的速度将是一条直线,其平方等于曲线面积ABGE。
完毕。
因为,在直线AE上取一段已知极小线段,令物体位D时直线EMG的处所在DLF;如果向心力使得一条直线,其平方等于面积ABGE,正比于落体的速度,则该面积将正比速度的平方;即,如果把在D和E处的速度记为V和V+I,则面积ABFD将正比于VV,而面积ABGE正比于VV+2VI+II;由减法,面积DFGE正比于2VI+II,所以 将正比于
将正比于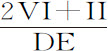 ;即,如果取这些量刚产生时的最初比值,则长度DF正比于量
;即,如果取这些量刚产生时的最初比值,则长度DF正比于量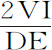 ,所以也正比于该量的一半
,所以也正比于该量的一半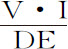 ,但物体掠过极小线段DE所用时间正比于该线段,反比于速度V;而力正比速度的增量I,反比于时间;所以,如果取这些量刚产生时的最初比值,则力正比于
,但物体掠过极小线段DE所用时间正比于该线段,反比于速度V;而力正比速度的增量I,反比于时间;所以,如果取这些量刚产生时的最初比值,则力正比于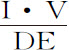 ,即正比于长度DF。所以正比于DF或EG的力将使物体以正比于其平方等于面积ABGE的直线的速度下落。
,即正比于长度DF。所以正比于DF或EG的力将使物体以正比于其平方等于面积ABGE的直线的速度下落。
完毕。
而且,由于掠过极小的给定长度DE所用的时间反比于速度,因而也反比于其平方等于面积ABFD的直线;又由于线段DL,因而刚产生的面积DLME,反比于同一直线,则时间正比于面积DLME,所有时间的和将正比于所用面积的和;即(由引理4的推论),掠过AE所用的全部时间正比于整个面积ATVME。
证毕。
推论Ⅰ.令P为物体应由之开始下落的处所,使得当它受到任意已知的均匀向心力(如常见的引力)的作用时,在处所D获得的速度,等于另一物体受任意力作用下落到同一处所D时所获得的速度。在垂线DF上取DR,它比DF等于该均匀力比在处所D的另一个力。作矩形PDRQ,分割面积ABFD等于该矩形,则A为另一个物体所由之下落的处所。因为作矩形DRSE,由于面积ABFD比面积DFGE等于VV比2VI,所以等于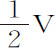 比I,即等于总速度的一半比下落物体受变化力作用产生的速度增量;用类似方法,面积PQRD比面积DRSE等于总速度的一半比下落物体受均匀力作用产生的速度增量;而由于这些增量(考虑到初始时间的相等性)正比于产生它们的力,即,正比于纵坐标DF,DR,因而正比于新生面积DFGE,DRSE;所以,整个面积ABFD,PQRD相互间的比正比于总速度的一半;所以,由于这些速度相等,它们也相等。
比I,即等于总速度的一半比下落物体受变化力作用产生的速度增量;用类似方法,面积PQRD比面积DRSE等于总速度的一半比下落物体受均匀力作用产生的速度增量;而由于这些增量(考虑到初始时间的相等性)正比于产生它们的力,即,正比于纵坐标DF,DR,因而正比于新生面积DFGE,DRSE;所以,整个面积ABFD,PQRD相互间的比正比于总速度的一半;所以,由于这些速度相等,它们也相等。
推论Ⅱ.如果任意物体被由任意处所D以给定速度向上或向下抛出,并且所受到的向心力的定律已给定,则它在任意其他场所,如e 的速度,可以这样求出:作纵坐标eg ,取该速度比在处所D的速度等于其平方为矩形PQPD,再加上曲线面积DFge ,如果处所e 低于处所D,或减同一面积DFge ,如果处所e 高于D的直线,比其平方刚好等于矩形PQRD的直线。
推论Ⅲ.时间也可以这样求得:作纵坐标em 反比于PQRD+或-DFge 的平方根,取物体掠过线段De 的时间比另一物体受均匀力由P下落到达到D所用的时间等于曲线面积DLme 比乘积2PD·DL。因为,物体受均匀力作用掠过线段PD的时间比同一物体掠过线段PE所用的时间等于PD与PE比值的平方根;即(极小线段DE刚刚产生),等于PD与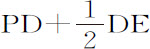 或2PD与2PD+DE的比值,由减法,它比物体掠过小线段DE所用的时间,等于2PD比DE,所以,等于乘积2PD·DL比面积DLME;两个物体掠过极小线段DE的时间比物体以变化运动掠过线段De 的时间,等于面积DLME比面积DLMe ;所以,上述时间中的第一个与最后一个的比等于乘积2PD·DL比面积DLme 。
或2PD与2PD+DE的比值,由减法,它比物体掠过小线段DE所用的时间,等于2PD比DE,所以,等于乘积2PD·DL比面积DLME;两个物体掠过极小线段DE的时间比物体以变化运动掠过线段De 的时间,等于面积DLME比面积DLMe ;所以,上述时间中的第一个与最后一个的比等于乘积2PD·DL比面积DLme 。
