第六章 巴斯噶定理
Chaper VI. Pascal's Theorem
§31 关于巴斯噶定理能否证明的两条定理
前面已经说过,德沙格定理(定理53)可以用公理Ⅰ,Ⅱ,Ⅳ* 证明,这就是说,实质上用空间公理而不再用合同公理,就可以证明;在§23中曾经指出下述事实:若不用第一组中的空间公理和合同公理Ⅲ,则即使允许用连续公理 ,也还不能证明德沙格定理。
在§14中从公理Ⅰ1~3 ,Ⅱ~Ⅳ推证了巴斯噶定理(定理40),在§22中也同样地推证了德沙格定理,所以都是未用空间公理,而主要地用了合同公理。因此发生了下述问题:是否也能够在援引空间的关联公理之下 ,不用合同公理 ,而证明巴斯噶定理,我们的研究将要指出,在这方面巴斯噶定理完全和德沙格定理不同,表现在证明前者时,阿基米德公理的容许或排除 ,对它的成立具有决定性的影响。由于在本章中一般不假设合同公理,所以,必须给阿基米德公理以如下的形式,作为根据:
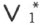 (线段计算的阿基米德公理) 设在一直线g 上给定一条线段A 和两个点A 和B ,则恒能求得一些点A 1 ,A 2 ,…,A n-1 ,A n ,使得B 在A 和An 之间,而且线段AA 1 ,A l A 2 ,…,A n-1 A n 等于线段a ;所谓等于是指在线段计算的意义下的等于,而线段计算按照§24根据公理Ⅰ,Ⅱ,Ⅳ* 和德沙格定理所能在g 上引进的【68】 。
(线段计算的阿基米德公理) 设在一直线g 上给定一条线段A 和两个点A 和B ,则恒能求得一些点A 1 ,A 2 ,…,A n-1 ,A n ,使得B 在A 和An 之间,而且线段AA 1 ,A l A 2 ,…,A n-1 A n 等于线段a ;所谓等于是指在线段计算的意义下的等于,而线段计算按照§24根据公理Ⅰ,Ⅱ,Ⅳ* 和德沙格定理所能在g 上引进的【68】 。
我们研究的主要结果可以综合成下述的两条定理:
定理57 根据公理Ⅰ,Ⅱ,Ⅳ ,V1 ,即不用合同公理而借助于阿基米德公理,能证巴斯噶定理(定理40)。
定理58 根据公理Ⅰ,Ⅱ,Ⅳ* ,即不用合同公理也不用阿基米德公理,不能 证巴斯噶定理(定理40)。
根据普遍的定理56,在这两条定理的叙述中,也可以不要求空间公理I4~8 ,而要求有一个具有德沙格定理(定理53)的平面几何。
§32 阿基米德数系中的乘法交换律
定理57和定理58的证明,实质上根据算术的运算律和基本事实之间的某种相互关系。这种关系的知识本身也有兴趣。我们先证下述两条定理。
定理59 对于一个阿基米德数系,乘法的交换律是其余的运算律的一个必然的推论;这就是说,若一个数系具有§13中所列举的性质1~11,13~17,则必然它也适合性质12。
证明 首先注意:若a 是这数系的任意一个数,而且
n =1+1+…+1
是一个正有理整数,则对于a 和n 乘法交换律恒成立;实际上
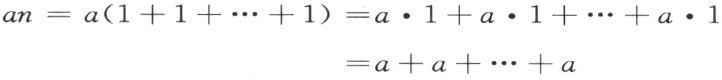
而且同样地
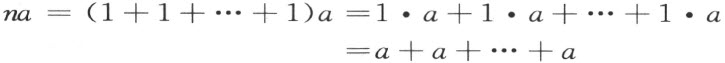
现在假设和我们的论断相反,数系中有两个数a ,b ,对于它们交换律不成立,显然,我们能够假设
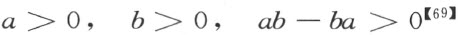
因为§13中的要求5,存在一个数c (>0),使得
(a +b +1)c =ab -ba
再者,取一数d ,同时适合下述不等式
d >0,d <1,d <c
最后,用m 和n 表示使得下述不等式
md <a ≤(m +1)d
nd <b ≤(n+1)d
分别成立的两个非负的有理整数。m 和n 这两个数的存在是阿基米德定理(§13中的定理17)的直接推论。考虑到本证明开始时的注意,我们从上两个不等式经由乘法得到

这不等式和数c 的决定矛盾,因此定理59得证。
§33 非阿基米德数系中的乘法交换律
定理60 对于一个非阿基米德数系,乘法交换律不是 其余的运算律的一个必然的推论;这就是说,存在一个数系,它具有§13中所列举的性质1~11,13~16——即根据§28,一个德沙格数系——但其中乘法交换律(12)不 成立。
证明 设t 是一个参数,而且T 是下述形式的、含有有限项或无穷多项的任意一个式子。

其中,r 0 (≠0),r 1 ,r 2 ,…是任意有理数,n 是任意一个有理整数 。还把0这个数添加到这些式子的域T 中。两个这样形式的式子T 叫做相等,如果它们之中的所有的对应的数n ,r 0 ,r 1 ,r 2 …都成对的相等。再设S 是另一个参数,而且S 是下述形式的、含有有限项或无穷多项的任意一个式子:
。还把0这个数添加到这些式子的域T 中。两个这样形式的式子T 叫做相等,如果它们之中的所有的对应的数n ,r 0 ,r 1 ,r 2 …都成对的相等。再设S 是另一个参数,而且S 是下述形式的、含有有限项或无穷多项的任意一个式子:
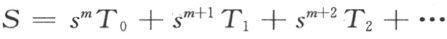
其中,T 0 (≠0),T 1 ,T 2 …是具有形式T 的式子,m 是任意一个有理整数 。把0这个数添加到具有形式S 的全体式子的集合,再规定下述的运算律,把这集合看做一个复数系Q (s ,t )。
。把0这个数添加到具有形式S 的全体式子的集合,再规定下述的运算律,把这集合看做一个复数系Q (s ,t )。
首先,参数s 和t 本身的计算遵循§13中的规则7~11,而规则12换成下述公式

容易看出,这里的规定是无矛盾的。
现在,设S′ ,S ″是具有形式S的任意两个式子:
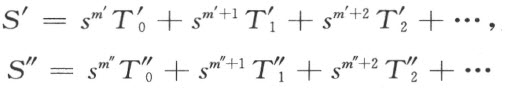
显然,我们能够逐项相加,作成一个新的式子S′ +S″ ;它仍旧有S 的形式,而且同时唯一的决定了;S′ +S″ 这式子叫做由S′ ,S″ 所表出的数的和。
把S′ ,S″ 这两个式子照通常一样的逐项相乘,我们又得到一个下述形式的式子。
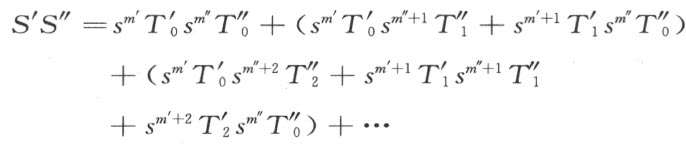
这个式子,利用公式(1)之后,显然变成一个唯一决定的具有形式S的式子;所得到的式子叫做S′ 所表示的数乘以S″ 所表示的数的积。
在计算方法如此规定的情形下,§13中的运算律1~44和6~11显然正确【70】 。§13中的规则5的正确性,也不难证明。为了这个目的,姑且设给定了具有形式S的两个式子是
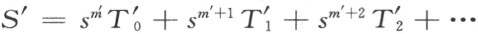
和
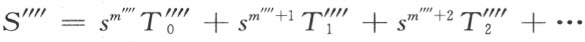
注意根据我们的规定,T ′0 中的第一个系数r ′O 必非0。现在比较方程

两端中S 的幂;首先唯一地决定一个整数m ″,作为幂指数,然后依次地决定式子

使得式子
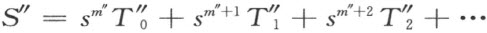
在公式(1)条件之下适合方程(2)。对于方程

也有相似的结果。这样便完成了所需要的证明。
最后,要使我们的数系Q (s,t )的数能够排成顺序,我们作下述规定:按照在表示一个数的式子S中T 0 的第一个系数r O <0或者r O >0,这个数就分别叫做<0或者>0。若a 和b 是这复数系中的任意两个数,按照a -b <0或者a -b >0,就分别说a <b 或者A >b 。在如此规定的情形下,立刻看出,§13中的规则13~16也有效,即Q (s,t )是一个德沙格数系(参看§28)。
§13中的规则12在我们的复数系Q (s,t )中不 满足,如同方程(1)所指出的;因此定理60完全证明了。
由于定理59,所以在刚才所建立的数系Q (s,t )中,阿基米德定理(§13中的定理17)不成立。
§34 关于巴斯噶定理的两条命题的证明(非巴斯噶几何)
若在一种空间几何中,全体公理Ⅰ,Ⅱ,Ⅳ 都满足,那么德沙格定理(定理53)也成立,而且,根据§28中的最后一条定理,在这几何的每一对相交的直线上能够引进线段计算,适合§13中的规则1~11,13~16。若再在这几何中假设阿基米德公理V1 ,则对于这个线段计算阿基米德定理(§13的定理17)显然成立,从而,根据定理59,乘法交换律也成立。从所附的图(图76)可见,乘法交换律不是别的,正是对于这两条轴的巴斯噶定理。因此证明了定理57。
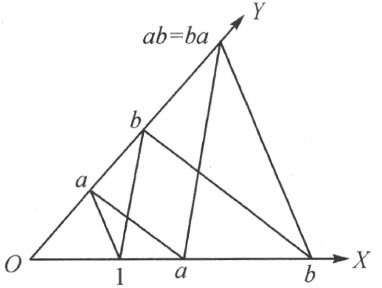
图 76
要证明定理58,取§33中所引进的德沙格数系Q (s,t ),而且按照§29中所描写的方法用这数系来建立一种空间几何,在这几何中全体公理Ⅰ,Ⅱ,Ⅳ* 都满足。虽然如此,巴斯噶定理不成立,因为乘法交换律在这个德沙格系数Q (s,t )中不成立。如此建立的“非巴斯噶几何 ”,由于这里所证明的定理57,必然也同时是一个“非阿基米德几何 ”。
即使这空间几何是任意高维的一种几何的一部分(这高维的几何中除点、直线、平面之外,还有别种元素;而且作为根据的有一组相应的关联公理,顺序公理,以及平行公理),在我们的假设之下,巴斯噶定理还显然不能证明。
§35 利用巴斯噶定理来证明任意交点定理
首先,证明下述重要的事实:
定理61 只用公理Ⅰ1~3 ,Ⅱ,Ⅳ* ,因而不用合同公理和连续公理,能从巴斯噶定理(定理40)证明德沙格定理(定理53)。
证明 (1) 定理53的两部分的每一部分,显然是另一部分的直接推论。因此,只需要证明其中的一部分,例如第二部分。首先,我们增加假设,在附加的假设之下完成证明。
设三角形ABC 和A′B′C′ 的位置如下(图77):对应顶点的连线通过一点O ,而且AB 平行于A′B′ ,AC 平行于A′C′ 。我们再假设,直线OB′ 和A′C′ 不平行,直线OC′ 和A′B′ 也不平行。现在作OB′ 的通过A 的平行线,交直线A′C′ 于一点L ,交直线OC′ 于一点M 。其次再假设直线LB′ 既不平行于OA ,又不平行于OC 。直线AB 和LB′ 断然不平行,即它们有一交点N;把N连到M 和O 。
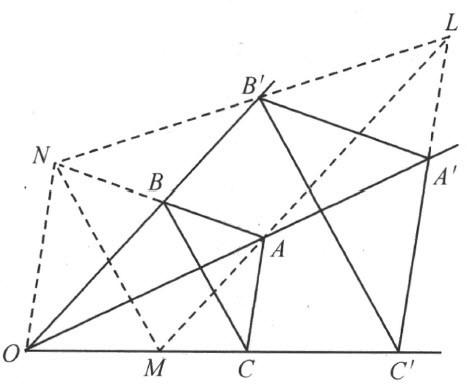
图 77
根据作图,巴斯噶定理能应用到构形ONALA′B′ 上去,因此可知,ON 平行于A′L ,也平行于CA 。现在,巴斯噶定理也能应用到构形ONMACB 和ONMLC′B′ ,而得到MN 既平行于CB ,也平行于C′B′ 。所以边CB 和C′B′ 平行。
这证明中所作的附加假设,可以一个一个地去掉。去掉附加假设的这部分的证明,我们这里省略了【71】 。
设现在有一种平面几何,其中除公理Ⅰ1~3 ,Ⅱ,Ⅳ* 之外,巴斯噶定理还成立。定理61告诉我们,在这几何中德沙格定理也成立。所以在这几何中我们能按照§24引进线段计算;而且根据§34,对于这个计算,巴斯噶定理和乘法交换律同时成立,这就是说,这计算法遵循§13中的所有运算律1~12。
如果把相当于巴斯噶定理或德沙格定理的内容的一个图形叫做巴斯噶构形或德沙格构形,那么§24~§26和§34中的结果可综述如下:在我们的线段计算中,每一次应用运算律(§13的定理1~12)可以表为有限个巴斯噶构形和德沙格构形的一个组合,而且,既然通过适当的辅助点和辅助直线的作图(如同在证明定理61时所作的),德沙格构形能表为巴斯噶构形的组合,所以在我们的线段计算中,每一次应用所说的运算律可以表为有限个巴斯噶构形的组合。
按照§27中所说的和乘法交换律,在这线段计算中,一个点用一对实数(x,y )表示,一条直线用三个实数的比【72】 (u :v :w )表示,其中前两个不同时是零,点和直线位置关联的条件是方程
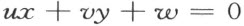
而且两直线(u :v :w )和(u′:v′:w′ )平行的条件是
u :v =u′:v′
设在如此给定了的几何中,有一条纯粹的交点定理。所谓一条纯粹的交点定理,所指的是具有下述性质的定理:只含有关于点和直线的位置关联以及关于直线的平行性的叙述,而同时不用其他关系(如合同和垂直)。平面几何的每一条这种的纯粹的交点定理都可以表述如下:
首先任意取一组有限个点和直线,然后按照预定的方式作这些直线中的某些任意平行线,在这些直线中的某些直线上取任意点,而且通过这些点中的某些点作任意直线;在按照预定的方式作了连线,交点以及通过已经存在的点的平行线之后,终于得到一组有限条直线,它们就是定理所论断的、通过同一个点或互相平行的直线。
开始时我们完全任意取了点和直线,把它们的坐标看做是参数P 1 …,P n ,然后我们又在有限度的任意性之下取了点和直线,它们的若干坐标能够看做是另一些参数P n+1 ,…,P r ,其余的都将由P 1 ,…,P r 这些参数决定了。以后再作出的所有的连线,交点和平行线的坐标,都是依赖于这些参数的诸有理式A (P 1 ,…,P r )。在这样的情形下,所要证明的交点定理的内容化为下述的论断:当参数值相同时,某一些这种的式子取相同的值;换句话说,交点定理就是说:当参数P 1 ,…,P r ,用所讨论的几何中所引进的线段计算中的任意元素代入时,这些参数的某一些完全确定的有理式R (P 1 ,…,P r )都等于零。既然这些元素的域是无穷的,我们从一条已知道的代数定理得到下述结论:在 §13中的运算律 1~12的基础之上 ,这些式子R (P 1 ,…,Pr )恒 等于零【73】 。但是要想证明式子R (P 1 ,…,P r )在我们的线段计算中恒等于零,根据我们在上文所证明了的关于应用运算律的事实,应用巴斯噶定理就足够了。这样,我们证明了下述结论:
定理62 设一种平面几何中,公理Ⅰ1~3 ,Ⅱ,Ⅳ* 都满足,而且巴斯噶定理正确。这几何中的每一条纯粹的交点定理,可以通过作适当的辅助点和辅助直线,表为有限个巴斯噶构形的组合。
于是,利用巴斯噶定理,交点定理的证明就不需要再求助于合同公理和连续公理。
历史的注记
关于第五章和第六章的发展的研究始于韦纳(Hermann Wiener)“关于几何学的基础和建立”(über Grundlagen und Aufbau der Geometrie)一文中所作的探讨。此文是1891年在哈雷(Halley)举行的自然研究会议上所作的报告(参看韦纳于Jahresber.d.Deutschen Mathem-Vereiaigung,Bd.I 45—48页(1892)上所发表的文章)。韦纳也是在“Bereichten. der Kgl. Sächs Ges. d. Wiss., Leipzig 1890, 1891, 1893上所连续刊登“可换的双镜面反射变换”(Verta uschbare Zweispiegelige Verwandschaften)的作者.
————————————————————
(1) 这里所指出的定理61的证明,源于赫森堡“从巴斯噶定理证明德沙格定理”(Beweis des Desarguesschen Satzes Aus dem pascalschen; Math. Ann.卷61)。
