《世界的和谐》导读

《世界的和谐》导读

杨建邺

（华中科技大学　教授）

• Chinese Version Introduction •

开普勒直率地承认毕达哥拉斯和柏拉图为他的理念上的老师，他坚信他们的理想的宇宙图式是被完美的数学音乐统治的。他的天体和谐的观点的与众不同之处在于天体的音乐头一次被认为是复调音乐。……他不停地强调，复调音乐是古人所不知（将伽利略《古代音乐与现代音乐的对话》引为他的经典），他声称，他的新天文学在宇宙哲学中将是一个伟大的进步，就像复调音乐在音乐中一样。

《世界的和谐》导读 - 图1

开普勒用正多面体说明行星的运动。

《世界的和谐》 ⁽¹⁾ 是德国天文学家开普勒（Johannes Kepler，1571—1630）最辉煌的一部著作，出版于1619年。读者面前的这本书，不是《世界的和谐》的全文，只是其中的第五卷。

《世界的和谐》全书分为五卷：第一卷几何学，第二卷构型学，第三卷形而上学，第四卷谐音学，第五卷天文学。前两卷属于基础知识介绍：第一卷讨论圆内接正多边形的演示和构型；第二卷讨论如何把正多边形按一定的原则配置成正多面体的组合系列，以及由此表现出来的数的和谐。这两卷均以欧几里得的《几何原本》为蓝本，由一系列定理、公式逻辑地组成。后三卷以前两卷的数学、构型为依据逐步展开。第三卷把与正多面体构型相对应的数的关系，用来解释音乐中感受到的谐音（值得一提的是，在第三卷的附录里，开普勒还大胆地把和谐的原理扩大到人间事物上，“天上地下，只要和谐持续着，一切都生机勃勃，一旦和谐受到了干扰，一切都会杂乱无章”，这种深刻而伟大的信念，至今仍然是人类社会和自然界运行的最高原则）；第四卷是在确立了和谐的几何原型之后，着重寻求几何学、音乐及行星运动间和谐比例之间的联系；第五卷说明了谐音原理也可以用行星角速度极值来表示。

在第五卷里，开普勒提出了十个问题：

1．五种正多面体的形状；

2．五种正多面体与和谐比例的关系；

3．天体和谐所必需的天文学原理概要；

4．与行星运动相关事物中表现出和谐的比例；

5．音乐的音高或音阶，各种和谐、大调和小调，都在星星 ⁽²⁾ 的视运动中表现出来；

6．某音调或调式，必以某种方式表现于行星的运动；

7．六颗行星的和谐比例彼此不同，就像四声部对位；

8．四声部表现于行星运动就是女高音、女低音、男高音和男低音；

9．每颗行星运动特有的偏心率，起源于行星运动的和谐比例；

10．结语——关于太阳的一些猜想。

这十个问题在本书里分属于十章，其中第三章的标题是“研究天体和谐所必需的天文学原理之概要”；这一章的第八节以谐音理论为依据，给出了著名的“行星运动第三定律”（又称“和谐定律”），揭示了行星在天空运行中的时空关系。第三定律的发现是开普勒最重要的科学成就之一，由此奠定了他作为现代天文学的开创者的地位。

《世界的和谐》不仅是宇宙结构和谐观的壮丽诗卷，也是近代科学史上第一个具有严谨逻辑的科学体系。开普勒所处的时代，正是科学发生伟大变化的时期，这个时期科学正努力从古希腊和中世纪的一些科学偏见中挣脱出来；这是一个史无前例的变革和发展的时期。正是在这关键的变革时代，开普勒的发现为后来牛顿的伟大发现铺平了道路。

开普勒深知这本书的重要价值，所以在第五卷的序言中抑制不住自己的欢乐写道：

出人意料的是，我惊奇地发现，这本书的几乎整个第三卷在1500年前就已经讨论了天体的和谐。不过在那个时候，天文学还远没有成熟，托勒密通过一种不幸的尝试，可能已经使人陷入了绝望。他就像西塞罗（Cicero）笔下的西庇阿（Scipio），似乎讲述了一个令人惬意的毕达哥拉斯之梦，却没有对哲学有所助益。然而粗陋的古代哲学竟能与时隔15个世纪的我的想法完全一致，这极大地增强了我把这项工作继续下去的力量。……从18个月前透进来的第一缕曙光，到3个月前的一天的豁然开朗，再到几天前思想中那颗明澈的太阳开始尽放光芒，我始终勇往直前，百折不回。我要纵情享受那神圣的狂喜，以坦诚的告白尽情嘲弄人类：我窃取了埃及人的金瓶，却用它们在远离埃及疆界的地方给我的上帝筑就了一座圣所。如果你们宽恕我，我将感到欣慰；如果你们申斥我，我将默默忍受。总之书是写成了，骰子已经掷下去了，人们是现在读它，还是将来子孙后代读它，这都无关紧要。既然上帝为了他的研究者已经等了6000年，那就让它为读者等上100年吧。

为了让读者能够更好地理解这本书，读者需要大致了解开普勒的人生经历和他的学术思想。

一、天体的运动只不过是某种永恒的复调音乐

当读者翻到这本书的49页的时候，将会看到一段奇怪的五线谱。读者也许会惊讶地想到：这是一阕什么乐曲？是巴赫的《勃兰登堡协奏曲》？是舒伯特的《野玫瑰》？还是贝多芬的《第五交响曲》？也许你想问的问题还不少，其中还会有一个共同的疑问：这本书不是讲世界的和谐吗？怎么会出现一段五线谱？而且前后还有不少论述这些乐谱的段落。

这段乐谱在音乐史上没有什么地位，它既不是巴赫、舒伯特的作品，也不是舒曼和贝多芬以及任何一位作曲家的作品，但在物理学史以及人类认识宇宙的历史上，却有重大的价值。开普勒是毕达哥拉斯（Pithagoras，公元前约560—公元前约480）的忠实信徒，对音乐和天文学之间的密切关系，有着很深刻的看法。他在书中曾经写道：

天体的运动只不过是一首带有不谐和调音的（理智上的，而不是听觉上的）永恒的复调音乐 ⁽³⁾ ，犹如某种切分或终止式（人们据此模仿那些自然界的不谐和音），趋向于固定的、被预先规定的解决（每一个结束乐句都有六项，就像六个声部一样），并通过那些音区分和表达出无限的时间。因此，人类作为造物主的模仿者，最终能够发现不为古人所知的和谐歌唱的艺术，以使其能够通过一种多声部的人造的协奏曲，用不到一个小时的短暂时间去呈现整个时间的永恒；人通过音乐这上帝的回声而享受到天赐之福的无限甜美，从这种快感中他可以在某种程度上品尝到造物主上帝在自己的造物中所享有的那种满足。

美国科学作家杰米·詹姆斯（Jammie James）在他写的《天体的音乐——音乐、科学和宇宙的自然秩序》（The Music of Celestial Body——Music，Science，and the Nature Order of Cosmos ）一书中说：

二、毕达哥拉斯的信徒

开普勒于1571年12月27日生于德国中部符腾堡（Württemberg）地区的小镇魏尔（Weil）。他刚刚出生的时候体质极为孱弱，接生婆还以为这个婴儿未见得能够存活下来。

他的祖父曾经是魏尔镇十分活跃的新教倡导人，还一度担任镇长。到了父母这一代，家事开始衰落，始终没有脱离贫困之苦。父亲脾气暴躁，母亲非常任性，很难相处。父亲为躲避家里婆媳无止境的争吵，长期在军队服役，成为一位职业军人。后来在一次征战结束回家途中，突然因病死去。开普勒共有4个兄弟姊妹，3个夭折，活下来的只有他和弟弟，而弟弟又是一个癫痫患者。开普勒早年的命运十分凄惨：3岁时遭遇肆虐欧洲的传染病天花，不仅损坏了他的面容，还使得他一只手半残，视力也受到损害；而家境的贫寒又使他饱受穷苦之累，有时穷得只能乞住于乡村旅店之中，9岁时为了生活他做过佣人，直到12岁才在他人的帮助下回到学校。

人间的倾轧、无穷尽的苦难和亲人的死亡，从小在开普勒的心灵上留下了深深的伤痕。幸好他没有被苦难的命运击倒，反而由此磨炼了意志，寻求到解脱的办法。他从小就喜欢到教堂做晚祷，因为教堂那高高的圆形穹顶，管风琴美妙的和声在大厅的穹顶上回旋袅绕，对在苦难中的开普勒来说，就像是上帝的福音。《圣经》的引导、管风琴美妙的和声和诗歌班童声合唱，和谐地融合在一起，使他的心灵受到了很大的震撼。他得到了人间不能给予他的温暖、希望和力量，也从小就迷上了音乐。在肃穆静谧、和谐美妙的氛围里，这个残忍、粗暴、丑恶的世界，似乎远远地离他而去，在他面前展示的是美妙的音乐旋律，也孕育了他朦胧而美丽的梦想。

凭借与生俱来的禀赋加上后天的刻苦，1588年开普勒17岁时进入图宾根（Tübingen）大学神学院。在进神学院以前，开普勒对天文学并没有多大兴趣，他热衷的是神学，希望日后能当一个牧师，为上帝传播福音。没想到在图宾根神学院，由于天文学教授马斯特林（Michael Masterlin，1550—1631）的影响，他的兴趣开始转向了天文学，并接受了哥白尼的日心说。他曾经说过：

早在图宾根时期，当我仔细地领会著名的马斯特林的教导时，我感到迄今为止对于宇宙结构的惯常观念是多么笨拙！因此，哥白尼使我欢欣鼓舞，我的老师马斯特林在他的讲座中经常提及哥白尼。我不仅在同学们的讨论中反复主张他的观点，而且对于引起地球转动的第一次运动（恒星天空的革命）的问题进行了仔细的讨论。我已经积极开始从事这个工作，即把地球对于太阳的运动建立在物理学的基础上，如果你愿意，也可以说，是把运动建立在形而上学的基础上，犹如哥白尼把地球对于太阳的运动建立在数学的基础上。……在这一方面，哥白尼远胜过托勒密。

在神学院求学期间，他甚至写了一卷论述哥白尼理论的短文。1591年，开普勒以全班第二名的优秀成绩毕业于图宾根神学院。毕业后，开普勒本来想在教会中找到一个职位，但由于他信奉被教会视为洪水猛兽的哥白尼日心说，从而失去了担任教会职务的可能性。

1594年，在马斯特林的帮助下，开普勒在奥地利格拉茨（Graz）神学院谋到一个数学讲师的职务。从此，他把当牧师的想法抛到了九霄云外，一心一意开始研究行星问题。开普勒以他渊博的知识和过人的天分很快就在格拉茨神学院得到校方高度的好评：“毫不夸张地说，开普勒是一位年轻的、受过良好教育的和虚怀若谷的教师。我们这样的学院能够拥有他这样出色的教师，真是万幸。”

教书之余，开普勒继续研究行星运动的规律。开普勒信奉毕达哥拉斯主义。毕达哥拉斯发现数和音乐之间存在令人惊讶的和谐关系。英国著名数学家、诗人和科学作家布伦诺斯基（Jacob Bronovski，1908—1974）在他写的《人的上升》（The Ascent of Man ）一书中写道：

毕达哥拉斯发现，发出悦耳音的和弦对应于整数的分弦点。对于毕达哥拉斯学派的人来说，这个发现里面有一股神秘的力量。自然与数字之间的和谐如此确切，因而使他们相信，不仅仅自然的声音，而且自然所有特征性的尺度，都一定有一些简单的数字来表达其和谐之处。例如，毕达哥拉斯或其弟子相信，我们应该能够计算出天体的轨道（希腊人在结晶体上画的画认为天体围绕地球转动），比如使其与音乐的间隔产生关系。他们感觉到，自然当中所有的规律都有音乐性，天体的运行在他们看来就是球体的音乐。

毕达哥拉斯学派认为，数先于自然界整体，它的特征内在于音阶、天体和宇宙万事万物。离开了数，就没有任何事物能够存在或者被认识。研究宇宙万事万物的唯一途径，就在于研究大自然内在的数学结构。这种结构的外在表现就是数的和谐，就是对称和美。这种和谐是宇宙万事万物共同的内在本质。正是这种内在的、先验的共同本质，使得人类具有正确认识宇宙的可能性。这种观点，在现代科学探究中也会常常被重复提到。例如杨振宁在一次访谈中就说过：

杨振宁：当我们发现自然界的一个秘密时，一种敬畏之情就会油然而生，好像我们正在瞻仰一件我们不应瞻仰的东西一样。

莫耶斯：不应该瞻仰？难道属于禁区？

杨振宁：是的。因为它具有一种神圣的色彩，一种力量的张力。当你面对它时，你会自然而然地产生一种感觉：它不应该被我们凡人窥视到。我一直把这种情结看做是一种最深的宗教情结。当然，这让我想到一个没有人能够回答的问题：为什么自然界是这样而不是那样？为什么最终可以把大自然这些强大的力量，都简化为一些简单而又美丽的方程式呢？这个问题有许多人探讨过，争论过，但始终都得不到答案。不过，事实在于，我们既然有认识它的可能，就有进一步深入认识的可能。而这正是吸引我们不断前进的原因所在。我们想建造一些机器，不是因为我们想把40亿美元的资金随意挥霍掉，也不是因为我们沉迷于将发现的基本粒子进一步分类编目。这些都绝对不是真正的原因，真正的原因在于大自然具有一种神秘的、里面含有力量的东西——而且，还有异乎寻常的美。

开普勒同样认为“大自然这些强大的力量，都简化为一些简单而又美丽的方程式”，因而行星运动的真实动因，应该到隐含有数的和谐精神的音乐里去寻找。

三、五种正多面体带来的灵感

在格拉茨神学院任职期间，开普勒最感兴趣的问题是：为什么行星有6颗？（当时只发现了6颗行星——水星、金星、地球、火星、木星和土星，其他行星是在他去世后才发现的）它们的轨道半径为什么恰好是8∶15∶20∶30∶115∶195这样一个比例？

这似乎纯粹是一个数字游戏，可是你可别小看它。从古到今，这种游戏所蕴含的美感常常给人以巨大的启迪，吸引着许多爱思考的人作出重大的科学发现。开普勒在《宇宙的奥秘》一书里说：

犹如创造眼睛是为了颜色，创造耳朵是为了音调，同样人类的智慧被创造是为了理解量，而不是为了理解任何别的事物。越是接近作为事物的源泉的纯数量，就越是能够正确地掌握这个事物。越是远离事物的量，就越是会陷入黑暗并出现错误。是我们智慧的本性使我们对于神圣事物的概念的研究复苏，这些概念是建立在量的范畴的基础之上的。如果丧失了这些概念，神圣的事物就只能用纯粹虚无来定义。

开始的时候，开普勒试着用平面几何图形的组合来推出行星轨道，结果失败了。

1595年7月的一天，灵感突然来了：“啊呀，我多傻啊！行星在空间运动，我怎么在平面上研究这些几何图形呢？应该用立体图形！”

思路一开，很快就有了可喜的突破。当时人们知道5种“规则的多面体”（即正多面体），古希腊数学家还证明过，大自然只可能有5种正多面体。柏拉图（Plato，公元前427—公元前347）在《蒂迈欧卷》里指出，这5种规则多面体是“神的形象的天体”，开普勒接受了这种观念，并曾说过“我企图证明，上帝在创造宇宙和规定宇宙秩序的时候，曾考虑到5种规则的几何立体（从毕达哥拉斯和柏拉图时代我们就已经知道它们），祂按照它们的大小，确定天体尺寸、数目、比例及其运动关系。”

开普勒的设想是，如果把5种正多面体与6个球形套合起来，不就有6个球吗？6个球的半径恰好对应6个行星的轨道——这实在是太美妙了！开普勒相信，这就是只有6个行星的奥秘所在！开普勒的具体方法是这样的：开始以一个球形作地球的轨道，在这个球形外面配一个正12面体，这个正12面体的12个面与球形相切，12面体外面作一个圆球，这个圆球是火星的运动轨道；火星球外面作正4面体，再在它外面作一个圆球，得出木星轨道；木星球外作一立方体，立方体外面的球就是土星轨道；在地球轨道的球形内作正20面体，20面体内的球形是金星的轨道；金星球内作正8面体，其内的球就是水星的轨道。根据这种方法得出各轨道半径的比，与观测结果大体相同（差别大致上在5％以内），这使得开普勒非常兴奋：

我永远无法用语言来描述我从自己的发现中获得的快乐。现在我再也不惋惜失去的时间，再也不厌倦工作，无论有多大困难，我也不回避计算。日日夜夜我不停地从事计算，直到我看见用公式的语言表达的句子与哥白尼的轨道完全吻合，直到我的欢乐被风吹走。我相信在这件事情上我已经正确地掌握了这个问题，我向全能而仁慈的上帝发誓，在第一个机会中我要把上帝的智慧这个令人惊叹的奇迹印刷出来公布于世。尽管这些研究尚未终结，在我的基本思想中尚有某些不明确的结论，这些发现我可以为自己保留，至于其他可能的结论，如果有谁关注这个问题，他应该和我一道做出尽可能多的发现以荣耀上帝的名，并且一致歌颂以使赞美和荣耀归于全智全能的创造者。

杰米·詹姆斯在《天体的音乐》一书中也写道：

“当他开始向第三维的跳跃的时候，最后的晴空霹雳震撼了他，完美的立体数字是5，正好是描述行星天体间的区间所需要的数字。这完美的立体，相当恰当地被称做毕达哥拉斯学派的立体和柏拉图的立体，这么叫是因为它们完美地左右对称；它们的正面都是相同形状和大小的有规则的多角形。这是几何的事实。”

1596年底，开普勒把他的这一发现写进了《宇宙的奥秘》（Mysterium Cosmogra phicum ）一书，在书中他又一次热情洋溢地写道：

七个月以前，我曾许诺写出一部将会使学者们认为是优雅的、令人惊叹的、远胜于一切历书的著作，现在，我把她奉献给你们。这部著作卷幅虽小，都是我微薄努力的结晶，而且论述的是一个奇妙的课题。如果你们期望成熟——毕达哥拉斯在两千多年前就已经论述过这一课题。如果你们追求新奇——这是我本人第一次向全人类提出这一课题。如果你们要广度——再没有比宇宙更宏伟更广阔的了。如果你们向往尊严——没有什么能比上帝的壮丽殿堂更尊贵更瑰丽。如果你们想知道奥秘——自然界中没有比这更（或从来没有比这更）奥妙的了。只有一个原因使我的论题不能让每个人都感到满意，因为无思想者是看不到其用处的。圣保罗告诫异教徒要从自己身上去反思上帝，就像从水或镜子中反照出太阳一样。难道我们基督徒就不该乐于进行这种反思？因为我们责无旁贷的使命就是以真正的方式去称颂、崇拜和赞美上帝啊。我们这样做得越虔诚，就越能深刻地认识上帝创造的天地万物及其宏伟。神的忠实仆人——大卫赞美道：诸天述说他的荣耀，穹苍传扬他的手段。那么，苍天和星星会说话吗？它们能够像人一样赞美上帝吗？不，当我们说它们自己赞美上帝时，只是因为它们为人类提供了赞美上帝的思想。所以，下面我们就来解开苍天和大自然的歌喉，以使它们再次高唱……

开普勒还提出了一个含糊但却很有启发性的猜想：太阳将沿着光线辐射方向给每个行星一种推动作用，使它们沿着各自轨道运动，而且猜测这种作用对于较远的行星会减弱。这个猜想虽然模模糊糊也不正确，但却帮助他后来发现了一条重要定律。

这本书使得年轻的开普勒一举成名。当他50岁的时候，他还没有忘记这本书给他带来的启示：“我整个的生活方向，我的研究和著作无不从这本小书出发。”

现在我们知道，开普勒所重视的五种正立方体图形与行星运动轨道只是碰巧合适，而且即使在当时与观测资料也并不完全符合。在更多的行星发现以后，这种图形就失去了价值。正如詹姆斯所说：

开普勒追逐天体音乐的幻想是在浪费他的时间。对于像泡利 ⁽⁴⁾ 这样的人来说，天堂就像坟墓一样寂静，并且是开普勒自己开创的“数学的逻辑思想”使它们变得沉默的。然而，显然开普勒的意图是用（或者在需要的地方发明）大部分现代天文的和数学的方法来挽救毕达哥拉斯学派的宇宙观。他的工作做得太好了；在开普勒之后，天体的音乐从科学中不可挽回地分开了，永远地退到模糊的深奥的幽深处。然而，开普勒是最后一位试图向这些隐秘处照射光亮的伟大的科学家。

但是，我们切不可低估开普勒的这次可贵的努力，他的《宇宙的奥秘》至少有两点开创性的价值：一是公开宣传哥白尼日心说，而且他的理论完全建立在这个学说的基础之上；二是他不仅仅试图用数的和谐来解释天文现象，而且试图找出现象后面的物理学原因。这与希腊天文学传统很不相同，已经具有现代天文学的理念。

诚如爱因斯坦（Albert Einstein，1879—1955，1921年获得诺贝尔物理学奖）所说，“在根本没有确信自然界是受规律支配的”情形下，开普勒曾经勇于去寻找“规律”，这本身就很了不起。找到的立脚点不合适这是可以理解的。正多面体的设想虽然错了，但是他用数字关系来研究天体运动规律，不能不说是一个伟大的创举。

1598年，奥地利爆发了严重的宗教冲突，开普勒只得逃到匈牙利。1599年，开普勒把他的《宇宙的奥秘》一书寄给刚到布拉格的第谷，并将自己的困境和疑难问题告诉了第谷。第谷对于开普勒的著作十分欣赏，于是在几次通信后，第谷就邀请开普勒到布拉格共同工作。他在信中写道：“来吧，作为朋友而不是客人，和我一起用我的仪器观测。”

四、八分的误差引出了伟大的发现

1600年初，开普勒来到了布拉格与第谷一起工作，开始了科学史上极富成效的合作。开普勒曾经说：

我认为，正当第谷和他的助手全神贯注研究火星问题时，我能来到第谷身边，这是“神的意旨”，我这样说是因为仅凭火星就能使我们揭示天体的奥秘，而这奥秘由别的行星是永远揭示不了的……。

第谷对于自己的观测资料本来是十分保密的，从不让外人过目。但开普勒到他身边工作后，第谷十分欣赏这个年轻人，因此很快就允许开普勒接触他极为珍贵的火星观测资料，并让开普勒和他共同研究火星的运动。

合作约一年时间，第谷因病去世。第谷在临终时，曾把他的全家人召到他的床前，要求家人保存他的资料，并委托助手开普勒继续编辑、校订和出版他的行星表。第谷没有选错人，因为开普勒不仅在1627年正式出版了《鲁道夫星表》（将星表命名为鲁道夫，是为了纪念第谷的赞助人鲁道夫皇帝），而且他还利用第谷的观测资料，发现了伟大的行星运动规律。

还有一件罕为人知的事，也许更能说明第谷选对了人。第谷死后，第谷的家人除了脾气像第谷一样暴躁以外，还非常贪婪。他们结成一帮把开普勒看成外人，违背死者的遗愿，不愿意把第谷的观测资料给开普勒。开普勒可以说费尽了心机，耍了不少花招，才使得这些极为宝贵的资料由他保管，没有散失。我们可以设想一下，如果这些宝贵的资料散失了，人类文明史会遭到多大的损失！要知道，牛顿正是在开普勒铺就的道路上走向成功的！

第谷的死对开普勒未尝不是一件好事，因为第谷根本不相信哥白尼的日心说，这就使得相信日心说的开普勒在第谷身边左右为难，施展不开手脚。第谷去世后，开普勒倒是可以自由自在地放开手脚大干起来。

当开普勒开始独立用第谷的观测资料研究火星运动时，发现火星如果真是做圆周运动的话，那就与第谷的观测资料有8′的误差（即1°的8/60）。在这一误差面前，开普勒清醒而敏锐地认定，在研究中他必须坚持三个基本原则：一是哥白尼的日心说；二是第谷观测资料的准确性 ⁽⁵⁾ ；三是毕达哥拉斯数的和谐。

这时，开普勒以非凡的创造性精神大胆扬弃一些不符合观测的传统观念。火星的运动轨道偏离圆轨道已经比较明显，与哥白尼认为行星运动一定是圆周运动的观点有了矛盾——以前第谷就因为这一点而怀疑和否定哥白尼的日心说。但开普勒既没有因此怀疑日心说，也没有怀疑第谷的观测资料，而是独辟蹊径地认为哥白尼的日心说里的“圆周运动”值得怀疑。这种怀疑在当时可绝不是一件简单的事。英国学者詹姆斯·麦卡里斯特（James McAllister）在他写的《美与科学革命》（Beauty and Revolution in Science ）一书中指出：

17世纪初与哥白尼生活的时代一样，圆周被赋予了巨大的形而上学和审美价值。比如，在文学意象中圆周继续被看成最重要的图形。比较起来，椭圆被看成审美上不悦人的。尽管今天我们通常把圆周看成椭圆的一种特殊情况，即两个轴长度相等的情况，但在16世纪和17世纪初期，椭圆则被看成扭曲的和不完美的圆周。

17世纪初期的天文学家都具有对圆周的这一偏爱，开普勒也不例外。许多人都认为圆周是适于天体运动的唯一形状。

1602年，开普勒决定摒弃火星运行轨道是圆周的假说，而把它视为卵形。这年10月他曾经指出：“行星轨道不是圆。这一结论是显而易见的——有两边朝里面弯，而相对的另两边朝外凸伸。这样的曲线形状为卵形。行星的轨道不是圆，而是卵形。”

在作出火星轨道是卵形这一结论之后，开普勒又花了3年时间才最终确定火星的轨道实际上是椭圆。而且发现火星椭圆运动轨道的猜想与观测资料非常一致。这样，古希腊以来统治天文学两千余年的星体必作圆周运动这一“符咒”，被一笔勾销。进一步的研究证明，不仅仅是火星，而且所有行星运动的轨道都是椭圆，太阳在椭圆的一个焦点上。这就是开普勒的“行星运动第一定律”（也称“椭圆定律”）。

接着，开普勒又证实，行星在椭圆轨道上，有时离太阳远，有时离太阳近，离太阳远时行星运动得比较慢，离太阳近时则运动得较快。这样，星体作神圣的“匀速”运动也被抛弃。不过还有一点让开普勒聊以自慰的是，行星沿椭圆轨道上的运动还是遵循着一种规律的，它们并不是信马由缰地乱蹦瞎窜。这个规律就是开普勒第二定律：由行星到太阳联一条线（学名叫“矢径”），这条线在相同的时间内扫过的面积相等（所以这个定律也称“面积定律”）。

“均匀性”这一和谐的“美学标准”总算以另一种面貌展现在人们面前！

这里值得注意的是，第一定律的发现有第谷的观测资料为契机，那么第二定律发现的契机是什么？原来，在确定行星沿椭圆轨道运动以后，开普勒迫切希望了解：“为什么行星偏爱椭圆运动？行星运动的原因是什么？”这是以前天文学家包括哥白尼从未提出过的问题。

1605年，开普勒在写给一位朋友的信中表达了他追求的目标：

我一心想探讨其中的物理原因。我的目标是想证明天体的机器不宜比作神圣的有机体，而应该比作一座时钟。因为几乎所有这些各种各样的运动，只是借助于单一的、十分简单的磁力而形成的，就像时钟的各种运动只是由于一个重锤造成的一样。此外，我还可证明，这个物理概念可以通过计算和几何学表示出来。

这就是说，开普勒认为天体仿佛是一个大钟，被一个单一的力所驱动，而且这个力与地球上所具有的力应该具有同质性。这是一个天才的、划时代的预言，也是开普勒不同于同时代天文学家的独特之处。

开普勒与英国物理学家吉尔伯特（William Gilbert，1544—1603）一样，认为太阳是一个巨大的磁石，绕太阳旋转的每一个行星是小的磁石。行星正是靠着太阳的这种磁力绕太阳旋转；在旋转的时候，行星时而北极面向太阳，时而南极面对太阳，于是太阳对各个行星时而吸引、时而排斥。正是这一物理学原因使得行星偏离正圆轨道而沿着椭圆轨道运转。这种磁力作用又使开普勒“看”到了“矢径”，并由此推出了面积定律！

英国剑桥大学研究员米歇尔·霍金斯（Michael Hoskin）在他主编的《剑桥插图天文学史》里，对开普勒用磁力思考行星的运动这件事情写道：

这种物理直觉后来被证明是具有决定性的。例如，在关键的时刻，它导致开普勒认识到他必须将行星轨道与真实的、物理上的太阳联系起来；……它使得开普勒将他的注意力集中到了由太阳之力造成的实际的行星轨道上，而他的前辈们则全神贯注于分立的几何结构——本轮等等——所生成的轨道上。

开普勒将他的这些新发现写进《新天文学》（Astronomia Nova ）一书，它的全称是《新天文学：基于原因或天体的物理学，关于行星运动的有注释的论述》，1609年出版。开普勒在书里表达了他的信念：研究地面物体运动的物理学和研究天体运动的天文学“彼此密切相关，没有一种可以离开另一种而达到完美”。他力图用一个动力学理论，代替古希腊的只有几何结构的天文学理论。因此，开普勒是现代天体力学的奠基人。

开普勒提出的理论，由于与传统的天体作圆周匀速运动的美学标准不一致，受到了朋友们和同事们的强烈反对。他的朋友、德国天文家法布里修斯（David Fabricius，1564—1617）对开普勒说：“你用你的椭圆废除了天体运动的圆周性和均匀性，当我的思考越是深入，我越觉得这种情况荒谬。……如果你能保留正圆轨道，并且用另外的小本轮证明你的椭圆轨道的合理性，那情况会好得多。”

开普勒的另一个朋友英国哲学家罗伯特·弗拉德（Robert Fludd，1574—1637）在他的《宏观世界历史》中，极力谴责开普勒的数学“粗俗”、“低俗”，以及“开普勒太快地陷入了污秽和泥土里，太牢固地受到看不见的脚镣的束缚而不能让他自由”。

这意味着法布里修斯和弗拉德并不相信第谷的观测资料，他们绝对相信的是传统的美学标准。甚至于连非常重视实验观测的伽利略（Galilei Galileo，1564—1642）都不相信椭圆轨道，在他1632年出版的《关于两大世界体系的对话》（Dialogue Concerning the Two Chief World Systems ）一书中写道：“只有圆周运动能够自然地适宜于以最佳配置组成宇宙的各个组成部分。”

伽利略像当时许多天文学家一样，没有摆脱传统的审美观念，他没有把他的反传统的智慧和勇气延伸到这个问题上。他坚持认为天体运动是一种与地球上物体运动截然不同的天然的、无始无终的、最完美、最和谐的匀速圆周运动，是一种惯性运动（伽利略错误地认为匀速圆周运动是一种惯性运动），因而这种运动不需要力的作用，可以无止境地继续运动下去。正是由于这一错误的结论，使伽利略忽视了对万有引力的探索，没有把他在地面上得到的运动学和动力学规律扩展到天体运动上。这一错误还影响到其他人对万有引力的探索。

五、世界的和谐

开普勒在提出了行星运动第一定律和第二定律以后，对已经取得的成就仍然感到很不满意，这是因为各行星虽然各有自己的椭圆轨道半径和运动的速率，但是这些时间和空间量彼此之间没有联系，各行其道，似乎没有什么规律可循。对开普勒这位出色的音乐欣赏家和坚信数学、音乐、天体运动应该处于一个和谐的体系之内的人来说，他相信宇宙一定有一种内在的和谐规则隐藏在什么地方，使各行星之间遵守某种简单的数学规律的制约，不会彼此毫无关系。

正是因为他有这种坚定的信念，在发现第一和第二定律之后的十年里，开普勒又不知疲倦地继续观测行星运动和分析第谷的观测资料。1618年5月，开普勒终于从各个行星运动的观测数据中，发现一种内在的规律：

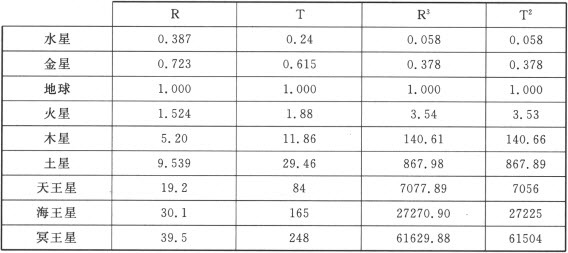
《世界的和谐》导读 - 图2

（表中R表示行星与太阳的平均距离；T表示行星绕太阳转动一周的时间）

由表中右边两列数据可以得到：T² ＝R³

这就是开普勒的行星运动第三定律：“行星绕太阳转动一周的时间（称公转周期）的平方，正比于它们与太阳平均距离的立方。”

这个定律又称“和谐定律”，它揭示了行星对太阳的距离和其公转周期之间的内在联系，这是一种时空的数学关系，一种隐藏的对称性。在本书第三章的第八部分，开普勒抑制不住内心巨大的喜悦叙述了这个著名的定律：

我在22年前由于有些地方尚不明了而置于一旁的《宇宙的奥秘》中的一部分，必须重新加以完成并在此引述。因为借助于第谷·布拉赫的观测，通过黑暗中的长期摸索，我弄清楚了天球之间的真实距离，并最终发现了轨道周期之间的真实比例关系。这真是——

虽已姗姗来迟，仍在徘徊观望，

历尽茫茫岁月，终归如愿临降。

倘若问及确切的时间，应当说，这一思想发轫于今年，即公元1618年的3月8日，但当时计算很不顺意，遂当做错误置于一旁。最终，5月15日来临了，我又发起了一轮新的冲击。思想的暴风骤雨一举扫除了我心中的阴霾，我在第谷的观测上所付出的17年心血与我现今的冥思苦想之间获得了圆满的一致。起先我还当自己是在做梦，以为基本前提中就已经假设了结论，然而，这条原理是千真万确的，即任何两颗行星的周期之比恰好等于其自身轨道平均距离的3/2次方之比，尽管椭圆轨道两直径的算术平均值较其长径稍小。

开普勒大悟：“天体运动不是别的，不过是几种声音汇成一种连续的音乐。这种音乐只能为心智所领悟，不能被人的耳朵听见。”

1618年5月27日开普勒完成了《世界的和谐》（Harmonice Mundi ）一书，1619年出版。这本书基本上是《宇宙的奥秘》一书的延续、修正和扩展。开普勒从几何学、音乐、占星学和天文学四个方面证实，宇宙结构是由和谐原理支配的。他不只是罗列出各种和谐关系，而是让和谐本身构成了一种普遍的科学理论基础。以前，哥白尼的学说用34个正圆解释了托勒密需要77个正圆才能解释的天体运动，而现在，开普勒只要7个椭圆，就把哥白尼用34个正圆都说不清的问题作出了成功的解释。这就使得宇宙的结构显得比以前更加和谐。从中我们可以悟出两个特点：一是开普勒对观测到的事实采取一种新的态度，从22年前用一个正多面体组合的几何模型作为解释的主要工具，22年后，他关注运动本身及其隐藏的数学关系，从静止不动的宇宙走向了运动着的宇宙；二是他成功地用几何、代数来表达物理的定律，从比较简单的几何关系走向了比较复杂的函数关系——行星运动第三定律。这两个特点对天文学和物理学的发展具有深远的影响。

行星运动第三定律的提出对现代科学的发展具有重大价值。可惜这个定律是如何发现的，开普勒没有详细说明。

开普勒显然非常重视这本书的出版，他高兴地写道：

在我见到托勒密“天体和谐”前很久我就坚定相信世界的和谐。在22年前，一当我发现天体轨道之中的5种正多面体时，我就更加肯定天体一定是和谐的，我还对我的朋友们作过许诺，一定要找到这种和谐。这本书在我尚未肯定我的发现（16年前，我作为一件事努力地去寻找）时就已命名。为了这个发现，我结识了第谷·布拉赫；为了这个我定居布拉格；也为了这个我把我生命中最美好的那部分时光奉献给了天文学的沉思。终于在我最意想不到的地方，我揭露而且认识了它的真理。自我第一次瞥见它的微光还不到18个月，自它破晓以来只有3个月，见到真理的阳光才只几天，它无比美妙地注视着我，突然来到我的面前。没有什么能制止我……

后来，开普勒根据他的行星运动三大定律制定的《鲁道夫星表》与观测到的行星位置充分吻合，因而又具有巨大的经验价值。正是这种经验价值，迫使许多天文学家先后承认了开普勒的理论。

詹姆斯·麦卡里斯特在《美与科学革命》一书中写道：

……起初天文学家很难确定开普勒理论的经验价值，他们熟悉圆周的数学性质却很少熟悉椭圆的数学性质，因而不能顺当地从该理论导出预言并用天文观测数据验证。1627年以后，开普勒理论的经验价值更为明显易见，此时开普勒出版了《鲁道夫星表》（Tabulae Rudolphinae ）。它汇编了用于预言月亮和行星位置的数据表和规则，依据的是开普勒的定律。本质上，它是对开普勒理论的观测结果的表格化，这样人们就容易对开普勒理论进行经验检验。天文学家很快发现，《鲁道夫星表》中提出的预言与观测到的行星位置充分吻合——甚至包括水星的观测位置，而这颗行星一直是最不受天文模型约束的。……许多同时代的天文学家都是由于有使用《鲁道夫星表》的经历而最终承认开普勒理论有巨大的经验价值。

德国天文学家克鲁格教授（Peter Crüger）的话表明了开普勒理论对他的影响：“我不再理会行星轨道的椭圆形式带给我的困扰。”

伏尔泰（Voltaire，1694—1778）说得更加犀利，他说：“我们以前都是瞎子。”

比开普勒晚出生两个世纪的黑格尔（G．W．F．Hegel，1770—1831）同样高度评价开普勒关于宇宙有序和谐的深刻信念，他把这一信念提升为开普勒的“伟大发现的唯一理由”。在黑格尔看来，开普勒的有序和谐是一种伟大的哲学思想，一种超越时代、超越历史和具有永久生命力的伟大哲学思想。

爱因斯坦在1930年为纪念开普勒逝世300周年发表的纪念文章《约翰内斯·开普勒》中写道：

在我们这个令人焦虑和动荡不定的时代，难以在人性中和在人类事务的进程中找到乐趣，在此时想起像开普勒那样高尚而淳朴的人物，就特别感到欣慰。在开普勒所生活的时代，人们还根本没有确信自然界是受着规律支配的。他在没有人支持和极少有人了解的情况下，全靠自己的努力，专心致志地以几十年艰辛的、坚忍的工作，从事行星运动的经验研究以及这运动的数学定律的研究。使他获得这种力量的，是他对自然规律存在的信仰。这种信仰该是多么深挚呀……

六、一生颠沛流离的开普勒

开普勒几乎终生都在贫穷中度日。虽然他名义上是德国皇帝宫廷天文学家，但却长年拿不到薪水。他是历史上数理天文学的先驱，但却没办法用天文学的职位养活自己和12个孩子。他只能靠算命来使一家人不致活活饿死。

1630年10月，开普勒迫于生活无法维持，只好亲自去雷根斯堡（Regensburg）向国会要求付给他近20年的欠薪。不幸的是由于饥寒交迫，在11月2日到雷根斯堡后不久他就病倒了。11月15日，开普勒这位奋斗一生的哲人，在穷困潦倒中悲惨地离开了人世。

11月17日，他被葬在城堡外面圣彼得堡公墓里；墓碑上刻的是他生前给自己留下的墓志铭：

我曾测天高，

今欲量地深，

上天赐我灵魂，

凡俗的肉体安睡地下。

后来由于战争连绵不断，他的坟墓已经消失得无影无踪。

开普勒一生颠沛流离，长期处于贫困艰难生活之中。不断失去亲人的巨大痛苦始终没有离开过他：他结过两次婚，两任妻子为他生下11个孩子，第二任妻子还给他带来一个继女，一共是12个孩子。他自己的11个孩子只有3个孩子最后活了下来，两任妻子也在他之前因病去世。他的母亲由于被控为“巫婆”而险遭烧死，经开普勒冒死抢救总算没有死于酷刑。命运给他带来的忧患和打击无法细数，但他顽强坚韧地挺过来了，并且从宇宙和谐的信仰中寻找到无比的欢乐和慰藉。爱因斯坦在1949年曾经感叹地说过：

应当知道开普勒是在何等艰难的条件下完成这项巨大的工作的。他没有因为贫困，也没有因为那些有权支配着他的生活和工作条件的同时代人的不了解，而使自己失却战斗力或者灰心丧气。而且他所研究的课题还给宣扬真理的他以直接的危险。但开普勒还是属于这样的一类少数人，他们要是不能在每一领域里都为自己的信念进行公开辩护，就绝不甘心。

18世纪德国诗人诺瓦利斯（Novalis，1772—1801）用诗句表达了他对开普勒的钦佩和仰慕：

向着您，我转过身来，高贵的开普勒，您的智力创造了一个神圣的精神宇宙，在我们的时代里，被视为智慧的东西是什么？是屠杀一切，使高尚的东西变低微，使低微的东西纷纷扬起，甚至使人类精神在机械的法则之下屈服。 ⁽⁶⁾

捷克作家布诺德（Max Brod，1884—1968）在他的《第谷·布拉赫的赎罪》（The Redemption of Tycho Brahe ）一书中说：

开普勒使第谷对他充满了敬畏之情。开普勒全心全意致力于实验工作、完全不理会叽叽嚓嚓的谄言的宁静心理，在第谷看来，就几乎是一种超人的品质。这儿有点不可理喻的地方，即似乎缺乏某种情感，有如极地严寒中的气息……

————————————————————

(1) 国内更多的人翻译为《宇宙的和谐》。

(2) 这里指的是行星。

(3) 复调音乐（polyphony）：广义而言，指由两个或更多相对独立的声部构成的音乐（参阅Monophony），与主调音乐（homophony）形成对比。在复调音乐中，能听出各声部是独立进行的，在节奏上它们互不依靠。……更具体地说，复调音乐指各声部关系密切、互相补充、彼此间有相互作用的力度关系的多声部织体。——摘自《不列颠百科全书》13卷（1999年）394页。

(4) 泡利（Wolfgang Pauli，1900—1958），瑞士籍奥地利物理学家，1954年因为发现量子力学中的不相容原理获得诺贝尔物理学奖。

(5) 开普勒曾经写道：“我们应该仔细倾听第谷的意见。他花了35年的时间全心全意地进行观察……我完全信赖他，只有他才能向我解释行星轨道的排列顺序。”“第谷掌握了最好的观察资料，这就如他掌握了建设一座大厦的物质基础一样。”

(6) 引自车桂《倾听天上的音乐——哲人科学家开普勒》。