第二编
动 电 学
·Part II Electrokinematics·

不少人抱着极大的热情研究麦克斯韦的著作,常常遇到极大的困难,于是他们不得不放弃系统全面理解麦克斯韦的希望……麦克斯韦的理论是什么?我只能说,麦克斯韦的理论就是麦克斯韦方程的体系。
——赫兹(周兆平译)

1831年的爱丁堡
第十四章 电 流
230.〕 我们在第45节中已经看到,当一个导体处于电平衡时,导体各点的势必然相同。
如果两个导体A和B被充了电,以致A的势高于B的势,则当用和它们二者相接触的一条金属线把它们接通时,A的一部分电荷就会过渡到B,而A和B的势就会在很短的时间内变为相等。
231.〕 在这一过程的进行中,在导线C中观察到某些现象,这些现象叫做电流 〔1〕 。
其中第一种现象就是正电从A到B而负电从B到A的转移。这种转移也可以通过使一个绝了缘的小物体交替地和A及B相接触而用一种更慢的方式来达成。利用我们可称之为电运流的这种过程,每一个物体所带电的一个个的小部分可以转移到另一个物体上。不论在哪一种事例中,某一电量或带电状态都在物体之间的空间中沿着某一路径从一个地方运动到另一个地方。
因此,不论我们对电的本性有何见解,我们都必须承认所描述的过程构成电的一种流动。这种流动可以描述为正电从A到B的流动,或负电从B到A的流动,或这两种流动的组合。
按照菲希诺尔的学说和韦伯的学说,这是一种正电的流动和一种恰好相等的负电沿相反方向而通过相同物质的流动的组合。为了理解韦伯关于某些最有价值的实验结果的叙述,记住这种有关电流之组成的极其牵强的假说是必要的。
如果我们像在第36节中一样假设,在单位时间之内,有P个单位的正电从A转移到B而有N个单位的负电从B转移到A,则按照韦伯的学说,应有P=N,而P或N就应该被取为电流的数值。
与此相反,我们对P和N之间的关系不作任何假定,而只注意流动的结果,那就是P+N个单位的正电从A到B的转移,从而我们将把P+N看成电流的真实量度。因此,韦伯将称之为1的电流,我们将称之为2。
论恒稳电流
232.〕 在处于不同势的两个绝缘导体之间的流动事例中,过程很快地就会因二物体的势的相等而停止,从而电流在本质上就是一种“瞬变电流”。
但是也有一些办法可以使导体之间的势差保持恒定,在那种情况下,电流就将以一种均匀的强度作为一种“恒稳电流”而继续流动。
伏打电池组
产生恒稳电流的最方便的方法是利用一个伏打电池组。
为了明确起见,我们将描述丹聂耳的恒势电池组:
一种硫酸锌的溶液放在一个多孔性的素烧瓷瓶子中,而这个瓶子又放在一个装有硫酸铜饱和溶液的容器中。一块锌浸在硫酸锌中,而一块铜浸在硫酸铜中。在液面以上,有导线焊在锌上和铜上。这一套东西,就叫做丹聂耳电池组的一个电池或单元。见第272节。
233.〕 如果这个电池通过放在一个不导电的底座上而被绝缘,而使连在铜上的导线和一个绝了缘的导体A相接触,使连在锌上的导线和另一个绝了缘的并和A用相同金属制成的导体B相接触,则可以利用一个精密的静电计来证明,A的势比B的高出某一个数量。这个势差叫做丹聂耳单元的“电动势”。
如果A和B现在从电池断开并利用一根导线互相连接起来,一个瞬变电流就会从A流向B,而A和B的势就会变成相等。然后A和B又可以被电池所充电,而这种过程就可以重复进行,只要电池还能工作就行。但是,如果A和B用一根导线连接起来,而且像从前那样仍和电池连接着,则电池将在C中保持一个恒定的电流,而且也在A和B之间保持一个恒定的势差。我们即将看到,这个势差并不等于电池的总电动势,因为一部分电动势要被用来在电池本身中保持电流。
若干个电池串联起来,即用金属把第一个电池的锌和第二个电池的铜相接,如此等等,就叫做一个“伏打电池组”,这样一个电池组的电动势是它所由组成的各电池的电动势之和。如果电池组被绝了缘,作为整体它可能带电,但是铜端的势永远比锌端的势大,而二者之差就是它的电动势,不论这两个势的绝对值是什么。电池组中的那些电池可以有很不相同的构造,含有不同的化学溶液和不同的金属,如果当没有电流通过时没有化学反应继续进行的话。
234.〕 现在让我们考虑两端互相绝缘的一个电池组。铜端将带正电或玻璃电,而锌端将带负电或树胶电。
现在设用一根导线把电池组的两端连接起来。于是一个电流就出现,并在一个很短的时间内达到一个恒定值。这时它就叫做一个“恒稳电流”。
电流的性质
235.〕 电流形成一条回路,沿着从铜到锌的方向通过导线,并从锌到铜通过溶液。
如果把任何一条把一个电池的铜和其次一个电池的锌连接起来的导线切断,回路就被切断,电流就会停止,而连在铜上的导线的端点的势就会比连在锌上的导线的端点的势高出一个常量,这就是回路的总电动势。
电流的电解作用
236.〕 只要回路是断开的,电池中就没有化学作用在继续进行,但是一旦回路接通,每一个丹聂耳电池中的锌块就会开始溶解,而在它的铜块上就会有铜沉积下来。
硫酸锌的量将增加,硫酸铜的量将减少,除非有更多的硫酸铜不断地被加进来。
被溶解的锌的量,和所沉积的铜的量,在整个回路中的每一个丹聂耳电池中都相同,不论各锌板的大小如何;而且,如果任何一个电池是具有不同的构造的,它里边的化学作用也会在数量上和丹聂耳电池中的化学作用有一个恒定的比值。例如,如果其中一个电池是由浸在用水稀释过的硫酸中的两个铂板构成的,就会有氧在电流进入液体处的那个板上放出,也就是在和丹聂耳电池的铜用金属连接着的那个板上放出,并有氢在电流离开液体处的板上即和丹聂耳电池的锌相连的那个板上放出。
氢的体积正好是在相同时间内放出的氧的体积的两倍,而氧的重量正好是氢的重量的八倍。
在回路的每一电池中,每一种溶解了的、沉积了的或分解了的物质的重量,等于一个叫做该物质之化学当量的量乘以电流的强度和电流流动的时间。
关于确立这一原理的那些实验,见法拉第《实验研究》的系列七和系列八。关于这一法则的表观例外的考察,见密勒的《化学物理学》和魏德曼的《动电》。
237.〕 用这种方式分解的物质,叫做“电解质”。这种过程叫做“电解”。电流进入和离开电解质的地方叫做“电极”。其中电流所由进入电解质的电极叫做“阳极”,而电流所由离开电解质的电极叫做“阴极”。电解质分解而成的组分叫做“离子”:出现在阳极处的离子叫做“阴离子”,而出现在阴极处的离子叫做“阳离子”。
我相信这些名词是由法拉第在惠威耳博士的协助下制订的。其中前三个即电极、电解和电解质已经得到公认,而其中出现这种组分的分解和传递的导电模由叫做“电解导电”。
如果有一种均匀的电解质放在一根变截面的管子中,而电极装在这根管子的两端,则我们发现当电流通过时阴离子就出现在阳极上而阳离子就出现在阴极上,这些离子的数量是电化学地等价的,而且是共同和电解质的某一个量等价的。在管子的其他部分,不论截面是大是小,是均匀的还是变化的,电解质的成分都保持不变。因此,通过管子的每一截面进行的电解的数量都相同。因此,在截面小的地方,作用必然比在截面大的地方更强,但是在给定时间内通过任一完整截面的每一种离子的数量对所有的截面来说都是相同的。
因此,电流的强度可以用给定时间内的电解数量来量度。可以很方便地测量电解产物的数量的一种仪器叫做“电量计”。
这样量得的电流强度在回路的每一部分处都相同,而且在任一给定时间以后出现在电量计中的电解产物的总量,和在同一时间内通过任一截面的电量成正比。
238.〕 如果我们在一个电池组的回路中接入一个电量计并在任何部分把回路切断,我们就可以假设电流的测量是如下进行的。设断路的两端是A和B,并设A是阳极而B是阴极,让一个绝了缘的球交替地接触A和B,则它在每一次行程中都会把某一个可测量的电量从A带到B。这个电量可以用一个静电计来测量,它也可以通过用球的静电电容去乘回路的电动势而被算出。就这样,电就在一个过程中被一个绝了缘的球从A带到B,这个过程可以叫做“运流”。与此同时,电解在电量计和电池组的各电池中持续进行,而每一个电池中的电解数量可以和被绝缘球带过去的电量相比较。被单位电量所电解的物质的量,叫做该物质的“电化当量”。
如果用一个普通大小的球和一个可以摆弄的电池组来这样进行,这个实验就将是极其繁难和麻烦的,因为在一个可觉察数量的电解质被分解以前,必须来来回回搞了许许多多次。因此,实验必须被认为只是一种说明,而电化当量的实际测量则是用不同的方式进行的。但是这个实验也可以看成电解过程本身的一种说明。因为,如果我们把电解导电看成运流的一种,在这种运流中一个电化当量的阴离子携带着负电向阳极方向运动,而一个电化当量的阳离子携带着正电向阴极方向运动,而电的总传递量则是一个单位,那么我们就将得到有关电解过程的一种概念。就我所知,这种概念是和已知的事实并不抵触的,尽管由于我们对电的本性和化学化合物的本性不够了解,它可能只是实际上发生的事情的一种很不完善的表象。
电流的磁作用
239.〕 奥斯特发现,放在直线电流附近的一个磁铁,倾向于使自己变得垂直于通过电流和磁铁的平面。见第475节。
假如一个人把自己的身体摆得沿着电流线的方向,使得从铜经过导线到锌的电流将从他的头流向脚,而且他的脸则向着磁铁的中心,则当电流在流时,磁铁的指北极将倾向于指向人的右手。
这种电磁作用的本性和规律,将在我们进行到本书第四编时再行讨论。目前我们所要谈到的是这样一个事实:电流有一种在电流外面起作用的磁效应;通过这种效应,电流的存在可以被确定,电流的强度可以被测量,而不必断开电路或在电流本身中接入任何仪器。
已经确定,磁作用的大小正比于由电量计中的电解产物来测量的电流强度,而和电流所流过的导体的本性完全无关,不论导体是金属还是电解质。
240.〕 通过它的磁效应来指示一个电流的强度的仪器,叫做“电流计”。
电流计通常包括一个或多个用丝包线绕成的线圈,线圈内挂着一个轴线水平的磁铁。当电流在导线中通过时,磁铁就倾向于把自己摆在轴线垂直于线圈平面的方位上。如果我们假设线圈的平面是摆得和地球的赤道面相平行的,而电流是沿着太阳的表观运动方向从东向西在线圈中运行的,则线圈中的磁铁将倾向于把自己摆得使它的磁化和看成大磁铁的地球的磁化方向相同,地球的北极和罗盘指针指向南方的那一端相类似。
电流计是测量电流强度的最方便的仪器。因此我们将假设在电流规律的研究中制造这样一种仪器的可能性,而把仪器的原理留到我们的第四编中再来讨论。因此,当我们说一个电流具有某一强度时,我们就假设测量是用电流计来完成的。
第十五章 电导和电阻
241.〕 如果我们在一个保持着恒定电流的电路中用一个静电计来测定不同点上的电势,我们就会发现,在由温度均匀的单独一种金属构成的任何一段电路上,任何一点的势都比沿电流方向来看是更远一些的任何其他点的势大一个量,这个量依赖于电流的强度,并依赖于所研究的那一段电路的本性和尺寸。这一路段两端的势差,叫做作用在它上面的“外电动势”。如果所考虑的一段电路不是均匀的而却包含着从一种物质到另一种物质的过渡、从金属到电解质的过渡或从较热部分到较冷部分的过渡,则除了外电动势以外,还可能存在必须考虑在内的“内电动势”。
电动势、电流和电阻之间的关系,是由G. S. 欧姆博士在1827年发表的一篇题为《动电序列的数学研究》的论文中首先研究了的,该论文的英译本见泰勒的《科学论文集》(Taylor, Scientific Memoirs)。在均匀导体的事例中,这些研究的结果通常称为“欧姆定律”。
欧姆定律
作用在电路任一部分的两端之间的电动势,是电流强度和该部分电路的电阻的乘积。
这里引用了一个新的名词,导体的“电阻”,它被定义为电动势和所产生的电流强度之比。欧姆曾经用实验证明,电阻一词是和一个实在的物理量相对应的,就是说,它有一个确定的值,只有当导体的本性改变时这个值才会改变。没有这种证明,名词的引用就将是没有任何科学价值的。
总之,第一,一个导体的电阻不依赖于通过导体的电流强度。
第二,电阻不依赖于导体所在的势,也不依赖于导体表面上的电分布的密度。
它完全依赖于构成导体的材料的本性、导体各部分的聚集态和导体的温度。
导体的电阻可以测量到它的值的万分之一乃至十万分之一的精确度,而且已经测试过的导体是如此之多,以致我们关于欧姆定律之真确性的信心现在是很大的了 〔2〕 。在第六章中,我们将追索它的应用和推论。
电流的生热
242.〕 我们已经看到,当一个电动势使一个电流通过一个导体而流动时,电就从高势的地方转移到低势的地方。假如这种转移是通过运流来进行的,也就是通过在一个球上带着一个个的电荷从一个地方到另一个地方来的运动进行的,电力就会对球做功,而这种功就将需要说明。在一些干堆电路中,它也确实以一种部分的方式得到了说明;在那些电路中,电极被作成钟形,而运送电的小球则像一个摆似地在两个钟之间运动并交替地敲响它们。用这种办法,电作用被弄得和摆的摆动步调一致并把钟声传到远处。在导线的事例中,我们有同样的从高势处到低势处的电转移而没有任何的外功被作出。因此,能量守恒原理就引导我们到导体中去寻找内功。在一种电解质中,内功部分地表现为电解质组分的被分离。在其他导体中,它完全转化为热。
在这一事例中,转化为热的能量等于电动势和通过的电量的乘积。但是电动势等于电流和电阻的乘积,而电量等于电流和时间的乘积。由此可见,热量乘以热功当量就等于电流强度的平方乘以电阻再乘以时间。
在克服电阻中由电流产生的热量,曾由焦耳博士测定过。他首次确定了,在给定时间内产生的热量正比于电流的平方,而且后来又通过所有各有关量的仔细的绝对测量,证实了方程JH=C2 Rt,式中J是焦耳的热功当量,H是热量,C是电流强度,R是电阻,而t是电流流动的时间。电动势、功和热之间的这些关系,由W. 汤姆孙爵士在一篇关于机械效应对电动势测量之应用的论文中第一次作出了充分的解释 〔3〕 。
243.〕 初看起来,电的传导理论和热的传导理论之间的类似性是完全的。如果我们取两个在几何上相似的体系,假设第一个体系中任一点上的热导率正比于第二个体系中对应点上的电导率,而且令第一个体系中任一部分处的温度正比于第二部分中对应点上的电势,则通过第一个体系中任一面积的热流将正比于通过第二个体系中对应面积的电流。
于是,在我们已经作出的说明中,既然电的流动对应于热的流动,而电势对应于温度,那么电就倾向于从高势处流向低势处,正如热倾向于从高温处流向低温处一样。
244.〕 因此,电势理论和温度理论可以弄成互相例示的形式,然而在电现象和热现象之间却有一个引人注目的差别。
用一根丝线把一个导电物体挂在一个闭合的导电容器中并使容器带电。容器和它内部所有东西的势将立即升高,但是,不论容器被多么强烈地充了电,不论它里边的物体是否和它相接触,容器内部都不会出现任何带电的迹象,而且当物体被拿出时它也不会显示任何电效应。
但是如果容器被加热到一个高的温度,器内的物体也将达到相同的温度,但那要在一段相当长的时间以后,而且,如果后来把它拿出来,它就会是热的,而且它会保持为热的,直到它继续放了一段时间的热以后。
两种现象的差别在于这样一件事实:物体能够吸热和放热,而在电的方面它们却没有对应的性质。不向物体供应一定量的热,就不可能使它热起来,而所需的热量依赖于物体的质量和比热,但是一个物体的电势却可以用上述方法提高到任何程度而不必把任何的电传给该物体。
245.〕 另外,假设一个物体首先被加热然后被放在闭合容器中。容器的外表面起先将和周围的物体温度相同,但它不久就会热起来,而且将保持为较热,直到内部物体所有的热都被放掉为止。
进行一个对应的电学实验是不可能的。不可能使一个物体带电,然后把它放在一个中空容器中,而使容器的外表面起初并不显示任何的带电现象,但是后来却带了电。法拉第曾经徒劳地寻求过的所谓“绝对电荷”,正是某种这一类的现象。
热可以隐藏在一个物体的内部而没有外部作用,但是却不可能把一个电量隔离起来,以阻止它和一个种类相反的相等电量处于经常的感应之中。
因此,在电现象中就没有任何东西和一个物体的热容量相对应。这可以从本书所肯定的学说中立刻推出来;那学说就是,电和一种不可压缩的流体服从相同的连续性条件。因此就不可能通过把一个附加的电量挤入任何物质中而使它得到一个体电荷。参阅第61、111、329、334各节。
第十六章 接触物体之间的电动势
接触中的不同物质的势
246.〕 如果我们把一个中空导电容器的势定义为器内空气的势,我们就可以借助于在第一编第221节中描述了的一个静电计来确定这个势。
如果现在取两个用不同金属例如铜和锌做成的中空容器,并使它们互相处于金属接触之中,然后检测每一个容器中的空气的势,则锌质容器中的空气的势和铜质容器中的空气的势相比将是正的。势差依赖于各容器的内表面的本性;当锌是光亮的而铜上附有一层氧化物时,势差最大。
由此可见,当两种金属互相接触时,通常会有一个电动势从一种金属向另一种金属作用着,以促使一种金属的势超过另一种金属的势。这就是伏打有关“接触电”的理论。
如果我们取一种金属例如铜作为标准,那么,如果铁在和势为零的铜相接触时的势是I而锌在和势为零的铜接触时的势为Z,则锌在和势为零的铁相接触时的势将是Z-I,如果各金属周围的媒质保持相同的话。
这种结果对任何三种金属都是对的。由这种结果可知,温度相同的任何两种金属相接触时的势差,等于它们和第三种金属相接触时二势之差,因此,如果一个电路由温度相同的任意几种金属所形成,则各金属一经得到了它们的适当的势,电路中就将存在一种电平衡,从而电路中就不会有电流继续存在。
247.〕 然而,如果电路由两种金属和一种电解质所构成,则按照伏打的理论,电解质将倾向于使和它接触着的两种金属的势变成相等,于是金属接触点上的电动势就不再是被平衡掉的,而一个连续的电流就会得到保持。这个电流的能量由发生在电解质和金属之间的化学作用来提供。
248.〕 然而,电效应也可以不用化学作用来产生,如果我们能够用任何别的办法来使相接触的两种金属的势相互接近的话。例如,在W. 汤姆孙爵士所作的一个实验中 〔4〕 ,一个铜漏斗被放在和一个竖直的锌圆筒相接触的位置上,从而当使一些铜屑通过漏斗时,它们就在锌筒的中部互相分开并离开漏斗而落入放在下面的绝缘接收器中。于是接收器就被发现为带负电,而且它的电荷将随着碎屑的不断下落而增加。与此同时,里边放了铜漏斗的那个锌筒就会越来越多地带正电。
如果现在用一根导线把锌筒和接收器连接起来,导线中就会有一个正电流从锌筒流向接收器。每一片铜屑都由于感应而带了负电,而铜屑流就形成从漏斗到接收器的一个负电流,或者换句话说,形成从接收器到铜漏斗的一个正电流。于是正电流就(由铜屑携带着)通过空气从锌流到铜,并通过金属连线而从铜流到锌,正如在普通的电池电路中一样。但是,在这一事例中,保持电流的力不是化学作用而是重力,这种重力使铜屑下落,尽管有带正电的漏斗和带负电的铜屑之间的电吸引力。
249.〕 接触电理论的一种引人注目的证实曾由珀耳帖的发现所给出。他曾发现,设有一个电流通过两种金属的接触点,当电流沿一个方向流动时接触点就发热,而当它沿相反方向流动时接触点就变冷。必须记得,一个电流在通过一种金属时永远产生热,因为它会遇到电阻。因此,整个导体中的冷却效应必然永远小于发热效应。从而我们就必须区分每一种金属中由普通的电阻而引起的发热和两种金属接头处的热的产生或吸收。我们将把前者称为由电流引起的热的摩擦产生,而正如我们已经看到的那样,这种热量正比于电流的平方,从而不论电流沿正方向还是沿负方向流动热量都是相同的。我们可以把第二种效应叫做珀耳帖效应,它随着电流的变号而变号。
在由两种金属形成的组合导体的一个部分中,产生的总热量可以表示成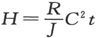 -ΠCt,式中H是热量,J是热功当量,R是导体的电阻,C是电流,而t是时间;Π是珀耳帖效应的系数,也就是单位电流在单位时间内在接触点上吸收的热量。
-ΠCt,式中H是热量,J是热功当量,R是导体的电阻,C是电流,而t是时间;Π是珀耳帖效应的系数,也就是单位电流在单位时间内在接触点上吸收的热量。
喏,产生的热和在导体中反抗电力所做的功是在力学上等价的;就是说,它等于电流和产生电流的电动势的乘积。由此可见,如果E是使电流通过导体而流动的那个外电动势,则有JH=CEt=RC2 t-JΠCt,从而E=RC-JΠ。
由这一方程可以看到,推动电流通过组合导体所需要的外电动势,比只由它的电阻所要求的电动势小一个电动势JΠ。因此JΠ就代表在接触点上沿正方向发生作用的电动势。
由W. 汤姆孙爵士 〔5〕 作出的这种热的动力理论对区域性电动势之确定的应用,具有很大的科学重要性,用导线把组合导体的两个点和一个电流计或验电器的两个极连接起来的那种普通方法,将由于导线和组合导体物质接头处的接触力而成为无用的。另一方面,在热学方法中,我们知道能量的唯一来源是电流,而除了使那一部分导体变热以外电流在电路的一部分中不作任何的功。因此,如果我们能够测量电流的大小和产生的或吸收的热量,我们就能确定促使电流通过那一部分导体时所需要的电动势,而且这种测量是和电路其他部分中的接触力效应完全无关的。
用这种方法测定的二金属接头处的电动势,并不能说明在第246节中描述的那种伏打电动势。后者通常是比本节所述的这种电动势大得多的,而且有时是符号相反的。因此,认为一种金属的势应该用和它接触着的空气的势来量度的那种假设就必然是错误的,而且伏打电动势的较大部分不应该到两种金属的接头处去找,而应该到把金属和形成电路之第三种单元的空气或其他媒质的一个或两个分界面上去找。
250.〕 塞贝克发现,当接触点处于不同的温度时,由不同金属构成的电路中出现温差电流;这就表明,一个闭合电路中的接触势并不是永远互相平衡的。然而很明显,在由均匀温度下的不同金属构成的闭合电路中,接触势必然互相平衡。因为,假若不是这样,电路中就会出现电流,而这个电流就可以带动一个机器或在电路中产生热,也就是说可以做功,而与此同时却没有能量的任何消耗,因为电路到处的温度相同,而且也没有化学变化或其他的变化发生。由此可见,如果在由两种金属a和b的接触点上当电流从a流到b时珀耳帖效应用Πab 来代表,则对由同温下的两种金属构成的电路来说,应用Πab +Πba =0,而对由三种a、b、c构成的电路来说,我们必有Πbc +Πca +Πab =0。
由这一方程可知,三个珀耳帖效应并不是独立的,而是其中一个可由另外两个推出。例如,如果我们假设c是一种标准金属,并写出Pa =JΠac 和Pa =JΠbc ,则有JΠab =Pa -Pb 。
Pa 这个量是温度的函数,并取决于金属a的本性。
251.〕 马格努斯也曾证明,如果一个电路是由单独一种金属构成的,电路中就不会形成任何电流,不论导体的截面和温度怎么变化 〔6〕 。
既然在这种事例中存在热传导以及由此引起的能量耗散,我们就不能像在以前的事例中那样把这一结果看成显而易见的。例如,电路两部分之间的电动势可能取决于电流是从导体的较粗部分流向较细部分还是相反,也可能取决于它是迅速地或缓慢地从较热部分流向较冷部分还是相反,而这就会使得由一种金属构成的不均匀加热的一个电路中的电流成为可能。
因此,利用和在珀耳帖现象的事例中相同的推理,我们就得到,如果电流在单一金属导体中的通过会引起任何的热效应,而当电流反向时该效应也反向,则这只有当电流从高温处流向低温处或从低温处流向高温处时才是可能发生的,而且,如果当从温度为x处流到温度为y处时在导体中产生的热是H,则JH=RC2 t-Sxy Ct,而倾向于保持这一电流的电动势则是Sxy 。
如果x、y、z是一个均匀电路中三个点上的温度,则按照马格努斯的结果,我们必有Syz +Szx +Sxy =0。因此,如果我们假设x是零温度,并令Qx =Sxz 而Qy =Syz ,我们就得到Sxy =Qx -Qy ,式中Qx 是温度x的一个函数,其函数形式取决于金属的本性。
如果我们现在考虑由两种金属a和b构成的一个电路,设电流从a流入b处的温度为x而它从b流入a处的温度为y,则电动势将是
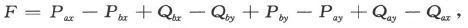
式中Pax 代表金属a在温度x下的P值,或者说
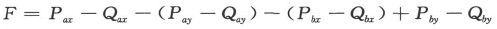
既然在非均匀加热的不同金属的电路中一般是存在温差电流的,那就可以推知P和Q一般对同一金属和同一温度来说是不同的。
252.〕 Q这个量的存在最初是由W. 汤姆孙爵士在我们已经提到的论文中作为由克明 〔7〕 发现的温差电反转的一种推论而证实了的;克明发现,某些金属在温差电系列中的次序在高温下和在低温下是不同的,从而对一个确定的温度来说两种金属可以是无分轩轾的。例如,在由铜和铁构成的一个电路中,如果一个接触点保持在常温而另一个接触点的温度被提高,则有一个电流在热接触点上从铜流入铁中,而且电动势不断增大,直到热接触点达到一个温度T时为止,而按照汤姆孙的研究,这个温度约为284℃。当热接触点的温度进一步升高时,电动势就变小,而到最后,如果温度升得够高,电流就会反向。电流的反向可以通过升高冷接触点的温度来更容易地得到。如果两个接触点的温度都高于T,则电流在热接触点上从铁流入铜中,也就是和在两个接触点的温度都低于T时观察到的电流方向相反。
由此可见,如果一个接触点的温度是中性温度T,而另一个接触点则较热或较冷,电流就总是将在中性温度的接触点上从铜流入铁中。
253.〕 由这一事实出发,汤姆孙推理如下:
假设另一个接触点处于一个低于T的温度。电流可被用来带动一个机器或在一根导线中产生热,而能量的消耗必将由从热到电能的转变来补充,也就是说热必须在电路的某个地方消失。现在,在温度T下,铜和铁是势均力敌的,从而在热接触点上不会有可逆的热效应,而在冷接触点上则由珀耳帖原理将由电流产生热。由此可见,热可以消失的唯一所在就是电路的铜段或铁段,因此,或是铁中一个从热到冷的电流将冷却铁,或是铜中一个从冷到热的电流将冷却铜,或是两种效应都可能发生。{这种推理假设温差接触点在有电流通过时只作为一个热机而起作用,而在形成接触点的物质的能量方面没有任何别的变化(例如像电池组中那样的变化)。}通过一系列精心设计的巧妙实验,汤姆孙成功地探测到了电流在流过温度不同的导体部分时的可逆的热作用,而且他发现电流在铜中和铁中将产生相反的效应 〔8〕 。
当一种物质性的流体在一根管子中从热的部分流到冷的部分时,它就使管子变热,而当它从冷的部分流到热的部分时,它就使管子变冷,而且这些效应依赖于流体的比热。假如我们假设电无论正负都是一种物质性的流体,我们就将可能通过非均匀加热导体中的热效应来量度电流体的比热。现在汤姆孙的实验证明,铜中的正电和铁中的负电都把热从热处带到冷处。由此可见,假如我们假设正电或负电是可以被加热和被冷却并能够把热传给其他物体的一种流体,我们就会发现这种命题对正电而言被铁所否定而对负电而言被铜所否定,从而我们将不得不放弃这两种假说。
关于电流对非均匀加热的单一金属的可逆效应的这种科学预见,又是应用能量守恒学说来指明科学研究新方向的一个很有教育意义的范例。汤姆孙也曾经应用热力学第二定律来指明了我们用P和Q来代表的那些量之间的关系,而且也研究了沿不同方向有着不同结构的那些物体的可能的温差电性质。他也在实验上研究了这些性质通过压力、磁化等等而得到发展的那些条件。
254.〕 泰特教授 〔9〕 近来研究了接触点温度不相同的由不同的金属构成的电路中的电动势。他发现,一个电路的电动势可以很准确地用公式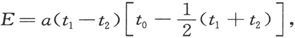 来表示,式中t1 是热接触点的绝对温度,t2 是冷接触点的绝对温度,而t0 是两种金属相互中立时的温度。因子α是取决于构成电路的两种金属的本性的一个系数。这条定律曾由泰特教授和他的学生们在相当大的温度范围内进行了验证,而且他希望把温差电路弄成一种测温仪器,使之可以应用于他的关于热传导的实验中,以及汞温计不便于应用或其温度范围不足的其他事例中。
来表示,式中t1 是热接触点的绝对温度,t2 是冷接触点的绝对温度,而t0 是两种金属相互中立时的温度。因子α是取决于构成电路的两种金属的本性的一个系数。这条定律曾由泰特教授和他的学生们在相当大的温度范围内进行了验证,而且他希望把温差电路弄成一种测温仪器,使之可以应用于他的关于热传导的实验中,以及汞温计不便于应用或其温度范围不足的其他事例中。
按照泰特的理论,汤姆孙称之为电的比热的那个量在每一种金属中都和温度成正比,尽管它的量值乃至正负号是随金属的不同而不同的。他由此而用热力学的原理导出了下述的结果。设ka t 、kb t 、kc t是三种金属a、b、c的比热,而Tbc 、Tca 、Tab 是每两种金属互相中立时的温度,则方程
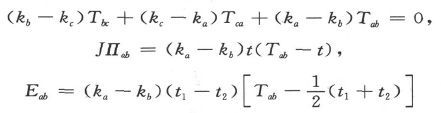
将表示一个温差电路的各中立温度,珀耳帖效应的值和电动势之间的关系。
第十七章 电解导电
255.〕 我已经叙述过,当一个电流在电路的任一部分通过一种叫做“电解质”的化合物时,它的通过就是由一种叫做“电解”的化学过程伴随着的;在这种过程中,化合物被分解成两种叫做“离子”的成分,其中一种叫做“阴离子”,或带负电的成分,它出现在阳极处,或电流进入电解质的地方,另一种叫做“阳离子”,出现在阴极处,或电流离开电解质的地方。
电解的全面考察有很大一部分属于化学,正如也有一部分属于电学一样。我们将从电学的观点来考虑它,而不考虑它在化合物的构造理论方面的应用。
在所有的电现象中,电解似乎是最有可能向我们提供一种关于电流之真实本性的实在识见的现象,因为我们发现普通物质的流动和电的流动都形成同一现象的本质性的部分。
也许正是由于这个原因,在目前还很不完善的我们关于电的概念状况下,电解的理论才是如此不能令人满意的。
由法拉第确立了的并迄已被比茨、希托尔夫等人的实验所证实了的基本电解定律如下:
在给定时间内由一个电流的通过而分解的一种电解质的电化当量数,等于在同一时间由电流所传递的电量的单位数。
一种物质的电化当量,就是通过该物质的单位电流在单位时间内所电解的该物的数量,或者换句话说,就是当单位电量通过时电解的数量。当电量的单位是用绝对单位定义的时,每一种物质的电化当量的值就可以用格令或克来计算。
不同物质的电化当量正比于它们的普通的化学当量。然而,普通的化学当量只是各物质互相化合时的数值比,而电化当量则是物质的一种具有确定量值的性质,它的量值依赖于电量的单位。
每一种电解质都包括两种组分,它们在电解过程中出现在电流进入和离开电解质的地方而不出现在任何别的地方。因此,如果我们设想在电解质的内部画一个曲面,则用沿相反方向通过曲面的各组分的电化当量数来量度的通过该面而进行的电解的数量,将正比于通过该曲面的总电流。
因此,沿相反方向而通过电解质的那些离子的实际传递,就是电流通过电解来传导的那种现象的一个部分。在电流所通过的那种电解质中的每一点上,也有阴离子和阳离子的两个物质流,它们和电流具有相同的流线,并且在量值上和电流成正比。
因此就可以极其自然地假设,离子流就是电的对流,而特别说来,每一个阳离子是带有一个确定的正电荷的;这一电荷在一切阳离子上都相同,而每一个阴离子则带有一个相等的负电荷。
于是,离子通过电解质的反向运动就将是电流的一种完备的物理表象。我们可以把这种离子运动和扩散过程中气体和液体互相通过的运动相比较;这两种过程间有一种区别,那就是,在扩散中,不同的物质只是互相混合的,而且混合物是不均匀的,而在电解中,不同的物质是化合的,而且电解质是均匀的。在扩散中,一种物质在一个给定方向上的运动的决定性原因就在于每单位体积中的该物质数量沿该方向的减小,而在电解中,每一种离子的运动都起源于作用在带电分子上的电动势。
256.〕 克劳修斯 〔10〕 曾经在物体的分子骚动理论方面进行过许多的研究;他曾假设一切物体的分子都处于一种经常骚动的状态,但是在固体中,每一个分子永远不会离它的原始位置远于一定的距离,而在流体中,一个分子在从它的原始位置运动离开一定的距离以后,却有同样的可能性来继续远离或开始回向原位置。因此,在表观上静止的一种流体中,各分子是不断地改变着自己的位置,并无规则地从流体的一部分过渡到另一部分的。在化合物的流体中,他假设不仅仅化合物的分子是这样运动的,而且在发生于各化合物分子之间的碰撞中,组成化合物分子的那些分子还常常分开并交换伙伴,从而某一个别原子就时而和某一个种类相反的原子相结合,时而又和另一个那种原子相结合。克劳修斯假设这种过程是一直在液中进行着的;但是当一个电动势作用在液体上时,起先在一切方向并无不同的分子运动就会受到电动势的影响,从而带正电的分子就比趋于正极具有较大的倾向趋于负极,而带负电的分子则有较大的倾向沿相反的方向而运动。因此,阳离子在其自由阶段内就将努力奔向阴极,但是它们却不断因为和阴离子短期配对而耽误行程,而阴离子也是不断地在离子群中挤着前进的,不过是沿着相反的方向。
257.〕 克劳修斯的理论使我们能够理解,尽管一种电解质的实际分解需要一个有限大小的电动势,怎么电解质中的电传导还会服从欧姆定律,使得电解质中每一个哪怕是最微弱的电动势都产生一个量值与之成正比的电流。
按照克劳修斯的理论,电解质的离解和复合即使当没有电流时也是不断进行着的,而最微弱的电动势就足以使这种过程得到某种程度的方向性,并从而产生离子流和作为现象之一部分的电流。然而,在电解质中,离子根本不会以有限的数量被释放,而正是这种离子的释放才要求一个有限的电动势。在电极那儿,离子会积累起来,因为相继到来的那些离子不是在那里找到很容易和它们结合的反号的离子,而却发现自己置身于不能与之结合的同类离子群中。产生这种效应所要求的电动势是有一个有限量值的,而且它也形成一个反向的电动势,并当其他电动势被取消时将产生一个反向的电流。当由于离子在电极上的积累而引起的这种逆电动势被观察到时,电极就叫做被“极化”了。
258.〕 确定一个物体是不是一种电解质的最好的方法就是把它放在两个铂电极之间并给它通一段时间的电流,然后,把电极从电池组切断而把它们接在一个电流计上,并观察是否有一个由电极的极化而引起的反向电流通过电流计。这样一个电流既然起源于不同物质在两个电板上的积累,它也就是物质曾被来自电池组的原有电流所电解的一个证明。当用直接的化学方法来探测分解产物在电极上的出现有困难时,这种方法常常可以应用。见第271节。
259.〕 到此为止,电解理论都显得是很令人满意的。它借助于电解质的物质组分流来解释了我们不理解其本性的电流,而那些组分的运动虽然不能为肉眼所见但却是很容易证实的。正如法拉第所指明的那样,这种理论也解释了为什么在液态下可以导电的一种电解质当凝固以后却不是一种导体。这是因为,除非各分子能够从一个地方运动到另一个地方,就不能出现任何的电解导电,因此,为了成为一种导体,物质就必须通过融解或溶解而处于液态。
但是,如果我们继续下去,并假设电解质中的离子确实带有一定数量的正的或负的电荷,从而电解电流不过是一种对流,我们就会发现这种诱人的假说会把我们引导到很困难的处境中去。
首先,我们必须假设,在每一种电解质中,每一个阳离子当在阴极上被释放时都会传给阴极一个正电荷,而这个正电荷不仅对该阳离子来说而且对所有其他的阳离子来说都应该是相同的。同样,每一个阴离子在被释放时也将传给阳极一个负电荷,其数值和由阳离子传递的正电荷相等而符号相反。
如果我们不是考虑单独一个离子而是考虑形成该离子的一个电化当量的一群离子,则所有离子上的总电荷就像我们已经看到的那样是一个正的或负的单位电量。
260.〕 我们还不知道在任何一种物质的一个电化当量中共有多少个分子,但是由许多物理考虑所制订的化学分子理论却假设一个化学当量中的分子数对一切物质来说都是相同的。因此在关于分子的思索中我们就可以假设一个化学当量中的分子数N;这在目前还是一个未知的数,但是我们在以后可以设法确定它 〔11〕 。
因此,每一个分子当从化合态中被释放时都带走一个电荷,其量值是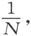 其符号对阳离子为正而对阴离子为负。我们将把这个确定的电荷叫做分子电荷。假如它是已知的,它就将是最自然的电量单位。
其符号对阳离子为正而对阴离子为负。我们将把这个确定的电荷叫做分子电荷。假如它是已知的,它就将是最自然的电量单位。
到此为止,我们通过在追索分子的带电和放电方面运用我们的想象而增大了我们的概念的精确性。
离子的释放和正电从阳极被送到阴极是同时的事件。离子当被释放时是不带电的,从而在化合状态下它们就将带有如上所述的分子电荷。
然而,分子的带电虽然谈起来容易,想象起来却并非容易。
我们知道,如果两种金属被放得在任一点上互相接触,则它们的表面的其余部分将带电,而如果这些金属做成平板的形式,而且中间由一个很窄的空气间隙所隔开,每个板上的电荷就可以变得相当大,当一种电解质的两种组分互相化合时,可以设想发生了某种类似的情况。可以假设,每一对分子将在一个点上互相接触,而它们的表面的其余部分则由于接触电动势而带了电。
但是,要想解释电有现象,我们就必须证明为什么这样产生的每一个分子上的电荷具有一个确定的数量,以及为什么当一个氯分子和一个锌分子相结合时,其分子电荷与一个氯分子和一个铜分子相结合时的分子电荷相同,尽管氯和锌之间的电动势比氯和铜之间的电动势大很多。如果分子的带电是接触电动势的效应,为什么强弱不同的电动势应该产生恰好相等的电荷呢?
然而,假设我们通过简单地肯定分子电荷的常量值来跳过这一困难,并假设我们为描述上的方便而把这个常量分子电荷称为电的一个分子。
这个说法尽管很粗略,而且和本书的其余部分也不协调,但是它却使我们至少能够清楚地叙述关于电解的已知情况,并领会那些突出的困难。
每一种电解质必须被看成它的阴离子和阳离子的二元化合物。阴离子或阳离子或两种离子都可以是组合物体,从而一个阴离子或阳离子可以是由简单物体的若干个分子{原子}所构成的。一个阴离子和一个阳离子相结合,就形成电解质的一个分子。
为了在电解质中作为一个阴离子而起作用,起作用的分子必须带有我们已经称之为电分子的一个负电荷,而为了作为一个阳离子而起作用,分子则必须带有一个电分子的正电荷。
这些电荷,只有当各分子作为阴离子和阳离子而在电解质中互相化合时才是联系在分子上的。
当各分子被电解时,它们就把电荷带到电极那儿去,而当从化合中被释放时它们就作为不带电的物体而出现。
如果同一个分子能够在一种电解质中作为阳离子而起作用,而在另一种电解质中则作为阴离子而起作用,而且也能够参加到不是电解质的化合物中去,我们就必须假设当作为阳离子而起作用时它就得到一个正电荷,当作为一个阴离子而起作用时它就得到一个负电荷,而当不在电解质中时它就不带电荷。
例如,碘在金属碘化物和氢碘酸中是作为阴离子而起作用的,但是在碘的溴化物中却据说是作为阳离子而起作用的。
这种分子电荷的学说可以作为一种方法,我们可以用这种方法来记住有关电解的许多事实。然而,当我们终于理解了电解的真实本性时,我们仍然保持任何形式的分子电荷学说的可能性却是非常小的,因为那时我们将已经得到一种可靠的基础来建立一种真实的电流理论,并从而不再依赖于这些暂时性的学说了。
261.〕 我们关于电解的知识的最重要步骤之一曾经是一些次级化学过程的认知;当各离子从电极那儿被放出时,这些次级过程就会出现。
在许多事例中,在电极那儿被发现的并不是电解质的实际离子,而是这些离子对电极的作用的产物。
例如,当一种硫酸苏打溶液被一个也通过了稀硫酸的电流所电解时,在硫酸苏打中的阳极和硫酸中的阳极上将得出相等数量的氧,而在各阴极处就得到相等数量的氢。
但是,如果电解在U形管或加了多孔壁障的容器之类的适当容器中进行,从而每一电极周围的物质都可以分别检查的话,那就会发现,在硫酸苏打中的阳极处,既存在一个当量的氧也存在一个当量的硫酸,而在阴极处则既存在一个当量的氢也存在一个当量的苏打。
初看起来,按照盐类构造的旧理论,似乎是硫酸苏打被电解成了它的组分硫酸和苏打,而溶液中的水则同时被电解成了氧和氢。但是这种解释将引导人们承认,通过稀硫酸并电解了一个当量的水的同一个电流,当它通过硫酸苏打的溶液时就既电解一个当量的水又电解一个当量的硫酸盐,而这就将是和电化当量定律相矛盾的。
但是,如果我们假设硫酸苏打的组分不是SO3 和Na2 O而是SO4 和Na2 (不是硫酸和苏打而是硫酸根和钠),则硫酸根将运动到阳极并被放出;但是由于不能自由存在,它将分解成硫酸和氧,各一当量。与此同时,钠也在阴极上被放出并在那里使溶液中的水分解,形成一当量的苏打和一当量的氢。
在稀硫酸中,收集在两个电极处的气体是水的组分,即一个体积的氧和两个体积的氢。阳极处的硫酸也有所增多,但它的量不等于一当量。
纯水是不是一种电解质是有疑问的。水的纯度越大,它在电解导电中的电阻就越大。极少的一点杂质就足以引起水的电阻的很大的减低。不同观察者所测定的水的电阻很不一致,从而我们还不能认为它是一个确定的量。水越纯电阻越大,从而假如我们能得到真正纯的水,它到底还能否导电就是很可疑的了 〔12〕 。
只要水还被看成一种电解质,而事实上它是被当作电解质的典型的,那就有很强的理由认为它是一种二元化合物,而且两个体积的氢是在化学上和一个体积的氧相等价的。然而,如果我们承认水不是一种电解质,我们就可以自由地假设一个体积的氧和一个体积的氢是在化学上等价的。
气体的分子运动论引导我们假设,在理想气体中,相同的体积中永远包含着相同数目的分子,而且比热的主要部分,即依赖于分子彼此之间的骚动的那一部分,对于一切气体的相同数目的分子来说是相同的。因此我们就更喜欢一种化学体系,在那里,体积相等的氧和氢被认为是等价的,而水是由两个当量的氢和一个当量的氧化合而成的,从而或许是不能直接电解的。
尽管电解现象充分确立了电现象和化合现象之间的密切关系,但是并非每一种化合物都是一种电解质这一事实却表明,化合过程是比任何单纯的电现象复杂程度更高的。例如,尽管金属是良导体,而且它们在接触带电的序列中占据着不同的位置,但是金属的一些结合物却甚至在液态下也不能被一个电流所分解 〔13〕 。作为阴离子而起作用的那些物质的多数结合物都不是导体,从而也不是电解质。此外我们还有许多化合物,它们包含着和一些电解质的组分相同的组分,但不是按当量的比例来包含的;这些化合物也不是导体,从而也不是电解质。
关于电解中的能量守恒
262.〕 试考虑包括一个电池组、一条导线和一个电解池的任一电路。
在单位电荷通过电路的任一截面的过程中,不论是在伏打电池中还是在电解池中,每一种物质都将有一个电化当量被电解。
和任一给定的化学过程相等价的机械能的数量,可以通过把由该过程引起的全部能量转化为热并乘以焦耳的热功当量而换算成力学单位来确定。
在这种直接方法不适用的地方,如果我们能够估计由各物质在归结到同一末状态的过程中放出的热,即首先考虑它在过程以前的状态,然后考虑它在过程以后的状态,则过程的热当量将是这两个热量之差。
在化学作用保持一个伏打电路的事例中,焦耳发现在伏打电池中发生的热少于由电池中的化学过程所造成的热,而其多余的热量则是在连接导线中发出的,或者,如果电路中有一个电机,一部分热量就可以用机器所作的机械功来说明。
例如,如果伏打电池的两极首先是用短而粗的导线连接,而后改用长而细的导线连接的,则对被溶解的每一格令锌来说,电池中产生的热量在第一事例中将比在第二事例中更大,但是导线中产生的热量在第二事例中却比在第一事例中为大。对于被溶解的每一格令锌来说,在电池中发生的热量和在导线中发生的热量之和在两个事例中是相同的。这一点已由焦耳用直接的实验确证过了。
电池中产生的热量和导线中产生的热量之比等于电池电阻和导线电阻之比,因此,假如导线被做得电阻够大,则几乎全部的热量都将是在导线中产生的,而假如它被做得有够大的导电本领,则几乎全部的热量都将是在电池中产生的。
设导线被做得具有很大的电阻,则以力学单位计的在导线中产生的热量就等于传送过去的电量和传送中所受到的电动势的乘积。
263.〕 现在,在电池中的一个电化当量的物质经历引起电流的那种化学过程的时间之内,一个单位的电量将通过导线。因此,由一个单位电量的通过所产生的热量,在这一事例中就是用电动势来量度的。但是这一热量就是一个电化当量的物质当经历所给的化学过程时所产生的,不论是在电池中还是在导线中产生。
由此就得到首先由汤姆孙证明了的重要定理如下(Phil, Mag, Dec. 1851):
“以绝对单位计的一个电化学仪器的电动势,等于作用在一个电化当量的物质上的化学作用的机械当量 〔14〕 。”
许多化学作用的热当量已由安德鲁斯、赫斯、否尔和则耳伯曼、汤姆孙等人所测定,而由这些热当量就可以通过乘以热功当量而推得它们的机械当量。
这一定理不仅使我们能够根据纯粹的热数据来计算不同的伏打装置的电动势,并计算在不同的事例中达成电解所必需的电动势,而且也提供了实际地测量化学亲和势的手段。
长时间以来人们已经知道,化学亲和势,或者说指向某些化学变化之发生的那种趋势,在某些事例中是比在另一些事例中更强的,但是这一趋势的任何适当的量度却都没能得出,直到证明了这一趋势在某些事例中恰恰和一个电动势相等价,从而可以按照测电动势的相同原理来加以测量时为止。
因此,在某些事例中,化学亲和势被归结成了一个可测量的量的形式;这样一来,化学过程的整个理论,它们的进行速率的理论,一种物质被另一种物质所置换的理论,等等,就变得比化学亲合势被看成一种特别的、不能归结为数字测量的量时更好理解多了。
当电解产物的体积大于电解质的体积时,在电解过程中就要反抗压强而做功,如果一个电化当量的电解质当在压强p下被电解时体积增大了v,则在单位电荷通过时反抗压强所做的功是vp,而电解所要求的电动势必须包括等于vp的用来完成这一机械功的一个部分。
如果电解产物是气体,它们像氧和氢那样比电解质稀薄得多,而且很准确地服从玻意耳定律,则vp在相同的温度下将很近似地等于常量,而电解所要求的电动势将不会在任何可觉察的程度上依赖于压强 〔15〕 。因此,曾经发现,通过把气体的分解限制在一个小空间中来核对稀硫酸的电离,是不可能的。
当解产物是液体或固体时,vp这个量将随着压强的增大而增大,因此,如果v是正的,则压强的增大将增大电解所要求的电动势。
同样,电解中所作的任何其他种类的功也将影响电动势的值;例如,如果有一个竖直的电流在一种硫酸锌溶液中的两个锌质电极之间流过,则当电流在溶液中向上流时,将比它向下流时要求一个较大的电动势,因为,在第一种事例中,电流将把锌从下面的电极带到上面的电极,而在第二种事例中则从上面的电极带到下面的电极。为此目的而要求的按每英尺计算的电动势,小于丹聂耳电池的电动势的百万分之一。
第十八章 电解极化
264.〕 当一个电流在以金属电极为边界的一种电解质中通过时,各离子在电极上的积累就引起一种叫做“极化”的现象;这种现象就在于有一个电动势沿着和电流相反的方向发生作用,从而引起电阻的一个表观增量。
当所用的是一个连续的电流时,电阻显示为从电流开始时迅速增大;而最后则达到一个将近恒定的值。如果装着电解质的容器的形状发生改变,则电阻也发生改变,其改变的方式和一个金属导体形状的相似改变将改变其电阻的那种方式相同,但是一个附加的依赖于电极之本性的表观电阻永远必须被加在电解质的真实电阻上。
265.〕 这些现象曾经引导某些人假设,需要一个有限的电动势来使一个电流通过一种电解质。然而,通过楞茨、诺依曼、比兹、魏德曼 〔16〕 、帕耳佐 〔17〕 以及近来的F. 考耳劳什和W. A. 尼波耳特 〔18〕 、斐兹杰惹和特罗顿 〔19〕 等人的研究,已经证明电解质本身中的导电,在和金属导体中的导电相同的精确度下服从欧姆定律,而电解质边界面上的电极表面上的表观电阻则完全是由极化引起的。
266.〕 所谓极化现象在连续电流的事例中通过电流的减小而表现出来;电流减小就表示有一个反对电流的力。电阻也被感受为一种反对电流的力,但是我们可以通过在一瞬间取消或反转电动势来分辨这两种现象。
阻力永远是和电流方向相反的,而克服阻力所必需的外电动势则正比于电流强度,而且当电流的方向改变时它的方向也改变。如果外电动势变为零,电流就干脆停止。
另一方面,由极化所引起的电动势则存一个固定的方向,和引起极化的电流方向相反。如果产生电流的电动势被取消,极化{电动势}就沿相反的方向产生一个电流。
两种现象之间的区别可以比拟为通过一个长毛细管和通过一个普通口径的管子把水打入高处的水槽中时的区别。在第一种事例中,如果我们取消打水的压力,水流就会干脆停止。在第二种事例中,如果我们取消压力,水就会从水槽中再向下流。
为了使这种机械比喻再加全面,我们只需假设水槽具有中等的深度,从而当一定量的水被打入时水就会溢出来。这就将代表由极化引起的总电动势有一个最大限度。
267.〕 极化的起因看来是由于在电极上出现了电极之间的流体的电分解产物。电极的表面变得在电的方面不相同了,从而就在电极之间引起了一个电动势,其方向和引起极化的电流方向相反。
由于它们的存在而引起极化的那些离子,并不是处于完全自由的状态,而是处于以相当的力附着的电极表面上的状态。
由极化引起的电动势依赖于覆盖电极的离子密度,但却并不正比于这一密度,因为电动势并不像密度增长得那么快。
离子的这种沉积总是倾向于变成自由的或是扩散到液体中去,或是作为气体而逸出,或是作为固体而下沉。
极化的这种耗散率,当极化程度很小时是非常小的,而在极化接近极限值时则是非常大的。
268.〕 我们在第262节中已经看到,在任何电解过程中起着作用的电动势,在数值上等于该过程对物质的一个电化当量所造成的结果的机械当量。如果过程引起参加过程的各物质的内能的一种降低,就像在一个伏打电池中那样,则电动势是沿着电流的方向的。如果过程引起各物质的内能的增高,就像在一个电解池中那样,则电动势是和电流方向相反的,而这种电动势就叫做极化{电动势}。
在电解持续进行而各离子是在自由状态下在电极上被分离的那种恒稳电流的事例中,我们只要用适当的手续测量被分出的离子的内能并把它和电解质的内能相比较,就可以计算电解所要求的电动势。这将给出最大的极化。
但是,在电解过程的最初阶段,沉积在电极上的离子并不是处于自由状态,从而它们的内能也小于自由状态中的内能,尽管比它们结合为电解质时的内能要大一些。事实上,当沉积层很薄时,和电极相接触的离子是处于一个可以比拟为离子与电极相化合的那种状态,但是当沉积密度增大时,后来的部分就不再和电极结合得那么紧密,而只是附着在它上面而已了;而到了最后,如果沉积层是气体,它就会作为气泡而逸出;如果是液体,就会通过电解液而扩散;如果是固体,就形成一种沉淀。
因此,当研究极化时,我们必须考虑:
(1)沉积层的面密度,我们用σ来代表它。量σ代表沉积在单位面积上的离子的电化当量数。既然所沉积的每一个电化当量都对应于被电流传递了的一个单位电量,我们就可以把σ或是看成物质的面密度或是看成电的面密度。
(2)极化电动势,我们用p来代表它。p这个量就是当通过电解质的电流非常弱,以致电解质的固有电阻在电极之间并不造成任何可觉察的势差时二电极之间的势差。
电动势p在任何时刻都在数值上等于在该时刻进行着的那种电解过程的和一个电化当量的物质相对应的机械当量。必须记得,这种电解过程就造成离子在电极上的沉积,而它们在沉积时所处的状态则依赖于电极表面的可以因先前的沉积而改变的实际状态。
由此可见,任一时刻的电动势都依赖于各电动极的以前历史。很粗略地说来,它是沉积密度σ的函数:当σ=0时p=0,而且p比σ更快得多地趋于一个极限值。然而p是σ的函数的说法不能被认为是准确的。更准确一些的说法或许是,p是沉积物的表面层的化学状态的函数,而且这个状态按照某种和时间有关的规律而依赖于沉积密度。
269.〕 (3)我们必须考虑到的第三个问题就是极化的耗散。当不受外界强制时,极化就减小,其减小率部分地依赖于极化强度或沉积密度,部分地依赖于周围媒质的本性和电极所受到的化学的、力学的或热学的作用。
如果我们确定一个时间T,使得按照沉积的耗散率来看,整个的沉积将在T内被消除,则我们可以把T叫做耗散时间的模量。当沉积密度很小时:T是很大的,可能以天计或以月计,当沉积趋于它的极限值时T就迅速地减小,而且也许会是一秒的一个很小的分数。事实上,耗散率很快地增加,以致当电流强度保持不变时分离开的气体不是增大沉积密度而是刚一形成就会作为气泡而逸出。
270.〕 因此,当极化很弱时和当极化达到其极限值时,电解池中各电极的极化状态就是很不相同的。例如,如果把一些带有铂电极的稀硫酸电解池串联起来,并且把一个小电动势例如单一丹聂耳电池的电动势接到电路中,这个电动势就会在一段非常短的时间内产生一个电流,因为,在一段很短的时间之后,由各电解池的极化所引起的电动势就会把丹聂耳电池的电动势平衡掉。
在如此微弱的极化状态下,耗散将是很小的,而且它将通过很缓慢的气体吸收和液体中的扩散来进行。这种耗散的速率由一个非常弱的电流来指示,这一电流继续流动而没有任何显著的气体分离。
如果我们在极化状态的很短的建立时间内忽略这种耗散,并且用Q来代表电流在这一时间内传递的电量,那么,如果A是一个电极的面积,而σ是假设为均匀的沉积密度,就有Q=Aσ。
如果现在我们把电解装置的电极从丹聂耳电池断开并把它们接在一个能够测量通过它的总电量的电流计上,则当极化消失时就会有一个近似等于Q的电量被放掉。
271.〕 因此我们就可以把这种实际上是一种形式的里特尔次级电堆的装置的作用和一个莱顿瓶的作用相比较。
次级电堆和莱顿瓶都能够被充以一定数量的电,然后也可以把电再放掉。在放电过程中,一个近似等于所充电荷的电量将沿相反方向流过去,充入的和放掉的电量之差,部分地起源于耗散;这种过程在少量充电的事例中是很慢的,但是当充电超过某一限度时,过程就变得非常地快,充电和放电之差的另一部分起源于这样一件事实:当二电极连接了一段足以产生一次表观上完全的放电的时间,从而电流已经完全消失以后,如果我们把电极分开,过了一段时间以后再把它们接起来,我们就会得到和原先的放电方向相同的第二次放电。这叫做剩余放电,而且是莱顿瓶的一个现象,正如是次级电堆的现象一样。
因此,次级电堆在许多方面都可以和莱顿瓶相比拟。然而也有某些重要的区别。莱顿瓶的电荷精确地正比于充电的电动势,也就是正比于两个表面的势差的,而对应于单位电动势的电荷就叫做瓶的电容,是一个恒量。可以称为次级电堆之电容的对应的量,当电动势增大时却是增大的。
莱顿瓶的电容依赖于相对的两个面积依赖于两个表面之间的距离,并依赖于二者之间的媒质的本性,但是却不依赖于金属表面本身的本性。次级电堆的电容依赖于电极表面的面积,但是却不依赖于电极之间的距离,而且它既依赖于电极之间的流体的本性也依赖于电极表面的本性。次级电堆中每一个单元中的电极之间的最大势差比起充电莱顿瓶的电极之间的最大势差来是很小的,因此,为了得到较大的电动势,就必须使用由许多单元构成的电堆。
另一方面,次级电堆中的电荷面密度却比可以积累在一个莱顿瓶表面上的电荷面密度大得多,以致竟使瓦尔莱先生 〔20〕 在描述大电容的电容器的制造时从经济观点出发建议使用浸在稀酸中的金片或铂片而不使用由绝缘材料隔开的锡箔感应片。
储存在莱顿瓶中的能量的形式是导电表面之间的电介质的约束状态;我曾经在电极化的名称下描述过这种状态,当时指出了目前已知的和这一状态相伴随的那些现象,并且指示了我们对实际发生的事情的了解方面的不足。参阅第62、111节。
储存在次级电堆中的能量的形式是电极表面上的物质层的化学条件,其中包括电解质离子和电极物质之间的从化学结合到表面聚集、机械附着和简单并列的那种变化的关系。
这种能量的所在之处是电极的表面附近而不是电极物质的全部,而且它的存在形式可以叫做电解极化。
在联系到莱顿瓶而研究了次级电堆以后,读者还应该把伏打电池组和某种形式的起电机作一比较,例如和在第211节中描述过的那种起电机作一比较。
近来瓦尔莱先生曾经发现 〔21〕 ,对于稀硫酸中的铂片来说,一平方英寸的电容是175到542微法拉以上,而且电容是随着电动势而增加的,当电动势是丹聂耳电池电动势的0.02倍时电容约为175,当电动势是丹聂耳电池电动势的1.6倍时电容约为542。
但是莱顿瓶和次级电堆之间的比较还可以进行得更远,正如在由杜夫 〔22〕 所作的下述实验中那样。只有当莱顿瓶的玻璃是冷的时,它才能保存电荷,在不到100℃的温度下,玻璃就变成一个导体。如果把装有水银的一根试管放入一个装了水银的容器中,并把一对电极分别接在内部的外部的水银上,这种装置就构成一个莱顿瓶,它在常温下可以保存一个电荷。如果把各电极接到一个伏打电池组的电极上,只要玻璃是冷的,就不会有电流通过。但是如果仪器被慢慢加热,一个电流就会开始通过,而且它的强度会随着温度的升高而迅速地增大,尽管玻璃还是像从前那样硬。
这个电流显然是电解电流,因为如果把电极从电池组上断开并把它们接在一个电流计上,就会有一个相当大的由玻璃表面的极化所引起的反向电流通过。
如果当电池组还在起作用时仪器被冷却,电流就会像从前那样被冷的玻璃所阻止,但是表面的极化却还在。水银可以被取走,玻璃表面可以用硝酸和水洗净,然后换上新的水银。如果这时再把仪器加热,则玻璃刚一热到可以导电,极化电流立刻就会出现。
因此,我们可以把100℃的玻璃看成一种电解质,尽管表面看来它是一种固体。而且有相当的理由可以相信,在一种电介质有一个很小的导电程度的多数事例中,导电都是电解性的。极化的存在可以看成电解的一种决定性的证据,而且如果一种物质的电导率是随着温度而增大的,我们就有很好的理由来推测导电是电解性的 〔23〕 。
关于恒定的伏打元件
272.〕 当用一个内部出现着极化的伏打电池组来做一系列实验时,极化在电流不通的时间内将变小,从而当它再开始流时,电流就会比在它流了一段时间以后时更强一些。另一方面,如果允许电流通过一条短的支路而把电路的电阻减小,则当使电流重新通过普通的电路时,由于使用短电路而引起的大极化,电流强度在一开始时就会比它的正常强度要小一些。
电流方面的这些不规则性,在涉及精密测量的实验中是非常讨厌的。为了消除这些不规则性,必须消除极化,或至少是尽可能地减小极化。
当一块锌板被浸入硫酸锌溶液或稀硫酸中时,它的表面上似乎没有多大的极化。极化的主要部分出现在负金属的表面上,当负金属所浸入的液体是稀硫酸时,就可以看到它的表面布满了由液体的电分解而产生的氢气泡。这些气泡当然会通过阻止液体和金属相接触而减小接触面积并增大电路的电阻。但是,除了可以看到气泡以外,肯定还有一层或许并非处于自由状态的氢膜附着在金属上,而正如我们看到的那样,这层薄膜能够沿相反的方向产生一个电动势,它必然会减小电池组的电动势。
曾经采取了各种方案来消除这个氢膜。它可以通过机械方法而在某种程度上被减小,例如搅动液体或擦拭负金属的表面。在斯密的电池组中,负板是竖直的,而上面涂有很细的铂粉,气泡很容易从这种表面上逸出,而且在上升的过程中引起一种液流,而这种液流就有助于把新形成的其他气泡带走。
然而一种更有效得多的方法就是利用化学手段。化学手段是两种。在格罗夫的和本生的电池组中,负板被浸入于一种富含氧的液体中,从而氢就不是覆盖极板而是和这种物质相结合。在格罗夫的电池组中,极板是浸在强硝酸中的铂板。在本生的电池组中,极板是浸在同一种酸中的碳板。铬酸也被用于同一目的,而且有一个优点就是它没有由硝酸的还原而产生的那种烟雾。
一种不同的除氢方式就是用铜来作为负金属,并在表面上涂一层氧化物。然而当用它作为负极时,这种氧化物会很快地消失。为了更新它,焦耳曾经建议把铜板做成圆盘状,把它的一半浸入液体中并慢慢转动它,于是空气就对轮流暴露出来的部分起作用。
另一种办法就是用一种电解质来作为液体,该电解质的阳离子是比锌负得多的一种金属。
在丹聂耳电池组中,一个铜板被浸在一种硫酸铜的饱和溶液中。当电流通过溶液而从锌流到铜时,没有氢出现在铜板上而只有铜沉积在它上面。当溶液是饱和的而电流并不太强时,铜就作为真正的阳离子而起作用,而阴离子SO4 则向着锌运动。
当这些条件并不满足时,氢就会在阴极上出现,但是它立刻就会和溶液发生作用,并留下铜而和SO4 形成硫酸。当出现这种情况时,靠近铜板的硫酸铜就会被硫酸所取代,溶液变成无色的,而氢气就又开始引起极化。用这种方式沉积下来的铜比由真正的电解所沉积下来的铜在结构上更加松脆。
为了保证和铜相接触的液体是被硫酸铜所饱和的,必须在铜附近的液体中放一些硫酸铜的晶体,以便当溶液由于铜的沉积而变得较稀时可以有更多的晶体被溶解。
我们已经看到,靠近铜的液体必须被硫酸铜所饱和。更加必要的是锌所浸入的液体中应该没有硫酸铜。如果任何这种盐跑到锌的表面上去,它就会被还原,而铜就会在锌上沉积下来。于是锌、铜和液体就会形成一种小电路,而电解作用就在该电路中迅速地进行,而锌就被一种对电池组并无任何有用效应的作用所不断地腐蚀掉。
为了避免这一点,锌就被浸在稀硫酸或硫酸锌溶液中,而为了避免硫酸铜溶液和这种液体互相混合,两种液体就被一个用膀胱或素烧瓷作的屏障互相隔开;这种屏障允许电解通过它来进行,但是却很有效地阻止了各液体通过可见的液流而互相混合。
在某些电池组中,是用锯末来阻止液流的。然而格喇汉的实验却证明,如果使用这样一种隔离物,扩散过程就将进行得差不多和液体直接接触但没有可见的液流时同样地快;而且情况或许是,如果采用一个减弱扩散的屏障,它就将按相同的比例增大元件的电阻,因为电解导电是一种过程,它的数学规律和扩散的规律形式相同,从而对一种过程的干预必将同样地干预另一种过程。唯一的区别就在于,扩散是永远进行的,而电流则只有当电池组起作用时才会存在。
在一切形式的丹聂耳电池中,最后的结果都是硫酸铜总有办法到达锌那里并对电池组进行破坏。为了无限期地阻止这种结果,W. 汤姆孙爵士 〔24〕 曾经按照下面的形式制造了丹聂耳电池组。
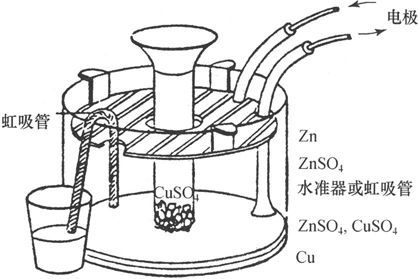
图22
在每一个电池中,铜板都是水平地放在底部的,铜板的上面倒上了硫酸锌的饱和溶液。锌被做成格子状,水平地放在溶液的表面附近,一根玻璃管竖直地插在溶液中,其下端刚好在铜板表面的上方,硫酸铜的晶体通过此管被放下去,并溶解在液体中,形成密度比纯硫酸锌的密度还要大的一种溶液,从而除了通过扩散以外不可能达到锌那儿。为了阻滞扩散过程,用玻璃管和棉花做成一个虹吸管,把它的一端放在锌和铜的中间,而其另一端则在电池外面的一个容器中,于是液体就从它的深度的中部被很慢地抽走。为了保证它的位置,在必要时从上面添入水或硫酸锌的稀溶液。这样,通过液体而扩散上来的硫酸铜的一大部分在到达锌以前就会被虹吸管所抽走,而锌就被一种几乎不含硫酸铜的并在电池中缓缓向下流动的液体所包围,而这种流动就会进一步阻止硫酸铜向上运动。在电池组的作用时间内,铜会沉积在铜板上,而SO4 则通过液体而慢慢地运动到锌,并和锌化合而形成硫酸锌。于是,底部的液体就通过铜的沉积而变稀,而上部的液体则通过锌的加入而变浓。为了阻止这种作用改变各液层的密度顺序并从而在容器中引起不稳定性和可见液流,必须注意保证管子中有充分的硫酸铜晶体,并在上方加入足够稀的硫酸锌溶液,使它比电池中的任一其他液层都要轻。
丹聂耳电池组绝不是常用电池组中的最强大的一种。格罗夫电池的电动势是丹聂耳电池的电动势的192,000,000倍,而本生电池的电动势是丹聂耳电池的电动势的188,000,000倍。
丹聂耳电池的电阻通常大于同样尺寸的格罗夫电池的电阻和本生电池的电阻。
然而,在一切要求精确测量结果的事例中,这些缺点却抵不过一个优点,那就是,在电动势的恒定性方面,丹聂耳电池胜过一切已知的装置 〔25〕 。它还有能够长时间地正常工作和不放出任何气体的优点。
第十九章 线性电流
论线性导体组
273.〕 任何一个导体可以当作一个线性导体来处理,如果它被安排得适当,使是电流在它的表面的两个部分之间永远按相同的方式而通过;那两个部分表面叫做它的电极。例如,设有任意形状的一块金属,除了两个地方以外整个的表面都被一种绝缘材料所覆盖,而在那两个地方,暴露着的导体表面则和用理想导电材料做成的电极相连接;这样一块金属就可以看成一个线性导体。因为,如果使电流从一个电极流入而从另一个电极流出,则流线将是确定的,而电动势、电流和电阻之间的关系将由欧姆定律来表示,因为物体每一部分中的电流都将是E的线性函数。但是,如果有多于两个的一些可能的电极,则导体中可以有多于一个的独立电流通过,而这些电流可以不互相共轭。参阅第282a和282b节。
欧姆定律
274.〕 设E是一个线性导体中从电极A1 到电极A2 的电动势。(参阅第69节)。设C是沿该导体的电流强度,这就是说,设有C个单位的电量在单位时间内沿方向A1 A2 通过每一个截面,并设R是导体的电阻,则欧姆定律的表示式是
串联的线性导体
275.〕 设A1 、A2 是第一个导体的电极,并设第二个导体被摆得有一个电极和A2 相连接,于是第二个导体就以A2 、A3 为其两个电极。第三个导体的电极可以用A3 和A4 来代表。
设沿着这些导体的电动势用E12 、E23 、E34 来代表,对其他导体依此类推。设各导体的电阻是R12 ,R23 ,R34 ,等等。于是,既然各导体是串联的从而有一个相同的电流C通过它们,我们由欧姆定律就有
如果E是体系的合电动势而R是合电阻,则我们由欧姆定律必有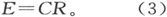
现在 
把这一结果和(3)式相比较,我们就得到 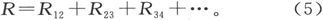
或者说,串联导体的电阻是分别考虑的各导体的电阻之和。
串联导体的任一点上的势
设A和C是串联导体的电极而B是二者之间的一个点,设a、c和b分别是这些点的势。设R1 是从A到B的那一部分的电阻,R2 是从B到C的那一部分的电阻,而R则是从A到C的整个体系的电阻,那么,既然a-b=R1 C,b-c=R2 C,而a-c=RC,B点的势就是 
当A点和B点的势已给定时,此式就确定B点的势
并联的线性导体
276.〕 设有一些导体ABZ、ACZ、ADZ并排摆放,使得它们的两端都和相同的两个点A、Z相接。这些导体被说成是联成一个“多重弧”,或称并联。
设这些导体的电阻分别是R1 、R2 、R3 ,而其电流是C1 、C2 、C3 ,此外并设并联导体的电阻是R,而其总电流是C。于是,既然A和Z上的势对一切导体都相同,我们就有相同的势差,用E来代表。于是我们就有E=C1 R1 =C2 R2 =C3 R3 =CR,但是C=C1 +C2 +C3 ,故得到 
或者说,并联导体的电阻的倒数,等于各分导体的电阻倒数之和。
如果我们把一个导体的电阻的倒数叫做导体的电导,我们就可以说,并联导体的电导是各分导体的电导之和。
并联导体的任一分支中的电流
由以上的各方程可以看出,如果C1 是并联导体的任一分支中的电流而R1 是该分支的电阻,则有 
式中C是总电流,而R是以上确定的并联导体的电阻。
截面均匀的导体的纵向电阻
277.〕 设一块立方形给定材料对平行于它的边棱的电流而言的电阻是ρ,而立方形的棱长为一个长度单位,则ρ叫做“该材料的单位体积的比电阻”{电阻率}。
现在考虑一个用相同材料做成的角柱形的导体,其长度为l而截面为1。这就相当于l个立方体串联在一起。因此这一导体的电阻就是lρ 。
最后,考虑一个长度为l而均匀截面为s的导体,这就相当于s个上面那样的导体相并联。因此这一导体的电阻就是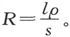 当我们知道了一条均匀导线的电阻时,如果我们能够测量它的长度和截面,我们就能确定制成导线的材料的比电阻。
当我们知道了一条均匀导线的电阻时,如果我们能够测量它的长度和截面,我们就能确定制成导线的材料的比电阻。
细导线的截面积可以通过测定样品的长度、重量和比重来最准确地确定。比重的测定有时是不方便的;在那种情况下,就用一根单位长度和单位质量的导线的电阻来作为“单位长度的比电阻”。
如果r是一根导线的这种比电阻,l是它的长度而m是它的质量,则有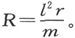
关于这些方程中所含各量的量纲
278.〕 一个导体的电阻就是作用在它上面的电动势和所引起的电流之比。导体的电导就是这个量的倒数,或者换句话说就是电流和引起电流的电动势之比。
现在我们知道,在静电单位制中,一个电量和带此电量的导体的势之比就是导体的电容,而且这是用长度单位来量度的。如果导体是一个放在无限场中的球,则这个长度是球的半径,因此,电量和电动势之比就是一个长度,但是电量和电流之比是一个时间,在该时间之内电流传递了那个电量。由此可见,电流和电动势之比就是长度和时间之比,换句话说就是一个速度。
导体的电导在静电单位制中是以速度单位计的;这一事实可以通过假设一个半径为r的球被充电到势V然后用所给的导体把球接地来加以验证。设球逐渐缩小,使得当电量通过导体而流走时球的势永远保持为V。于是球上的电荷就在任何时刻都是rV,而电流就是 但是V是一个常量,故电流就是
但是V是一个常量,故电流就是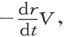 而通过导体的电动势则是V。
而通过导体的电动势则是V。
导体的电导是电流和电动势之比,或者说是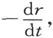 也就是说,它就是当电荷被允许通过导体流到地上时球的半径必须收缩以便保持其势不变的那个收缩速度。
也就是说,它就是当电荷被允许通过导体流到地上时球的半径必须收缩以便保持其势不变的那个收缩速度。
因此,在静电单位制中,导体的电导是一个速度,从而具有量纲[LT-1 ]。
因此导体的电阻具有量纲[L-1 T]。
单位体积的比电阻具有量纲[T],而单位体积的比电导则具有量纲[T-1 ]。
系数的数值只依赖于时间的单位,而这一单位在不同的国家中是相同的。
单位重量的比电阻具有量纲[L-3 MT]。
279.〕 以后我们将发现,在电磁单位制中,导体的电阻是用一个速度来表示的,从而在该单位制中导体的电阻就具有量纲[LT-1 ]。
导体的电导当然是这个量的倒数。
单位体积的比电阻在这一单位制中具有量纲[L2 T-1 ],而单位重量的比电阻则具有量纲[L-1 T-1 M]。
论一般的线性导体组
280.〕 一个线性导体组的最普遍事例就是用 个线性导体成对连接起来的n个点A1 ,A2 ,…,An 。设连接任何一对点例如Ap 和Aq 的那一导体的电导(即电阻的倒数)用Kpq 来代表。并设从Ap 到Aq 的电流是Cpq 。设Pp 和Pq 分别是点Ap 和点Aq 处的电势,而如果有任何电动势沿着导体从Ap 指向Aq ,就用Epq 来代表它。
个线性导体成对连接起来的n个点A1 ,A2 ,…,An 。设连接任何一对点例如Ap 和Aq 的那一导体的电导(即电阻的倒数)用Kpq 来代表。并设从Ap 到Aq 的电流是Cpq 。设Pp 和Pq 分别是点Ap 和点Aq 处的电势,而如果有任何电动势沿着导体从Ap 指向Aq ,就用Epq 来代表它。
由欧姆定律,从Ap 到Aq 的电流是 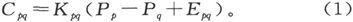
在这些量之间,我们有下列一组关系式:
导体的电导在正反两个方向上是相同的,或者说 
电动势和电流是有方向{译:应作“正负”}的量,故有
设P1 ,P2 ,…,Pn 分别是A1 ,A2 ,…,An 上的势,并设Q1 ,Q2 ,…,Qn 是单位时间内分别在这些点上进入体系中的电量。这些电量肯定服从“连续性”条件。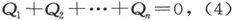 因为电既不能在体系中无限积累也不能在体系中无限产生。
因为电既不能在体系中无限积累也不能在体系中无限产生。
在任一点AP 上,“连续性”条件是 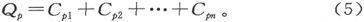
利用方程(1)把各电流的值代入此式中,就得到
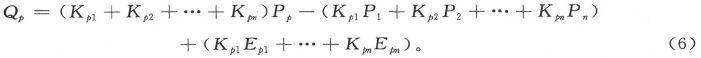
符号Kpp 并不出现在此式中,因此让我们设它的值是
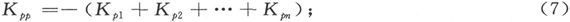
也就是说,设Kpp 是和相聚于Ap 点的一切导体的电导之和相等而反号的一个量。于是我们就可以把Ap 点处的连续性条件写成
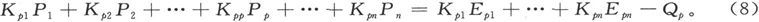
在这一方程中令p等于1,2,…,n,我们就将得到种类相同的n个方程,由此就能定出n个势P1 ,P2 ,…,Pn 。
然而如果我们把方程组(8)加起来,既然由(3)、(4)和(7)可知结果恒等于零,那就只会有n-1个独立的方程,这些方程将足以确定各点间的势差,而不能确定任一点的绝对势。然而在计算体系中的电流时并不需要任何绝对势。
如果我们用D来代表行列式
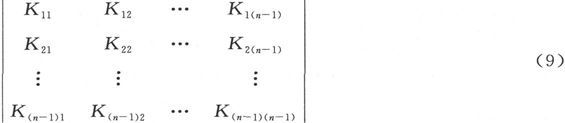
并用Dpq 代表Kpq 的子行列式,我们就能求得Pp -Pn 的值
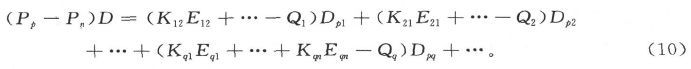
同理也可以定出任一其他点例如Aq 的势比An 的势大出的值。然后我们就能由方程(1)定出Ap 和Aq 之间的电流,并从而完全地解出问题。
281.〕 现在我们将演证体系中任意二导体的一种倒易性,这是和我们已经在第86节中演证过的静电倒易性相对应的。
在Pp 的表示式中Qq 的系数是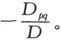 在Pq 的表示式中,Qp 的系数是
在Pq 的表示式中,Qp 的系数是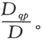
喏,Dpq 和Dqp 的区别只在于把Kpq 代成Kqp ,但是由方程(2)可知这两个符号是相等的,因为导体沿正反方向的电导相同。由此即得 
由此可知,由于在Aq 点通入一个单位电流而在Ap 引起的那一部分势,等于由于在Ap 点通入一个单位电流而在Aq 引起的那一部分势。
我们可以由这一定理推出一种更切实用的形式。
设A、B、C、D是体系中的任意四点,并设由于一个电流从A进入并从B离开体系而使C点的势比D点的势大出一个量P。于是,如果一个相等的电流Q从C进入并从D离开体系,则A点的势将比B点的势大出同一个量P。
如果引入一个电动势E,使它在从A到B的导体中起作用,而如果这就引起一个从X到Y的电流C,则引入到从X到Y的导体中的同一个电动势E将引起从A到B的相等的电流C。
电动势E可以是一个伏打电池组的电动势,这时必须注意保证导体的电阻在引入电池组的以前和以后是相同的。
282a.〕 如果有一个电动势Epq 沿着导体Ap Aq 起作用,则很容易求出沿着体系中的另一导体Ar As 引起的电流是Krs Kpq Epq (Drp +Dsq -Drq -Dsp )÷D。
如果 
那就不会有电流,但是由(11)可知,同样的方程也成立,如果当电动势沿Ar As 起作用时在Ap Aq 中没有电流的话。由于这种倒易关系式,所谈到的两个导体就被说成是共轭的。
共轭导体的理论曾由基尔霍夫研究过,他曾按照下面这种避免考虑势的方式叙述了线性导体组的条件。
(1)(“连续性”条件。)在体系的任一点上,流向该点的一切电流之{代数}和等于零。
(2)在由一些导体构成的任何完整回路中,沿回路计算的电动势之和等于每一导体中的电流和该导体的电阻的乘积之和。
我们可以通过针对完整回路来把形如(1)的各方程加起来而得到这一结果,这时各个势必然不再出现。
〔26〕 282b.〕 如果一些导线形成一个简单的网络,而且我们假设绕着每一个网络都有一个电流在周流,则形成两个网格之公共边的那条导线中的实际电流,将是周流于二网格中的二电流之差,这时当电流按反时针的方向运行时就把它算作正的。在这种情况下,很容易建立下列定理:设任意网格中的电流是x,电动势是E,而总电阻是R,并设和x在其中周流的那个网格具有公共边的各相邻网格中的周流电流是y,z,…,而各公共边的电阻是s,t,…,则有Rx-sy-tz-…=E。
为了举例说明这一法则的应用,我们将取所谓惠斯登电桥,并采用第347节中的图形和符号,于是我们就得到三个方程,它们代表这一法则在三个回路OBC、OCA、OAB的事例中的应用,而三个回路中的周流电流则分别是x、y、z;方程就是
(α+β+γ)x-γy-βz=E,
-γx+(b+γ+α)y-αz=0,
-βz-αy+(c+α+β)z=0。
由这些方程,我们现在就可以定出支路OA中的电流计电流z-y的值,但是读者请参阅第347节及以后各节,那里讨论了这一问题以及和惠斯登电桥有关的其他问题。
体系中产生的热
283〕 由第242节可知,单位时间内由一个电流C在电阻为R的一个导体中产生的热量的机械当量是 
因此我们必须确定体系中一切导体上的RC2 类型的量的和。
对于从Ap 到Aq 的导体来说,电导是Kpq ,而电阻Rpq 则满足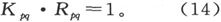
按照欧姆定律,这一导体中的电流是 
然而我们将假设,电流的值不是由欧姆定值给出而是Xpq ,而且

为了确定体系中产生的热,我们必须求出形如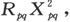
或 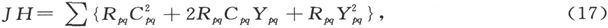
的各量之和。
代入Cpq 的值产记得Kpq 和Rpq 之间的关系,这一关系式就变成
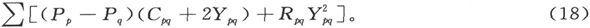
现在,既然C和X都必须满足Ap 处的连续性条件,我们就有

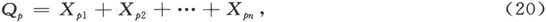
因此就得到 
因此,将(18)式的各项相加,我们就得到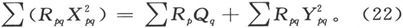
现在,既然R永远为正而Y2 也必为正,上式中的最后一项必然是正的。因此,当每一导体中的Y都为零时,也就是当每一导体中的电流都由欧姆定律给出时,上式的左端必为极小值 〔27〕 。
由此就得到下列的定理:
284〕 在任何不包含内电动势的导体组中,由按照欧姆定律而分布的电流所产生的热量,小于由按照和电流的供入和流出的实际条件不相矛盾的任何其他方式而分布的电流所产生的热量。
当欧姆定律得到满足时,实际产生的热量的机械当量是∑Pp Qp ,也就是说,它等于在各个外电极上供入的电量和各该供电处的势的乘积之和。
第六章附录
在第280节中研究了的电流分布规律,可以表示成很容易记住的法则如下。
让我们把其中一个点例如An 的势取作零势,那么,如果有一个电量Qs 流入As 中,则在正文中已经证明一点Ap 处的势应是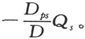 D和Dps 各量可按下述法则求出:D就是每次取(n-1)个电导的各乘积之和,而略去所有包括了形成闭合回路的各支路电导的乘积的那些项。Dps 就是每次取(n-2)个电导的各乘积之和,而略去所有包含支路Ap An 或As An 的电导的那些项,或是包含本身形成闭合回路或借助于Ap As 或As An 可以形成闭合回路的各支路电导的乘积的那些项。
D和Dps 各量可按下述法则求出:D就是每次取(n-1)个电导的各乘积之和,而略去所有包括了形成闭合回路的各支路电导的乘积的那些项。Dps 就是每次取(n-2)个电导的各乘积之和,而略去所有包含支路Ap An 或As An 的电导的那些项,或是包含本身形成闭合回路或借助于Ap As 或As An 可以形成闭合回路的各支路电导的乘积的那些项。
我们由方程(11)看到,沿支路Aq Ar ,作用着的一个电动势Eqr 的效应,和Q处的一个强度为Kqr Eqr 的源头以及R处的一个相同强度的尾闾的效应相同,从而上一法则将包括这一事例。然而这一法则的应用结果可以更简单地叙述如下。如果一个电动势Epq 沿着导体Ap Aq 而起作用,则沿另一导体Ar As 引起的电流是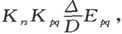 式中D按上述法则得出,而∆=∆1 -∆2 。这里的∆1 是这样得出的:在每次取(n-2)个电导的各乘积的和式中,选取既包含Ap Ar 的电导(或和Ap Ar 一起形成闭合回路的各支路电导的乘积)又包含Aq As 的电导(或和As Aq 一起形成闭合回路的各支路电导的乘积)的那些乘积,而从如此选出的各项中略去所有包含Ars 或Apq 的电导的那些项,或是所有包含本身形成或和Ar As 或Ap Aq 一起形成闭合回路的那些支路电导的乘积的那些项。∆2 和∆1 相对应,不过要分别取Ap As 、Aq Ar 来代替Ap Ar 和As Aq 。
式中D按上述法则得出,而∆=∆1 -∆2 。这里的∆1 是这样得出的:在每次取(n-2)个电导的各乘积的和式中,选取既包含Ap Ar 的电导(或和Ap Ar 一起形成闭合回路的各支路电导的乘积)又包含Aq As 的电导(或和As Aq 一起形成闭合回路的各支路电导的乘积)的那些乘积,而从如此选出的各项中略去所有包含Ars 或Apq 的电导的那些项,或是所有包含本身形成或和Ar As 或Ap Aq 一起形成闭合回路的那些支路电导的乘积的那些项。∆2 和∆1 相对应,不过要分别取Ap As 、Aq Ar 来代替Ap Ar 和As Aq 。
如果一个电流在P进入而在Q离开,则电流和Ap 、Aq 之间的势差之比是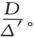
这里的∆′是每次取n-2个电导的乘积之和,而略去所有包含Ap Aq 的电导或包含和Ap Aq 一起形成闭合回路的支路电导之积的那些项。
在这些表示式中,所有包含形成闭合回路的各支路电导之积的那些项都应略去。
我们可以举例来说明这些法则,即把它们用于一个很重要的事例,那就是用6个导体连接起来的4个点的事例。让我们用1、2、3、4来代表这4个点。
于是D=每次取3个电导的乘积之和,但是要略去4个乘积K12 K23 K31 、K12 K24 K41 、K13 K34 K41 、K23 K34 K42 ,因为它们对应于四个闭合回路(123)、(124)、(134)、(234)。
于是就有D=(K14 +K24 +K34 )(K12 K13 +K12 K23 +K13 K23 )+K14 K24 (K13 +K23 )+K14 K34 (K12 +K23 )+K34 K24 (K12 +K13 )+K14 K24 K34 。
让我们假设有一个电动势E沿着(23)而作用,则通过支路(14)的电流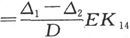
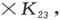 ∆1 =K13 K24 (根据定义),∆2 =K13 K43 。由此可见,如果没有电流通过(14),则K13 K24 -K12 K43 =0,这就是(23)和(14)可以共轭的条件。
∆1 =K13 K24 (根据定义),∆2 =K13 K43 。由此可见,如果没有电流通过(14),则K13 K24 -K12 K43 =0,这就是(23)和(14)可以共轭的条件。
通过(13)的电流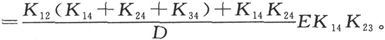
当一个电流在(2)进入而从(3)流出时,网络的电导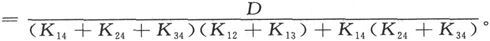
如果我们有5个点,则(23)和(14)相共轭的条件是
K12 K34 (K15 +K25 +K35 +K45 )+K12 K35 K45 +K34 K51 K52
=K13 K24 (K15 +K25 +K35 +K45 )+K13 K52 K54 +K24 K51 K53 。
第二十章 三维空间中的导电
电流的本性
285.〕 设在任一点取一个面积元dS和x轴相垂直,并设有Q个单位的电量在单位时间内从负侧向正侧通过这一面积,那么,如果当dS无限缩小时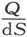 变为等于u,则u叫做给定点上电流沿x方向的“分量” 〔28〕 。
变为等于u,则u叫做给定点上电流沿x方向的“分量” 〔28〕 。
同样我们可以定义v和w,它们分别是电流沿y方向和z方向的分量。
286.〕 为了定义电流在给定点O上沿任一其他方向OR的分量,设l、m、n为OR的方向余弦;于是,如果我们分别在A、B、C三点上从x、y、z轴上截取等于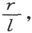
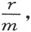 和
和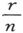 的线段,则三角形ABC将垂直于OR。
的线段,则三角形ABC将垂直于OR。
这个三角形ABC的面积将是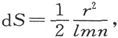 而通过减小r,这个面积将无限地减小。
而通过减小r,这个面积将无限地减小。
通过三角形ABC而离开四面体ABCO的电量,必然等于通过三个三角形OBC、OCA和OAB而进入这个四面体的电量。
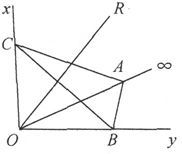
图23
三角形OBC的面积是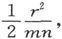 而垂直于它的平面的电流分量是u,故单位时间内通过这个三角形的电量就是
而垂直于它的平面的电流分量是u,故单位时间内通过这个三角形的电量就是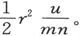
单位时间内分别通过三角形OCA和OAB而流进来的电量是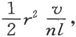 和
和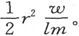
如果γ是电流在OR方向上的分量,则单位时间内通过ABC而离开四面体的电量是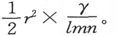 既然这一电量等于通过另外三个三角形流进来的电量,就有
既然这一电量等于通过另外三个三角形流进来的电量,就有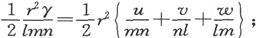 乘以
乘以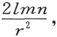 我们就得到
我们就得到 
如果我们令u2 +v2 +w2 =Γ2 ,并取l′、m′、n′,使之满足u=l′Γ,v=m′Γ,和w=n′Γ;就得到 
由此可见,如果我们可以把合电流定义为一个矢量,其量值是Γ,其方向余弦是l′、m′、n′,而γ则代表沿着和合电流有一夹角θ的一个方向的电流分量,就有

这就表明,电流的分解规律和速度、力以及其他矢量的分解规律相同。
287.〕 为了确定一个给定的曲面可以是一个流面的条件,设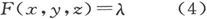
是一族曲面的方程,其中每一个平面通过令l取一个常数值来给出。于是,如果我们令

则沿λ增大的方向画出的法线的方向余弦是
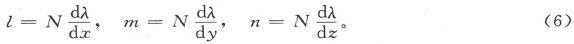
因此,如果γ是沿曲面法线的电流分量,则有
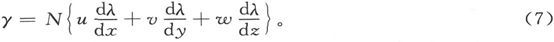
如果γ=0,就没有电流通过曲面,从而曲面就可以叫做一个“流面”,因为各流线是在这个曲面上的。
288.〕 因此,流面的方程就是 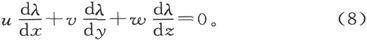
如果这一方程对一切的λ值都成立,则族中的一切曲面都将是流面。
289.〕 设有另外一族曲面,其参数为λ′,那么,如果这些曲面也是流面,我们就将有

如果有第三族流面,其参数为λ″,则有 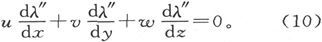
如果在这三个方程中消去u、v和w,我们就得到
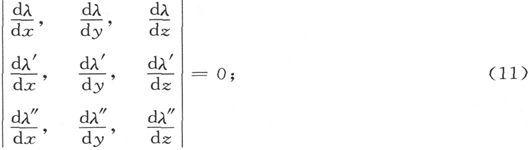
或者说 
这就是说,λ″是λ和λ′的某一函数。
290.〕 现在考虑四个曲面,其参数是λ、λ+δλ、λ′以及λ′+δλ′。这四个曲面包围成一个方截面的管子,我们称之为管δλ. δλ′。既然这个管子是由一些没有电流通过的曲面包围而成的,我们就可以称之为一个“流管”。如果我们在管上取两个截面,则通过一个截面流进来的电量必然等于通过另一个截面流出去的电量,从而这个电量就在一切截面上都相同,让我们用Lδλ. δλ′来代表它,此处L是定义特定流管的参数λ和λ′的函数。
291.〕 如果δS代表由一个垂直于x的平面在一个流管上切出的截面,则我们由自变数的变化理论得到 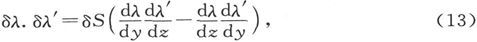
而由电流分量的定义就得到 
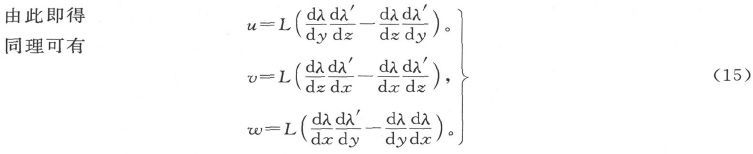
292.〕 当函数λ和λ′中的一个函数为已知时,总可以定义另一个函数使它的L等于1。例如,让我们取yz平面,在上面画一系列平行于y的等距线来代表这一平面在族λ′中切出的截面。换句话说,设函数由当x=0时λ′=z这个条件来确定。那么,如果我们令L=1,从而(当x=0时)λ=∫udy,则在平面(x=0)上通过任一部分的电量将是

由yz平面在各流面上切出的截面的本性既已确定,各流面在别处的形状就可以由条件式(8)和(9)来确定。这样确定的两个函数λ和λ′就足以通过把L代成1以后的方程(15)来确定每一点上的电流。
关于流线
293.〕 设已经选定一系列λ的值和λ′的值,相邻值之差为1。由这些值定义的两系列曲面将把空间分成许多方形截面的流管,通过每一流管的将是一个单位电流。通过假设电流的单位很小,电流的细节就可以在任意的精确度下用这些流管来反映,于是,如果画一个任意曲面和这一组流管相交截,则通过这一曲面的电流的数量将由它所交截的流管数目来表示,因为每一个流管载有单位电流。
各曲面的实际交线可以叫做“流线”。当单位取得够小时,和曲面相交的流线就近似地等于和它相交的流管数,因此我们可以认为,各流线不仅表示着电流的方向而且表示着电流的强度,因为通过一个截面的每一条流线都对应于一个单位电流。
关于电流层和电流函数
294.〕 包括在一族流面(例如λ′)中的两个相邻流面之间的一层导体,叫做一个“电流层”。这一层内的流线,由函数λ来确定。如果λA 和λP 分别代表点A和点P上的λ值,则从右向左越过在层上从A画到P的任何线的电流是λP -λA 〔29〕 。如果AP是在层上画出的一条曲线上的一个线段元ds,则从右向左越过这一线段元的电流是
根据函数λ,可以完全地确定层中的电流分布;这一函数叫做“电流函数”。
两侧以空气或其他非导电媒质为界的任何金层薄层或导电物质薄层,都可以看成一个电流层,层中的电流分布可以利用一个电流函数来表示。参阅第647节。
“连续性”方程
295.〕 如果我们把(15)中的三个方程分别对x、y、z微分,记得L是λ和λ′的一个函数,我们就得到 
在流体力学中,对应的方程叫做“连续性方程”。它所表示的连续性是存在上的连续性,也就是表示的这样一件事实:一种物质实体不可能离开空间的一个部分到达另一部分而并不经过二者之间的空间。它不能简单地从一个地方消失和在另一个地方出现,而是必须沿着一条连续的路径而运动。因此,如果画一个闭合曲面,包围一个地方而不包围另一个地方,则一种物质实体在从一个地方运动到另一个地方时必将越过这个闭合曲面。流体力学中最普遍的方程形式是 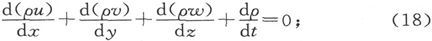
式中ρ代表实体的数量和它所占的体积之比,这时体积应是体积元;(ρu)、(ρv)和(ρw)代表单位时间内越过一个面积元的实体数量和面积元之比,而各面积元分别垂直于x、y和z轴。在这样的理解下,方程就适用于任何的物质实体,不论是固体还是流体,不论运动是连续的还是非连续的,只是该实体的各部分的存在是连续的就行。如果任何一种东西,尽管不是一种实体,但是却满足在时间和空间中连续存在的条件,则这一方程将表示那种条件。在物理科学的其他部门中,例如在电学量和磁学量的理论中,形式相似的方程也存在。我们将把这样的方程叫做“连续性方程”,以指示他们的形式,尽管我们可能并不认为这些量有什么物质性,甚至并不认为它们在时间和空间中有什么连续存在。
如果在方程(18)中令ρ=1,也就是说,如果假设实体是均匀的和不可压缩的,则我们在电流的事例中求得的方程(17)将和方程(18)完全相同。在流体的事例中,这个方程也可以按照在流体力学中给出的任何一种证明方式来确立。在其中一种证明方式中,我们在某一个数量的流体的运动过程中追索它的变形过程。在另一种方式中,我们把注意力集中在一个空间体积元上,并考虑进入和离开该体积元的一切流体。前一种方法不能应用于电流,因为我们并不知道电在物体中的运动速度,甚至不知道它是沿着电流的正方向还是负方向而运动的。我们所知道的一切,只是在单位时间内越过单位面积的电量的代数值,这是和方程(18)中的(ρu)相对应的一个量。我们没有任何办法来确定因子ρ的或因子u的值,从而我们不能追索一部分电量在物体中的运动。另一种研究方法,即考虑通过一个体积元的各壁面的各个电量的方法,对电流是适用的,而且从我们已经给出的形式来看也许是更加可取的,但是既然这种方法可以在任何流体力学著作中找到,我们也就用不着在这里重述了。
通过一个给定曲面的电量
296.〕 设Γ是曲面的任意点上的合电流。设dS是曲面的一个面积元,而ε是Γ和曲面的外向法线之间的夹角,则通过曲面的电流将是∬ΓcosεdS,积分遍及于该曲面。
正如在第21节中一样,在任何闭合曲面的事例中,我们可以把这一积分变换成
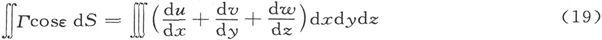
的形式,三重积分的积分限就是曲面所包括的界限。这就是闭合曲面上的外向通量的表示式。既然在一切恒稳电流的事例中这一通量不论积分限是什么都等于零,被积函数就必须为零,而这样我们就能得到连续性方程(17)。
第二十一章 三维空间中的电阻和电导
关于电流和电动势之间的最普遍的关系
297.〕 设任意点上的电流分量为u、v、w。设电动强度的分量为X、Y、Z。
任意点上的电动强度就是作用在位于该点的一个单位正电荷上的合力。它可以起源于(1)静电作用,这时如果V是势,就有 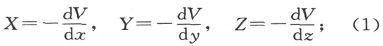
或起源于(2)电磁感应,其规律将在以后加以考查;或起源于(3)该点本身上倾向于沿给定方向产生电流的温差电作用或电化学作用。
一般说来,我们将假设X、Y、Z代表一点上的实际电动强度的分量,不论力的起源是什么,但是有时我们也将考查假设它完全起源于势的变化时所将得到的结果。
由欧姆定律,电流正比于电动强度。由此可知X、Y、Z必然是u、v、w的线性函数。
因此我们可以采用“电阻方程”如右: 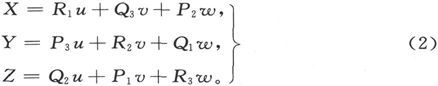
我们可以把各个系数R叫做沿各坐标轴方向的纵向电阻系数。
各系数P和Q可以叫做横向电阻系数。它们指示的是沿一个方向产生电流时所要求的沿另一方向的电动强度。
假如我们能够假设一个固体可以看成一个线性导体组,则由线性组中任意二导体的倒易性(第281节),我们可以证明平行于y产生单位电流所要求的沿z的电动强度,等于平行于z产生单位电流所要求的沿y的电动强度。这就将表明P1 =Q1 ,同理我们将得到P2 =Q2 和P3 =Q3 。当这些条件得到满足时,系数组就被说成是“对称的”。当条件不满足时,系数组就被说成是“非对称的”{译注:原文是Skew system,易引起误解,今略改。}
我们有很强的理由相信在每一个实际事例中系数组都是对称的 〔30〕 ,但是我们也将考查承认非对称可能性的某些后果。
298.〕 u、v、w这些量可以用一组方程来表示成X、Y、Z的线性函数,我们把这一组方程称为“电导方程”。

我们可以把各个系数r叫做“纵向电导系数”,而把各个p和各个q叫做“横向电导系数”。
各个电阻系数是和各个电导系数互逆的。这种关系可以定义如下。
设[PQR]是电阻系数行列式,而[pqr]是电导系数行列式,于是就有
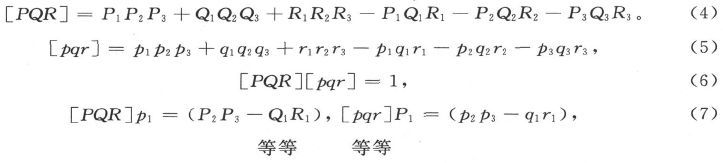
其他的方程可以通过将各符号P、Q、R、p、q、r按各下标1、2、3进行轮换来得出。
热的产生率
299.〕 为了求出电流在单位时间内克服电阻而产生热时所做的功,我们把电流分量和对应的电动强度分量相乘。于是我们就得到单位时间内消耗的功W的表示式如下:
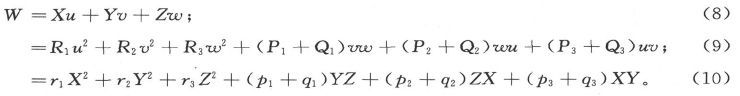
通过坐标轴的适当选择,可以从(9)中消去含u、v、w的乘积的各项,或是从(10)中消去含X、Y、Z的乘积的各项。然而,把W简化成R1 u2 +R2 v2 +R3 w2 的坐标系通常并不同于把它简化成r1 X2 +r2 Y2 +r3 Z2 的坐标系。
只有当系数P1 、P2 、P3 分别等于Q1 、Q2 、Q3 时两个坐标系才会重合。
如果我们像汤姆孙 〔31〕 那样写出 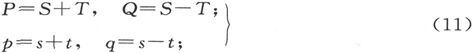
我们就得到 
和 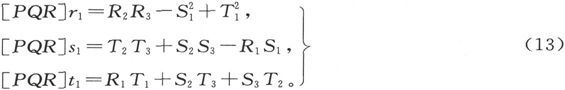
因此,如果我们使S1 、S2 、S3 不再存在,则各系数s并不会也不再存在,除非各系数T等于零。
稳定条件
300.〕 既然电的平衡是稳定的,用于保持电流的功就必须永远是正的。W必为正的条件是三个系数R1 、R2 、R3 和三个表示式 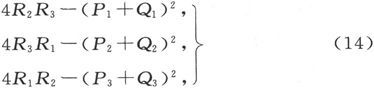
必须都是正的。
关于电导系数也有类似的条件。
均匀媒质中的连续性方程
301.〕 如果我们把电动强度的各分量写成势的导数,则连续性方程

在均匀媒质中将变成
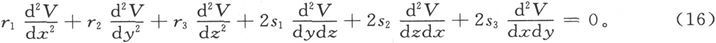
如果媒质是不均匀的,则会有起源于电导系数从一点到另一点的变化的一些项。
这一方程对应于各向异性媒质中的拉普拉斯方程。
302.〕 如果我们令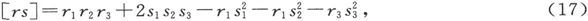
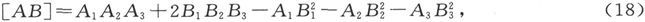
式中 
等等,则A、B组将和r、s组互逆,而如果我们令
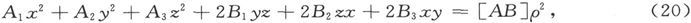
我们就会发现 
是方程的一个解 〔32〕 。
在各系数T为零的事例中,各系数A和B变成与第299节中的各系数R和S相等同。当T不等于零时,情况并不是这样的。
因此,在电从一种无限的、均匀的然而并非各向同性的媒质中的一个中心流出的事例中,等势面就是一些椭球,对其中每一个椭球来说ρ是常量。这些椭球的轴各沿电导的主轴,而这些轴并不和电阻的主轴相重合,除非体系是对称的。
通过方程(16)的变换,我们可以取电导的主轴作为x、y、z轴。于是形如s和B的系数将简化为零,而每一个形如A的系数将和对应的形如r的系数互为倒数。p的表示式将是 
303.〕 电阻和电导的完整方程组的理论就是三变数线性函数组的理论;这种理论在协变理论 〔33〕 和物理学的其他部门中有其实例。处理这种问题的最合适的方法,就是哈密顿和泰特用来处理一个矢量的线性矢量函数的那种方法。然而我们不准备明显地引用四元数的符号。
各系数T1 、T2 、T3 可以看成一个矢量T的直角分量,该矢量的量值和方向是固定在物体中的,和坐标轴的方向无关。对于t1 、t2 、t3 也有相同的情况,它们是另一个矢量t的分量。
矢量T和t的方向通常并不一致。
现在让我们把z轴取成和矢量T相重合,并相应地变换电阻方程。这时它们的形式将是 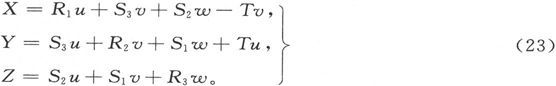
由这些方程看来,我们可以把电动强度看成两个力的合力;其中一个力依赖于各系数R和S,而另一个力则只依赖于T,依赖于R及S的分力和电流的关系,与椭球切面的垂线和矢径的关系相同。另一个依赖于T的分力等于T和垂直于T的电流分量的乘积,其方向垂直于T和电流,并永远指向电流分量沿正方向绕T转动90°时所指的方向。
如果我们把电流和T都看成矢量,由T引起的电动强度分量就是乘积“TX电流”的矢量部分。
系数T可以叫做“旋转系数”。我们有理由相信它在任何已知的物质中都是不存在的。如果存在的话,它应该在一些磁体中被找到,那些磁体有一种沿着一个方向的也许是由物质内的旋转现象所引起的极化 〔34〕 。
304.〕 于是,假设不存在任何旋转系数,我们就将指明可以怎样对在第100a~100e节中给出的汤姆孙定理进行推广,来证明电流在给定时间内在一个体系中产生的热量是一个唯一的极小值。
为了简化代数计算,设坐标轴选得可以把表示式(9)简化为三项,而且在现有的事例中也把表示式(10)简化为三项;然后让我们考虑这时简化为
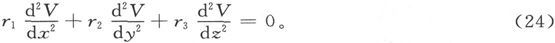
的普遍特征方程(16)。另外,设a、b、c是x、y、z的满足条件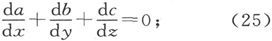
的三个函数,并设 
最后,设三重积分
遍及于一个空间,该空间的边界如第100a节所述;也就是说,在某些部分上,V是常量而在另一些部分上矢量a、b、c的法向分量已经给定,而且前一个条件还附加着一个限制,即这一分量在整个边界面上的积分应为零。于是,当u=0,v=0,w=0时W将是一个极小值。
因为,我们在这一事例中有r1 R1 =1,r2 R2 =1,r3 R3 =1;从而由(26)即得
但是既然 
第三项就因为积分限上的条件而等于零。
因此(28)式中的第一项就是W的唯一的极小值。
305.〕 由于这一定理在电学理论中有很大的重要性,在不用分析运算的形式下给出下述最普遍事例的证明就可能是有用的。
让我们考虑电通过一个任意形状的、均匀或不均匀的导体的传播情况。
这时我们知道:
(1)如果我们沿着路径并沿着电流的方向画一条线,则这条线必然从高势的地方引向低势的地方。
(2)如果体系各点的势按一个给定的均匀的比例而变化,则按照欧姆定律,电流也将按相同的比例而变化。
(3)如果某种势分布引起某种电流分布,而第二种势分布引起第二种电流分布,则其势为第一种和第二种分布中的势之和或差的第三种势分布将引起第三种电流分布,而这种分布通过给定有限曲面的总电流将等于在第一种和第二种分布中通过该曲面的总电流之和或差。因为,由欧姆定律,由于势的改变所引起的附加电流是和由原有势分布所引起的原有电流无关的。
(4)如果势在整个一个闭合曲面上是常量,而且曲面内没有任何的电极或内禀电动势,则闭合曲面内部不会有电流,而其内部各点的势将等于曲面上的势。
假如闭合曲面中有电流,则电流必然或是形成闭合曲线,或是其起点和终点都位于曲面之内或之上。
但是,既然电流必须从高势处流到低势处,它就不能形成闭合曲线。
既然曲面内没有任何电极,电流的起点和终点就不可在闭合曲面之内,而既然曲面上各点的势都相同,也不可能有任何电流沿着从曲面上一点到另一点的线而流动。
由此可见曲面内部没有任何电流,从而也不可能有任何势差,因为这样一个势差将引起电流,而因此闭合曲面内的势就到处都和曲面上的势相同。
(5)如果没有任何电流通过一个闭合曲面的任何部分,而又没有任何电极或内禀电动势位于曲面之内,则曲面内部将没有电流,而势将是均匀的。
我们已经看到,电流不能形成闭合曲线或是起始或终止于曲面之内,而既然根据假设它又不通过曲面,那就不可能有任何电流,从而势就是不变的。
(6)如果势在一个闭合曲面的一部分上是均匀的,而曲面的其余部分上又没有电流通过,则根据相同的理由可知势在曲面内部将是均匀的。
(7)如果一个物体的一部分表面的每一点上的势为已知,而在其余部分表面的每一点上通过的电流为已知,则物体内部各点上只能存在一种势分布。
因为,假若在物体内的任一点上可以有两个不同的势值,设在第一种事例中为V1 而在第二种事例中为V2 ,并且让我们设想第三种事例,那时物体每一点的势是第一、二两种事例中的势的差值。那么,在势为已知的那一部分表面上,第三种事例中的势将是零,而在所通过的电流为已知的那一部分表面上,则第三种事例中的电流将为零,于是由(6)可知,曲面内到处的势都将是零,或者说V1 和V2 并无差值。因此就只有一种可能的势分布。这一定理是对的,不论固体是以一个还是以若干个闭合曲面为其边界面。
一个形状给定的导体的电阻的近似计算
306.〕 这里考虑的导体,其表面被分成三部分。在其中第一部分上,势被保持为一个常量。在第二部分上,势有一个不同于第一部分上的值的常量值。表面的整个其余部分都不允许电通过。我们可以假设第一部分和第二部分上的条件是通过在导体上加了两个用理想导电材料做成的电极来满足的,而其余表面上的条件则是通过用一种完全不导电的材料盖住它来满足的。
在这些条件下,导体任何部分的电流将简单地正比于两个电极之间的势差。把这个势差称为电动势,从一个电极到另一个电极的总电流就等于电动势和整个导体的电导的乘积,而导体的电阻就是电导的倒数。
只有当一个导体近似地处于上述这样的条件下时,它才能被说成有一个确定的整体电阻。两头接在大铜块上的用细导线绕成的线圈就近似地满足这些条件,因为大电极中的势差不多是常量,而同一电极上各点之间的任何势差和二电极之间的势差比起来是可以忽略不计的。
计算这样的导体的电阻的一种很有用的方法,据我所知是由瑞利勋爵最初在一篇论文“关于共振理论” 〔35〕 中提出的。
这是建筑在下面的想法上的。
如果导体任一部分的比电阻被改变而其余部分的比电阻保持不变,则整个导体的电阻将变大,如果该部分的电阻是增大了的,而整个导体的电阻将变小,如果该部分的电阻是减小了的。
这一原理可以认为是不言而喻的,但是可以很容易地证明,一个导体组在取为电极的二点之间的电阻表示式的值,是随着组内每一导体电阻的增加而增加的。
由此可以推知,如果在导体物质中画一个任意形状的曲面,而且进一步假设这个曲面是一个由理想导电物质构成的无限薄的层,则整个导体的电阻将减小,除非曲面是导体在自然状态下的一个等势面;在后一情况下,把该面做成理想导体不会产生任何效应,因为它已经是处于平衡的了。
因此,如果我们在导体内部画出一系列曲面,其中第一个曲面和第一个电极相重合,其最后一个曲面和第二个电极相重合,而中间的各曲面以导体的不导电表面为边界,而且并不相交,另外,如果我们假设这些曲面中的每一个曲面都是一个无限薄的理想导电层,我们就将得到一个体系,其电阻肯定不大于原有导体的电阻,而且只有当我们所选的那些曲面是自然等势面时,该体系的电阻才等于原有导体的电阻。
计算人为体系的电阻是比原有问题容易得多的一种运算。因为整体电阻就是包括在相邻曲面之间的所有各物质层的电阻之和,而每一物质层的电阻可以求出如下:
设dS是物质层表面的一个面积元,v是层的垂直于面积元的厚度,p是比电阻,E是完全导电曲面之间的势差,而dC是通过dS的电流,于是就有 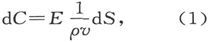
而通过物质层的总电流就是 
积分遍及以导体的不导电表面为其边界的整个物质层。
由此可见,物质层的电导就是 
而物质层的电阻是这个量的倒数。
如果物质层是以两个曲面为其边界面的,而函数F在该二曲面上的值分别是F和F+dF,则有 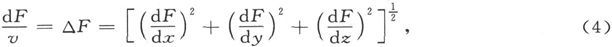
而该层的电阻就是 
为了求出整个人为导体的电阻,我们只要对F求积分,于是就得到

自然状态下的导体的电阻大于如此求得的值,除非我们所选的曲面全部都是自然等势面。另外,既然R的真实值是各个R1 值的绝对最大值,它就可以这样来求出:所选可曲面对真实等势面的微小偏离,将引起R的一个比较小的误差。
这种确定电阻值下限的方法显然是完全普遍的,而且是可以应用于任何形状的导体的,即使比电阻ρ是在导体内以任意方式变化的也无妨。
最熟知的例子就是确定变截面直导线的电阻的普通方法。在这一事例中,所选的各面是一些垂直于导线轴的平面,各物质层具有平行的表面,而截面为S、厚度为dS的层的电阻就是 
而长度为s的整个导线的电阻就是 
式中S是横截面,而且是s的函数。
在导线的截面随长度而缓慢变化的事例中,这一方法给出的结果和真实值很接近,但结果其实只是一个下限,因为真实的电阻永远大于这种结果,截面完全均匀的事例除外。
307.〕 为了求出电阻的上限,让我们假设在导体中画出的一个曲面被弄成不导电的。此事的效应必然是增大导体的电阻,除非该曲面是自然电流面之一。借助于两组曲面,我们可以形成一组管子,它们将完全限定电流,而这些不导电曲面的效应,如果有任何效应的话,将是使电阻超过它的自然值。
每一根管子的电阻,可以用已经给出的计算细导线电阻的办法来计算,而整个导体的电阻是所有各管电阻倒数之和的倒数。这样求出的电阻大于自然电阻,除了各管和自然流线相一致时以外。
在已经考虑过的事例中,导体的形状是一个拉长了的旋转体;让我们沿物体的轴来测量x,并设任一点上的截面半径为b。设一组非导电曲面是通过轴线的一些平面,对其中每一个平面来说φ是不变的;设另一组曲面是一些旋转曲面,其方程是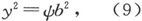 式中
式中 是介于0和1之间的一个数字。
是介于0和1之间的一个数字。
让我们考虑由各面φ和φ+dφ、 和
和 +d
+d 、x和x+dx限定的一根管子的一段。
、x和x+dx限定的一根管子的一段。
垂直于轴线的管子截面是 
如果θ是该管和轴线之间的夹角,则有 
管子的元段的真实长度是dx secθ,而其真实截面积是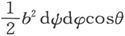 因此它的电阻是
因此它的电阻是
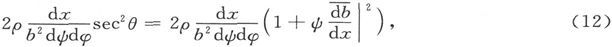
令 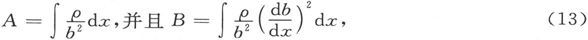
积分遍及导体的全部长度x,则管d dφ的电阻是
dφ的电阻是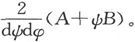 而其电导是
而其电导是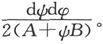
整个导体的电导是各管电导之和。为了求出这一电导,我们必须把此式从φ=0积分到φ=2π,并从 =0积分到
=0积分到 =1。结果是
=1。结果是 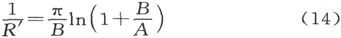
这一结果可以小于但不能大于导体的真实电导。
当 永远是一个小量时,
永远是一个小量时, 也将很小,从而我们可以把这个电导表示式展开,于是
也将很小,从而我们可以把这个电导表示式展开,于是
此式第一项, 就是我们用以前的方法所应得到的电导的上限。因此,真实的电导就小于第一项而大于整个的级数。电阻的上限就是此式的倒数,或者说
就是我们用以前的方法所应得到的电导的上限。因此,真实的电导就小于第一项而大于整个的级数。电阻的上限就是此式的倒数,或者说
如果除了认为电流受到各曲面φ和 的限制以外还假设通过每一根管子的电流和d
的限制以外还假设通过每一根管子的电流和d dφ成正比,我们就将得到这一附加约束下的电阻值
dφ成正比,我们就将得到这一附加约束下的电阻值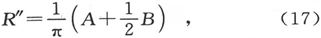 〔36〕
〔36〕
此值显然大于上一值,而由于附加的约束,这也是理所当然的。在瑞利勋爵的论文中这就是所作的假设,而文中给出的电阻上限就具有(17)的值,它比我们在(16)中得到的稍大一些。
308.〕 我们现在必须应用相同的方法来求出当一个半径为a的圆柱导体的一端和一个很大的电极相接时必须对导体的长作出的改正量。这时我们可以假设电极是用另一种金属制成的。
为了得到电阻的下限,我们可以假设有一个无限薄的用理想电物质制成的圆片被放在圆柱的一端和大块电极之间,以便使圆柱的端面上具有一个到处相同的势。于是圆柱内部的势将只是它的长度的函数,而且,如果我们假设电极和圆柱接触的部分近似地是平面,而且它的一切线度都比圆柱的直径大得多,则势的分布将是由放在无限媒质中的一个圆盘形导体所引起的那种势分布。见第151、177节。
如果E是圆片和电极最远部分之间的势差,C是从圆片的表面出发而进入电极中的电流,而ρ′是电极的比电阻,那么,如果Q是我们将假设为像在第151节中那样分布在圆片上的电量,我们就看到,电动强度在圆上的积分是

因此,如果从一点到电极的导线长度是L,而导线的比电阻是ρ,则从该点到电极上不靠近接触面的任何一点的电阻是 而且此式可以写成
而且此式可以写成

此处括号中的第二项就是在计算一根圆柱或导线的电阻时必须加在它的长度上的一个量,而这肯定是一个微不足道的改正量。
为了理解主要误差的本性,我们可以注意,尽管我们曾经假设导线中的电流直到圆片为止是在整个截面上均匀分布的,但是从圆片到电极的电流却不是均匀分布的,而是在任一点上都反比于通过该点的最短弦的(第151节)。在实际情况下,通过圆片的电流将不是均匀的,但它也不像所假设的情况一样从一点到一点变化得那么快。实际情况下的圆片的势将不是均匀的而是从中间到边沿逐步减小。
309.〕 其次我们将通过把圆片中的电流约束成各点均匀来确定一个大于真实电阻的量。我们可以假设,为此目的而引入的电动势是垂直于圆片的表面而作用着的。
导线中的电阻将和以前相同,但是电极中的发热率将是电流和势的乘积的面积分。任何一点的流动率将是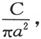 而势将和面密度为σ的带电表面的势相同,此处
而势将和面密度为σ的带电表面的势相同,此处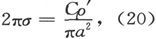
ρ′是比电阻。
因此我们必须确定圆片均匀地带有面密度为σ的电荷时的势能。
〔37〕 密度σ均匀的一个圆片的边沿上的势,很容易求出为4aσ,在圆片边沿上增加宽度为da的一条时所做的功是2πaσda。4aσ,而圆片的总势能就是此式的积分,或者说是

在电传导的事例中,电阻为R′的电极中的功率是C2 R′。但是,由普遍的导电方程可知,穿过圆片的单位面积的电流应是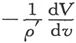 或
或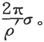 如果V是圆片的势而ds是它的面积元,则功率
如果V是圆片的势而ds是它的面积元,则功率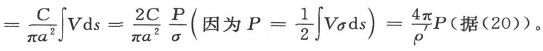
因此我们就有 
于是,由(20)和(21)即得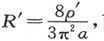 而必须加在圆柱长度上的改正量就是
而必须加在圆柱长度上的改正量就是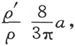 这个改正量大于真实值。因此,必须加在长度上的改正量是
这个改正量大于真实值。因此,必须加在长度上的改正量是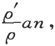 n是一个数字,介于
n是一个数字,介于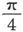 和
和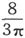 之间,或者说介于0.785和0.849之间。
之间,或者说介于0.785和0.849之间。
〔38〕 利用二级近似,瑞利勋爵曾经把上限减小到0.8282。
第二十二章 不均匀媒质中的导电
关于在两种导电媒质的分界面上必须满足的条件
310.〕 有两个条件是电流分布必须普遍满足的,即势必须连续的条件和电流的“连续性”条件。
在两种媒质的分界面上,第一个条件要求分界面两侧相距无限近的两个点上的势应该相等。这里所说的势,应理解为借助于一个用给定金属制成的电极而接在所给点上的一个静电计所测得的势。如果势是用第222、246节所描述的那种把电极放在金属中一个充有空气的空腔中的办法来测量的,则如此测得的靠近不同金属的点上的势将相差一个量,该量依赖于两种金属的温度和种类。
界面上的另一个条件是,通过任一面积元的电流当在两种媒质中测量时应该相等。
于是,如果V1 和V2 是两种媒质中的势,则在分界面的任一点上,有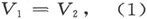
而且,如果u1 、v1 、w1 和u2 、v2 、w2 是两种媒质中的电流分量,而l、m、n是分界面法线的方向余弦,则有 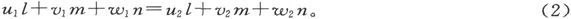
在最普遍的事例中,各分量u、v、w是V的导数的线性函数,其形式由方程

来给出,此处X、Y、Z分别是V对x、y、z的导数。
让我们考虑一种分界面的事例,分界面一侧的媒质具有这些电导系数,而其另一侧则是电导系数等于r的一种各向同性的媒质。
设X′、Y′、Z′是各向同性媒质中的X、Y、Z的值,于是我们在分界面上就有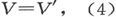
或 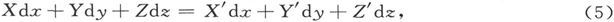
当 
这一条件导致 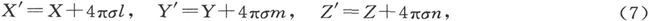
式中σ是面密度。
在各向同性媒质中,我们还有 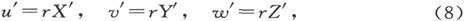
从而分界面上的电流条件就是 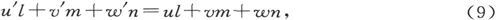
或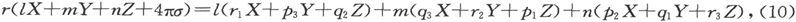
由此即得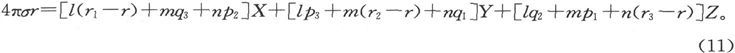
量σ代表分界面上的电荷面密度。在结晶的和有结构的物质中,它依赖于分界面的方向和垂直于分界面的力。在各向同性物质中,系数p和q是零而各个系数r都相等,从而就有 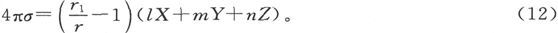
式中r1 是物质的比电导,r是外部媒质的比电导,而l、m、n是向着比电导为r的媒质画出的法线的方向余弦。
当两种媒质都为各向同性时,条件可以大为简化,因为,如果k是单位体积的比电阻,就有 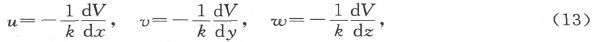
从而如果v是分界面任一点上从第一种媒质向第二种媒质画的法线,则连续性条件是

如果θ1 和θ2 分别是第一种媒质和第二种媒质中的流线和分界面法线所夹的角,则这些流线的切线和该法线位于同一平面上,且在法线的两侧,而且有

此式可以叫做流线的折射定律。
311.〕 作为电在穿越两种媒质的分界面时所必须满足的条件的例子,让我们假设分界面是半径为a的球面,球面内、外的比电阻为k1 和k2 。
设把球面之内和之外的势能都按体谐函数展开,并设其依赖于面谐函数Si 的部分在球面之内和之外分别是


在分界面上,r=a,我们应有 
由这些条件式,我们得到方程
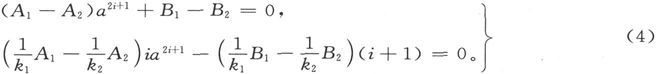
当我们知道了四个量A1 、A2 、B1 、B2 中的两个量时,这些方程就足以导出其余的两个量。
让我们假设A1 和B1 是已知的,于是我们就得到A2 和B2 的下列表示式,
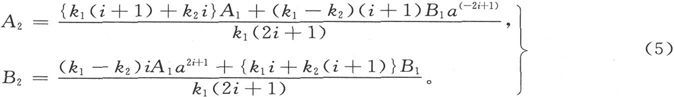
用这种办法,我们可以针对由同心球面分成的任意多层媒质来求出势的谐函数展式中每一项所必须满足的条件。
312.〕 让我们假设第一个球面的半径是a1 ,并设有第二个球面,其半径a2 大于a1 ,而在这个球面以外,比电阻是k2 。如果在这些球面内没有电荷的正负源头,那就不会有V的无限值,从而我们将有B1 =0。
于是我们就求得外面媒质中的系数A3 和B3 的表示式
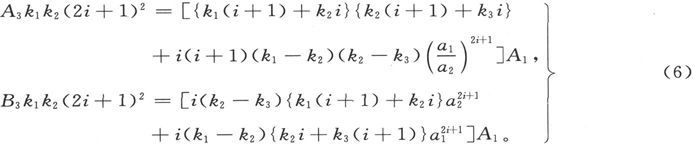
外部媒质中的势值,部分地依赖于外部的电源,这种电源独立于内部不均匀物质球的存在而引起电流,而同时势值也部分地依赖于引入不均匀球而造成的干扰。
第一部分必然只依赖正阶次的体谐函数,因为它不可能在球内有无限值。第二部分必然依赖于负阶次的体谐函数,因为它在距球心无限远处必须为零。
由此可见,由外电动势引起的势必须展成正阶体谐函数的级数。设A3 是形如A3 Si ri 的一个体谐函数的系数。于是我们就能由(6)求得内球的对应系数A1 ,并由此导出A2 、B2 和B3 。在这些系数中,B2 代表由于引入不均匀球而对外部媒质中的势所造成的影响。
现在让我们假设k3 =k1 ,于是情况就变成,一个k=k2 的中间球壳把k=k1 的一种媒质分成了内外两部分。
如果我们令 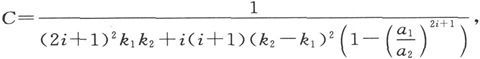
就得到 
未受干扰的系数A3 和它在壳内部的值A1 之差是
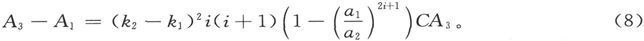
既然不论k1 、k2 的值是什么这一差值都永远和A3 同号,那就可以知道,不论球壳的导电性能比其余媒质的性能是好还是坏,球壳所占据的空间中的电作用都是比没有球壳时更弱一些的。如果球壳是比其余其质更好的一个导体,它就倾向于使内球各点的势变为相等。如果它是一个较坏的导体,它就倾向于阻止电流达到内球。
实心球的事例可以通过令a=0而由此事例推得,它也可以独立地被算出。
313.〕 谐函数展式中最重要的项是i=1的那一项,对该项来说有
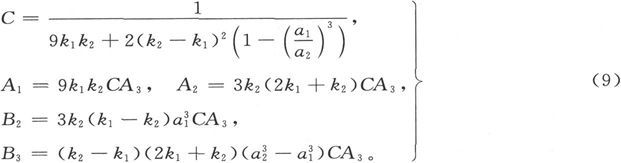
比电阻为k2 的实心球的事例可以通过令a1 =0而从此式推出,于是我们就有

很容易由普遍表示式证明,在由电阻为k2 的球壳包围的电阻为k1 的球核的事例中,B3 的值和电阻为K而具有外球半径的一个均匀实心球的事例中的值相同,此处
314.〕 设有几个半径为a1 而其比电阻为k1 的球放在一种比电阻为k2 的媒质中,各球相距较远,以致它们对电流路线的干扰效应可以看成是相互独立的,那么,如果所有这些球都包括在一个半径为a2 的球中,则离此球心很大距离r处的势将有如下的形式。

式中B的值是 
n个小球的体积和包围它们的大球体积之比是 
因此,离球很远处的势的值可以写成

喏,假如半径为a2 的整个球都是用一种比电阻为K的材料制成的,我们就将得到

为了使一个表示式和另一个表示式相等价,应有
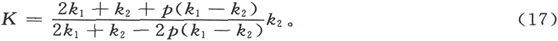
因此这就是一种组合媒质的比电阻,该媒质包括一种比电阻为k2 的媒质,里边分散着一些比电阻为k1 的小球,所有小球的体积和整个球的体积之比是p。为了使这些球的作用可以没有依赖于它们的干涉的效应,它们的半径应该比它们的距离小得多,从而p必然是个很小的分数。
这一结果也可以用别的方法来求得,但是此处给出的求法只重复了已经得到的关于单一球的结果。
当各球之间的距离并非远大于它们的半径而且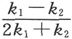 也相当大时,结果中就会出现一些其他的项;我们现在不考虑那些项。由于这些项的存在,各球的某些分布方法将使组合媒质的电阻在不同方向上有不同的值。
也相当大时,结果中就会出现一些其他的项;我们现在不考虑那些项。由于这些项的存在,各球的某些分布方法将使组合媒质的电阻在不同方向上有不同的值。
电像原理的应用
315.〕 作为例子,让我们考虑由一个平界面分开的两种媒质,并且让我们假设有一个电的源头位于第一种媒质中,离分界面的距离是a,单位时间内从源头流出的电量是S。
假若第一种媒质是无限延伸的,任一点P上的电流就将沿着SP方向的,而P点的势则将是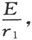 此处
此处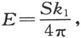 而r1 =SP。
而r1 =SP。
在实际事例中,各条件可以通过在第二种媒质取S的一个像I来加以满足,此时IS垂直于分界面并被该面所平分。设r2 是任一点离开I的距离,则在分界面上有


设第一种媒质中任一点的势V1 是由放在S点上的一个电量E和放在I点上的一个电量E2 所引起的,而第二种媒质中任一点的势V2 是由放在S上的像电量E1 所引起的,那么,如果 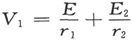 而
而
则边界条件V1 =V2 给出 
而条件 
则给出 
由此即得 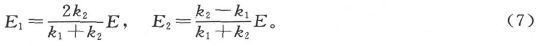
因此,第一种媒质中的势就是由S处的电荷E和I处的电荷E2 按照静电理论而即将在空气中引起的势,而第二种媒质中的势则是由S处的电荷E1 所将在空气中引起的势。
第一种媒质中任一点上的电流和该媒质为无限时由源头S和放在I处的源头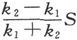 所引起的电流相同,第二种媒质中任一点上的电流和该媒质为无限大时由放大S处的源头
所引起的电流相同,第二种媒质中任一点上的电流和该媒质为无限大时由放大S处的源头 所起的电流相同。
所起的电流相同。
于是,在由平面边界分开的两种媒质的事例中,我们就有一种完备的电像理论。不论第一种媒质中有些什么性质的电动势,它们在第一种媒质中引起的势都可以通过把它们的直接效应和它们的像的效应结合起来而得出。
如果我们假设第二种媒质是一种理想导体,则k2 =0,而I处的像就和S处的源头相等并异号。这就是汤姆孙静电理论中的那种电像的事例。
如果我们假设第二种媒质是一种理想绝缘体,则k2 =∞,而I处的像就和S处的源头相等并同号。这就是流体运动学中当流体以一个刚性平面为界面时的像的事例 〔39〕 。
316.〕 在分界面被假设为一个理想导体的表面时非常有用的反演法,是不能应用于比电阻不相等的两种导体的分界面的更普遍事例的。然而,二维空间中的反演法却是适用的,正如在第190节中给出的更普遍的变换法一样 〔40〕 。
分隔两种媒质的平板中的导电
317.〕 其次让我们考虑一种厚度为AB的平板媒质,其比电阻为k2 ;它分隔开两种媒质,其比电阻为k1 和k2 设在第一种媒质{k2 }中有一个源头S,试考虑其在该媒质中引起的势的改变。
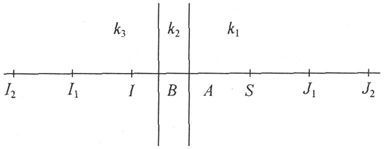
图24
势将等于由一系列电荷引起的势,各电荷放在通过S的平板法线上的某些点上。
令 AI=SA,BI1 =SB,AJ1 =I1 A,BI2 =J1 B,AJ2 =I2 A,等等,
我们就有一系列点,彼此之间的距离等于平板厚度的两倍。
318.〕 第一处媒质中任一点P上的势是 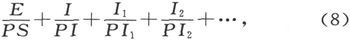
在第二种媒质中的一点P′上,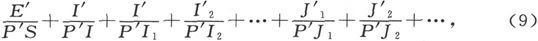
在第三种媒质中的一点P″上, 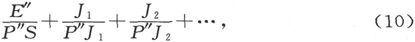
式中I、I′等等代表放在I等点上的假想电荷,而撇号表示势是要在平板内部取的。
于是,按照第315节,我们由关于通过A点的分界面的条件就得到
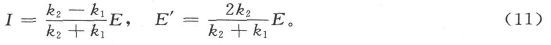
对于通过B点的分界面,我们有 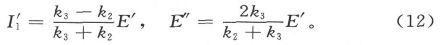
同样,又是对于通过A点的分界面, 
而对于通过B点的分界面则有 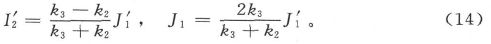
如果令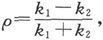
 则我们得到第一种媒质中的势的表示式如下,
则我们得到第一种媒质中的势的表示式如下,
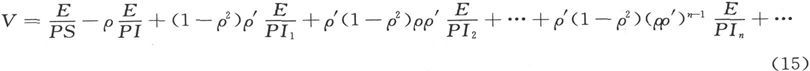
关于第三种媒质中的势,我们得到
如果第一种媒质和第三种媒质相同,则有k1 =k3 和ρ=ρ′,而平板另一侧的势就将是
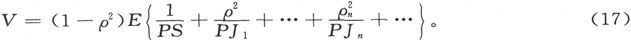
如果平板是比其余媒质好得多的导体,则ρ很近似地等于1。如果平板几乎是一种理想绝缘体,则ρ近似地等于-1,而如果平板在导电性能上和其余的媒质相差很小,则ρ是一个正的或负的小量。
这一事例的理论是由格林在他的《磁感应理论》(Essay, p. 65)中首次给出的。然而他的结果只有当ρ近似地等于1时才是正确的 〔42〕 。他所引用的量g是由下列方程来和ρ相联系的:
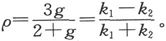 如果令
如果令 我们就将得到一个磁感应问题的解,那种磁感应是由放在磁化系数为k的无限平板中的一个磁极所引起的。
我们就将得到一个磁感应问题的解,那种磁感应是由放在磁化系数为k的无限平板中的一个磁极所引起的。
论层状导体
319.〕 设一个导体是由导电系数不同的两种物质的交替层构成的,物质层的厚度为c和c′。要求的是组合导体的电阻系数和电导系数。
设各层的平面垂直于z。设和第二种层有关的符号用撇号来区分,并用横线来标明和组合导体有关的量,例如 于是就有
于是就有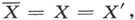
首先我们必须根据第297节中的电阻方程或第298节中的电导方程,把u、u′、v、v′、Z和Z′用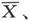
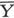 和
和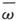 表示出来。如果用D代表电阻系数的行列式,我们就得到
表示出来。如果用D代表电阻系数的行列式,我们就得到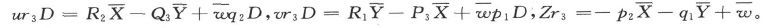
各符号加了撇号的类似方程就给出u′、v′和Z′的值。既经借助于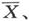
 和
和 求出
求出
 和
和 我们就可以写出分层导体的电导方程。如果令
我们就可以写出分层导体的电导方程。如果令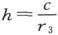 和
和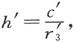 我们就得到
我们就得到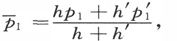
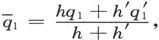

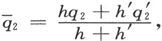
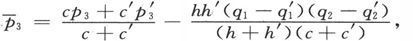
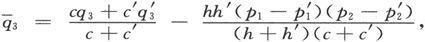
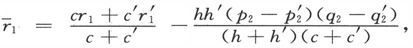
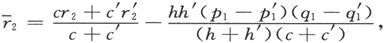
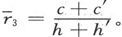
320.〕 如果构成各层的两种物质都不具备第303节的那种旋转性,则任一P或的值将等于和它对应的Q或q的值。由此可以推知,在分层导体中也有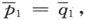
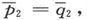
 或者说,层化并不会造成任何的旋转性,除非单纯材料的一种或两种具备这种旋转性。
或者说,层化并不会造成任何的旋转性,除非单纯材料的一种或两种具备这种旋转性。
321.〕 如果我们现在假设并不存在任何旋转性,而且x、y、z轴是主轴,则p系数和q系数为零,从而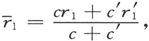

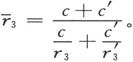
如果我们从电导r和r′不同的两种各向同性的媒质开始,那么,既然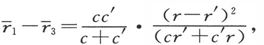 分层的结果就将是,电阻在和各层相垂直的方向上为最大,而在各层平面上的一切方向上则都相等。
分层的结果就将是,电阻在和各层相垂直的方向上为最大,而在各层平面上的一切方向上则都相等。
322.〕 试取一种比电导为r的各向同性物质,把它切成厚度为a的非常薄的薄片,并把这些薄片和一些比电导为s而厚度为k1 a的薄片交替地叠合起来。
设这些薄片垂直于x轴。然后把这种组合导体切成厚度为b的厚得多并垂直于y的片子,并把它们和比电导为s和厚度为k1 b的片子交替起来。
最后,把这种新导体再切成厚度为c的更加厚的并垂直于z的片子,并把它们和比电导为s而厚度为k3 c的片子交替起来。
这三次手续的结果,将是把比电导为r的物质切成线度为a、b和c的一些长方体,其中b远小于c而a远小于b,然后把这些长方体嵌在比电阻为s的物质中,使得它们之间的距离在z方向上是k1 a,在y方向上是k2 b,而在z方向上是k3 c。这样形成的导体在x、y和z方向上的比电导通过按次序应用三次第321节中的结果来求得。我们于是就得到
这种研究的精确性全靠长方体的三个线度具有不同的数量级,从而我们可以忽略在他们的边角等处所必须满足的条件。如果我们令k1 、k2 和k3 都等于1,则有

如果r=0,也就是说,如果构成各长方体的物质是一种理想绝缘体,就有
如果r=∞,就是说,如果各长方体是一些理想导体,则有
在每一个事例中,如果k1 =k2 =k3 ,则可以r1 ,r2 和r3 具有递升的数量级,从而最大的比电导出现在长方体最大线度的方向上,而最大的比电阻则出现在最小线度的方向上。
323.〕 设在一个长方形的导电固体中从一个顶角到对面的顶角开一个导电通路,设这条通路是一根用绝缘材料包着的导线,其横向线度很小,以致除了由导线所传导的电流以外,固体的电导并不受其他影响。
设长方体在各坐标轴方向上的线度为a、b、c,并设从原点到(abc)点的通路的电导是abcK。
在通路两端作用着的电动势是aX+bY+cZ,而如果C是通路中的电流,则C′=Kabc(aX+bY+cZ)。
穿越bc面的电流是bcu,而这就包括由固体的电导所引起的电流和通路的电导所引起的电流,或者说bcu=bc(r1 X+p3 Y+q2 Z)+Kabc(aX+bY+cZ),或u=(r1 +Ka2 )X+(p3 +Kab)Y+(q2 +Kca)Z。同样也可以求出v和w的值。被通路的效应所改变了的各电导系数将是r1 +Ka2 ,r2 +Kb2 ,r3 +Kc2 ,p1 +Kbc,p2 +Kca,p3 +Kab,q1 +Kbc,q2 +Kca,q3 +Kab。
在这些表示式中,由通路的效应所引起的p1 等等的值的增量等于q1 等等的值的增量。由此可见,p1 和q1 的值不能由于在固体的每一体积元中引入线性通路而变成不相等,因此,如果第303节中那种旋转性起初在固体中并不存在,它是不会通过这种方法而被引入的。
324.〕 试构成线性导体的一种构架,使它具有任意给定的形成对称组的电导系数。
设空间被分成许多相等的小立方体,其中一个如图所示。设O、L、M、N各点的坐标和势如下
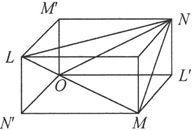
图25
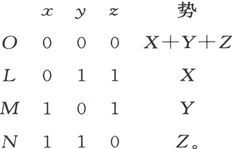
把这四个点用六个导体OL,OM,ON,MN,NL,LM,连接起来,各导体的电导分别是A,B,C,P,Q,R。
沿着这些导体而起作用的电动势将是Y+Z,Z+X,X+Y,Y-Z,Z-X,X-Y,而电流则是A(Y+Z),B(Z+X),C(X+Y),P(Y-Z),Q(Z-X),R(X-Y).在这些电流中,沿着x的正方向而送电的电流就是沿着LM、LN、OM和ON而流动的那些,而所送的电量就是u=(B+C+Q+R)X+(C-R)Y+(B-Q)Z。同理得到v=(C-R)X+(C+A+R+P)Y+(A-P)Z;w=(B-Q)X+(A-P)Y+(A+B+P+Q)Z;由此,我们通过和第298节中的导电方程相比较就得到4A=r2 +r3 -r1 +2p1 ,4P=r2 +r3 -r1 -2p1 ,4B=r3 +r1 -r2 +2p2 ,4Q=r3 +r1 -r2 -2p2 ,4C=r1 +r2 -r3 +2p3 ,4R=r1 +r2 -r3 -2p3 。
第二十三章 电介质中的导电
325.〕 我们已经看到,当有电动势作用在一种电介媒质上时,它就在媒质中引起一种我们曾称之为电极化的状态,而且我们曾经把这种状态描述成由媒质中的电位移和我们设想由电介质分成的每一个体积元上的表面电荷所构成;在各向同性媒质中电位移的方向和电动势的方向相同,体积元上的正电荷出现在电动势所指向的面上,而其负电荷则出现在电动势所由开始的面上。
当电动势作用在一种导电媒质上时,它也引起所谓的电流。
喏,电介媒质也是或多或少的非理想导体,如果有例外也是很少见的,而且许多并非良导体的媒质也显示电介感应的现象。因此我们就被引导到一种媒质的状态的研究,在那种媒质中感应和传导是同时在进行着的。
为了简单,我们将假设媒质在每一点上都为各向同性,但不一定在不同点上是均匀的。在这种情况下,由第83节可知泊松方程变为

式中K是“比感本领”。
电流的“连续性方程”变为 
式中r是相对于单位体积而言的比电阻。
当K或r是不连续的时,这些方程必须被变换成适用于不连续界面的那些方程。
在一种严格均匀的媒质中,r和K都是常量,从而我们就得到
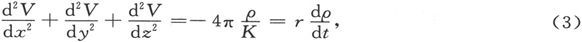
由此即得 
或者,如果我们令 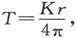 就得到
就得到
这一结果表明,在任何外电动势对其内部起初以任何方式带电的均匀媒质的作用下,内部的电荷永远将以一个不依赖于外力的速率而衰减,从而最后在媒质内部将不再有任何电荷,而在此以后,任何外力都不能在媒质的任何体内部分引起或保持一个电荷,如果电动势、电极化和电导之间的关系保持不变的话。当破坏性放电发生时,这些关系就不再成立,从而内部电荷就可能出现。
关于通过一个电容器的导电
326.〕 设C是一个电容器的电容,R是它的电阻,而E是作用在它上面的电动势,也就是两个金属极的表面之间的势差。
于是,电动势起点处的一个表面上的电量将是CE,而沿着电动势的方向而通过电容器材料的电流将是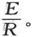
如果带电状态被假设为是由在电容器形成其一个部分的电路中起作用的一个电动势E所引起的,而且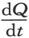 代表该电路中的电流,则有
代表该电路中的电流,则有 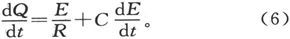
把一个电动势为E而包括各电极连接导线在内的电阻为r的一个电池接入电路中,就有 
由此可见,在任何时刻t1 ,应有
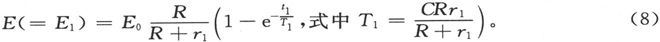
其次,把电路r1 切断一段时间t2 ,这时r1 为无限大,我们由(7)就得到
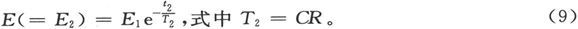
最后,用一根电阻为r3 的导线把电容器的两个表面连接一段时间t3 ,则在(7)中令E=0,r1 =r3 ,我们就得到 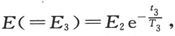 式中
式中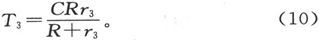
如果Q3 是在时间t3 内流过这一导线的总电量,则有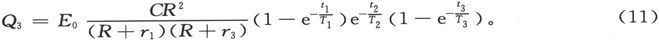
用这种办法,我们就可以在电容器被充电一段时间t1 然后被绝缘一段时间t2 以后求出通过一根把它的两个表面连接起来的导线而进行总放电。如果像通常那样充电时间长得足以得到全部的电荷,而且放电时间也足以得到完全的放电,则所放的电是
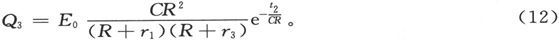
327.〕 在这样的一种电容器中,当起初以任意方式充电其次通过一根小电阻的导线而放电然后被绝缘时,是不会出现任何新的带电现象的。然而,在多数的实际电容器中,我们却发现在放电和绝缘以后,一个新的电荷会逐渐长成,它和原有电荷同号,但强度较小。这就叫做残余电荷。为了说明它,我们必须承认电介媒质的构造是和我们刚刚描述过的有所不同的。然而我们却将发现,由不同种类的媒质小块堆集而成的一种媒质,将具有这种性质。
组合电介质理论
328.〕 为了简单起见,我们将假设电介质由一些不同材料的平面层所组成的,其面积为一个单位,而电力则是沿着各层的法线方向起作用的。
设a1 、a2 等等是不同层的厚度。X1 、X2 等等是各层中的合电力。p1 、p2 等等是各层中的传导电流。f1 、f2 等等是电位移。u1 、u2 等等是部分地起源于传导而部分地起源于电位移变化的全电流。r1 、r2 等等是对单位体积而言的比电阻。K1 、K2 等等是比感本领。k1 、k2 等等是比感本领的倒数。E是一个电池组所引起的电动势;该电池组接在从最后一层接到最初一层的电路中,而我们假设那电路由一些良导体构成。Q是直到时刻t为止通过电路的这一部分的总电量。R0 是电池和连线的电阻。σ12 是第一、二层的分界面上的电荷面密度。
于是,在第一层中,我们由欧姆定律得到 
由电位移理论得到 
由全电流的定义得到 
在其他各层中也有相似的方程,而每一层中的各量都带有属于该层的下标。
为了确定任何一层上的面密度,我们有一个形如 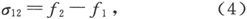
的方程,而为了确定其变化,我们有 
对t微分(4)并使结果和(5)相等,我们就得到例如 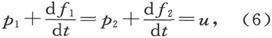
或者,照顾到(3),就有 
就是说,全电流在所有各层中都相同,并等于通过导线和电池组的电流。
由于有方程(1)和(2),我们也有 
由此我们通过对u的逆运算就能求出X1 , 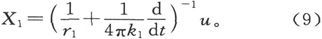
总电动势是 
或 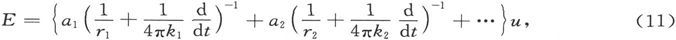
这是外电动势E和外电流u之间的一个方程。
如果r和k之比在所有各层中都相同,则方程简化为
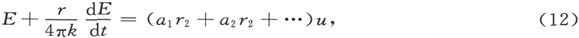
这就是我们在第326节中已经分析过的事例,在那种事例中我们发现不可能出现任何残余电荷现象。
如果有n种物质具有不同的r和k之比,普遍方程(11)在执行了逆运算以后就将是对E为n阶而对u为(n-1)阶的一个以t为自变数的线性微分方程。
由方程的形式可以显然看出,不同层的顺序是无关紧要的,因此,如果有若干个相同物质的层,我们可以假设它们合并成一层而并不改变现象。
329.〕 现在让我们假设,起初f1 、f2 等等都是零,而一个电动势E0 突然发生了作用,让我们求出它的瞬时效应。
把(8)对t求积分,我们就得到 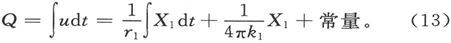
现在,既然X1 在这一事例中永远是有限的,当t很小时∫X1 dt以就必然是很小的,因此,既然X1 起初为零,瞬时效应就将是 
因此,由方程(10)就得到 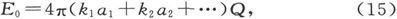
而如果C是用这种瞬时方式测量的体系电容,就有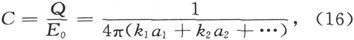
这就是当忽略各层的电导时我们即将得到的同样的结果。
其次让我们假设,电动势继续均匀作用了一段无限长的时间,或是一直作用到在体系中建立了一个等于p的均匀的传导电流的时候。
于是我们就有X1 =r1 p1 ,等等,从而由(10)就有 
如果R是体系的总电阻,则 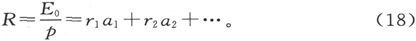
在这一状态下,我们由(2)得到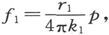 从而就有
从而就有 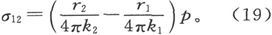
如果我们现在突然用一个电阻很小的导体把两边的层接起来,E就将突然地从它的原有值E0 变成零,而且一个电量Q就将流过该导体。
为了确定Q,我们注意到,如果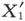 是新的X1 值,则由(13)可得
是新的X1 值,则由(13)可得
于是,令E=0,由(10)即得 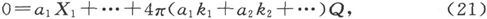
或 
由此即得Q=-CE0 ,式中C是由方程(16)给出的电容。因此,瞬时的放电量等于瞬时的充电量。
其次让我们假设,在这一放电之后,连线立即被切断。这时我们将有u=0,从而由方程(8)即得 
式中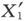 是放电以后的初始值。
是放电以后的初始值。
由此可见,在任一时刻t,我们由(23)和(20)就得到
因此,任一时刻的E值
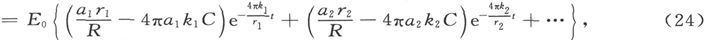
而任何时间t以后的放电量是EC,这叫做残余放电。
如果r和k之比在一切层中都相同,则E的值将减小到零。然而,如果这一比值并不相同,让我们把各项按这一比值的递减次序排列起来。
所有系数之和显然是零,从而当t=0时E=0。各系数也是按量值递减的次序排列的,而当t为正时各个指数也是如此排列的。因此,当t为正时E将为正 〔43〕 ,从而残余放电永远和原始放电同号。
当t为无限大时所有的项都不复存在,除非有一层是一种理想的绝缘体;在那种事例中,该层的r1 是无限大,从而整个体系的R也是无限大,而且E的末值也不是零而是

由此可见,当某些层而不是所有的层是理想的绝缘体时,一种残余放电可以永远地保持在体系中。
330.〕 其次我们将假设体系首先通过一个电动势E的长久持续作用而被充了电,来确定通过一根电阻为R0 的长期接在体系的两个边界层上的导线的总放电量。
在任一时刻,我们有 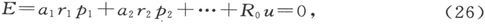
另外,由(3)即得 
由此可见, 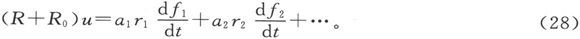
对t求积分以得出Q,我们就有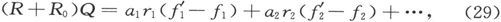
式中f1 和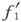 是f1 的初值和末值。
是f1 的初值和末值。
在这一事例中,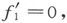 而且由(2)(20)得到
而且由(2)(20)得到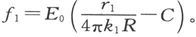
由此即得 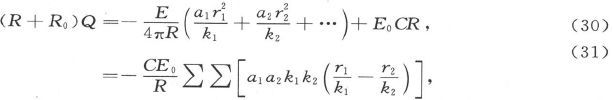
式中的求和遍及属于每一对层的这种形式的量。
由此可见Q永远是负的,也就是说,放电是和用来对体系充电的电流方向相反的。
这种研究表明,一种由种类不同的物质层构成的电介质可以显示所谓的电吸收现象和残余放电现象,尽管构成它的各种物质当单独存在时全部不显示这些现象。各物质不是分成层而是按其他方式分布的那种事例的研究,也将导致类似的结果,尽管计算可能是更加复杂的。因此我们可以得出结论说,在由种类不同的部分构成的物质中,可以预期出现电吸收的现象,即使那些部分是微观地小的 〔44〕 。
由此绝不能推断,每一种显示这种现象的物质都是如此组合而成的,因为它可能指示均匀物质所可能具备的一种新式的电极化,而且在某些事例中这种电极化可类似于电化学极化而不那么类似于电介极化。
这一研究的目的只是要指出所谓电吸收的真正数学特性,并且指明它和热现象是多么的根本不相同,尽管初看起来二者是类似的。
331.〕 让我们取任一物质的一块厚板并在一面对它加热,这样就会引起通过它的一个热流,而如果这时我们把加了热的一面突然冷却到和另一面相同的温度并让平板自行变化,则加过热的那一面将由于体内的热传导而再次变得热一些。
现在,和这种现象完全类似的一种电现象也可以产生,而且实际上是出现在电报电缆中的,然而它的数学规律虽然和热现象的规律精确相符,但这却是和分层电容器的规律完全不同的。
在热的事例中,存在热在物质中的真正吸收,结果使物质变热。在电的方面造成一个真正类似的现象是不可能的,但是我们可以在一种课堂演示实验的形式下用下述的方法来模拟它。
设A1 、A2 等等是一系列电容器的内表面而B0 、B1 、B2 等等是它们的外表面。
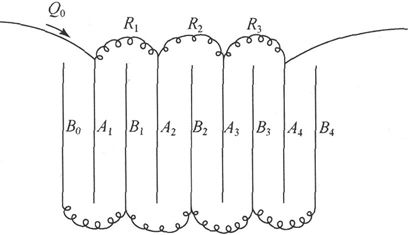
图26
设A1 、A2 等等用一些电阻为R的连接物串联起来,并且使一个电流从左向右通过这一系列。
让我们首先假设B0 、B1 、B2 各板是各自绝缘和没有电荷的。于是每一个B板上的总电量必然保持为零,而既然各个A板上的电量是和对面的板上的电量相等而反号的,这些A板也将不带电,从而人们也就不会观察到电流的任何改变。
但是,让我们把所有的B板都连接起来并把它们每一个都接地。这时,既然A1 的势是正的而各个B板的势是零,A1 就将带正电而B1 就将带负电。
设P1 、P2 等等是各板A1 、A2 等等的电势而C是每一个板的电容;如果我们假设一个等于Q0 的电量通过了左侧的导线,Q1 通过了连接物R1 ,余类推,则存在于A1 板上的电量是Q0 -Q1 ,从而我们就有Q0 -Q1 =CP1 。同理得到Q1 -Q2 =CP2 ,余类推。
但是由欧姆定律,我们有
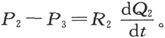
我们曾经假设各板的C值是相同的,如果假设各导线的R值也相同,我们就将得到一系列形式如下的方程,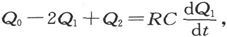
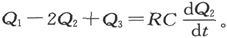
如果共有n个电量有待确定,而且如果或是总电动势或是某种等价的条件已经给定,则确定其中任一电量的微分方程将是线性的和n阶的。
利用这样装置起来的一部仪器,瓦尔莱先生做到了模拟一根12,000英里长的电缆的电作用。
当使一个电动势沿着左端的导线起作用时,流入体系中的电首先就被用来对从A1 开始的不同电容器充电,而只有过了相当一段时间以后,电流的一个很小的部分才会在右端出现。如果在R1 、R2 等处把一些电流计接在电路中,它们就会一个跟着一个地受到影响,而当我们向右端看过去时,相等指示之间的时间间隔是越来越大的。
332.〕 在电缆的事例中,传导电线和外面的导体是由一个用硬橡胶或其他绝缘材料制成的包皮隔开的。于是每一段电缆都变成一个电容器,其外表面永远处于零势。因此,在一段给定的电缆中,传导电线表面上的自由电量就等于势和看成一个电容器的那段电缆的电容的乘积。
如果a1 、a2 是绝缘包皮的外半径和内半径,而K是比感本领,则由第126节可知电缆的单位长度的电容是 
设v是电线任一点上的势,我们可以认为这个势在同一截面的不同部分上是相同的。
设Q是从电流开时以后流过了这一截面的总电量,则在时刻t存在于x处和x+δx处的二截面之间的电量是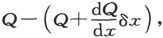 或者说
或者说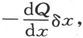 而按照以上的论述,这应该等于cvδx,从而就有
而按照以上的论述,这应该等于cvδx,从而就有 
另外,任一截面上的电动势是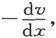 而由欧姆定律就得到
而由欧姆定律就得到 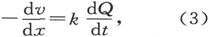
式中k是导体单位长度的电阻,而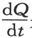 是电流强度。从(2)和(3)中消去Q,我们就得到
是电流强度。从(2)和(3)中消去Q,我们就得到

为了得到电缆的任意点上在任意时刻的势,这就是必须求解那个偏微分方程。它和傅立叶所给出的确定一个物质层中任意点上的温度的方程完全相同,在那个物质层中热是沿层的法线方向在流动的。在热的事例中,C代表单位体积的热容量,此量被傅立叶写成CD,而k代表热导率的倒数。
如果包皮不是一种理想绝缘体,而k1 是包皮对径向导电而言的单位长度的电阻,ρ1 是绝缘材料的比电阻,那就很容易证明 
方程(2)将不再成立,因为电不但被用在把导线充电到cv所代表的程度,而且还会以v/k1 所代表的速率而流失。因此,电的消耗率将 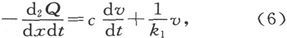
和(3)式相比较,我们由此即得 
而这就是傅里叶所给出的一根棒或一个环中的导热方程 〔45〕 。
333.〕 假如我们曾经假设当一个物体的势被提高时,它就在整个的物质内部带电,就好像电被挤压到它里边一样,我们就会得到恰恰是这种形式的一些方程。很可惊奇的是,由于受到电和热之间这种类似性的蒙蔽,欧姆本人就抱有这样一种见解,并从而通过一种错误的见解而被引导着还在这些方程的适用性的实在原因被推测到的很久以前,就用傅里叶的方程来表示了电通过长导线而传导的正确规律。
电介质性质的机械例示
334.〕 如图所示,五根截面积相等的管子A、B、C、D和P连成一条回路,A、B、C和D是竖直的和相等的,而P则是水平的。
A、B、C、D的下半段充有水银,它们的上半段和水平管P中充有水。
一个带阀门的管子把A、B的下端和C、D的下端接通,而一个活塞P可以在水平管中滑动。
让我们在开始时假设四根管子中的水银水平面是等高的,用A0 、B0 、C0 、D0 来代表,活塞的位置是P0 ,而且阀门Q是关住的。

图27
现在让活塞从P0 移动一段距离a而到达P1 。那么,既然所有管子的截面都相等,A和C中的水银液面就将上升一个距离而到达A1 和C1 ,而B和D中的水银则将下降一个相等的距离a而到达B1 和D1 。
活塞两侧的压力差将由4a来代表。
这种装置可以用来代表受到一个电动势4a作用的电介质的状态。
管D中多出的水可以看成代表电介质一侧的正电荷,而管4中多出的水银则可以代表另一侧的负电荷。于是,管P中活塞靠近D的一边多出的压力就代表电介质正侧高出的势。
如果活塞可以随便活动,它就将回到P0 并在那里保持平衡。这就代表电介质的完全放电。
在“放电”过程中,整个管子中都存在液体的反向运动,而这就代表我们曾经假设存在于电介质中的电位移的变化。
我曾经假设管子体系的每一部分中都充满了不可压缩的液体,为的是要代表所有电位移的一种性质,即在任何地方都不存在电的真正积累。
现在让我们考虑当活塞位于P1 时打开阀门Q所引起的效应。
A1 和D1 的液面将保持不变,但是B和C的将变为相同并将与B0 和C0 相重合。
阀门Q的打开就代表电介质中存在一个部分,它具有一个很小的导电性能,但是并不扩展到全体而形成一种导电通路。
电介质两面的电荷仍然是被绝缘的,但是它们的势差却减小了。
事实上,活塞两侧的压力差在液体通过Q的过程中将从4a降到2a。
如果我们现在关上阀门Q并让活塞自由运动,它就会在P2达到平衡,而所放的电则显然将只是电荷的一半。
A和B中的水银液面将比原始液面高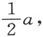 而C和D中的液面则比原始液面低
而C和D中的液面则比原始液面低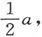 这一情况用水平表面A2 、B2 、C2 、D2 而来表示。
这一情况用水平表面A2 、B2 、C2 、D2 而来表示。
如果现在活塞被固定而阀门被打开,则水银将从B流到C,直到两管中的液面又回到B0 和C0 时为止。这时在活塞P的两侧将出现一个等于a的压力差。如果阀门被关住而活塞又可以随便活动,它就又会在P2 和P0 的中点P3 上达到平衡。这就对应于当一种充了电的电介质首先被放电然后自己存在时所观察到的那种残余电荷。电介质将慢慢地恢复其电荷的一部分,而如果这一部分电荷又被放掉,则第三个电荷又将形成,但是各电荷逐个减小。在例示实验的情况下,每一个电荷都是前一电荷的一半,而等于原电荷的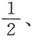
 等等的各次放电则形成一个级数,其和等于原始电荷。
等等的各次放电则形成一个级数,其和等于原始电荷。
如果我们不是时而打开、时而关住阀门,而是让它在整个实验过程中处于几乎关住而又并不完全关住的状态,我们就会有一个事例,和一种电介质的带电状况相类似,该电介质是一种理想绝缘体,但却显示一种称为“电吸收”的现象。
为了代表在电介质中存在真实导电的事例,我们必须或是使活塞有漏洞,或是在管A的顶部和管D的顶部建立一种联系。
用这种办法,我们可以构造一种机械例示来代表任何一种电介质的性质;在这种例示中,两种电用两种实在的液体来代表,而电势差则用压力差来代表。充电和放电用活塞P的运动来代表,而电动势则用作用在活塞上的合力来代表。
第二十四章 电阻的测量
335.〕 在电科学的当前状况下,一个导体的电阻的测定可以看成电学中的基本工作,正如重量的测定是化学中的基本工作一样。
这一点的理由就在于,其他电学量例如电量、电动势、电流等等的绝对测量,在每一事例中都要求一系列很繁复的操作,通常包括时间的观测、距离的测量和惯性矩的测定,而这些操作,至少是其中的某些操作在每一次新的测定中都必须重复进行,因为把一个电量单位、电动势单位或电流单位保持在不变的状态以便随时用来进行直接的比较是不可能的。
但是,人们发现,当用适当选定的材料做成的一个适当形状的导体的电阻一旦被测定了时,它就会在相同的温度下保持相同的值,从而这个导体就可以当作一个标准电阻来使用,而别的导体的电阻就可以和这个电阻相比较,而且电阻的比较是一种可以达到很高精确度的操作。
当电阻的单位既经选定时,就可以在“电阻线圈”的形式下做成这种单位的一些物质性的样品来供电学家们使用,这样,在世界的每一部分,电阻就都可以用相同的单位来表示。这些单位电阻线圈,在目前就是可以保存、复制并应用于测量目的的那种物质性电学标准的唯一范例 〔46〕 。也很重要的电容的量度,由于有电吸收的干扰影响,现在还是有缺点的。
336.〕 电阻的单位可以是完全任意的,就如在雅考比的原器事例中那样。那种原器是一条确定的铜线,质量为22.4932克,长度为7.61975米,而直径为0.667毫米。这种原器的一些复制品曾由莱比锡的莱瑟尔制成,而且可以在不同的地方见到。
按照另一种方法,单位可以定义为具有确定尺寸的一部分确定物质的电阻。例如,西门子的单位被定义为一个水银柱的电阻,水银柱的长度为一米,截面积为一平方毫米,而温度为0℃。
337.〕 最后,单位可从参照静电单位制或电磁单位制来定义。在实践中,电磁单位制是在一切的电报操作中被应用的,从而实际上被应用的唯一系统化的单位也就是这一单位制中的单位。
正如我们在适当的地方即将看到的那样,在电磁单位制中,电阻是一个具有速度量纲的量,从而是可以用速度的单位来量度的。参阅第628节。
338.〕 按照这一单位制来进行的最早的实际测量是由韦伯作出的,他用毫米每秒来当作了自己的单位。W. 汤姆孙爵士后来采用了英尺每秒来作为单位,但是许多电学家现在已经同意采用大英协会的单位,那是一个电阻,当表示为一个速度时等于一千万米每秒。这个单位的大小比韦伯单位的大小更适用,因为韦伯单位太小。这种单位有时称为B. A. 单位,但是为了把它和电阻定律的发现者的姓氏联系起来,这种单位被称为“欧姆”。
339.〕 为了记忆它在绝对单位制中的值,知道一点是很有用的,那就是,一千万被认为是沿巴黎子午线测量的从地极到赤道的距离。因此,在一秒钟内从地极沿子午线运动到赤道的一个物体就具有一个在电磁单位制中理应代表一欧姆的速度。
我说“理应”代表,因为,如果更精确的研究竟然证明按照大英协会的物质标准制成的“欧姆”实际上并不是用这个速度来表示的,电学家们也不会改换他们的标准,而只会应用一个改正量 〔47〕 。同样,一米理应是某一地球象限弧的一千万分之一,然而尽管人们发现这一点并不绝对正确,一米的长度却并没有被改动,而是地球的线度被用一个不那么简单的数字来表示了。
按照大英协会的单位制,这一单位的绝对值原先是被选得尽可能近似地代表由电磁单位制导出的一个量的。
340.〕 当代表这一抽象量的一个物质单位已经做成时,其他的标准就可以通过复制这一单位而被制成;这是可以达到很大精确度的一个过程,例如比按照一个标准英尺来复制英尺要准确得多。
用最耐久的材料做成的这些复制品被分送到世界各地,从而假若原始标准被失去,也不太可能在获得复制品方面遇到任何困难。
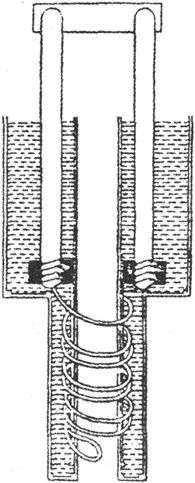
图28
但是,例如西门子的单位是不必费什么事就可以复制得很准确的,因此,既然一欧姆和一西门子单位之间的关系是已知的,即使没有一个标准来据以复制,标准欧姆也是可以重新制成的,尽管所费的功夫比直接复制要大得多而得到的精确度要小得多。
最后,标准欧姆也可以通过最初确定它的那种电磁方法来重新制造。这种方法比根据秒摆来确定英尺要费事得多,它或许比上述的方法更不精确。另一方面,以一种和电科学的进步相适应的精确度而借助于欧姆来确定电磁单位,却是一种顶重要的物理研究,而且是很值得重复进行的。
制造了用来代表欧姆的实际电阻线圈,是用两份银和一份铂制成的导线,其直径从0.5到0.8毫米,其长度从1到2米。这些导线焊在粗壮的铜电极上。导线本身包着两层丝绸,嵌在固体石蜡中,并包从薄铜外壳,以便很容易把它调到电阻准确地等于一欧姆的那一温度。这个温度被标明在线圈的绝缘支柱上(参阅图28)。
关于电阻线圈的形状
341.〕 一个电阻线圈是一个导体,它很容易被接到电路中去并从而在电路中引入一个已知电阻。
线圈的两极或两端必须做得不会因为连接方式而引起可觉察的误差。对于量值较大的电阻来说,用粗铜线或粗铜棒来做电极也就够了,电极的头上经过很好地汞齐化,而且这一头应该压在汞杯中平坦的齐化铜的表面上。
对于非常大的电阻来说,用厚黄铜块来做电极就够了,连接物应该是用铜或黄铜做成的楔子,可以插入电极的间隙中。这种方法被发现是很方便的。
电阻线圈本身是用丝绸包得很好的导线,其两端永久性地焊在电极上。
线圈必须适当装配,以便很容易观察它的温度。为此目的,导线被绕在一根管子上,外面套着另一个管子,这样它就可以被放到一个水容器中,而水就可以接触它的里面和外面。
为了避免线圈中电流的电磁效应,导线先双起来然后绕在管子上,这样,在线圈的任何部分就都在导线的相邻部分中有着相等而反向的电流。
当有必要使两个线圈保持相同的温度时,有时把两根导线并排在一起然后绕成线圈。当保证电阻的相等比知道电阻的绝对值更加重要时,例如在惠斯登电桥的等臂中(第347节),这种方法就是特别有用的。
当最初尝试测量电阻时,用得很多的是用裸导线绕在绝缘材料圆筒上的螺旋沟槽中而制成的线圈,这种线圈叫做可变电阻器。不久人们就发现,用这种线圈来比较电阻时所能够达到的精确度,是和利用其接线方式不比利用可变电阻器所能做到的接线方式更完善的任何仪器来得到的精确度不相容的。然而,在并不要求精确测量的地方,可变电阻器仍然被用来调节电阻。
电阻线圈通常是用那些电阻最大而其随温度的变化又最小的金属制成的。德银很好地满足这些条件,但是有些德银的品种却会逐年改变其性质。因此,为了制造标准线圈,曾经使用过几种纯金属,也使用过铂和银的一种合金,而且人们发现,在若干年内,这些东西的相对电阻在现代精确度的范围内是并不改变的。
342.〕 要得到很大的电阻,例如几兆欧姆的电阻,导线必须不是很细就是很长,从而线圈的制造就是昂贵而困难的。因此就曾有人建议用碲或硒来作为制造大电阻标准器的材料。一种很巧妙而又很容易的制造方法近来已由菲利普斯提出 〔48〕 。在一块胶木或磨砂玻璃上画一条很细的铅笔线。这条石墨细丝的两端被接在两个金属电极上,然后把整条细丝用绝缘漆覆盖起来。如果竟然发现这样一条铅笔线的电阻保持不变,这就将是得到若干兆欧姆电阻的最好的方法。
343.〕 有一些装置可以用来很容易地把电阻线圈接到一个电路中去。
例如,其电阻按2的幂次递增为1、2、4、8、16等等的一系列线圈,可以串联起来装在一个箱子里。
电极用结实的黄铜块制成,适当地排列在箱子的外面,使得通过插入一个黄铜制的塞子或楔子作为旁路,对应的线圈可以排除于电路之外。这种装置是西门子引入的。
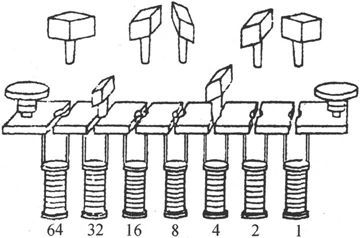
图29
电极之间的每一个间隙都标有对应线圈的电阻值,从而如果想使箱中的电阻等于107,我们只要就把107按二进制写成64+32+8+2+1或1101011。然后我们就从和64、32、8、2、1相对应的洞中把塞子拔出来,而剩下16和4处的塞子。
这种建筑在二进制上的方法是这样的:所要求的单个线圈的数目最小,而且可以最容易地加以检验。因为,如果我们有另一个等于1的线圈,我们就可以检验1和1′的品质,然后是1+1′和2的品质,然后是1+1′+2和4的品质,如此类推。
这种装置的唯一缺点就是它要求人们熟悉二进制计数法,而这通常是那些用惯了十进制记数法的人们并不熟悉的。
344.〕 为了用来测量电导而不是电阻,一个电阻箱也可以按另一种方法来装配。
各个线圈可以这样装配:每个线圈的一端都接在一块长而厚的金属上,这就形成电阻箱的一个极,线圈的另一端和在上述事例中一样接在一块结实的黄铜上。
电阻箱的另一个极是一块黄铜长板,通过在此板和线圈极之间插入一个黄铜塞子,可以把这个极板通过任何一组给定的线圈而和第一个极连接起来。这时箱子的电导就是各该线圈的电导之和。
图30
在图30中,各线圈的电阻是1、2、4等等,塞子插在2和8处,从而箱子的电导是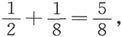 而箱子的电阻则是
而箱子的电阻则是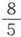 或1.6。
或1.6。
这种组合线圈来测量分数电阻的方法是由W. 汤姆孙爵士在多重弧法的名称下引入的。参阅第276节。
论电阻的比较
345.〕 如果E是一个电池组的电动势,R是电池组和包括用来测量电流的电流计在内的连接线的电阻,如果当电池组的连线被接通时电流强度是I,而当附加电阻r1 、r2 被接入电路中时电流强度是I1 、I2 ,则由欧姆定律可得
E=IR=I1 (R+r1 )=I2 (R+r2 )。
消去电池组的电动势E和电池组及其连线的电阻R,我们就得到欧姆的公式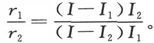 这种方法要求测量I、I1 和I2 的比值,而这就意味着要求一个有着绝对刻度的电流计。
这种方法要求测量I、I1 和I2 的比值,而这就意味着要求一个有着绝对刻度的电流计。
如果电阻r1 和r2 相等,则I1 和I2 相等,而我们就可以用一个不能测量电流比值的电流计来检验电流的相等。
但是这却应该被看成一种测定电阻的有毛病的方法,而不是一种切合实用的方法。电动势E不能严格地保持恒定,而电池组的内阻也非常不稳定的,因此,在一种方法中即使假设这些量在一段短时间内保持不变,这种方法也是不可靠的。
346.〕 电阻的比较可以利用两种方法中的任一种来很精确地进行;在这两种方法中,所得的结果都和R及E的变化无关。
其中第一种方法依赖于差绕电流计的应用。这种仪器中有两个线圈,线圈中的电流互相独立,从而当使两个电流沿相反的方向流动时,它们就对指针发生相反的作用,而且当电流之比是m和n之比时,它们对电流计指针的合效应就是零。
图31
设I1 、I2 是通过电流计的两个线圈的电流,则指针的偏转可以写成δ=mI1 -nI2 。
现在让电池组的电流分头流入电流计的两个线圈中,并把电阻A和B分别接在第一个和第二个线圈上,设各线圈及其连线的其余电阻分别是α和β,设电池组及其C、D之间的连线的电阻为r,而其电动势为E。
于是,关于C、D之间的势差,我们由欧姆定律就得到I1 (A+α)=I2 (B+β)=E-Ir,而且,既然I1 +I2 =I,就有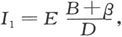
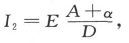
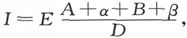 式中D=(A+α)(B+β)+r(A+α+B+β)。
式中D=(A+α)(B+β)+r(A+α+B+β)。
因此,电流计指针的偏转就是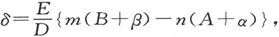 而如果没有能够观察到的偏转,我们就知道括号中的量和零之差不能超过某一小量,该小量依赖于电池组的强度、装置的优劣、电流计的精确度和观察者的能力。
而如果没有能够观察到的偏转,我们就知道括号中的量和零之差不能超过某一小量,该小量依赖于电池组的强度、装置的优劣、电流计的精确度和观察者的能力。
现在设用另一个导体A′来代替A,并设A′被调节得使电流计指针仍没有显著的偏转。这时显然在初级近似下就有A′=A。
为了确定这一估计的精确性,设在第二次观察中得到的变化了的量用撇号来区分,就有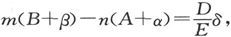
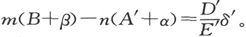 由此即得
由此即得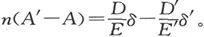
设δ和δ′不是在表观上都等于零,而是被观察到彼此相等,则方程右端不会等于零,除非我们能够确知E=E′。事实上,这种方法只是已经描述过的方法的一种修改形式。
这种方法的优点在于这样一件事实:观察到的是任何偏转的不存在;换句话说,这是一种“调零法”,即根据观察来断定一个力的不存在的方法,在那种观察中如果一个力和零的差值超过某一小量,它就会引起一个可以观察到的效应。
调零法在可以应用的地方是有很大价值的,但是只有当我们能够使两个种类相同的相等而相反的量一起进入实验中时,这种方法才能应用。
在我们遇到的事例中,δ和δ′是一些小得很难观察的量,从而E值的任何改变都不会影响结果的精确度。
这种方法的实际精确度,可以通过进行若干次分别调节A′的观察并比较每次观察结果和所有结果的平均值来加以确定。
但是,通过使A′从调整值偏离一个已知量,例如通过在A或B处增加一个等于A或B的百分之一的电阻,然后观察电流计指针的偏转,我们就能估计和百分之一的误差相对应的偏转度数。为了求出实际的精确度,我们必须估计可能观察不到的那一最小的偏转,并把它和由百分之一的误差所引起的偏转相比较。 〔49〕
如果必须比较的是A和B,而且A和B交换了位置,则第二个方程变成m(A+β)-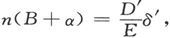 由此即得
由此即得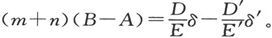
如果m和n、A和B、α和β、E和E′都近似地相等,则有
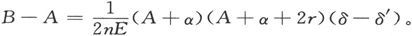
这里的δ-δ′可以看成可观察的电流计最小偏转。
如果电流计的导线被做得更长一些和更细一些而总的质量不变,则n将按导线长度而变化,而α则按长度的平方而变化。因此,当 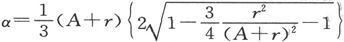
时就将有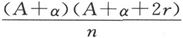 的一个最小值。
的一个最小值。
如果我们假设和A相比电池组的电阻r是可以忽略的,则上式给出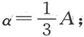 或者说,电流计的每一个线圈的电阻应该是待测电阻的三分之一。
或者说,电流计的每一个线圈的电阻应该是待测电阻的三分之一。
这时我们就得到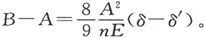
如果我们让电流只通过电流计中的二线圈之一,而由此引起的偏转是∆(假设偏转确切地正比于致偏力),则有 如果r=0而
如果r=0而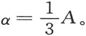 由此即得
由此即得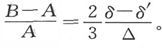
在差绕式的电流计中,两个电流被调得对悬挂着的指针引起相等而相反的效应。每一电流作用在指针上的力,不但依赖于电流的强度,而且依赖于导线各圈相对于指针的位置。由此可见,除非线圈被绕得很仔细,m和n之比可能会随指针的位置而变,因此,在每一次实验过程中,如果预料会有指针位置的任何变化,那就有必要用适当的方法来确定这一比值。
另一种调零法要用到惠斯登电桥。这种方法只要求一个普通的电流计,而所观察到的指针的零偏转不是起源于两个电流的相反效应,而是起源于导线中电流的不存在。因此,作为观察到的现象,我们不但有一个零偏转而且有一个零电流,从而电流计线圈的不规则性或任何种类的变化都不会引起任何误差。电流计只要够灵敏,可以探测电流的存在和方向就行了,它用不着以任何方式测定电流的值或把该值和另一个电流的值互相比较。
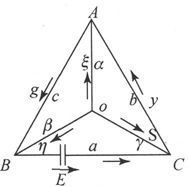
图32
347.〕 惠斯登电桥本质上就是连接着四个点的六个导体。借助于接在B和C之间的一个伏打电池组,使一个电动势E作用于二点之间。另外两点O和A之间的电流用一个电流计来测量。
在某一情况下这个电流变为零。这时导体BC和OB就被说成是互相共轭的;这就意味着在其他四个导体的电阻之间有一个关系式,而这个关系式就被利用来测量电阻。
如果OA中的电流是零,则O点的势必然等于A点的势。现在,当我们知道B点和C点的势时,我们就可以利用第275节所给出的法则来确定O点和A点的势,如果OA中没有电流的话。我们得到,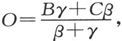
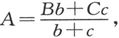 由此即得条件式bβ=cγ,式中b、c、β、γ分别是CA、AB、BO和OC的电阻。
由此即得条件式bβ=cγ,式中b、c、β、γ分别是CA、AB、BO和OC的电阻。
为了确定用这种方法所能得到的精确度,我们必须在这一条件并非确切地得到满足时确定OA中的电流强度。
设A、B、C和O是四个点。设沿着BC、CA和AB而流动的电流是x、y和z,而这些导体的电阻是a、b和c。设沿着OA、OB和OC而流动的电流是ξ、η、ζ,而电阻是α、β和γ。设有一个电动势E沿着BC而起作用。试求沿OA的电流ζ。
设A、B、C和O上的势用A、B、C和O来代表。导电方程是ax=B-C+E,αξ=O-A,by=C-A,βη=O-B,cz=A-B,γζ=O-C;并有连续性方程ξ+y-z=0,η+z-x=0,ζ+x-y=0。
把体系看成由三个回路OBC、OCA和OAB构成,各回路中的电流分别为x、y、z,并对每一个回路应用基尔霍夫的法则,我们就可以消去势O、A、B、C和电流ξ、η、ζ的值,而得到关于x、y、z的方程如下:(a+β+γ)x-γy-βz=E,-γx+(b+γ+α)y-αz=0,-βx-αy+(c+α+β)z=0。
由此可见,如果令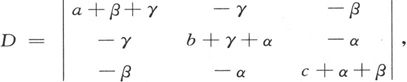 我们就得到ζ=
我们就得到ζ=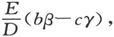 和
和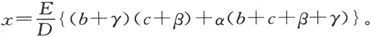
348.〕 D的值可以写成对称式
D=abc+bc(β+γ)+ca(γ+α)+ab(α+β)+(a+b+c)(βγ+γα+αβ) 〔50〕 ,
或者,既然我们假设电池组是在a上而电流计是在α上,我们就可以把a换成电池组的电阻B而把α换成电流计的电阻G。于是我们就得到
D=BG(b+c+β+γ)+B(b+γ)(c+β)+G(b+c)(β+γ)+bc(β+γ)+βγ(b+c)。
假如使电动势沿着OA发生作用,而OA的电阻仍为α,并把电流计接在BC上,而BC的电阻仍为a,则D的值将仍然相同,而由沿OA作用的电动势E在BC中引起的电流将等于沿BC作用的电动势E在OA中引起的电流。
但是,如果我们简单地摘掉电池组和电流计,而且不改变它们各自的电阻就把电池组接在O和A之间而把电流计接在B和C之间,则我们必须在D中把B和G二值互换。如果互换之后的D值是D′,我们就得到
D-D′=(G-B){(b+c)(β+γ)-(b+γ)(β+c)}=(B-G){(b-β)(c-γ)}。
让我们假设,电流计的电阻大于电池组的电阻。
让我们也假设,在原来的位置上,电流计把两个具有最小电阻β、γ的导体的接头和两个具有最大电阻b、c的导体的接头连接了起来;或者换句话说,我们将假设,如果b、c、γ、β各量是按照大小次序排列的,则b和c是互接的而γ和β是互接的。由此可见,b-β和c-γ这两个量同号,因此它们的乘积是正的,从而D-D′和B-G同号。
因此,如果电流计是连接了两个最大电阻的接头和两个最小电阻的接头的,而且电流计电阻大于电池组电阻,则D的值将小于二者互换时的值,而电流计的偏转值则将较大。
因此,在一个给定体系中得到最大电流计偏转的规则如下:
在电池组电阻和电流计电阻这两个电阻中,应把较大的一个电阻接在其他四个电阻中的两个最大电阻的接头和两个最小电阻的接头之间。
349.〕 我们将假设我们必须测定导体AB和AC的电阻之比,而且作法就是在导体BOC上找到一个点O,使得当A点和O点用一根中间接着电流计的导线连接起来,而电池组是在B、C之间起作用时,电流计指针没有可以觉察到的偏转。
导体BOC可以设想为被划分成若干等份的一根具有均匀电阻的导线,这样,BO和OC的电阻之比就可以立即读出。
我们也可以不是把整个的导体做成一根导线而只在靠近O点处接上这样一根导线,而在每一侧的其他部分则可以采用一些其电阻为精确已知的任意形式的线圈。
现在我们将使用另外一套符号,而不再使用开始时使用的那种对称的符号。
设BAC的总电阻是R。设c=mR而b=(1-m)R。设BOC的总电阻是S。设β=nS而γ=(1-n)S。
n的值是直接读出的,而m的值则当不存在可觉察的电流计偏转时由n的值推出。
设电池组及其连线的电阻是B,而电流计及其连线的电阻是G。
像以前一样,我们得到
D=G{BR+BS+RS}+m(1-m)R2 (B+S)+n(1-n)S2 (B+R)+(m+n-2mn)BRS,而如果ξ是电流计导线中的电流,则有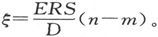
为了得到最精确的结果,我们必须使指针的偏转和(n-m)的值相比要尽可能地大。这一点可以通过适当选择电流计的规格和标准电阻线来做到。
当我们在第716节中讲到量电流学时就将证明,当电流计导线的形状改变而其质量保持不变时,单位电流引起的指针偏转是正比于导线长度的,但是电阻却像长度的平方一样地增大。由此就可以证明,当电流计导线的电阻等于电路其余部分的常量电阻时,最大的偏转就出现。
在现有的事例中,如果δ是偏转,则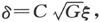 式中C是某一常数,而G是随导线长度的平方而变的电流计电阻。我们由此就得到,在D的表示式中,如果δ是最大值,则必须令包含G的部分等于表示式的其余部分。
式中C是某一常数,而G是随导线长度的平方而变的电流计电阻。我们由此就得到,在D的表示式中,如果δ是最大值,则必须令包含G的部分等于表示式的其余部分。
如果我们也令m=n,正如当我们作出了正确的观察时所应有的情况那样,我们就发现G的最佳值是G=n(1-n)(R+S)。
这一结果很容易通过考虑从A到O通过体系的电阻而求得,这时要记得BC和AO相共轭,从而对这一电阻没有任何效应。
同样我们即将发现,如果电池组的作用表面的总面积已经给定,则由于在这一事例中E正比于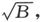 电池组的最佳装配就出现在
电池组的最佳装配就出现在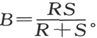
最后我们将确定那个S值,它使n值的一个给定改变量将引起最大的电流计偏转。
把ξ的表示式对S求导线,我们发现它当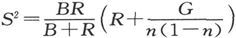 时有最大值。
时有最大值。
如果我们必须进行许多次电阻测量,而所测的实际电阻具有接近相同的值,则为此目的而专门准备一个电流计和一个电池组是值得的。在这一事例中,我们发现最佳装配是S=R,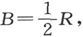 G=2n(1-n)R,而且如果
G=2n(1-n)R,而且如果 则
则
关于惠斯登电桥的应用
350.〕 我们已经论述了惠斯登电桥的普遍理论,现在我们将考虑它的一些应用。
可以作得最准确的是两个相等电阻的比较。
让我们假设β是一个标准电阻线圈。而我们想要调节γ使它的电阻等于β的电阻。
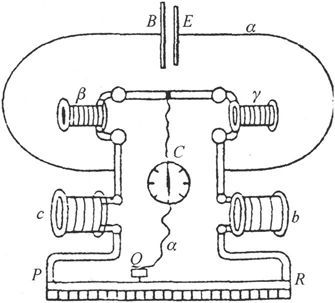
图33
准备另外两个线圈b和c,它们是相等的或接近相等的。把这四个线圈的电极插入水银杯中,并使电池组的电流分成两路,一路是β和γ而另一路是b和c。线圈b和c是用一根导线PR连接的,该导线的电阻要尽可能地均匀,并且附有等分的标尺。
电流计的导线把β、γ的接头和导线PR上的一点Q相连接,并且变动接触点Q,直到当先接通电池组电路而后接通电流计电路时观察不到电流计指针的偏转时为止。
然后交换线圈β和γ的位置,并找出Q点的一个新位置。如果新位置和旧位置相同,我们就知道β和γ的交换并没有引起电阻比例方面的变化,从而γ就是调好了的。如果Q点必须移动,这种变动的方向和大小就将显示为使γ和β的电阻相等所要求的γ的导线长度改变量的性质和数量。
线圈b和c,再加上它们到零读数点的滑线PR上的那一段,如果二者的电阻分别等于滑线上b格和c格的电阻,那么,如果x是第一种情况下的Q点读数,而y是第二种情况下的Q点读数,则有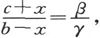
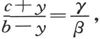 由此即得
由此即得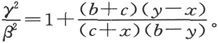
既然b-y近似地等于c+x,而且二者都比x或y大得多,我们就可以把上式写成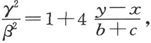 从而就有
从而就有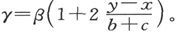
当γ已经尽可能地调好时,我们把b和c换成例如电阻变为十倍的另外两个线圈。
这时在β和γ之间保留着的差值将比使用原来的线圈b和c时引起Q点位置的十倍大的差别,从而利用这种办法我们就可以继续提高电阻比较的精确度。利用滑线接触法来调节可以进行得比利用电阻箱更加迅速,而且还可以连续变化。
电池组绝不可以代替电流计而接在滑线上,因为强电流在接触点上的通过将损坏滑线的表面。因此,这种装配就适用于电流计电阻大于电池组电阻的情况。
当待测电阻γ、电池组电阻a和电流计电阻α已经给定时,奥立沃·亥维赛先生曾经证明(Phil. Mag., Feb. 1873)其他各电阻的最佳值是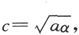
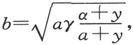
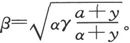
关于小电阻的测量
351.〕 当一个短而粗的导体被接入电路中时,它的电阻比由接触不良或焊接不好之类的不可避免的缺点所造成的电阻还要小得多,从而就不能用按上述方式做的实验来得出正确的电阻值。
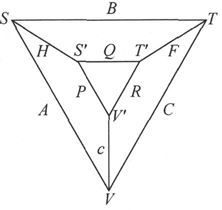
图34
这样一些实验的目的通常是测定物质的比电阻,而且当物质不能做成又长又细的导线时,或是当既要测量纵向导电的电阻又要测量横向导电的电阻时,这种实验就常被采用。
W. 汤姆孙爵士 〔51〕 曾经描述了一种适用于这些事例的方法,我们将把这种方法看成一组九个导体的例子。
这种方法的最重要部分就在于不是测量导体的整个长度的电阻,而是测量靠它两端不远处的两个记号之间的那一段的电阻。
我们所要测量的,就是其强度在导体的任一截面都均匀分布而其流动方向则平行于导体轴线的那个电流所遇到的电阻。喏,在端点附近,当电流借助于电极而被引入时,不论是焊接的、汞齐化的还是简单地压在导体两端上的电极,通常电流在导体中的分布都是不够均匀的。在离开端点一段小距离的地方,电流就变得基本上均匀了。读者可以自行检视第193节中的考察和图片;在那儿,一个电流从一条边上被送入了一片有着平行边的导体中,而很快就变得和两边平行了。
图35
要比较的是一些导体在某些记号S、S′之间和T、T′之间的电阻。
导体被串联起来,而且通过尽可能好的接法被接入一个电阻很小的电池组的电路中,一根滑线SVT的两端在S点及T点和导体相接触,而另一根滑线S′V′T′则在S′点及T′点和导体相接触。
电流计的导线接在这些滑线的V点和V′点上。
滑线SVT和S′V′T′具有很大的电阻,以致由于S、T、S′或T′处的接触不良而引起的电阻和滑线的电阻比起来可以忽略不计;V、V′二点要取得适当,以使每一导线通向两个导体的支路电阻之比近似地等于两导体的电阻之比。
用H和F代表导体SS′和TT′的电阻。
用A和C代表支路SV和VT的电阻。
用P和R代表支路S′V′和V′T′的电阻。
用Q代表连接器S′T′的电阻。
用B代表电池组及其连线的电阻。
用G代表电流计及其连线的电阻。
体系的对称性可以由线路图35看出。
电池组B和电流计G相共轭的条件,在这一事例中是 〔52〕
现在,导体Q的电阻是弄得尽可能地小的。假如它等于零,条件就将简化为 从而所要比较的两个导体的电阻之比就将是C和A之比,就像在通常形式的惠斯登电桥中一样。
从而所要比较的两个导体的电阻之比就将是C和A之比,就像在通常形式的惠斯登电桥中一样。
在现有的事例中,Q的值和P或R相比都是很小的,因此,如果我们选择V、V′二点,使得R和C之比近似地等于P和A之比,则方程中的最后一项将变为零,而我们就将有F∶H=C∶A。
这种方法的成功,在某种程度上依赖于滑线和被测导体在S、S′、T、T′点上的接触良好性。在马提森和霍金 〔53〕 所应用的下述方法中,这一条件就不必要了。
352.〕 如图36所示,待测的导体按以上已经描述的方式排列,其接通处要尽量完善,而所要比较的是第一个导体上S、S′之间的电阻和第二个导体上T′、T之间的电阻。
图36
两个导电的尖端或刀口被固定在一块绝缘材料上,从而它们之间的距离可以精确测量。这个仪器放在被测试的导体上,从而它和导体的两个接触点就是隔着一段已知的距离SS′的。这些接触物中的每一个都接着一个水银杯,而电流计的一个极就可以插入杯中。
仪器的其他部分就像在惠斯登电桥中一样安排得有电阻线圈或电阻箱A和C,和一根带着滑动接触器的导线,而电流计的另一个极O就接在这个接触点上。
现在把电流计接在S和Q上,调节A1 和C1 并调节Q的位置(即Q1 ),使得电流计的导线中没有电流。
于是我们就知道,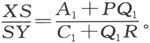 式中XS、PQ1 等等代表各该导体的电阻。
式中XS、PQ1 等等代表各该导体的电阻。
由此我们得到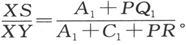
现在把电流计的电极接在S′上,并(通过把一些电阻线圈从一边挪到另一边)从C向A搬运电阻,直到可以通过把Q放在滑线的某点例如Q2 上而得到电流计导线中的电平衡。设现在C和A的值是C2 和A2 ,并设A2 +C2 +PR=A1 +C1 +PR=R。
于是我们就和以前一样得到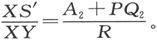 由此即得
由此即得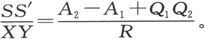
按同样办法,把仪器放在第二个导体的TT′段上,并且再次调动电阻,当电极位于T′时我们就得到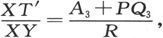 而当电极位于T时则得到
而当电极位于T时则得到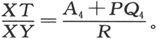 由此即得
由此即得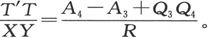
现在我们可以推出SS′和T′T的电阻之比了,因为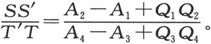
当并不要求很大的精确度时,我们就不必使用电阻线圈A和C,这时我们就得到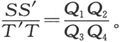
一根一米长的滑线上的Q点位置读数,不能精确到十分之一毫米,而且由于温度、摩擦等等的不相等,滑线的电阻可能在不同的部分变化颇大。因此,当要求很高的精确度时,就要在A和C两处引入电阻颇大的线圈,而这些线圈的电阻之比就可以比滑线在Q点被分成的两部分的电阻之比被测得更准确。
必须知道,在这种方法中,测定的精确度简直和S、S′或T、T′等处的接触的完善性完全无关。
这种方法可以叫做应用惠斯登电桥的差分用法,因为它依赖于分别作出的一些观察结果的比较。
这种方法中的精确性的一个根本条件就是,在完成测定所要求的四次观测过程中,各连接部分的电阻应该保持相同。因此,为了发现电阻的任何变化,观测系列永远必须重复进行 〔54〕 。
关于大电阻的比较
353.〕 当要测量的电阻很大时,体系中不同点上的势的比较,可以借助于一个精密的静电计来进行,例如借助于第219节中的象限静电计来进行。
如果要测量其电阻的那些导体是串联的,而且借助于一个电动势很大的电池组使一个相同的电流通过这些导体,则每一导体两端的势差将正比于该导体的电阻。因此,通过把静电计的两极先接在第一个导体的两端而后再接在第二个导体的两端,就可以测定该两导体的电阻之比。
这是测定电阻的最直接的方法。它涉及一个读数可靠的静电计的应用,而且我们必须有某种保证,可使电流在实验过程中保持不变。
四个大电阻的导体也可以像惠斯登电桥那样地接起来,而桥路本身则可以包括一个静电计的而不是一个电流计的两极。这种方法的好处就在于,为了引起静电计的偏转,并不要求任何持久的电流,而电流计则非有一个电流通过不能偏转。
354.〕 当一个导体的电阻非常大,以致用任何既有的电动势送进去的通过它的电流都小得无法用一个电流计来直接测量时,就可以用一个电容器来在一段时间内积累电荷,然后,让电容器通过一个电流计而放电,所积累的电量就可以被估计出来。这就是布来特和克拉克用来测试海底电缆接头的那种方法。
355.〕 但是,测量这样一个导体的电阻的最简单方法,就是把一个电容很大的电容器充电,并把它的两个表面和一个静电计的两个极接起来,而同时也和导体的两端接起来。如果E是静电计所指示的势差,S是电容器的电容,Q是电容器任一表面上的电荷,R是导体的电阻而x是导体中的电流,则由电容器理论可得Q=SE。
由欧姆定律,E=Rx,而由电流的定义,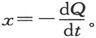
由此即得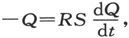 从而就有
从而就有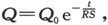 式中Q0 是起初t=0时的电荷。
式中Q0 是起初t=0时的电荷。
同理,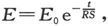 式中E0 是静电计的原始读数,而E是在时间t以后的读数。由此我们就得到
式中E0 是静电计的原始读数,而E是在时间t以后的读数。由此我们就得到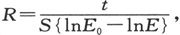 此式按绝对单位给出了R。在这一表示式中,关于静电计刻度的单位值的知识是不必要的。
此式按绝对单位给出了R。在这一表示式中,关于静电计刻度的单位值的知识是不必要的。
如果电容器的电容S是在静电单位制中作为若干米而被给出的,则R也是在静电单位制中作为一个速度的倒数而被给出的。
如果S是在电磁单位制中被给出的,则它的量纲是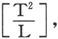 而R就是一个速度。
而R就是一个速度。
既然电容器本身并不是一个理想的绝缘体,那就有必要进行两个实验。在第一个实验中,我们测定导体本身的电阻R0 ;而在第二个实验中,我们测定当导体和电容器的两极相接时电容器的电阻,于是导体的电阻R就由下式给出,
这种方法曾由西门子先生应用过。
测定电流计电阻的汤姆孙方法 〔55〕
356.〕 一种和惠斯登电桥相似的装置曾被W. 汤姆孙爵士很有好处地应用于电流计在实际使用中的电阻的测定。在这方面,W. 汤姆孙爵士受到了曼斯方法的启发。参阅第357节。
设电池组仍像从前那样接在第347节的图中的B和C之间,但是电流计却接在CA上而不接在OA上。如果bβ-cγ=0,则导体OA和BC共轭,而且,由于BC上的电池组并不在OA中产生电流,任何其他导体中的电流强度就都和OA上的电阻无关。因此,如果电流计接在CA上,它的偏转就将保持相同,不论OA上的电阻是小还是大。因此,我们就可以观察电流计的偏转当O和A被一个导体接通时是否和不被接通时相同,而且,如果我们通过适当调节各导体的电阻而得到了这一结果,我们就知道电流计的电阻是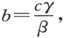 式中c、γ和β是电阻已知的电阻线圈。{译按:原文如此,其意义当是“线圈的已知电阻”。}
式中c、γ和β是电阻已知的电阻线圈。{译按:原文如此,其意义当是“线圈的已知电阻”。}
图37
可以注意,在电流计中并无电流的意义上,这不是一种调零法;但是所观察的是一个负效应,即当接通某一支路时电流计的偏转不变,而在这种意义上,这正是一种调零法。这样一种观察比同一电流计的两次不同偏转相等的观察更有价值,因为在后一事例中有一定的时间来让电池组的强度或电流计的灵敏度发生变化,而当我们可以随便重复某些变动而偏转则保持不变时,我们却可以确信电流是和这些变动完全无关的。
一个电流计线圈的电阻的测定很容易通过在OA上接入另一个电流计而用惠斯登电桥来按普通方法完成。利用现在所描述的方法,电流计本身却被用来测量它自己的电阻。
测定电池组电阻的曼斯方法 〔56〕
357.〕 电池组正在起作用时的电阻的测定,是困难程度更大得多的,因为人们发现,在通过它的电流发生变化以后的一段时间内,电池组的电阻会有相当的变化。在通常用来测量一个电池组的电阻的许多方法中,通过电池组的电流强度在操作过程中是会发生这样的变化的,从而就使所得的结果很可怀疑了。
在没有这种缺点的曼斯方法中,电池组被接在BC上而电流计被接在CA上。然后O和B之间的电路就被交替地接通和断开。
喏,如果OB和AC是共轭的,则不论OB的电阻如何变化,电流计指针的偏转都会保持不变。这可以看成在第347节中已经证明的那种结果的一个特例,也可以通过从该节那些方程中消去z和β而直接看出,那时我们就有
(aα-cγ)x+(cγ+cα+cb+bα)y=Eα。
如果y和x无关并从而和β无关,我们就必有aα=cγ。这样就由c、γ、α得出了电池组的电阻。
当条件式aα=cγ得到满足时,通过电流计的电流由下式给出,
为了检验这种方法的精确度,让我们假设条件式cγ=aα近似地而不是准确地得到满足,并假设y0 是当O和B被一个电阻可忽略的导体接通时通过电流计的电流,而y1 是C和B完全断开时通过电流计的电流。
图38
为了求出这些值,我们必须在y的普通公式中令β等于0和∞,然后比较所得的结果。
y的普遍值是 式中D代表第348节中的同一个表示式。令β=0,
式中D代表第348节中的同一个表示式。令β=0,
我们得到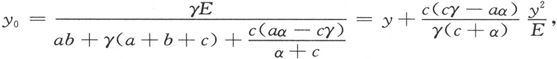 近似地,令β=∞,我们得到
近似地,令β=∞,我们得到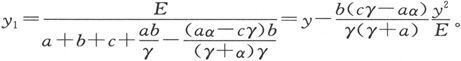
由这些值,我们即得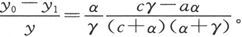
导体AB的电阻c应该等于电池组的电阻a;α和γ应该相等并尽可能地小;而b应该等于a+γ。
既然一个电流计当指针偏转很小时最为灵敏,我们在接通O和B以前就应该利用固定的磁体把指针弄到靠近零点的地方。
在这种测量电池组电阻的方法中,电流计中的电流在操作过程中是不受任何干扰的,因此我们就可以针对任何给定的电流计中的电流强度来确定电池组的电阻,以确定电流强度如何影响电阻 〔57〕 。
如果y是电流计中的电流,当开关合上时通过电池组的电流是x0 ,而当开关断开时的电流是x1 ,此处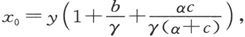
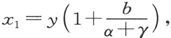 则电池组的电阻是
则电池组的电阻是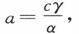 而电池组的电动势是
而电池组的电动势是
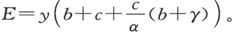
第356节中确定电流计电阻的方法和这里的方法只有一点不同,那就是电路的通断是在O、A之间而不是在O、B之间,从而通过把α和β互换和把a和b互换,我们就在这一事例中得到
关于电动势的比较
358.〕 在装置中没有电流通过时比较伏打装置及温差装置的下述方法,只需要一组电阻线圈和一个恒定电池组。
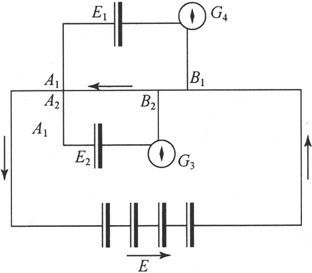
图39
设电池组的电动势E大于所要比较的任何一个发电装置的电动势,那么,如果把一个足够大的电阻R1插入到初级回路EB1 A1 E中的A1 、B1 二点之间,则从B1 到A1 的电动势可以弄成等于发电装置E1 的电动势。如果现在把这一装置的电极接在A1 、B1 二点上,就不会有电流通过该装置。在发电装置E1 的电路上接一个电流计G1 ,并调节A1 和B1 之间的电阻直到电流计不指示任何电流时为止,我们就得到方程E1 =R1 C式中R1 是A1 和B1 之间的电阻,而C是初级回路中的电流强度。
同样,取第二个发电装置并把它的电极接在A2 和B2 上,使得电流计G2 不指示任何电流,就得到E2 =R2 C,式中R2 是A2 和B2 之间的电阻。如果电流计G1 和G2 的观察是同时进行的,初级回路中的C值在两个方程中就是相同的,从而我们就得到E1 ∶E2 =R1 ∶R2 。
用这种方法,就可以比较两个发电装置的电动势。一个发电装置的绝对电动势既可以在静电学上借助于一个静电计来测量又可以在电磁学上借助于一个绝对电流计来测量。
在这种方法中,在进行比较的时间内没有任何电流通过其中任何一个发电装置。这种方法是波根道夫方法的一种修订形式;这是由拉提摩·克拉克先生提出的,他曾经得出了下列的各电动势的值:

一伏特就是等于100,000,000厘米—克—秒单位的一个电动势。
第二十五章 关于物质的电阻
359.〕 按照电在它们中通过的情况,不同的物质可以分成三类。
第一类包括所有的金属及其合金、某些硫化物以及含金属的其他化合物,此外还包括煤化焦炭形态的碳和晶体形态的硒。
在所有这些物质中,导电都是在不引起物质的分解或化学本性的改变的情况下进行的,不论在物质的内部还是在电流进入和离开物体的地方都如此。在所有这些物质中,电阻是随温度的升高而增大的 〔58〕 。
第二类包括称为电解质的那些物质;其所以称为电解质,是因为电流和物质变成出现在电极上的两种成分的那种分解相伴随。通常说来,一种物质只有当处于液体形态时才是一种电解质,但是某些表观上是固体的胶体,例如100℃下的玻璃,也是电介质 〔59〕 。按照B. C. 布罗迪爵士的实验来看,似乎某些气体也可以被很强的电动势所电解。
在所有通过电解而导电的物质中,电阻都随着温度的升高而减小。
第三类包括一些物质,它们的电阻如此之大,以致只有利用最精巧的方法才能探测电在它们中的通过。这些物质叫做电介质。属于这一类的有相当多的当融解时是电解质的固体,有一些液体例如松节油、石油精、融解的石蜡等等,还有所有的气体和蒸汽。金刚石形态的碳和非晶态的硒也属于这一类。
这一类物体的电阻比起金属的电阻来是非常大的,它随着温度的升高而减小。由于这些物质的电阻很大,人们很难确定我们勉强在它们中得到的微弱电流是不是和电解相伴随。
关于金属的电阻
360.〕 在电学的研究中,没有任何部分比金属电阻的确定有更多的和更精确的实验。在电报工作中,最重要的就是用来制造电线的金属应有尽可能小的电阻。因此在选定材料以前必须进行电阻的测量。当线路上出了故障时,故障的位置通过测量电阻就能立即确定,而现在占用了那么多人的这种测量就要用到用金属做成的电阻线圈,而那种金属的电学性质也必须经过仔细的测试。
金属及其合金的电学性质曾由马提森、佛格特、霍金、西门子等先生很仔细地研究过,它们在把精密的电学测量引入到实际工作中来的方面作出了许多贡献。
从马提森博士的研究可以看出,温度对电阻的影响在相当多的纯金属中是近似相同的100℃时的电阻和0℃时的电阻之比是1.414比1,或者说是100比70.7。对纯铁来说,比值是1.6197,而对铊来说则是1.458。
金属的电阻曾由V. W. 西门子博士 〔60〕 在广阔得多的温度范围内观察过,其范围从冰点扩展到350℃,而且在某些事例中扩展到1000℃。他发现,电阻随温度的升高而增加,但是增加率却随温度的升高而减小。他发现有一个公式既和马提森博士在低温度下观察到的电阻符合得很好,也和他自己在1000℃的范围内的观察结果符合得很好;那公式就是 式中T是从-273℃算起的绝对温度,而α、β、γ是一些常量。例如,对于
式中T是从-273℃算起的绝对温度,而α、β、γ是一些常量。例如,对于
由这一类的想法可知,一个炉子的温度,可以通过观察放在炉中的一根铂丝的电阻来加以测定。
马提林博士发现,当两种金属结合成合金时,合金的电阻在多数事例中都大于按照各成分金属的电阻及其性质来算出的电阻。在金和银的合金的事例中,合金的电阻既大于纯金的又大于纯银的电阻,而且,在各成分的一定限度的比例范围之内,合金的电阻几乎不随比例的变化而变化。基于这种原因,马提森博士就建议用两份重量的金和一份重量的银的合金来作为复制电阻单位的一种材料。
温度变化对电阻的效应,通常在合金中比在纯金属中要小。
因此普通的电阻线圈是用德银制成的,因为这种合金的电阻很大而其随温度的变化很小。
银和铂的一种合金也被用来制造标准线圈。
361.〕 某些金属的电阻当金属被退火时就会改变,从而只有当一根金属丝通过反复地升到高温而不再显示电阻的永久变化时,它才能够可靠地被当作一种电阻的标准。有些金属丝即使没有遭受温度的变化也会在时间过程中改变自己的电阻。因此确定汞的比电阻就是重要的。汞这种金属是液体,从而永远有相同的分子结构,而且很容易通过蒸馏或用硝酸处理来加以提纯。W. 西门子和C. F. 西门子曾经很细心地测定了这种金属的电阻,他们引用了这个电阻来作为一种标准。他们的研究曾经得到了马提森和霍金的实验的补充。
汞的比电阻是由观察到的一根长度为l并充有质量为w的汞的管子的电阻按下述方式推出的。
没有任何玻璃管的内径是到处完全相同的,但是,如果把少量的汞装入管中使它占据管子的一个长度λ,而这个长度的中点到管子一端的距离是x,则这一点附近的截面积s将是 式中C是一个相同的常量。
式中C是一个相同的常量。
充满整个管子的汞的质量是 式中n是沿管子等距排列的在那里测量λ的各点的数目,而ρ是单位体积的质量。
式中n是沿管子等距排列的在那里测量λ的各点的数目,而ρ是单位体积的质量。
整个管子的电阻是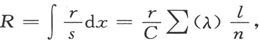 式中r是单位体积的比电阻。
式中r是单位体积的比电阻。
由此可得 从而单位体积的比电阻就是
从而单位体积的比电阻就是
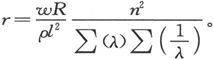
为了求出单位长度和单位质量的电阻,我们必须用密度来乘这个量。
由马提森和霍金的实验可知,长度为一米而质量为一克的均匀汞柱在0℃时的电阻是13.071大英协会单位;由此可见,如果汞的比重是13.595,则长度为一米而截面积为一平方毫米的汞柱的电阻是0.96146大英协会单位。
362.〕 在下面的表中,是按照马提森的实验 〔62〕 得出的电阻,R是长度为一米而质量为一克的一个柱体在0℃下以大英协会单位计的电阻,而r是一个立方厘米体积以厘米每秒计的电阻,这时假设一个大英协会单位等于0.98677地球象限弧。
关于电解质的电阻
363.〕 电解质电阻的测量,由于电极上的极化而成为很困难的;这种极化导致观察到的金属电极之间的势差大于实际上产生电流的那个电动势。
这一困难可以用各种方法来克服。在某些情况下我们可以用适当材料的电极来消除极化,例如在硫酸锌溶液中用锌电极。通过把电极的表面做得比要测其电阻的那一部分电解质的截面大得多,并通过沿相反的方向交替地在短时间内接通电流,我们可以在电流的通过激起任何相当强的极化以前进行测量。
最后,通过进行两个不同的实验,我们也可以估计极化的总效应;在这两个实验中,电流在一个实验中在电解质中经过的路程要比在另一个实验中的路程长得多,而电动势则调节得使两个实验中的实际电流和它们流动的时间都接近相同。
364.〕 在帕耳佐夫博士 〔64〕 的实验中,电极被做成大圆盘的形状,放在分开的扁平容器中,容器中充有电解质,另外把一个很长的充有电解质的虹吸管的两端插在两个容器中,以便把它们连接起来。用了两个不同长度的这种虹吸管。
观察到的这些虹吸管中的电解质的电阻是R1 和R2 ;然后在这些虹吸管中充入汞,测得它们的电阻是 和
和
于是就由公式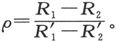 求出了形状相同的一部分汞和一部分电解质在0℃下的电阻之比。
求出了形状相同的一部分汞和一部分电解质在0℃下的电阻之比。
为了从各个ρ值推出长度为一厘米而截面积为一平方毫米的电解质的电阻,我们必须用汞在0℃下的r值去乘这些ρ值。参阅第361节。
帕耳佐夫给出的结果如下:
| 硫酸和水的混合物 | ||
| 温度 | 电阻和汞电阻之比 | |
| H2 SO4 ……15℃ | 96950 | |
| H2 SO4 +14H2 O……19℃ | 14157 | |
| H2 SO4 +13H2 O……22℃ | 13310 | |
| H2 SO4 +499H2 O……22℃ | 184773 | |
| 硫酸锌和水 | ||
| ZnSO4 +33H2 O……23℃ | 194400 | |
| ZnSO4 +24H2 O……23℃ | 191000 | |
| ZnSO4 +107H2 O……23℃ | 354000 | |
| 硫酸铜和水 | ||
| CuSO4 +45H2 O……22℃ | 202410 | |
| CuSO4 +105H2 O……22℃ | 339341 | |
| 硫酸镁和水 | ||
| MgSO4 +34H2 O……22℃ | 199180 | |
| MgSO4 +107H2 O……22℃ | 324600 | |
| 盐酸和水 | ||
| HC1+15H2 O……23℃ | 13626 | |
| HCl+500H2 O……23℃ | 86679 |
365.〕 F. 考耳劳什先生和W. A. 尼波耳特先生 〔65〕 曾经测定了硫酸和水的混合物的电阻。他们使用了磁电式的电流,其电动势变动于格罗夫电池的电动势的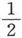 到
到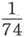 之间,而借助于一个铜—铁温差电偶,他们把电动势减到了格罗夫电池电动势的
之间,而借助于一个铜—铁温差电偶,他们把电动势减到了格罗夫电池电动势的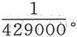 他们发现,在整个的电动势范围之内,欧姆定律是适用于这种电解质的。
他们发现,在整个的电动势范围之内,欧姆定律是适用于这种电解质的。
在含有大约三分之一的硫酸的混合物中,电阻有最小值。
电解质的电阻随温度的升高而减小。每增加1℃时的电导增时百分比列在下面的表中:
以0℃下的汞电阻表出的硫酸和水的混合物在22℃下的电阻。据考耳劳什和尼波耳特。
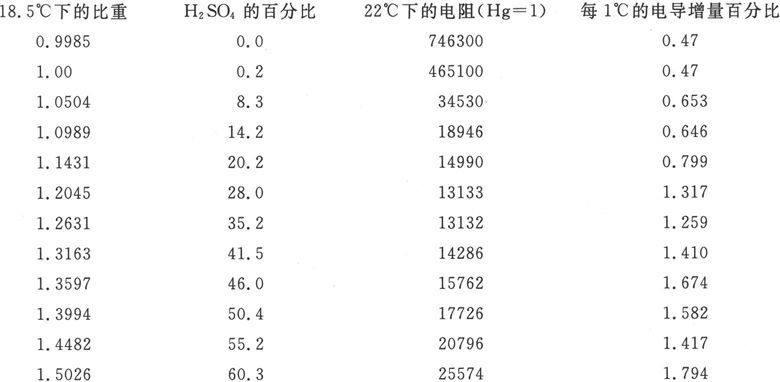
关于电介质的电阻
366.〕 关于古塔波胶和在电报电缆的制造中用作绝缘媒质的其他材料,曾经进行过许多的电阻测定,为的是要确定这些材料作为绝缘质的价值。
通常测定是在材料已经用作导线的包皮以后才进行的,而导线就被用作一个电极;电缆被浸入一个水槽中,槽中的水就被用作另一个电极。于是电流就是透过用绝缘质制成的一个面积很大而厚度很小的圆柱形包皮而流动的。
经发现,当电动势开始作用时,电流绝不是恒定的,就如电流计所指示的那样。最初的效应当然是一个强度相当大的瞬变电流,总的电量被用来把绝缘体的表面充电到和电动势相对应的面电荷分布。因此,最初的电流就不是电导的一种量度而是绝缘层电容的一种量度。
但是,即使在这种电流已经衰减掉以后,剩下来的电流也还不是恒定的,而且也并不指示物质的真实电导。人们发现电流至少在半小时之内还要继续减小,因此,如果过了一段时间以后再来按电流确定电阻,得到的值将大于刚一加上电池组就进行确定的电阻值。
例如,对于胡波尔的绝缘材料来说,10分钟结束时的表观电阻是一分钟结束时的表观电阻的四倍,而19小时结束时的表观电阻则是一分钟结束时的表观电阻的22倍。当电动势的方向倒转时,电阻就降到等于或低于起初的电阻,然后又逐渐增高。
这些现象似乎起源于古塔波胶的一种状态;由于没有更好的名称,我们可以把这种状态叫做极化,并且一方面把它和一系列级联充电的莱顿瓶的状态相比拟,而另一方面又把它和第271节中的里特尔次级电堆相比拟。
如果把若干个大电容的莱顿瓶用一些电阻很大的导体(例如高更实验中的湿棉线)串联起来,则作用在这一串莱顿瓶上的一个电动势将产生一个电流,而正如一个电流计所指示的那样,这个电流将逐渐减小,直到各个莱顿瓶已经完全充电时为止。
这样一串东西的表观电阻将增大,而如果各个莱顿瓶的电介质是一种理想绝缘体,则表观电阻将无限地增大。如果电动势被取消,而把这一串东西的两端连接起来,那就可以观察到一个反向的电流,而其总电量在理想绝缘体的事例中将和正向电流的总电量相同。在次级电堆的事例中也观察到类似的效应,所不同的是最后的绝缘不是那么好,而且每单位面积的电容要大得多。
在用古塔波胶等等为包皮的电缆事例中,人们发现,在加上电池组半小时以后,若把导线和外电极连接起来,就会出现一个反向电流;这个电流将持续一段时间,并逐渐使体系还原到原来的状态。
这些现象是和由莱顿瓶的“残余放电”所指示的那些现象种类相同的,只除了极化的数量在古塔波胶等等中比在玻璃中要大得多。
这种极化状态似乎是材料的一种有向的性质;为了造成这种状态,不但要有一个电动势,而且要按照位移或其他方式而有一个相当大的电量的通过,而这种通过是需要相当的时间的。当极化状态已经建成时,就有一个内电动势在物质内部沿相反的方向而作用着;这种电动势将继续存在,直到它已经产生了一个总量等于第一个电流的反向电流,或是极化状态已经通过物质中的真实导电而暗暗消失时为止。
我们曾经称之为残余放电、电的吸收、起电或极化的那种现象的整个理论,是值得仔细研究的,而且是也许会导致有关物体之内部结构的重要发现的。
367.〕 多数电介质的电阻是随温度的升高而减小的。例如,古塔波胶在0℃时的电阻约为它在24℃时的电阻的20倍。布莱特先生和克拉克先生曾经发现,下面的公式可以给出和他们的实验相符的结果。如果r是古塔波胶在百分温度计T度下的电阻,则在T+t度下的电阻将是R=r×Ct ,式中C是一个常数,其数值随古塔波胶品种的不同而在0.8878和0.9之间变动。
霍金先生曾经证实了这样一件稀奇的事实:只有当古塔波胶已经达到了它的末温度若干小时以后,它的电阻才能达到它的对应值。温度对弹性橡皮的电阻的影响,不像对古塔波胶电阻的影响那么大。当受到压力时,古塔波胶的电阻将有颇大的增加。
用在不同电缆中的不同古塔波胶的一立方米的电阻,以欧姆为单位,如下表所示 〔66〕 :

368.〕 根据第271节所描述的布夫实验算出的下面这个表,表示了不同温度下一立方米玻璃的以欧姆为单位的电阻。

369.〕 C. F. 瓦尔莱先生 〔67〕 近来曾经考察了电流通过稀薄气体的条件,他发现电动势E等于一个常量E0 和一个按照欧姆定律而依赖于电流的部分,即E=E0 +RC。
例如,使某一根管子中开始出现电流时所需要的电动势,是323个丹聂耳电池的电动势,而304个电池的电动势就刚刚足以维持电流了。按照电流计的测量,电流强度正比于比304多出的电池数目。例如,对于305个电池,偏转为2;对于306个电池,偏转为4;对于307个电池,偏转为6;如此等等,直到380,那就是304+76,这时偏转为150,或76×1.97。
由这些实验可以看出存在电极的一种极化,其电动势等于304个丹聂耳电池的电动势,而且直到此值为止,电动势是被用来建立这种极化状态的。当最大极化已经建成时,比304个电池电动势多出的部分电动势就被用来按照欧姆定律维持电流了。
因此,一种稀薄气体中的电流规律,和通过一种电解质的电流规律很相像;在电解质中,我们是必须照顾到电极的极化的。
联系到这一课题,我们必须研讨汤姆孙的结果;那就是,曾经发现,在空气中产生一个火花所需要的电动势不是正比于距离而是正比于距离加一个常量。和这个常量相对应的电动势可以看成电极极化的强度。
370.〕 魏德曼先生和吕耳曼先生 〔68〕 近来研究了电在气体中的通过。电流是用霍耳兹起电机来产生的,放电发生于充有稀薄气体的一个金属容器中的球形电极之间。放电通常是不连续的,相继放电之间的时间阶段利用一个和霍耳兹起电机的轴一起转动的镜子来测量。放电系列的像借助于一个具有分格物镜的测日计来观察;测日计被调节好,使每一次放电的一个像和下一次放电的另一个像相重合。利用这种方法,得到了很自洽的结果。经发现,每次放电的电量不依赖于电流强度和电极材料,而是依赖于气体的种类和密度,并依赖于电极的距离和形状。
这些研究证实了法拉第的下列叙述 〔69〕 :使一个导体的带电表面上开始出现一次破坏性放电时所需要的电张力(参阅第48节),当所带的是负电时将比所带的是正电时稍小,但是当一次放电确已发生时,一次在正电表面上开始的放电所放出的电却要多得多。这些研究也倾向于支持在第57节中提出过的假说,那就是,凝聚在电极表面上的气体层在现象中起重要的作用。而且这些研究也指示出来,这种凝聚是在正电极上最大的。
注 释
〔1〕 原书还引用了“电矛盾”(electric conflict)一词作为“电流”的同义语。——译注
〔2〕 关于针对各种金属导体对欧姆定律所作的验证,见B. A. Report 1866 p. 36上克里斯陶的文章,他证明了一条导线对无限弱的电流而言的电阻和它对很强的电流而言的电阻约相差百分之10-10 ;关于针对电解质对该定律所作的验证,见B. A. Report 1886上斐兹杰惹和特罗顿的文章。
〔3〕 Phil. Mag., Dec. 1851.
〔4〕 North British Review, 1864, p. 353;以及Proc. R. S. June 20, 1867.
〔5〕 Proc. R. S. Edin., Dec. 15, 1851;以及Trans. R. S. Edin., 1854.
〔6〕 勒·罗意曾经证明,当各截面上存在突然的变化,以致在一段可以和分子距离相比的距离上出现有限大小的温度改变时,这一结果就是不成立的。
〔7〕 Cambridge Transactions, 1823.
〔8〕 'On the Electrodynamic Oualities of Metals.' Phil. Trans., Part Ⅲ, 1856.
〔9〕 Proc. R. S. Edin., Session 1870~1871, p. 308,亦见Dec. 18, 1871.
〔10〕 Pogg. Ann. ci. p. 338(1857).
〔11〕 见第5节的小注。
〔12〕 见F. Kohlrausch, 'Die Eiektrische Leitungsfähigkeit des im Vacuum distillirten Wassers.' Wied. Ann. 24, p. 48. Bleekrode Wied. Ann. 3, p. 161,曾经证明纯盐酸不是导体。
〔13〕 见Roberts-Austen, B. A. Report, 1887.
〔14〕 只有当电池中不存在可逆的热效应时,这一定理才是适用的;当存在这种效应时,电动势p和化学作用的机械当量ω之间的关系用方程p-θ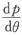 =ω来表示,式中θ是电池的绝对温度。见v. Helmholtx, 'Die Thermodynamik chemischer Vorgänge.' Wissenschaftliche Abhandlungen, ii. p. 958.
=ω来表示,式中θ是电池的绝对温度。见v. Helmholtx, 'Die Thermodynamik chemischer Vorgänge.' Wissenschaftliche Abhandlungen, ii. p. 958.
〔15〕 这一结果是和热力学第二定律相矛盾的;按照该定律,压强的增大将增大电解所要求的电动势。见J. J. Thomson's 'Applications of Dynamics to Physics and Chemistry,' p. 86. v. Helmholtz, 'Weitere Untersuchungen die Electrolyse des Wassers betreffend.' Wied. Ann. 34, p. 737.
〔16〕 Klektricität, i, 568, bd. j.
〔17〕 Berlin. Monatsbericht, July, 1868.
〔18〕 Pogg. Ann. bd. exxxviii. s. 286 (October, 1869).
〔19〕 B. A. Report, 1887.
〔20〕 C. F. Varley, 'Klectric Telegraphs, &c, 'Jan. 1860中的论述。
〔21〕 Proc. R. S., Jan. 12, 1871. 至于有关这一课题的其他研究,见Wiedemanns Elektricität, bd. ii. pp. 744~771.
〔22〕 Annalen der Chemic und Pharmacie, bd. xc. 257 (1854).
〔23〕 当时人们显然还不熟悉半导体。——译注
〔24〕 Proc. R. S., Jan. 19, 1871.
〔25〕 当要求一个标准电动势时,现在最常用的是一个克拉克电池。关于制造和使用这样一个电池的注意事项,见Lord Rayleigh的论文“The Clark Cell as a Staudard of Electromotive Force., Phil. Trans. part ii. 1885.”
〔26〕 此节摘录J. A. 弗莱明先生所作的麦克斯韦教授的演讲,参阅弗莱明的论文,见Phil. Mag., xx. p. 221, 1885.
〔27〕 我们可以用同样的办法证明,当不同支路中有电动势时,各电流将满足∑RC2 -2∑EC为极小值,式中E是支路中的电动势而C是支路中的电流。我们把这个量叫做F。如果我们用沿各回路流动的那些独立电流把F表示出来,则各导体中的电流分布x,y,z,…可由方程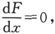
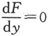 来求出。
来求出。
例如,在第382节所考虑的惠斯登电桥的事例中,就有F=ax2 +by2 +cz2 +β(x-z)2 +γ(y-x)2 +α(z-y)2 -2Ex,从而该节中的方程就是和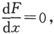
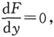
 等价的。这常常是求出电流按导体的分布的最方便的办法。第281节中的倒易性也可以很容易地用这种办法推出。
等价的。这常常是求出电流按导体的分布的最方便的办法。第281节中的倒易性也可以很容易地用这种办法推出。
〔28〕 此处定义的是电流密度的分量。——译注
〔29〕 所谓“越过AP的电流”是指通过由曲面λA 、λP 、λ′和λ′+1所包围而成的那一流管的电流。
〔30〕 参阅第303节的注。
〔31〕 Trans. R. S. Edin., 1853—1854, p. 165.
〔32〕 假设通过变换 
能使(16)式的左端变成 
为了做到这一点,我们看到r1 ξ2 +r2 η2 +r3 ζ2 +2s1 ηζ+…必须和(aξ+a′η+a″ζ)2 +(bξ+b′η+b″ζ)2 +(cξ+c′η+c″ζ)2 。相等同,我们用U来代表此式。
如果我们利用方程 
消去ξ,η,ξ,则因为AB组和rs组互逆,我们就得到U=A1 x2 +A2 y2 +A3 z2 +2B1 yz+…
但是我们由(1)和(3)看到X=aξ+a′η+a″ζ;Y=bξ+b′η+b″ζ;Z=cξ+c′η+c″ζ;由此即得U=X2 +Y2 +Z2 。
但是由(2)可见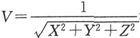 满足微分方程,从而
满足微分方程,从而 必须满足该方程。
必须满足该方程。
〔33〕 见Thomson and Tait's Natural Philosophy, §154。
〔34〕 霍耳先生关于磁性对永久电流的作用的发现(Phil. Mag. ix. p. 225; x. p. 301, 1880),可以用一种说法来描述,即放在磁场中的一个导体有一个旋转系数。参阅霍普金孙(Phil. Mag. x. p. 430, 1880)。
〔35〕 Phil. Trans., 1871, p. 77. 见第102a节。
〔36〕 Lord Rayleigh, Theory of Sound, ii. p. 171.
〔37〕 见Cayley教授的论文,London Math. Soc. Proc. vi. p. 38. VOL. I.
〔38〕 Phil. Mag. Now. 1872, p. 344. 随后瑞利勋爵得到了0.8242作为上限。参阅London Math. Sac. Prac. vii. p. 74,并见Theory of Sound, vol. ii. Appendix A. p. 291.
〔39〕 类似的考虑将给出由放在一种电介质中的S点上的一个电荷所引起的电场,该电介质的比感本领是K1 ,由一个平面和比感本领为K2 的另一种电介质分平。在这一事例中,如果电荷=K1 E而K1 k1 =1=K2 k2 ,则正文中的V1 和V2 将表示势。
〔40〕 参阅Kirchhoff, Pogg. Ann. lxiv. 497, and lxvii. 344; Quineke. Pogg. revii. 382; Smith, Proc. R. S. Edin., 1869~1870, p. 79. Holzmüller, Einfuhrung in die Theoris der isogonalen Verwandschaften, Leipzig, 1882. Guedhard, Journal de Physique, t. i. p. 483, 1882. W. G. Adams, Phil. Mag. iv. 50, p. 548, 1876; G. C. Foster and O. J. Lodge, Phil. Mag. iv. 49, pp. 385, 453; 50, p. 475, 1879 and 1880; O. J. Lodge, Phil. Mag. (5), i. 373, 1876.
〔41〕 这些表示式可以利用关系式 来简化为定积分,式中J0 代表零阶贝塞耳函数。
来简化为定积分,式中J0 代表零阶贝塞耳函数。
由此可见,如果我们把S取作坐标原点,而把平板的法线取作x轴,就有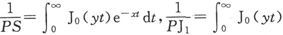
 式中c是平板的厚度,
式中c是平板的厚度, 等等。把这些值代入(15)中,我们就看到V等于
等等。把这些值代入(15)中,我们就看到V等于
 当y=0、x=2nc而n为整数时,此式的值很容易求出。
当y=0、x=2nc而n为整数时,此式的值很容易求出。
〔42〕 见Sir W. Thomson's 'Note on Induced Magnetism in a Plate,' Camb. 和Dub. Math. Journ, Nov. 1845,或Reprint, art. ix. §156.
〔43〕 如果我们把(24)写成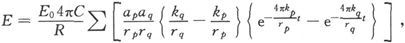 或许就可以更容易地看到这一点。
或许就可以更容易地看到这一点。
〔44〕 罗兰和尼科耳斯曾经证明,很均匀的冰洲石晶体并不显示电吸收,Phil. Mag. xi. p. 414, 1881. 穆索达发现,尽管单独考虑时石蜡和二甲苯并不显示残余电荷,一层石蜡上加一层二甲苯却显示这种现象,Wied. Ann. 40, 331, 1890.
〔45〕 Théorie de la Chaleur,第105节。
〔46〕 作为电动势之标准的克拉克电池,现在可算是这种说法的一个例外。
〔47〕 瑞利爵士和席维克先生的实验已经证明,大英协会单位只是0.9867地球象限弧每秒,从而它比所拟议的值约小百分之1.3。1884年在巴黎召开的国际电学家会议采用了一个新的电阻单位,即“法定欧姆”,它被定义为一个长度为106厘米而截面积为1平方毫米的水银柱在0℃下的电阻。
〔48〕 Phil. Mag, July; 1870.
〔49〕 这种研究采自韦伯的关于量电流学的论文,见Göttingen Transactions, x. p. 65.
〔50〕 D是每次取三个电阻的各乘积之和,比时应略去交于一点的任意三个电阻的乘积。
〔51〕 Proc. R. S., June 6, 1861.
〔52〕 这一条件可以通过在第五章附录中给出的法则来导出。
〔53〕 Laboratory. Matthiessen and Hockin on Alloys.
〔54〕 关于小电阻的另一种比较方法,见Lord Rayleigh, Proceedings of the Cambridge Philosophical Society, vol. v. p. 50.
〔55〕 Proe. R. S., Jan. 19, 1871.
〔56〕 Proc. R. S., Jan. 19, 1871.
〔57〕 在Philosophical Magazine for 1877, vol. i. pp. 515~525上,奥立沃·亥维赛先生曾经作为曼斯方法的一个缺点而指出了,如果方程aα=cγ成立,则由于电池组的电动势依赖于通过电池组的电流,故当开关合上和开断时电流计指针的偏转不可能是相同的。洛治先生描述了曼斯方法的修订形式,这是他成功地应用了的。
〔58〕 对于这一说法,碳是一种例外;而佛森诺近来曾经发现,一种锰铜合金的电阻当温度升高时是减小的。
〔59〕 考耳若什曾经证实,银的卤化物在固态下是电解导电的,见Wied. Ann. 17. p. 642, 1882.
〔60〕 Proc. R. S., April 27, 1871.
〔61〕 卡林达先生近来在卡文迪什实验室中所作的关于铂的电阻的实验已经证明,这些表示式是和高温下的事实不一致的。西门子的关于铂的公式要求电阻的温度系数在高温下变为常量并等于0.0021,而实验却似乎在很高的温度下指示着一个慢得多的增加率,如果不是减小率的话。见H. L. Callendar. 'On the Practical Measurement of Temperature,' Phil Trans. 178 A. pp. 161~230.
〔62〕 Phil. Mag., May, 1865.
〔63〕 更新的实验已经给出了汞的比电阻的不同值。下面是在0℃下对长度为一米而截面为一平方毫米的汞柱的电阻测定结果,以大英协会单位计:Lord Rayleigh and Mrs. Sidgwick, Phil. Trans. Part I. 1883…95412, Glazebrook and Fitzpatrick, Phil. Truns. A. 1888…95352, Hutchinson and Wilkes, Phil. Mag. (5). 28. 17. 1889…95341.
〔64〕 Berlin Monatsbericht, July, 1868.
〔65〕 Pogg., Ann. cxxxviii. pp. 280, 370, 1869.
〔66〕 Jenkin's Cantor Lectures.
〔67〕 Proc. R. S., Jan, 12, 1871.
〔68〕 Berichte der Königl Sächs. Gesellschaft, Leipzing, Oct. 20, 1871.
〔69〕 Exp. Res., 1501.