附录B

不可逆性与动力论方法

Appendix B

普里戈金和他的所谓“布鲁塞尔学派”中的同事们的工作可能很好地代表了下一次的科学革命，因为他们的工作不仅与自然，而且与社会本身开始了新的对话。

布鲁塞尔自由大学校景（彭丹歌摄）。

相关的动力学

第10章给出的描述不可逆性的概念框架，其简单性主要来自时间T和刘维算符L之间的简单关系（参见式8.22）。这使得我们明确地构造出用划分表达的T的本征函数（亦见附录A），并且最终得出变换算符Λ和熵算符M。

除了K流动的情形，T的L这种简单关系是不可能得到的。于是我们不得不转向现代形式的动力论方法（参见第8章）。这里，我们愿意给出一些定性的论述，并强调与第10章的类比。然后，我们将指出说明量子力学的势散射的某些结果。详细的说明见文献［3］。

利用算符P和Q（参见式8.29），刘维方程可以分成一个联立的方程组

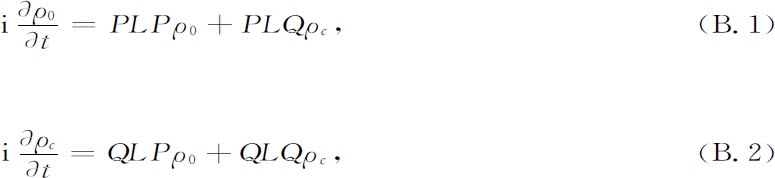
其中Pρ＝ρ₀ 是动量分布或能量分布，于是ρ_c 描述出空间的相关。因此ρ₀ 又叫做“相关的真空度”。我们从方程组B.1，B.2看出，相关ρ_c 可以这样地从真空度中通过QLP被创造，通过QLQ被传播，且通过PLQ被消灭。

从给定的ρ₀ 和ρ_c 在某瞬间的条件出发，方程2.2和2.3可以用不同的方法来求解。讨论它们的一种便利方法涉及到L的预解式：（z-L）^-1 。z在上半平面（即Ⅰm z≥0）的值和正的时间联系在一起，z在下半平面（即Ⅰm z≤0）的值和负的时间相联系。

如在式8.31中那样，我们把L的预解式分解为几个部分预解式之和，相当于把单位元分解为P和Q：

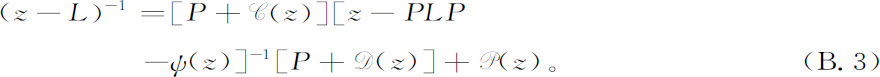
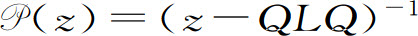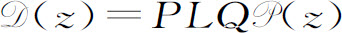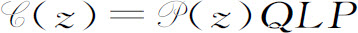用这种方法，我们引入了动力论描述的几个基本算符，即传播算符 Q，消灭算符 ，产生算符 ，以及碰撞算符 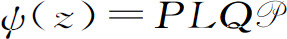（z）QLP（亦见式8.34）。

用这些定义可以容易地导出所谓“广义主方程”^[1] ：

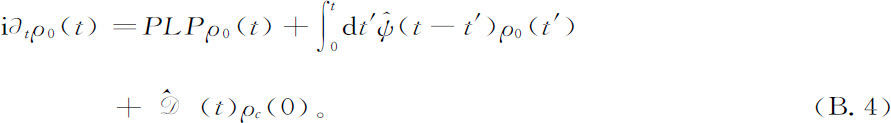
此处，比如说核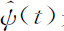 是由碰撞算符ψ（z）的逆拉普拉斯变换给出的。碰撞和相关之间的对偶性明显地出现在方程B.4中：某瞬时t真空度分量ρ₀ （t）的变化率是正定的，受到它在早些时候的值ρ₀ （t′）的影响（以非马尔可夫的方式），但它只在初始时刻受到相关ρ_c （0）的影响。这样的相关可以被称做碰撞前的相关，因为它们在任何以算符ψ表示的碰撞生效之前出现。与此类似，新的相关可以从早些时候的相关真空度ρ₀ （t′）中通过 诞生出来，不过这样的碰撞后的相关不以任何方式影响到不相关部分ρ₀ （t）的变化。如果广义主方程B.4中对初始相关的记忆渐渐淡漠而消失了，那么随着时间的延续，该变化将渐渐地被碰撞的效果所支配。

如我们在第6章已看到的，碰撞前的相关和碰撞后的相关间，其区别在分析洛喜密脱佯谬时起着决定性作用。一个简单的例子就是散射。这时我们有两种效果：一种是碰撞过程使粒子弥散（也就是说，它使得速度分布变得更加对称），另一种是在被散射的粒子与散射体之间产生了相关。实行速度反演（即在某个有限距离处放一个球面镜，并在球心处设一个靶子），可以明显看到相关的出现。简要地说，散射的作用如下：在正过程中，它把速度分布变得更加对称，而且出现相关；在逆过程中，速度分布变得更加不对称，而且相关消失。因此，通过对相关的考虑，可以在正过程（其顺序为碰撞—→相关）和逆过程（其顺序为相关—→碰撞）之间引入一个物理的分布。

如广义主方程B.4所说明的，长时间的行为与初态的制备是密切相关的。必须认识到，对所研究的系统来说，初始条件不能按照实验者或观察者的意愿任意地选择：初始条件本身一定是某个以前的动力学变化的结果。因此，表述一个对初态的选择原则，断定在自然界中只能制备或观察瞬态的碰撞前的相关，就成为十分自然的事了。

在对广义主方程B.4的研究中，人们作了大量的工作。应当记住，式B.4不过是刘维方程的另一种写法。因此，式B.4依然是描述决定论的时间可逆过程的。向不可逆性的过渡只能靠时间对称破缺变换Λ。

让我们考虑一下运动不变量。从式B.4可以推测出有两类不变量：一类是“奇异不变量”，它们通过抵消碰撞前相关的碰撞效果而维持它们的常数值；另一类是“规则不变量”，它们是碰撞不变量。为了简化起见，在这个讨论中我们将假定只出现规则不变量。这样，我们可以得到这样的一些分布，当t→+∞时它们趋向一个规则不变量（就是说，趋向于平衡态的分布），但当t→-∞时它们趋向一个奇异不变量，反之亦然^[2] 。作为选择原则的第二定律排除了第二类分布以及所有其他在t→+∞时不趋向平衡态的分布。我们已研究出的表达这些基本性质的方法就是所谓“子动力学”理论。简要地说，这个方法如下：

在z＝+i0的邻域中抽出预解式的适当的奇异点，这样我们就可以定义所谓“面向未来”的算符Π，该算符有如下性质：Π是一个幂等算符，Π² ＝Π（由于这个原因，我们又称它为“投向”算符），并且Π和刘维算符对易：［Π，L］_- ＝0。这就是我们为什么讲子动力学的原因。通过同样的步骤，但是考虑z＝-i0的邻域，我们还可定义所谓“面向过去”的算符Π′，它有这样的性质：Π′² ＝Π′，［Π′，L］_- ＝0。通过某个L反演，可以从Π得到Π′。Π算符和Π′算符是不同的（Π′≠Π），但它们是有关联的。实际上，无论Π或Π′，均不是厄米算符（Π≠Π^† ；Π′≠Π′^† ），但它们是“星－厄米”算符——就是说，当同时施行厄米共轭和L反演时，它们保持不变（参见第8章），即

Π和Π′还有另一些对称的性质（B.3），这里将不用到它们。重要的是，Πρ只对那些在t→+∞时趋于规则不变量的分布函数ρ才是确定的（同样，Π′ρ对那些在t→-∞时趋于规则不变量的ρ才是确定的）。

让我们对我们的论述和玻耳兹曼的最初表述作一简短的比较。玻耳兹曼考虑的是没有相关性的初始条件——就是说只有一个P分量（这相当于分子混沌状态）。虽然玻耳兹曼要挑选出一类特殊初始条件的革命思想看来比什么都重要，但他本人对此思想的实现是不能令人满意的。事实上，P并不和L对易，［P，L］_- ≠0，因此，随着时间的延续，任何分布函数都将获得一个Q分量。而且P对于L反演来说是不变量，P＝P′，因而玻耳兹曼的考虑不能得出时间的一个优惠方向来。

下一步是构造变换算符Λ。这是利用下面形式的关系式来做的：

式中λ是哈密顿量（H＝H₀ +λV）中的耦合常数。一旦我们有了Λ，我们也就有了微观熵算符M（参见式8.3）。

现在让我们回过来讨论与第10章概念框架的关系。我们将再次把φ_n 称作M的本征函数或本征分布（参见10.27）

于是我们可以把内部时间定义为算符，使它具有M的本征函数并且使它的本征值就是从“钟表上”读出的时间值：

但是与K流动不同，我们希望T与运动的幺正算符U_t 间有一个简单的关系。随着时间的延续，φ_n 可能以极复杂的方式变为混合的，这个问题目前正被人们研究。

现在让我们转向一个例子。

超空间中的量子力学散射理论

不可逆性起源于经典系统或量子系统，而且在两种情形下，都只是在刘维算符L具有连续谱时，不可逆性才能出现。因此，对于量子系统，必须考虑大系统的极限（参见附录C）。

第3章中已提到，量子理论可以用波函数ψ在希尔伯特空间中表述出来，或者用密度算符ρ在我们所谓“超空间”中表述出来。系统态的时间变化，在第一种情形中可通过薛定谔方程3.17用哈密顿算符H来表达；在第二种情形中，可通过刘维-冯·诺伊曼方程3.36来表达，其中包括了与H对易的刘维超算符L。

因为作用在“超空间”上的L是因式化超算符的差（参见式3.35）

所以超空间中的变化算符（参见式3.36）也取因式化的形式

看上去，从希尔伯特空间转到超空间，似乎什么也没有得到，但是当把不可逆性包括在描述中时，就不是这样了。实际上，假如果真存在着一种可能性把可观察量的代数扩大，以便包括不可逆性的话，那么相应的可观察量就只能被定义成一个不可因式分解的算符（参见附录C）。这样，不可逆性就引出了不能包括在希尔伯特空间框架中的可观察量，因此超空间在对可适用于量子系统的第二定律所做的一切表述中都起着中心的作用，而且在希尔伯特空间描述和超空间描述之间的简单对应关系B.10消失了。

不可因式分解的算符的引入，导致量子理论基本描述的重大变化，因为纯态和混合态在超空间中须受到同等待遇。于是，不可逆性只能出现在由于某种固有的运动不稳定性而使得用经典轨道或量子波函数所作的描述已失去物理意义的时候。在两种关系中，不可逆性都导致“非局域性”，因为可以实现的态既不能约化为相空间中的“点”，也不能约化为希尔伯特空间中的“纯态”。不可逆性的微观理论所提出来的基本问题，在势散射的简单例子里已经遇到^[3] 。这就是我们将在此处集中讨论的问题。

这时，哈密顿量H包括一个动能部分H₀ 和一个（有限范围的）势V：

这个分解相当于用投影算符P和Q去分解式8.30。

薛定谔方程3.17的一般解很容易用哈密顿量的本征态表达出来，如式3.21那样。按照这个观点，散射理论归结为寻找幺正算符U的问题，这个幺正算符U把H在未扰动的基底中对角化（即在该基底中H₀ 是对角算符）。

当不存在束缚态时，由于H的谱与H₀ 的谱是吻合的，所以方程

在适当的边界条件下得出默勒（Möller）算符U_± ^[4] 。它们对未扰动基底向量｜k〉的作用得到H的入射本征态和出射本征态：

作为趋向于大体积的极限过程的结果，U_± 或｜k^± 〉含有一些称为分布的奇异函数，这必须谨慎地加以处理。

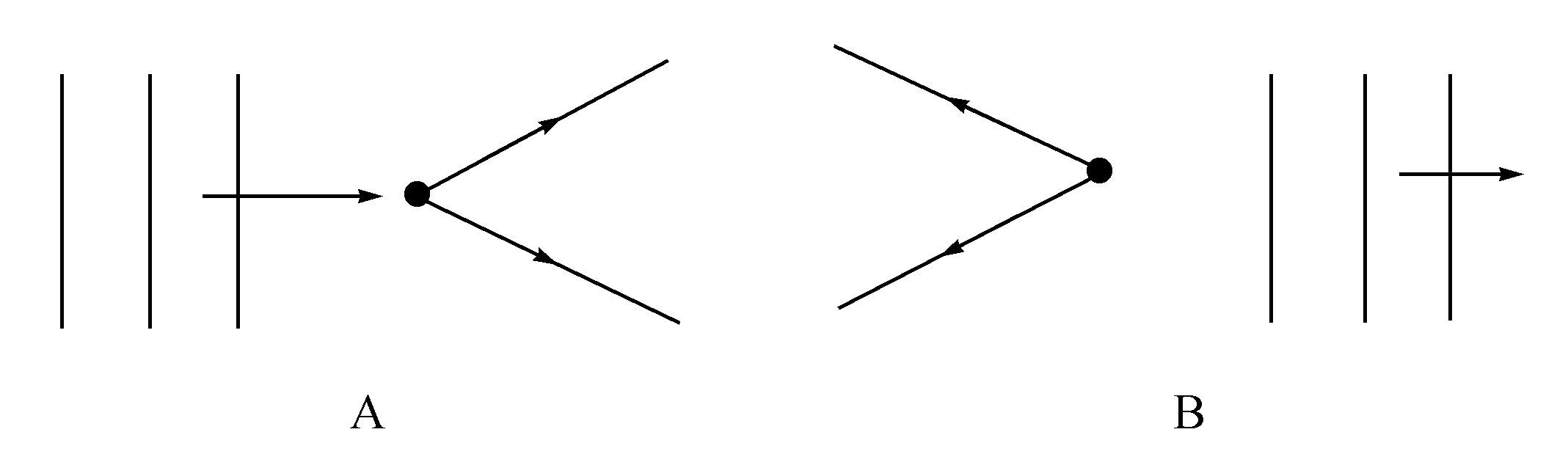
图B.1　散射的｜k⁺ 〉态（A）和散射的｜k^- 〉态（B）

散射态的物理意义在每一种关于散射理论的教科书中均有讨论。入射态｜k⁺ 〉描述的是带有一个处于平面波态的入射粒子和一个处于（比如说球面）散射波态的出射粒了的那些态。出射态｜k^- 〉包括一个出射平面波和一个入射球面波。一般地说，在物理直觉的基础上，一类定态解，即｜k⁺ 〉，对应于实际的实验；而｜k^- 〉永远不可能被制备或观察。这个重要的论述是作为一些“技术上的”特别考虑，比如对实现适当初始条件的“实践上的”不可能性的考虑结果而提出的。因此，十分令人感到满意的是，我们能够给出一个比较深刻的理由，证明排除入射球面波（以及更一般地，排除“超前”势）是合理的。因为我们证明了只有相应于出射球面波的那些态才在面向未来的耗散半群中。这种情形非常类似于第10章所使用的收缩纤维和膨胀纤维。这里，和K流动的情形一样，也无法描述什么“公共的未来”。

有关本附录上一节所包括的那个方法，我们在这里只能再补充几点说明。

在大系统的极限下用波函数描述散射，涉及到适当的解析开拓，即李普曼-斯温格（Lippman-Swinger）方法。对于研究波函数的二次泛函（式3.32）的密度算符来说，这一点也是对的。但是对密度算符，这个解析开拓并非仅仅包括取解析连续波函数的平方。

这个观察和范霍夫（van Hove）所作的评述有密切关系，范霍夫指出，必须把散射看做是波函数与其复共轭间“结构干涉”的结果，因此不能独立地去解决散射的时间变化，因为它们给出密度算符的时间变化。

这段话影响到量子论中时间的真正含义。因为可观察量的期望值以二次形式依赖于（与时间有关的）波函数，所以有一个“双倍”时间相关性。但是当要引入像碰撞那样的过程（不可逆过程就发源于此）时，必须把这个双倍的时间序列重新排到一个单个的事件序列中去。换句话说，在密度算符本身的层次上必须直接实现解析开拓。这样，子动力学算符Π和变换算符Λ就可以明确地构造出来。基本的结果是，Λ可以作用到随出射波｜k⁺ 〉收缩的态上，同时作用到包含｜k^- 〉发散的态上。

此外，截面现在极清楚地作为如下刘维算符的Λ变换而出现（参见式8.7）：

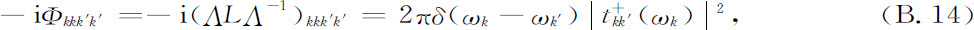
其中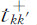 是通常的转移矩阵或散射理论中的t矩阵的元素（带有一个具有正虚部的自变量）。当然，这个公式是经典的。但值得注意的是，截面绝不可能从幺正变换中得出。实际上可以从有关L的公式B.9验证出，L_iijj 这样的元素等于零，经过一个幺正变换后，仍然为零。因此，像散射截面或寿命这一类概念，实际上是一个包括不可逆性的非幺正描述的组成部分。

参考文献

［1］I. Prigogine，C. George，F. Henin and L. Rosenfeld Chemica Scripta 4 （1973）：5.

［2］I. Prigogine and C. George，Proc. Natl. Acad. Sci. U. S. A. 80 （1983）：4590.

［3］C. George，F. Mayné and I. Prigogine，Advances in Chemical Physics，（1984）.

［4］见任何散射理论教科书，如M.L. Goldberger，K. M. Watson，Collision Theory，Wiley（1964）.