附录C

熵、测量和量子力学中的叠加原理

Appendix C

在20世纪的科学史中，普里戈金对中国传统文化和中国传统哲学思想高度关注，除了从生物学转向科学技术史的李约瑟之外，可能难有第二人可以与之相比。

普里戈金在为中国学者编著的《普利高津与耗散结构理论》一书的“序”中写道：“我相信，我们正是站在一个新的综合、新的自然观念的起点上。也许我们最终有可能把强调定量描述的西方传统和着眼于自发组织世界描述的中国传统结合起来。”

布鲁塞尔自由大学校景（彭丹歌摄）。

纯态和混合态

正如第3章所表明的，我们得出了量子力学中在纯态（波函数）和由密度矩阵表示的混合态之间的基本区别。在量子力学中占支配地位的纯态有点儿类似在经典力学中的轨道：正如薛定谔方程指出的（见方程3.17和3.18），随着时间的演化，纯态变换成另一些纯态。此外，可观察量被定义为把希尔伯特空间中的一个矢量映射成它自己的厄米算符。这些算符再次保持纯态，于是量子力学的基本规律被表述得甚至不需求助与混合态相对应的密度矩阵描述。采用后者只被当做是一种实践上的便利或近似。这类似于在经典力学中所考虑的情形。在经典动力学中，与纯态相对应的基本要素是动力学系统中的轨道（可专门参阅第2章和第7章）。

在第3章中，量子力学是完备的吗？这个问题已被提出。我们已经看到，之所以不顾过去的50年中量子力学已有的惊人成功而提出这个问题，其原因之一是它难以体现测量过程（见第3章“测量问题”一节）。我们已看出，测量过程把一个纯态转换为一个混合态，因而不能用薛定谔方程来描述，薛定谔方程是把一个纯态转换为另一个纯态。

尽管有过许多的讨论（参见文献［1］的极好的叙述），这个问题离开解决还很远。以迪斯帕格纳特的话来说（见文献［1］第161页）：“（测量）问题被一群有影响的理论物理学家当做是不存在的或价值不大的问题，而他们的人数较少但却在稳定增长的同事们则认为是提出了几乎不可克服的难题。”

在这个论战中，我不愿意采取过分强硬的立场，因为就当前的目的而言，测量过程只是对量子力学中不可逆性问题的一个说明。

不论人们采取什么立场，纯态和混合态的基本区别以及纯态在理论中占优惠地位这两点必须放弃。因而问题是要对纯态和混合态之间区别的消失提供一个基本的根据。值得注意的事实是作为理论的基本对象的熵算符M（见第8章“不可逆性以及经典力学和量子力学表述的扩展”一节）的引入恰好需要取消纯态与混合态之间区别。

本附录的目的是简略地给出这个叙述的一个证明。至于更详细的情形，读者可参考米斯拉、库巴奇和我的文章^[2] ，本附录是在这篇文章的基础上写成的。

熵算符和运动生成元

为什么我们必须越出量子力学的标准表述的范围？在量子力学的标准表述中，按照薛定谔方程（式3.17）哈密顿算符是运动的生成元。假设我们具有（见方程7.27，为了方便起见，我们改变D的符号）

于是D可看做微观熵产生算符。看来很自然地要假设M和D的测量彼此相容，正如大家所熟知的，这意味着：

对于后面讨论的全部内容来说，方程C.2作为“充分条件”来考虑。这个条件可以减弱，可是在这里我们不想进行更详细的讨论。

至于一个算符M为什么不能满足条件C.1和C.2，其基本理由是哈密顿算符H在量子力学中扮演着一个双重角色（见第8章“粒子和耗散：非哈密顿的微观世界”一节的）：除了生成时间演化外，它也表示系统的能量，因此它必须是有下界的，即

为了看出哈密顿量H为正与条件C.1和C.2之间的不能共存性，让我们考虑等式

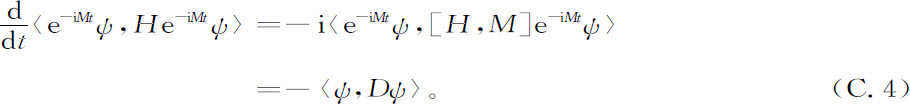
在这里，最后的等式是由M与D的对易得出的，所以有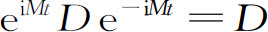 。从0到t积分式C.4的两边，现在得出：

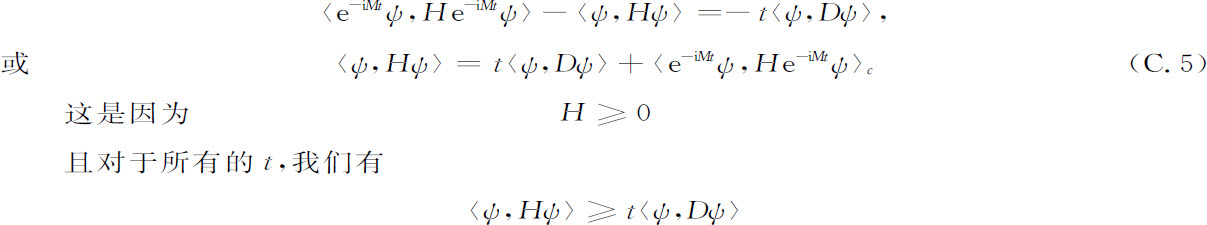
可是，除D＝0的平凡情况以外，显然这是不可能的。

在量子力学通常的表述中熵算符的不存在和定义一个时间算符T的不可能（是泡利^[3] 所指出的），这两者之间存在着令人感兴趣的联系。这样的一个时间算符应当是正则共轭于时间演化群的生成元H；或（同样可参见第3章“量子力学是完备的吗？”一节和第8章“熵算符的构成和变换理论：面包师变换”一节）

然而，如果存在一个满足式C.6的自伴算符T，则一个满足式C.1和式C.2的熵算符M可以通过直接取M为T的一个单调函数来得到：

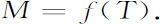
这样，在量子力学中定义熵算符M的不可能性，在量子力学中时间算符的不存在，以及时间-能量测不准关系的解释与证实等问题都是联系在一起的。它们共同起因于如下事实：在通常的量子力学的表述中，时间平移群的生成元H同样也是系统的能量算符。于是，为了有可能去定义熵算符M，克服这个简并性是必要的。达到这个目的最简单的道路是采用所谓的量子力学的刘维表述（见第3章“薛定谔表象和海森伯表象”一节），在这个表述中的基本对象是描述时间演化的密度算符群。正如第3章所指出的，现在时间平移群的生成元是由方程（见式3.35和式3.36）

所定义的刘维算符。因此让我们来研究M的存在与由刘维算符生成的时间演化之间的联系。

熵超算符

采用量子力学的刘维表述所得到的最重要的优点是时间演化群的生成元L在物理上不再被限制为有下界的。真的，如果H的谱从零扩展到+∞，则L的谱是整个实践。于是，定义M作为“超算符”的可能性（见第8章“不可逆性以及经典力学和量子力学表述的扩展”一节）不会被上面给出的讨论所排除，M应满足关系式

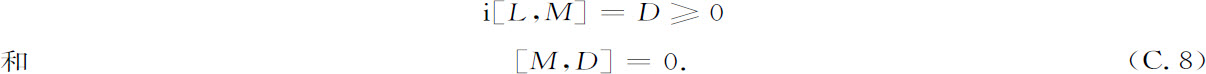
如同在经典力学中一样，我们必须外加补充条件（见第2章“遍历系统”一节）；M不能存在于下面两种情形之中：

（1）H有纯粹的分立谱，

（2）H有连续但有界的谱。

在物理学的语言中，这意味着对于一个有限而广延的包含有限数目的粒子的系统熵超算符不可能存在。这清楚地表明，与经典力学相比问题要复杂得多——因为在附录A中，对于只包含单个自由度的有限的经典系统我们已经构成了M。

现在熵超算符M的重要性质是它必须是不能因式分解的，这意味着Mρ不采取

的形式，式中A₁ 与A₂ 是通常的自伴算符。首先应注意，如果M是可以因式分解的，采用诸如保持厄米性等一般的性质，它可写成如下更简单的形式

这样一个可因式分解的算符应保持纯态。确实，它应当简单地把｜ψ〉转变成A｜ψ〉（见方程3.30）。

因此，M的不可因式分解是一个很重要的性质。确实，如果Mρ是由式C.10所给出的，不难加以证实，M的对易关系（式C.8）可导致如下的对于A的关系：

式中c是一个实数。

出现的三种情况（对应于c＝0，c＞0，和c＜0）能分别地排除如下：

（1）c＝0，上面给出的讨论表明［H，A］＝D₁ ＝0。然后，这与式C.10一起导致关系式

这意味着M是一个运动不变量。

（2）c＞0，在这个情形中，有

这个情形能通过与本附录上一节所述形式上的类似来加以研究，正的算符D扮演H的角色，A起着M的作用，cA² 起着D的作用，因此我们可以直接计算出A² ＝0，因此M如同被式C.10所给出的那样。

这样，上面所进行的讨论引导我们得出如下的结论：对于无限的量子系统，存在着扩大可观察量的代数以包括表示非平衡熵的算符M的可能性。可是，算符M只可以被定义为一个不可因式分解的超算符。于是，在可观察量中间包括熵算符（必须是不可因式分解的），要求纯态失去它在理论中占据的优惠地位，要求在同等的基础上对待纯态和混合态。在物理上，这意味着对于具有作为一个可观察量的熵的系统，在纯态与混合态之间的区别必须不再有运算上的意义，并且应当在实现量子态的相干叠加的可能性上加以限制（见第3章“测量问题”一节）。

明显地，作为我们的熵算符理论的一个逻辑上的结果而得出的这个结论，应当依据关于纯态和混合态之间失去区别的物理原因的分析，而得到进一步的阐释。

我们已经一再讨论了经典系统的情形（见第三、七、八、九章）我们已经看出目前存在两个已知的机制导致运动的不稳定性，这不稳定性又禁止对十分确定的轨道的“观察”。可以预斯，具有一个熵算符的量子系统，其纯态与混合态之间丧失区别的物理原因就是上面讨论的不稳定性的某种适当的量子类似。

另外，如同在经典力学中那样，可以存在一种以上的机制。一个机制可能是存在类似与经典系统强混合性质的；另一个可能是存在量子系统的庞加莱突变（见第8章“熵算符和庞加莱突变”一节）。在附录B中，我们讨论了经典系统的一个简单的例子。在那里当z→0，渐近碰撞算符Ψ（z） 不等于零。类似的情况存在于量子情形且在动力学方程的推导中起着重要的作用（看式8.34）。当然，量子不稳定性机制的严格的数学表述是未来的工作。虽然如此，令人满意的是：当热力学第二定律通过算符M的存在被解释成一种动力学原理时，它要求我们放弃纯态和混合态的区别，恰巧在这种场合这种区别被认为是在物理上不可观察的。

参考文献

［1］B. d'Espagnat，Conceptual Foundations of Quantum Mechanics，2d ed.（Menlo Park，California：Benjamin，1976）.

［2］B. Misra，I. Prigogine，and M. Courbage，Proceedings of the National Academy of Sciences，U. S. A. 76（1979）：3607.

［3］见M. Jammer，The Philosophy of Quantum Mechanics（New York：Wiley-Interscience，1974），p. 141.