第四章 环中线性的和变化的热运动
·Chapter IV of the Linear And Varied Movement of Heat in A Ring·
三角级数现在被称为傅立叶级数,表明数学家们对傅立叶贡献的肯定和赞赏。它常作为正交级数的范例出现在数学分析中,并给微分方程、积分方程和解析函数等数学理论提供了统一的数学联系。

欧塞尔街景
第一节 问题的通解
238 表示环中的热运动的方程已经在第105目中叙述过;它是

现在的问题是要对这个方程积分:我们可以把它简写成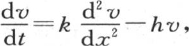 其中k表示
其中k表示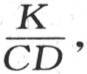 h表示
h表示 x表示包含在环的一点m和原点O之间的弧长,v是在一给定时间t之后在点m所观察到的温度。首先我们假定v=e-ht u,u是一个新的未知数,由此我们推出
x表示包含在环的一点m和原点O之间的弧长,v是在一给定时间t之后在点m所观察到的温度。首先我们假定v=e-ht u,u是一个新的未知数,由此我们推出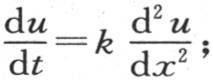 由于这个方程可以通过在前一个方程中令h=0而导出,所以它属于表面辐射为0的情况:我们由此得出结论,由于介质的作用,环的不同点会逐渐冷却,而这个条件不会以任一方式干扰热分布的规律。
由于这个方程可以通过在前一个方程中令h=0而导出,所以它属于表面辐射为0的情况:我们由此得出结论,由于介质的作用,环的不同点会逐渐冷却,而这个条件不会以任一方式干扰热分布的规律。
事实上,只要对方程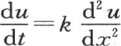 积分,我们就可以得到在同一时刻对应于这个环的不同点的u值,如果热在其中传导而在表面无任何损失,那么我们就能确定固体所处的状态;若有损失,为了确定固体在同一时刻所处的状态,我们只需用一个分数e-ht 乘不同点在同一时刻所取的所有u值就够了。因此,表面所受到的冷却并不改变热分布的规律;唯一的结果是每一点的温度都比它在没有这一条件时要小,由于这个原因,温度随分数e-ht 的逐次幂而降低。
积分,我们就可以得到在同一时刻对应于这个环的不同点的u值,如果热在其中传导而在表面无任何损失,那么我们就能确定固体所处的状态;若有损失,为了确定固体在同一时刻所处的状态,我们只需用一个分数e-ht 乘不同点在同一时刻所取的所有u值就够了。因此,表面所受到的冷却并不改变热分布的规律;唯一的结果是每一点的温度都比它在没有这一条件时要小,由于这个原因,温度随分数e-ht 的逐次幂而降低。
239 由于该问题简化成了方程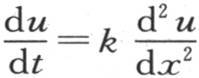 的积分,所以,我们首先选择可以赋予变量u的最简单的特殊值;然后由这些特殊值组成一般的值,我们要证明这个一般值和这个积分一样广泛,它包含一个x的任意函数,更准确地说,当根据问题所需要的形式安排后,它就是这个积分本身,因此,不可能有任何不同的解。
的积分,所以,我们首先选择可以赋予变量u的最简单的特殊值;然后由这些特殊值组成一般的值,我们要证明这个一般值和这个积分一样广泛,它包含一个x的任意函数,更准确地说,当根据问题所需要的形式安排后,它就是这个积分本身,因此,不可能有任何不同的解。
首先可以注意到,如果对u给定特殊值aemt sinnx,m和n服从条件m=-kn2 ,那么这个方程成立。因此,可以把函数e-kn2 t sinnx看做是u的一个特殊值。
为了使这个值能适合于这个问题,当r表示环的平均半径,距离x以量2πr增加时,它应当不变。因此,2πnr应当是圆周2π的i倍;这给出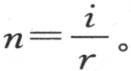
我们可以取i为任一整数;我们假定它总是正的,因为,若它是负的,我们则只需在值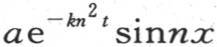 中改变系数a的符号就够了。这个特殊值
中改变系数a的符号就够了。这个特殊值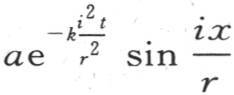 只有在表示这个固体的初始状态时,才满足所提出的问题。现在,当取t=0时,我们得到
只有在表示这个固体的初始状态时,才满足所提出的问题。现在,当取t=0时,我们得到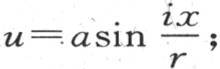 这样,假定u的初始值实际上由
这样,假定u的初始值实际上由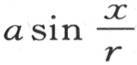 来表示;也就是说,假定不同点的初始温度与经过那些点的半径和经过原点的半径之间的角的正弦成正比,那么,环内部的热运动就严格由方程
来表示;也就是说,假定不同点的初始温度与经过那些点的半径和经过原点的半径之间的角的正弦成正比,那么,环内部的热运动就严格由方程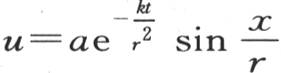 来表示,如果我们考虑表面的热耗,那么我们得到
来表示,如果我们考虑表面的热耗,那么我们得到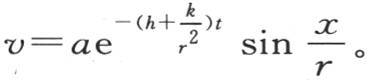 所讨论的这种情况是我们所能设想的所有情况中最简单的情况,在这种情况下,变化的温度保持它们的初始比,并且任一点的温度都随对每一点都相同的一个分数的逐次幂而降低。
所讨论的这种情况是我们所能设想的所有情况中最简单的情况,在这种情况下,变化的温度保持它们的初始比,并且任一点的温度都随对每一点都相同的一个分数的逐次幂而降低。
如果我们假定初始温度与弧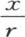 的两倍的正弦成正比,那么我们可以观察到同样的性质;一般地,当已知温度由
的两倍的正弦成正比,那么我们可以观察到同样的性质;一般地,当已知温度由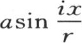 表示,i是任一整数时,亦如此。
表示,i是任一整数时,亦如此。
只要把量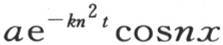 取作u的特殊值,我们也能得到同样的结果:在这里,我们也有
取作u的特殊值,我们也能得到同样的结果:在这里,我们也有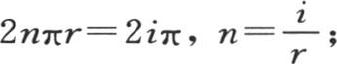 因此,如果初始温度由
因此,如果初始温度由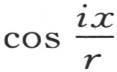 来表示,那么方程
来表示,那么方程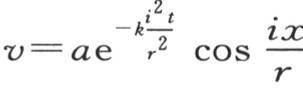 就表示环内的热运动。
就表示环内的热运动。
在已知温度与弧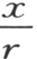 的倍数的正弦或余弦成正比的所有这些情况中,在这些温度之间所建立的比例在冷却的无穷时间中一直存在。如果初始温度由函数
的倍数的正弦或余弦成正比的所有这些情况中,在这些温度之间所建立的比例在冷却的无穷时间中一直存在。如果初始温度由函数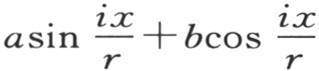 表示,i是任一整数,a和b是任意两个系数,则情况相同。
表示,i是任一整数,a和b是任意两个系数,则情况相同。
240 现在让我们转到初始温度没有我们刚才所假定的这种关系,而是由任一函数f(x)所表示的一般情况上来。让我们对这个函数给定形式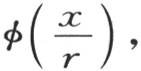 因而我们有
因而我们有
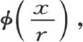 并且,让我们设想函数
并且,让我们设想函数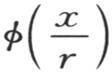 被分解成受恰当系数作用的多重弧的正弦或者是余弦级数。我们写下方程
被分解成受恰当系数作用的多重弧的正弦或者是余弦级数。我们写下方程
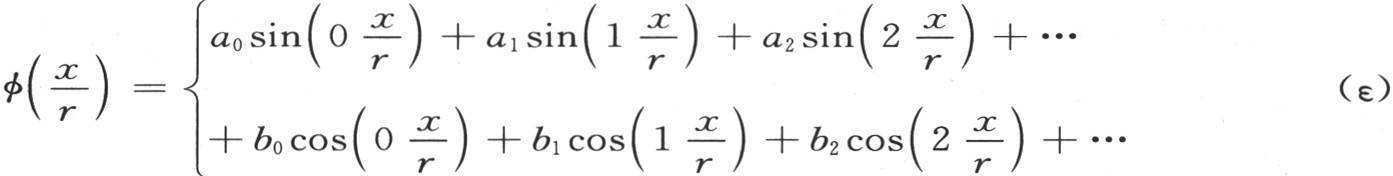
可把数a0 ,a1 ,a2 ,…,b0 ,b1 ,b2 ,…看做是已知的,且事先已计算出。显然,这时u的值将由方程
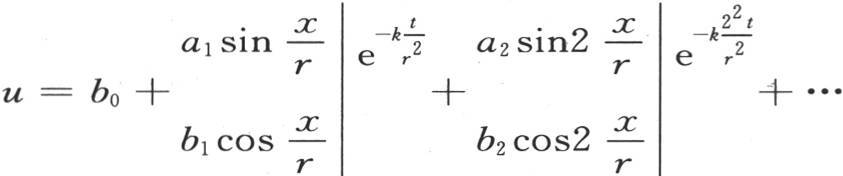
来表示。
事实上,
第一,这个u值满足方程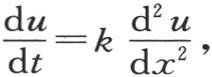 因为它是几个特殊值的和;
因为它是几个特殊值的和;
第二,当我们用环的圆周的任一倍数使距离x增加时它不发生变化;
第三,它满足初始状态,因为只要取t=0,我们就得到方程(ε)。
因此,这个问题的所有条件都得到满足,剩下的只是用e-ht 来乘这个u值。
241 随着时间的增加,组成u值的每一项都变得愈来愈小;因此温度系统不断趋于正常和稳定的状态,在这种状态下,温度u与常数b0 的差由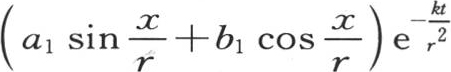 【1】 来表示。因此,我们在前面所考虑过的,由此而构成一般值的这些特殊值,从这个问题本身导出它们自身的起源。它们每一个都表示一旦形成就能自我存在的一种基本状态;这些值与热的物理性质有一种自然而必然的联系。
【1】 来表示。因此,我们在前面所考虑过的,由此而构成一般值的这些特殊值,从这个问题本身导出它们自身的起源。它们每一个都表示一旦形成就能自我存在的一种基本状态;这些值与热的物理性质有一种自然而必然的联系。
为了确定系数a0 ,a1 ,a2 ,…,b0 ,b1 ,b2 ,…,我们应当运用第234目的方程(Π),我们在前一章的最后一节已经证明了这个方程。
设这个方程中由X所表示的整个横坐标是2πr,设x是可变横坐标,f(x)表示环的初始状态,则积分应当从x=0取到x=2πr;这样我们有
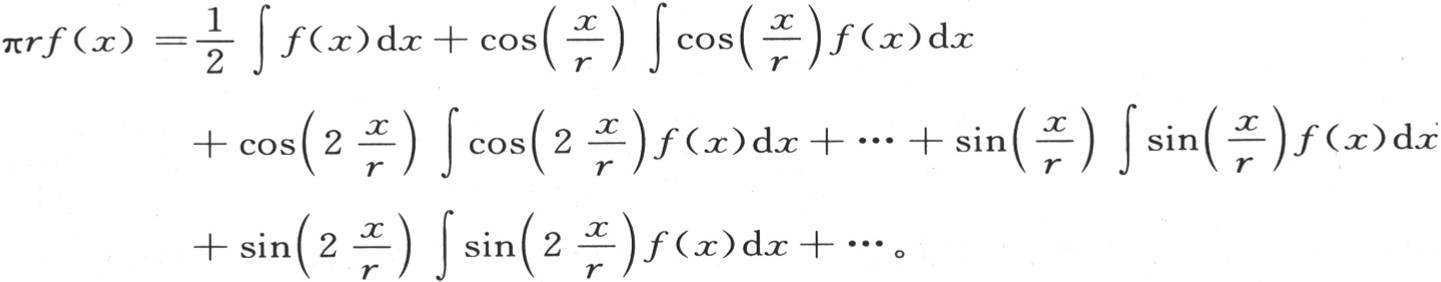
如此,在已知a0 ,a1 ,a2 ,…;b0 ,b1 ,b2 ,…的值时,如果把它们代入方程,则我们有包含这个问题全解的下述方程:

所有的积分都应当从x=0取到x=2πr。
用以形成v值的第一项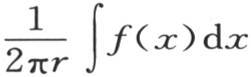 显然是平均初始温度,即,如果所有初始温度处处都一样分布,那么每一点都有这种温度。
显然是平均初始温度,即,如果所有初始温度处处都一样分布,那么每一点都有这种温度。
242 无论给定的函数f(x)的形式如何,前面的方程(E)都可以应用。我们考虑两种特殊情况,即:第一,当环因热源的作用已经上升到它的永恒温度时突然撤掉热源所发生的情况;第二,当半环处处等加热后再突然与初始温度处处为0的另外半个环联结起来时所发生的情况。
我们在前面已经看到,环的永恒温度由方程v=aαx +bα-x 表示;量α的值是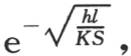 此处l是生成截面的周长,S是这个截面的面积。 【2】
此处l是生成截面的周长,S是这个截面的面积。 【2】
如果假定有一个热源并且热源唯一,那么在与热源所占据的那一点相对的点上,方程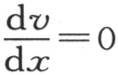 必然成立。因此这一点满足条件aαx -bα-x =0。为使计算方便,让我们把分数
必然成立。因此这一点满足条件aαx -bα-x =0。为使计算方便,让我们把分数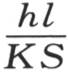 看做是等于一个单位的,并且让我们取环半径为三角函数表的半径,这样我们就有v=aex +be-x ;因此,环的初始温度由方程v=be-π (e-π+x +eπ-x )来表示。
看做是等于一个单位的,并且让我们取环半径为三角函数表的半径,这样我们就有v=aex +be-x ;因此,环的初始温度由方程v=be-π (e-π+x +eπ-x )来表示。
剩下的只是应用一般方程(E),用M表示平均初始温度(第241目),我们有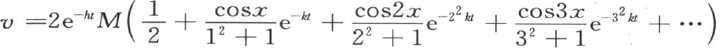 。 【3】
。 【3】
这个方程表示一个固体环在某一点加热并且升至驻温后,撤除热源,让它在空气中冷却时的变化状态。
243 为了给出一般方程(E)的第二种应用,我们假定初始热是这样分布的:它使包含在x=0到x=π之间的半环处处温度都等于1,另一半的温度为0。所要求的是确定经过时间t之后的环的状态。
在这种情况下,表示初始状态的函数f(x)是这样的:只要变量包含在0到π之间,它的值就是1。由此得到,我们应当假定f(x)=1,并且只在x=0到x=π之间取积分,由假定,这个积分的另一部分为0。我们首先得到下面的方程,这个方程给出所提出的函数的展开式,从x=0到x=π,它的值是1,从x=π到x=2π,它的值是0: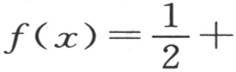

现在如果我们在这个一般方程中用我们刚才所得到的值代替常系数,那么我们有方程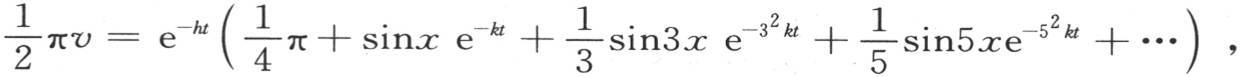 它表示环的每一点的温度变化所服从的规律,并且指明它在任一给定时间之后的状态:我们只限于前面两个应用,并只对由方程(E)所表示的通解增加某些观察结果。
它表示环的每一点的温度变化所服从的规律,并且指明它在任一给定时间之后的状态:我们只限于前面两个应用,并只对由方程(E)所表示的通解增加某些观察结果。
244 第一,如果假定k是无穷的,那么环的状态就表示成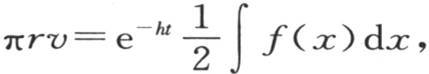 或者,当用M表示平均初始温度时(第241目),v=e-ht M。每一点的温度突然变得等于平均温度,且所有不同点都总是保持相等的温度,这是我们承认无穷传导率(infinite con ducibility)的假定的一个必然结果。
或者,当用M表示平均初始温度时(第241目),v=e-ht M。每一点的温度突然变得等于平均温度,且所有不同点都总是保持相等的温度,这是我们承认无穷传导率(infinite con ducibility)的假定的一个必然结果。
第二,如果环半径是无穷小的,我们将有同样的结果。
第三,为了得到在时间t之后的环的平均温度,我们应当从x=0到x=2πr取积分∫f(x)dx,并且除以2πr。在这些界限内u值的不同部分积分,然后假定x=2πr,我们会发现除第一项外,这些积分的总值为0;因此,在时间t之后,平均温度值是量e-ht M。所以,环的平均温度以同样的方式下降,仿佛它的热导率是无穷的一样;在这个固体中由热传导所引起的变化对这一温度没有影响。
在我们刚才所考虑的三种情况中,温度与分数e-h 的幂成正比地降低,或者同样地,与一条对数曲线的纵坐标成正比地降低,横坐标等于所历经的时间。这个规律人们早已知道,但必须注意,除非物体体积很小,否则它一般不成立。前面的分析告诉我们,如果环的直径不是很小的,那么一个确定点的冷却在开始时就不服从那条规律;平均温度则不同,它总是与一条对数曲线的纵坐标成正比地降低。此处应当记住,我们假定环的生成截面的面积非常小,以至于同一截面的不同点在温度上没有明显的差别。
第四,如果我们要确定在一给定时间内经过环的一个已知部分的表面所逃逸的热量,那么我们应当应用积分hl∫dt∫vdx,应当在相对于这一时间的区间内取积分。例如,如果我们取x的区间为0到2πr,t的区间为0到∞;即,如果我们希望确定在冷却的全过程中从整个表面所逃逸的全部热量,那么我们应当在积分之后得到等于全部初始热量的一个结果,或是2πrMCDS,M是平均初始温度。
第五,如果我们希望确定在一给定时间内经过环的一个确定截面流过多少热量,那么我们应当运用积分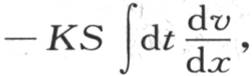 用
用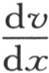 表示在所讨论的那一点上所取的那个函数的值。
表示在所讨论的那一点上所取的那个函数的值。
245 热在这个环中势必随我们应当注意到的一条规律分布。历经时间增加得愈多,在方程(E)中构成v值的那些项相对于它们前面的项就愈小。因此,存在某个t值,对于这个值,热运动开始明显地由方程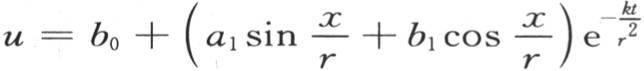 来表示。
来表示。
在冷却的无穷时间内,同一关系仍然存在,在这个状态下,如果我们选择环上位于同一直径两端的两个点,用x1 和x2 表示它们各自与原点的距离,用v1 和v2 表示它们在时间t时的相应温度;那么我们有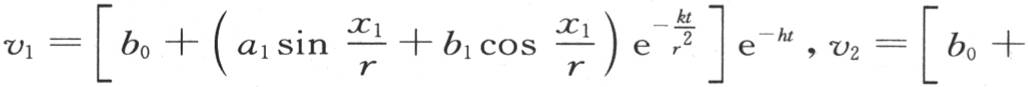
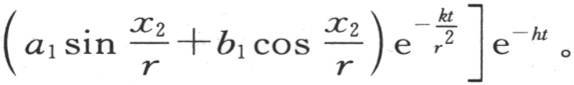
两段弧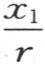 和
和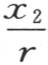 的正弦只是符号不同;量
的正弦只是符号不同;量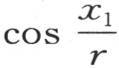 和
和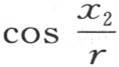 同样如此;这样,
同样如此;这样,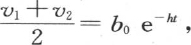 因此,相对的两点的温度的半和(half-sum)给出一个量b0 e-ht ,如果我们选择位于另一个直径两端的两点,则这个量仍然如此。正如我们在上面已经看到的,量b0 e-ht 是时间t后的平均温度值。因此,任意两个相对点的温度的半和都不断随环的平均温度而降低,并在冷却持续一段时间后表示它的值而无明显误差。让我们更详细地考查由方程
因此,相对的两点的温度的半和(half-sum)给出一个量b0 e-ht ,如果我们选择位于另一个直径两端的两点,则这个量仍然如此。正如我们在上面已经看到的,量b0 e-ht 是时间t后的平均温度值。因此,任意两个相对点的温度的半和都不断随环的平均温度而降低,并在冷却持续一段时间后表示它的值而无明显误差。让我们更详细地考查由方程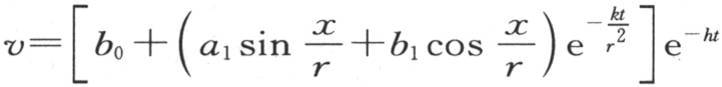 所表示的终极状态所存在的情况。
所表示的终极状态所存在的情况。
如果我们首先考查环上使我们有条件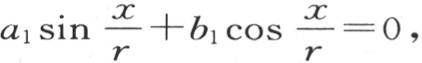 或者是
或者是 的点,那么我们会看到,这一点在每一时刻的温度都是环的平均温度:在直径上相对的点亦如此;因为后一个点的横坐标也满足上面的方程
的点,那么我们会看到,这一点在每一时刻的温度都是环的平均温度:在直径上相对的点亦如此;因为后一个点的横坐标也满足上面的方程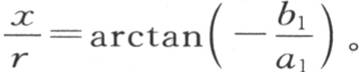
让我们用X表示这两点的第一个所处的距离,我们有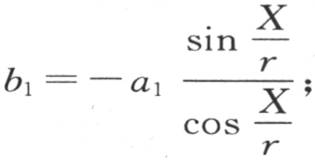 代入b1 的这个值,我们有
代入b1 的这个值,我们有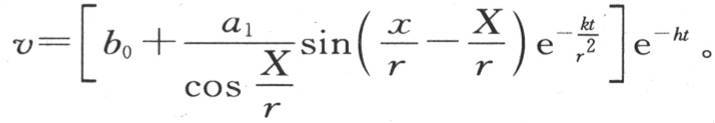
如果我们现在把对应于横坐标X的点作为横轴的原点,用u表示新的横坐标x-X,那么我们有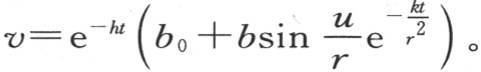
在横坐标u为0的原点,以及在相对的点上,温度v总等于平均温度;这两个点把环圆周分成状态相似符号相反的两个部分;其中一部分的每一点都有超过平均温度的温度,且那个超出量与离原点距离的正弦成正比。另一部分的每一点都有比平均温度低的温度,并且这个亏损量与相对点的超出量相等。热的这种对称分布在冷却的整个期间都存在,在受热的一半的两端,沿冷的一半的方向形成两股热流,它们的作用是不断使环的每一半都趋于平均温度。
246 现在我们可以注意到,在给出v值的一般方程中,每一项都有
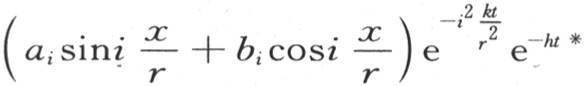
的形式。因此,相对于每一项,我们都能导出与前面类似的结论。事实上,用X表示使系数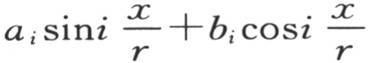 等于0的距离,我们有方程
等于0的距离,我们有方程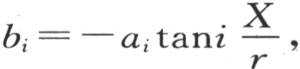 作为这个系数的值,这个代换给出
作为这个系数的值,这个代换给出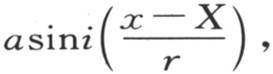 a是一个常数。由此得到,当取其横坐标是X的点为坐标系原点,用u表示新的横坐标x-X时,作为v值的这一部分的替换式,我们有函数
a是一个常数。由此得到,当取其横坐标是X的点为坐标系原点,用u表示新的横坐标x-X时,作为v值的这一部分的替换式,我们有函数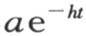
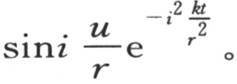
* 在英译本中,此式没有e-ht 这个因子,但法文《文集》本中有。虽然这里要讨论的内容是此式括号内的内容,与这些因子无关,但考虑到这里所说的“每一项”的完整性,我们还是加上这个因子。——汉译者
如果v值的这个特殊部分是单独存在的,结果使所有其他部分的系数都为0,那么环的状态就由函数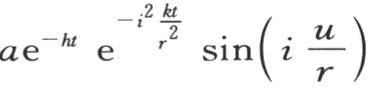 来表示,并且每一点的温度就与这一点与原点距离的i倍的正弦成正比。这个状态与我们曾描述过的状态类似:它与它的不同之处在于,总是具有与环的平均温度相等的相同温度的点的数目不只是2,而是一般等于2i。每一个这样的点和结点(node)都把环的两个毗邻的部分分开,这两部分处于相似的状态中,只是符号相反。因此,我们发现圆周被分成几个相等的部分,它们的状态交替地为正和负。热流量可能在这些结点上是最大的,并且指向状态为负的部分,在与两个相邻结点等距的那些点上,它为0。在这些温度之间所存在的比率在冷却的整个阶段一直保持,这些温度一起以与分数
来表示,并且每一点的温度就与这一点与原点距离的i倍的正弦成正比。这个状态与我们曾描述过的状态类似:它与它的不同之处在于,总是具有与环的平均温度相等的相同温度的点的数目不只是2,而是一般等于2i。每一个这样的点和结点(node)都把环的两个毗邻的部分分开,这两部分处于相似的状态中,只是符号相反。因此,我们发现圆周被分成几个相等的部分,它们的状态交替地为正和负。热流量可能在这些结点上是最大的,并且指向状态为负的部分,在与两个相邻结点等距的那些点上,它为0。在这些温度之间所存在的比率在冷却的整个阶段一直保持,这些温度一起以与分数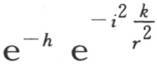 成正比的速度迅速地变化。
成正比的速度迅速地变化。
如果我们逐次对i给定值0,1,2,3,…,那么我们就可以确定热在一个固体环中传导时所能呈现的所有正常状态和基本状态。当某个这样的简单形式一旦形成时,它就自我保持,并且在这些温度之间所存在的这些比是不变的;但是,无论这些初始比如何,并且无论环以何种方式受热,这个热运动都可以分解成与我们刚才所描述的运动相似的几个简单运动,这些简单运动都一起完成而相互之间无任何干扰。在这些状态的每一个中,温度都与到一个固定点的距离的某个倍数的正弦成正比。在同一时刻对一个单点所取的所有这些部分温度的和,就是那一点的实际温度。于是构成这个和的某些部分的温降要比其他部分快得多。由此得到,与i的不同值对应的,以及其叠加确定总的热运动的环的这些基本状态,在某种意义上一个接一个地消失。它们很快就对温度值不产生任何明显的影响,在它们之中只剩下第一个,其中i是最小的。如此,我们就形成了关于热据以在环中分布,且据以在其表面耗散的规律的精确思想。环的这种状态变得愈来愈对称,它很快变得与它所具有的一个自然倾向所趋于的状态混淆不清,这个状态在于不同的点的温度逐渐变得与计量到原点距离的弧的同一倍数的正弦成正比。初始分布在这些结果中不发生任何变化。
第二节 分离物体之间的热传导
247 我们现在不得不注意前面的分析与应当用来确定分离物体间的热传导规律的分析的一致性;因此,我们将得到环的热运动问题的第二个解。这两个结果的比较将指明在对连续物体的热传导方程积分时我们所遵循的方法的真正基础。首先,我们将考查两个相同物体之间的热传导这种极其简单的情况。
假定体积相等、物质相同的两个立方体m和n受热不等;设它们各自的温度是a和b,并设它们具有无穷热导率。如果我们把这两个物体放得相互挨着,那么每一个的温度就会突然变得与平均温度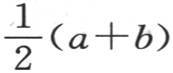 相等。假定这两块物体被一个非常小的区间分开,我们从第一块物质上分出一个无穷薄的薄层,使得这个薄层与第二块物质连起来,并在接触之后又立即回到第一块物质上。因此,当在同一无穷小区间上连续地交替移动时,这个交换薄层就把较热物体的热传到不怎么热的物体上去;问题是要确定若它们所包含的热在其表面无任何损失时,在一给定时间之后,每个物体的热将是怎样的。我们并不假定连续固体中的热传导以某种类似于我们刚才所描述的方式完成:我们只希望用分析来确定这样一种假定的结果。
相等。假定这两块物体被一个非常小的区间分开,我们从第一块物质上分出一个无穷薄的薄层,使得这个薄层与第二块物质连起来,并在接触之后又立即回到第一块物质上。因此,当在同一无穷小区间上连续地交替移动时,这个交换薄层就把较热物体的热传到不怎么热的物体上去;问题是要确定若它们所包含的热在其表面无任何损失时,在一给定时间之后,每个物体的热将是怎样的。我们并不假定连续固体中的热传导以某种类似于我们刚才所描述的方式完成:我们只希望用分析来确定这样一种假定的结果。
由于这两块物质都具有无穷热导率,所以包含在一个无穷薄的薄层中的热量就会骤然增加到与之接触的那块物质的热量中去;并且产生一种公共温度,这一温度等于热量的和除以物质的和的商。设ω是从较热物体上分离出来的无穷薄的薄层的物质,它的温度是a;设α和β是与时间t对应的变化温度,它的初始值是a和b。在薄层ω从物体m上分出来,m变成m-ω时,ω有和这块物质一样的温度α,当它一接触受温度β作用的第二块物体时,它就与这块物体一起同时呈现出等于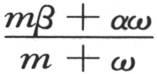 的温度。薄层ω保持后一温度又回到其物质为m-ω,温度为α的第一块物体上。这样我们得到第二次接触之后的温度
的温度。薄层ω保持后一温度又回到其物质为m-ω,温度为α的第一块物体上。这样我们得到第二次接触之后的温度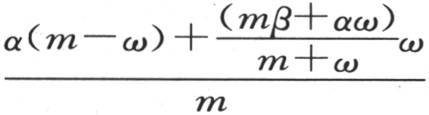 或者是
或者是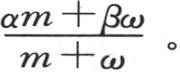
在时间间隔dt之后,变化温度α和β变成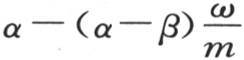 和
和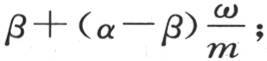 这两个值通过去掉ω的高次幂而得到。因此我们有
这两个值通过去掉ω的高次幂而得到。因此我们有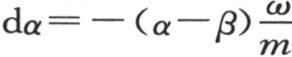 和
和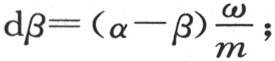 具有初始温度β的物体在某一时刻内得到等于mdβ或者是(α-β)ω的热量,它同时也是第一个物体所失去的热量。由此我们看到,在所有其他条件相同时,在一时刻内从受热多的物体传到受热少的物体中去的热量与这两个物体的实际温差成正比。在时间被分成几个相等的区间后,无穷小量ω可以用kdt来代替,k是物质的单位的数目,它的总和所包含的ω的倍数与一个单位的时间所包含的dt的倍数一样多,因此我们有
具有初始温度β的物体在某一时刻内得到等于mdβ或者是(α-β)ω的热量,它同时也是第一个物体所失去的热量。由此我们看到,在所有其他条件相同时,在一时刻内从受热多的物体传到受热少的物体中去的热量与这两个物体的实际温差成正比。在时间被分成几个相等的区间后,无穷小量ω可以用kdt来代替,k是物质的单位的数目,它的总和所包含的ω的倍数与一个单位的时间所包含的dt的倍数一样多,因此我们有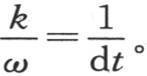 由此我们得到方程
由此我们得到方程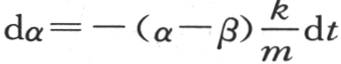 和
和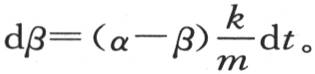
248 可以说,ω的作用,在于从这两个物体的一个中吸热,然后把这些热带给另一个物体,所以,如果我们对ω的体积赋予更大的值,那么,这种传导将更快;为了表示这个条件,我们有必要以同样的比率增加进入这两个方程的量k。我们也可以保持ω的值不变而假定这个薄层在给定时间内完成更多次数的移动,这亦由更大的k值来表明。因此,这个系数在某种意义上表示传导速度,或者是表示热从一个物体传到另一物体的能力,即它们的相互热导率。
249 把前面两个方程相加,我们有dα+dβ=0,如果我们用一个方程减去另一个方程,则我们有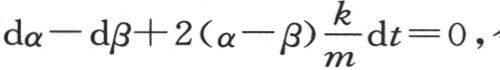 令α-β=y,
令α-β=y,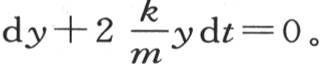 取积分,并以初始值为a-b这个条件来确定常数,则我们有
取积分,并以初始值为a-b这个条件来确定常数,则我们有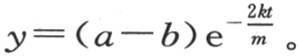 温差y随一条对数曲线,或者是随分数
温差y随一条对数曲线,或者是随分数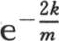 的逐次幂而减少。作为α和β的值,我们有
的逐次幂而减少。作为α和β的值,我们有
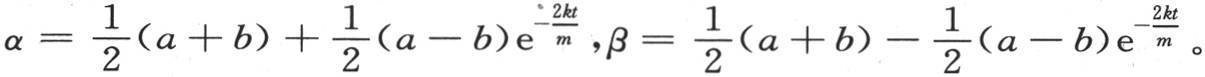
250 在前面的情况下,我们假定使传导得以完成的无穷小物质ω总是单位物质的同一部分,或者同样地,我们假定计量相互热导率的系数k是一个常量。为使所讨论的研究更一般化,我们应当把常数k看做是两实际温度α和β的函数,这样我们就有两个方程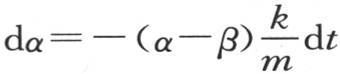 和
和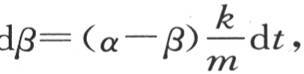 在这两个方程中,k等于α和β的一个函数,我们用φ(α,β)来表示它。当α和β极接近于它们的终极温度时,容易确定变化温度α和β所遵循的规律。设y是等于α和终极值
在这两个方程中,k等于α和β的一个函数,我们用φ(α,β)来表示它。当α和β极接近于它们的终极温度时,容易确定变化温度α和β所遵循的规律。设y是等于α和终极值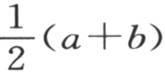 或者是c之差的一个新未知数。设z是等于差c-β的第二个未知数。我们用它们的值c-y和c-z代替α和β;由于问题是求y和z的值,所以当我们假定它们很小时,在这个代换结果中我们只需保留y和z的一次幂就行了。因此我们得到两个方程
或者是c之差的一个新未知数。设z是等于差c-β的第二个未知数。我们用它们的值c-y和c-z代替α和β;由于问题是求y和z的值,所以当我们假定它们很小时,在这个代换结果中我们只需保留y和z的一次幂就行了。因此我们得到两个方程
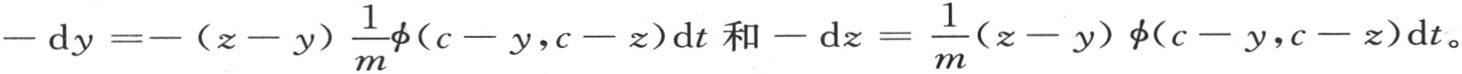
展开在符号φ下的那些量、并略去y和z的高次幂,我们得出
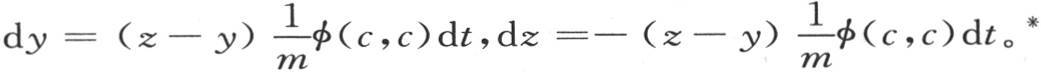
由于量φ是常数,我们得到,前面这两个方程对差z-y给出与我们在上面对α-β的值所得到的一个类似的结果。
* 在英译本中,这两式中的因子φ(c,c)是φ,这里是根据法文《文集》本改正的。另外,英译本在这里错了两个标点符号,但使叙述的意思大为改变,有兴趣的读者应参考法文《文集》。——汉译者
我们由此得出结论,如果在开始时被假定为常数的系数k由变化温度的任一函数表示,那么这些温度在无穷时间内所经历的最后变化仍然服从同样的规律,就像这种相互热导率是常数一样。这个问题实际上是要确定在实际温度不同的无数相同物体中的热传导的规律。
251 假定每个等于m的n个棱柱形物体被安排在同一直线上,并且受不同温度a,b,c,d,…的作用;假定除最后一个物体外,从这不同物体的每一个上都分出一个无穷薄的薄层,它们每一个的质量为ω,同时这些薄层依次从第一个物体向第二个物体,从第二个物体向第三个物体,从第三个物体向第四个物体等转移,接触之后,这些薄层又立即回到它们原来由之分出的物体上;在这双重运动所发生的次数和所存在的无穷小时刻dt的次数一样多时,我们要求温度变化所服从的规律。
设a,β,γ,δ,…,ω是对应于同一时间t,继初始值a,b,c,d,…之后的变化值。当这些薄层ω从前n-1个物体上分出并且与相邻物体接触时,不难看到温度变为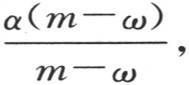
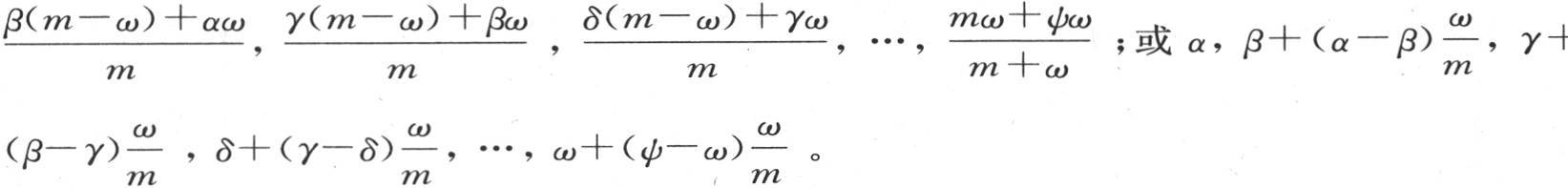
当这些薄层ω回到它们原来的位置时,我们根据同一规则得到新的温度,这些温度在于用热量的和除以这些物质的和,并且,在时刻dt之后,作为α,β,γ,δ,…的值,我们有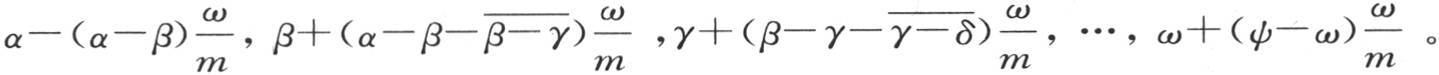
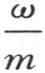 的系数是序列α,β,γ,…ψ,ω中所取的两个相邻差的差。对于
的系数是序列α,β,γ,…ψ,ω中所取的两个相邻差的差。对于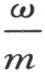 的第一个和最后一个系数,我们也可以把它们看做是二阶差。这只需假定项α的前面有一个等于α的项,项ω的后面有一个等于ω的项就够了。因此,和前面一样,一旦用kdt代替ω,我们就有下述方程:
的第一个和最后一个系数,我们也可以把它们看做是二阶差。这只需假定项α的前面有一个等于α的项,项ω的后面有一个等于ω的项就够了。因此,和前面一样,一旦用kdt代替ω,我们就有下述方程:
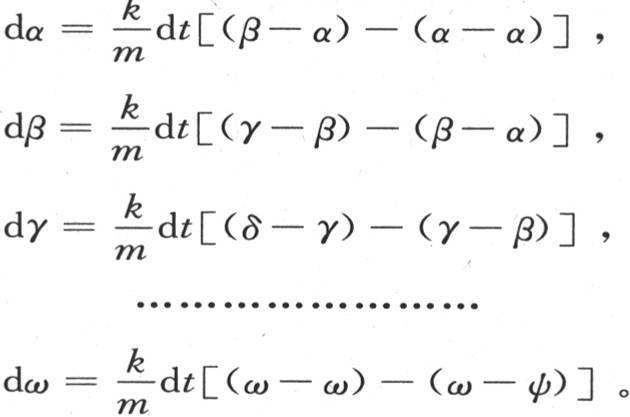
252 为了对这些方程积分,根据已知的方法,我们假定α=a1 eht ,β=a2 eht ,γ=a3 eht ,…,ω=an eht ;h,a1 ,a2 ,a3 ,…是必须确定的常数。作代换后,我们有下述方程:
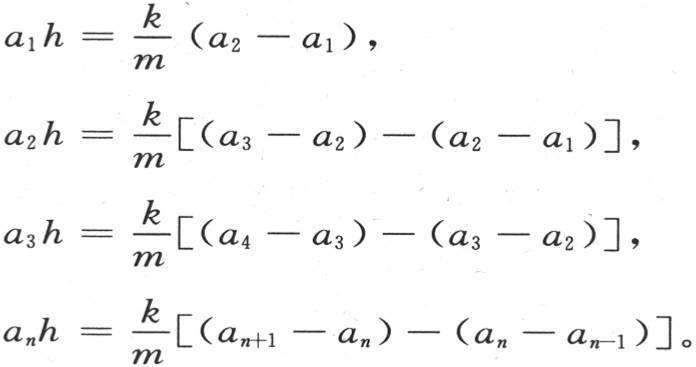
如果我们把a1 看做是已知量,那么我们得到用a1 和h所表示的a2 ,然后是用a2 和h表示的a3 ,所有其他未知量a4 ,a5 ,…亦如此。第一个和最后一个方程可以写成下面的形式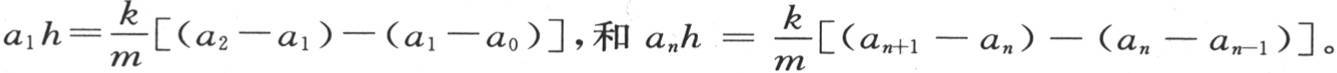
保持两个条件a0 =a1 和an =an+1 不变,则a2 的值包含h的一次幂,a3 的值包含h的二次幂,如此直到an+1 ,它包含h的n次幂,如此,当an+1 变得等于an 时,为确定h,我们有一个n次方程,a1 仍然待定。
由此得出,我们将得到n个h值,并且,根据线性方程的性质,α的一般值由n个项组成,量α,β,γ,…由如
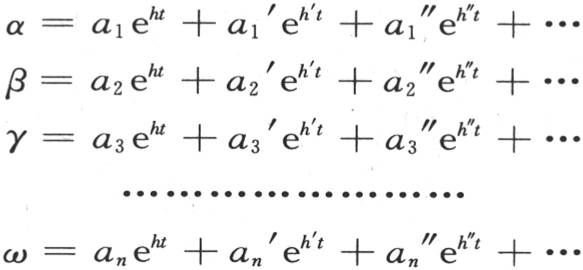
这样的一些方程来确定。
h,h′,h″,…的值有n个,并且等于h的n次代数方程的n个根,正如我们将要看到的,它的所有根都是实根。
第一个方程的系数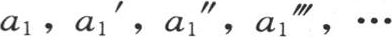 是任意的;至于下面各行的系数,它们由类似于前面那些方程的n个方程组来确定,现在的问题是要建立这些方程。
是任意的;至于下面各行的系数,它们由类似于前面那些方程的n个方程组来确定,现在的问题是要建立这些方程。
253 用字母q代替 我们有下述方程
我们有下述方程
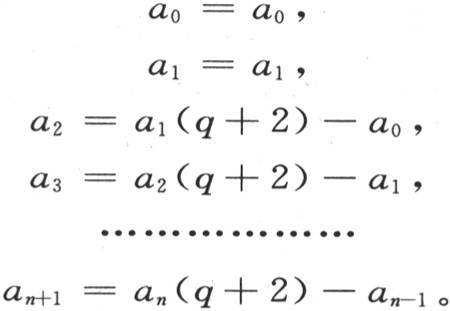
我们看到,这些量属于一个循环级数,这个递推级数的关系系数(scale of relation)由两个项(q+2)和-1组成。因此,适当确定量A,B和u,则我们可以用方程am =Asinmu+Bsin(m-1)u表示通项am 。我们首先由假定m=0,然后假定m等于1,来求A和B,这个假定给出a0 =a1 -Bsinu,a1 =Asinu,因此,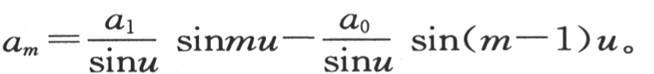
然后在一般方程am =am-1 (q+2)-am-2 中代入am ,am-1 ,am-2 ,…的值,则我们得到sinmu=(q+2)sin(m-1)u-sin(m-2)u,比较这个方程和下面的方程sinmu=2cosusin(m-1)u-sin(m-2)u, 【4】 它表示以算术级数增加的弧的正弦的一个已知性质,则我们得到q+2=2cosu,或q=-2versinu; 【5】 剩下的只是确定弧u的值。
由于am 的值是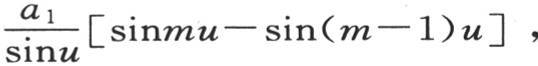 所以,为满足条件an+1 =an ,我们肯定有方程sin(n+1)u-sinnu=sinnu-sin(n-1)u,因此我们推出sinnu=0,或
所以,为满足条件an+1 =an ,我们肯定有方程sin(n+1)u-sinnu=sinnu-sin(n-1)u,因此我们推出sinnu=0,或 π是半圆周,i是任一整数,如0,1,2,3,4,…(n-1);由此我们得出q或
π是半圆周,i是任一整数,如0,1,2,3,4,…(n-1);由此我们得出q或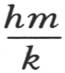 的n个值。因此,给出
的n个值。因此,给出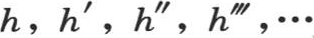 的值的含h的方程的所有根都是负实数根,它们由方程
的值的含h的方程的所有根都是负实数根,它们由方程
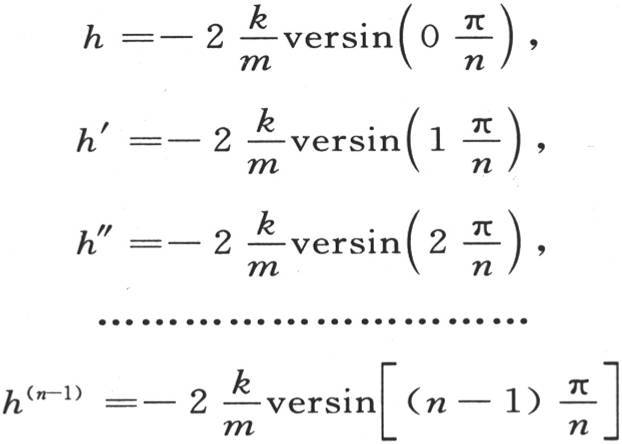
所提供。
这样,假定我们已经把半圆周π分成n等分,为形成u,我们取i个这样的部分,i小于n,取a1 为任一量,并使
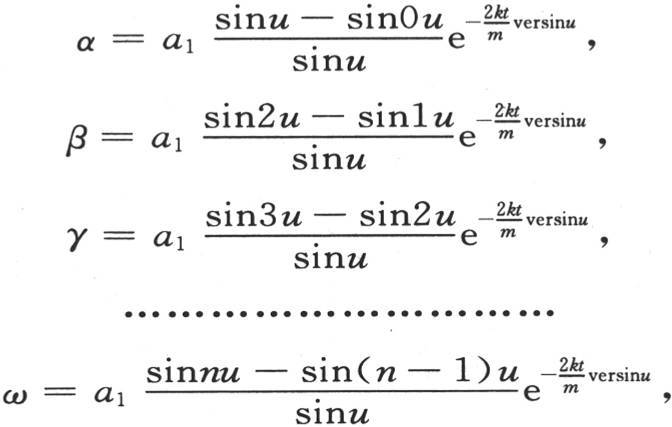
则我们满足这些微分方程。
由于存在我们可能为u所取的n个不同的弧,即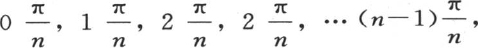 所以α,β,γ,…也有n组特殊值,这些变量的一般值是这些特殊值的和。
所以α,β,γ,…也有n组特殊值,这些变量的一般值是这些特殊值的和。
254 我们首先看到,如果弧u为0,则在α,β,γ,…的值中乘以a的那些量就都变得等于1,因为当弧u变为0时,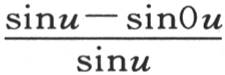 取值为1;在下面的方程中所能看到的那些量亦如此。由此我们得出,常数项应当进入α,β,γ,…,ω的一般值。
取值为1;在下面的方程中所能看到的那些量亦如此。由此我们得出,常数项应当进入α,β,γ,…,ω的一般值。
此外,把对应于α,β,γ,…的所有特殊值相加,则我们有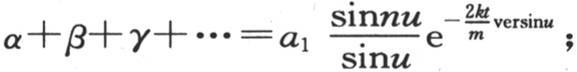 这是只要弧u不为0,则右边就化为0的方程。但是在u为0的情况下,我们会看到n是
这是只要弧u不为0,则右边就化为0的方程。但是在u为0的情况下,我们会看到n是 的值。这样我们一般有α+β+γ+…=na1 ;现在,由于这些变量的值是a,b,c,…,所以我们必然有na1 =a+b+c+…;由此得到,应当进入α,β,γ,…,ω的每个一般值的常数项是
的值。这样我们一般有α+β+γ+…=na1 ;现在,由于这些变量的值是a,b,c,…,所以我们必然有na1 =a+b+c+…;由此得到,应当进入α,β,γ,…,ω的每个一般值的常数项是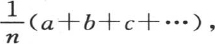 即是所有初始温度的均值。
即是所有初始温度的均值。
至于α,β,γ,…,ω的一般值,它们由下述方程表示:
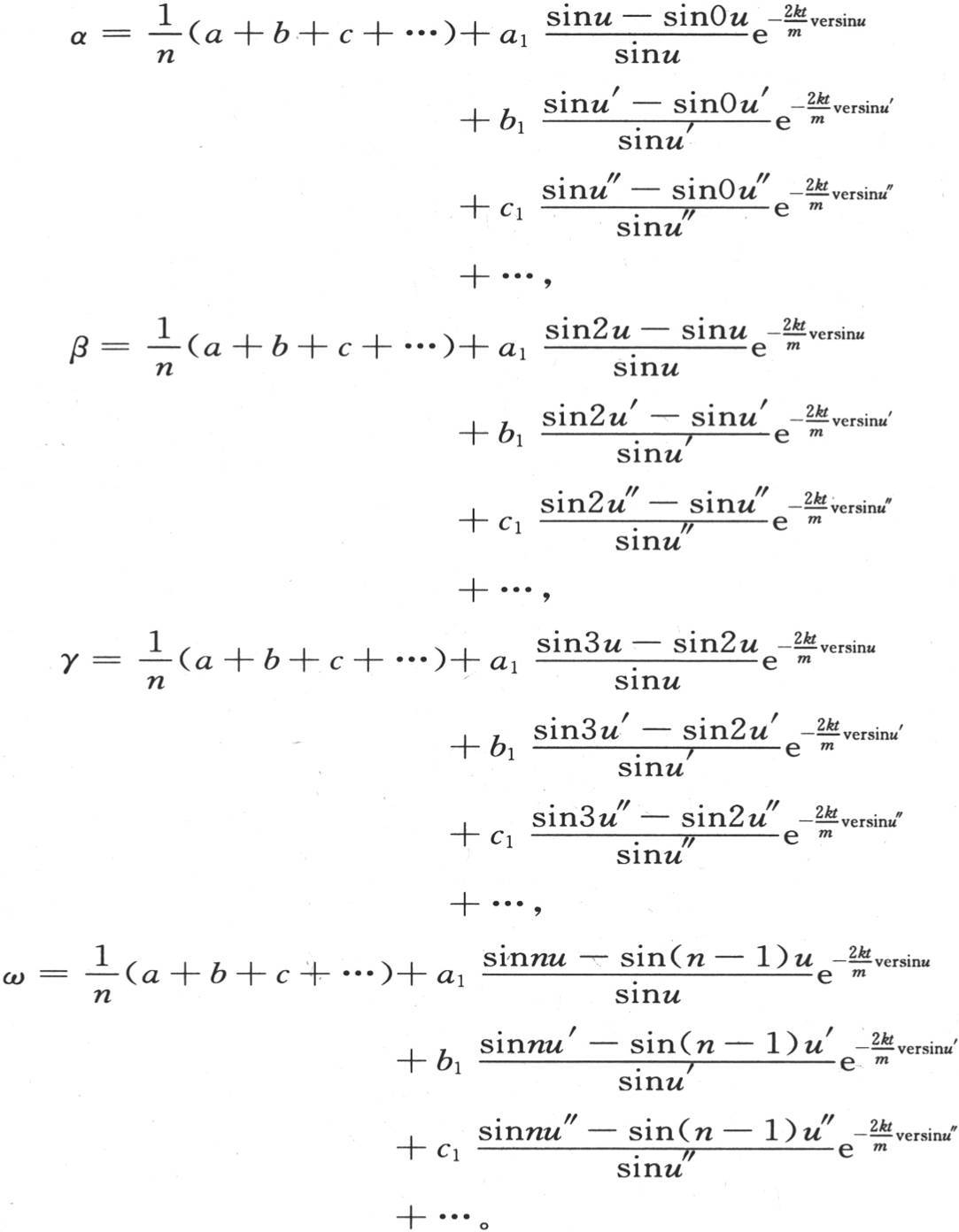
此处u,u′,u″,…表示 的不同倍数。 【6】
的不同倍数。 【6】
255 为了确定常数a,b,c,d,…,我们应当考虑系统的初始状态。事实上,当时间为0时,α,β,γ,…的值应当等于a,b,c,…;这样,为了确定这n个常数,我们有n个类似的方程。量sinu-sin0u,sin2u-sinu,sin3u-sin2u,…,sinnu-sin(n-1)u,可以∆sin0u,∆sinu,∆sin2u,∆sin3u,…,∆sin(n-1)u这样的方式标明;如果初始均温用C表示,那么适合于确定这些常数的方程是
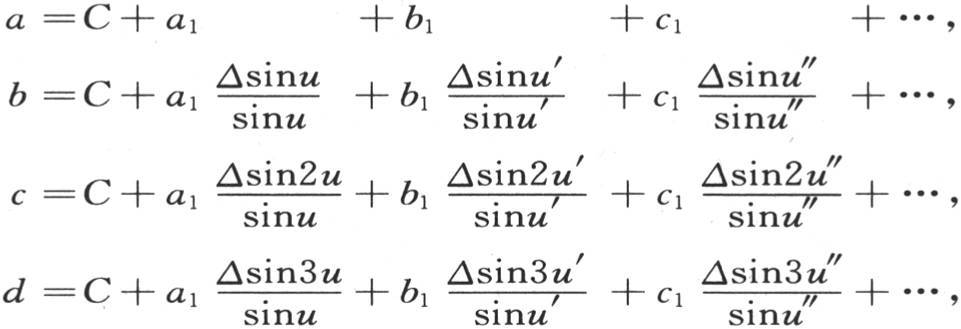
由于量a1 ,b1 ,c1 ,d1 和C由这些方程来确定,所以我们完全知道变量α,β,γ,δ,…,ω的值。
一般地,我们可以在这些方程中实施未知数的消元,并确定量a,b,c,d,…的值,即使方程的数目无穷也亦可如此;在下面几目中,我们将应用这个消元过程。
256 一旦考查给出变量α,β,γ,…,ω的一般值的这些方程,我们就会看到,随着时间的增加,每个变量的值的逐项极不相等地变小;因为,由于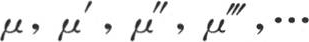 的值是
的值是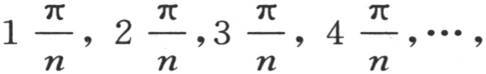 所以指数
所以指数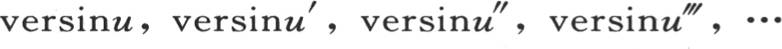 变得愈来愈大。如果我们假定时间t是无穷的,那么只有每个值的第一项存在,这些物体的每一个的温度就变得等于平均温度
变得愈来愈大。如果我们假定时间t是无穷的,那么只有每个值的第一项存在,这些物体的每一个的温度就变得等于平均温度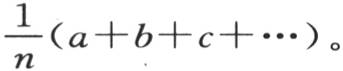 由于时间t连续增加,所以某个变量的值的每一项就与一个分数的逐次幂成正比地减少,对于第二项,这个分数是
由于时间t连续增加,所以某个变量的值的每一项就与一个分数的逐次幂成正比地减少,对于第二项,这个分数是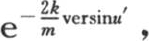 对于第三项,是
对于第三项,是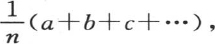 以此类推。由于这些分数中最大的一个是对应于最小u值的分数,所以我们得到,为了确定温度的终极变化所服从的规律,我们只需考虑前两项就够了;因为随着时间的增加,所有其他项都变得无比地小。因此,温度α,β,γ,…的终极变化由下述方程表示:
以此类推。由于这些分数中最大的一个是对应于最小u值的分数,所以我们得到,为了确定温度的终极变化所服从的规律,我们只需考虑前两项就够了;因为随着时间的增加,所有其他项都变得无比地小。因此,温度α,β,γ,…的终极变化由下述方程表示:
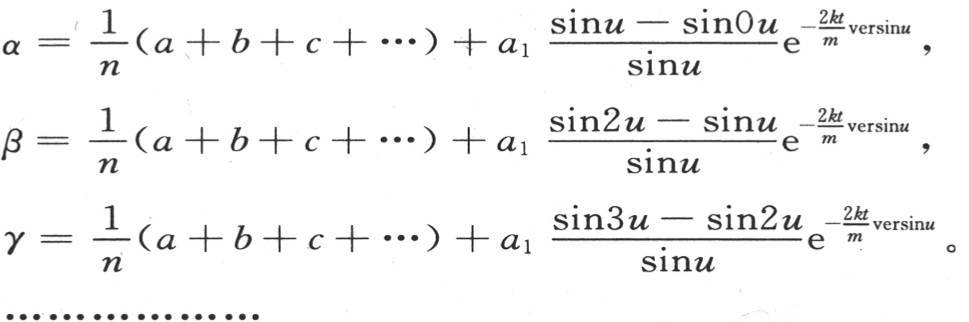
257 如果我们把半圆周分成n等分,并且,在画出这些正弦后,取两个相邻正弦的差,那么,这n个差就与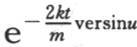 的系数成正比,或者,与α,β,γ,…,ω的值的第二项成正比。由于这个原因,后面这些α,β,γ,…,ω的值就使得终极温度和平均初始温度
的系数成正比,或者,与α,β,γ,…,ω的值的第二项成正比。由于这个原因,后面这些α,β,γ,…,ω的值就使得终极温度和平均初始温度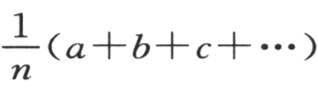 的差总与相邻正弦的差成正比。这些物体开始无论以什么样的方式加热,热分布最后都根据一条不变的规律而完成。如果我们在它们与平均温度相差无几时测量过最后阶段的温度,那么我们就会看到,任一物体的温度和均温之差都随同一分数的逐次冪而不断减少;比较它们自己之间的不同物体在同一时刻所取的温度,我们也会看到,当半圆周被分成n等分时,实际温度和平均温度之差与相邻正弦的差成正比。
的差总与相邻正弦的差成正比。这些物体开始无论以什么样的方式加热,热分布最后都根据一条不变的规律而完成。如果我们在它们与平均温度相差无几时测量过最后阶段的温度,那么我们就会看到,任一物体的温度和均温之差都随同一分数的逐次冪而不断减少;比较它们自己之间的不同物体在同一时刻所取的温度,我们也会看到,当半圆周被分成n等分时,实际温度和平均温度之差与相邻正弦的差成正比。
258 如果我们假定相互传热的这些物体数目无穷,那么,对于弧u,我们得到一个无穷小的值;因此,在这个圆上所取的相邻正弦的差与相应弧的余弦成正比,因为当弧u无穷小时,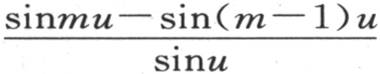 等于cosmu。在这种情况下,在同一时刻所取的温度不同于它们都必须趋于的均温的那些温度的量,与对应于被分成无穷多等分的圆周上不同点的余弦成正比。如果把这些导热物体相互等距地放在半圆周π的周长上,那么任一物体所位于其端点的弧的余弦,就是那个物体的温度之所以仍不同于均温的那个量的大小。因此,处在所有物体中间的那个物体是最快达到均温的物体。处在中间的某一边的物体都有一过高的温度,随着它们离中间位置愈远,它们超出均温也愈多;处在另一边的物体的温度都低于均温,它们与均温的差和相反的一边与均温的差一样大,只是意义相反。最后,这些差不管是正还是负,它们都同时与同一分数的逐次幂成正比地减少;因此,它们在同一时刻仍然由同一半圆周的余弦值来表示。除个别情况外,一般地,这就是终极温度所服从的规律。系统的初始状态不改变这些结果。我们现在开始处理和前面的问题属于同一类型的第三个问题,这个问题的解将给我们提供许多有用的注记。
等于cosmu。在这种情况下,在同一时刻所取的温度不同于它们都必须趋于的均温的那些温度的量,与对应于被分成无穷多等分的圆周上不同点的余弦成正比。如果把这些导热物体相互等距地放在半圆周π的周长上,那么任一物体所位于其端点的弧的余弦,就是那个物体的温度之所以仍不同于均温的那个量的大小。因此,处在所有物体中间的那个物体是最快达到均温的物体。处在中间的某一边的物体都有一过高的温度,随着它们离中间位置愈远,它们超出均温也愈多;处在另一边的物体的温度都低于均温,它们与均温的差和相反的一边与均温的差一样大,只是意义相反。最后,这些差不管是正还是负,它们都同时与同一分数的逐次幂成正比地减少;因此,它们在同一时刻仍然由同一半圆周的余弦值来表示。除个别情况外,一般地,这就是终极温度所服从的规律。系统的初始状态不改变这些结果。我们现在开始处理和前面的问题属于同一类型的第三个问题,这个问题的解将给我们提供许多有用的注记。
259 假定n个相等的棱柱形物体等距地放在一个圆的圆周上。具有理想热导率的所有这些物体都有已知的实际温度,这些温度都彼此不同;它们都不可能让它们所含的任一部分的热从其表面逃逸;从第一个物体上分出一个无穷薄的薄层,把它连接到第二个物体上,第二个物体在第一个物体的右边,同时,从第二个物体上分出同样一个薄层,它从左向右移动,并连接到第三个物体上,其他所有物体亦如此,在同一时刻从它们之上分出一个无穷薄的薄层,并连接到下一个物体上。最后,同样这些薄层后来又立即返回,连接到它们由之分出的那些物体上。
我们假定热通过这种往复运动在这些物体之间传导,这种运动在间隔相等的每一时刻内完成二次;问题是要求出这些温度根据什么规律而变化:即,当这些温度的初始值被给定时,就需要确定在任一给定时间之后每个物体的新的温度。
我们用a1 ,a2 ,a3 ,…ai ,…,an 表示其值任意的初始温度,用α1 ,α2 ,α3 ,…αi ,…,αn 表示历经时间t之后的同一温度值。量α的每一个显然都是时间t和所有初始值a1 ,a2 ,a3 ,…,an 的一个函数:需要确定函数α。
260 我们用ω表示从一个物体移到另一个物体上的这个无穷薄的薄层的物体。我们可以注意到,首先,当这些薄层已经从它们原来为一体的那些物体上分出来,与位于右边的那些物体分别接触时,包含在不同物体中的热量就变成(m-ω)α1 +ωαn ,(m-ω)α2 +ωα1 ,(m-ω)α3 +ωα2 ,…,(m-ω)αn +ωαn-1 ;用物体m除这些热量的每一个,则对于新的温度值,我们有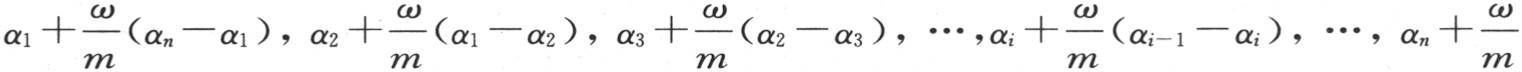
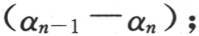 即为了求出在第一次接触后温度的新的状态,我们应当把薄层已由之分出的物体的温度超过它已连接其上的物体的温度的超出量加到它以前所有的温度值上去。由这同一规则,我们得到第二次接触后的温度是
即为了求出在第一次接触后温度的新的状态,我们应当把薄层已由之分出的物体的温度超过它已连接其上的物体的温度的超出量加到它以前所有的温度值上去。由这同一规则,我们得到第二次接触后的温度是
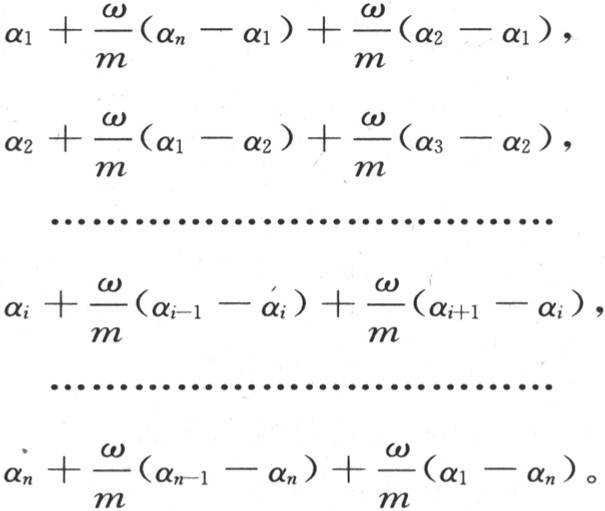
由于时间被分成一些相等的时刻,所以用dt表示这种时刻的间隔,并假定ω包含在k个单位物体中,k与包含在时间单位中的dt的倍数相同,这样我们有ω=kdt。把dα1 ,dα2 ,dα3 ,…,dαi ,…,dαn 叫做温度α1 ,α2 ,…,αi ,…,αn 在时刻dt内所得到的无穷小增量,则我们有下述微分方程:
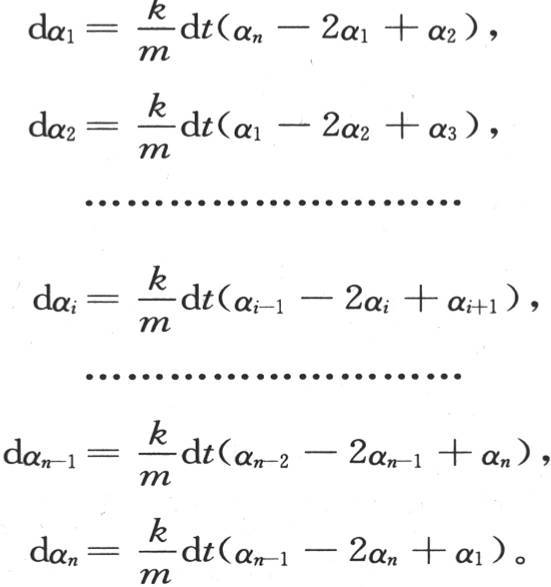
261 为了解这些方程,首先,根据已知的方法,我们假定α1 =b1 eht ,α2 =b2 eht ,…,αi =bi eht ,αn =bn eht 。
量b1 ,b2 ,b3 ,…,bn 是待定常数,指数h也是待定常数。容易看出,如果α1 ,α2 ,…,αn 的值服从下面的条件:
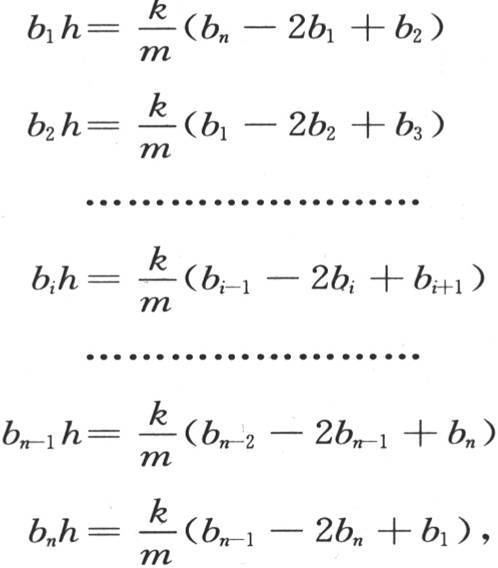
那么它们满足这些方程。
令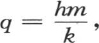 从最后一个方程开始,我们有
从最后一个方程开始,我们有
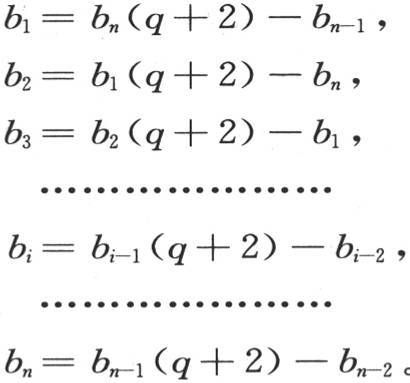
由此得到,不用b1 ,b2 ,b3 ,…bi ,…,bn ,我们可以取把整个圆周2π分成n等分而得到的n个连续的正弦。事实上,用u表示弧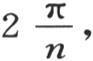 则如所说的,其数目为n的量sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u属于一个递推级数,该级数的关系系数有两项,2cosu和-1:因此,我们总有条件siniu=2cosusin(i-1)u-sin(i-2)u。
则如所说的,其数目为n的量sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u属于一个递推级数,该级数的关系系数有两项,2cosu和-1:因此,我们总有条件siniu=2cosusin(i-1)u-sin(i-2)u。
这样,不用b1 ,b2 ,b3 ,…,bn ,而取量sin0u,sin1u,sin2u,…,sin(n-2)u。则我们有q+2=2cosu,q=-2versinu,或者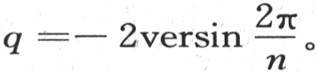
我们已经在前面用q代替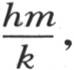 因此h的值是
因此h的值是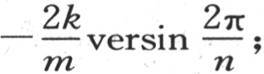 当在方程中代入bi 和h的这些值时,我们有
当在方程中代入bi 和h的这些值时,我们有
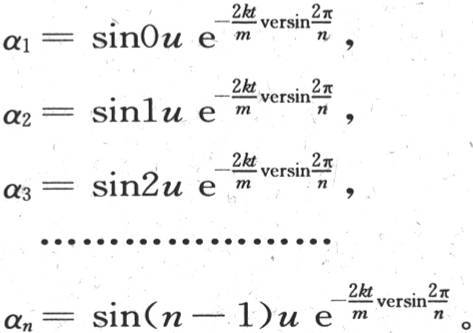
262 上面这些方程只对所提出的问题提供一个非常特殊的解;因为,如果我们假定t=0,那么作为α1 ,α2 ,α3 ,…,αn 的初始值,我们有量sin0u,sin1u,sin2u,…,sin(n-1)u,一般地,这些量不同于已知值α1 ,α2 ,α3 ,…αn :但是上面的解值得注意,因为正如我们即将看到的,它表示属于所有可能情况的事件,并表示温度的终极变化。我们由这个解看到,如果初始温度α1 ,α2 ,α3 ,…,αn 与正弦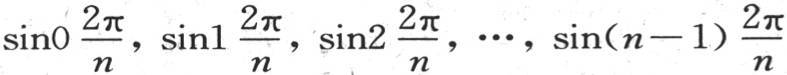 成正比,那么它们将仍然保持与同样这些正弦成正比,我们会有方程
成正比,那么它们将仍然保持与同样这些正弦成正比,我们会有方程
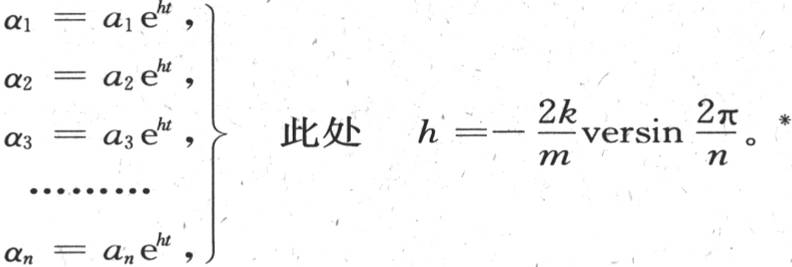
* 英文版中,左边一列等式中的e的指数是负的,即e-ht ,但右边等式是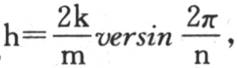 即等式右边是正的。这样处理虽然不错,但与下面的叙述相抵。现依法文《文集》本改正。——汉译者
即等式右边是正的。这样处理虽然不错,但与下面的叙述相抵。现依法文《文集》本改正。——汉译者
由此,如果等距地位于圆周上的这些物体有与落到过第一点的直径上的垂线成正比的初始温度,那么这些温度将随时间变化,但总保持与那些垂线成正比,并且这些温度将随其比为分数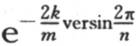 的一个几何级数的项同时降低。
的一个几何级数的项同时降低。
263 为了建立通解,我们首先可以注意到,不用b1 ,b2 ,b3 ,…,bn ,我们可以取与被分成n等分的圆周的分点相对应的n个余弦。量cos0u,cos1u,cos2u,…,cos(n-1)u中的u表示弧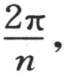 这些量也组成一个递推级数,该级数的关系系数由两个项2cosu和-1组成,由此,我们可以通过下述方程来满足微分方程:
这些量也组成一个递推级数,该级数的关系系数由两个项2cosu和-1组成,由此,我们可以通过下述方程来满足微分方程:
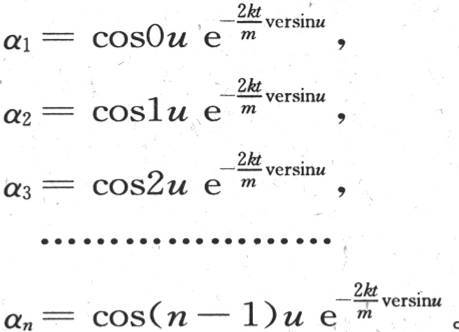
和前面两个解无关,我们可以为b1 ,b2 ,b3 ,…,bn 的值选择量sin0·2u,sin1·2u,sin2·2u,sin3·2u,…,sin(n-1)2u;或者选择cos0·2u,cos1·2u,cos2·2u,cos3·2u,…,cos(n-1)2u。
事实上,每个这样的级数都是递推的,并且由n个项所组成;关系系数有两项,2cos2u和-1;如果我们延续这个级数n个项,那么我们会得到分别等于前n项的另外n个项。
一般地,如果我们用u1 ,u2 ,u3 ,…,un 表示弧 那么我们可以为b1 ,b2 ,b3 ,…,bn 的值取n个量sin0ui ,sin1ui ,sin2ui ,sin3ui ,…,sin(n-1)ui ;或者是cos0ui ,cos1ui ,cos2ui ,cos3ui ,…,cos(n-1)ui 。与这每个级数所对应的h值可以由方程
那么我们可以为b1 ,b2 ,b3 ,…,bn 的值取n个量sin0ui ,sin1ui ,sin2ui ,sin3ui ,…,sin(n-1)ui ;或者是cos0ui ,cos1ui ,cos2ui ,cos3ui ,…,cos(n-1)ui 。与这每个级数所对应的h值可以由方程 给出。
给出。
我们可以对i给出从i=1到i=n的n个不同的值。
把b1 ,b2 ,b3 ,…,bn 的这些值代到第261目的方程中去,则我们有由下述结果所满足的第260目中的微分方程:
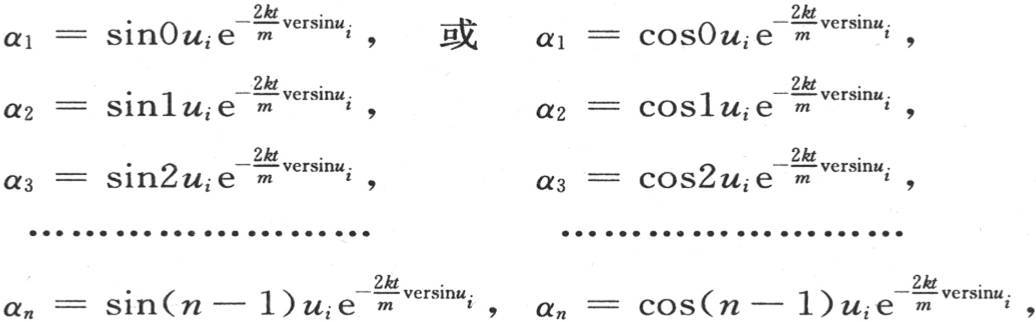
264 变量α1 ,α2 ,α3 ,…,αn 来自为这些变量所找到的几个特殊值的和,通过构造这每个变量α1 ,α2 ,α3 ,αn 的值,我们同样可以满足第260目的那些方程;进入某个变量的一般值的每一项也可以乘以任一常系数。由此得到,若用A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…,An ,Bn 表示任一组系数,那么为了表示某个变量,例如αm+1 的一般值,我们可以取方程
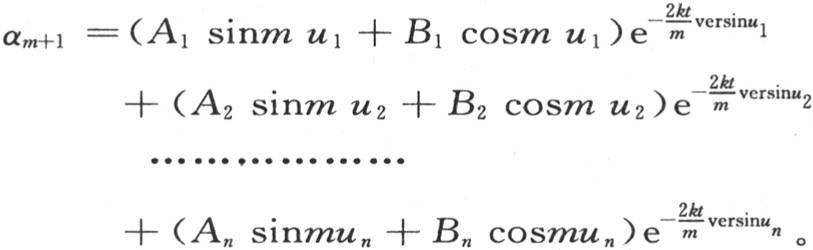
进入这个方程的量A1 ,A2 ,A3 ,…,An ,B1 ,B2 ,B3 ,…,Bn 是任意的,弧u1 ,u2 ,u3 ,…,un 由方程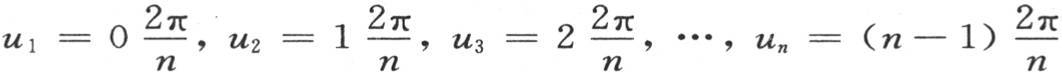 给出。
给出。
这样,变量α1 ,α2 ,α3 ,…,αn 的一般值由下述方程表示:
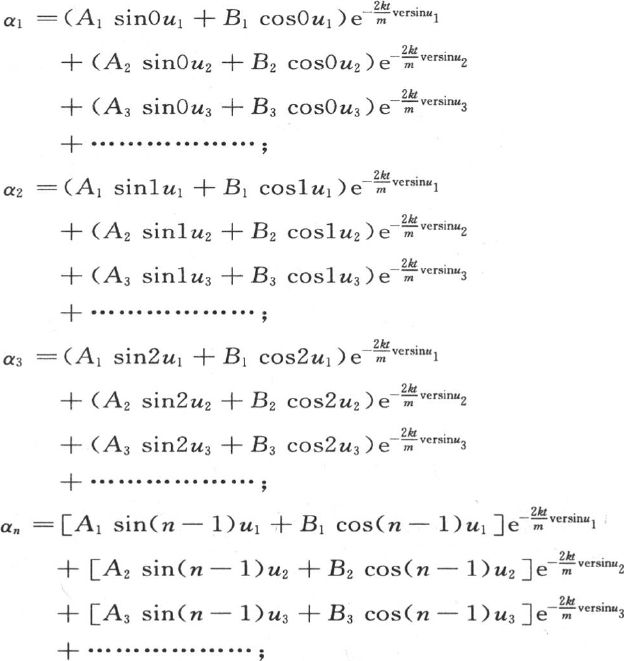
265 如果我们假定时间为0,那么值α1 ,α2 ,α3 ,…,αn 肯定变得和初始值a1 ,a2 ,a3 ,…,an 相同。我们由此得到n个方程,它们用来确定系数A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…。容易看出,未知数的个数总等于方程的个数。事实上,进入这些变量某一个的值的项数依不同的量versinu,versinu2 ,versinu3 ,…的个数而定,一旦把圆周长2π分成n等分,我们就能得到这些不同的量。现在,如果我们只计算那些不同的量,那么,量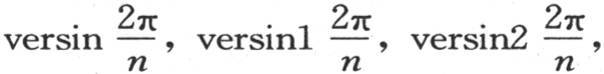 …的个数就比n小得多。若数n是奇数,就用2i+1来表示,若n是偶数,就用2i来表示。i+1总表示不同正矢的个数。另一方面,当在量
…的个数就比n小得多。若数n是奇数,就用2i+1来表示,若n是偶数,就用2i来表示。i+1总表示不同正矢的个数。另一方面,当在量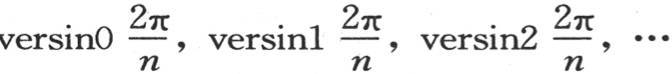 的级数中,我们得出一个正矢
的级数中,我们得出一个正矢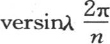 等于前面某个正矢
等于前面某个正矢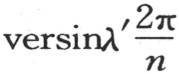 时,包含这个正矢的方程的两项就只构成一项;有同一正矢的两个不同的弧uλ 和uλ′ 也有同一个余弦,并且正弦只在符号上不同。容易看到,有同一正矢的弧uλ 和uλ′ 是这样的:uλ 的任一倍数的余弦等于uλ′ 的同一倍数的余弦,并且,uλ 的任一倍数的正弦与uλ′ 同一倍数的正弦只在符号上不同。由此得到,当我们把每个方程的两个对应项合成一项时,进入这些方程的两个未知数Aλ 和Aλ′ 就由单个未知数,即Aλ -Aλ′ ,来代替。至于两个未知数Bλ 和Bλ′ ,它们也由单个未知数,即Bλ +Bλ′ ,来代替:由此得到,在所有情况下,未知数的个数都等于方程的个数;因为项数总是i+1。我们应当加上,由于未知数A乘以一个零弧的正弦,所以它自行从第一项中消掉。此处,当数n是偶数时,则在每个方程的最后可以看到一个某未知数在其中自行消失的项,因为该项乘以一个零正弦;因此,当数n为偶数时,进入这些方程的未知数的个数等于2(i+1)-2;因此,在所有情况下未知数的个数都与方程的个数相同。
时,包含这个正矢的方程的两项就只构成一项;有同一正矢的两个不同的弧uλ 和uλ′ 也有同一个余弦,并且正弦只在符号上不同。容易看到,有同一正矢的弧uλ 和uλ′ 是这样的:uλ 的任一倍数的余弦等于uλ′ 的同一倍数的余弦,并且,uλ 的任一倍数的正弦与uλ′ 同一倍数的正弦只在符号上不同。由此得到,当我们把每个方程的两个对应项合成一项时,进入这些方程的两个未知数Aλ 和Aλ′ 就由单个未知数,即Aλ -Aλ′ ,来代替。至于两个未知数Bλ 和Bλ′ ,它们也由单个未知数,即Bλ +Bλ′ ,来代替:由此得到,在所有情况下,未知数的个数都等于方程的个数;因为项数总是i+1。我们应当加上,由于未知数A乘以一个零弧的正弦,所以它自行从第一项中消掉。此处,当数n是偶数时,则在每个方程的最后可以看到一个某未知数在其中自行消失的项,因为该项乘以一个零正弦;因此,当数n为偶数时,进入这些方程的未知数的个数等于2(i+1)-2;因此,在所有情况下未知数的个数都与方程的个数相同。
266 为了表示温度α1 ,α2 ,α3 ,…,αn 的一般值,前面的分析给我们提供这样一些方程:
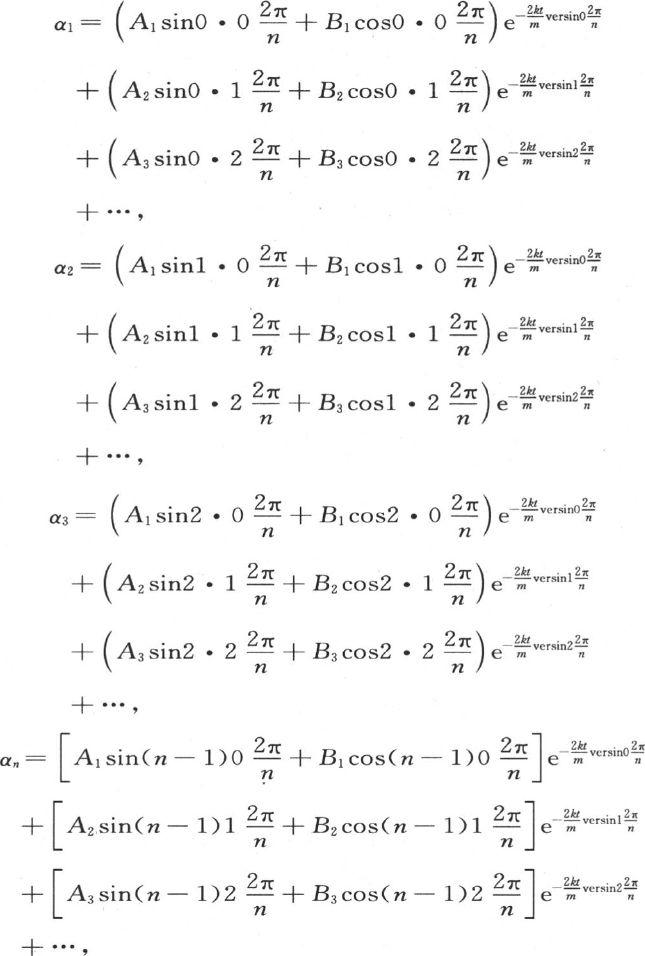
为了建立这些方程,我们应当在每个方程中依次延续包含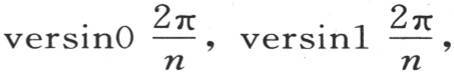
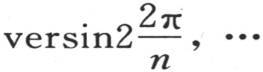 的项,直到我们包括了每个不同的正矢为止;并且,从出现一个正矢等于前面一个正矢的那个项开始,我们应当略去所有后面的项。
的项,直到我们包括了每个不同的正矢为止;并且,从出现一个正矢等于前面一个正矢的那个项开始,我们应当略去所有后面的项。
这些方程的个数是n。如果n是一个等于2i的偶数,则每个方程的项数就是i+1;如果方程个数n是由2i+1所表示的一个奇数,则项数仍然等于i+1。最后,在进入这些方程的量A1 ,B1 ,A2 ,B2 ,…之间,存在一些应当略去的量,因为它们在乘以零正弦后自行消掉。
267 为了确定进入前面这些方程的量A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…,我们应当考虑已知的初始状态:假定t=0,并且不用α1 ,α2 ,α3 ,…,而用给定的量α1 ,α2 ,α3 ,…,它们是温度的初始值。这样,为了确定A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…,我们有下述方程:
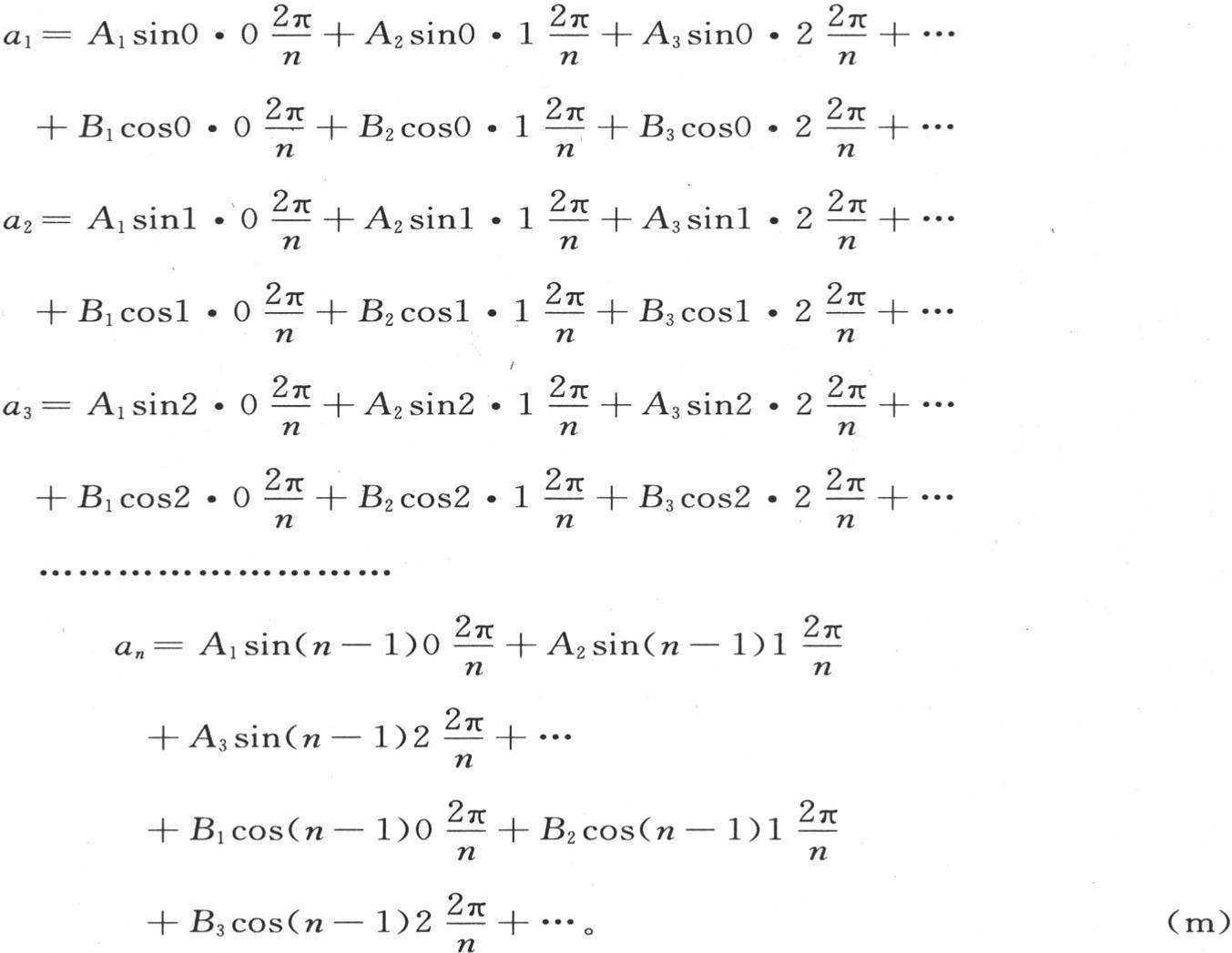
268 在个数为n的这些方程中,未知量是A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…,所需要的是进行消元并求出这些未知数的值。首先我们可以注意到,同一个未知数在每一个方程中有不同的乘数,这些乘数序列组成一个递推级数。事实上,这个序列是以算术级数增加的弧的正弦序列,或者是同样这些弧的余弦序列;它可以表示为sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,或者是cos0u,cos1u,cos2u,cos3u,…,cos(n-1)u。
如果所讨论的未知数是Ai+1 或者是Bi+1 ,则弧u就等于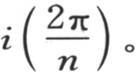 如此,为了用前面的那些方程确定未知数Ai+1 ,我们应当把这一个一个的方程和这一系列乘数sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u合并,用这个序列的相应项乘每一个方程。如果我们取如此乘过的方程的和,那么除需要确定的未知数外,我们就消去了所有其他的未知数。如果我们要求Bi+1 的值,则情况亦如此。我们应当用那个方程中Bi+1 的乘数乘每个方程,然后取所有这些方程的和,需要证明的是,通过这样的运算,除唯一的一个未知数外,我们事实上消去了其他所有的未知数。为此,只需标明下面三点就够了:第一,如果我们逐项乘下面两个序列sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,sin0v,sin1v,sin2v,sin3v,…,sin(n-1)v,那么,除了当弧u和v相同这种情况之外,换句话说,除了当每个这样的弧被认为是等于
如此,为了用前面的那些方程确定未知数Ai+1 ,我们应当把这一个一个的方程和这一系列乘数sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u合并,用这个序列的相应项乘每一个方程。如果我们取如此乘过的方程的和,那么除需要确定的未知数外,我们就消去了所有其他的未知数。如果我们要求Bi+1 的值,则情况亦如此。我们应当用那个方程中Bi+1 的乘数乘每个方程,然后取所有这些方程的和,需要证明的是,通过这样的运算,除唯一的一个未知数外,我们事实上消去了其他所有的未知数。为此,只需标明下面三点就够了:第一,如果我们逐项乘下面两个序列sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,sin0v,sin1v,sin2v,sin3v,…,sin(n-1)v,那么,除了当弧u和v相同这种情况之外,换句话说,除了当每个这样的弧被认为是等于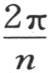 的部分圆周长的倍数这种情况之外,乘积的和sin0u sin0v+sin1u sin1v+sin2u sin2v+…就等于0;第二,如果我们逐项乘两个序列cos0u,cos1u,cos2u,…,cos(n-1)u,cos0v,cos1v,cos2v,…,cos(n-1)v,那么除u等于v的情况外,乘积的和就等于0;第三,如果我们逐项乘两个序列sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,cos0v,cos1v,cos2v,cos3v,…,cos(n-1)v,那么乘积的和就总等于0。
的部分圆周长的倍数这种情况之外,乘积的和sin0u sin0v+sin1u sin1v+sin2u sin2v+…就等于0;第二,如果我们逐项乘两个序列cos0u,cos1u,cos2u,…,cos(n-1)u,cos0v,cos1v,cos2v,…,cos(n-1)v,那么除u等于v的情况外,乘积的和就等于0;第三,如果我们逐项乘两个序列sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,cos0v,cos1v,cos2v,cos3v,…,cos(n-1)v,那么乘积的和就总等于0。
269 让我们用q表示弧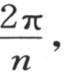 用μq表示弧u,用νq表示弧v;μ和ν是小于n的正整数。对应于前两个序列的两项的积用sinjμqsinjνq,或
用μq表示弧u,用νq表示弧v;μ和ν是小于n的正整数。对应于前两个序列的两项的积用sinjμqsinjνq,或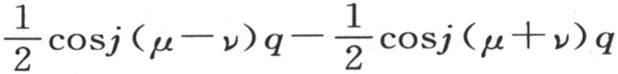 来表示,字母j表示序列0,1,2,3,…,(n-1)的任一项;现在不难证明,如果我们对j给定其从0到(n-1)的n个连续值,那么和
来表示,字母j表示序列0,1,2,3,…,(n-1)的任一项;现在不难证明,如果我们对j给定其从0到(n-1)的n个连续值,那么和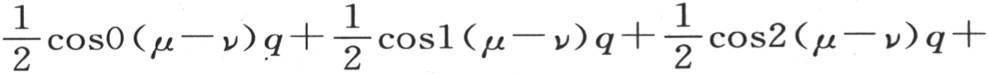
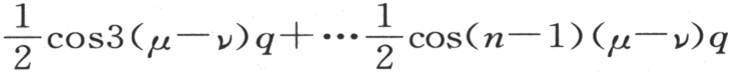 就取0值,级数
就取0值,级数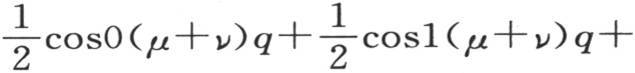
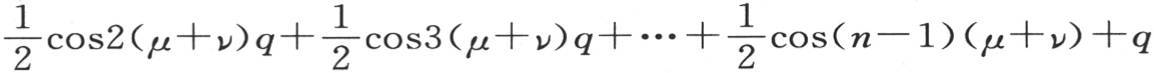 亦如此。
亦如此。
事实上,用α表示弧(μ-ν)q,这个弧必然是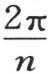 的一个倍数,则我们有循环级数cos0α,cos1α,cos2α,…,cos(n-1)α,它的和为0。
的一个倍数,则我们有循环级数cos0α,cos1α,cos2α,…,cos(n-1)α,它的和为0。
为了表明这一点,我们用s表示这个和,由于关系系数的两个项是2cosα和-1,所以我们用-2cosα和1依次乘方程s=cos0α+cos1α+cos2α+cos3α+…+cos(n-1)α的两边;这样,把这三个方程相加,我们就会看到,按照递推级数,中项被消掉。
如果现在我们注意到,由于nα是整个圆周的一个倍数,所以量cos(n-1)α,cos(n-2)α,cos(n-3)α,…分别和那些由cos(-α),cos(-2α),cos(-3α),…所表示的量相同,那么我们得到2s-2scosα=0;因此一般地,所求的这个和应当是0。
用同样的方法我们得到,属于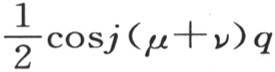 的展开式的项的和为0。应当除开由α所表示的弧为0的情况;这时,我们有1-cosα=0;即,弧u和v是相同的。在这种情况下,项
的展开式的项的和为0。应当除开由α所表示的弧为0的情况;这时,我们有1-cosα=0;即,弧u和v是相同的。在这种情况下,项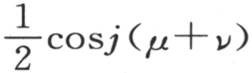 仍然给出一个其和为0的展开式;但是量
仍然给出一个其和为0的展开式;但是量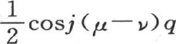 提供一些相同的项,它们每一个都取值
提供一些相同的项,它们每一个都取值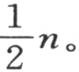
同样地,我们可以得到后两个序列逐项积的和的值或者是∑(cosjμq cosjνq)的值;事实上,我们可以用量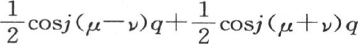 代替cosjuq cosjνq,这样,和在前面的情况一样,我们得到
代替cosjuq cosjνq,这样,和在前面的情况一样,我们得到 为0,并且,除μ=ν的情况外,
为0,并且,除μ=ν的情况外,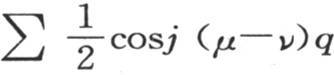 为0。由此得到,当弧u和v不同时,后两个序列逐项积的和或者是∑cosjμq cosjνq总等于0,当u=v时,它等于
为0。由此得到,当弧u和v不同时,后两个序列逐项积的和或者是∑cosjμq cosjνq总等于0,当u=v时,它等于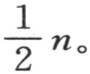 所要注意的只是当我们取0作为表示前两个序列逐项积的和∑sinjμq sinjνq的值时,弧μq和νq均为0的情况。
所要注意的只是当我们取0作为表示前两个序列逐项积的和∑sinjμq sinjνq的值时,弧μq和νq均为0的情况。
当μq和νq都为0时所取的和∑cosjμq cosjνq的情况不同;后两个序列逐项积的和显然等于n。
至于两个序列sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,cos0u,cos1u,cos2u,cos3u,…,cos(n-1)u的逐项积的和,正如可以由前述分析容易断定一样,它在所有情况下都为0。
270 这些序列的比较提供下面的结果。如果我们把圆周2π分成n等分,使弧u由这些等分的一个整数μ所组成,并标明弧u,2u,3u,…,(n-1)u的端点,那么从三角函数量的已知性质得到,量sin0u,sin1u,sin2u,sin3u,…,sin(n-1)u,当然,或者是量cos0u,cos1u,cos2u,cos3u,…,cos(n-1)u形成由n个项所组成的一个递推周期级数(a recurring periodic series):如果我们把与弧u或者是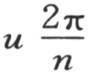 对应的两个序列中的一个和与另一个弧v或者是
对应的两个序列中的一个和与另一个弧v或者是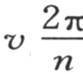 所对应的序列作比较,并且把这两个相比较的序列逐项相乘,那么当弧u和v不同时,这些积的和为0。如果弧u和v相等,那么当我们合并正弦的两个序列,或者当我们合并余弦的两个序列时,这些积的和就等于
所对应的序列作比较,并且把这两个相比较的序列逐项相乘,那么当弧u和v不同时,这些积的和为0。如果弧u和v相等,那么当我们合并正弦的两个序列,或者当我们合并余弦的两个序列时,这些积的和就等于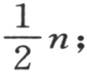 但是如果我们把一个正弦序列和一个余弦序列合并,则积为0。如果我们假定弧u和v等于0,那么显然,只要这两个序列中的一个由正弦组成,或者两者都由正弦组成,那么逐项积的和就为0,但是,如果所合并的序列都由余弦组成,则这些积的和等于n。一般地,逐项积的和或者是等于0,或者是等于
但是如果我们把一个正弦序列和一个余弦序列合并,则积为0。如果我们假定弧u和v等于0,那么显然,只要这两个序列中的一个由正弦组成,或者两者都由正弦组成,那么逐项积的和就为0,但是,如果所合并的序列都由余弦组成,则这些积的和等于n。一般地,逐项积的和或者是等于0,或者是等于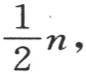 或者是等于n;此外,已知的公式将直接导致同样的结果。在这里,它们是作为三角学基本定理的明显结论而被推导出来的。
或者是等于n;此外,已知的公式将直接导致同样的结果。在这里,它们是作为三角学基本定理的明显结论而被推导出来的。
法文《文集》本的编者M.加斯东·达布在此给出了一个脚注来说明这个和为什么等于0。脚注如下:等式cosiα-2cosαcos(i-1)α+cos(i-2)α=0,可用于所有的i值,我们一般有
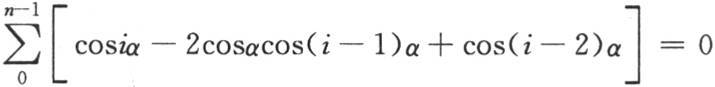
或者
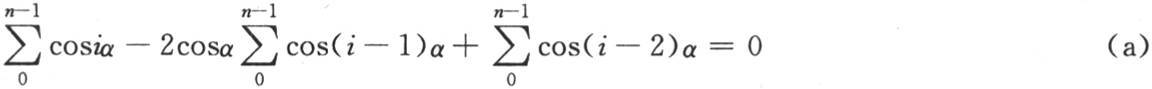
在傅立叶的这部著作中,nα是2π的倍数,因此我们有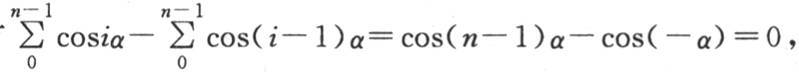
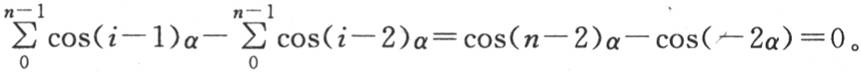 方程(a)中的三个和完全相等,用和s来代替它们的值,我们正好得到2s(1-cosα)=0。——汉译者
方程(a)中的三个和完全相等,用和s来代替它们的值,我们正好得到2s(1-cosα)=0。——汉译者
271 我们通过这些注记不难完成前述方程的未知数消元。未知数A1 因有0系数而自行消去;为了求出B1 ,我们应当用那个方程中的系数乘每一个方程的两边,把所有这样乘过的方程相加,我们得到a1 +a2 +a3 +…+an =B1
为了确定A2 ,我们应当用那个方程中A2 的系数乘每个方程的两边,用q表示弧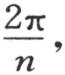 在把这些方程加起来后,我们有,
在把这些方程加起来后,我们有,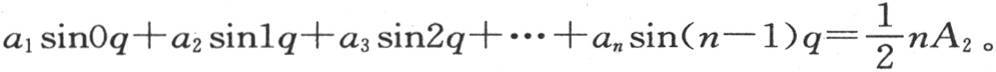
同样,为了确定B2 ,我们有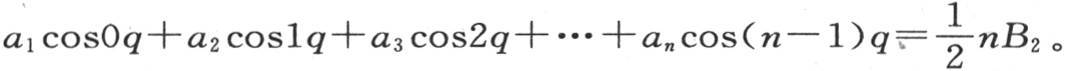
一般地,通过用相应方程中未知数的系数乘每个方程的两边,我们可以求出每一个未知数。因此我们得到下述结果:
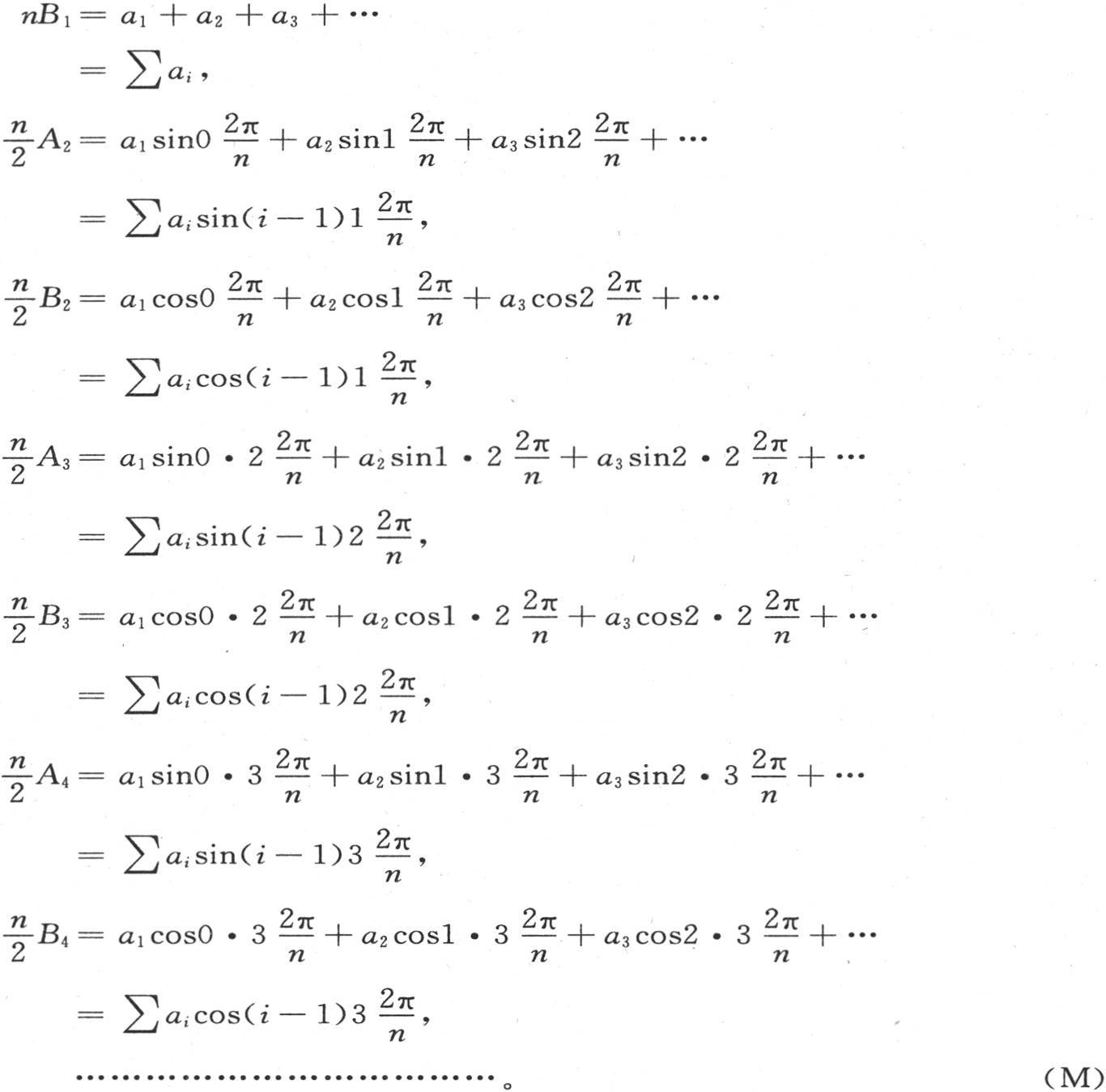
为了得到由符号∑所指明的展开式,我们必须对i给出它的n个连续值1,2,3,4,…,并且取和,在这种情况下,我们一般有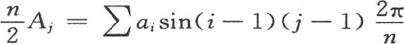 和
和
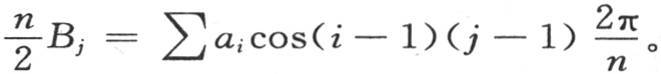
如果我们对整数j给出它所能取的所有连续值1,2,3,4,…,那么这两个式子给出我们的方程,如果我们通过对i给出它的n个值1,2,3,4,…n来展开符号∑下的项,那么我们就得到A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…的值,第267目的方程(m)就完全解出来了。
272 现在我们把系数A1 ,B1 ,A2 ,B2 ,A3 ,B3 ,…的已知值代入第266目的方程(μ)中,并得到下述值:
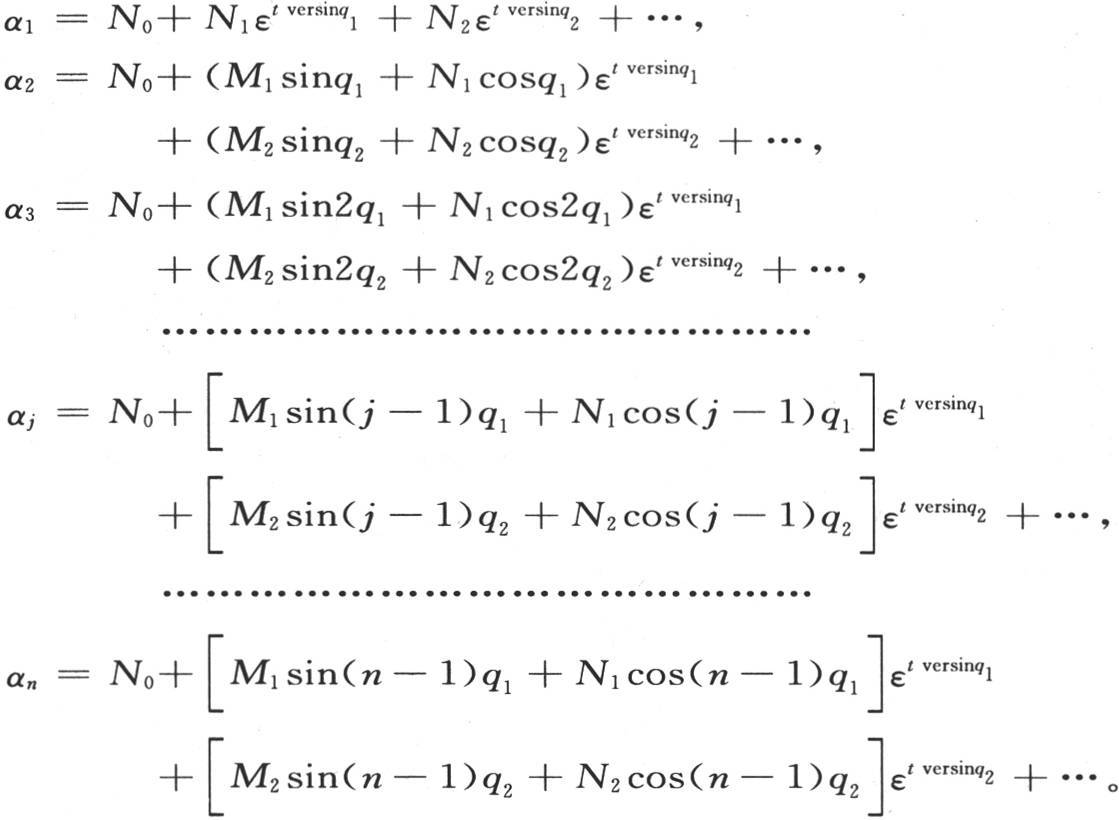
在这些方程中,
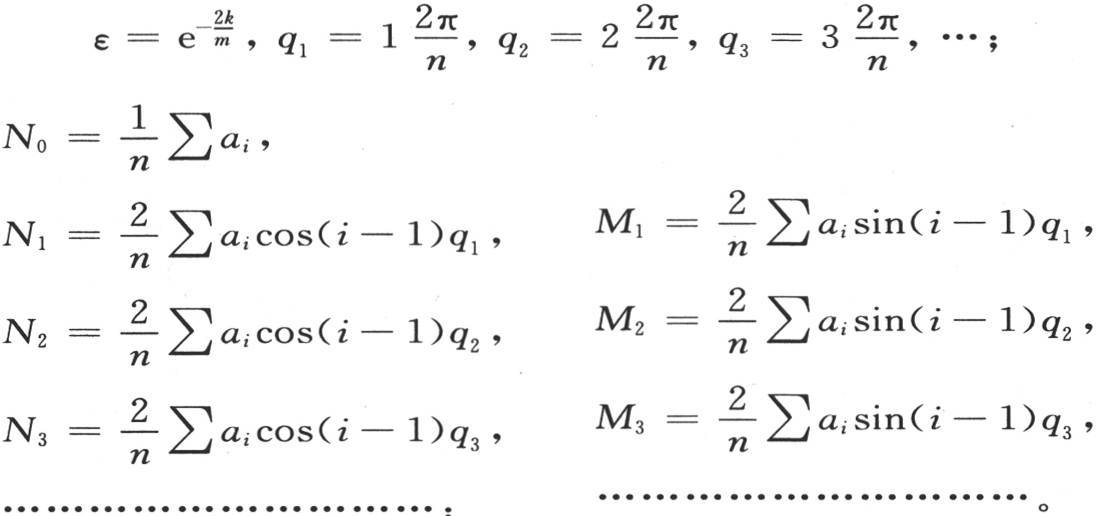
273 我们刚才所确定的方程包含了所提出的问题的全解,它由一般方程
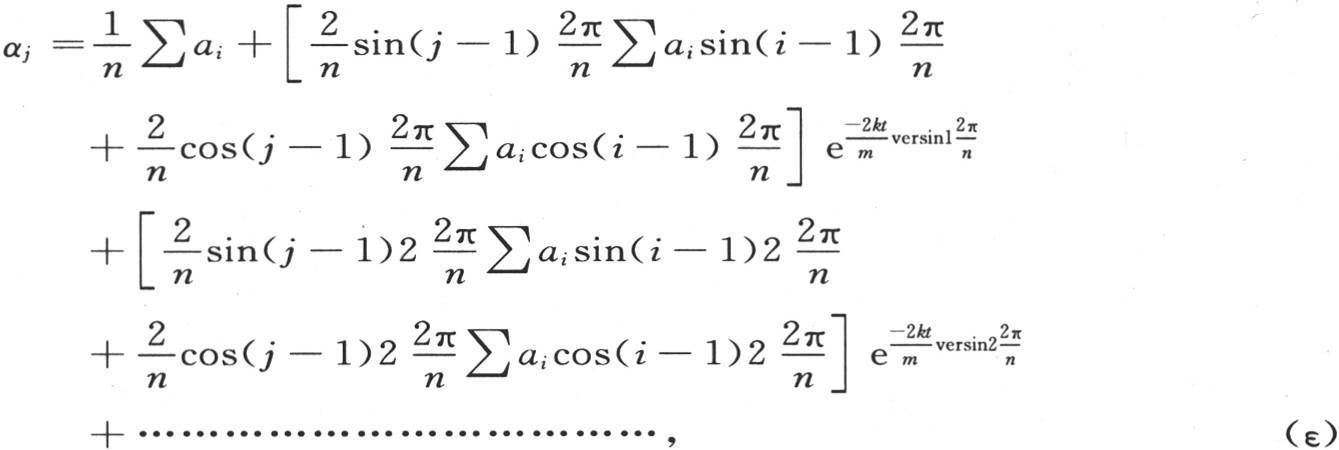
来表示。进入这个方程的,只有已知量,即a1 ,a2 ,a3 ,…,an ,它们是初始温度,k是热导率的大小,m是物质的值,n是受热物体的个数,t是历经时间。
由前面的分析得到,如果数目为n的几个相等的物体被安排在一个圆上,在得到任一初始温度后开始以我们曾假定的方式相互传热;用m表示每个物体的物质,t表示时间,k表示某个常系数,那么,每个物体的变化温度肯定是量t,m,k,和所有初始温度的一个函数,它由一般方程(ε)给出。我们首先用指示我们希望确定其温度的物体的位置的数字来代替j,即,1表示第一个物体,2表示第二个物体,…;然后,对于进入符号∑下的字母i,我们给出它的n个连续值1,2,3,…,n,并取所有这些项的和。至于进入这个方程的项数,肯定和属于逐个弧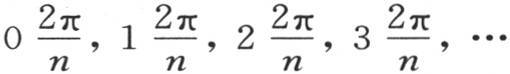 的不同正矢的个数一样多,也就是说,无论数n因其为奇数或者是偶数而等于(2λ+1)或者是2λ,进入这个方程的项数都总是λ+1。
的不同正矢的个数一样多,也就是说,无论数n因其为奇数或者是偶数而等于(2λ+1)或者是2λ,进入这个方程的项数都总是λ+1。
274 为了给出应用这个公式的一个例子,让我们假定第一个物体是首先唯一被加热的物体,因此初始温度a1 ,a2 ,a3 ,…,an 除第一个外都是0。显然,包含在第一个物体中的热量逐渐分布到所有其他物体之中,因此这个热传导规律由方程
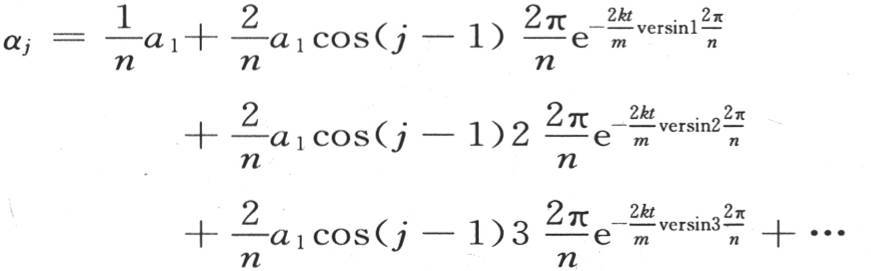
来表示。
如果只有第二个物体被加热,温度a1 ,a2 ,a3 ,a4 ,…,an 为0,那么我们有
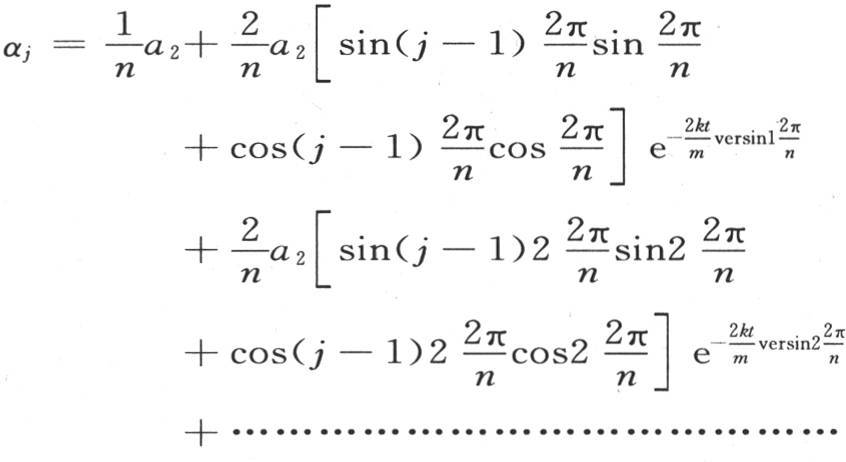
如果除a1 和a2 之外,所有初始温度都假定为0,那么对于aj 的值,我们得到在前面两个假定的每个中所得到的那些值的和。一般地,从第273目中的一般方程(ε)不难得到,为了求热的初始量在这些物体中据以分布的规律,我们可以分别考虑初始温度除一个物体的之外都为0的那些情况。在把除一个物体之外的所有其他物体看做受0度温度作用时,我们可以假定包含在这个物体中的热量只由自身向其他所有物体传导;关于每个个别物体所得到的初始热,在作出这个假定后,通过把同一物体在前面每个假定下应得到的所有温度相加,我们就可以确定在一给定时间之后,任一个这样的物体的温度。
275 如果在给出αj 的值的一般方程(ε)中,我们假定时间无穷,那么我们得到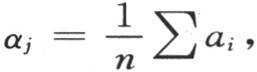 因此每一个这样的物体都达到平均温度,这个结果是显然的。
因此每一个这样的物体都达到平均温度,这个结果是显然的。
随着时间值的增加,第一项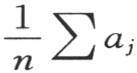 相对于后面各项或相对于它们的和就变得愈来愈大。第二项相对于其后各项的情况亦如此;当时间变得相当大时,αj 的值就由方程
相对于后面各项或相对于它们的和就变得愈来愈大。第二项相对于其后各项的情况亦如此;当时间变得相当大时,αj 的值就由方程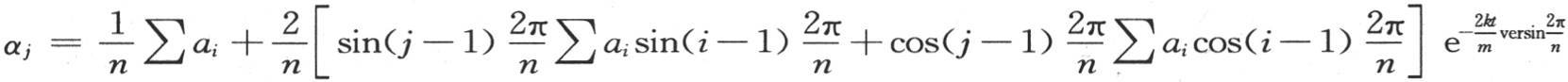 来表示而无明显的误差。
来表示而无明显的误差。
用a和b表示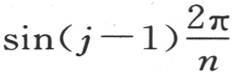 和
和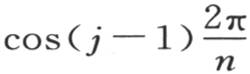 的系数,用ω表示分数
的系数,用ω表示分数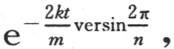 我们有
我们有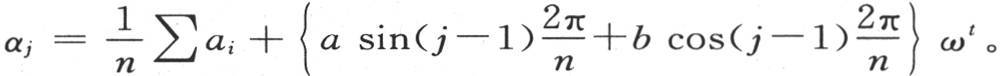 量a和b是常数,即与时间和字母j无关,字母j指示其变化温度为αj 的物体的顺序。这两个量对所有物体都相同。因此,对于每一个物体,变化温度αj 和终极温度
量a和b是常数,即与时间和字母j无关,字母j指示其变化温度为αj 的物体的顺序。这两个量对所有物体都相同。因此,对于每一个物体,变化温度αj 和终极温度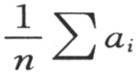 的差与分数ω的逐次幂成正比地减少。那个最终极限和同一物体的变化温度之差总是随一个分数的逐次幂减少而结束。无论这个物体的温度变化被看做是怎样的,这个分数总是相同的;用uj 来表示弧
的差与分数ω的逐次幂成正比地减少。那个最终极限和同一物体的变化温度之差总是随一个分数的逐次幂减少而结束。无论这个物体的温度变化被看做是怎样的,这个分数总是相同的;用uj 来表示弧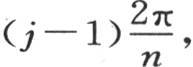 则我们可使ωt 的系数或者是(asinuj +bcosuj )处于Asin(uj +B)的形式之下,同时A和B按a=AcosB,b=AsinB这样的方式来取。如果我们要确定相对于温度为αj+1 ,αj+2 ,αj+3 ,…的逐个物体的ωt 的系数,我们就必须把
则我们可使ωt 的系数或者是(asinuj +bcosuj )处于Asin(uj +B)的形式之下,同时A和B按a=AcosB,b=AsinB这样的方式来取。如果我们要确定相对于温度为αj+1 ,αj+2 ,αj+3 ,…的逐个物体的ωt 的系数,我们就必须把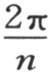 或者是
或者是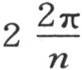 等加到uj 上去;因此我们有方程
等加到uj 上去;因此我们有方程
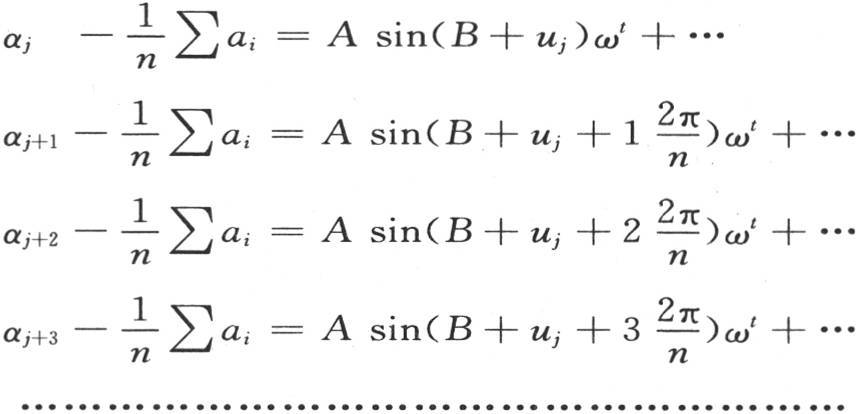
276 我们由这些方程看到,在每个方程右边只保留第一项时,这些实际温度与终极温度的差就由前面那些方程来表示。这样,这些差随下述规律而变化:如果我们只考虑一个物体,那么当时间以等分增加时,所讨论的变差,即这个物体的实际温度超过终极和共同温度的超出量,就随一个分数的逐次幂而减少;如果我们在同一时刻比较所有这些物体的温度,那么所讨论的差就与被分成若干等分的圆周的逐个正弦成正比地变化。尽管每个物体在同一时刻所产生的温度由其圆周被等分的圆的纵坐标来表示,但是,同一物体在不同的逐个相等时刻所产生的温度却由其轴被等分的一条对数曲线的纵坐标来表示。正如我们在前面所注意到的,不难看出,如果初始温度确乎如此,即这些温度和平均温度或者是终极温度的差与多重弧的逐次正弦成正比,那么这些差就都同时减少,并且仍保持与同一正弦成正比。这个规律,它同时也控制初始温度,不会为这些物体的相互作用所干扰,并一直保持到它们都达到一共同温度为止。对于每一个物体,这个差将随同一个分数的逐次幂而减少。相同物体序列间的热传导所服从的最简规律就是如此。这个规律一旦在初始温度之间建立起来,它就自我保持,当它不控制初始温度,即当这些温度与平均温度的差不与多重弧的逐次正弦成正比时,所说的这个规律就总是趋于形成,并且,这个变化的温度系统很快就以与由一个圆的纵坐标和一条对数曲线的纵坐标所确定的温度明显重合而结束。
由于在一个物体的温度超过平均温度的超出量之间,后来的差与该物体所处的端点的弧的正弦成正比,由此得到,如果我们考虑位于同一直径两端的两个物体,那么,第一个物体的温度超过平均温度和不变温度的量就和这一不变温度超过第二个物体的温度的量一样大。由此,如果我们在每一时刻取其位置相反的两个物体的温度和,那么我们得到一个不变的和,这个和对于处在同一直径两端的任意两个物体有相同的值。
277 表示分离物体的变化温度的公式不难应用到连续物体的热传导上去。为了给出一个引人注目的例子,我们将通过已建立的一般方程来确定环中的热运动。
假定物体的数目n不断增加,同时每个物体的长度以同一比例减少,于是这个系统的长度有一个等于2π的不变值。因此,如果物体的数目n依次是2,4,6,8,直到无穷,那么这每个物体将是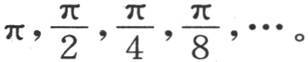 还应当假定,热的传导能力以同一比例随质量数m而增加;因此,在只有两个质量时k所表示的量,在有4个时,就翻成两倍,在有8个时,就翻成4倍,等等。用g表示这个量,则我们看到,数k必须依次由g,2g,4g等来代替。如果我们现在转到一种连续物体的假定上来,那么我们就应当用每一个无穷小物质的值,基元dx,来代替m;应当用
还应当假定,热的传导能力以同一比例随质量数m而增加;因此,在只有两个质量时k所表示的量,在有4个时,就翻成两倍,在有8个时,就翻成4倍,等等。用g表示这个量,则我们看到,数k必须依次由g,2g,4g等来代替。如果我们现在转到一种连续物体的假定上来,那么我们就应当用每一个无穷小物质的值,基元dx,来代替m;应当用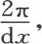 来取代物体的数目;不用k,而改用
来取代物体的数目;不用k,而改用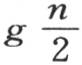 或者是
或者是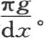
至于初始温度a1 ,a2 ,a3 ,…,an ,它们取决于弧x的值,当把这些温度看做是这同一变量的相继状态时,一般的值ai 就表示x的一个任意函数。这样,指标i就肯定由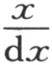 来代替。关于量α1 ,α2 ,α3 ,…,它们是由两个量x和t所决定的可变温度。用v表示这个变量,我们有v=φ(x,t)。指标j标明这些物体当中的一个所占据的位置,应当由
来代替。关于量α1 ,α2 ,α3 ,…,它们是由两个量x和t所决定的可变温度。用v表示这个变量,我们有v=φ(x,t)。指标j标明这些物体当中的一个所占据的位置,应当由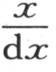 来代替。因此,为了把以前的分析应用于以环的形式组成一个连续物体的无数薄层的情况,我们应当用量
来代替。因此,为了把以前的分析应用于以环的形式组成一个连续物体的无数薄层的情况,我们应当用量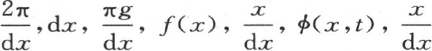 等来代替它们所对应的n,m,k,ai ,i,aj ,j等。让我们在第273目的方程(ε)中作这些代换,用
等来代替它们所对应的n,m,k,ai ,i,aj ,j等。让我们在第273目的方程(ε)中作这些代换,用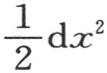 代替versindx,用i和j代替i-1和j-1。第一项
代替versindx,用i和j代替i-1和j-1。第一项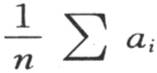 变成从x=0取到x=2π的积分
变成从x=0取到x=2π的积分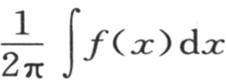 的值;量
的值;量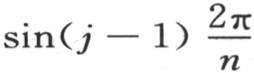 变成sinjdx或者是
变成sinjdx或者是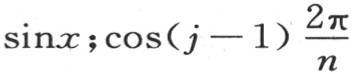 的值是
的值是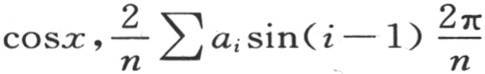 的值是
的值是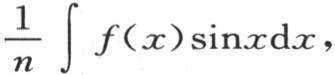 该积分从x=0取到
该积分从x=0取到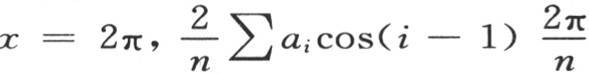 的值是
的值是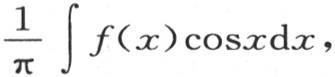 该积分同样从x=0取到x=2π。因此我们得到方程
该积分同样从x=0取到x=2π。因此我们得到方程
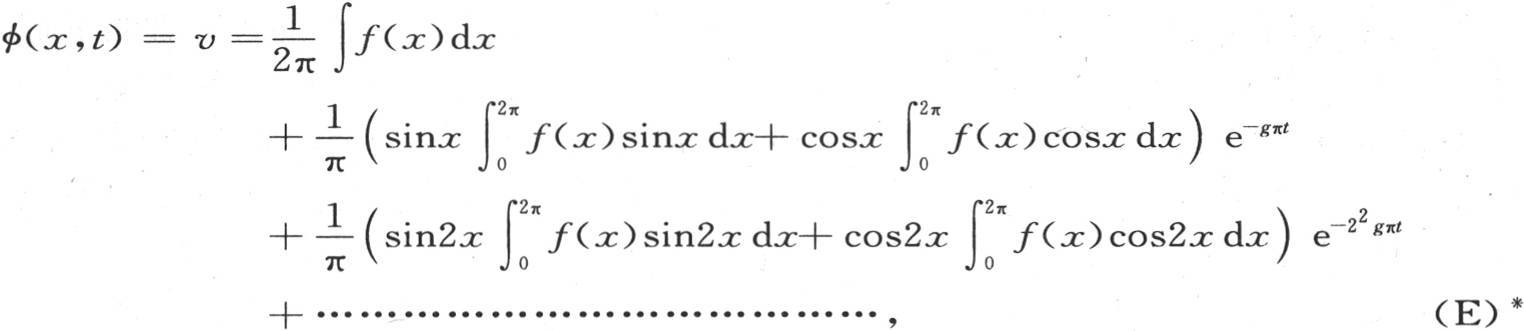
* 在英译本中,方程(E)以及本章后面几目中的积分号都是不定积分号。此处依法文《文集》本修改。——汉译者
用k表示量gπ,我们有
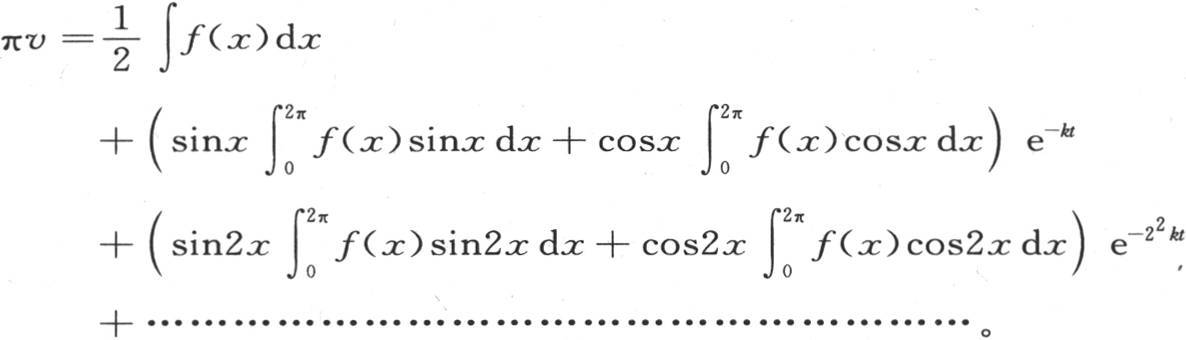
278 这个解与上一节第241目所给出的解相同;这引出几点注记。
第一,为了得到表示环的热运动的一般方程,无须求助于偏微分方程的分析。这个问题可作为物体的数目有限的问题来解决,然后再假定该数目无穷。这种方法本身具有清晰性,并引导我们最初的研究。通过一个自然而然地被指明的过程,以后就容易转到更简洁的方法上来。我们看到,满足偏微分方程并组成一般值的那些特殊值的挑选,由其系数为常数的线性微分方程的已知规则导出。此外,正如我们在上面所看到的,这个挑选建立在这个问题的物理条件之上。
第二,为了从分离物体的情况过渡到连续物体的情况,我们假定系数k与物体数n成正比地增加。数k的这种连续变化,是根据我们以前所证明的,即同一棱柱的两个薄层之间所流过的热量与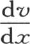 的值成正比而得来的,x表示与这个截面对应的横坐标,v表示温度。的确,如果我们假定系数k不是与物体数目成正比地增加,而是对那个系数保持一个常数值,那么,一旦取n为无穷,我们就得到与在连续物体中所看到的相反的结果。热扩散将无限地慢,无论物体以何种方式加热,在一个有限的时间内,某一点的温度都不会发生明显的变化,这与事实矛盾。每当我们要考虑无穷多个分离的导热物体,并希望过渡到连续物体的情况上去时,我们就必须对计量传导速度的系数k赋予与组成给定物体的无穷小物体的数目成正比的一个值。
的值成正比而得来的,x表示与这个截面对应的横坐标,v表示温度。的确,如果我们假定系数k不是与物体数目成正比地增加,而是对那个系数保持一个常数值,那么,一旦取n为无穷,我们就得到与在连续物体中所看到的相反的结果。热扩散将无限地慢,无论物体以何种方式加热,在一个有限的时间内,某一点的温度都不会发生明显的变化,这与事实矛盾。每当我们要考虑无穷多个分离的导热物体,并希望过渡到连续物体的情况上去时,我们就必须对计量传导速度的系数k赋予与组成给定物体的无穷小物体的数目成正比的一个值。
第三,如果在我们为表示v或者是φ(x,t)的值而得出的上一个方程中假定t=0,那么这个方程就必然表示初始状态,由此可见,我们有在前面第233目中所得到的方程(p),即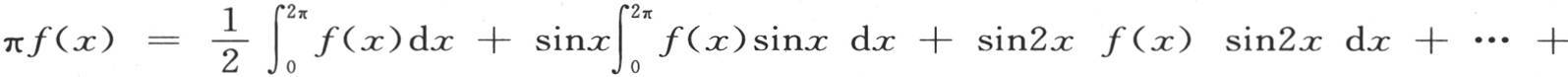
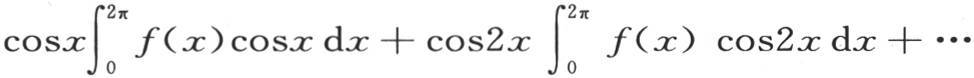
因此,在所给定的区间之间以多重弧的正弦级数或者是余弦级数给出一个任意函数的展开式的定理,由分析的基本规则导出。在这里,我们得到通过方程
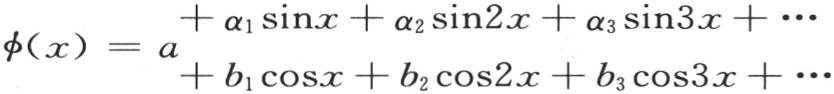
的逐次积分而使所有系数除一个之外全部都消掉所应用的这个过程的起点。这些积分与第267和271目方程(m)中的不同未知数的消元相对应,并且,通过这两种方法的比较我们清楚地看到,第279目的方程(B)对0到2π之间的所有x值都成立,而把它应用到超出这个界限的x的值则不成立。
279 函数φ(x,t),它满足这个问题的这些条件,并且其值由第277目的方程(E)来确定,可以表示如下:
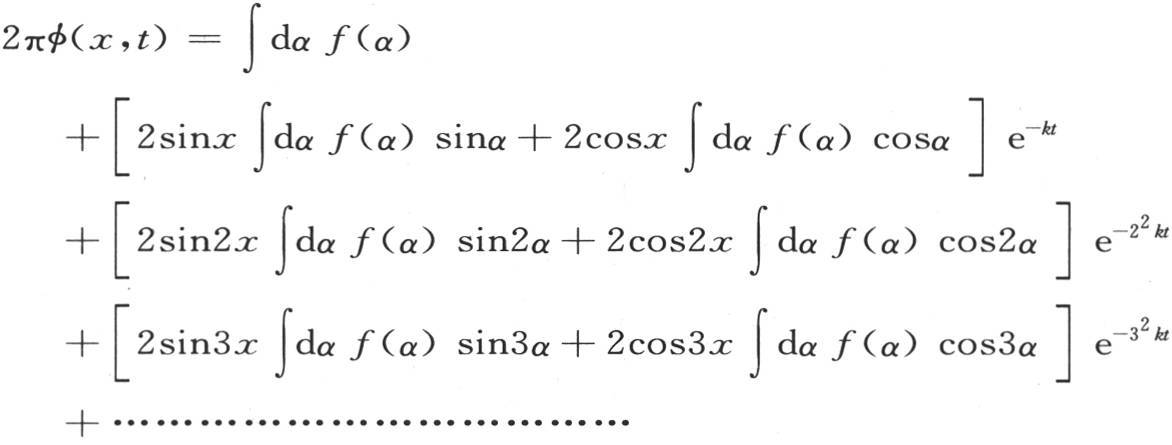
或者是
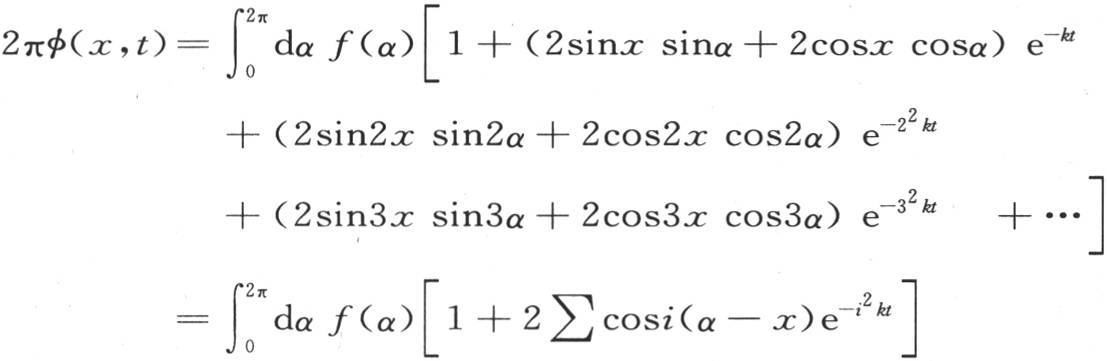
符号∑影响数i,并指明这个和应当从i=1取到i=∞。我们也可以把第一项包括到符号∑之下,这样我们有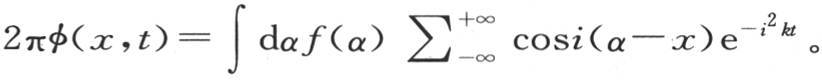 这时我们必须对i给定从-∞到+∞的所有整数值;这由写在符号∑之后的-∞和+∞所指明,i的这些值中有一个是0。这就是这个解的最简洁的表达式。为了展开该方程的右边,我们假定i=0,然后假定i=1,2,3,…,并且,除对应于i=0的第一项外,使每个结果都翻一倍,当t为0时,函数φ(x,t)必然表示温度等于f(x)的初始状态,因此我们有恒等方程
这时我们必须对i给定从-∞到+∞的所有整数值;这由写在符号∑之后的-∞和+∞所指明,i的这些值中有一个是0。这就是这个解的最简洁的表达式。为了展开该方程的右边,我们假定i=0,然后假定i=1,2,3,…,并且,除对应于i=0的第一项外,使每个结果都翻一倍,当t为0时,函数φ(x,t)必然表示温度等于f(x)的初始状态,因此我们有恒等方程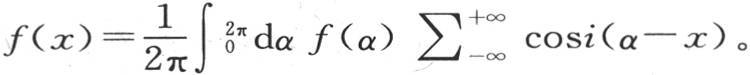 (B)我们已经把应当在其中取积分和的上下限符号加到符号∫和∑上去。无论函数f(x)在从x=0到x=2π的区间内有怎样的形式,这个定理都普遍成立;用给出第235目中F(x)的展开式的方程所表示的情况同样如此;我们在后面会看到,我们可以不用前面的考虑而直接证明方程(B)成立。
(B)我们已经把应当在其中取积分和的上下限符号加到符号∫和∑上去。无论函数f(x)在从x=0到x=2π的区间内有怎样的形式,这个定理都普遍成立;用给出第235目中F(x)的展开式的方程所表示的情况同样如此;我们在后面会看到,我们可以不用前面的考虑而直接证明方程(B)成立。
280 不难看出,这个问题不可能有与第277目的方程(E)所给出的不同的解。事实上,函数φ(x,t)完全满足问题的条件,根据微分方程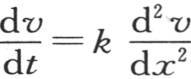 的性质,其他方程不可能有同一性质。为了使我们自己确信这一点,我们应当认为当固体的第一个状态由一个给定的方程v1 =f(x)来表示时,流数
的性质,其他方程不可能有同一性质。为了使我们自己确信这一点,我们应当认为当固体的第一个状态由一个给定的方程v1 =f(x)来表示时,流数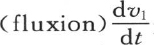 是已知的,因为它等于
是已知的,因为它等于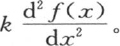 因此,用v2 或者是
因此,用v2 或者是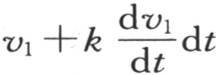 表示第二个时刻开始时的温度,我们就可以从初始状态和从这个微分方程推出v2 的值。同样我们可以确定在每一时刻开始时固体任一点的温度值v3 ,v4 ,…,vn 。现在函数φ(x,t)满足初始状态,因为我们有φ(x,0)=f(x)。此外,它也满足这个微分方程;因此,如果它被微分,那么和从微分方程(a)的逐次应用所得出的结果一样,它对
表示第二个时刻开始时的温度,我们就可以从初始状态和从这个微分方程推出v2 的值。同样我们可以确定在每一时刻开始时固体任一点的温度值v3 ,v4 ,…,vn 。现在函数φ(x,t)满足初始状态,因为我们有φ(x,0)=f(x)。此外,它也满足这个微分方程;因此,如果它被微分,那么和从微分方程(a)的逐次应用所得出的结果一样,它对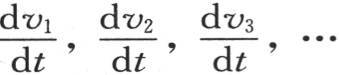 给出同样的值。这样,如果在函数φ(x,t)中我们对t依次给出值0,ω,2ω,3ω,…,iω来表示时间元,那么,我们会得到同样的值v1 ,v2 ,v3 ,v4 ,…,正如我们可以通过方程
给出同样的值。这样,如果在函数φ(x,t)中我们对t依次给出值0,ω,2ω,3ω,…,iω来表示时间元,那么,我们会得到同样的值v1 ,v2 ,v3 ,v4 ,…,正如我们可以通过方程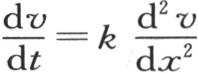 的连续应用而从初始状态所能得出的结果一样。因此,满足微分方程和初始状态的每一个函数ψ(x,t)必然与函数φ(x,t)重合:因为当我们在它们之中假定t依次等于0,ω,2ω,3ω,…,iω时,每一个这样的函数都给出同一个x的函数。
的连续应用而从初始状态所能得出的结果一样。因此,满足微分方程和初始状态的每一个函数ψ(x,t)必然与函数φ(x,t)重合:因为当我们在它们之中假定t依次等于0,ω,2ω,3ω,…,iω时,每一个这样的函数都给出同一个x的函数。
我们由此看到,这个问题只可能有一个解,如果我们以任一种方式发现一个满足微分方程和初始状态的函数ψ(x,t),那么我们可以断定它和由方程(E)所给出的前一个函数相同。
281 同一注记可应用于其对象是变化的热运动的所有研究;它显然正好从一般方程的形式得出。
由于这同一原因,方程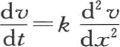 的积分可能只包含一个x的任意函数。事实上,当我们对时间t的某个值给定x的函数v的一个值时,显然,我们就确定了v对应于任一时间的所有其他值。因此,我们可以任意选择对应于某个状态的x的函数,这样就确定了两个变量x和t的一般函数。方程
的积分可能只包含一个x的任意函数。事实上,当我们对时间t的某个值给定x的函数v的一个值时,显然,我们就确定了v对应于任一时间的所有其他值。因此,我们可以任意选择对应于某个状态的x的函数,这样就确定了两个变量x和t的一般函数。方程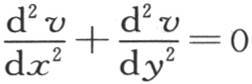 的情况则不同,这种情况在前一章中应用过;它属于不变的热运动。它的积分包含x和t的两个任意函数:但是,只要把终极状态和永恒状态看做是由它前面的状态,因而是由给定的初始状态所产生的,我们就可以把这个研究转化为可变运动的研究。
的情况则不同,这种情况在前一章中应用过;它属于不变的热运动。它的积分包含x和t的两个任意函数:但是,只要把终极状态和永恒状态看做是由它前面的状态,因而是由给定的初始状态所产生的,我们就可以把这个研究转化为可变运动的研究。
我们所给出的积分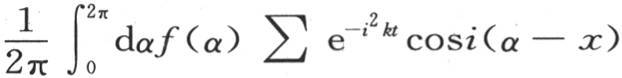 包含一个任意函数f(x),并且和通积分有相同的范围,通积分也只包含x的一个任意函数,更准确地说,它就是以适合于这个问题的形式而被给出的这个积分本身。事实上,由于方程v1 =f(x)表示初始状态,v=φ(x,t)表示继它之后的变化状态,所以我们正好从受热物体的形式看到,当用x±i2π代替x,i是任一整数时,v的值不发生变化。函数
包含一个任意函数f(x),并且和通积分有相同的范围,通积分也只包含x的一个任意函数,更准确地说,它就是以适合于这个问题的形式而被给出的这个积分本身。事实上,由于方程v1 =f(x)表示初始状态,v=φ(x,t)表示继它之后的变化状态,所以我们正好从受热物体的形式看到,当用x±i2π代替x,i是任一整数时,v的值不发生变化。函数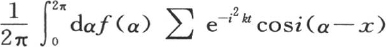 满足这个条件;当我们假定t=0时,它也表示初始状态,因为这时我们有
满足这个条件;当我们假定t=0时,它也表示初始状态,因为这时我们有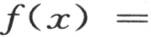
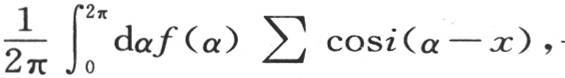 一个在上面第235和279目已经证明且不难验证的方程。最后,这同一函数满足微分方程
一个在上面第235和279目已经证明且不难验证的方程。最后,这同一函数满足微分方程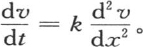 无论t值如何,温度v都正好由一个收敛级数来给定,不同的项表示其组合形成总体运动的那些部分运动。随着时间的增加,高阶部分状态迅速变化,但是它们的影响变得微不足道;因此,应当对指数i所给定的那些值的数目不断减少。在一定时间之后,温度系统就明显地由一旦对i给定值0、±1和±2就能得到的那些项来表示,或者是只由对i给定0和±1所得到的项,或者是最后,只由这些项的第一项,即
无论t值如何,温度v都正好由一个收敛级数来给定,不同的项表示其组合形成总体运动的那些部分运动。随着时间的增加,高阶部分状态迅速变化,但是它们的影响变得微不足道;因此,应当对指数i所给定的那些值的数目不断减少。在一定时间之后,温度系统就明显地由一旦对i给定值0、±1和±2就能得到的那些项来表示,或者是只由对i给定0和±1所得到的项,或者是最后,只由这些项的第一项,即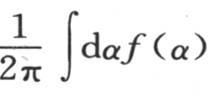 来表示;因此,在这个解的形式和服从于分析的物理现象的进程之间存在着明显的联系。
来表示;因此,在这个解的形式和服从于分析的物理现象的进程之间存在着明显的联系。
282 为了得到解,我们首先考虑满足微分方程的函数v的简单值:这样,我们形成与初始状态一致,因而具有属于这个问题所有普遍性的一个值。我们可以采用一个不同的过程,并从这个积分的另一表达式导出同样的解;一旦这个解已知,这些结果就容易变换,如果我们假定环的平均截面的直径无限增加,那么,正如我们在后面将要看到的,函数φ(x,t)就得到一个不同的形式,并且与在定积分符号下只含单个任意函数的积分相同。这后一个积分也可以应用到这个实际问题上去,但是,如果我们只限于这种应用,那么我们就只有关于这类现象的很不完善的知识;因为这些温度值不由收敛级数来表示,当时间增加时,我们不能区分彼此相继的状态。因此应当把这个问题所假定的周期形式归之于表示初始状态的函数;但是一旦以这种方式改变那个积分,我们就得到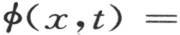
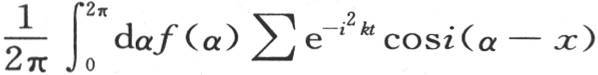 而不会有别的结果。
而不会有别的结果。
正如在本书之前的研究报告中所证明的,我们从最后这个方程不难过渡到所讨论的积分上来。要从这个积分本身得到这个方程不会更难。这些变换使这些分析结果的一致性更加显然;但是它们并没有对这个理论增加任何东西,并没有构成任何不同的分析。在下面几章的一章中,我们将考查可由方程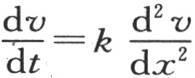 的积分所假定的不同形式,它们不得不具有的相互联系,以及它们应当在其中被应用的情况。
的积分所假定的不同形式,它们不得不具有的相互联系,以及它们应当在其中被应用的情况。
为了建立表示环的热运动的积分,我们有必要把一个任意函数分解成一个多重弧的正弦和余弦级数;对符号sin和cos下的变量起作用的数是自然数1,2,3,4,…。在下面的问题中,任意函数再次被化成一个正弦级数;但是,在符号sin下的这个变量的系数不再是数1,2,3,4,…:这些系数满足一个定义方程,该方程的根都是不可通约的,并且数目无穷。
第四章第1节注。佛罗伦萨的吉列尔莫·利布里(Guglielmo Libri)是在杜隆和珀蒂建立的冷却定律的假定上研究热运动问题的第一个人。见他的“关于热理论的论文”(Mémoire sur la théorie de la chaleur),《克雷尔学报》,第7卷,第116—113页,柏林,1831年。(1825年在法兰西科学院宣读)。利布里先生使解依赖于一组偏微分方程,就像它们是线性方程那样处理这些方程。凯兰(Kelland)先生以不同的方法讨论了这些方程,见他的《热的理论》(Theory of Heat),第69—75页,剑桥,1837年。所得到的主要结果是环的任一直径的两个相对的端点的平均温度在同一时刻相同。——A. F.
注释
【1】 式中的a,和b,在英译本中,是a和b,此处是按法文《文集》本改定的。——汉译者
【2】 在法文《文集》本中,环的永恒温度的方程是v=aα-x +bαx ,1807年的研究报告则与英译本相同。按理算,应是《文集》本有误。——汉译者
【3】 在英译本中,此式右边括号内每一项中带e的因式,其指数均为正,但法文《文集》本和1807年的研究报告则为负。故改之。——汉译者
【4】 在上面一个方程以及这一个方程中,法文《文集》本与英译本有点不同,英译本中的m,在法文本中是m′,它表示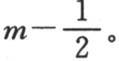 我们把法文《文集》本中的相关叙述转译如下:
我们把法文《文集》本中的相关叙述转译如下:
……则我们得到sinm′u=(q+2)sin(m′-1)u-sin(m′-2)u,m′表示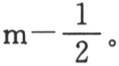
比较这个方程和下面的方程:sinm′u=2cosusin(m′-1)u-sin(m′-2)u,该方程表示一个已知的性质,我们因而得到q+2=2cosu或者q=-2versinu;剩下的只是确定弧u的值。——汉译者
【5】 versin,正矢,即versinθ=1-cosθ。傅立叶经常用“sinusvers”或者是“sinv”来表示正矢。——汉译者
【6】 英文本中没有这句话,但法文《文集》本中有。——汉译者
