第九章 热扩散
·Chapter IX Of the Diffusion of Heat·
虽然傅立叶的理论在学术界引起过争议,但作为一名科学家,一个有学问的人,他的品行却从未遭受过非议。傅立叶有极好的口才、广泛的兴趣和丰富的想象力,为人正直、诚实、热情。教学上循循善诱。工作起来一丝不苟。

格勒诺布尔市景
第一节 无穷直线中的自由热运动
342 这里,我们考虑在一个同质固体中的热运动,这个固体的长、宽、高都是无穷的。这个固体被无穷密并且与公共轴垂直的无数平面所分割;并且首先假定这个固体只有一部分已经被加热,即只有包含在两个平行平面A和B之间的那一部分被加热,这两个平面A和B的距离是g;其他所有部分取初始温度为0;不过包含在A和B之间的任一平面都有一给定的初始温度,这一初始温度可看做是任意的,并且在平面上的每一点都相同;不同平面上的温度则不同。因此,由于这个固体的初始温度已经被定义,所以需要用分析来确定所有的后继状态。所讨论的这种运动完全是线性的,并且沿平面的轴的方向进行,因为显然,由于平面上每一点的初始状态是一样的,所以在垂直于轴的任一平面上不可能有任何热传导。
代替无穷固体,我们可以假定很细的一个棱柱,它的侧面完全不透热。这时,这种运动就可以仅仅看做是无穷直线运动,该直线是棱柱所有截平面的公共轴。当我们对固体已经被加热的部分的所有点赋予完全任意的温度,而取固体其他所有点的初始温为0时,这个问题就更一般了。无穷固体中的热分布规律应当有一个简单而显著的特征;因为这种运动不受表面障碍或介质作用的干扰。
343 由于每一点的位置涉及三个直角坐标轴,我们在这三个轴上测定坐标x,y,z,所以,所求的温度是变量x,y,z和时间t的函数。这个函数v或者是φ(x,y,z)满足一般方程
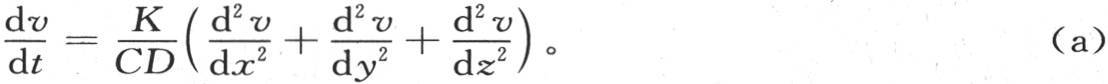
此外,它必然表示初始状态,这个初始状态是任意的;因此,用F(x,y,z)表示在时间为0,即在热扩散开始时在任一点所取的给定温度值,我们必定有

因此我们应当找到一个四变量x,y,z,t的函数v,该函数满足微方程(a)和定义方程(b)。
在我们前面所讨论的问题中,这个积分服从于由表面状态所决定的第三个条件:因此,这一分析更加复杂,其解需要运用指数项。当这个解只需满足初始条件时,这个积分形式就简单得多了;并且不难立即确定三维的热运动。但是,为了阐明理论的这一部分,并且确定扩散根据什么规律而进行,我们最好首先考虑线性运动,同时把它分解成下面的两个问题:我们在后面会看到它们怎样应用于三维的情况。
344 第一个问题:一条无穷直线的一部分ab在所有点上都被升高到温度1;直线的其他点的实际温度为0;假定热不能扩散到周围介质中去;我们不得不确定在一给定时间之后这条直线的状态是怎样的。我们可以使这个问题更一般,这就是假定第一,包含在a和b之间的点的初始温度是不等的,并且由任一曲线的纵坐标表示,我们首先把该曲线看做是由两个对称部分所组成的(见图16);第二,部分热通过固体表面而扩散,该固体是一个非常细而无穷长的棱柱。
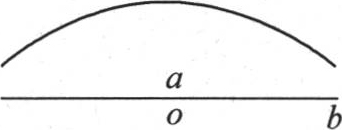
图16
第二个问题在于确定一端受恒温作用的一个无穷长棱柱棒的后继状态。这两个问题的解取决于方程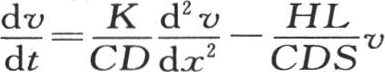 的积分(第105目),这个方程表示线性热运动。v是与原点距离为x的点在历经时间t之后所必然具有的温度;K,H,C,D,L,S表示内热导率,表面热导率,比热,密度,垂直截面的围道和这个截面的面积。
的积分(第105目),这个方程表示线性热运动。v是与原点距离为x的点在历经时间t之后所必然具有的温度;K,H,C,D,L,S表示内热导率,表面热导率,比热,密度,垂直截面的围道和这个截面的面积。
345 在第一个例子中考虑热在一条无穷直线中自由传导的情况,这条直线的一部分ab已经得到任一初始温度;其他所有点的初始温度为0。我们在这根棒的每一个点上都建立一个平面曲线的纵坐标,以表示在那一点的实际温度,我们看到,对于某个时间值t,这个固体的状态由这条曲线的形状来表示。用v=F(x)表示与给定初始状态相对应的方程,为使研究更为简单,首先假定这条曲线的初始形状由两个对称的部分组成,这样我们有条件F(x)=F(-x)。设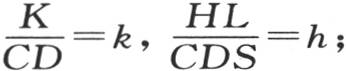 在方程
在方程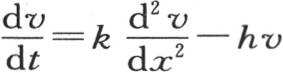 中令v=e-ht u,我们有
中令v=e-ht u,我们有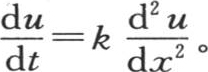
假定u的一个特殊值,即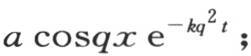 a和q是任意常数。设a1 ,a2 ,a3 ,…是对应于系数a的一组值,q1 ,q2 ,q3 ,…是q的一组任意值, 【1】 则我们有
a和q是任意常数。设a1 ,a2 ,a3 ,…是对应于系数a的一组值,q1 ,q2 ,q3 ,…是q的一组任意值, 【1】 则我们有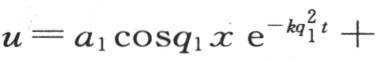
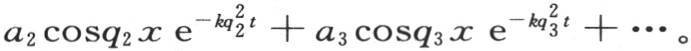 首先假定,作为某一条曲线的横轴q,值q1 ,q2 ,q3 ,…以无穷小的度数增加;因此它们等于dq,2dq,3dq,…;dq是这根横轴的常微分;其次假定值a1 ,a2 ,a3 ,…与同一曲线的纵坐标Q成正比,并假定它们等于Q1 dq,Q2 dq,Q3 dq,…,Q是q的某个函数。由此得到u的值可以表示成:
首先假定,作为某一条曲线的横轴q,值q1 ,q2 ,q3 ,…以无穷小的度数增加;因此它们等于dq,2dq,3dq,…;dq是这根横轴的常微分;其次假定值a1 ,a2 ,a3 ,…与同一曲线的纵坐标Q成正比,并假定它们等于Q1 dq,Q2 dq,Q3 dq,…,Q是q的某个函数。由此得到u的值可以表示成: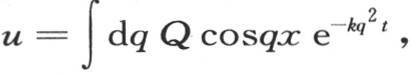 Q是一个任意函数f(q),这个积分可以从q=0取到q=∞。现在困难被简化成适当确定函数Q了。
Q是一个任意函数f(q),这个积分可以从q=0取到q=∞。现在困难被简化成适当确定函数Q了。
346 为了确定Q,我们应当假定在u的表达式中t=0,并使u等于F(x)。因此我们有条件方程F(x)=∫dqQ cosqx。
如果我们用q的任一个函数代替Q,并且把这个积分从q=0积到q=∞,那么我们会得到x的一个函数:需要解决的是问题的逆,即需要确定,在对Q作代换后,q的什么函数最后给出函数F(x),这是一个值得注意的问题,它的解需要仔细加以考虑。
展开积分号,我们记必然导出Q值的方程如下:F(x)=dq Q1 cosq1 x+dq Q2 cosq2 x+dq Q3 cosq3 x+…。
为了使右边除某一项外其他所有项都消掉,用dx cosrx乘两边,然后对x从x=0到x=nπ积分,此处n是一个无穷大的数,r表示等于q1 ,q2 ,q3 ,…之中的、或者同样地,等于dq,2dq,3dq,…之中的任一个量。设qi 是变量q的任一个值,qj 是另一个值,即我们为r所取的值,我们有r=j dq和q=i dq。然后把无穷大的数n看做是表示含基元dq的单位长度多少倍的数,因此我们有 取积分,我们得到,只要r和q取不同的量,积分∫dx cosqx cosrx的值就为0;但是当q=r时,它的值是
取积分,我们得到,只要r和q取不同的量,积分∫dx cosqx cosrx的值就为0;但是当q=r时,它的值是 这由积分除保留右边某一项,即除保留含qj 或者是r的项外消去所有其他项这一事实得出。对这同一项起作用的函数是Qj ,因此我们有
这由积分除保留右边某一项,即除保留含qj 或者是r的项外消去所有其他项这一事实得出。对这同一项起作用的函数是Qj ,因此我们有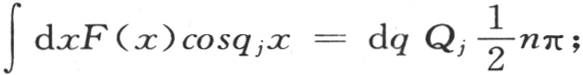 对n dq代之以它的值1,我们有
对n dq代之以它的值1,我们有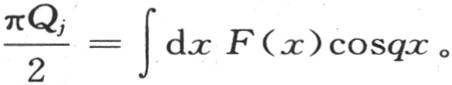 因而一般地,我们得到
因而一般地,我们得到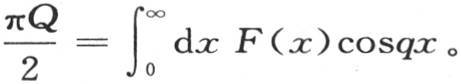 所以,为了确定满足所提出的条件的函数Q,我们应当用dx cosqx乘已知函数F(x),并且取从x等于0到x等于无穷的积分,同时用
所以,为了确定满足所提出的条件的函数Q,我们应当用dx cosqx乘已知函数F(x),并且取从x等于0到x等于无穷的积分,同时用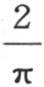 乘这个结果;即我们由方程
乘这个结果;即我们由方程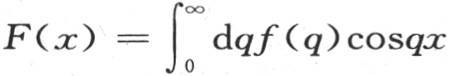 推出
推出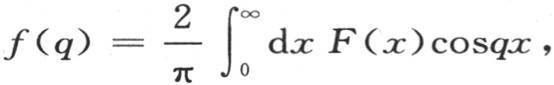 函数F(x)表示仅中间部分受热的一个无穷棱柱的初始温度。在这个表达式中用f(q)的值代替F(x),我们得到一般方程
函数F(x)表示仅中间部分受热的一个无穷棱柱的初始温度。在这个表达式中用f(q)的值代替F(x),我们得到一般方程
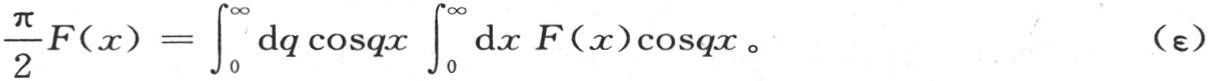
347 如果我们在v的表达式中用我们所得到的这个值代替函数Q,那么我们有下面的积分,它包含所提出的问题的全解,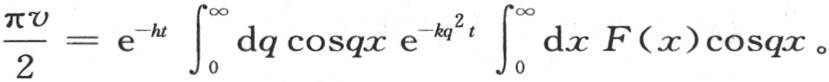
由于对x的积分是从x=0取到x等于无穷,所以结果是q的一个函数;然后相对q从q=0到q=∞取积分,我们就得到v等于x和t的一个函数,它表示固体的连续状态。由于对x的积分使变量x消去,所以在v的表达式中可以用任一变量α来代替它,积分在同一区间内取,即从α=0取到α=∞。这样,我们有 F(α)cosqa,或者是
F(α)cosqa,或者是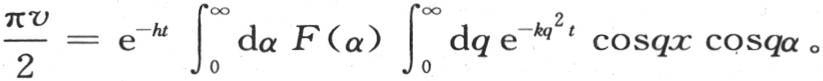
对q的积分给出x,t和α的一个函数,在对α取积分时,我们得到只有x和t的一个函数。在后一个方程中不难完成对q的积分,并且因此会改变v的表达式。一般地,我们可以对方程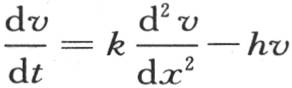 的积分给出不同的形式,它们都表示x和t的同一个函数。
的积分给出不同的形式,它们都表示x和t的同一个函数。
348 首先假定包含在a和b之间从x=-1到x=1的所有点的初始温度都有共同值1,所有其他点的初始温度是0,函数F(x)由这个条件给出。这时,对x的积分从x=0取到x=1,因为由假定,这个积分的其他部分为0。因此我们得到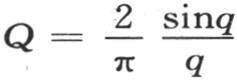 和
和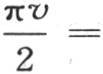
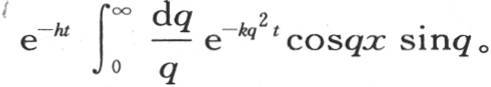
如前面所见到的,我们不难把右边变成一个收敛级数;它严格表示固体在一给定时刻的状态,如果我们在其中令t=0,那么它表示初始状态。
因此,如果我们对x给定包含在-1到1之间的任一个值,那么函数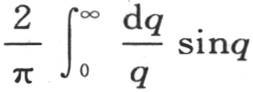
 就等于1;但是如果对x给定-1到1区间之外的任一个值时,则这个函数为0。由此我们看到不连续函数也可以用定积分来表示。
就等于1;但是如果对x给定-1到1区间之外的任一个值时,则这个函数为0。由此我们看到不连续函数也可以用定积分来表示。
349 为了给出前面公式的第二种用法,让我们假定这根棒的某一点已经由同一热源的恒定作用而被加热,并假定它已经达到其永恒状态,已知这个状态由一条对数曲线表示。
需要确定的是在撤掉热源后热扩散以什么规律进行。用F(x)表示温度的初始值,我们有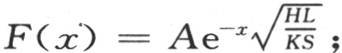 A是最热的那一点的初始温度。为简化这一研究,让我们令A=1,
A是最热的那一点的初始温度。为简化这一研究,让我们令A=1,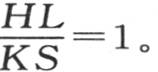 这时我们有F(x)=e-x ,由此我们推得
这时我们有F(x)=e-x ,由此我们推得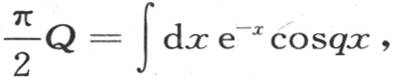 从x等于0到x等于无穷取积分,则
从x等于0到x等于无穷取积分,则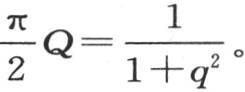 因此,含x和t的v值由下述方程给出:
因此,含x和t的v值由下述方程给出: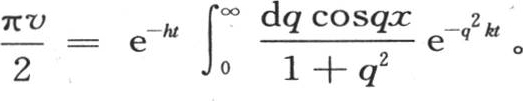
350 如果我们令t=0,那么我们有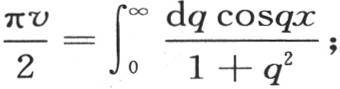 它对应于初始状态。因此,表达式
它对应于初始状态。因此,表达式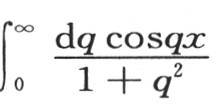 等于e-x 。我们应当注意,根据假定,当x变成负数时,表示初始状态的函数F(x)不改变它的值。在初始状态形成之前由热源所传递的热同等地从点0向左右两边传导,点0直接得到这些热:由此得到,其方程为
等于e-x 。我们应当注意,根据假定,当x变成负数时,表示初始状态的函数F(x)不改变它的值。在初始状态形成之前由热源所传递的热同等地从点0向左右两边传导,点0直接得到这些热:由此得到,其方程为 的曲线由两个对称的分支组成,这两个分支由一条对数曲线的一部分在y轴的左右两边重复而形成,这条对数曲线的这一部分在y轴的右边,这条对数曲线的方程是y=e-x 。这里,我们看到不连续函数由定积分表示的第二个例子。当x为正时,函数
的曲线由两个对称的分支组成,这两个分支由一条对数曲线的一部分在y轴的左右两边重复而形成,这条对数曲线的这一部分在y轴的右边,这条对数曲线的方程是y=e-x 。这里,我们看到不连续函数由定积分表示的第二个例子。当x为正时,函数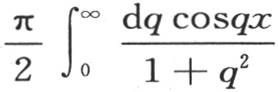 等于e-x ,但是当x为负时,它是ex 【2】 。
等于e-x ,但是当x为负时,它是ex 【2】 。
351 正如我们即将看到的,一端受恒温作用的无穷长棒的热传导问题可以简化成一条无穷直线的热扩散问题;但是必须假定初始热不是同等地作用于这个固体的两个相邻部分,而是以相反的方式分布;即若用F(x)表示与这条直线中点距离为x的一点的温度时,距离为-x的相对点的初始温度值为-F(x)。
这第二个问题与前面的问题差别甚小,并且可以用类似的方法来解:不过这个解也可以根据我们用来确定一个有限体积的固体中的热运动的分析导出。
假定无穷棱柱棒的一部分ab已经以任一方式被加热,见(图16* ),并且相对的部分aβ处于类似的状态中,只是符号相反;这个固体的所有其余部分的初始温度为0。同时假定周围介质保持恒温0度不变,它或者从这根棒那里得到热,或者通过棒的外表面向这根棒传热。要求的是在一给定时间t之后,与原点距离为x的点的温度将是怎样的。
图16*
我们首先考虑这根被加热的棒有有限长度2X,并且受某种外因作用,这种作用使它在两端保持恒温0度不变;然后我们令X=∞。
352 我们先运用方程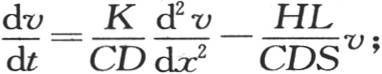 或者是
或者是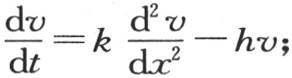 令v=e-ht u,我们有
令v=e-ht u,我们有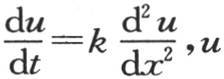 的一般值可表示如下:
的一般值可表示如下: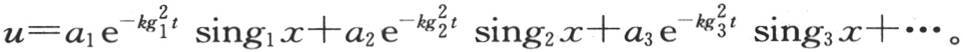 这时令x=X,它应当使v的值为0,为了确定这一系列指数g,我们有条件singX=0或者是gX=iπ,i是一个整数。
这时令x=X,它应当使v的值为0,为了确定这一系列指数g,我们有条件singX=0或者是gX=iπ,i是一个整数。
因此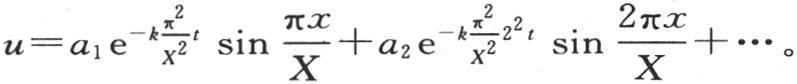
剩下的只是求一系列常数a1 ,a2 ,a3 ,…,令t=0,我们有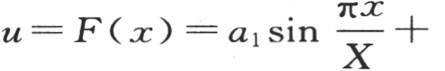
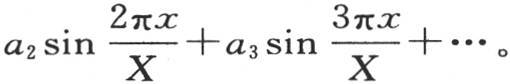
设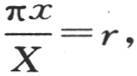 并且用f(r)表示F(x)或者是
并且用f(r)表示F(x)或者是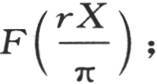 我们有f(r)=a1 sinr+a2 sin2r+a3 sin3r+…。
我们有f(r)=a1 sinr+a2 sin2r+a3 sin3r+…。
我们以前曾得到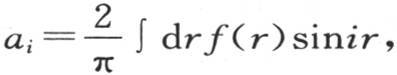 积分从r=0取到r=π。因此
积分从r=0取到r=π。因此
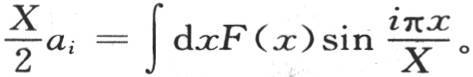
对x的这个积分必须从x=0取到x=X。作这些代换,我们建立方程
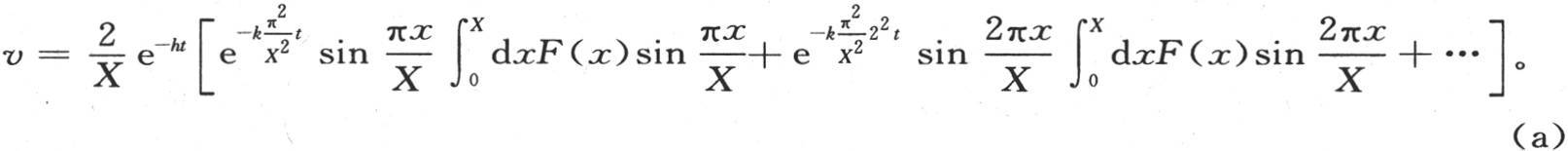
353 如果棱柱有以2X所表示的有限长度,那么上述方程就是解。这是我们到现在为止所建立的这些原理的一个明显的推论;现在只需假定长度X是无穷的。设X=nπ,n是一个无穷大的数;同时q是一个变量,它的无穷小增量dq都相等;我们用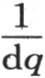 代替n。由于进入方程(a)的级数的通项是
代替n。由于进入方程(a)的级数的通项是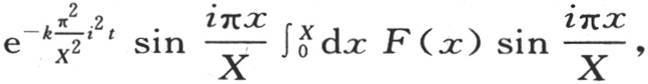 所以我们用
所以我们用 表示数i,它是可变的,且变成无穷大。因此我们有
表示数i,它是可变的,且变成无穷大。因此我们有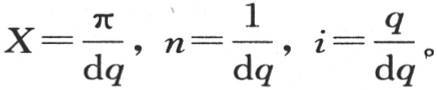
在所说的项中作这些代换,我们得到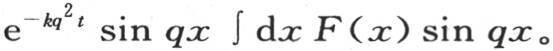 每一个这样的项都必须用X或者是
每一个这样的项都必须用X或者是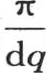 来除,因而变成无穷小量,这个级数的和不过是一个积分,它必须相对q从q=0到q=∞积分。因此
来除,因而变成无穷小量,这个级数的和不过是一个积分,它必须相对q从q=0到q=∞积分。因此
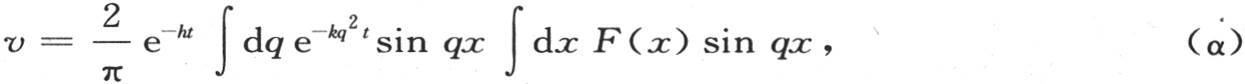
对x的这个积分应当从x=0取到x=∞。我们也可以写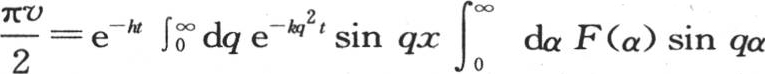 或者是
或者是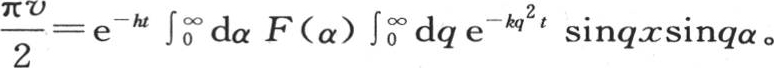
方程(α)包含问题的通解;并且,用任意一个服从或者是不服从于连续性规律的函数来代替F(x),我们都总能够根据x和t来表示温度的值:只是应当注意函数F(x)与由两个相等的并且交变的部分所组成的一条曲线相对应 【3】 。
354 如果棱柱中的初始热以这样一种方式分布:表示初始状态的曲线FFFF(图17)由位于固定点O的左右两条相等的弧所组成,那么变化的热运动就由方程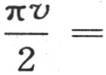
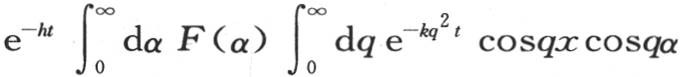 来表示。
来表示。
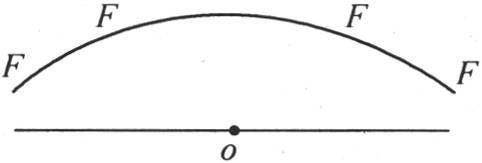
图17
如果表示初始状态的曲线ffff(图18)由两个相似并且交变的弧组成,那么给出温度值的积分就是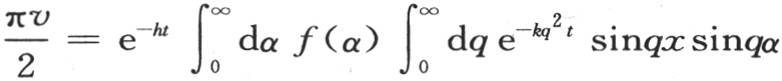
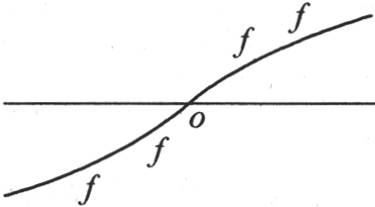
图18
如果我们假定初始热以任一方式分布,那么不难根据前面的二个解导出v的表达式。事实上,无论表示给定的初始温度的函数φ(x)怎样,它都总可以分解成两个其他函数F(x)+f(x),其中一个对应于曲线FFFF,另一个与曲线ffff相对应,因此,我们有这样三个条件:F(x)=F(-x),f(x)=-f(-x),φ(x)=F(x)+f(x)。
我们在第233第234目中已经使用过这个注记。我们也知道,每一个初始状态都引起仿佛独立存在的一个可变的部分状态。这三个不同状态的合成并不把变化引进到分别由它们每一个所引起的温度中去。由此得到,用v代表由表示全函数φ(x)的初始状态所产生的变化温度,我们肯定有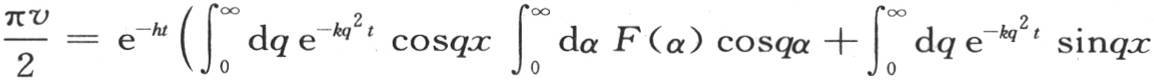
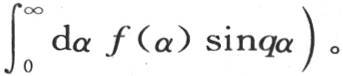
如果我们在-∞到+∞之间对α取这些积分,那么显然,我们会使这个结果翻一倍。这样,在前面的方程中,我们可以略去左边的分母2,并且在这第二种形式中对α从α=-∞到a=+∞取这些积分。我们还不难看到,我们可以用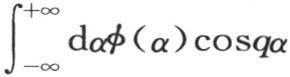 来代替
来代替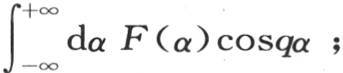 因为,由函数f(α)所服从的这个条件可以得出,我们应当有
因为,由函数f(α)所服从的这个条件可以得出,我们应当有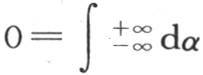
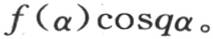 我们也可以用
我们也可以用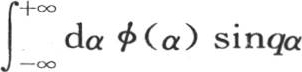 代替
代替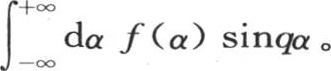 因为我们显然有
因为我们显然有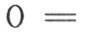
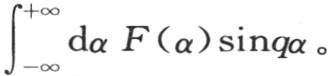 由此我们得到
由此我们得到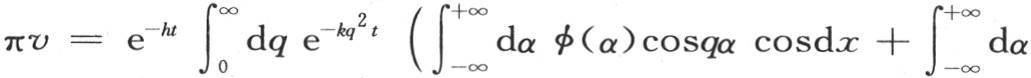
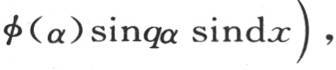 或者是
或者是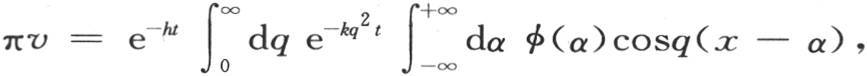 或者是
或者是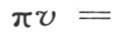
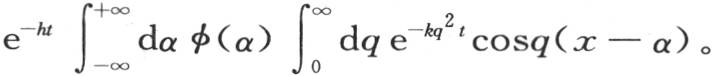
355 这第二个问题的解清楚地指明在我们刚才所运用的定积分和我们对一个有限形状的固体所运用的分析结果之间有什么样的联系。在这一分析所提供的收敛级数中,当我们对表示长度的量给出无穷值时;这些项的每一个都变得无穷小,并且除一个积分之外级数和为0。我们也可以用同样的方法而无需用任何物理上的考虑,直接从我们在第三章所应用过的这些不同三角级数得到这些定积分;我们只需给出这些变换的某些例子就够了,这些例子中的结果是值得注意的。
356 在由第188目和第222目中所给出的方程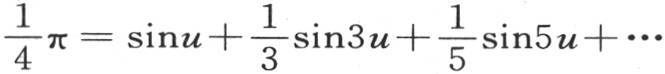 中,我们用量
中,我们用量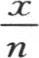 来代替u;x是一个新变量,n是一个等于
来代替u;x是一个新变量,n是一个等于 的无穷大的数;q是由等于dq的无穷小量逐次相加而形成的一个量。我们用
的无穷大的数;q是由等于dq的无穷小量逐次相加而形成的一个量。我们用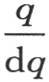 表示变数i。如果在通项
表示变数i。如果在通项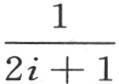
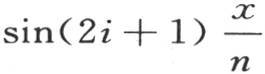 中,我们让i和u代之以它们的值,那么这个项就变成
中,我们让i和u代之以它们的值,那么这个项就变成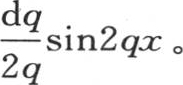 这样,级数和是
这样,级数和是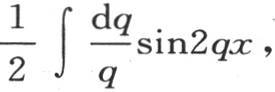 积分从q=0取到q=∞;因此我们有方程
积分从q=0取到q=∞;因此我们有方程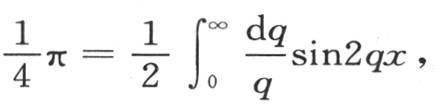 无论x有怎样的正值,这个等式都成立。令2qx=r,r是一个新变量,我们有
无论x有怎样的正值,这个等式都成立。令2qx=r,r是一个新变量,我们有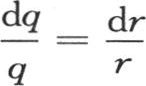 和
和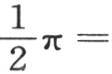
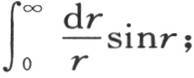 人们知道定积分
人们知道定积分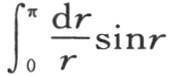 的这个值已经有一段时间了。如果在假定r为负时我们从r=0到r=-∞取这个积分,那么我们显然会得到反号的结果
的这个值已经有一段时间了。如果在假定r为负时我们从r=0到r=-∞取这个积分,那么我们显然会得到反号的结果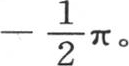
357 我们刚才对等于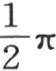 或者是
或者是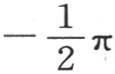 的积分
的积分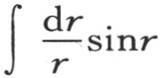 的值所作的注记可以用来弄清表达式
的值所作的注记可以用来弄清表达式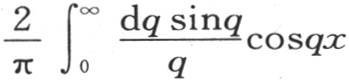 的性质,这个式子的值我们已经求出(第348目),它随x在或不在1到-1之间而等于1或0。
的性质,这个式子的值我们已经求出(第348目),它随x在或不在1到-1之间而等于1或0。
事实上,我们有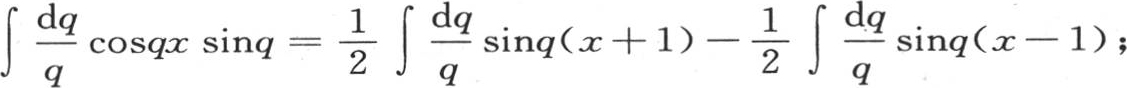 第一项随x+1是一个正数或者是负数而等于
第一项随x+1是一个正数或者是负数而等于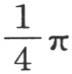 或者是
或者是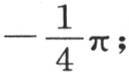 第二项
第二项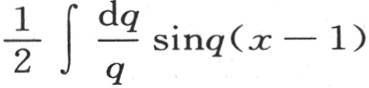 随x-1是正数或者是负数而等于
随x-1是正数或者是负数而等于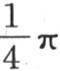 或者是
或者是 这样,如果x+1和x-1有相同的符号,那么整个积分为0;因为,在这种情况下这两项相互抵消。但是,如果这些量有不同的符号,即如果我们同时有x+1>0并且x-1<0,那么这两项加起来,这个积分的值就是
这样,如果x+1和x-1有相同的符号,那么整个积分为0;因为,在这种情况下这两项相互抵消。但是,如果这些量有不同的符号,即如果我们同时有x+1>0并且x-1<0,那么这两项加起来,这个积分的值就是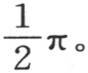 因此,定积分 【4】
因此,定积分 【4】 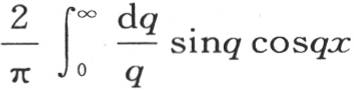 是x的一个函数,如果变量x取包含在1到-1之间的任一个值,则它等于1;对于其他不包含在区间1到-1之间的每一个x的值,这个函数等于0。
是x的一个函数,如果变量x取包含在1到-1之间的任一个值,则它等于1;对于其他不包含在区间1到-1之间的每一个x的值,这个函数等于0。
358 我们还能够从进入这些积分的级数的变换推出两个式子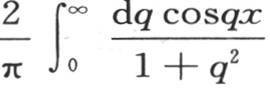 和
和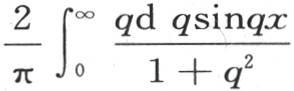 的性质 【5】 ,第一个式子在x为正时等价于e-x ,x为负时等价于ex 。第二个在x为正时等价于e-x ,在x为负时等价于-ex ,因此当x为正时这两个积分有相同的值,当x为负时它们有反号值。它们一个由曲线eeee来表示(图19),另一个由曲线εεεε表示(图20)。
的性质 【5】 ,第一个式子在x为正时等价于e-x ,x为负时等价于ex 。第二个在x为正时等价于e-x ,在x为负时等价于-ex ,因此当x为正时这两个积分有相同的值,当x为负时它们有反号值。它们一个由曲线eeee来表示(图19),另一个由曲线εεεε表示(图20)。
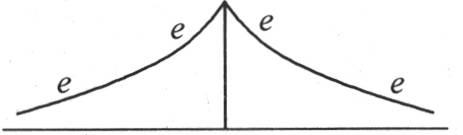
图19
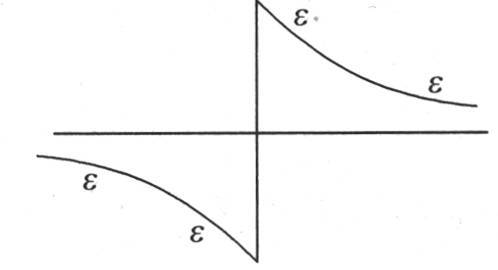
图20
我们(在第226目)所得到的方程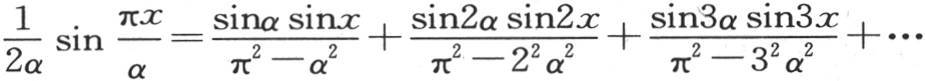 立即给出积分
立即给出积分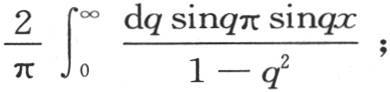 如果x包含在0到π之间,那么这个表达式 【6】 等价于sinx,只要x超过π,则它的值为0。
如果x包含在0到π之间,那么这个表达式 【6】 等价于sinx,只要x超过π,则它的值为0。
359 同一变换适用于一般方程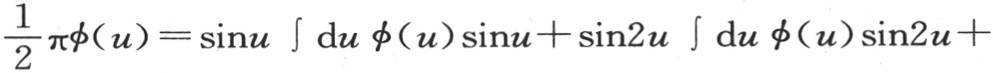 …。令
…。令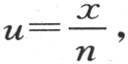 用f(x)表示φ(u)或者是
用f(x)表示φ(u)或者是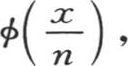 并在这一分析中引入量q,若q得到等于dq的一些无穷小增量,则n等于
并在这一分析中引入量q,若q得到等于dq的一些无穷小增量,则n等于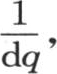 i等于
i等于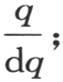 把这些值代入通项
把这些值代入通项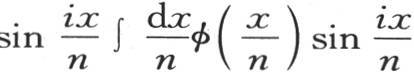 中,我们得到dq sinqx∫dxf(x)sinqx。对u的积分从u=0取到u=π,因此,对x的积分应当从x=0取到x=nπ,或者从x等于0取到x等于无穷大。
中,我们得到dq sinqx∫dxf(x)sinqx。对u的积分从u=0取到u=π,因此,对x的积分应当从x=0取到x=nπ,或者从x等于0取到x等于无穷大。
因此我们得到由方程
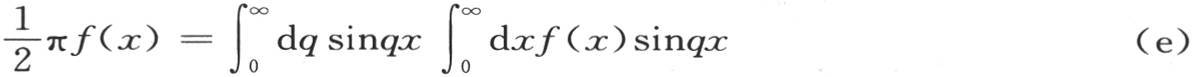
所表示的一个一般的结果,由此,用Q表示q的一个函数,使得我们有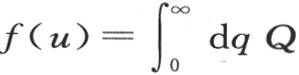
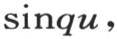 其中f(u)是一个已知函数的方程,则我们有
其中f(u)是一个已知函数的方程,则我们有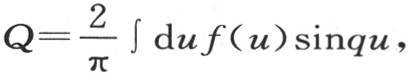 积分从u等于0取到u等于无穷大。我们已经解决了一个类似的问题(第346目),并证明了一般方程
积分从u等于0取到u等于无穷大。我们已经解决了一个类似的问题(第346目),并证明了一般方程
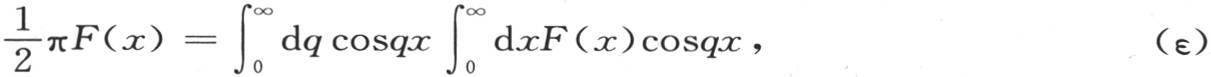
它与前面的方程类似。
360 为了给出这些定理的应用,让我们假定f(x)=xr ,方程(e)的右边通过这个代换变成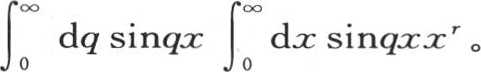
积分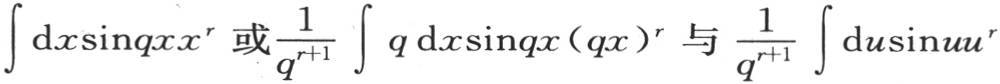 等价,后一个积分从u等于0取到u等于无穷。
等价,后一个积分从u等于0取到u等于无穷。
设μ是积分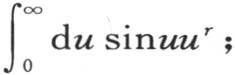 剩下的事情是构造积分
剩下的事情是构造积分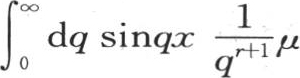 或者是
或者是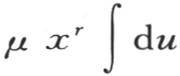
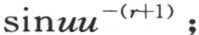 用ν表示最后这个积分,它从u等于0取到u等于无穷,作为两个连续积分的结果,我们有项xr μν。根据方程(e)所表示的条件,这时我们肯定有
用ν表示最后这个积分,它从u等于0取到u等于无穷,作为两个连续积分的结果,我们有项xr μν。根据方程(e)所表示的条件,这时我们肯定有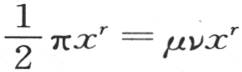 或者是
或者是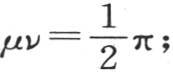
因此,这两个超越数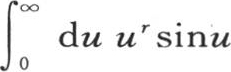 和
和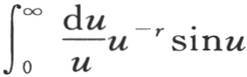 的积是
的积是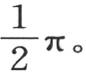 例如,如果
例如,如果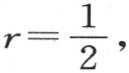 那么我们得到已知的结果
那么我们得到已知的结果

同样我们得到

从这两个方程我们还可以得到下述结果 【7】 ,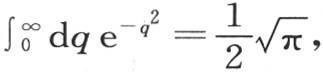 这个结果已被运用了一段时间了。
这个结果已被运用了一段时间了。
361 通过方程(e)和(ε),我们可以解决也属于偏微分分析的下面一个问题。为了使表达式∫dqQ e-qx 能够与一个已知函数相等,我们应当把变量q的一个什么函数放到从q等于0到q等于无穷大的积分的积分号之下呢 【8】 ?然而,无需为不同的结果而停下来,对这些结果的考查会使我们远离我们的主要目的,我们只限于下述结果,该结果由合并两个方程(e)和(ε)而得到。
可以把它们置于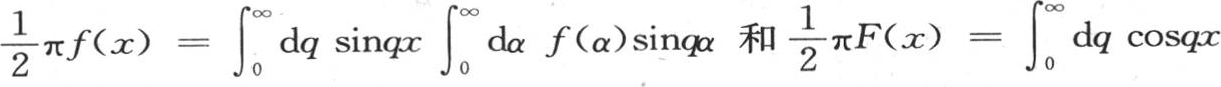
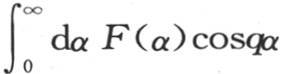 的形式之下。
的形式之下。
如果我们对α从-∞到+∞取这两个积分,那么每个积分的结果将翻一倍,这是两个条件f(α)=-f(-α)和F(α)=F(-α)的必然结论。
因此我们有两个方程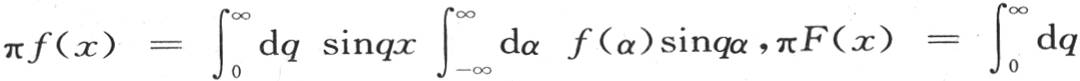
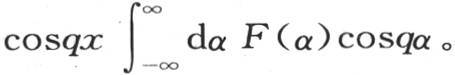
前面我们已经注意到,任一函数φ(x)总可以分解成两个其他的函数,其中一个F(x)满足条件F(x)=F(-x),另一个f(x)满足条件f(x)=-f(-x)。因此我们有两个方程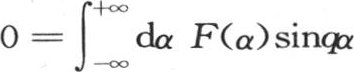 和
和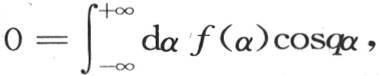 因此我们得到
因此我们得到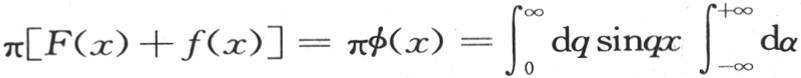
 和
和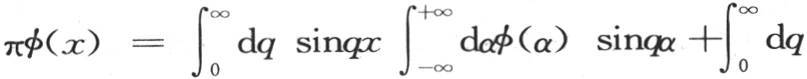
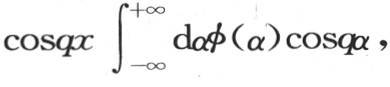 或者是
或者是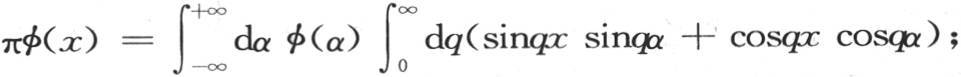 或者是最后 【9】 ,
或者是最后 【9】 ,
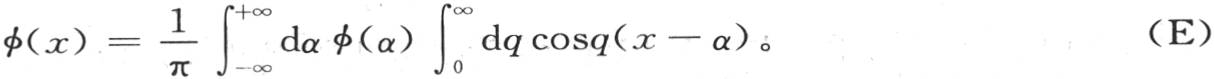
对q的积分给出x和α的一个函数,第二个积分使变量α消掉。因此,由定积分∫dq cosq(x-α)所表示的函数有一个特殊性质,即如果我们用任一函数φ(α)和dα乘它,并在无穷大的界限之间对α取它的积分,那么结果等于πφ(x);因此这个积分的作用就是把α变成x,并乘以数π。
362 我们可以直接从第234目所陈述的定理推出方程(E),第234目的这个定理给出任一函数F(x)以多重弧的正弦和余弦展开的展开式。我们从上一个命题过渡到我们刚才通过对体积赋予无穷值所证明的那些命题。在这种情况下,级数的每一项都变成微分量 【10】 。把函数变换成三角级数,这是热的解析理论的基本原理的一部分;要解决由这一理论所决定的问题,就应当使用这部分原理。
把任意函数化成定积分,例如化成由方程(E)和由导出方程(E)的两个基本方程所表示的定积分,这引出一些不同的结果,我们在此省略了这些结果,因为它们与物理问题没有什么直接的联系。我们只注意同样的方程有时以不同的形式出现在分析中就行了。例如我们得到这样一个结果,
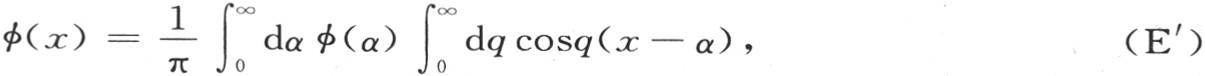
它与方程(E)的不同在于对α所取的积分区间是0到∞,而不是-∞到+∞。
在这种情况下我们应当注意到,当x为正时,两个方程(E)和(E′)对右边给出相等的值。如果变量是负的,方程(E′)就总是对右边给出一个为0的值。方程(E)则不同,无论我们对x给定正值和负值,它的右边都等于πφ(x)。至于方程(E′),它解决下面这个问题。求一个x的函数,使得如果x为正,那么函数的值为φ(x),如果x为负,则函数值总为0 【11】 。
363 对这个偏微分方程的积分给出我们在下一目中将要指明的一种不同的形式时,我们也可以解决无穷直线中的热传导问题。我们先来研究热源恒定的情况。
假定初始热以任一方式分布在整个无穷长棒中,在所传递的一部分热经外表面而扩散的同时,我们使截面A保持一恒温不变。需要确定在一给定时间之后棱柱的状态,这是我们向自己所提出的第二个问题的目的。用1表示末端A的恒温,用0表示介质温度,我们把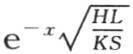 作为与末端距离为x的点的终极温度,或者,若为简便起见,假定量
作为与末端距离为x的点的终极温度,或者,若为简便起见,假定量 等于1,则仅用e-x 作为这一温度。用v表示历经时间t之后这同一点的变化温度,为了确定v,我们有方程
等于1,则仅用e-x 作为这一温度。用v表示历经时间t之后这同一点的变化温度,为了确定v,我们有方程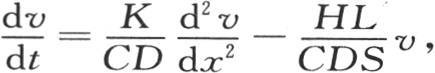 现在设
现在设 我们有
我们有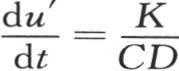
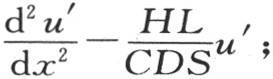 或者用k代替
或者用k代替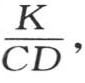 用h代替
用h代替 则有
则有
如果我们令u′=e-ht u,那么我们有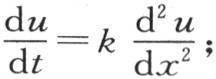 u′或者是
u′或者是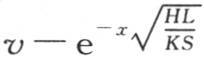 的值是实际温度与终极温度的差值;这个差u′愈来愈趋于0,其终极值就是0,这个差在开始时等于
的值是实际温度与终极温度的差值;这个差u′愈来愈趋于0,其终极值就是0,这个差在开始时等于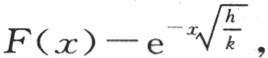 F(x)表示位于距离x处的点的温度。设f(x)是初始温度超过终极温度的超出量,我们应当为u′找到一个满足方程
F(x)表示位于距离x处的点的温度。设f(x)是初始温度超过终极温度的超出量,我们应当为u′找到一个满足方程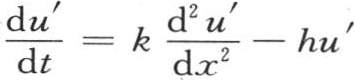 , 【12】 并且其初始值是f(x),终极值是0的函数。在点A或者是x=0处,由假定,量
, 【12】 并且其初始值是f(x),终极值是0的函数。在点A或者是x=0处,由假定,量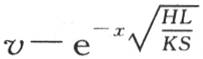 有一个等于0的常数值。由此我们看到,u′表示热的超出量,这个量在开始时在棱柱中聚集,然后,或者是通过向无穷远处传导,或者是通过向介质扩散而逃逸。因此,为了表示在一条无限延长的直线中端点A均匀受热时所产生的作用,我们应当设想,第一,这条直线也向点A的左边延长,并且右边每一点现在受到温度的初始超出量的影响;第二,点A左边的另一半直线处于相反的状态中;这样,与点A距离-x的点有初始温度-f(x):这时热开始在这根棒的内部自由运动,并在表面扩散。
有一个等于0的常数值。由此我们看到,u′表示热的超出量,这个量在开始时在棱柱中聚集,然后,或者是通过向无穷远处传导,或者是通过向介质扩散而逃逸。因此,为了表示在一条无限延长的直线中端点A均匀受热时所产生的作用,我们应当设想,第一,这条直线也向点A的左边延长,并且右边每一点现在受到温度的初始超出量的影响;第二,点A左边的另一半直线处于相反的状态中;这样,与点A距离-x的点有初始温度-f(x):这时热开始在这根棒的内部自由运动,并在表面扩散。
点A保持0度,并且所有其他点明显达到同一状态。如此,我们能够把外部热源不断传递新热的情况看做是初始热通过固体内部而传导的情况。因此,我们能以和第347和353目中热扩散的相同方法解决所提出的问题;不过为了在这样一个新问题中增加解的方法,我们将以不同于我们至今所考虑过的形式来使用这个积分。
364 方程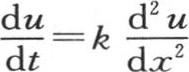 由假定u等于e-x ekt 而被满足。也可以把x和t的这个函数放到一个定积分的形式之下,这个定积分很容易从
由假定u等于e-x ekt 而被满足。也可以把x和t的这个函数放到一个定积分的形式之下,这个定积分很容易从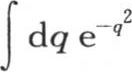 的已知值中推出。事实上,当这个积分从q=-∞取到q=+∞时,我们有
的已知值中推出。事实上,当这个积分从q=-∞取到q=+∞时,我们有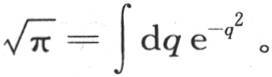 因此我们也有
因此我们也有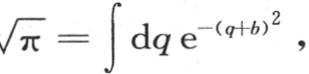 b是任一常数,这个积分的积分区间和前面的一样。由方程
b是任一常数,这个积分的积分区间和前面的一样。由方程 通过令b2 =kt,我们得出
通过令b2 =kt,我们得出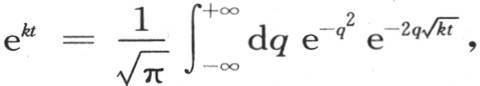 因此前面的u或者是e-x ekt 的值等价于
因此前面的u或者是e-x ekt 的值等价于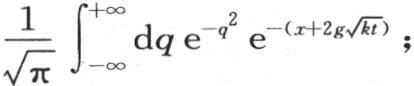 我们还应假定u等于函数
我们还应假定u等于函数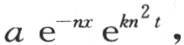 a和n是两个任意常数;同样我们可以得到这个函数等价于
a和n是两个任意常数;同样我们可以得到这个函数等价于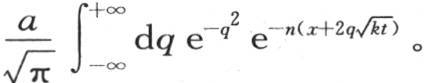 因此一般地,我们可以把u的这个值看做是无数这样的值的和,所以我们有
因此一般地,我们可以把u的这个值看做是无数这样的值的和,所以我们有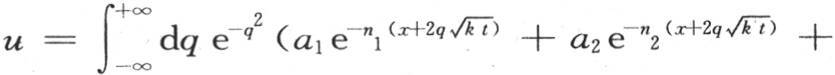
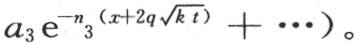 常数a1 ,a2 ,a3 ,…,和n1 ,n2 ,n3 ,…是待定的,这个级数表示
常数a1 ,a2 ,a3 ,…,和n1 ,n2 ,n3 ,…是待定的,这个级数表示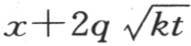 的任一个函数;因此我们有
的任一个函数;因此我们有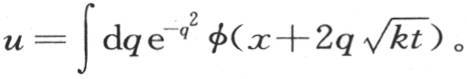 这个积分应当从q=-∞取到q=+∞,u的这个值必然满足方程
这个积分应当从q=-∞取到q=+∞,u的这个值必然满足方程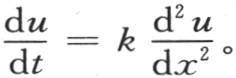 在我们已经开始从事我们的热理论研究时,这种包含一个任意函数的积分还不为人所知,我们于1807年11月把这个积分递交给法国科学院:它现在已经由拉普拉斯 【13】 先生的一个成果给出,该成果构成综合工艺学校研究报告第8卷的一部分;我们仅仅由它来确定线性热运动。我们由它得出
在我们已经开始从事我们的热理论研究时,这种包含一个任意函数的积分还不为人所知,我们于1807年11月把这个积分递交给法国科学院:它现在已经由拉普拉斯 【13】 先生的一个成果给出,该成果构成综合工艺学校研究报告第8卷的一部分;我们仅仅由它来确定线性热运动。我们由它得出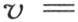
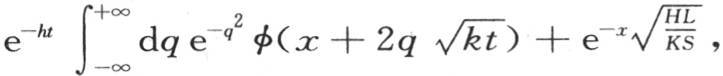 当t=0时,u的值是
当t=0时,u的值是 或者是f(x);所以
或者是f(x);所以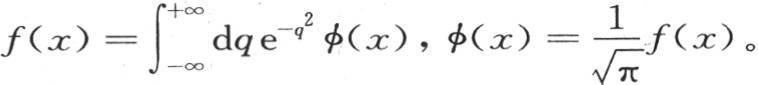 因此进入这个积分的任意函数由已知函数f(x)所确定,并且我们有下面的方程,
因此进入这个积分的任意函数由已知函数f(x)所确定,并且我们有下面的方程,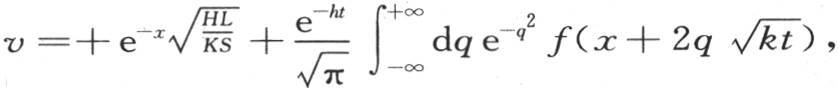 它包含这个问题的解,不难用一个作图来表示这个解。
它包含这个问题的解,不难用一个作图来表示这个解。
365 让我们把前面的解用到直线AB的所有点的温度都为0,端点A因受热而仍然保持1度的情况中去。由此得到,当x不为0时,F(x)的值为0。因此只要x不为0,f(x)就等于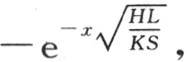 当x为0时,它等于0。另一方面,只要令x为负,f(x)的值就必然变号,因此我们有条件f(-x)=-f(x)。我们由此知道不连续函数f(x)的性质;当x超过0时它变成
当x为0时,它等于0。另一方面,只要令x为负,f(x)的值就必然变号,因此我们有条件f(-x)=-f(x)。我们由此知道不连续函数f(x)的性质;当x超过0时它变成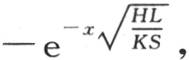 当x小于0时它变成
当x小于0时它变成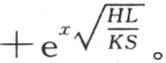 我们现在应当用量
我们现在应当用量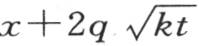 来代替x。为了求u或者是
来代替x。为了求u或者是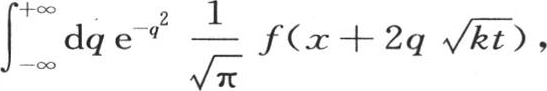 我们应当先从
我们应当先从 到
到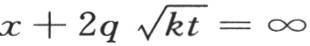 取积分,然后从
取积分,然后从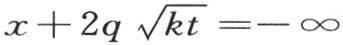 到
到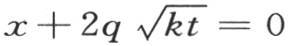 取积分。对于第一部分,我们有
取积分。对于第一部分,我们有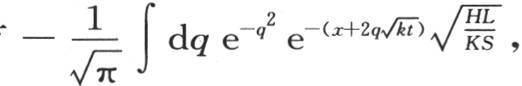 用k的值
用k的值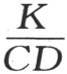 来代替k,我们有
来代替k,我们有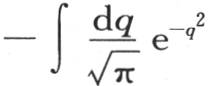
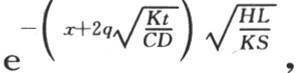 或者是
或者是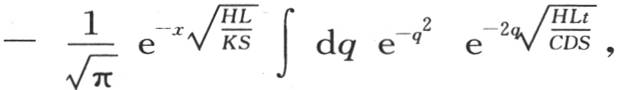 或者是
或者是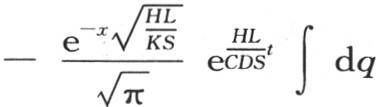
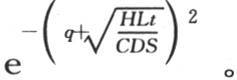 用r表示量
用r表示量 则前面的表达式变成
则前面的表达式变成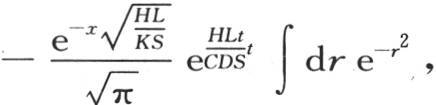 由假定,这个积分
由假定,这个积分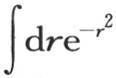 应当从
应当从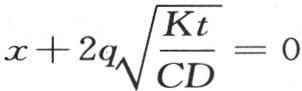 积到
积到 或者是从
或者是从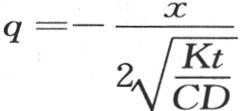 积到q=∞,或者是从
积到q=∞,或者是从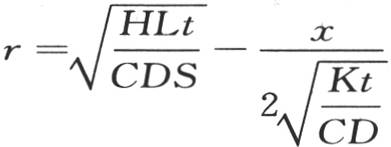 积到r=∞。这个积分的第二部分
积到r=∞。这个积分的第二部分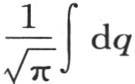
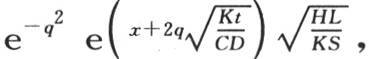 或者是
或者是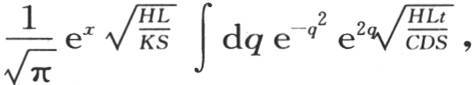 或者是
或者是 r表示量
r表示量 由假定,积分
由假定,积分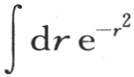 应当从
应当从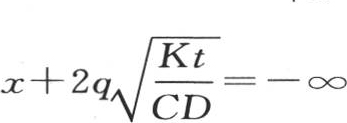 积到
积到 或者是从q=-∞积到
或者是从q=-∞积到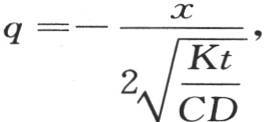 即从r=-∞积到
即从r=-∞积到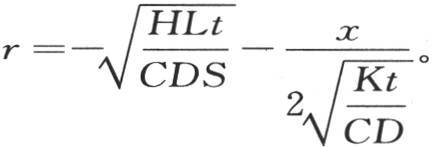 根据函数
根据函数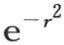 的性质,最后两个积分限可以用这样两个来代替:
的性质,最后两个积分限可以用这样两个来代替: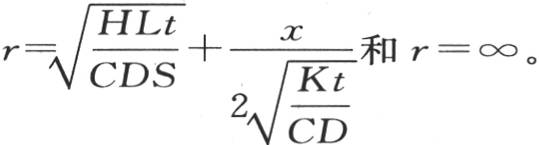 由此得到u的值因而表示成:
由此得到u的值因而表示成: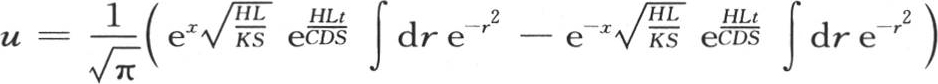 , 【14】 第一个积分应当从
, 【14】 第一个积分应当从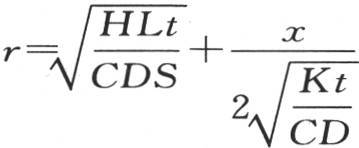 取到r=∞,第二个从
取到r=∞,第二个从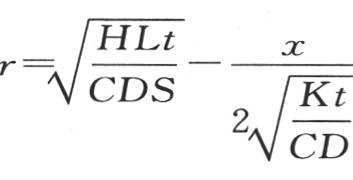 取到r=∞。让我们现在用ψ(R)来表示从r=R到r=∞的积分
取到r=∞。让我们现在用ψ(R)来表示从r=R到r=∞的积分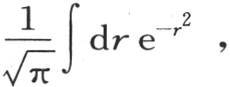 我们有
我们有
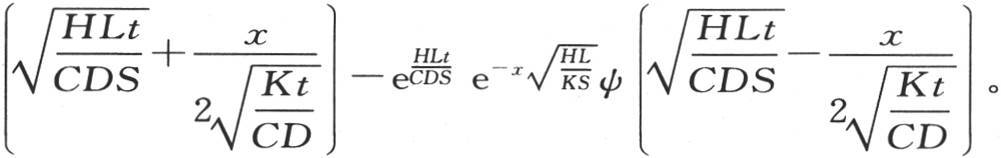 因此,与
因此,与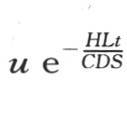 等价的u′可以表示成
等价的u′可以表示成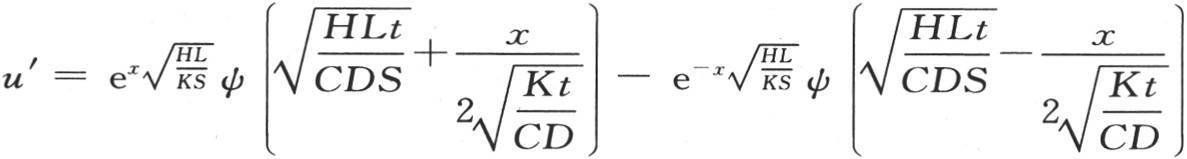 来表示,并且
来表示,并且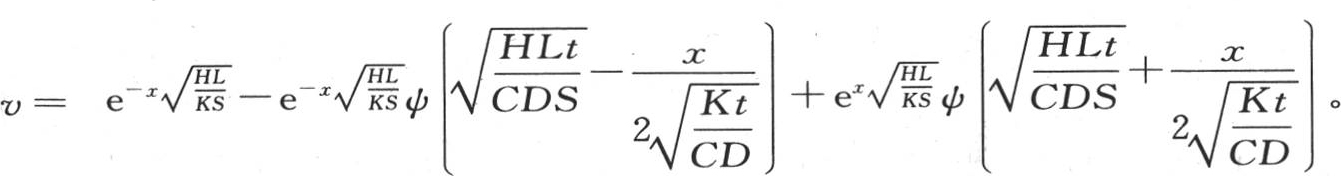 人们知道由ψ(R)所表示的这个函数已经有一段时间了,我们不难用收敛级数或者是用连分式,来计算在我们用已知量代替R时,这个函数所得到的值;因此,这个解的数值应用不存在任何困难 【15】 。
人们知道由ψ(R)所表示的这个函数已经有一段时间了,我们不难用收敛级数或者是用连分式,来计算在我们用已知量代替R时,这个函数所得到的值;因此,这个解的数值应用不存在任何困难 【15】 。
366 如果使H变成0,那么我们有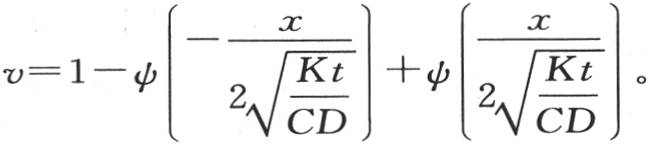
这个方程表示一根无穷长的棒中的热传导,除端点的那些点外,这根棒的所有点的温度在开始时都为0,端点的温度保持1不变。我们假定热不可能通过棒的外表面而逃逸;或者同样地,假定这根棒的厚度无穷大。因此,当假定这个无穷厚的壁的所有部分在开始时初始温度均为0,表面受恒温1的作用时,这个v值指明热在由一个无穷平面所限定的固体中传导时所遵循的规律。指出这个解的几个结果不会是完全无用的。
用φ(R)表示从r=0取到r=R的积分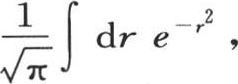 当R是一个正数时,我们有
当R是一个正数时,我们有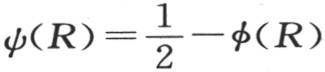 和
和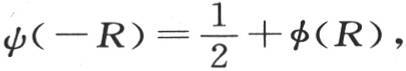 因此ψ(-R)-ψ(R)=2φ(R)并且
因此ψ(-R)-ψ(R)=2φ(R)并且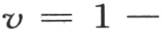
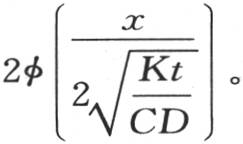 展开积分φ(R),我们有
展开积分φ(R),我们有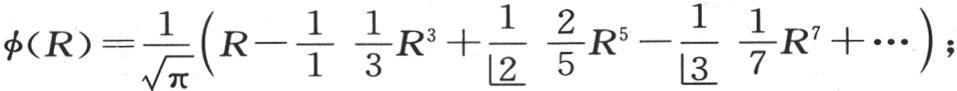 因此
因此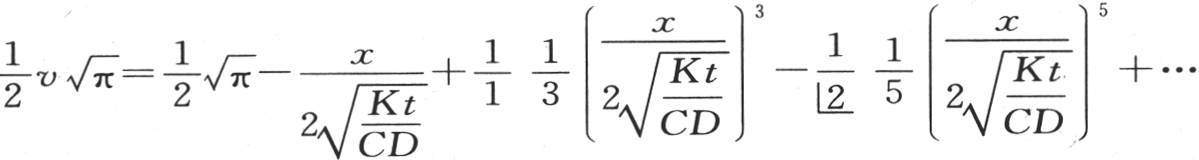
第一,如果我们假定x为0,则我们得到v=1;
第二,如果x不为0,我们假定t=0,那么含x的项的和就表示从r=0取到r=∞的积分 并且它必然等于
并且它必然等于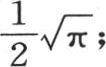 因此v为0;
因此v为0;
第三,处在不同深度x1 ,x2 ,x3 ,…的不同点在不同时间t1 ,t2 ,t3 ,…之后达到同一温度,时间t1 ,t2 ,t3 ,…与深度x1 ,x2 ,x3 ,…成正比;
第四,为了比较在一个无穷小时刻内流过这个固体内与受热面距离x的截面S的热量,我们应当取量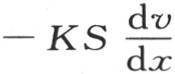 的值,我们有
的值,我们有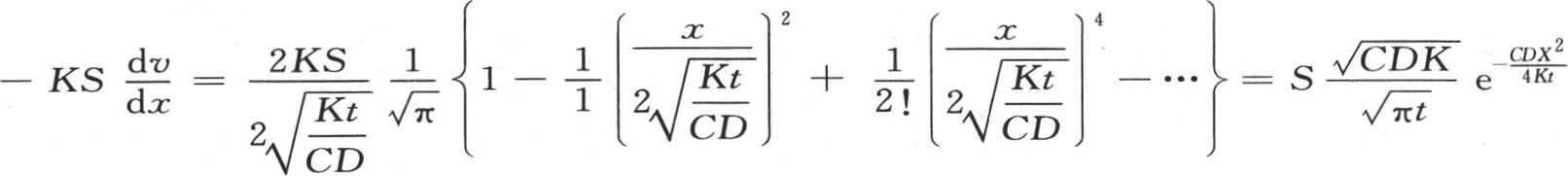 ; 【16】 因此量
; 【16】 因此量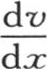 的表达式与积分符号完全分离。前面那个在受热固体面上的值变成
的表达式与积分符号完全分离。前面那个在受热固体面上的值变成 它表明面上的热流量怎样随量C,D,K,t而变化;为求在时间t内热源向这个固体传递多少热,我们应当取积分
它表明面上的热流量怎样随量C,D,K,t而变化;为求在时间t内热源向这个固体传递多少热,我们应当取积分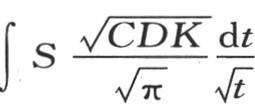 或者是
或者是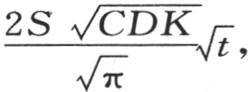 因此,所得到的热与历经时间的平方根成正比地增加。
因此,所得到的热与历经时间的平方根成正比地增加。
367 我们可以用一个类似的方法来处理热扩散的问题,这个问题也依赖于方程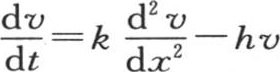 的积分。用f(x)表示一条直线中与原点距离x的点的初始温度,我们现在要确定在时间t之后这同一点应该有怎样的温度。令v=e-ht z,我们有
的积分。用f(x)表示一条直线中与原点距离x的点的初始温度,我们现在要确定在时间t之后这同一点应该有怎样的温度。令v=e-ht z,我们有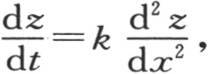 因此
因此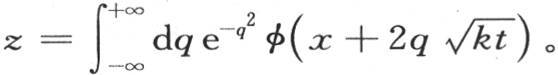 当t=0时,我们肯定有
当t=0时,我们肯定有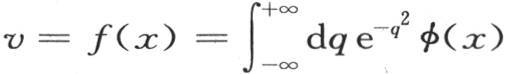 或者是
或者是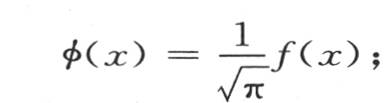 因此
因此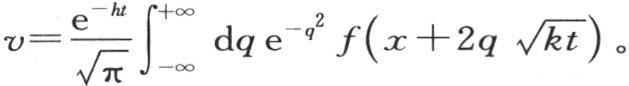
为了把这个一般表达式应用到这条直线从x=-α到x=α的部分被均匀加热,而这个固体的其他所有部分保持0度的情况中去,我们应当认为,由假定,乘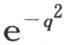 的因子
的因子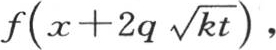 在函数符号下处在-α到α之间时,取常数值1,并且这个因子的所有其他值为0。因此积分
在函数符号下处在-α到α之间时,取常数值1,并且这个因子的所有其他值为0。因此积分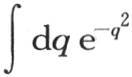 应当从
应当从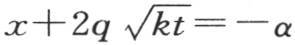 取到
取到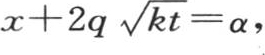 或者从
或者从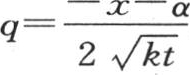 取到
取到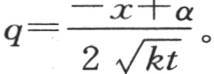 和上面一样,用ψ(R)表示从r=R取到r=∞的积分
和上面一样,用ψ(R)表示从r=R取到r=∞的积分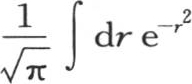 【17】 ,我们有
【17】 ,我们有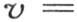
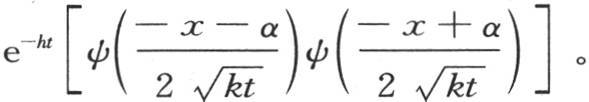
368 接下来我们把一般方程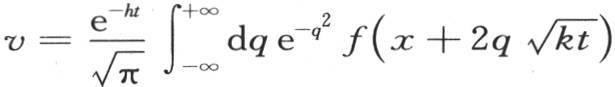 用到由强度恒为1的热源所加热的无穷长棒已经达到固定温度,然后在保持0度的介质中自由冷却的情况中去。为此,我们只需注意,只要在函数符号下的变量x是正的,由f(x)所表示的初始函数就等价于
用到由强度恒为1的热源所加热的无穷长棒已经达到固定温度,然后在保持0度的介质中自由冷却的情况中去。为此,我们只需注意,只要在函数符号下的变量x是正的,由f(x)所表示的初始函数就等价于 并且,当受符号f作用的这个变量小于0时,这个初始函数就等价于
并且,当受符号f作用的这个变量小于0时,这个初始函数就等价于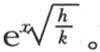 因此
因此 第一个积分应当从
第一个积分应当从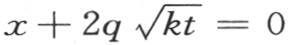 取到
取到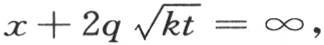 第二个积分从
第二个积分从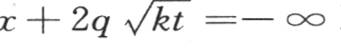 取到
取到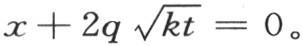
v值的第一部分是 或者是
或者是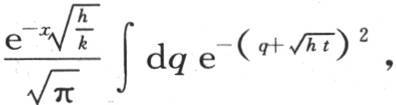 或者是令
或者是令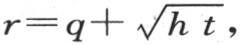 则是
则是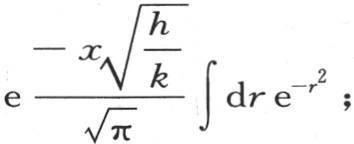 这个积分应当从
这个积分应当从 取到q=∞,或者是从
取到q=∞,或者是从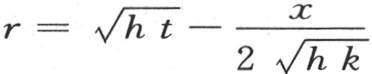 取到r=∞。
取到r=∞。
v值的第二部分是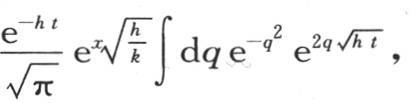 或者是令
或者是令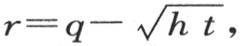 则是
则是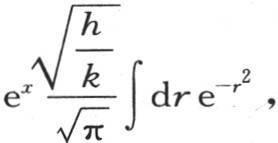 这个积分应当从r=-∞取到
这个积分应当从r=-∞取到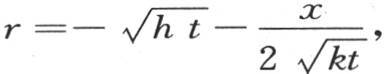 或从
或从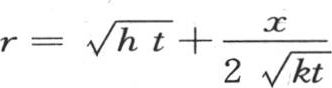 取到r=∞,由此我们得到下式:
取到r=∞,由此我们得到下式: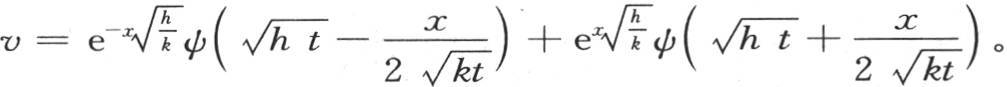
369 为了表示一根细棒在给定区间x=-α和x=+α的中点均匀受热的热扩散的规律,我们曾得到(第367目)方程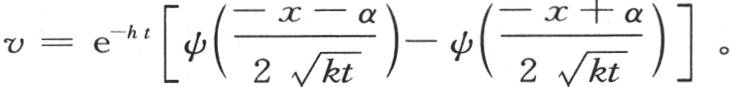 我们在前面曾用一种不同的方法解决过这同一个问题,在假定α=1时,我们得到了方程
我们在前面曾用一种不同的方法解决过这同一个问题,在假定α=1时,我们得到了方程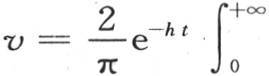
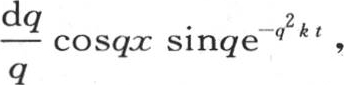 (第348目)
(第348目)
为了比较这两个结果,我们在每一个中假定x=0;再一次用ψ(R)表示从r=0取到r=R的积分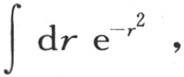 我们有
我们有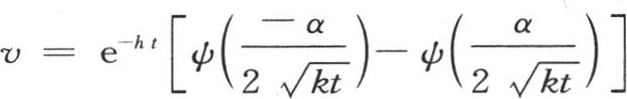 。 【18】 或者是
。 【18】 或者是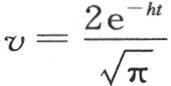
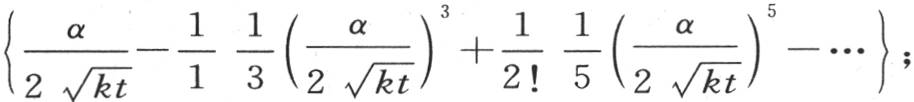 另一方面,我们应当有
另一方面,我们应当有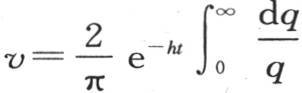
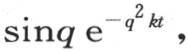 或者是
或者是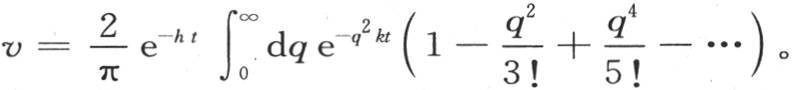
现在,从u=0到u=∞的积分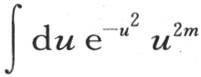 有一个已知值,m是任一正整数。一般地,我们有
有一个已知值,m是任一正整数。一般地,我们有 【19】 这时,令q2 kt=u2 ,前面的方程给出
【19】 这时,令q2 kt=u2 ,前面的方程给出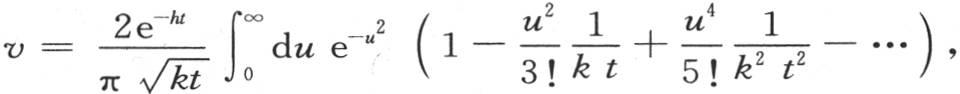 或者是
或者是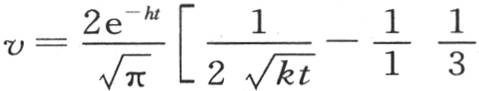
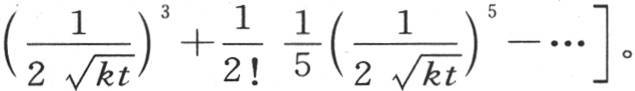
当我们假定α=1时,这个方程和前面的方程相同。由此我们看到,我们由不同过程所得到的积分导致同一个收敛级数,因此无论x如何,我们都得到两个恒等的结果。
和前面一样,在这个问题中,我们应当比较在一给定时刻内流过受热棱柱的不同截面的热量,这些量的一般表达式不含积分符号;不过,我们将绕过这些注记,以比较我们曾对表示无穷直线中热扩散方程的积分所给出的不同形式来结束本节。
370 为了满足方程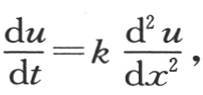 我们可以假定u=e-x ekt ,或者一般地,假定
我们可以假定u=e-x ekt ,或者一般地,假定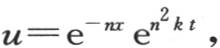 因此我们不难推出(第364目)积分
因此我们不难推出(第364目)积分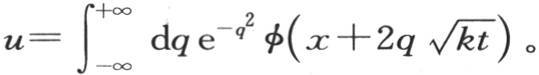
由已知方程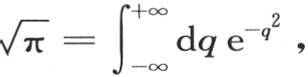 我们得出
我们得出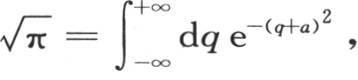 a是任一常数;因此我们有
a是任一常数;因此我们有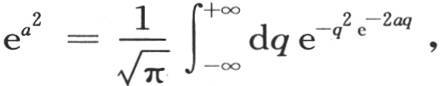 或者是
或者是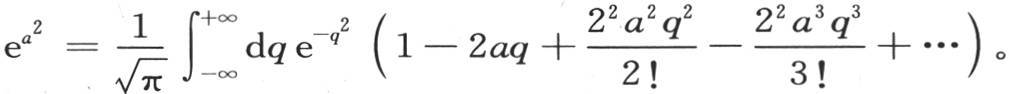 无论a值如何,这个方程都成立。我们可以把左边展开;通过各个项的比较,我们可以得到积分
无论a值如何,这个方程都成立。我们可以把左边展开;通过各个项的比较,我们可以得到积分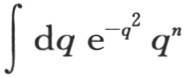 的已知值。当n是奇数时,这个值为0,当n是偶数2m时,我们得到
的已知值。当n是奇数时,这个值为0,当n是偶数2m时,我们得到
371 作为方程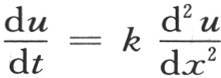 的积分,我们在前面用过表达式
的积分,我们在前面用过表达式
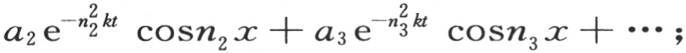 或者是
或者是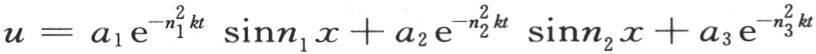
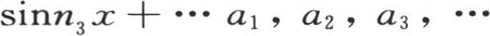 和n1 ,n2 ,n3 ,…是两组任意常数。这两个表达式都等价于积分
和n1 ,n2 ,n3 ,…是两组任意常数。这两个表达式都等价于积分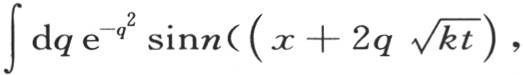 或者是
或者是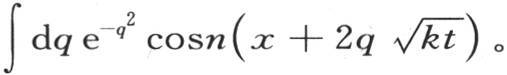
事实上,为了确定积分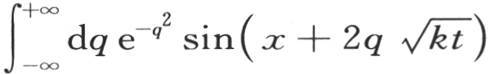 的值;我们对它给出下述形式
的值;我们对它给出下述形式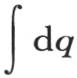
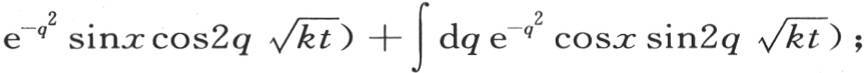 或者是
或者是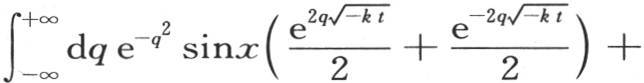
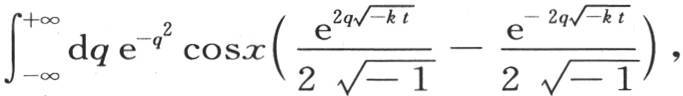 它等价于
它等价于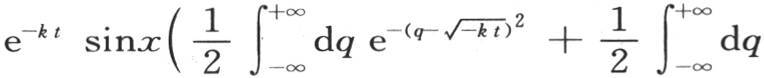
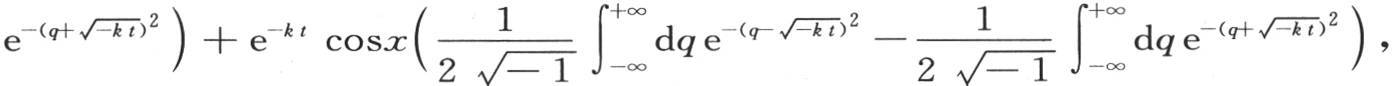 从q=-∞到q=∞的积
从q=-∞到q=∞的积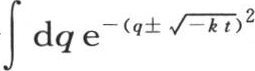 是
是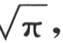 因此,对于积分
因此,对于积分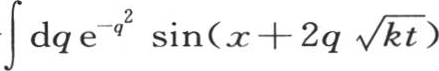 的值,我们有量
的值,我们有量 一般地,我们有
一般地,我们有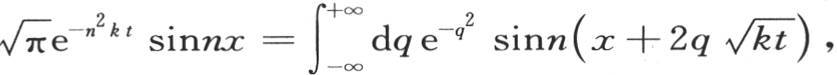 我们可以同样的方式确定积分
我们可以同样的方式确定积分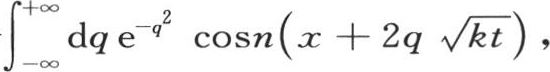 它的值是
它的值是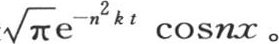
由此我们看到,积分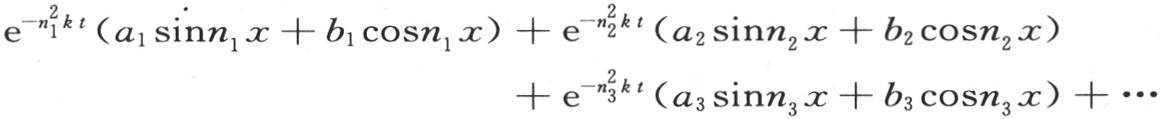
等价于
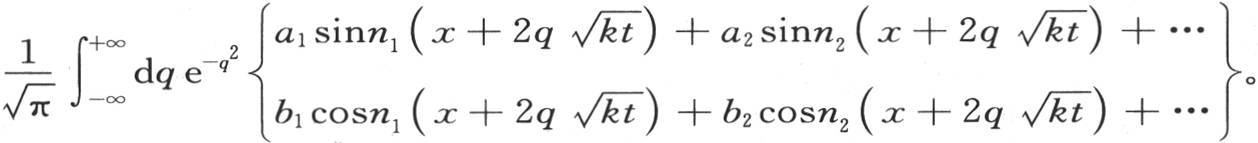
如我们在前面见过的一样,这个级数值表示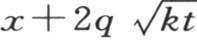 的任一个函数;因此,这个通积分可以表示成
的任一个函数;因此,这个通积分可以表示成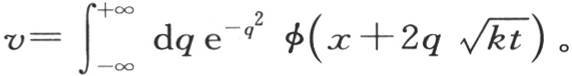 此外,方程
此外,方程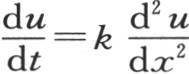 的积分可以用各种别的形式来表示 【20】 。所有这些表达式都必然恒等。
的积分可以用各种别的形式来表示 【20】 。所有这些表达式都必然恒等。
第二节 无穷固体中的自由热运动
372 正如我们在处理实立方体中的热传导问题时已经注意到的,方程

的积分立即提供带有四个变量的方程
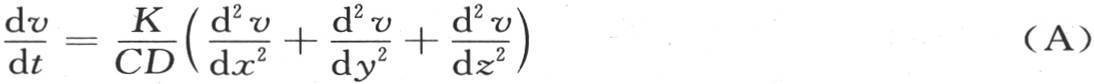
的积分。由于这个原因,我们只需一般地考察在线性情况下的热扩散作用就够了。当物体的体积有限时,热分布不断受到从固体介质向弹性介质过渡的干扰;或者,为了使用适合于分析的表达式,确定温度的函数不仅应当满足偏微分方程和初始状态,而且还应当服从由表面形状所决定的条件。在这种情况下,这个积分具有更难以确定的形式,并且,为了从一个线性坐标的情形过渡到三个正交坐标的情形,我们在考察这个问题时就更要小心得多:但是当这个实体未受到干扰时,附属条件本身就不会反对热的自由扩散。它的运动在所有方向上就都相同。
一条无穷直线的一点的变化温度v由方程
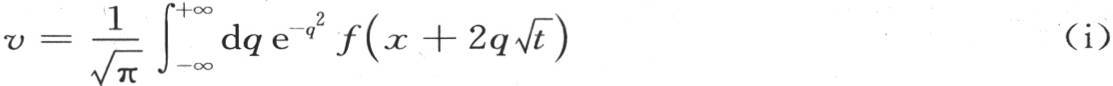
来表示。x表示定点0和点m之间的距离,点m的温度在历经时间t之后与v相等。我们假定热不可能通过这个无穷长棒的外表面而耗散,并且这根棒的初始状态由方程v=f(x)来表示。v值应当满足的微分方程是

但是为了简化这一研究,我们写成

它假定我们用等于 的另一个未知数来代替t。
的另一个未知数来代替t。
如果我们在x和若干常数的函数f(x)中用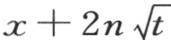 来代替x,并且如果在乘以
来代替x,并且如果在乘以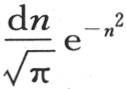 之后对无穷区间之间的n积分,那么如同我们在上面所证明的,表达式
之后对无穷区间之间的n积分,那么如同我们在上面所证明的,表达式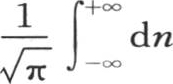
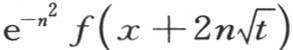 满足微分方程(b);即这个表达式具有对相对x的二阶流数和相对t的一阶流数给出相同值的性质。由此显然,如果我们用量
满足微分方程(b);即这个表达式具有对相对x的二阶流数和相对t的一阶流数给出相同值的性质。由此显然,如果我们用量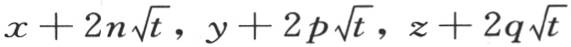 来代替x,y,z,那么对于三个变量的函数f(x,y,z),只要我们在乘以
来代替x,y,z,那么对于三个变量的函数f(x,y,z),只要我们在乘以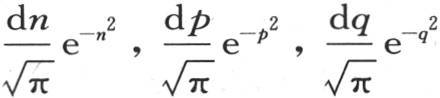 之后积分,这个函数就有同样的性质。事实上,我们因此而形成的函数,
之后积分,这个函数就有同样的性质。事实上,我们因此而形成的函数,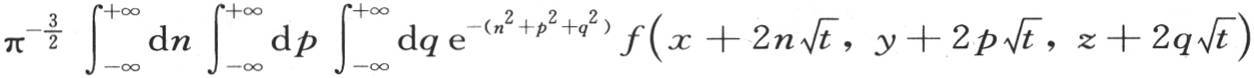 对相对t的流数给出三个项,这三个项就是通过对三个变量x,y,z的每一个取二阶流数所能得到的那些项。
对相对t的流数给出三个项,这三个项就是通过对三个变量x,y,z的每一个取二阶流数所能得到的那些项。
因此方程
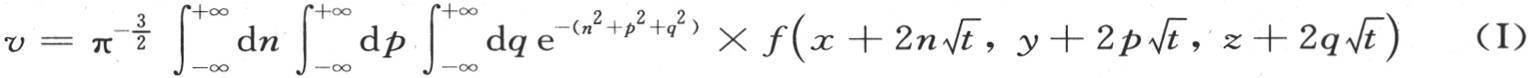
给出满足偏微分方程

的一个v值。
373 现在假定一种无定型实体(即充满无穷空间的一种物质)含有其实际分布已经给定的热量。设v=F(x,y,z)是表示这个初始且任意的状态的方程,因此其坐标为x,y,z的分子有与给定函数F(x,y,z)的值相等的初始温度。我们可以设想初始热包含在这种物质的某一部分中,这一部分开始的状态由方程v=F(x,y,z)所给出,其他所有点的初始温度为0。
我们需要确定这个温度系统在一给定时间之后是怎样的。变化温度v必然由应当满足一般方程(A)和条件φ(x,y,z,0)=F(x,y,z)的函数φ(x,y,z,t)来表示。现在这个函数的值由积分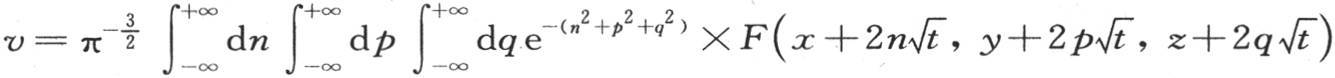 给出。事实上,这个函数v满足方程(A),如果我们在其中令t=0,那么我们得到
给出。事实上,这个函数v满足方程(A),如果我们在其中令t=0,那么我们得到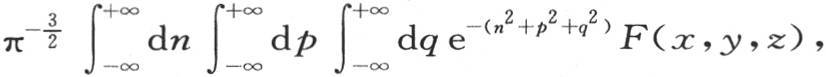 或者完成积分,我们得到F(x,y,z)。
或者完成积分,我们得到F(x,y,z)。
374 由于函数v或者是φ(x,y,z,t)在令t=0时表示初始状态,由于它满足热传导的微分方程,所以,它也表示在第二个时刻开始时所出现的状态,令第二个状态发生变化,我们可知同一函数表示这个固体的第三个状态及表示所有的后继状态。因此,我们刚才所确定的、包含三个变量x,y,z的一个完全任意的函数的v值给出这个问题的解,我们不可能假定有更一般的表达式,尽管这同一积分可以置于很不同的形式之下。
不用方程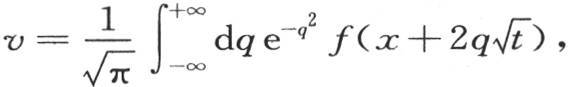 我们可以给出方程
我们可以给出方程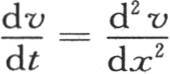 的积分的另一种形式;并且由它总容易推出属于三维情形的积分。我们将得到的结果必然和前面的相同。
的积分的另一种形式;并且由它总容易推出属于三维情形的积分。我们将得到的结果必然和前面的相同。
为了给出这一研究的一个例子,我们使用曾帮助我们构造指数积分的特殊值。
这样,取方程

让我们给定v一个很简单的值 它显然满足微分方程(b)。事实上,我们由此推出
它显然满足微分方程(b)。事实上,我们由此推出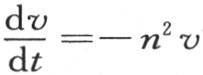 和
和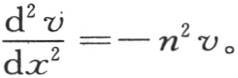 因此积分
因此积分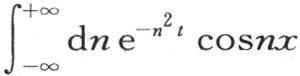 也属于方程(b);因为这个v值由无数特殊值的和所组成。现在积分是已知的,并且已知等于
也属于方程(b);因为这个v值由无数特殊值的和所组成。现在积分是已知的,并且已知等于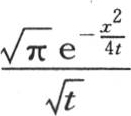 (见下一目)。因此最后这个x和t的函数也与微分方程(b)一致。而且不难直接验证特殊值
(见下一目)。因此最后这个x和t的函数也与微分方程(b)一致。而且不难直接验证特殊值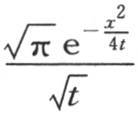 满足所说的方程。
满足所说的方程。
如果我们用x-α来代替变量x,α是任一常数,则会有同样的结果。这样,作为一个特殊值,我们可以运用函数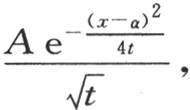 其中我们赋予α任一值。因此和
其中我们赋予α任一值。因此和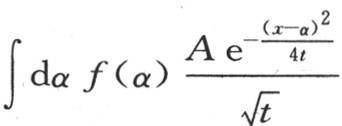 也满足微分方程(b);因为这个和由同一形式的无数特殊值乘以任一常数所组成。因此我们可以把下面的
也满足微分方程(b);因为这个和由同一形式的无数特殊值乘以任一常数所组成。因此我们可以把下面的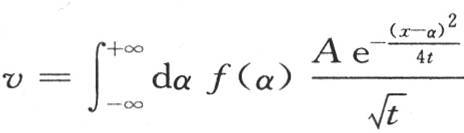 作为方程
作为方程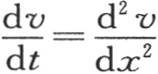 中的一个v值,其中A是一个常系数。如果在最后这个积分中我们假定
中的一个v值,其中A是一个常系数。如果在最后这个积分中我们假定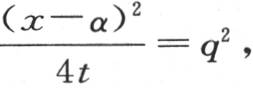 同时令
同时令 那么我们有
那么我们有

或者是
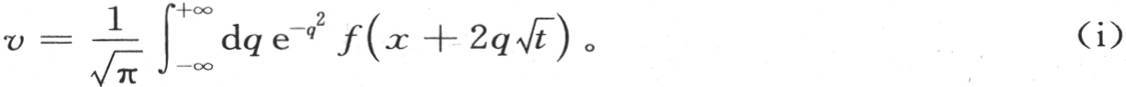
由此我们看到特殊值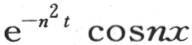 或
或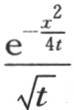 的运用怎样导致在一个有限形式下的积分。
的运用怎样导致在一个有限形式下的积分。
375 在我们计算积分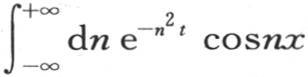 的值 【21】 时就可以揭示这两个特殊值相互之间所具有的联系。
的值 【21】 时就可以揭示这两个特殊值相互之间所具有的联系。
为了完成积分,我们应当展开因子cosnx并对n积分。这样我们得到表示一个已知的展开式的级数;不过这个结果更容易从下面的分析中导出。假定n2 t=p2 和nx=2pu,则积分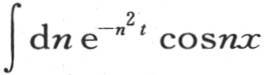 就变换成
就变换成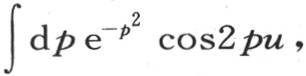 因此我们有
因此我们有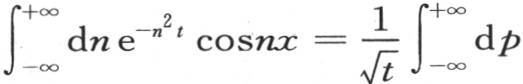
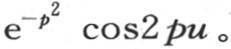
现在我们记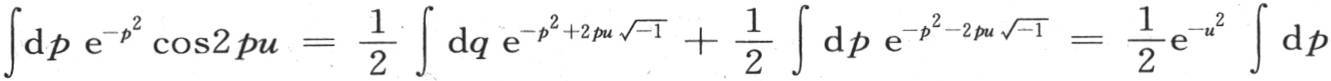
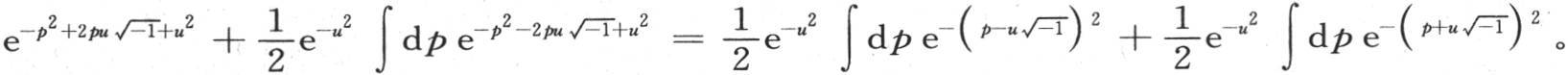
这时进入这两个项的每一个积分都等于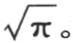 事实上,我们一般有
事实上,我们一般有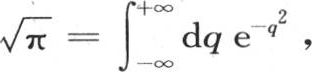 并且无论常数b如何,必然有
并且无论常数b如何,必然有 这时只要令
这时只要令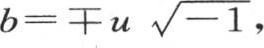 我们就得到
我们就得到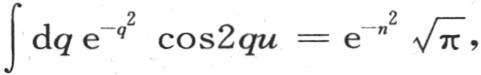 因此
因此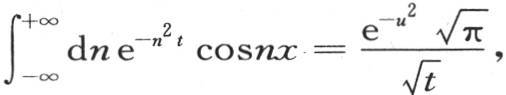 并且用u的值
并且用u的值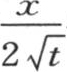 代替u,我们有
代替u,我们有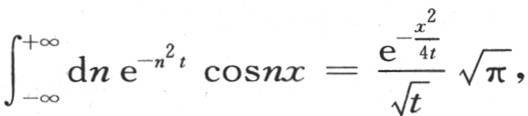 而且这个特殊值
而且这个特殊值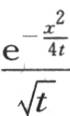 简单得足以直接呈现出来,而无需从值
简单得足以直接呈现出来,而无需从值 中推出。不管怎样,函数
中推出。不管怎样,函数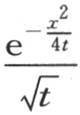 满足微分方程
满足微分方程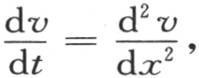 这是肯定的;因而无论α如何,函数
这是肯定的;因而无论α如何,函数 亦满足这个微分方程。
亦满足这个微分方程。
376 为了转到三维的情形上来,只需用另外两个类似的函数乘x和t的函数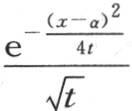 就够了,这两个类似的函数一个是y和t的函数,另一个是z和t的函数;这个积显然满足方程
就够了,这两个类似的函数一个是y和t的函数,另一个是z和t的函数;这个积显然满足方程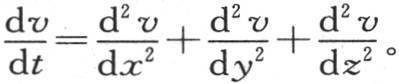
因此这时我们把v值表示成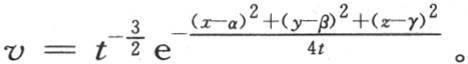
如果现在我们让右边乘以dα,dβ,dγ和量α,β,γ的任一个函数f(α,β,γ),那么,只要指明这个积分,我们就得到一个由无数特殊值乘以任意常数的和所构成的v值。
由此得到,函数v可以表示成
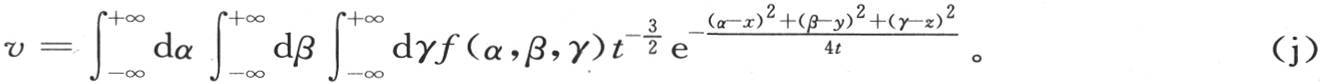
这个方程包含所提出的方程(A)的通积分。应当注意使我们得到这个积分的过程,因为它可以用于许多情形;当这个积分应当满足与表面有关的条件时它尤其有用。如果我们仔细考察它,那么我们会看到它所需要的变换都由问题的物理性质所指明。在方程(j)中,我们还可以改变这些变量。当取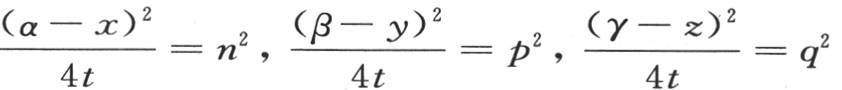 时,只要使右边乘以一个常系数A,那么我们就有
时,只要使右边乘以一个常系数A,那么我们就有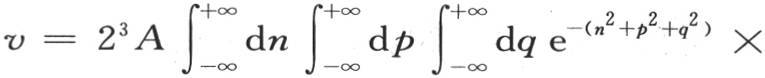
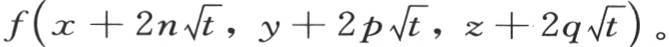
为了确定初始状态,在区间-∞到+∞之间取这三个积分,并且令t=0,我们得到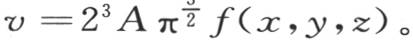 因此,如果我们用F(x,y,z)表示已知的初始温度,并对常系数A给定值
因此,如果我们用F(x,y,z)表示已知的初始温度,并对常系数A给定值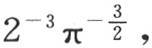 那么我们就得到积分
那么我们就得到积分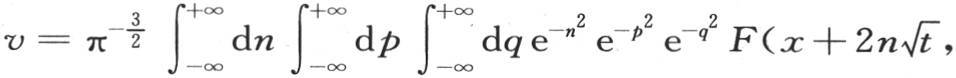
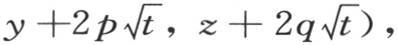 它和第372目的方程相同。
它和第372目的方程相同。
方程(A)的积分可以以几种其他形式来表示,从这些形式中可以选出最适合于所要解决的问题的形式。
一般地,在这些研究中,我们肯定会观察到,当两个函数φ(x,y,z,t)都满足微分方程(A),并且当它们对某个确定的时间值相等时,则它们相同。由这一原理得到,那些当我们在其中令t=0时就化为同一任意函数F(x,y,z)的积分,都有相同的普适度;它们必然是恒等的。
微分方程(a)的右边曾乘以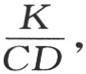 并且在方程(b)中我们假定了这个系数等于1。为了使这个量还原,只需在积分(i)或者是在积分(j)中用
并且在方程(b)中我们假定了这个系数等于1。为了使这个量还原,只需在积分(i)或者是在积分(j)中用 代替t就够了,我们现在指出由这些方程所得出的某些结果。
代替t就够了,我们现在指出由这些方程所得出的某些结果。
377 正如我们在第二章第9节中所明确证明的,从分析的一般原理可以得出,用做数e的指数 【22】 的函数可以只表示一个绝对数(an absolute number)。如果我们在这个指数中用 来代替未知数t,那么我们看到,由于K,C,D和t的量纲相对于长度单位是-1,0,-3和0,所以分母
来代替未知数t,那么我们看到,由于K,C,D和t的量纲相对于长度单位是-1,0,-3和0,所以分母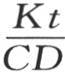 的量纲是2,分子的每一项的量纲也是2,因此,整个指数的量纲为0。让我们考虑t值逐渐递增的情况;为了简化这一研究,让我们首先运用方程
的量纲是2,分子的每一项的量纲也是2,因此,整个指数的量纲为0。让我们考虑t值逐渐递增的情况;为了简化这一研究,让我们首先运用方程

它来表示一条无穷直线中的热扩散。假定初始热包含在这条直线的一个已知部分中,即包含在从x=-h到x=+g中,并且假定我们赋予x一个确定的值X,X固定那条直线某一点m的位置。如果时间t无限增加,那么进入指数的项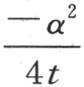 和
和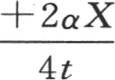 的绝对数就变得愈来愈小,因此在乘积
的绝对数就变得愈来愈小,因此在乘积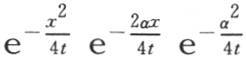 中,我们可以略去明显接近于1的后两个因子。由此我们得到
中,我们可以略去明显接近于1的后两个因子。由此我们得到

这是这条直线在很长时间之后的变化状态的表达式;它适用于这条直线的那些与原点的距离不比点m远的所有部分。定积分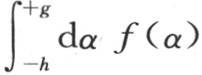 表示包含在这个固体中的全部热量B,并且我们看到,初始分布对很长时间之后的温度没有任何影响。它们只依赖于和B,而与热得以分布的规律无关。
表示包含在这个固体中的全部热量B,并且我们看到,初始分布对很长时间之后的温度没有任何影响。它们只依赖于和B,而与热得以分布的规律无关。
378 如果我们假定唯一处在原点的基元ω已经获得初始温度f,所有其他基元则在开始时取温度0,那么积ωf就等于积分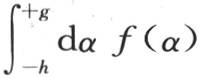 或者是B。常数f极其大,因为我们假定线段ω很小。
或者是B。常数f极其大,因为我们假定线段ω很小。
如果唯一处在原点的基元已经被加热,那么方程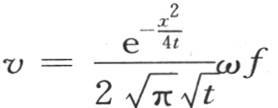 表示会发生的运动。事实上,如果我们给定x任一非无穷小的值a那么当我们假定t=0时,函数
表示会发生的运动。事实上,如果我们给定x任一非无穷小的值a那么当我们假定t=0时,函数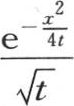 就是0。如果x的值是0,那么情况则不同。相反,在这种情况下,当t=0时,函数
就是0。如果x的值是0,那么情况则不同。相反,在这种情况下,当t=0时,函数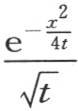 得到一个无穷值。如果我们把曲面理论的一般原理应用到其方程是
得到一个无穷值。如果我们把曲面理论的一般原理应用到其方程是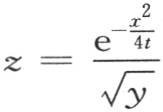 的面上去,那么我们可以清楚地确定这个函数的性质。
的面上去,那么我们可以清楚地确定这个函数的性质。
当我们假定全部初始热集中在唯一处在原点的基元上时,这时方程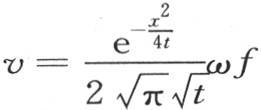 表示棱柱任一点的可变温度。这个假定虽然特殊,但属于一个一般的问题,因为在充分长的时间之后,这个固体的变化状态总是相同的,仿佛初始热原来曾集中在原点似的。根据以分布的这个规律对棱柱的变化温度影响很大;但是这个作用变得愈来愈弱,最后以简直不可察觉而结束。
表示棱柱任一点的可变温度。这个假定虽然特殊,但属于一个一般的问题,因为在充分长的时间之后,这个固体的变化状态总是相同的,仿佛初始热原来曾集中在原点似的。根据以分布的这个规律对棱柱的变化温度影响很大;但是这个作用变得愈来愈弱,最后以简直不可察觉而结束。
379 我们有必要注意,简化方程(y)对这条直线在点m以外的那一部分不适用,点m的距离已经由X来表明。
事实上,无论时间值多大,我们都可以选择一个x值,使得项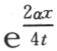 明显地与1不同,所以这个因子不可能被省略。因此我们应当设想我们已经在原点O的两边标明了两点m和m′,这两点位于某个距离X或者是-X上,我们逐渐增加时间值,同时观察直线在包含在m和m′之间的这一部分的相继状态。这些变化状态愈来愈收敛于由方程
明显地与1不同,所以这个因子不可能被省略。因此我们应当设想我们已经在原点O的两边标明了两点m和m′,这两点位于某个距离X或者是-X上,我们逐渐增加时间值,同时观察直线在包含在m和m′之间的这一部分的相继状态。这些变化状态愈来愈收敛于由方程

所表示的状态。无论赋予X的这个值怎样,我们总能够找到一个充分大的时间值,使得线段m′om的状态不是明显地不同于前面的方程(y)所表示的状态。
如果我们要求同一方程能适用于离原点更远的其他部分,那么就应当假定一个比前面更大的时间值。
在所有情况下表示任一直线的终极状态的方程(y)表明,在极长的时间之后,不同的点得到几乎相同的温度,同一点的温度以与自扩散开始后所历经的时间的平方根成反比地变化而结束。任一点的温度的减量总是变得与时间的增量成正比。
380 如果我们用积分

来确定在这条直线上处在与受热部分距离很远的点的变化状态,并且以此来表示也省略了因子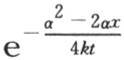 的终极条件,那么我们所得到的结果就不会是精确的。事实上,假定受热部分只从α=0延长到α=g,并且界限g相对于我们希望确定其温度的点的距离x很小;构成指数的量
的终极条件,那么我们所得到的结果就不会是精确的。事实上,假定受热部分只从α=0延长到α=g,并且界限g相对于我们希望确定其温度的点的距离x很小;构成指数的量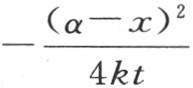 实际上简化成
实际上简化成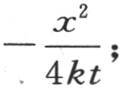 即两个量
即两个量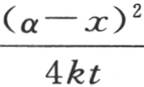 和
和 的比随x的值相对于α的值逐渐增大而愈来愈趋近于1;但是由此并不能得出我们可以在e的指数中用一个量来代替这两个量中的另一个。因此一般地,从属项的省略不可能发生在指数式或者是三角式中。放在正弦和余弦符号下或者放在指数符号e下的量总是绝对数,我们只能省略其值极小的那一部分的数;它们的相对值在此不重要。我们不允许通过考查x与α的比是否很大而项
的比随x的值相对于α的值逐渐增大而愈来愈趋近于1;但是由此并不能得出我们可以在e的指数中用一个量来代替这两个量中的另一个。因此一般地,从属项的省略不可能发生在指数式或者是三角式中。放在正弦和余弦符号下或者放在指数符号e下的量总是绝对数,我们只能省略其值极小的那一部分的数;它们的相对值在此不重要。我们不允许通过考查x与α的比是否很大而项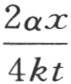 和
和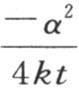 是否是很小的数来确定我们能否把表达式
是否是很小的数来确定我们能否把表达式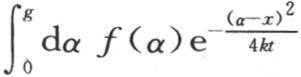 简化成
简化成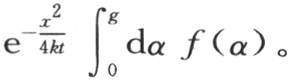 当历经时间t极大时,这个条件总存在;但它并不依赖于比
当历经时间t极大时,这个条件总存在;但它并不依赖于比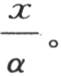
381 现在假定为使固体在包含在x=0到x=X之间的这一部分的温度能够很接近地由简化方程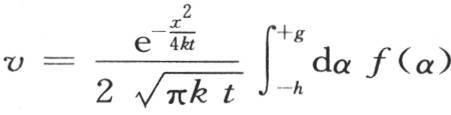 来表示,我们要确定应当历经多少时间,0和g可以是最初受热的部分的界限。
来表示,我们要确定应当历经多少时间,0和g可以是最初受热的部分的界限。
精确解由方程

所给出,近似解由方程

给出。k表示热导率的值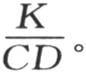 一般地,为了能使方程(y)代替前面的方程(i),就应当使我们省略的因子
一般地,为了能使方程(y)代替前面的方程(i),就应当使我们省略的因子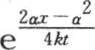 与1相差无几;因为,如果差是1或者
与1相差无几;因为,如果差是1或者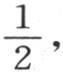 那么我们就会看到一个等于所计算的值或者是等于那个值的一半的误差。这样,设
那么我们就会看到一个等于所计算的值或者是等于那个值的一半的误差。这样,设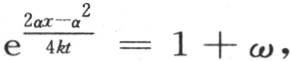 ω是一个像
ω是一个像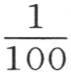 或者是
或者是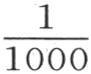 那样的小分数;我们由此得到条件
那样的小分数;我们由此得到条件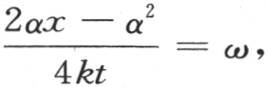 或者
或者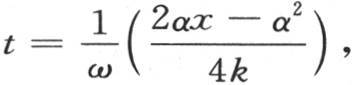 如果变量α可以得到的最大值g相对于x非常小,那么我们有
如果变量α可以得到的最大值g相对于x非常小,那么我们有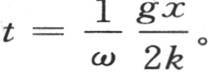
我们由这个结果看到,我们要以简化方程确定其温度的那些点与原点距离愈远,历经的时间值就必然愈大。因此,热就愈来愈倾向于依一条与最初的加热无关的规律而分布。在一定时间之后,扩散就明显地发生作用,即固体的状态只依赖于初始热的量,而与由这一热量所构成的分布无关。与原点充分接近的点的温度很快就严格无误地由简化方程(y)来表示;但是与热源相距很远的点则不同。这时我们仅仅在历经时间极长时才可以使用那个方程。数值应用使这个注记更加显而易见。
382 假定组成这个棱柱的物质是铁,这个固体已经受热的那部分长一分米,因此g=0.1。如果我们要确定在一给定时间之后与原点相距1米的点m的温度是怎样的,如果我们对这一研究使用近似积分(y),那么我们所出现的误差就随时间值愈大而愈小。如果历经时间超过三天半,那么这个误差就小于所求量的百分之一。
在这种情况下,包含在原点O和我们要确定其温度的点m之间的距离只比受热部分大10倍。如果这个比不是10而是100,那么,在历经的时间值超过一个月时,简化方程(y)就给出小于百分之一的温度。为使这个近似成为可接受的,一般我们必须做到,第一,量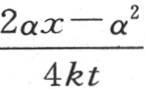 仅仅等于一个很小的分数,如
仅仅等于一个很小的分数,如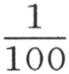 或者是
或者是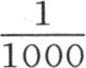 或者是更小;第二,必须注意的这个误差应当只有比我们以最敏感的温度计所观察到的很小的量还小得多的一个绝对值。
或者是更小;第二,必须注意的这个误差应当只有比我们以最敏感的温度计所观察到的很小的量还小得多的一个绝对值。
当我们所考虑的点与这个固体最初受热的那部分相距很远时,需要确定的温度就极其小;因此,在应用这个简化方程时我们会出现的误差就有很小的绝对值;但是这并不意味着我们有权使用那个方程。因为,如果所出现的误差尽管很小,但超过或者是等于所求的量,或者即使它是这个量的二分之一或者是四分之一,或者是可感觉到的一部分,那么我们还是应当拒绝这个近似。显然,在这种情况下,近似方程(y)不能表示这个固体的状态,我们也不能用它来确定两个或者是多个点同时出现的温度比。
383 由这个考查得到,我们不应当由积分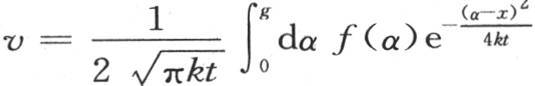 得出初始分布规律对远离原点的点的温度无影响的结论。这种分布的合成作用很快不再对靠近受热部分的点起作用;即它们的温度只依赖于初始热的量,而与这个量所构成的分布无关:但是很远的距离不能同时消除分布的痕迹,相反,它在很长的时间内保留它,并且延缓热扩散。因此,方程
得出初始分布规律对远离原点的点的温度无影响的结论。这种分布的合成作用很快不再对靠近受热部分的点起作用;即它们的温度只依赖于初始热的量,而与这个量所构成的分布无关:但是很远的距离不能同时消除分布的痕迹,相反,它在很长的时间内保留它,并且延缓热扩散。因此,方程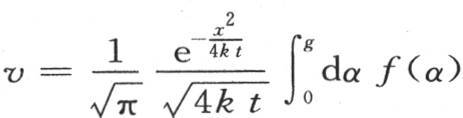 只在极长时间之后表示远离受热部分的点的温度。如果我们运用它而不考虑这个条件,那么我们会得到使实际结果翻两倍或者是三倍,甚至比实际结果无比大或者是无比小的结果。不仅对很小的时间值会出现这种情况,就是对很大的时间值,如1小时,1天或者是1年等,也会出现这种情况。最后,由于所有其他条件都相同,所以这些点与开始被加热的部分愈远,则这个表达式就愈不精确。
只在极长时间之后表示远离受热部分的点的温度。如果我们运用它而不考虑这个条件,那么我们会得到使实际结果翻两倍或者是三倍,甚至比实际结果无比大或者是无比小的结果。不仅对很小的时间值会出现这种情况,就是对很大的时间值,如1小时,1天或者是1年等,也会出现这种情况。最后,由于所有其他条件都相同,所以这些点与开始被加热的部分愈远,则这个表达式就愈不精确。
384 当热扩散在各个方向上产生时,如我们所看到的,这个固体的状态就由积分
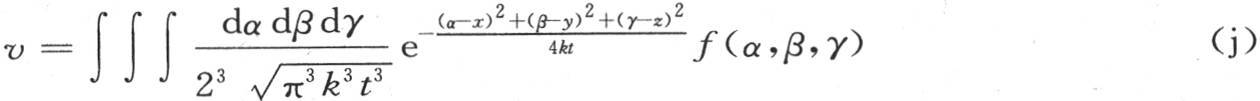
来表示。如果初始热包含在这个实体的一个确定的部分中,那么我们就知道构成这个受热部分的界限,在积分号下变化的量α,β,γ不可能得到超过这些界限的值。这时,假定我们在三个轴上标出了其距离为+X,+Y,+Z和-X,-Y,-Z的六个点,我们考虑在这些距离上过轴的六个平面所包含的这个固体的相继状态;我们看到,当时间值无限增加时,在积分符号下的e的指数简化成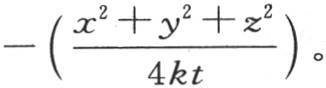 事实上,像
事实上,像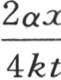 和
和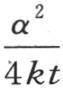 这样的项在这种情况下得到很小的绝对值,因为分子包含在固定区间之间,而分母却无限增加。因此,我们所省略的因子与1完全没有什么差别。所以在很大的时间值之后,这个固体的变化状态就由
这样的项在这种情况下得到很小的绝对值,因为分子包含在固定区间之间,而分母却无限增加。因此,我们所省略的因子与1完全没有什么差别。所以在很大的时间值之后,这个固体的变化状态就由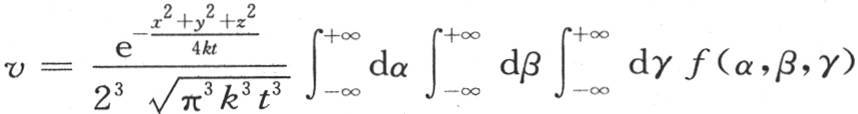 来表示。
来表示。
因子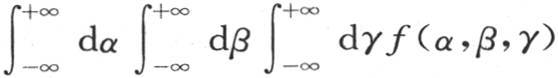 表示这个固体所包含的总热量B。因此,温度系统与热的初始分布无关,只仅仅依赖于它的量。我们应当假定,所有初始热原来都包含在唯一一个棱柱基元中,这个棱柱基元在原点,它极小的正交尺寸是ω1 ,ω2 ,ω3 。该基元的初始温度可以用一个极大的数f来表示,这个固体所有其他分子的初始温度是0。在这种情况下,积ω1 ω2 ω3 f等于积分
表示这个固体所包含的总热量B。因此,温度系统与热的初始分布无关,只仅仅依赖于它的量。我们应当假定,所有初始热原来都包含在唯一一个棱柱基元中,这个棱柱基元在原点,它极小的正交尺寸是ω1 ,ω2 ,ω3 。该基元的初始温度可以用一个极大的数f来表示,这个固体所有其他分子的初始温度是0。在这种情况下,积ω1 ω2 ω3 f等于积分
无论开始的加热如何,与很大的时间值相对应的这个固体的状态是相同的,就好像所有的热都曾集中在处在原点的唯一基元中似的。
385 现在假定我们只考虑相对受热部分的尺寸而言与原点相距很远的这个固体的那些点;我们先可以设想这个条件对简化在一般方程中的e的指数是充分的。事实上,这个指数是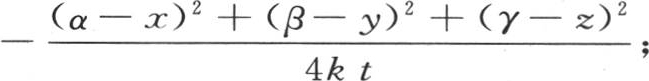 由假定,变量α,β,γ包含在有限的区间之间,因此,它们的值相对于远离原点的点的更大的坐标而言总是极小的。由此得到e的指数由两部分M+μ组成,其中一部分相对另一部分是很小的。然而,我们不能由比
由假定,变量α,β,γ包含在有限的区间之间,因此,它们的值相对于远离原点的点的更大的坐标而言总是极小的。由此得到e的指数由两部分M+μ组成,其中一部分相对另一部分是很小的。然而,我们不能由比 是一个很小的分数这一事实得出指数eM+μ 变得等于eM ,或者是变得与它只相差一个相对它的实际值而言非常小的量这样一个结论。我们决不能只考虑M和μ的相对值,而只能考虑μ的绝对值。为了使我们能够把精确积分(j)简化成方程
是一个很小的分数这一事实得出指数eM+μ 变得等于eM ,或者是变得与它只相差一个相对它的实际值而言非常小的量这样一个结论。我们决不能只考虑M和μ的相对值,而只能考虑μ的绝对值。为了使我们能够把精确积分(j)简化成方程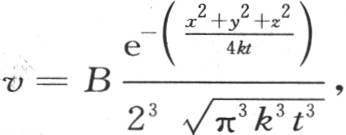 我们就应当使量纲为0的量
我们就应当使量纲为0的量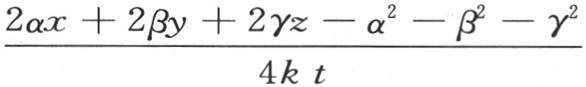 总是一个很小的数。如果我们假定从原点到我们要确定其温度的点m的距离相对于最初被加热的部分的长度非常大,那么我们就应当考察前面这个量是否总是一个很小的分数ω。为了使我们能够运用近似积分
总是一个很小的数。如果我们假定从原点到我们要确定其温度的点m的距离相对于最初被加热的部分的长度非常大,那么我们就应当考察前面这个量是否总是一个很小的分数ω。为了使我们能够运用近似积分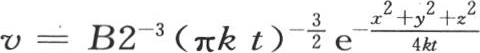 , 【23】 我们必须满足这个条件;但是这个方程不表示这个物体离热源很远的那部分的变化状态。相反,由于其他条件相同,随着我们要确定其温度的这些点与热源相距愈远,它给出的结果就愈不精确。
, 【23】 我们必须满足这个条件;但是这个方程不表示这个物体离热源很远的那部分的变化状态。相反,由于其他条件相同,随着我们要确定其温度的这些点与热源相距愈远,它给出的结果就愈不精确。
包含在这个实体的一个确定部分中的初始热不断贯穿到相邻的部分中去,并在各个方向上传导;仅仅只有极少的热量到达与原点相距很远的那些点。当我们从分析上表示这些点的温度时,这一研究的目的就不是要从数值上确定这些不可测的温度,而是要确定它们的比。现在这些量肯定依赖于初始热据以分布的规律,随着棱柱的这些部分离热源愈远,初始分布的作用就延续得更长。不过如果组成指数部分的项如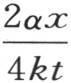 和
和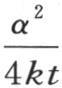 有无限递减的绝对值,那么我们就可以运用这些近似积分了。
有无限递减的绝对值,那么我们就可以运用这些近似积分了。
这个条件出现在为了确定与原点相距很远的点的最高温度而提出的那些问题中。事实上我们可以论证,在这种情况下,当我们要考虑的点离原点很远时,时间值以比距离更大的比值增加,并且与这些距离的平方成正比。只有在建立了这个命题之后,我们才能进行指数下的简化。这类问题是下一节的目的。
第三节 无穷固体中的最高温度
386 我们首先考虑一部分已经均匀受热的无穷长棒中的线性运动,我们将研究为使这条直线的一个已知点能够得到它的最高温度所应当历经的时间值。
让我们用2g来表示受热部分的范围,它的中点与距离x的原点0对应。由假定,与y轴的距离小于g并且大于-g的所有点有共同的初始温度f,其他所有截面取初始温度0。我们假定这个棱柱的外表面不会失热,或者同样地,我们对与轴垂直的截面赋予无穷大的面积。要确定的是与其距离为x的一个已知点的温度的极大值所对应的时间t如何。
我们在前面几目中已经看到,任一点的变化温度由方程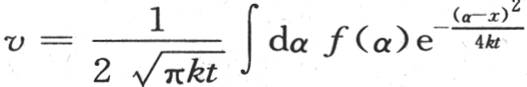 来表示。
来表示。
系数k表示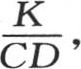 K是热导率,C是热容量,D是密度。
K是热导率,C是热容量,D是密度。
为了简化这一研究,令k=1,因而用t代替kt或者是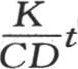 。 【24】 v的表达式变成
。 【24】 v的表达式变成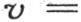
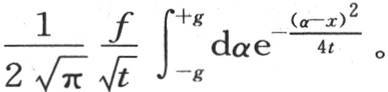
这是方程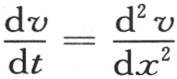 的积分。函数
的积分。函数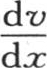 计量热流沿棱柱的轴所流过的速度。现在
计量热流沿棱柱的轴所流过的速度。现在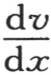 的这个值在实际问题中是已知的而不带任何积分号。事实上我们有
的这个值在实际问题中是已知的而不带任何积分号。事实上我们有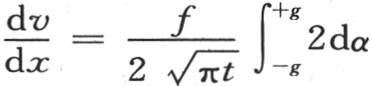
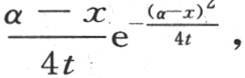 或者完成这个积分,
或者完成这个积分,
387 函数 也可以不用积分号来表示;现在它等于一阶流数
也可以不用积分号来表示;现在它等于一阶流数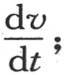 因此只要使计量任一点温度的瞬时增量的这个值
因此只要使计量任一点温度的瞬时增量的这个值 等于0,我们就有所求的x和t之间的关系,所以我们得到
等于0,我们就有所求的x和t之间的关系,所以我们得到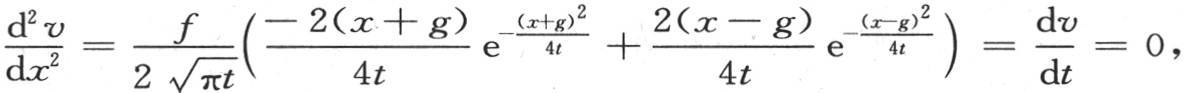 它给出
它给出
 因此我们得到
因此我们得到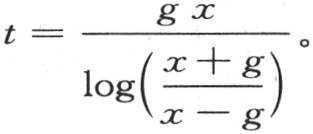
我们已经假定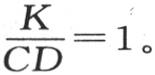 为了使系数还原,我们应当用
为了使系数还原,我们应当用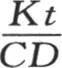 代替t,我们有
代替t,我们有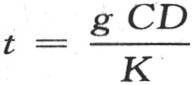
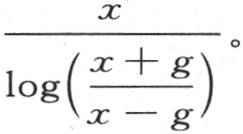
最高温度根据由这个方程所表示的规律而彼此相随。如果我们假定它表示作直线运动的一个物体的可变运动,x是所经过的距离,t是所历经的时间,那么这个运动物体的速度就是温度极大值的速度。
当量g无穷小时,即当初始热集中在位于原点的唯一基元中时,t值就化为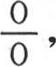 由微分或者是级数展开式,我们得到
由微分或者是级数展开式,我们得到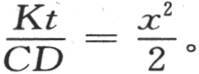
我们尚未考虑从棱柱表面所逃逸的热量;我们现在来考虑这个损耗,我们假定初始热包含在无穷棱柱棒的唯一一个基元中。
388 在前面的问题中,我们确定了一个无穷棱柱棒的变化状态,这个棱柱棒的一个确定部分自始至终受到初始温度f的作用。我们假定初始热分布在从x=0到x=b的一个有限长度中。
我们现在假定同一热量bf包含在从x=0到x=ω的一个无穷小基元中。因此受热薄层的温度是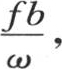 由此得到前面所说的,这个固体的变化状态由方程
由此得到前面所说的,这个固体的变化状态由方程

来表示;当进入微分方程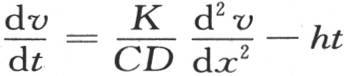 的系数
的系数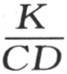 由k来表示时,这个结果成立。至于系数h,它等于
由k来表示时,这个结果成立。至于系数h,它等于 S表示棱柱截面的面积,l表示截面的围道,H表示外表面的热导率。
S表示棱柱截面的面积,l表示截面的围道,H表示外表面的热导率。
在方程(a)中代入这些结果,我们有

f表示平均初始温度,即如果初始热在这根棒长为l,或者是更简单地,在这根棒的长为一个测量单位的那一部分的点之间同等地分布,那么f就表示一个单点所具有的温度。需要确定的是与一个已知点的温度的极大值所对应的这个所历经的时间的值t。
为了解决这个问题,只需要从方程(a)推出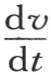 的值,并且使它等于0就够了;我们有
的值,并且使它等于0就够了;我们有
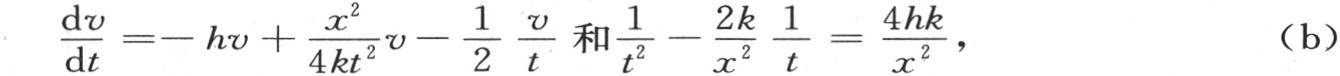
这样,为使处在距离x的点能得到它的最高温度所必须历经的时间值θ,就由方程

来表示。
为了确定最高温度V,我们注意方程(a)中的e-1 的指数是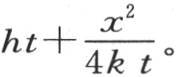 现在方程(b)给出
现在方程(b)给出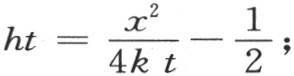 因此
因此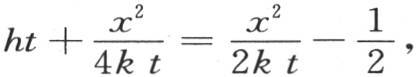 用
用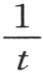 的已知值代替
的已知值代替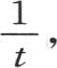 我们有
我们有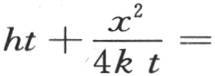
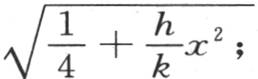 把e-1 的这个指数代入方程(a),我们有
把e-1 的这个指数代入方程(a),我们有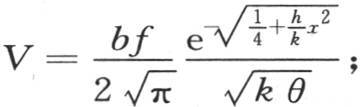 用
用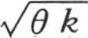 的已知值代替
的已知值代替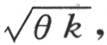 和极大值V的表达式一样,我们得到
和极大值V的表达式一样,我们得到
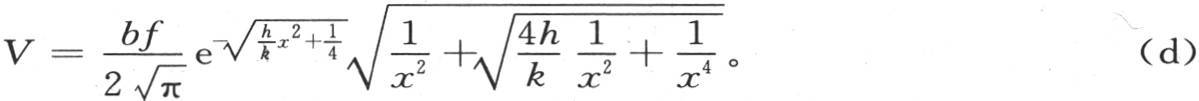
方程(c)和方程(d)包含问题的解;让我们用h和k的值 和来代替h和k;同时用
和来代替h和k;同时用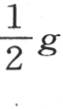 代替
代替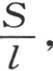 用g表示底为正方形的这个棱柱的半厚。为确定V和θ,我们有方程
用g表示底为正方形的这个棱柱的半厚。为确定V和θ,我们有方程
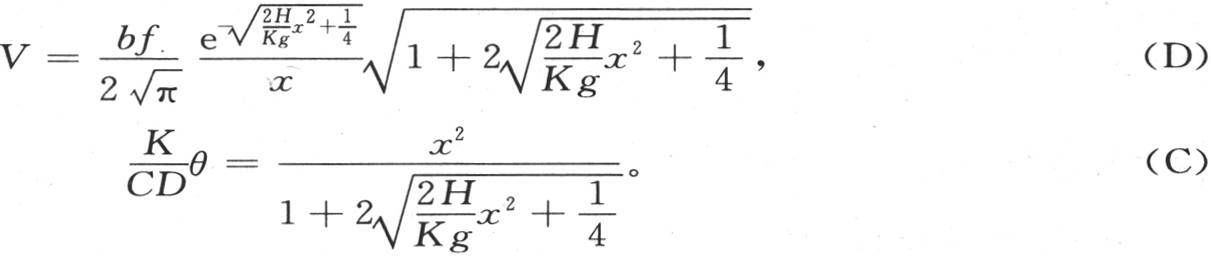
这两个方程适用于很长的细棒中的热运动。我们假定这个棱柱的中央已经受到一定热量的作用,该热量向末端传导,并通过凸面而扩散。V表示与初始热源相距x的点的温度的极大值;θ是自扩散开始一直到出现最高温度这一时刻为止所历经的时间。系数C,H,K,D表示和在前面的问题中一样的特定性质,g是由棱柱截面所形成的正方形的边长的一半。
389 为了用一个数值应用使这些结果更可理解,我们可以假定形成这个棱柱的物质是铁,正方形的边2g是一米的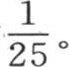
我们以前用我们的实验测定了H和K的值,C和D的值原来就是已知的。取米作为长度单位,取60进制的分作为时间单位,运用H,K,C,D的近似值,我们将确定与一个已知距离相对应的V和θ的值。对于我们所考虑的这个结果的考查来说,不需要很精确地知道这些系数。
我们首先看到,如果距离x大约是1.5米或者是2米,那么进入根号之下的项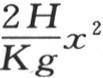 相对第二项
相对第二项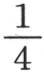 而言就有一个很大的值。这两项的比随距离的增加而增加。
而言就有一个很大的值。这两项的比随距离的增加而增加。
因此,随着热从原点移开,最高温度的规律就变得愈来愈简单。为了确定通过棒的全长而建立的正常规律,我们应当假定距离x是很大的,我们得到
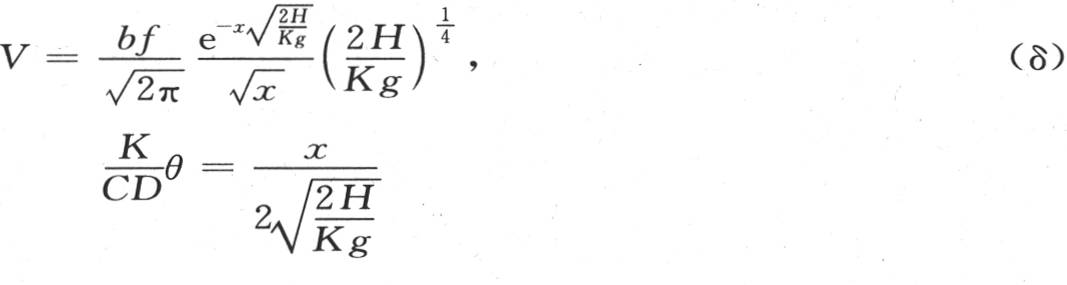
或者是

390 我们由第二个方程看到,与温度极大值所对应的时间和距离成正比地增加。因此,这种波速(如果无论怎样我们都可以把这个表达式应用于所讨论的运动的话)是恒定的,说得更准确些,它愈来愈趋于变成为恒定的,并在它从热的起点至无穷远的运动中都保持这个性质。
在第一个方程中我们还可以注意到,和在第一章第76目中可以看到的一样,如果我们以一固定温度f作用于原点,那么量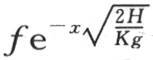 就表示这根棒的不同点所达到的永恒温度。
就表示这根棒的不同点所达到的永恒温度。
为了想象出V的值,我们应当设想热源所包含的初始热在这根棒的长为b或者是长为一个计量单位的部分中的分布是相同的。这一部分的每一点所达到的温度f在某种意义上是平均温度。如果我们假定处在原点的薄层在无穷时间内都保持恒定温度f不变,那么所有薄层就都达到其一般表达式为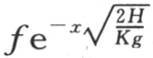 的固定温度,x表示薄层的距离。由一条对数曲线的纵坐标所表示的这些固定温度在距离相当大时是极小的;如所知,随着热源从原点被撤掉,它们就迅速下降。
的固定温度,x表示薄层的距离。由一条对数曲线的纵坐标所表示的这些固定温度在距离相当大时是极小的;如所知,随着热源从原点被撤掉,它们就迅速下降。
现在方程(δ)表明,这些每一点都可以达到的最高的固定温度都大大超过热扩散期间彼此相随的最高温度。为了确定后者的极大值,我们应当计算这个固定的极大值,使它乘以常数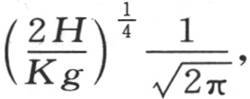 并除以距离x的平方根。
并除以距离x的平方根。
因此,作为除以横坐标平方根的一条对数曲线的纵坐标,这些最高温度在这条直线的整个范围内彼此相随,并且这种波动是均匀的。聚集在一个单点的热根据这个一般规律在这个固体的长度方向上传导。
391 如果我们把这个棱柱外表面的热导率看做是0,或者假定热导率K或者是厚度2g是无穷的,那么我们会得到很不同的结果。这时,我们可以省略项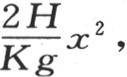 我们将有 【25】
我们将有 【25】

在这种情况下,极大值与距离成反比。因此波运动是不均匀的。我们应当注意这个假定纯粹是理论性的,如果热导率H不是0,而只是一个极小的量,那么波的速度在这个棱柱离原点很远的部分中就不是可变的。事实上,无论H的值怎样,只要这个值也像K和g的值那样是已知的,并且只要我们假定距离x无限增加,那么项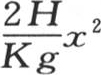 就总是变得比
就总是变得比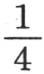 大许多。这些距离在开始时可能相对于项
大许多。这些距离在开始时可能相对于项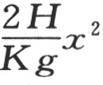 来说小得足以在根号下略去。这时这些时间与距离的平方成正比;但是随着热沿无穷长度的方向流动,传导规律发生变化,时间变得与距离成正比。初始规律,即与和热源极近的点有关的规律,与在很远直至无穷的部分所建立的终极规律大不相同;但是在中间的部分,最高温度根据由前面两个方程(D)和(C)所表示的混合规律而彼此相随。
来说小得足以在根号下略去。这时这些时间与距离的平方成正比;但是随着热沿无穷长度的方向流动,传导规律发生变化,时间变得与距离成正比。初始规律,即与和热源极近的点有关的规律,与在很远直至无穷的部分所建立的终极规律大不相同;但是在中间的部分,最高温度根据由前面两个方程(D)和(C)所表示的混合规律而彼此相随。
392 还需要确定对于热在物质实体内在各个方向上被传导至无穷远情况下的最高温度。根据我们已经建立的原理,这一研究不会有任何困难。
当一个无穷固体的一个确定部分已经受热,这个物体的所有其他部分取同一初始温度0时,热向四面八方传导,并且在一定时间之后,这个固体的状态就如同热最初曾集中在坐标原点的单个点上一样。当物体的这些点远离原点时,最后效应出现之前所应当历经的时间是极长的。每个在开始温度为0的这样的点受热微乎其微;随后它们的温度达到它们所能达到的极大值;并以逐渐减弱而结束,直到在这个物体中不留下任何显热(sensible heat)。这种变化状态一般由方程
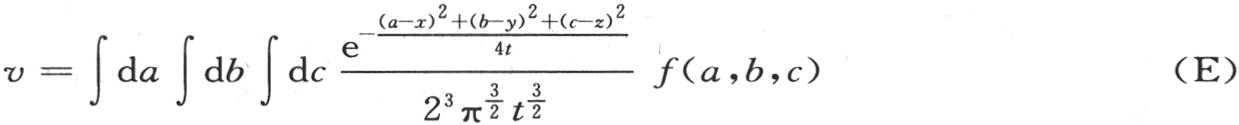
来表示。
我们应当在a=-a1 ,a=a2 ;b=-b1 ,b=b2 ;c=-c1 ,c=c2 的区间内取这些积分。
区间-a1 ,+a2 ,-b1 ,+b2 ,-c1 ,+c2 是已知的;它们包括这个固体最初被加热的整个部分。函数f(a,b,c)也是已知的。它表示坐标为a,b,c的一点的初始温度。这些定积分使变量a,b,c消掉,并为v保留x,y,z,t的一个函数和几个常数。为了确定在一个已知点m上与v的一个极大值所对应的时间θ,我们应当从前述方程推出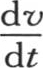 的值;因此我们建立一个含θ和点m的坐标的方程。于是我们由此可推出θ值。如果这时我们在方程(E)中用这个θ值代替t,那么我们就得到以x,y,z和一些常数所表示的最高温度V的值。
的值;因此我们建立一个含θ和点m的坐标的方程。于是我们由此可推出θ值。如果这时我们在方程(E)中用这个θ值代替t,那么我们就得到以x,y,z和一些常数所表示的最高温度V的值。
不用方程(E),让我们写v=∫da∫db∫dcPf(a,b,c),用P表示f(a,b,c)的乘数,我们有
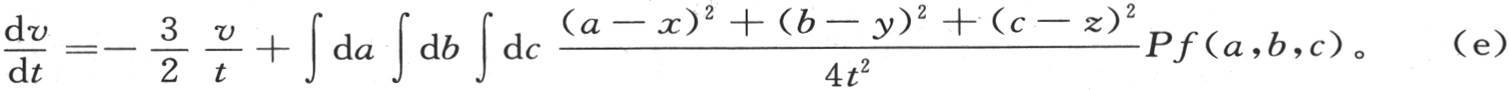
393 我们现在应当把最后这个表达式应用到这个固体远离原点的那些点上去。由于含初始热部分的任一点的坐标是变量a,b,c,并且我们要确定其温度的点m的坐标是x,y,z,所以这两点之间的距离的平方是(a-x)2 +(b-y)2 +(c-z)2 ;这个量作为一个因子进入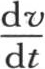 的第二项。
的第二项。
现在由于点m离原点很远,所以显然,这一点和受热部分任一点的距离∆与这同一点和原点的距离D相同;即随着点m离含坐标原点的初始热源愈来愈远,距离D和∆的最终比变成1。
由此得到,在给出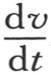 的值的方程(e)中,因子(a-x)2 +(b-y)2 +(c-z)2 可以用x2 +y2 +z2 或者是r2 来代替,r表示点m与原点的距离。于是我们有
的值的方程(e)中,因子(a-x)2 +(b-y)2 +(c-z)2 可以用x2 +y2 +z2 或者是r2 来代替,r表示点m与原点的距离。于是我们有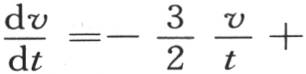
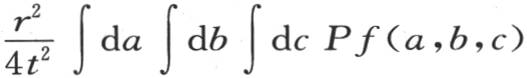 或者是
或者是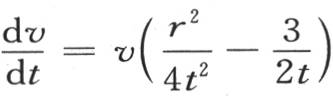
如果我们为了重新设立我们曾经假定等于1的系数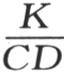 而用v的值来代替v,用
而用v的值来代替v,用 代替t,那么,我们有
代替t,那么,我们有
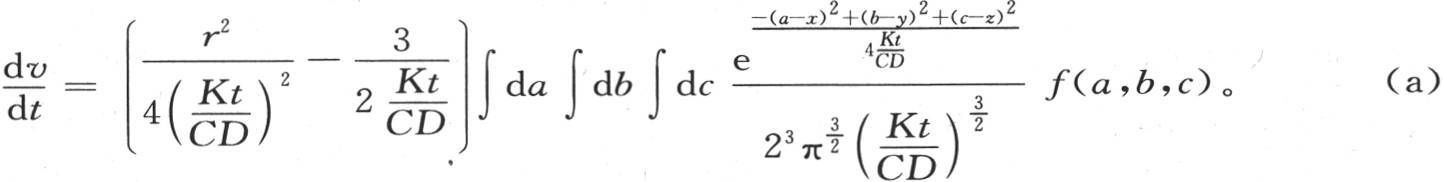
394 这个结果只属于这个固体与原点的距离相对热源的最大长度很大的那些点。我们应当时刻小心注意的是,从这个条件并不能得出我们可以忽略指数符号下变量a,b,c的结论。它们只有在这个符号之外时才可以略去。事实上,在积分符号下乘f(a,b,c)的这个项是几个像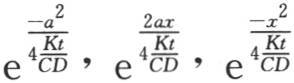 这样的因子的积。
这样的因子的积。
现在,比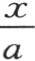 总是一个很大的数,这并不足以使我们能略去前两个因子。例如,如果我们假定a等于1分米,x等于10米,并且如果使热在其中得以传导的物质是铁,那么我们看到,在历经9小时或者是10小时之后。因子
总是一个很大的数,这并不足以使我们能略去前两个因子。例如,如果我们假定a等于1分米,x等于10米,并且如果使热在其中得以传导的物质是铁,那么我们看到,在历经9小时或者是10小时之后。因子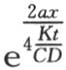 仍然比2大;所以若删去它,我们就会减少所求结果的一半。因此,当
仍然比2大;所以若删去它,我们就会减少所求结果的一半。因此,当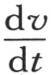 的值属于远离原点的点时,对任一时间来说,它都应当由方程(α)来表示。但是如果我们只考虑极大的时间值,该时间值与距离的平方成正比地增加,则情况就不同了:与这个条件相对应,我们应当省略包含a,b或者是c的那些项,即使它们在指数符号内也应省略。现在,正如我们开始证明的一样,当我们要确定一个很远的点所能达到的最高温度时,这个条件成立。
的值属于远离原点的点时,对任一时间来说,它都应当由方程(α)来表示。但是如果我们只考虑极大的时间值,该时间值与距离的平方成正比地增加,则情况就不同了:与这个条件相对应,我们应当省略包含a,b或者是c的那些项,即使它们在指数符号内也应省略。现在,正如我们开始证明的一样,当我们要确定一个很远的点所能达到的最高温度时,这个条件成立。
395 事实上,在所说的情况下,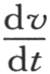 的值应当为0;因此我们有
的值应当为0;因此我们有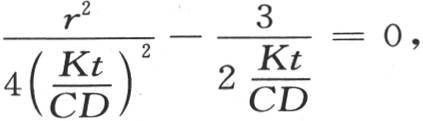 或者是
或者是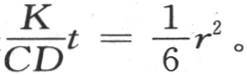
所以,为了使一个很远的点能够达到它的最高温度所应当历经的时间,就与这一点和原点的距离的平方成正比。 【26】
如果我们在v的表达式中用分母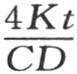 的值
的值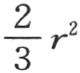 来代替分母
来代替分母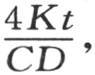 那么e-1 的指数
那么e-1 的指数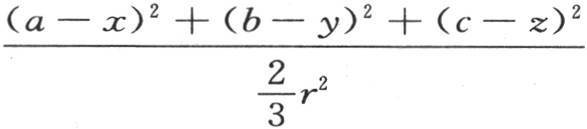 就简化成
就简化成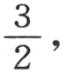 因为我们略去的因子相当于1。由此我们得到
因为我们略去的因子相当于1。由此我们得到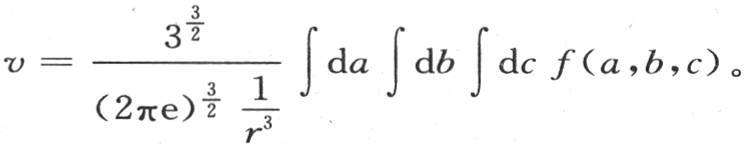
积分∫da∫db∫dcf(a,b,c)表示初始热量;半径为r的球的体积是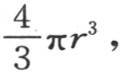 因此,当用f表示该球的每个分子所得到的温度时,如果我们在它的各部分之间分布所有的初始热,那么我们有
因此,当用f表示该球的每个分子所得到的温度时,如果我们在它的各部分之间分布所有的初始热,那么我们有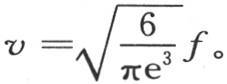
我们在本章所展开的这些结果指明包含在无穷固体的一个确定部分中的热逐渐贯穿到其初始温度为0的所有其他部分中去的规律。解决这个问题比解决前几章的问题要简单一些,因为通过对该固体赋予无穷体积,我们就消去了与表面有关的条件,而主要困难就在于这些条件的运用。无界固体中的热运动的一般结果是很引人注目的,因为这种运动不为表面障碍所干扰。它通过热的自然性质而自由地完成。严格地说,这一研究是对物体内的热辐射的研究。
第四节 积分的比较
396 热传导方程的积分呈现出不同的形式,有必要对这些不同形式进行比较。正如我们在本章第二节第372和376目中所看到的,不难把三维的情况归到线性运动的情况中去;因此对方程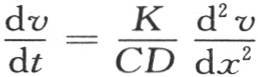 或者是对方程
或者是对方程

积分就够了。
为了从这个微分方程推出在一个确定形状的物体中的热传导规律,如在一个环中的热传导规律,我们应当知道这个积分,应当在某种适合于该问题的形式下得到它,后者是不可能以别的形式完成的一个条件。我们在1807年12月21日提交给法兰西研究院的研究报告中首次给出了这个积分(第124页第84目):它主要在于表示固体环的变化的温度系统的下述方程:
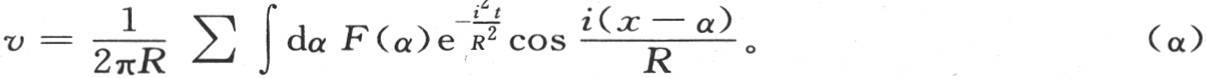
R是环的平均周长的半径;对α的积分应当从α=0取到α=2πR,或者同样地,从α=-πR取到α=πR;i是任一整数,和∑应当从i=-∞取到i=+∞;v表示在历经时间t之后在与位于原点的截面相距弧x的截面上的每一点所观察到的温度。我们用v=F(x)表示环上任一点的初始温度。我们应当对i给出逐个值0,+1,+2,+3,…,和-1,-2,-3,…,用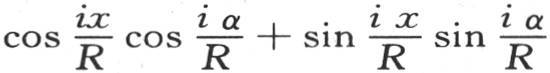 代替
代替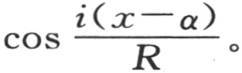
因此我们得到v值的所有项。这就是我们为表示环中变化的热运动(第四章第24目)所应当安排的方程(α)的积分形式。我们把环的生成截面(the generating section)的形状和大小设想成同一截面的点明显保持相同的温度这样一种情况。我们同时还假定环的表面不会失热。
397 由于方程(α)适用于所有的R值,所以我们可以在其中假定R是无穷的;在这种情况下,它给出下述问题的解。一根细而无穷长的实棱柱的初始状态已知,并且由v=F(x)来表示,求所有的后继状态。假定半径R在数值上包含三角函数表上的单位半径的n倍。用q表示依次变成dq,2dq,3dq,…,idq,…的一个变量,无穷数n由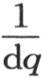 来表示,变数i则由
来表示,变数i则由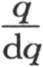 来表示。作这些代换以后,我们得到
来表示。作这些代换以后,我们得到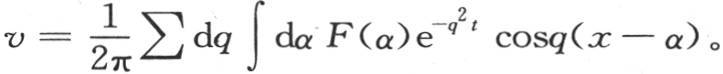
进入符号∑之内的项是一些微分量,因此这个符号变成一个定积分符号;所以我们有
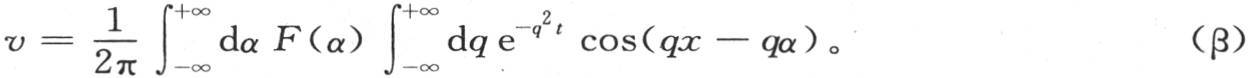
这个方程是方程(α)的积分的第二种形式;它表示在无穷长棱柱中的线性热运动(第七章第354目)。它是第一个积分(α)的明显推论。
398 我们可以在方程(β)中完成对q的定积分;因为根据我们已经证明过的一条引理(第375目),我们有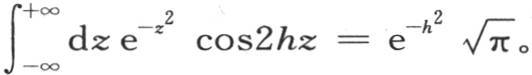
然后令z2 =q2 t,我们得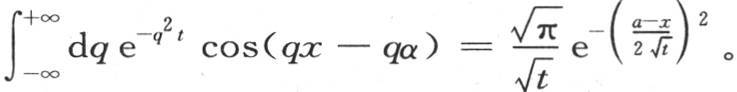
因此上一目的积分(β)就变成

如果我们用另一个未知量β代替α,令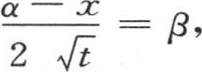 则我们得到
则我们得到
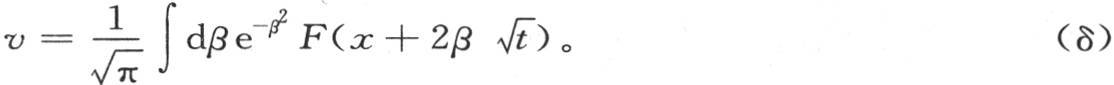
方程(a)的这个积分形式(δ) 【27】 在《综合工科学校研究报告》第8卷中由拉普拉斯先生给出,他是通过考虑表示这个积分的无穷级数而得到这个结果的。
方程(β),(γ),(δ)的每一个都表示无穷长棱柱中的线性热扩散。显然,它们是同一个积分的三种形式,并且不能认为其中一种比另外二种更一般。它们每一个都包含在积分(α)之中,它们通过对R给定一个无穷值而从积分(α)中导出。
399 我们不难以由某个变量的增幂所安排的级数来展开从方程(a)所推出的这个v值。这些展开式是自明的,我们本来不谈它们也行;不过它们引出的一些注记在积分研究中是有用的。用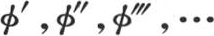 表示函数
表示函数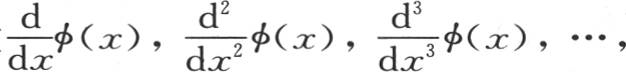 我们有
我们有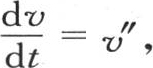 和v=c+∫dtv″;在这里,常数表示x的一个任意函数。用v″的值c″+∫dtvⅣ 来代替v″并且一直继续运用类似的代换,则我们得到
和v=c+∫dtv″;在这里,常数表示x的一个任意函数。用v″的值c″+∫dtvⅣ 来代替v″并且一直继续运用类似的代换,则我们得到
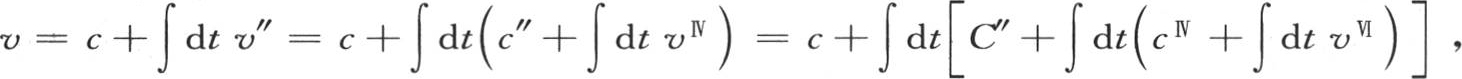
或者是
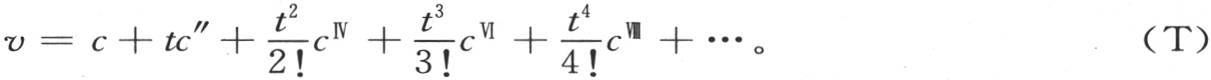
在这个级数中,c表示x的一个任意函数。如果我们要根据x的升幂来安排v值的展开式,那么我们运用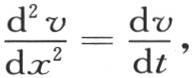 并且,用
并且,用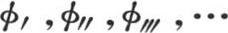 表示函数
表示函数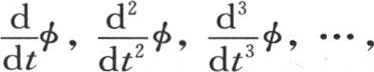 我们首先有
我们首先有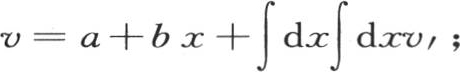 此处a和b表示t的两个任意函数。然后我们可以用
此处a和b表示t的两个任意函数。然后我们可以用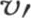 的值
的值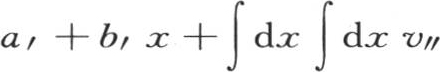 来代替
来代替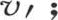 用
用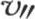 的值
的值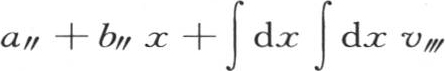 代替
代替 等等。通过连续代换,
等等。通过连续代换,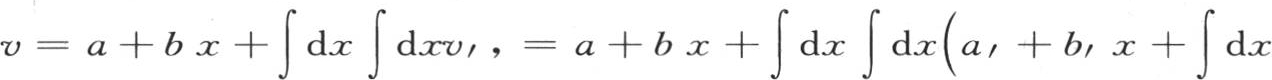
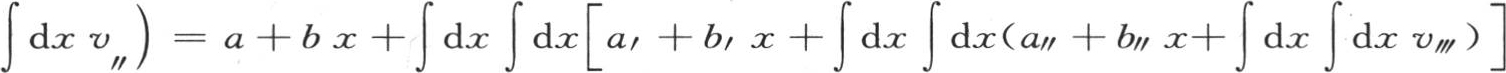 或者是
或者是
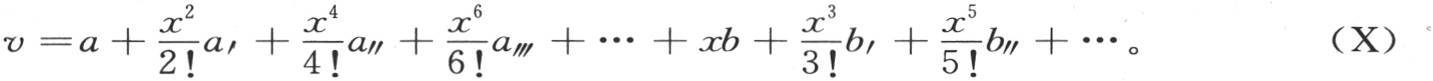
在这个级数中,a和b表示t的两个任意函数。
如果在由方程(X)所给定的这个级数中我们用两个函数φ(t)和ψ(t)来代替a和b,并根据t的升幂来展开它们,那么我们只得到x的一个唯一的任意函数,而不是两个函数a和b。我们把这个注记归功于泊松,他在《综合工科学校研究报告》第6卷第110页给出了这个注记。
相反,如果在由方程(T)所表示的级数中我们根据x的幂来展开函数c,那么在相对于x的相同幂来安排这个结果时,这些幂的系数就由t的两个完全任意的函数组成;只要进行这一研究,就不难验证这一点。
400 事实上,根据t的幂所展开的这个v值应当只含x的一个任意函数;因为微分方程(a)清楚地表明,作为x的一个函数,如果我们知道对应于t=0的这个v值,那么对应于t的后继值的这个函数v的其他值就由这个值所确定。
同样明显的是,这个函数v,当根据x的升幂而展开时,应当包含变量t的两个完全任意的函数。事实上,微分方程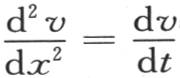 表明,作为t的一个函数,如果我们知道与x的一个确定值所对应的v值,那么我们不能由此得出与x的其他所有值所对应的v值。我们还必须给出与x的第二个值所对应的、作为t的一个函数的v值,如给出与第一个值挨得无穷近的值。这时,函数v的所有其他状态,即与x的其他所有值相对应的值,就被确定了。微分方程(a)属于一个曲面,该曲面任一点的纵坐标是v,两个水平坐标是x和t。由这个方程(a)显然可以得到,当我们给出过x轴的平面的垂直截面的形状时,这个曲面的形状就确定了:这也可以从问题的物理性质得出;因为显然,由于棱柱的初始状态被给定,所以所有后继状态也就确定了。但是,如果这个曲面仅仅只受过t和v的第一个垂直平面上所引的一条曲线的支配,那么我们就不能画出这个曲面。我们有必要进一步知道在与第一个垂直平面平行的第二个垂直平面上所作的曲线,我们可以假定它与第一个垂直平面挨得无穷近。同样这些注记适用于所有的偏微分方程,就所有情况而言,这个方程的阶并不确定任意函数的数目。
表明,作为t的一个函数,如果我们知道与x的一个确定值所对应的v值,那么我们不能由此得出与x的其他所有值所对应的v值。我们还必须给出与x的第二个值所对应的、作为t的一个函数的v值,如给出与第一个值挨得无穷近的值。这时,函数v的所有其他状态,即与x的其他所有值相对应的值,就被确定了。微分方程(a)属于一个曲面,该曲面任一点的纵坐标是v,两个水平坐标是x和t。由这个方程(a)显然可以得到,当我们给出过x轴的平面的垂直截面的形状时,这个曲面的形状就确定了:这也可以从问题的物理性质得出;因为显然,由于棱柱的初始状态被给定,所以所有后继状态也就确定了。但是,如果这个曲面仅仅只受过t和v的第一个垂直平面上所引的一条曲线的支配,那么我们就不能画出这个曲面。我们有必要进一步知道在与第一个垂直平面平行的第二个垂直平面上所作的曲线,我们可以假定它与第一个垂直平面挨得无穷近。同样这些注记适用于所有的偏微分方程,就所有情况而言,这个方程的阶并不确定任意函数的数目。
401 可以把从方程

所导出的第399目的级数(T)放在 的形式之下。根据D的幂展开这个指数,并且
的形式之下。根据D的幂展开这个指数,并且 代替Di ,同时把i看做是微分的阶,则我们有
代替Di ,同时把i看做是微分的阶,则我们有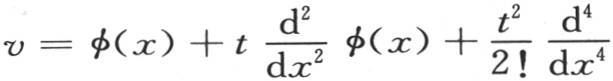
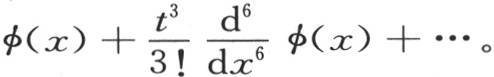
若采用同一记号,那么只含x偶次幂的级数(X)(第399目)的第一部分就可以表示成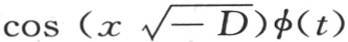 的形式。在把i看做是微分的阶时,根据x的幂来展开,并且用
的形式。在把i看做是微分的阶时,根据x的幂来展开,并且用 来代替Di 。通过相对x取积分,同时把函数φ(t)变成另一个任意函数,级数(X)的第二部分则可以从第一部分中导出。因此我们有
来代替Di 。通过相对x取积分,同时把函数φ(t)变成另一个任意函数,级数(X)的第二部分则可以从第一部分中导出。因此我们有 和
和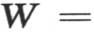
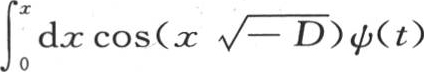 。 【28】
。 【28】
这个已知的简记法从积分和幂之间所存在的相似性导出。至于此处对它所作的运用,其目的是为了表示级数,且无需任何展开式而验证它们。这只需在这个简记法所使用的符号下进行微分就够了。例如,只对t进行微分,我们由方程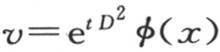 推出
推出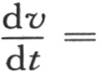
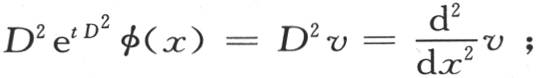 它恰好表明级数满足微分方程(a)。同样地,如果我们考虑级数(X)的第一部分,同时记
它恰好表明级数满足微分方程(a)。同样地,如果我们考虑级数(X)的第一部分,同时记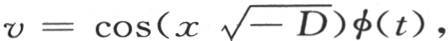 那么,仅仅对x微分两次,我们有
那么,仅仅对x微分两次,我们有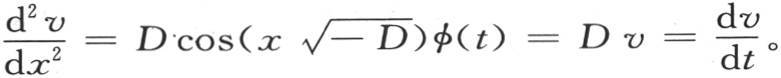
因此,这个v值满足微分方程(a)。
同样,我们可以发现,微分方程

以一个根据y的增幂而展开的级数给出v的表达式,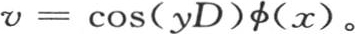
我们应当相对于y来展开,并且用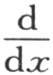 来代替D。事实上,我们由这个v值推得
来代替D。事实上,我们由这个v值推得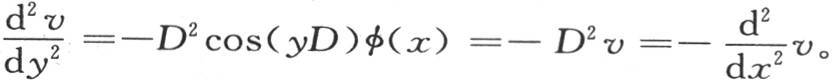
值sin(yD)ψ(x)也满足这个微分方程;因此v的一般值是v=cos(yD)φ(x)+W,此处W=sin(yD)ψ(x)。
402 如果所提出的微分方程是

如果我们要以根据t的幂所安排的级数来表示v,那么我们可以用Dφ来表示函数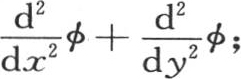 由于这个方程是
由于这个方程是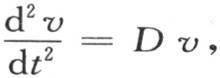 所以我们有
所以我们有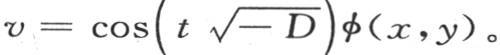
由此我们推出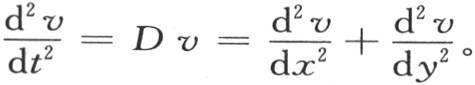 我们应当根据t的幂来展开前面的v值,用
我们应当根据t的幂来展开前面的v值,用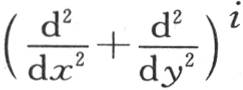 代替Di ,并把i看做是微分的阶。
代替Di ,并把i看做是微分的阶。
下面的值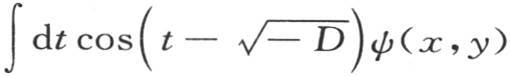 满足相同的条件;因此v的最一般的值是
满足相同的条件;因此v的最一般的值是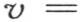
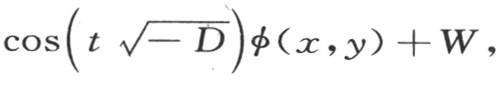 并且
并且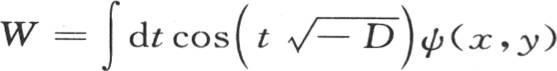 。 【29】 v是一个有三个变量的函数f(x,y,t)。如果我们取t=0,则我们有f=(x,y,0)=φ(x,y);用f′(x,y,t)表示
。 【29】 v是一个有三个变量的函数f(x,y,t)。如果我们取t=0,则我们有f=(x,y,0)=φ(x,y);用f′(x,y,t)表示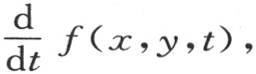 则我们有f′(x,y,0)=ψ(x,y)。
则我们有f′(x,y,0)=ψ(x,y)。
如果所提出的方程是

那么以根据t的幂所安排的一个级数所表示的这个v值就是v=cos(tD2 )φ(x,y),D表示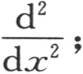 因此我们从这个值推出
因此我们从这个值推出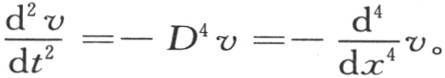
因此,可以只含x和y的两个任意函数的这个一般的v值是v=cos(tD2 )φ(x,y)+W,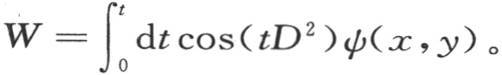 当用f(x,y,t)来表示v,用f′(x,y,t)表示
当用f(x,y,t)来表示v,用f′(x,y,t)表示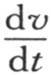 时,我们就不得不确定两个任意函数φ(x,y)=f(x,y,0),和ψ(x,y)=f(x,y,0)。
时,我们就不得不确定两个任意函数φ(x,y)=f(x,y,0),和ψ(x,y)=f(x,y,0)。
403 如果所提出的微分方程是
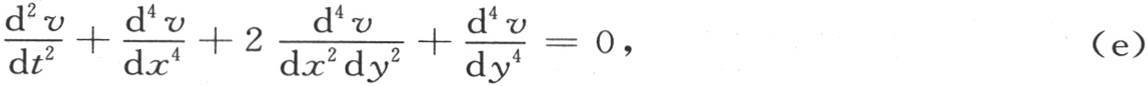
那么,我们可以用Dφ来表示函数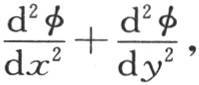 因此,可以通过把二项式
因此,可以通过把二项式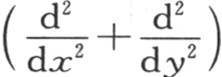 增加到二阶、同时把指数看做是微分的阶来形成DDφ或者是D2 φ。这样,方程(e)就变成
增加到二阶、同时把指数看做是微分的阶来形成DDφ或者是D2 φ。这样,方程(e)就变成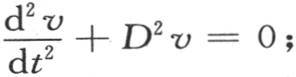 并且,根据t的幂所安排的v值是cos(tD)φ(x,y);因为由此我们推得
并且,根据t的幂所安排的v值是cos(tD)φ(x,y);因为由此我们推得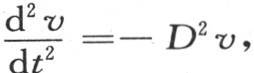 或者是
或者是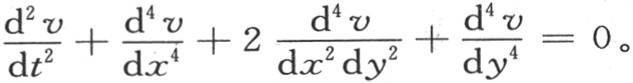
由于最一般的v值可以只含x和y的两个任意函数,这是这个方程形式的一个明显推论,所以它可以表示成v=cos(tD)φ(x,y)+∫dtcos(tD)ψ(x,y)。 【30】 用f(x,y,t)表示函数v,用f1 (x,y,t)表示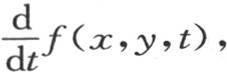 则函数φ和ψ可以确定如下:φ(x,y)=f(x,y,0),ψ(x,y)=f1 (x,y,0)。
则函数φ和ψ可以确定如下:φ(x,y)=f(x,y,0),ψ(x,y)=f1 (x,y,0)。
最后,设所提出的方程是
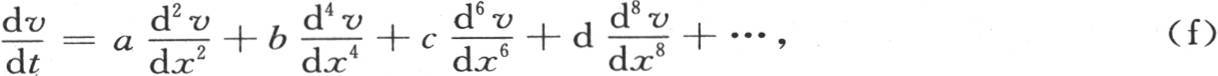
系数a,b,c是已知数,方程的阶是不定的。
这个最一般的v值可以只含x的一个任意函数;因为显然,仅仅由方程的这个形式可知,作为x的一个函数,如果我们知道对应于t=0的v值,那么对应于t的后续值的其他所有v值就都被确定了。因此,为了表示v,我们有方程v=etD φ(x)。
我们用Dφ表示表达式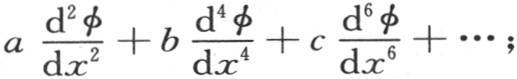 即为了形成v值,我们应当根据t的幂来展开量
即为了形成v值,我们应当根据t的幂来展开量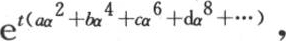 并且用
并且用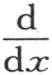 代替α,同时把α的幂看做是微分的阶。事实上,由于这个v值只对t微分,所以我们有
代替α,同时把α的幂看做是微分的阶。事实上,由于这个v值只对t微分,所以我们有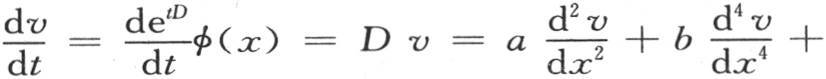
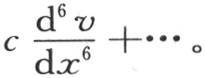 增加这个相同过程的重复应用没有什么用。对于很简单的方程。我们无需简化表达式;不过它们一般代替很复杂的研究。例如我们选择前面那些方程,是因为它们都与其解析表达式和热运动表达式相似的物理现象有关。前两个,(a)和(b),属于热的理论;后三个,(c),(d),(e),属于动力学问题;最后的(f)表示在瞬时传导超出极小距离时实体中所出现的热运动。我们有在贯穿透明介质的光热运动方面的这类问题的一个例子。
增加这个相同过程的重复应用没有什么用。对于很简单的方程。我们无需简化表达式;不过它们一般代替很复杂的研究。例如我们选择前面那些方程,是因为它们都与其解析表达式和热运动表达式相似的物理现象有关。前两个,(a)和(b),属于热的理论;后三个,(c),(d),(e),属于动力学问题;最后的(f)表示在瞬时传导超出极小距离时实体中所出现的热运动。我们有在贯穿透明介质的光热运动方面的这类问题的一个例子。
404 我们可以用不同的方法得到这些方程的积分。我们首先要指明这是由第361目中所阐明的定理带来的,我们现在重温这个定理。
如果我们考虑表达式
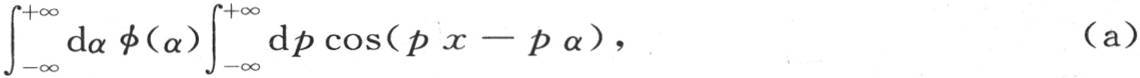
那么我们会看到,它表示x的一个函数;因为这两个对α和p的定积分使这两个变量消掉,并只保留一个x的函数。这个函数的性质显然依赖于我们将会为φ(α)所选定的函数。我们可以问,为使我们在两个定积分之后能得到f(x)的一个已知函数,函数φ(α)应当是怎样的。一般地,适合于不同物理现象的表达式的这些积分研究可以简化成类似于前面的问题。这些问题的目的是要确定积分符号下的这些任意函数,因此这个积分的结果可以是一个已知函数。例如不难看到,如果在前面的表达式(a)中我们可以确定φ(α),因而积分的结果是一个已知函数f(x),那么方程
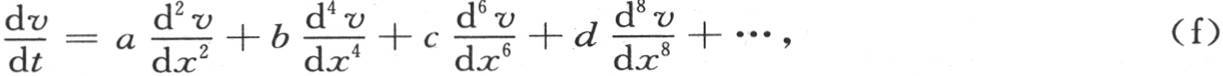
的通积分就是已知的。事实上,我们恰好建立一个特殊的v值,它表示成v=e-mt cospx,并且我们得到条件m=ap2 +bp4 +cp6 +…。 【31】
当对常数α给定任意一个值时,我们也可以取v=e-mt cos(px-pα),同样,我们有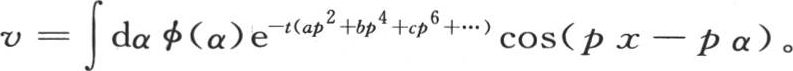 显然,这个v值满足偏微分方程(f);它只不过是一些特殊值的和。
显然,这个v值满足偏微分方程(f);它只不过是一些特殊值的和。
此外,假定t=0,对于v,我们应当得到x的一个任意函数。用f(x)表示这个函数,我们有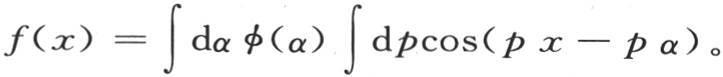
现在,由方程(f)的形式得到,最一般的v值可以只含一个x的任意函数。事实上,这个方程清楚地表明,作为x的一个函数,如果对于时间t的一个已知值,我们知道其v值,那么与其他时间值所对应的其他所有v值就必然被确定。由此严格得到,作为t和x的一个函数,如果我们知道满足微分方程的一个v值,此外,如果只要令t=0,x和t的这个函数就变成x的一个完全任意的函数,那么,所说的x和t的这个函数就是方程(f)的通积分。因此,整个问题简化成在上述方程中确定函数φ(α),使得两个积分的结果是一个已知函数f(x)。为使这个解是一般的,只需我们能够把f(x)看做是一个完全任意、甚至是不连续的函数就行了。因此,只需知道已知函数f(x)和未知函数φ(α)之间必定总是存在的关系就够了。现在,这种很简单的关系由我们所说的定理来表示。事实上,它在于当在无穷区间内取这些积分时函数φ(α)是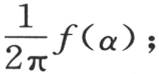 即我们有方程
即我们有方程
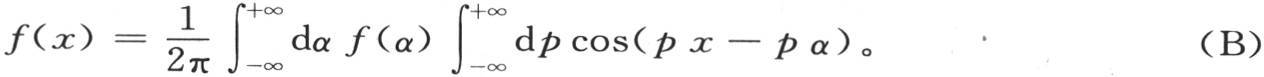
和所提出的方程(f)的通解一样,我们由此得到:

405 如果我们提出方程

它表示一块弹性板的横切振动运动 【32】 ,由这个方程的形式,我们应当认为最一般的v值可以只含x的两个任意函数;因为,当用f(x,t)表示这个v值,用f′(x,t)表示函数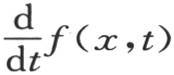 时,显然,如果我们知道f(x,0)和f′(x,0),即知道在第一个时刻的那些v值和
时,显然,如果我们知道f(x,0)和f′(x,0),即知道在第一个时刻的那些v值和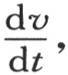 那么其他所有v值就都确定了。
那么其他所有v值就都确定了。
这还可以只从这个现象的性质推出。事实上,考虑静止状态下的一块直线弹性薄板:x是这块薄板上任一点与坐标原点的距离;这块薄板的平衡位置与水平面上的x轴重合,把这块薄板从它的平衡位置上拉开,它的形状就稍稍发生变化;这时它就处在由形变所产生的力的作用之中。假定这种位移是任意的,只是非常小,以至于对这块薄板所给定的初始形状是过x轴的垂直平面上所作的一条曲线的形状。这个系统将不断改变其形状,并在垂直平面中,在平衡线的两边不断运动。这种运动的最一般的条件由方程

来表示。
在水平面上,在与原点O相距x的平衡位置上的任一点m,在时间t结束时,已经过垂直高度v而从它的位置上离开。这个变程v是x和t的一个函数。v的初始值是任意的;它由任一函数φ(x)来表示。现在,从动力学的基本原理所推出的方程(d)表明,v对t所取的二阶流数或者是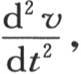 以及对x所取的四阶流数或者是
以及对x所取的四阶流数或者是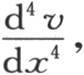 是x和t的两个函数,这两个函数只有符号上的差别。我们在此不讨论与这两个函数的不连续性有关的具体问题;我们只考虑积分的解析表达式。
是x和t的两个函数,这两个函数只有符号上的差别。我们在此不讨论与这两个函数的不连续性有关的具体问题;我们只考虑积分的解析表达式。
我们还可以假定,在任意移动这块薄板的不同点之后,我们在完成振动的垂直平面上对它们给予很小的初速。对任一点m所给定的初速取任意值。它由距离x的一个任意函数ψ(x)来表示。
显然,如果我们给定这个系统的初始形状或者是φ(x),以及初始冲量ψ(x),那么这个系统的所有后继状态就被确定。因此,在任一时间t之后表示这块薄板的相应形状的函数v或者是f(x,t),包含两个任意函数φ(x)和ψ(x)。
为了确定所要求的函数f(x,t),设想在方程

中,我们可以对v给出很简单的值u=cosq2 tcosqx,或者是u=cosq2 tcos(qx-qα);q和α表示既不含x也不含t的任意两个量。因此我们也有u=∫dαF(α)∫dqcosq2 t cos(qx-qα),无论积分区间是怎样的,F(α)都是一个任意函数。这个v值只不过是一些特殊值的和。
假定现在t=0,这个v值必然是我们用f(x,0),或者是φ(x)所表示的值。因此我们有φ(x)=∫dαF(α)∫dqcos(qx-qα)。
函数F(α)应当这样来确定:使得当两个积分完成时,结果应当是任意函数φ(x)。现在由方程(B)所表示的定理表明,当两个积分区间是-∞到+∞时,我们有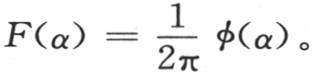
因此,u值由下述方程给定: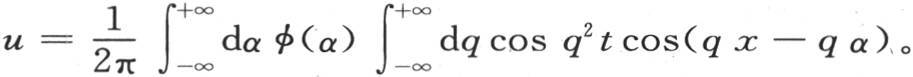
如果我们相对t来对这个u值积分,其中的φ变成ψ,那么显然,(由W所表示的)积分将再次满足所提出的微分方程(d),并且我们应当有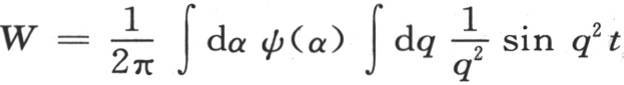
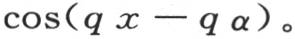
当t=0时,这个W值变成0;如果我们取表达式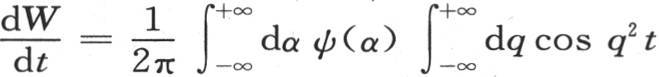
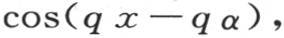 那么我们看到,只要在其中令t=0,它就变得等于ψ(x)。表达式
那么我们看到,只要在其中令t=0,它就变得等于ψ(x)。表达式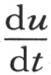 则不同;当t=0时,它变成0,并且当t=0时u变得等于φ(x)。
则不同;当t=0时,它变成0,并且当t=0时u变得等于φ(x)。
由此得到方程(d)的积分是
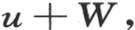 并且
并且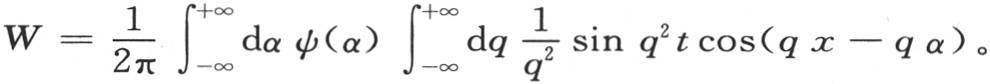
事实上,这个v值满足微分方程(d);同样,当我们令t=0时,它等于完全任意的函数φ(x);当我们在表达式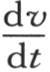 中令t=0时,它化为第二个任意函数ψ(x)。因此v值是所提出的方程的完全积分,并且不可能有更一般的积分了。
中令t=0时,它化为第二个任意函数ψ(x)。因此v值是所提出的方程的完全积分,并且不可能有更一般的积分了。
406 相对q进行积分,v值可以简化成更简单的形式。这个简化以及那些相同类型的其他式子的简化,取决于由方程(1)和(2)所表示的两个结果,这两个方程将在下一目中证明:
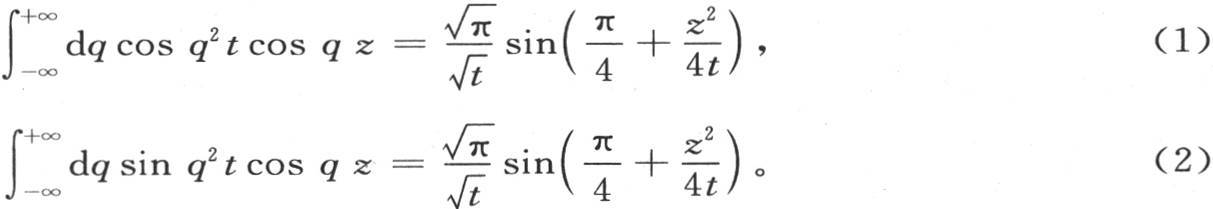
由此我们得到
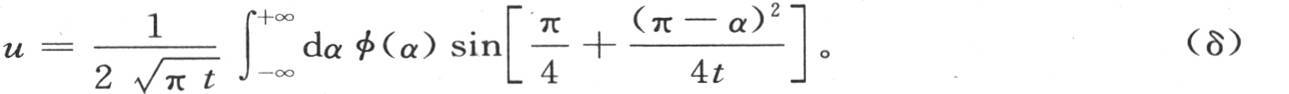
用另一个未知数μ表示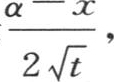 我们有
我们有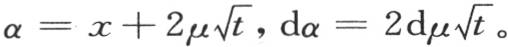 不用
不用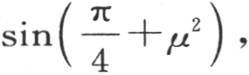 而代之以它的值
而代之以它的值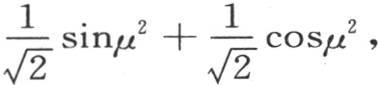 我们有
我们有
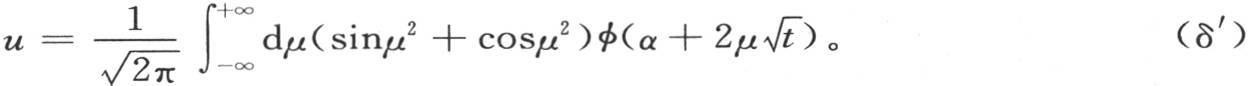
我们在一份具体的研究报告中已经证明,(δ)或者是(δ′),方程(d)的这些积分,清楚完整地表示一块无穷弹性薄板的不同部分的运动。它们包含这个现象的清晰的表达式,并且很容易阐明它的所有规律。我们正是主要从这个观点出发而提出它们,以引起几何学家们的注意的。它们表明振动在薄板的整个范围内怎样传递和建立,表明任意的和偶然的初始位移的作用怎样随着它从原点取消而逐渐改变,很快变得察觉不出来,只剩下这个系统特有的力,即弹性力的作用。
407 由方程(1)和(2)所表示的结果取决于定积分∫dxcosx2 ,和∫dxsinx2 ;设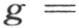
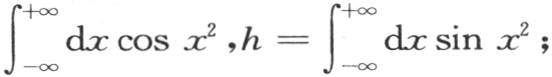 并且把g和h看做是已知数。显然,在前面两个方程中我们可以用y+b来代替x,b表示任一常数,积分区间仍然相同。因此我们有
并且把g和h看做是已知数。显然,在前面两个方程中我们可以用y+b来代替x,b表示任一常数,积分区间仍然相同。因此我们有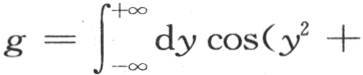
 现在不难看到,如果积分区间是-∞到+∞,那么含因子sin2by的所有积分都是0;因为sin2by与y同时变号。因此我们有
现在不难看到,如果积分区间是-∞到+∞,那么含因子sin2by的所有积分都是0;因为sin2by与y同时变号。因此我们有
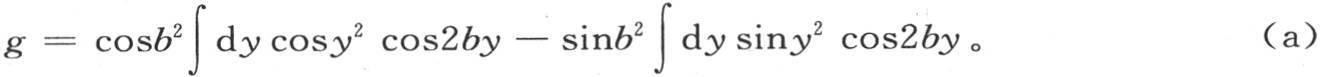
同样,h的方程给出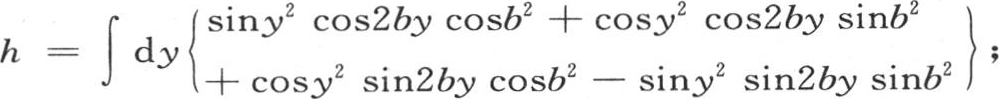 同样略去含sin2by的项,我们有
同样略去含sin2by的项,我们有
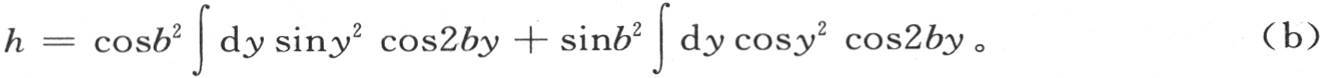
因此,两个方程(a)和(b)对g和h给出两个积分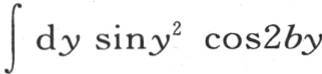 和
和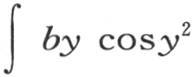 cos2by,我们分别用A和B来表示这两个积分。我们现在可以令y2 =p2 t,2by=pz;或者
cos2by,我们分别用A和B来表示这两个积分。我们现在可以令y2 =p2 t,2by=pz;或者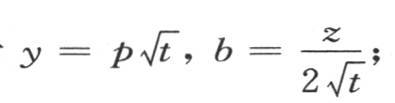 因此我们有
因此我们有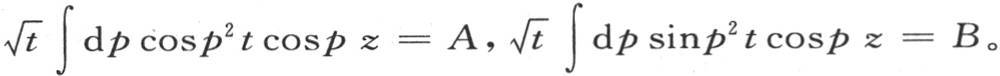
g和h的值 【33】 立即从已知结果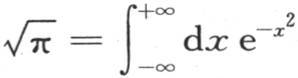 中推出。
中推出。
最后这个方程事实上是一个恒等式,因此,当我们用量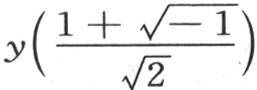 来代替x时,这个等式一定成立。这个代换给出
来代替x时,这个等式一定成立。这个代换给出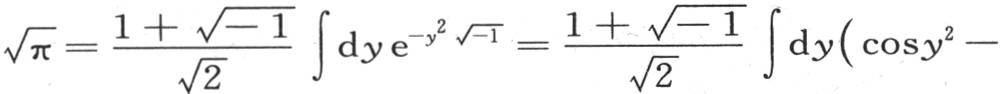
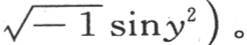
因此最后这个方程右边的实部是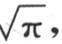 虚部是0。由此我们得出
虚部是0。由此我们得出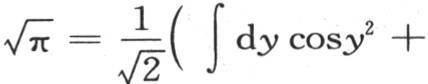
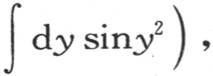 并且0=∫dycosy2 -∫dysiny2 ,或者是
并且0=∫dycosy2 -∫dysiny2 ,或者是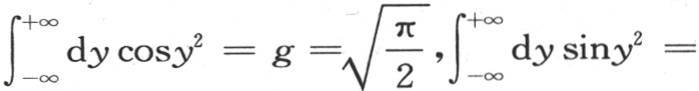
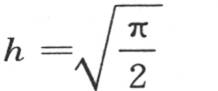
剩下的只是用方程(a)和(b)来确定两个积分∫dycosy2 cos2by和∫dysiny2 sin2by的值。
因此这两个积分可以表示成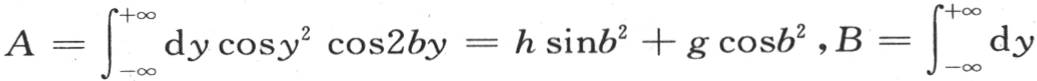
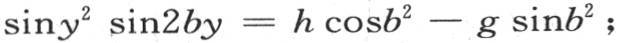 所以我们得出
所以我们得出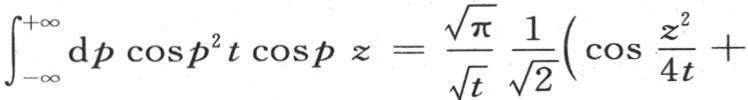
 用
用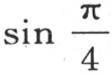 或者是
或者是 来代替则我们有
来代替则我们有
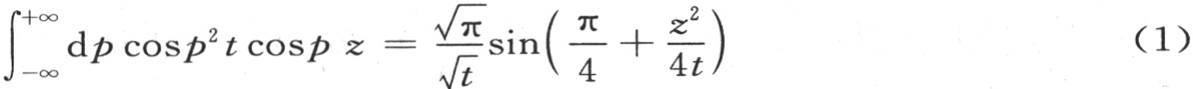
和
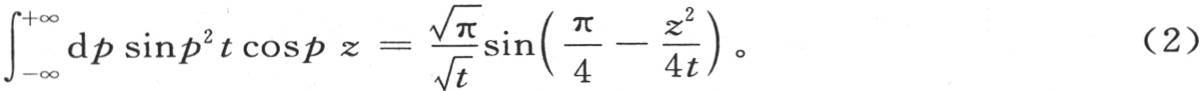
408 由第404目的方程(B)和第361目的方程(E)所表示的命题是用来求积分(δ)和前面那些积分的,它显然也对许多变量适用。事实上,在一般方程
 或者是
或者是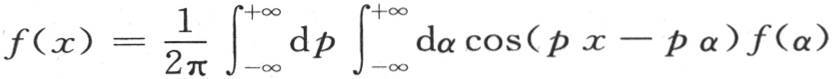 中,我们可以把f(x)看做是两个变量x和y的一个函数。这时函数f(α)是α和y的一个函数。现在我们把这个函数f(α,y)看做是变量y的一个函数,这样我们从第404目的同一个定理(B)得出
中,我们可以把f(x)看做是两个变量x和y的一个函数。这时函数f(α)是α和y的一个函数。现在我们把这个函数f(α,y)看做是变量y的一个函数,这样我们从第404目的同一个定理(B)得出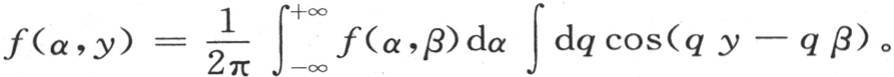
因此,为了表示两个变量x和y的任一个函数,我们有下述方程
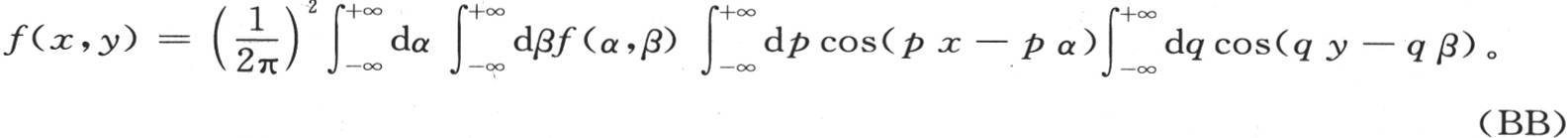
我们以同样的方式建立属于有三个变量的函数的方程,即
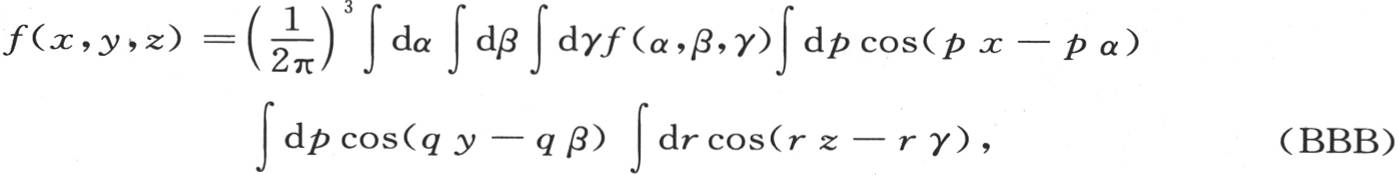
每一个积分都从-∞取到+∞。
显然,同一命题可以推广到包含任意数目的变量的那些函数上去。剩下来的是要表明这个命题怎样适合于求含二个以上的变量的方程的那些积分。
409 例如,由于微分方程是

所以我们希望确定作为(x,y,t)的一个函数的v值,使得:第一,只要假定t=0,v或者是f(x,y,t)就变成x和y的一个任意函数φ(x,y);第二,只要在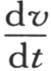 或者是f′(x,y,t)的值中令t=0,我们就得到第二个完全任意的函数ψ(x,y)。
或者是f′(x,y,t)的值中令t=0,我们就得到第二个完全任意的函数ψ(x,y)。
从微分方程(c)的形式我们可以推出,满足这个方程和前面两个条件的v值必然是通解。为了求这个积分,我们首先对v给出特殊值v=cosmtcospxcosqy。v的这个代换给出条件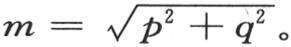 同样明显的是,不含x,y和t的那些量p,q,α,β和F(α,β)无论是怎样的,我们都可以记
同样明显的是,不含x,y和t的那些量p,q,α,β和F(α,β)无论是怎样的,我们都可以记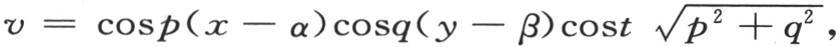 或者是
或者是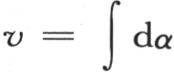
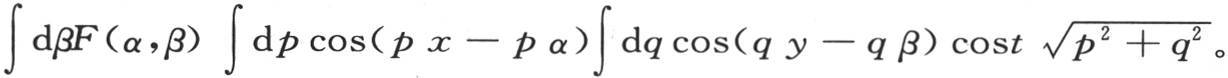 事实上,这个v值只不过是一些特殊值的和。
事实上,这个v值只不过是一些特殊值的和。
如果我们假定t=0,那么v必然变成φ(x,y)。因此我们有φ(x,y)=∫dα∫dβF(α,β)∫dpcos(px-pα)∫dqcos(qy-qβ)。
这样,问题就简化成确定F(α,β),使得所指明的积分结果能够成为φ(x,y)。现在只要比较最后这个方程和方程(BB),我们就会得到s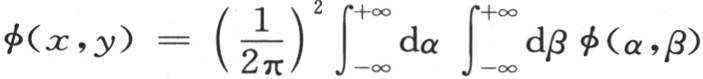
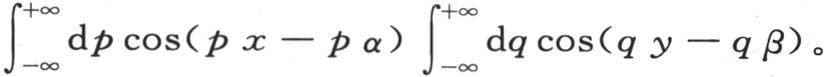
所以这个积分可以表示成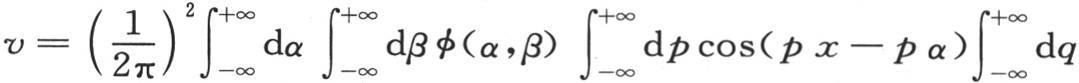
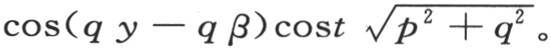
这样我们就得到这个积分的第一部分u,用W表示第二部分,它应当包含另外一个任意函数ψ(x,y),我们有v=u+W,并且我们应当把W看做是积分∫udt,只不过把φ变成ψ。事实上,当令t=0时,u就变成φ(x,y);同时W变成0,因为相对t的积分把余弦变成正弦。
此外,如果我们取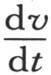 的值,并且令t=0,那么这时含一个正弦的第一部分就变成0,第二部分变成ψ(x,y)。因此方程v=u+W是所提出的方程的完全积分。
的值,并且令t=0,那么这时含一个正弦的第一部分就变成0,第二部分变成ψ(x,y)。因此方程v=u+W是所提出的方程的完全积分。
我们同样可以建立方程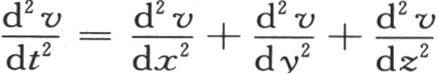 的积分。
的积分。
这只要引进一个新的因子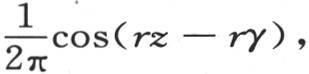 并且相对r和γ积分就够了。
并且相对r和γ积分就够了。
410 设所提出的方程是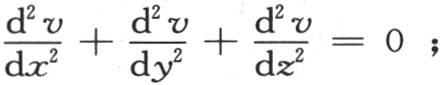 所需要的是把v表示成一个函数f(x,y,z),使得:第一,f(x,y,0)可以是一个任意函数φ(x,y);第二,只要在函数
所需要的是把v表示成一个函数f(x,y,z),使得:第一,f(x,y,0)可以是一个任意函数φ(x,y);第二,只要在函数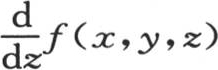 中令z=0,我们就得到第二个任意函数ψ(x,y)。由微分方程的形式显然得到,被确定的函数是所提出的方程的完全积分。
中令z=0,我们就得到第二个任意函数ψ(x,y)。由微分方程的形式显然得到,被确定的函数是所提出的方程的完全积分。
为了求这个方程,我们首先可以注意到,这个方程通过记v=cospxcosqyemz 而被满足,指数p和q是任意两个数,m的值是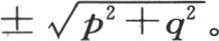
这时我们还可以记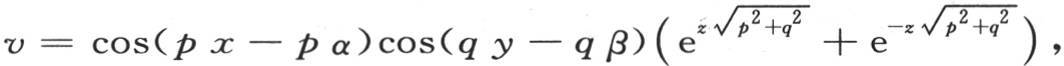 或者是
或者是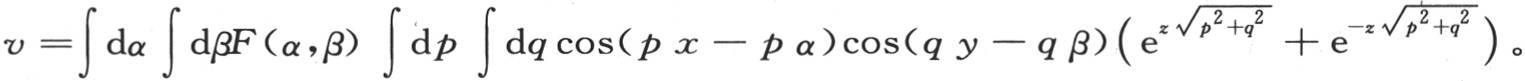
如果令z等于0,那么为了确定F(α,β),我们有下述条件
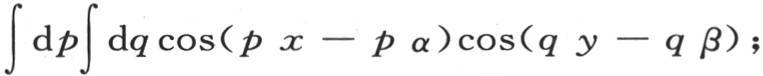 并且只要与方程(BB)进行比较,我们就看到
并且只要与方程(BB)进行比较,我们就看到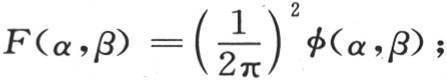 这样,作为这个积分第一部分的表达式,我们有
这样,作为这个积分第一部分的表达式,我们有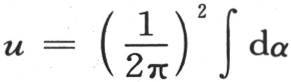
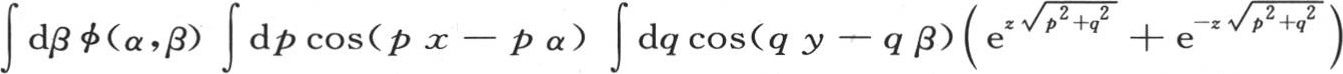 。 【34】
。 【34】
当z=0时u值简化成φ(x,y),同一代换使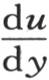 的值为0。
的值为0。
我们也可以相对z来对这个v值积分,并对这个积分给出下述形式,其中ψ是一个新的任意函数: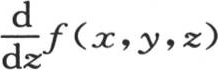
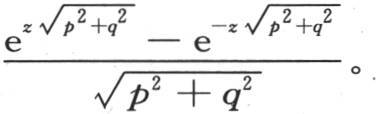
当z=0时W的值变成0,同一代换使函数 等于ψ(x,y)。因此所提出的方程的通解是v=u+W。
等于ψ(x,y)。因此所提出的方程的通解是v=u+W。
411 最后设这个方程是

所需要的是把v确定为一个函数f(x,y,t),它满足所提出的方程(e)和下面两个条件:即第一,f(x,y,t)中的这个代换t=0应当给出一个任意函数φ(x,y);第二,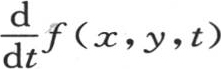 中的同一代换应当给出第二个任意函数ψ(x,y)。
中的同一代换应当给出第二个任意函数ψ(x,y)。
从方程(e)的形式和从我们在上面所阐明的原理显然得到,当我们确定了函数v,以致使它满足前面那些条件时,它是所提出的方程的完全积分。为了求这个函数,我们先写v=cospxcosqycosmt,因此我们推出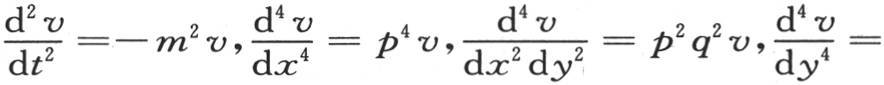
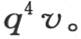
这时我们有条件m=p2 +q2 。因此我们可以写v=cospxcosqycost(p2 +q2 )或者是v=cos(px-pα)cos(qy-qβ)cos(p2 t+q2 t),或者是v=∫dα∫dβF(α,β)∫dp∫dq cos(px-pα)cos(qy-qβ)cos(p2 t+q2 t)。
当我们令t=0时,我们肯定有v=φ(x,y);它被用来确定函数F(α,β)。如果我们把这个方程和一般方程进行比较,那么我们得到,当在无穷区间内取这些积分时,F(α,β)的值是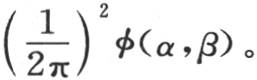 因此,作为这个积分的第一部分的表达式,我们有
因此,作为这个积分的第一部分的表达式,我们有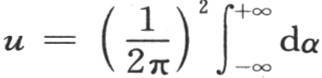
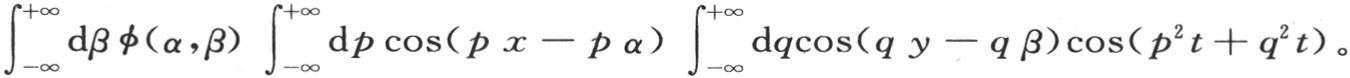
相对t来对u值进行积分,由于第二个任意函数由ψ来表示,所以我们看到积分的另一部分W表示成: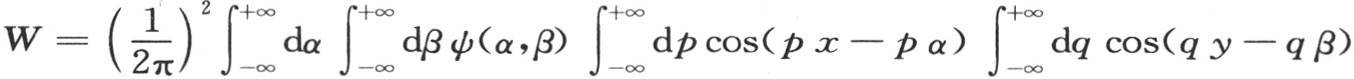
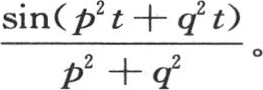
如果我们在u和W中令t=0,那么第一个函数变成φ(x,y),第二个函数变成0;如果我们也在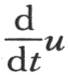 和在
和在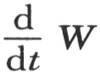 中令t=0,那么第一个函数就变成0,第二个变成ψ(x,y):因此v=u+W是所提出的方程的通解。
中令t=0,那么第一个函数就变成0,第二个变成ψ(x,y):因此v=u+W是所提出的方程的通解。
412 相对p和q施行两次积分,我们可以给予u值一个更简单的形式。为此,我们使用我们在第407目所证明了的两个方程(1)和(2),我们得到下述积分,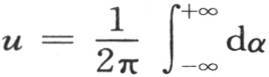
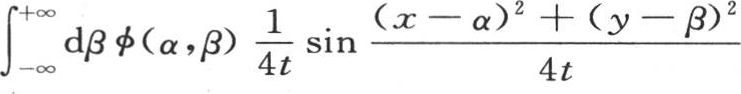 。 【35】
。 【35】
用u表示这个积分的第一部分,用W表示第二部分,它应当包含另一个任意函数,那么我们有
如果我们用μ和υ来表示两个新未知数,使得我们有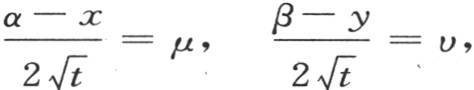 并且如果我们不用α,β,dα,dβ,而代之以它们的值
并且如果我们不用α,β,dα,dβ,而代之以它们的值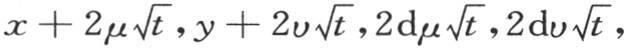 那么我们有这个积分的另一种形式,
那么我们有这个积分的另一种形式,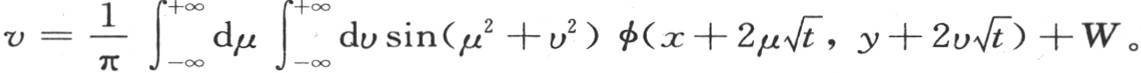
进一步扩大我们这些公式的应用会偏离我们的主题。前面那些例子与一些物理现象有关,这些物理现象的规律原来不为人们所知并且难以发现;我们选择它们,是因为人们一直徒劳地寻找至今的这些方程的积分与那些表示热运动方程的积分有引人注目的相似性。
413 在这些积分的研究中,我们还可以先考虑根据一个变量的幂所展开的级数,并且用方程(B)、(BB)所表示的定理对这些级数求和。这种分析的下面这个例子取自热的理论本身,我们认为这个例子是值得注意的。
我们在第399目已经看到,从方程

所导出、并且根据变量t的增幂以级数所展开的这个一般的v值,只包含x的一个任意函数;当根据x的增幂以级数展开时,它包含t的两个完全任意函数。
因此,第一个级数表示成:
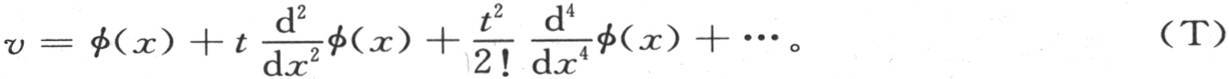
由第397目的(β)或者是由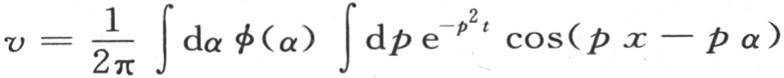 所表示的积分表示这个级数的和,并且包含唯一的任意函数φ(x)。
所表示的积分表示这个级数的和,并且包含唯一的任意函数φ(x)。
根据x的幂所展开的v值包含两个任意函数f(t)和F(t),因此被表示成
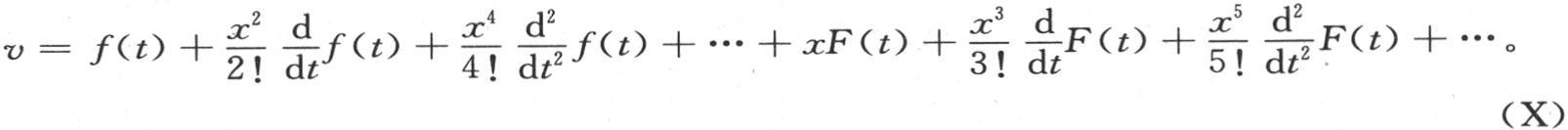
因此,与方程(β)无关,表示最后这个级数的和,并且含有两个任意函数f(t)和F(t)的这个积分,有另外一种形式。我们需要找到所提出的方程的这第二个积分,这个积分不可能比前面那个积分更一般,但是它包含两个任意函数。
我们可以通过对进入方程(X)的两个级数的每一个取和而得到它。显然,在一个x和t的函数形式下,如果我们知道含f(t)的第一个级数的和,那么,我们在用dx乘它之后应当相对x取这个积分并把f(t)变成F(t)。我们由此得到第二个级数。而且,只要确定进入第一个级数的奇数项的和就够了:因为,用μ表示这个和,用υ表示其他所有项的和,那么我们显然有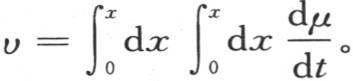
这时,剩下的是求μ的值。现在函数f(t)可以由一般方程(B)表示成
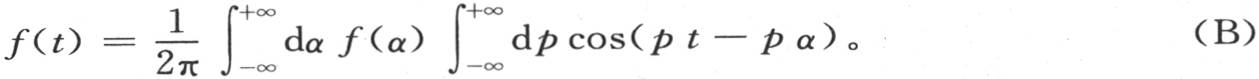
由此不难推出函数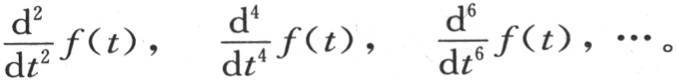
显然,微分相当于在方程(B)的右边、在符号∫dp之下写上相应的因子-p2 ,+p4 ,-p6 ,…。
这时,只要写上共同的因子cos(pt-pα),我们就有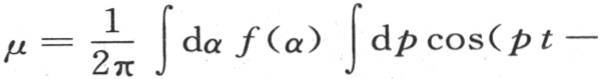
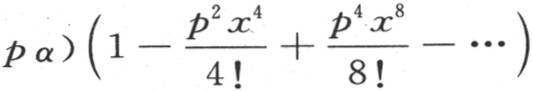
因此,问题在于求进入右边级数的和,这看来没有困难。事实上,如果y是这个级数的值,那么我们得出 或者是
或者是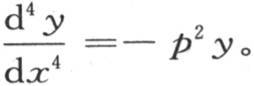
对这个线性方程进行积分,并确定那些任意常数,因此当x为0时y是1,并且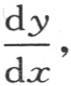
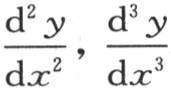 是0,作为级数的和,我们得到
是0,作为级数的和,我们得到 讨论这个研究的细节没什么用处;只要陈述结果就够了,作为所寻求的积分,它给出
讨论这个研究的细节没什么用处;只要陈述结果就够了,作为所寻求的积分,它给出
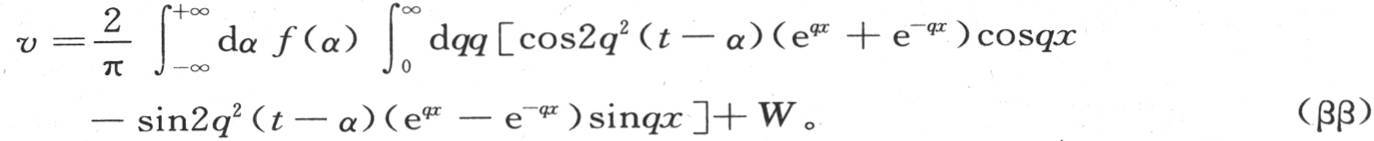
项W是积分的第二部分;它由第一部分相对x从x=0到x=x取积分,并把f变成F而形成。在这种形式下,积分包含两个完全任意的函数f(t)和F(t)。如果在v值中我们假定x为0,那么由假定,项W变成0,并且积分的第一部分变成f(t)。如果我们在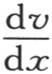 的值中作同一代换x=0,那么显然,第一部分
的值中作同一代换x=0,那么显然,第一部分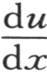 变成0。第二部分
变成0。第二部分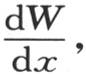 与第一部分只相差函数F,它代替f,所以化为F(t)。因此由方程(ββ)所表示的积分满足所有的条件,并且表示形成方程(X)右边的两个级数的和。
与第一部分只相差函数F,它代替f,所以化为F(t)。因此由方程(ββ)所表示的积分满足所有的条件,并且表示形成方程(X)右边的两个级数的和。
这就是在热的理论的几个问题中所应当选择的积分形式 【36】 ;我们看到,它与第397目的方程(β)所表示的形式是很不相同的。
414 我们可以采用非常不同的研究过程来用定积分表示那些代表微分方程的积分的那些级数的和。这些表达式的形式也依赖于这些定积分的上下限。让我们重温第311目的结果,对这种研究举一个例子。在那一目结束时的那个方程中,如果我们在函数φ的符号下写上x+tsinu,那么我们有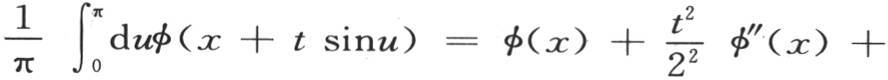
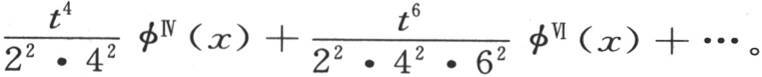
用v表示构成方程右边的这个级数的和,我们看到,为了使因子22 ,42 ,62 ,…的某一个在每一项中消去,我们应当对t微分一次,用这个结果乘以t,并再对t微分一次。由此我们得知v满足偏微分方程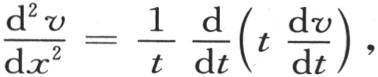 或者是
或者是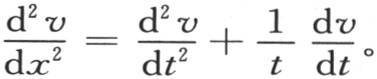
因此,为了表示这个方程的积分,我们有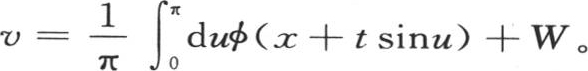
积分的第二部分W包含一个新的任意函数。
积分的这个第二部分W的形式与第一部分的形式大小不相同,并且它也可以用定积分来表示。由定积分所得到的这些结果随导出它们的研究过程而不同,也随这些积分的上下限而不同。
415 有必要仔细考查用来变换任意函数的一般命题的性质:因为这些定理的运用很广泛,我们由它们直接得到几个重要的物理问题的解,这些问题不可能用其他方法来处理。我们在我们开始的研究中所给出的下面几个证明对于揭示这些命题的真实性是很适合的。
在和第404目的方程(B)相同的一般方程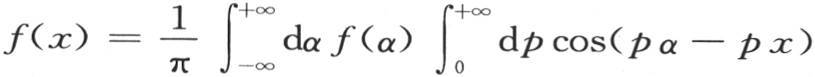 中,我们可以对p进行积分,我们得到
中,我们可以对p进行积分,我们得到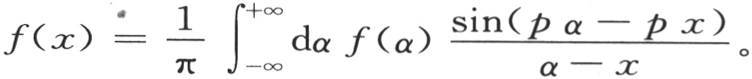
这时在最后这个表达式中,我们应当赋予p一个无穷值;如此,右边就表示f(x)的值。通过下面的作图,我们会看出这个结果是成立的。先考察定积分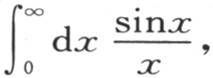 我们知道,在第356目中,它等于
我们知道,在第356目中,它等于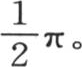 如果我们在x轴的上方作纵坐标为sinx的曲线和纵坐标为
如果我们在x轴的上方作纵坐标为sinx的曲线和纵坐标为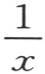 的曲线,然后使第一条曲线的纵坐标乘以相应的第二条曲线的纵坐标,那么我们可以把这个积看做是第三条曲线的纵坐标,这条曲线的形状是很容易确定的。
的曲线,然后使第一条曲线的纵坐标乘以相应的第二条曲线的纵坐标,那么我们可以把这个积看做是第三条曲线的纵坐标,这条曲线的形状是很容易确定的。
它在原点的第一个纵坐标是1,随后的纵坐标交替为正和负,这条曲线在x=π,2π,3π,…的点上截x轴,并且它愈来愈趋近于这个轴。
这条曲线的第二个分支,完全像第一个分支一样,在y轴的左边。积分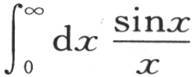 是包含在这条曲线和x轴之间,并且从x=0一直算到x为正无穷大的面积。
是包含在这条曲线和x轴之间,并且从x=0一直算到x为正无穷大的面积。
假定p是任一正数,定积分 和上面的积分有相同的值。事实上,设px=z;则所提出的积分变成
和上面的积分有相同的值。事实上,设px=z;则所提出的积分变成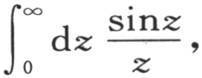 因此,它也等于
因此,它也等于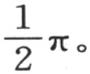 无论p是怎样的正数,这个命题都成立。例如,如果我们假定p=10,那么纵坐标为
无论p是怎样的正数,这个命题都成立。例如,如果我们假定p=10,那么纵坐标为 的这条曲线的正弦波(sinuosities)就比纵坐标为
的这条曲线的正弦波(sinuosities)就比纵坐标为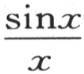 的正弦波要密得多和短得多;但是从x=0一直到x=∞的整个面积是一样的。
的正弦波要密得多和短得多;但是从x=0一直到x=∞的整个面积是一样的。
现在假定数p变得愈来愈大,并且它无限增加,即变成无穷大。纵坐标是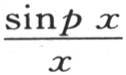 的这条曲线的正弦波就无限接近。它们的底是等于
的这条曲线的正弦波就无限接近。它们的底是等于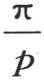 的无穷小长度。因此,如果我们比较保持在某个这样的区间
的无穷小长度。因此,如果我们比较保持在某个这样的区间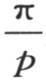 上的正面积和保持在随后的区间上的负面积,如果我们用X表示有限且充分大的横坐标,它与第一条弧的起点一致,那么我们看到,作为分母而进入纵坐标表达式
上的正面积和保持在随后的区间上的负面积,如果我们用X表示有限且充分大的横坐标,它与第一条弧的起点一致,那么我们看到,作为分母而进入纵坐标表达式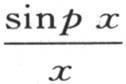 的横坐标x,在作为两个面积的底的两个区间中没有明显的差异。因此积分是一样的,就像x是一个常数一样。由此得到彼此相继的两个面积的和为0。
的横坐标x,在作为两个面积的底的两个区间中没有明显的差异。因此积分是一样的,就像x是一个常数一样。由此得到彼此相继的两个面积的和为0。
当x的值无穷小时则不同,因为在这种情况下区间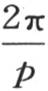 与x的值有一个有限比。由此我们知道,假定p是一个无穷大的数,则积分
与x的值有一个有限比。由此我们知道,假定p是一个无穷大的数,则积分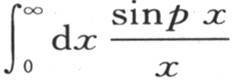 就完全由与x的极小值对应的前几项的和所组成。当横坐标有一个有限值X时,这个面积就不会变,因为构成它的那些部分两两交替地相互抵消。
就完全由与x的极小值对应的前几项的和所组成。当横坐标有一个有限值X时,这个面积就不会变,因为构成它的那些部分两两交替地相互抵消。
我们用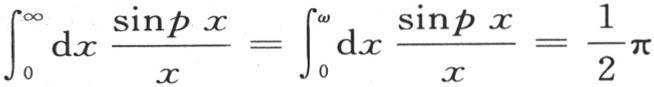 来表示这个结果。
来表示这个结果。
表示第二个积分的积分区间的量ω取无穷小的值;当这个区间是ω并且当它是∞时,这个积分的值是相同的。
416 如假定,取方程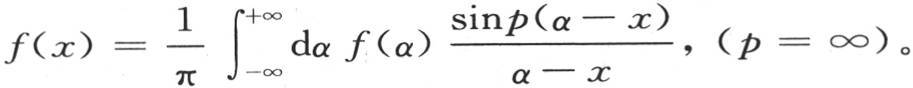
建立横坐标α的轴,在轴的上方作曲线ff,它的纵坐标是f(α)。这条曲线的形状是完全任意的;它的纵坐标可能只在它轨迹的一个或几个部分上有,而其他所有部分的纵坐标都是0。
在横坐标轴的上方还作一条曲线ss,它的纵坐标是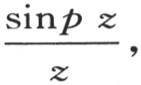 z表示横坐标,p表示一个很大的正数。这条曲线的中心,或者说对应于最大纵坐标p的点,可以放在横坐标α的原点O上,或者是放在任一横坐标的端点上。我们假定这个中心是依次移动的,并且离开点O向α轴右边的所有点转移。当这个中心到达点x,x是第一条曲线的一个横轴x的终点时,我们考察在第二条曲线的某个位置上所发生的情况。
z表示横坐标,p表示一个很大的正数。这条曲线的中心,或者说对应于最大纵坐标p的点,可以放在横坐标α的原点O上,或者是放在任一横坐标的端点上。我们假定这个中心是依次移动的,并且离开点O向α轴右边的所有点转移。当这个中心到达点x,x是第一条曲线的一个横轴x的终点时,我们考察在第二条曲线的某个位置上所发生的情况。
由于x的值被看做是常数,α是唯一的变量,所以第二条曲线的纵坐标变成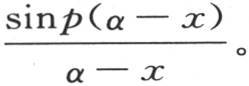
这时如果我们把这两条曲线耦合起来,构成第三条曲线,即如果我们把这两条曲线的每一个纵坐标相乘,并且用在α轴的上方所作的第三条曲线的纵坐标来表示这个积,那么这个积是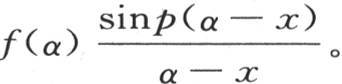
第三条曲线的整个面积,或者说包含在这条曲线和横轴之间的面积,由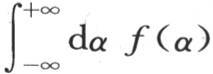
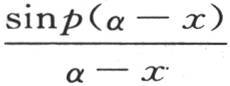 来表示。
来表示。
现在由于数p无穷大,所以第二条曲线的所有正弦波无限接近;我们不难看到,对于与点x有一个有限距离的所有点,定积分,或者是说第三条曲线的全面积,由交替为正或者是负的一些相等部分所构成,这些相等部分两两相互抵消。事实上,对于这些与点x有一定距离的点来说,当我们以小于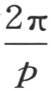 的量使这个距离增加时,f(α)的值的变化就无穷地小。分母α-x的情况亦如此,α-x测定那个距离。因此对应于区间
的量使这个距离增加时,f(α)的值的变化就无穷地小。分母α-x的情况亦如此,α-x测定那个距离。因此对应于区间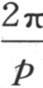 的面积是一样的,仿佛量f(α)和α-x不是变量一样。因此当α-x是一个有限量时这个全面积为0。所以我们可以在我们想怎么近就怎么近的区间内取这个定积分,并且它在那些区间内给出和在无穷区间内所给出的一样的结果。这样,整个问题就简化成在无穷近的点之间取积分,这些点一个在使α-x为0的点的左边,另一个在它的右边,即从α=x-ω到α=x+ω之间取积分,ω表示一个无穷小量。在这个区间内函数f(α)不变,它等于f(x),并且可以放到积分号外面去。因此表达式的值是f(x)与
的面积是一样的,仿佛量f(α)和α-x不是变量一样。因此当α-x是一个有限量时这个全面积为0。所以我们可以在我们想怎么近就怎么近的区间内取这个定积分,并且它在那些区间内给出和在无穷区间内所给出的一样的结果。这样,整个问题就简化成在无穷近的点之间取积分,这些点一个在使α-x为0的点的左边,另一个在它的右边,即从α=x-ω到α=x+ω之间取积分,ω表示一个无穷小量。在这个区间内函数f(α)不变,它等于f(x),并且可以放到积分号外面去。因此表达式的值是f(x)与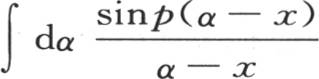 在区间α-x=-ω和α-x=ω内所取积分的积。
在区间α-x=-ω和α-x=ω内所取积分的积。
正如我们在上一目中所看到的,这个积分等于π;因此定积分等于πf(x),由此我们得到方程
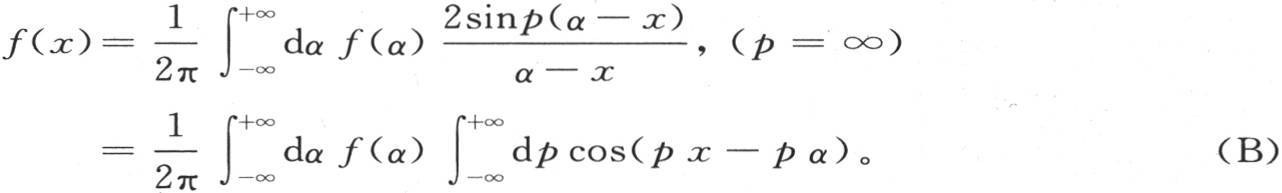
417 前面的证明假定一个一直为几何学生们所接受的无穷量的概念。考察由符号sinp(α-x)中的因子p的连续增加所引起的变化,我们不难以另一种形式提供同样的证明。这些考虑太熟悉了,以致我们无需重提它们。
重要的是我们应当注意到,这个证明所适合的函数f(x)是完全任意的,并且不受连续性规律的支配。因此我们可以设想这一研究涉及这样一个函数,它使得表示这个函数的纵坐标除了当横坐标包含在两个给定的界限a和b之间时有值外,其他所有的纵坐标都假定为0。因此这条曲线除了在从x=a到x=b的上述区间内有图形和轨迹外,它的其他所有部分都与α轴重合。
同一证明表明我们在此不考虑x的无穷值,而只考虑确定的实际值。对于包含在已知界限之间的x的奇异值,我们也可以依据同样这些原理来考察函数f(x)变成无穷时的情况;不过这些情况与我们所关心的主要目的没有联系,我们的目的是要对这些积分引入一些任意函数;当我们对x给定包含在已知界限之间的一个奇异值时,不可能有什么问题事实上会导致函数f(t)变成无穷的这样的假定。
一般地,函数f(x)表示一系列的值,或者是纵坐标,每一个这样的值或者是纵坐标都是任意的。由于对横坐标x给定了无穷多的值,所以存在同样多的纵坐标f(x)。所有这些纵坐标都有或正或负或为0的实数值。
我们不假定这些纵坐标都服从于一条共同的规律;它们以任一方式彼此前后相继,它们每一个都是被给定的,仿佛都是单个的量一样。
仅仅从问题的性质和从适合于它的分析可以得到,从一个纵坐标到下一个坐标的轨迹是以一种连续的方式进行的。但是这时涉及一些具体的条件,一般方程(B),若单独考虑,则与这些条件无关。它严格适合于那些不连续的函数。
现在假定,当我们对x给定包含在两个界限a和b之间的一个值时,函数f(x)与某个解析式相同,如sinx,e-x2 ,φ(x),等等,当x不在a和b之间时,f(x)的所有值均为0;在前面的方程(B)中,对α的积分的上下限这时变成α=α,α=b;由于这个结果和界限为α=-∞到α=+∞时的结果相同,所以,由假定,当α不在a和b之间时,φ(α)的每个值均为0。这时我们有方程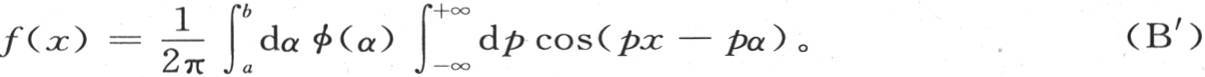
这个方程(B′)的右边是变量x的一个函数;因为两次积分会使变量α和p消掉,只有x和常数a和b保留下来。现在与右边等价的这个函数是这样的,它使得只要用包含在a和b之间的任一个值来代替x,我们就得到和在φ(x)中代入这个x值的一样的结果;并且,如果我们在右边用不在a和b之间的任一个值来代替x,则我们得到一个0结果。这时,如果在保持组成右边的其他所有量不变时,我们用靠得更近的界限a′和b′代替界限a和b,a′和b′都包含在a和b之间,那么,我们就会改变与右边相等的这个x的函数,并且这种改变的完成是这样的,它使得我们对x给定不包含在a′和b′之间的无论什么值时右边都变成0;而且,如果x的值在a′和b′之间,那么我们就有和在φ(x)中代入这个x值的相同的结果。
因此我们可以在方程(B′)的右边任意改变积分限。这个方程对包含在我们可能已经选定的任一界限a和b之间的x值总存在;并且,如果我们对x给定任何其他的值,那么右边就变成0。让我们用x为横坐标的一条曲线的可变纵坐标来表示φ(x);右边,其值为f(x),表示其形状依赖于界限a和b的第二条曲线的可变纵坐标,如果这两个界限是-∞和+∞,那么这两条曲线,一条的纵坐标是φ(x),另一条的纵坐标是f(x),就在它们历经的整个范围内完全重合。但是,如果我们对这两个界限给定别的值a和b,那么,这两条曲线就在它们与从x=a到x=b的区间相对应的轨迹的每一部分上完全重合。对于这个区间的左右两边,第二条曲线严格与x轴的每一点重合。这个结果是很惊人的,它确定由方程(B)所表示的命题的真实意义。
418 由第234目的方程(II)所表示的定理应当在这同一观点下来考虑。这个方程以多重弧的正弦和余弦级数展开任意函数f(x)。函数f(x)表示一个完全任意的函数,即表示或服从或不服从于一条共同规律的,并且满足包含在0到任一个量X之间的所有x值的一系列已知的值。
这个函数的值由下述方程表示,
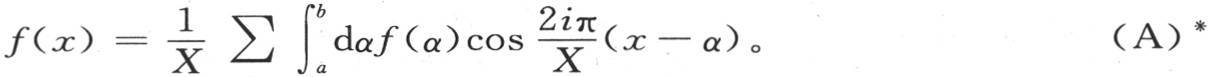
* 这里,方程(A)的右边的系数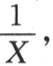 在英译本中,是
在英译本中,是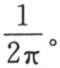 这里是根据法文《文集》本订正的。——汉译者
这里是根据法文《文集》本订正的。——汉译者
这个相对α的积分应当在界限α=a到α=b之间来取;界限a和b的每一个都是包含在0到X之间的任意量。符号∑对整数i起作用,指明我们应当对i给定每一个或正或负的整数值,即…,-4,-3,-2,-1,0,+1,+2,+3,+4,…并且应当取安排在符号∑下的项的和。在这些积分之后,右边变成只含变量x和常数a和b的一个函数。这个一般命题在于下面两点:第一,用包含在a和b之间的一个量代替x就能得到的右边的值等于若用同样的量代替函数f(x)中的x时所能得到的值;第二,包含在0到x之间,但不包含在a和b之间的每个其他的x值,代入右边后,给出0结果。
因此,函数f(x),或者是一个函数的一部分,都可以用三角级数来表示。
右边的值是周期性的,其周期是X,即当用x+X代替x时,右边的值不变。它的所有值都在周期X上连续重复。
与右边相等的这个三角级数是收敛的;这个表述的意义是,如果我们对变量x给定任一个值,级数各项的和就愈来愈趋近于、并且无限接近于一个确定的极限。如果我们用包含在0到X之间,但不包含在a和b之间的一个量来代替x,那么这个极限是0;但是如果代替x的这个量包含在a到b之间,那么这个级数的极限就有和f(x)一样的值。最后这个函数不受任何条件的限制,并且,它表示其纵坐标的曲线可以有任一形状;例如,一系列直线和曲线所形成的一条围道。我们由此看到,由于界限a和b,整个区间X以及函数的性质是任意的,所以这个命题有很广泛的意义;并且,由于它不仅表示一种解析性质,而且本质上还导致几个重要问题的解,所以有必要以不同的观点来考虑它,并且指明它的主要应用。我们在本书中给出了这个定理的几个证明。我们在下面几目的一目(423目 【37】 )中要谈到的证明具有亦可用于非周期函数的优点。
如果我们假定这个区间X是无穷的,级数的这些项变成微分量;那么正如我们在第353和355目中所看到过的,由符号∑所表明的和就变成一个定积分,方程(A)就变换成方程(B)。因此后一个方程(B)包含在前一个方程之中,并且属于区间X为无穷的情况:这时界限a和b显然是完全任意的常数。
419 由方程(B)所表示的定理还提供若干的分析应用,展开这些应用会使我们脱离本书的目的,不过我们将阐明导出这些应用的原理。
我们看到,在方程
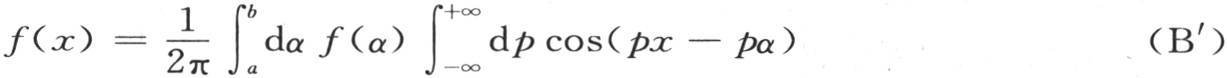
的右边,函数f(x)是这样变换的:它使得函数符号f不再作用于变量x,而是作用于一个辅助变量α。变量x只受余弦符号的作用。由此得到,为了使函数f(x)对x微分我们所希望的那样多次,只需要相对余弦符号下的x微分右边就行了。用i表示任一整数,这时我们有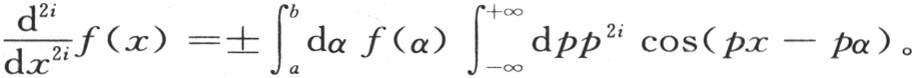 当i是偶数时我们取上符号,当i为奇数时我们取下符号。遵循正负号选择的同一规则,
当i是偶数时我们取上符号,当i为奇数时我们取下符号。遵循正负号选择的同一规则,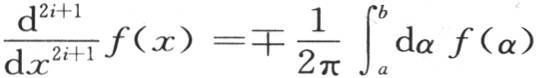
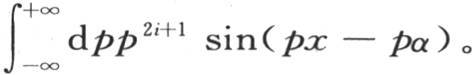
我们也可以连续几次相对x对方程(B)的右边进行积分;这只需在符号sin或者是cos前面写上p的一个负幂就够了。
同一注记适合于有限差和由符号∑所表示的求和,一般地,适合于对三角量起作用的分析运算。所说的这个定理的主要特征,就是要把函数的一般符号变换成一个辅助变量,并把变量x放到三角函数符号之下。通过这个变换,函数f(x)在某种意义上得到三角量的所有性质;因此,就像级数的微分、积分和求和适合于指数三角函数一样,它们也适合于一般意义上的函数。由于这个原因,这个命题的运用就直接给出带常系数的偏微分方程的积分。事实上,我们显然可以用特殊指数的值来满足这些方程;由于我们所说的这些定理给一般并且任意的函数赋予指数量的特征,所以它们不难导出完全积分的表达式。
正如我们在第413目中所看到的一样,当无穷级数包含同一函数的连续微分或者是连续积分时,同样的变换也给出这些级数和的一种简易方法;因为,由前面所说,这种级数的和就简化成一种代数项级数的和。
420 我们也可以运用所说的定理在函数的一般形式下进行由实部和虚部组成的二项式代换。这个分析问题是在偏微分方程运算开始时出现的;我们在此指出是因为它与我们的主要目的有直接联系。
如果我们在函数f(x)中用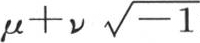 来代替x,那么结果由两部分
来代替x,那么结果由两部分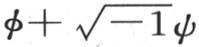 组成。这个问题是要用μ和ν来确定函数φ和ψ。如果我们用表达式
组成。这个问题是要用μ和ν来确定函数φ和ψ。如果我们用表达式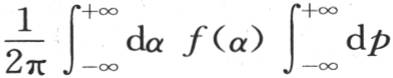 cos(px-pα)来代替f(x),那么我们很快就得到这个结果,因为这时问题简化成用
cos(px-pα)来代替f(x),那么我们很快就得到这个结果,因为这时问题简化成用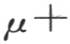
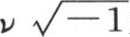 来代替余弦符号下的x,简化成计算实项和
来代替余弦符号下的x,简化成计算实项和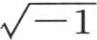 的系数。因此我们有
的系数。因此我们有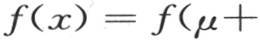

 ; 【38】 所以
; 【38】 所以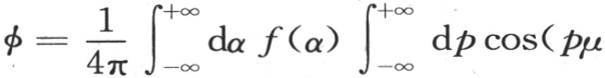
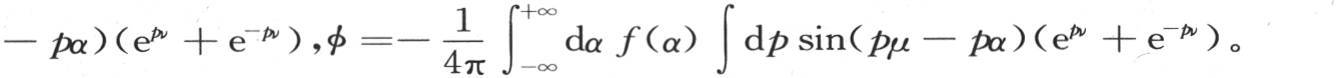
因此,当我们用二项式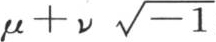 来代替变量x时,我们所能想象到的所有函数f(x),甚至是那些不服从于任何连续性规律的函数,就都化为
来代替变量x时,我们所能想象到的所有函数f(x),甚至是那些不服从于任何连续性规律的函数,就都化为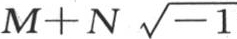 的形式。
的形式。
421 为了给出运用最后两个公式的例子,让我们考虑方程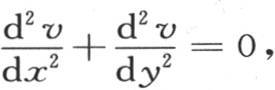 这个方程与矩形薄片中的均匀热运动有关。该方程的通解显然包含两个任意函数。这时假定我们由x知道当y=0时的v值,并且还知道当y=0时作为x的另一个函数
这个方程与矩形薄片中的均匀热运动有关。该方程的通解显然包含两个任意函数。这时假定我们由x知道当y=0时的v值,并且还知道当y=0时作为x的另一个函数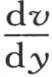 的值,那么我们可以由方程
的值,那么我们可以由方程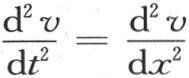 的积分推出所求的积分,上面这个方程是我们早已知道的;不过我们得到函数符号下的一些虚量:这个积分是
的积分推出所求的积分,上面这个方程是我们早已知道的;不过我们得到函数符号下的一些虚量:这个积分是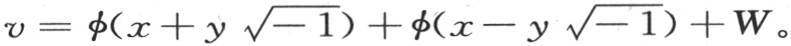
积分的第二部分通过对第一部分进行相对y的积分,并把φ变成ψ而得到。
这时剩下的事情是,为了把实部与虚部分开,对量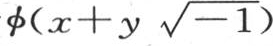 和
和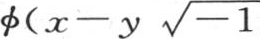 进行变换。遵循上一目的过程,我们得到积分的第一部分u,
进行变换。遵循上一目的过程,我们得到积分的第一部分u,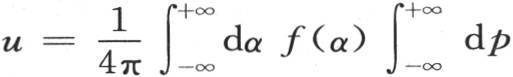
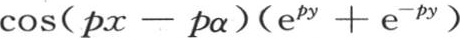 , 【39】 因此
, 【39】 因此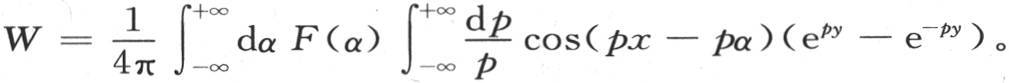
因此,由实项所表示的我们所提出的方程的完全积分,是v=u+W。事实上我们知道,第一,它满足微分方程;第二,只要在其中令y=0,则它给出v=f(x);第三,只要在函数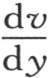 中令y=0,则结果就是F(x)。
中令y=0,则结果就是F(x)。
422 我们还可以注意到,我们可以从方程(B)推出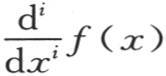 或者是积分∫i dxi f(x)的第i阶微分系数的一个很简单的表达式。
或者是积分∫i dxi f(x)的第i阶微分系数的一个很简单的表达式。
所求的这个表达式是x和指标i的某个函数。所需要的是确定这样一种形式下的这个函数:这种形式使数i不作为一个指标,而作为一个量进入这个函数,以便在同一公式中包括我们对i赋予任一正值和负值的每一种情况。为了得到这个表达式,我们注意到,如果i的各个值是1,2,3,4,5,…,那么表达式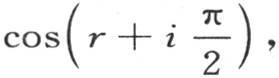 或者是
或者是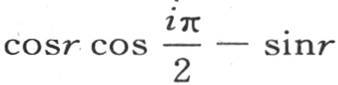
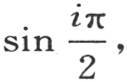 依次变成-sinr,-cosr,+sinr,+cosr,-sinr,…。当我们使i值增加时,同样的结果以同样的次序重复。在方程
依次变成-sinr,-cosr,+sinr,+cosr,-sinr,…。当我们使i值增加时,同样的结果以同样的次序重复。在方程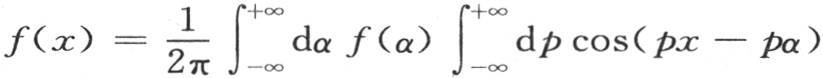 的右边,我们现在应当在余弦符号的前面写上因子pi ,在这个符号中加上项
的右边,我们现在应当在余弦符号的前面写上因子pi ,在这个符号中加上项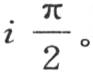 因此我们有
因此我们有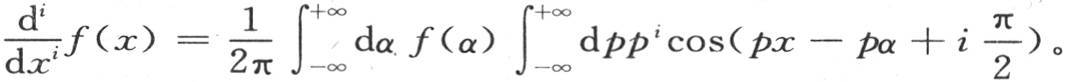
进入右边的数i可以是任一正整数或者是负整数。我们不打算把这些应用硬贴到一般的分析上去;用不同例子表明我们定理的应用就够了。如我们所说,第405目的(d)和第411目的(e)这两个四阶方程,属于动力学问题。直到我们在一篇《论弹性表面的振动的研究报告》(a Memoir on the Vibrations of Elastic Surfaces)中给出的这些方程的积分为止,人们还一直不知道它们,这个报告是在1816年6月6日科学院的一次会议上宣读的 【40】 (第6目§10—11,和第7目§13—14)。这个报告的内容主要是第406目的两个公式δ和δ′,以及两个积分,这两个积分,一个由第412目的第一个方程来表示,另一个由同一目的最后一个方程来表示。随后我们给出了同样这些结果的另外几个证明。这份研究报告还包含第409目的方程(c)的积分,其积分形式就是该目所采用的形式。至于第413目方程(a)的积分(ββ),它在此处系首次发表。
423 我们可以用一个更一般的观点来考虑由第418和417目方程(A)和(B′)所表示的这些命题。第415和416目中所指明的作图不仅适用于三角函数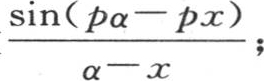 而且适合于其他所有的函数,并且只假定当数p变成无穷的时,我们通过在极近的界限之间取积分,就得到相对α积分的值。现在这个条件不仅属于三角函数,而且适用于无数其他的函数。因此我们得到任意函数f(x)在非常惊人的不同形式下的表达式;不过,我们在我们所进行的具体研究中没有使用这些变换。
而且适合于其他所有的函数,并且只假定当数p变成无穷的时,我们通过在极近的界限之间取积分,就得到相对α积分的值。现在这个条件不仅属于三角函数,而且适用于无数其他的函数。因此我们得到任意函数f(x)在非常惊人的不同形式下的表达式;不过,我们在我们所进行的具体研究中没有使用这些变换。
至于第418目中的方程(A)所表示的命题,同样不难用一些作图使它的成立变得显然,并且我们最初的是为这个定理运用了这些作图。我们现在只要指明这个证明过程就够了。
在方程(A)中,即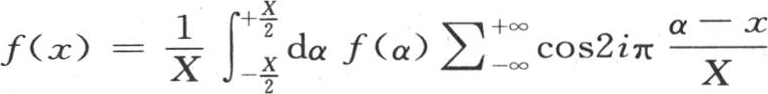 【41】 中,我们可以不用符号∑下所安排的那些项的和,而代之以它的值,这个值可从已知定理中导出。我们在前面第三章第3节中已经看到这种运算的不同例子。如果我们为了简化表达式而假定2π=X,并且用r表示α-x,则它给出结果
【41】 中,我们可以不用符号∑下所安排的那些项的和,而代之以它的值,这个值可从已知定理中导出。我们在前面第三章第3节中已经看到这种运算的不同例子。如果我们为了简化表达式而假定2π=X,并且用r表示α-x,则它给出结果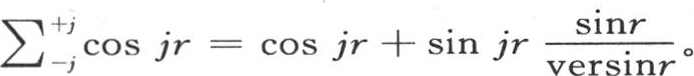
这时我们应当用dαf(α)乘这个方程的右边。假定数j无穷,并且从α=-π到α=+π积分。当横坐标是α纵坐标cosjr的曲线与横坐标是α纵坐标是f(x)的曲线相联时,即当相应的纵坐标相乘时,显然,在任一区间之间所取的这条派生曲线的面积,在数j无限增加时变成0。
只要项sinjr不乘以因子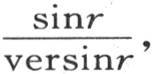 那么同样是这种情况;但是只要此较有相同横坐标并且纵坐标是sinjr,
那么同样是这种情况;但是只要此较有相同横坐标并且纵坐标是sinjr,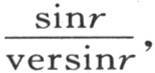 f(α)的这三条曲线,那么我们会清楚地看到,积分
f(α)的这三条曲线,那么我们会清楚地看到,积分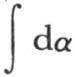
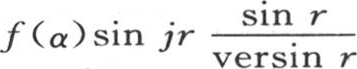 只有在某此无穷小区间内,即当纵坐标
只有在某此无穷小区间内,即当纵坐标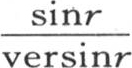 变成无穷时,才有实际的值。如果r或者α-x为0,这种情况就会出现;在α与x相差无穷小的区间内,f(α)的值与f(x)重合,因此积分变成
变成无穷时,才有实际的值。如果r或者α-x为0,这种情况就会出现;在α与x相差无穷小的区间内,f(α)的值与f(x)重合,因此积分变成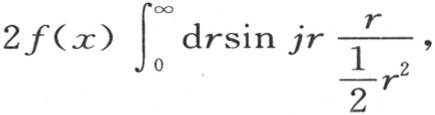 或者是
或者是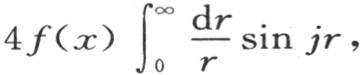 它等于第415和356目的2πf(x)。因此我们得到前面的方程(A)。
它等于第415和356目的2πf(x)。因此我们得到前面的方程(A)。
当变量x严格等于-π或者是+π时,作图将表明方程(A)的右边的值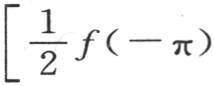 或者是
或者是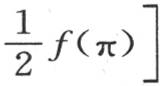 是怎样的。
是怎样的。
如果积分限不是-π和+π,而是另外的数a和b,它们都包含在-π到+π之间,那么我们由同一图形看到使方程(A)右边为0的x的值是怎样的。
如果我们设想在积分限之间f(α)的某些值变成无穷的,那么作图表明我们必须在何种意义上来理解这个一般命题。不过我们在此不考虑这类情况,因为它们不属于物理问题。
如果不限制在界限-π和+π之间,我们对这个积分给出更大的范围,选择更远的界限a′和b′,那么我们从同一图形知道方程(A)的右边由几项组成,并且无论函数f(x)是怎样的,它都使积分结果成为有限的。
如果我们用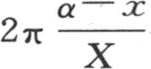 代替r,积分限是-X和+X,那么我们得到类似的结果。
代替r,积分限是-X和+X,那么我们得到类似的结果。
我们现在应当认为我们所得到的这些结果对于sinjr的无数不同的函数也成立。这只要这些函数得到交替为正或者是为负的值,使得在j无限增加时面积变成0就行了。我们可以改变因子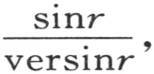 也可以改变积分限,并且我们可以假定这个区间是无穷的。这类表达式很一般,并且可以有很不同的形式。我们不可能耽误在这些展开式上,不过有必要展示一些几何作图的应用;因为它们无疑可以解决在极值和在奇异值上可能出现的问题;它们不能用来发现这些定理,但是它们证明这些定理,并且导出它们所有的应用。
也可以改变积分限,并且我们可以假定这个区间是无穷的。这类表达式很一般,并且可以有很不同的形式。我们不可能耽误在这些展开式上,不过有必要展示一些几何作图的应用;因为它们无疑可以解决在极值和在奇异值上可能出现的问题;它们不能用来发现这些定理,但是它们证明这些定理,并且导出它们所有的应用。
424 我们还不得不从另一方面来考虑同样的命题。如果我们比较与在环、球、矩形棱柱和圆柱中的变化热运动有关的每一个解,那么我们看到,我们不得不用如像a1 φ(μ1 x)+a2 φ(μ2 x)+a3 φ(μ3 x)+…这样一些项的级数来展开一个任意函数f(x)。
函数φ在方程(A)的右边是一个余弦或者是正弦,它在此由一个与正弦很不相同的函数所代替。数μ1 ,μ2 ,μ3 ,…不再是整数,而是由一个超越方程所给出,这个方程的根有无穷多个,并且都是实根。
问题在于求系数a1 ,a2 ,a3 ,…,ai 的值;它们已经由一些定积分而得到,这些定积分使未知数除保留一个外,其余的都消掉。我们现在来专门考察这个过程的性质以及由它所得到的精确结论。
为了给这个考察一个更确定的目的,我们以最重要的问题之一,即实心球中变化的热运动的问题为例。我们在第290目已经看到,为了满足热的初始分布,我们应当确定方程
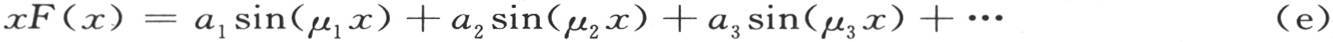
中的系数a1 ,a2 ,a3 ,…,ai 。
函数F(x)是完全任意的;它表示半径为x的球壳的已知的的初始温度的v值。数μ1 ,μ2 ,…,μi 是超越方程

的根μ。X是整个球的半径;h是有任一正值的已知的数值系数。在我们更早的研究中我们已经严格证明了所有的μ值或者是方程(f)的根都是实根 【42】 。这个论证由方程的一般理论导出,并且只需要我们假定知道每一个方程所可能有的虚根形式就行了。我们在本书中不谈及它,因为它的作用由使这个命题更加显然的作图所代替。此外,在确定圆柱体中变化的热运动时,我们已经从分析上处理了一个类似的问题(第308目)。如此,问题在于发现a1 ,a2 ,a3 ,…ai …,的数值,使得当我们在方程(e)的右边用包含在0到全长X之间的任何一个值来代替x时,它必然等于xF(x)。
为了得到系数ai ,我们曾经用dxsinμi x乘方程(e),然后在界限x=0和x=X之间积分,我们已经证明(第291目),每当指标i和j不同时,即当数μi 和μj 是方程(f)的两个不同的根时,积分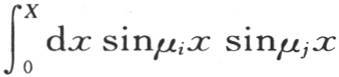 就取0值。由此得到,当定积分使右边除包含ai 的项之外其他所有的项都消掉时,为了确定这个系数,我们有
就取0值。由此得到,当定积分使右边除包含ai 的项之外其他所有的项都消掉时,为了确定这个系数,我们有
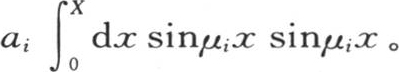 在方程(e)中代入系数ai 的这个值,我们由此导出恒等方程(ε),
在方程(e)中代入系数ai 的这个值,我们由此导出恒等方程(ε),
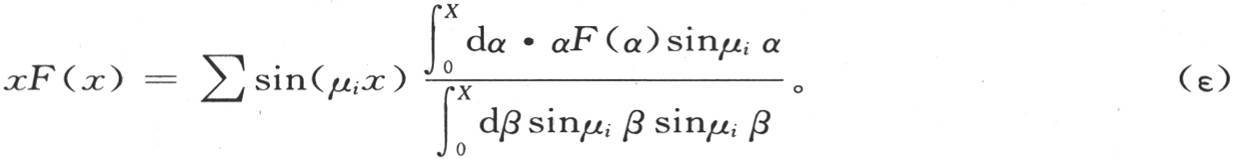
在右边,我们应当对i赋予其所有的值,即我们应当依次用方程(f)的所有的根μ来代替μi ,积分应当对α从α=0取到α=X,该积分使未知数α消掉。β也一样,它这样进入分母,使得项sinμi x乘以一个系数ai ,ai 的值只依赖于X和指标i。符号∑表示在对i给定其所有的值后我们应当写下所有项的和。
这时积分提供直接确定系数的一个很简单的方法;但是我们应当仔细考察这个过程的由来,这引出如下的注记。
第一,如果在方程(e)中我们省略了这些项的一部分,例如省略所有那些指标为偶数的项,那么只要用dxsinμi x乘这个方程,并且从x=0到x=X取积分,我们仍然得到ai 的相同的值,我们确定了这个值,我们就因此建立了一个不成立的方程;因为它只包含一般方程的一部分项,即那些指标是奇数的项。
第二,在确定了系数后我们所得到的,并且与(第291目)所说的其中令t=0并且v=f(x)的方程一样的这个完全方程(e)是这样的:它使得如果我们对x给定包含在0到X之间的任一个值,则两边必然相等;但是正如我们所注意到的,我们不能得出结论说,如果我们在为左边xF(x)选定一个服从于连续性规律的函数如sinx或者是cosx时,对x给定一个不包含在0到x之间的值,则这个性质仍然成立。一般地,综合方程(ε)适用于包含在0到X之间的x值。现在,确定系数ai 的这个过程既不解释为什么所有的根μi 应当进入方程(e),也不解释为什么这个方程只与包含在0到X之间的x值有关。
为了清楚地回答这些问题,只需回到作为我们分析基础的原理上来就够了。
我们把区间X分成等于dx的无数部分n,因此我们有ndx=X,用f(x)代替xF(x)之后,我们用f1 ,f2 ,f3 ,…,fi ,…,fn 表示f(x)的值,它对应于为x所安排的值dx,2dx,3dx,…,idx,…ndx;我们把一般方程(e)分成n项,因此n个待定系数a1 ,a2 ,a3 ,…,ai ,…,an 进入这个方程。如此,方程(e)表示n个一次方程,我们应当通过用x的n个值dx,2dx,3dx,…,ndx代替x来建立这些方程。这n个方程的方程组包含第一个方程的f1 ,第二个方程的f2 ,第三个方程的f3 ,第n个方程的fn 。为了确定第一个系数a1 ,我们用σ1 乘第一个方程,用σ2 乘第二个,用σ3 乘第三个,等等,把这些乘过的方程加起来。因子σ1 ,σ2 ,σ3 ,…,σn 必须以这样的条件来确定:它使得右边含a2 的所有项的和必须为0,并且后面的系数a3 ,a4 ,…,an 亦如此。这时把所有的方程相加,只有系数a1 进入结果,我们有一个确定这个系数的方程。然后我们重新用另一些因子ρ1 ,ρ2 ,ρ3 ,…,ρn 分别乘所有的方程,并且这样确定这些系数:使得只要把这些方程相加,所有的系数除a2 外就都被消掉。这样我们就有确定a2 的方程。继续类似的运算,并且总是选择新的因子,我们就会依次确定所有的待定系数。显然,这个消元过程正好就是在界限0到X之间的积分所产生的那个过程。第一组因子σ1 ,σ2 ,σ3 ,…,σn 是dxsin(μ1 dx),dxsin(μ1 2dx),dxsin(μ1 3dx),…,dxsin(μ1 ndx)。一般地,用来消去除ai 外的所有其他系数的那组因子是dxsin(μi dx),dxsin(μi 2dx),dxsin(μi 3dx),…,dxsin(μi ndx)。它们由通项dxsin(μi x)表示,在通项中,我们依次给出x的所有值dx,2dx,3dx,…,ndx。
我们由此看到,用来确定这些系数的过程与一次方程中的一般消元过程没有什么两样。方程的数目n等于待定系数a1 ,a2 ,a3 …,an 的数目,并且和已知量f1 ,f2 ,f3 ,…,fn 的个数相同。为这些系数所得到的值是按应当使这n个方程能同时成立的顺序而存在的值,即是按当我们对x给定包含在0到X之间的这n个值中的一个时方程(ε)成立的顺序而存在的值;由于数n是无穷的,所以得到,当在每一个中所代入的x值包含在0到X之间时,左边f(x)必然与右边相等。
上述证明不仅适合于形如a1 sinμ1 x+a2 sinμ2 x+a3 sinμ3 x+…+ai sinμi x的展开式,并且,在保持主要条件,即保持若i和j不同则积分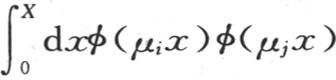 取0值这一条件时,它也适合于可以代替sin(μi x)的所有函数φ(μi x)。
取0值这一条件时,它也适合于可以代替sin(μi x)的所有函数φ(μi x)。
如果提出下述形式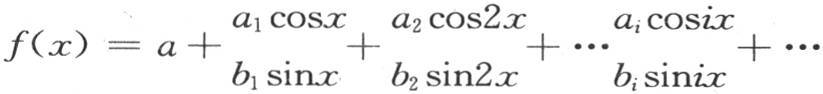 来展开f(x),那么量μ1 ,μ2 ,μ3 ,…,μi ,…是整数,并且若指标i和j不同则条件
来展开f(x),那么量μ1 ,μ2 ,μ3 ,…,μi ,…是整数,并且若指标i和j不同则条件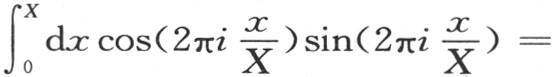 0总成立时,我们通过确定系数ai ,bi 而得到第192页的一般方程(Π),它与第418目的方程(A)相同。
0总成立时,我们通过确定系数ai ,bi 而得到第192页的一般方程(Π),它与第418目的方程(A)相同。
425 如果我们在方程(e)的右边省略与方程(f)的一个或者是多个根μi 相对应的一个或者是多个项,那么方程(ε)一般不成立。为了证明这一点,让我们假定方程(e)的右边少一个含μj 和aj 的项,我们可以用因子dxsin(μj dx),dxsin(μj 2dx),dxsin(μj 3dx),…,dxsin(μj ndx)分别乘以这n个方程;把它们相加,则右边所有项的和是0,因此所有待定系数都没有留下。左边的和,即值f1 ,f2 ,f3 ,…,fn 分别乘以因子dxsin(μj dx),dxsin(μj 2dx),dxsin(μj 3dx),…,dxsin(μj ndx)的和所形成的结果,就仍为0。这样,这种关系在已知量f1 ,f2 ,f3 ,…,fn 之间必然存在;并且它们不能看做是完全任意的,这与假定矛盾。如果这些量f1 ,f2 ,f3 ,…,fn 取任何值,则所说的这种关系就不可能存在,我们就不可能通过在方程(e)中省略如aj sin(μj x)这样的一个或者是多个项来满足所提出的条件。
因此在函数f(x)仍然待定时,即在f(x)表示与包含在0到X之间的x值所对应的这组无数任意常数时,就有必要在方程(e)的右边引进诸如aj sin(μj x)这样的所有项,这些项满足条件 指标i和j是不同的;但是,如果碰巧函数f(x)是这样的,它使得n个量f1 ,f2 ,f3 ,…,fn 由用方程
指标i和j是不同的;但是,如果碰巧函数f(x)是这样的,它使得n个量f1 ,f2 ,f3 ,…,fn 由用方程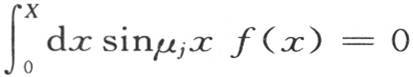 所表示的一种关系联系起来,那么显然,项aj sinμj x就可以在方程(e)中略去。
所表示的一种关系联系起来,那么显然,项aj sinμj x就可以在方程(e)中略去。
因此,有n类函数f(x),它们由方程(ε)的右边表示,其展开式不含与某些根μ所对应的一些项。例如,有我们省略指标为偶数的所有项这样的情况;我们在本书中已经看到各种这样的例子。但是,如果函数f(x)具有一切可能的普遍性,则这不成立。在所有这些情况下,我们应当假定方程(e)的右边是完全的,并且这个研究表明哪些项因它们的系数变成0而可以略去。
426 通过这个考察我们清楚地看到,在我们的分析中,与包含在0到X之间的n个x值相对应,函数f(x)表示这组n个数目的分离的量,并且这n个量取实数值,因而不是任意选取的无穷值。除一个其值已知的外,所有这些量都可以为0。
可能碰巧这组n个值f1 ,f2 ,f3 ,…,fn 由服从于一条连续性规律的函数来表示,如由x或者是x3 ,sinx或者是cosx,或者一般地,由φ(x)来表示;曲线OCO,它的纵坐标表示与横坐标x相对应的值,并且它处在从x=0到x=X的区间的上方,这时在这个区间中与纵坐标为φ(x)的曲线重合,由前面的规则所确定的方程(e)的系数a1 ,a2 ,a3 ,…,an 总满足这样的条件,即当在φ(x)和在方程(ε)的右边作代换时,包含在0到X之间的任一x值都给出相同的结果。
F(x)表示半径为x的球壳的初始温度。例如,我们可以假定F(x)=bx,即初始热与从圆心为0到表面为bx的距离成正比地增加。在这种情况下,xF(x)或者是f(x)等于bx2 ;对这个函数运用确定系数的规则,bx2 就以如α1 sinμ1 x+α2 sinμ2 x+α3 sinμ3 x+…+αn sinμn x这样的一些项的级数展开。
现在每一项sin(μi x)在根据X的幂而展开时都只含奇次幂,而函数bx2 是一个偶次幂。很值得注意的是,这个函数bx2 ,在表示从0到X这个区间的已知值的一个级数时,可以如像αi sinμi x这样一些项的级数展开。
我们已经证明了这些结果的严格精确性,这是分析中从来未曾有过的,并且我们表明了表示它们的命题的真实意义。例如我们在第223目已经看到函数cosx以多重弧的正弦级数展开,使得在给出这个展开式的方程中,左边只含变量的偶次幂,右边只含奇次幂。反过来说,只有奇数幂进入其中的函数sinx,在第225目中,被转换成只含偶数幂的余弦级数。
在与球有关的实际问题中,xF(x)的值由方程(ε)展开。如我们在第290目所看到的,这时我们应当在每一项中写上含t的指数因子,为了表示作为x和t的函数的温度v,我们有方程
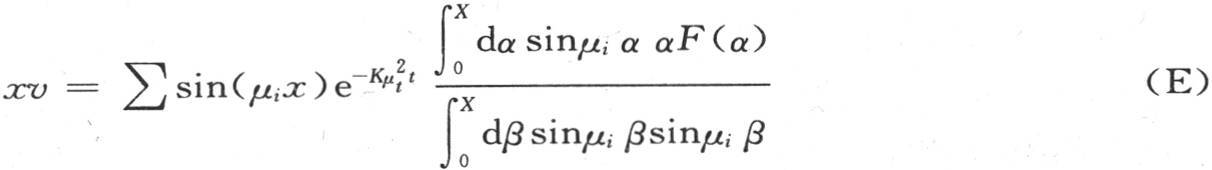
给出这个方程(E)的通解完全与函数f(x)的性质无关,因为这个函数在这里只表示无穷多的任意常数,这些任意常数与包含在0到X之间的同样多的x值相对应。
如果我们假定初始热只包含在这一实心球的一部分中,如包含在从x=0到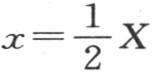 的部分中,并且外层的初始温度为0,那么在界限x=0到
的部分中,并且外层的初始温度为0,那么在界限x=0到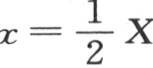 之间取积分∫dαsinμi αf(α)就够了。
之间取积分∫dαsinμi αf(α)就够了。
一般地,由方程(E)所表示的解适合于所有情况,并且展开式的形式不随函数的性质而变化。
现在假定在用sinx代替F(x)之后,我们用积分确定了系数ai ,并且我们建立了方程xsinx=a1 sinμ1 x+a2 sinμ2 x+a3 sinμ3 x+…。
无疑,只要对x给定包含在0到X之间的任一值,这个方程的右边就等于xsinx;这是我们的方法的一个必然结论。但是决不能由此得出在对x给定不包含在0到x之间的值时同样的性质仍然成立。在我们引用过的例子中我们看到很明显的反例。并且,除特殊情况外,我们可以说,组成这类方程的左边并且服从于一条连续性规律的函数,除x的值包含在0到X之间以外,不会与右边所表示的函数相同。
严格说来,方程(ε)是一个恒等式,它对于可能赋予变量x的所有值都成立;如果我们对变量x给定包含在0到X之间的值,则这个方程两边表示与一个已知函数f(x)重合的某个解析函数。至于对变量包含在某个界限之间的所有值都重合,而对其他值则不同的这些函数的存在性,由前面所有那些内容证明,并且这种考虑是偏微分方程理论的一个必要因素。
此外,显然方程(ε)和(E)不仅适用于其半径为x的实心球,而且还表示该球体构成它的一部分的一个无穷延伸固体的初始状态,以及表示它的其他的变化状态;当我们在这两个方程中对变量x给定比X更大的值时,它们就指这个无穷固体包住这个球体的那些部分。
这个注记也适用于用偏微分方程来解决的所有动力学问题。
427 为了把由方程(E)所给出的这个解应用到在开始时只有一个球层被加热,而所有其他球层取0初始温度的情况中去,我们只需在两个很近的界限α=r和α=r+u之间取积分∫dαsinμi ααF(α)就够了,r是受热层内表面的半径,u是这个薄层的厚度。
我们也可以分别考虑包含在限r+u和r+2u之间的另一个薄层初加热的合成作用;如果我们把属于第二个原因的可变温度加到在第一个薄层单独受热时我们所得到的温度上去,那么这两种温度的和就是这两个薄层在同时受热时所产生的温度。为了说明这两种温度的联合原因,只需在界限α=r和α=r+2u之间取积分∫dαsinμi ααF(α)就够了。更一般地,由于方程(E)可以置于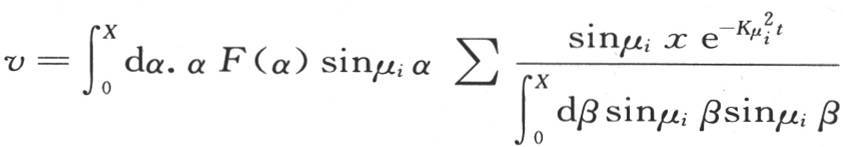 的形式之下,所以我们看到,不同薄层加热的整体作用是各部分作用的和,我们可以假定每个薄层单独被加热来确定各部分的作用。同一结论可推广到热理论的所有其他问题上去;这完全可从方程的性质导出,而积分形式则使之变得显然。我们看到,包含在一个固体的每个基元中的热产生其截然不同的作用,仿佛那个基元被单独加热,而所有其他基元取0初始温度一样。这些分离状态在某种意义上被叠加,并一起构成这个一般的温度系统。
的形式之下,所以我们看到,不同薄层加热的整体作用是各部分作用的和,我们可以假定每个薄层单独被加热来确定各部分的作用。同一结论可推广到热理论的所有其他问题上去;这完全可从方程的性质导出,而积分形式则使之变得显然。我们看到,包含在一个固体的每个基元中的热产生其截然不同的作用,仿佛那个基元被单独加热,而所有其他基元取0初始温度一样。这些分离状态在某种意义上被叠加,并一起构成这个一般的温度系统。
由于这个原因,我们应当把表示初始状态的这个函数式看做是完全任意的。进入可变温度表达式的定积分,在具有和受热固体一样的界限时,清楚地表明我们把属于每个基元初加热的所有的部分作用都统一起来了。
428 我们在此结束几乎完全致力于分析的这一节。我们所得到的积分不仅仅是满足微分方程的一般表达式;它们也以最不相同的方式表示作为问题之对象的自然作用。这是我们一直在考虑的主要条件,没有这个条件,研究结果在我们看来就只是一些无用的变换。当这个条件被满足时,这个积分,准确地说,就是这一现象的方程;就像一条曲线或者是一个曲面的有限方程使我们知道其形状的所有性质一样,它以同样的方式清楚地表示它的特征和进展。为了揭示这些解,我们不仅仅只考虑积分的一种形式;我们还希望直接得到适合于问题的那种形式。因此,表示半径已知的一个球中的热运动的积分,与表示一个圆柱体、乃至假定半径无穷的一个球中的热运动的积分,是非常不同的。现在每一个这样的积分都有一个不可能由另一个取而代之的确定形式。如果我们希望确定所讨论的物体中的热分布,那么就应当运用它。一般地,我们在我们的解中引进任一变化都会使它们失去表示这一现象的基本特征。
这些不同的积分可以互相导出,因为它们是共存的。不过这些变换需要很长的运算,并且几乎总是假定结果的形式预先知道。我们首先可以考虑那些体积有限的物体,然后从这个问题过渡到与无界固体有关的问题上去。这时我们可以用一个定积分来代替由符号∑所表示的和。因此这就是在本节开始时所说的方程(α)和(β)相互依赖。当我们假定半径无穷时,第一个方程就变成第二个方程。反过来我们也可以由第二个方程(β)导出与有限体积的固体相关的解来。
一般地,我们总是设法用最简单的方法得到每一个结果。我们所遵循的方法的要点如下:
第一,我们同时考虑由偏微分方程所给定的一般条件和完全确定问题的所有特殊条件,并进而建立满足所有这些条件的解析表达式。
第二,我们首先看到这个表达式包含有未知数进入其中的无数项,或者它等于包含一个或者是多个任意函数的一个积分。在第一种情况下,即当通项受符号∑的作用时,我们从特殊条件得到一个确定的超越方程,这个方程的根给出无穷多个常数的值。
当通项变成无穷小量时得到第二种情况;这时级数和变成一个定积分。
第三,我们可以用代数基本定理甚至用这个问题的物理性质来证明这个超越方程的所有根都是实根,并且有无穷多个。
第四,在简单的问题中,通项取正弦或者是余弦的形式;定义方程的根或是整数或是实数或是无理量,它们每一个都包含在两个确定的界限之间。
在更复杂的问题中,通项呈函数形式,它隐含地由一个可积的或者是不可积的微分方程所给出。不管怎样,定义方程的根是存在的,它们是数目无穷的实数。必然构成积分的这些部分的这个区别是很重要的,因为它清楚地表明解的形式和系数之间的必然联系。
第五,剩下来的只是确定依赖于初始状态的常数;这通过无数的一阶方程的未知数的消元来进行。我们用一个微分因子来乘以初始状态相关的这个方程,然后在所定义的界限之间对它积分,这些界限是运动在其中得以实现的这个固体的最普通的界限。
有些问题我们是通过逐次积分来确定系数的,如在那些其对象是驻温的研究报告中所看到的那样。在这种情况下我们考虑指数积分,它属于无穷固体的初始状态;不难得到这些积分 【43】 。
由这些积分得到,除了我们要确定其系数的那个项外,右边的所有项都消掉。在这个系数的值中分母变成0,我们总得到其积分限是固体界限的一个定积分,它的因子之一是属于那个初始状态的任意函数。结果的这个形式是必然的,因为如果固体的每一点都已单独受热,其他每一点的温度都为0,那么作为问题之对象的这个可变运动就由所有那些单独存在的运动混合而成。
当我们仔细考查用来确定这些系数的这个积分过程时,我们看到它包含一个完整的证明,并清楚地表明结果的性质,因此毫无必要用其他研究来检验它们。
我们迄今为止所提出的问题中最引人注目的,并且最适合于表明我们全部分析的,是圆柱体中的热运动问题。在其他研究中,这些系数的确定可能需要我们现在仍不清楚的一些研究过程。然而必须注意的是,即使不确定这些系数的值,我们也总可以得到这个问题的精确知识和作为问题之目的的这个现象的自然过程的精确知识;主要想法是简单运动。
第六,当所寻求的表达式包含一个定积分时,在积分符号下所安排的这些未知函数就或者由我们对定积分的任意函数式所给出的定理来确定,或者由一个更复杂的过程来确定,在第二部分可以看到几个这样的例子。
这些定理可以推广到任意个变量上去。它们在某种意义上属于定积分的一种逆方法;因为它们的作用是在符号∫和∑之下来确定未知函数,这些函数必须是这样的:它们使得积分的结果是一个已知函数。
不管方程包含有限的或者是无穷小的差,或者是两者都包含,同样这些原理都可应用到其他的几何问题、普通物理学问题和分析问题中去。
由这种方法所得到的解是全解,并且由一些通积分组成。不可能有别的更一般的积分。对这一课题所提出的反对意见全无根据,此处没有必要讨论这些意见。
第七,我们说过,每一个这样的解都给出适合于这个现象的方程,因为它在它的过程的整个范围内明显地表示它,并且便于用来在数值上确定它的所有结果。
由这些解所得到的函数由许多项所组成,这些项或者是有限的或者是无穷小的:但是这些表达式的形式决不是任意的;它由这个现象的物理特征所确定。由于这个原因,当函数值由与时间有关的一些指数进入其中的一个级数来表示时,它必然如此,因为,与这个级数的这些不同的项相对应,我们寻求其规律的这种自然效应实际上被分解成不同的部分。这些部分表示与这个具体条件相一致的如此之多的简单运动;对于每一个这样的运动,所有温度都降低,同时保持它们的初始化。在这种合成中,我们不应该把一个分析的结果归之于这些微分方程的这种线性形式,而应当把它归之于在实验中变得明显起来的一种实际效应。它也出现在我们考虑使运动消失的原因的动力学问题中;然而它必定属于热理论的所有问题,并且确定我们为得到它们的解所遵循的方法的性质。
第八,热的数学理论包括:首先,所有这些分析的要素的精确定义;其次,微分方程;最后,适合于基本问题的积分。这些方程可以由几种方式得到;同样这些积分可以通过在研究过程中引入某些变化而得到,或者其他一些问题可由此而解决。我们认为这些研究并不构成不同于我们自己的方法:而只是确认和增加它的结果。
第九,对我们的分析的主题所提出的反对意见是,在确定指数的这些超越方程有虚根时,我们有必要运用由它们所引起的、并且指明该现象某一部分的周期特征的一些项,然而这种反对意见没有根据,因为事实上所说的这些方程的根都是实根,并且这个现象没有哪一部分是周期的。
第十,有人说,为了切实解决这类问题,我们有必要在所有情况下都借助于以一般的形式来表示的某种积分形式;而且第398目的方程(γ)就是在这种意义下被提出的;但是这个区分是没有根据的,单个积分的这种使用在大多数情况下只会起到使研究不必要地复杂化的作用。此外,显然这个积分(γ)可以从我们在1807年为确定一个给定半径R的环中的热运动而给出的积分导出;这只需对R给定一个无穷值就够了。
第十一,有人曾经猜想,这种主要在于用一系列指数项来表示积分的,并且在于通过初始状态来确定这些项的系数的方法,不能解决一个棱柱在两端不等地失热这一问题;或者是猜想,至少这样以长长的运算来检验可以从积分(γ)导出这个解是很困难的。我们通过一个新的考查会看到,我们的方法直接适用于这个问题,甚至单单一个积分就够了 【44】 。
第十二,我们以多重弧的正弦级数展开了似乎只含变量偶次幂的一些函数,如cosx。我们用了一些收敛级数或者是一些定积分来表示一些不同的函数的一些不同的部分,或者是表示在某些界限之间不连续的函数的不同的部分,例如,计量一个三角形的纵坐标的函数。我们的证明清楚地表明这些方程严格成立。
第十三,我们在许多几何学家的著作中看到类似于我们所运用过的那些运算结果和过程。这些都是一种一般方法的特例,这种一般方法一直未曾建立,为了在哪怕最简单的问题中确定热分布的数学规律都必须建立这种一般方法。这个理论需要一种适合于它的分析,它的一个重要因素是分离函数的或者说是函数的各部分的解析表达式。
我们通过一个分离的函数或者是一个函数的一部分而理解一个函数f(x)在变量x包含在已知界限之间时取实际的值,并且如果该变量不在这些界限之间时,则它的值总是0。这个函数计量一条曲线的纵坐标,这条曲线包含任意形式的一条有限弧段,并且在所有其余的部分与横轴重合。
这个概念 【45】 并不与那些一般的分析原理相对立;我们甚至可以在丹尼尔·伯努利,柯西(Gauchy),拉格朗日和欧拉等人的著作中找到它最初的痕迹。人们一直认为显然不可能用多重弧的正弦级数或至少不能用三角函数的收敛级数来表示只有在变量的值包含在某个界限之内时才有实际的值、而所有其他值都为0的这样一个函数。然而我们完全澄清了分析的这个要点,并且同样无可争辩的是,分离的函数或者是函数的各部分,严格地由三角函数的收敛级数或者是定积分来表示。我们从我们研究的开始一直到现在都坚持这一结论,因为我们在此所涉及的不是一个抽象的和孤立的问题,而是与最有用和最广泛的思考密切相关的一个基本考虑。在我们看来,没有任何东西比几何作图更适合于论证这些新结果的真实性,更适合于提供分析因它们的表达式而使用的明了形式了。
第十四,我们用来建立热的解析理论的这些原理直接适用于对流体中的波运动的研究,这种运动曾部分地被热烈讨论过。它们也有助于弹性片、紧张可曲面和大面积平面弹性面等的振动研究,并且一般可用到依赖于弹性理论的那些问题上去。我们从这些原理所导出的解的性质会使数值应用变得容易,并且会提供清晰明了的结果而不至于使知识依赖于不可能实现的积分或者是消元,这些结果实际上确定问题的目的。我们把不满足这个基本条件的分析结果的每一个变换都视为多余的。
429 第一,我们现在对热运动的微分方程给出一些注记。
如果同一物体的两个分子挨得极近,并且温度不等,那么受热多的那个分子在某一时刻直接向另一个传递一定的热量;这个量与其极小温差成正比:即如果这个差翻成两倍、三倍或者是四倍的,并且其他所有条件保持不变,那么所传递的热就是两倍、三倍或者是四倍的。
这个命题表示一个一般的和不变的事实,它足以用来作为数学理论的基础。这时传递方式无疑是已知的,而与关于其原因的性质的每个假定无关,并且这种传递方式不可能根据两种不同的观点来考察。显然,这种直接传递在所有方向上进行,并且除两个极近的分子外,在不透热的流体或液体中不存在这种传递。
在任一体积的固体内部和在这些物体表面的热运动的一般方程是上述命题的必然结论。如同我们在我们1807年的第一份研究报告中所证明的那样,它们严格由它导出。我们通过一些引理不难得到这些方程,这些引理的证明和力学基本命题的证明一样精确。
通过运用积分来确定一个分子从它周围的分子那里所得到的全部热量,这些方程还可以从这同一个命题导出。这一研究不存在任何困难。由于这些引理直接给出这个热流的表达式,即给出过任一截面的热量的表达式,所以,所说的这些引理代替这些积分。两种计算显然应当得出相同的结果;由于在原理上没有差别,所以在结论中不可能有任何差别。
第二,我们在1811年给出了与表面有关的一般方程。如同人们认为它缺乏基础一样,它不从特例中推出,它也不可能从特例中推出;它所表示的命题具有一种不为归纳法所能发现的性质;我们不可能因某些物体而确认它,因另一些物体而忽视它;为使表面状态不可能在确定时间内历经无穷变化,它对所有物体都是必要的。在我们的研究报告中我们省略了证明细节,因为它们仅仅在于已知命题的应用。正如我们在援引的研究报告的第15目中所做的那样,在本书中给出这个原理和结果就够了。根据同样的条件,通过确定位于表面的每个分子所得到的和所传递的全部热量,也可以推出所说的一般方程。这些很复杂的运算在证明的性质上不会引起什么变化。
在热运动的微分方程研究中,可以假定物质不是均匀的,从热流量的解析表达式不难导出这个方程;这只需留下微分符号下计量热导率的系数就够了。
第三,牛顿是考虑物体在空气中的冷却定律的第一个人;他对空气以恒定速度移动所采用的定律随温差愈小而愈与观察一致;如果温差无穷小,则它严格成立。
阿蒙通(Amontons)对端点受一定的温度作用的一根棱柱中的热的确定做过一个引人注目的实验。在这种棱柱中温度降低的对数定律首次由柏林科学院的兰贝特(Lambert)给出。毕奥(Biot)和拉姆福德(Rumford)用实验确证了这条定律 【46】 。
原来,为了发现变化的热运动的微分方程,甚至在最简单的情况下,如在半径很小的柱面棱柱的情况下,都必须知道过棱柱极短部分的热量表达式。现在这个量不仅仅与界定薄层的两个截面的温差成正比。我们以最严格的方式证明,它也与薄层的厚度成反比,即如果同一棱柱的两个薄层厚度不等,如果在第一个中两个底面的温差和第二个中的一样,那么在同一时刻内经过这两个薄层的热量与厚度成反比。上面这个引理不仅适用于厚度无穷小的薄层;它也适用于任意长度的棱柱。热流量的这个概念是基本的,只要我们还没有这样一个概念,我们就不能对这种现象和表示它的方程建立精确的概念。
显然,一点的温度的瞬时增量与该点所得到的超过它所失去的热量的超出量成正比,并且这个结果应当由一个偏微分方程来表示。然而,问题不仅仅在于宣布这个命题,它不过是事实罢了;问题在于实际地建立这个微分方程,这需要我们从基本原理出发考虑这个事实。如果我们不是运用热流量的这个精确表达式而是省略这个表达式的分母,那么我们会由此产生一个困难,而这个困难决不是问题本身所固有的。如果我们不是以证明的这个原理开始,那么任何数学理论就都必然会出现一些类似的困难。这样,我们不仅不能建立微分方程,而且,对于一个方程来说,再没有什么比我们要表示不可比较的两个量的相等这样一种命题更矛盾的了。为了避免这个错误,只需注意一下前面引理的论证和结论就行了(第65、66、67和75目)。
第四,至于我们据以首次推出这些微分方程的思想,它们都是一直为物理学家们所承认的。我们不知道谁能把热运动想象成是由使一些不同的部分分开的那些面的简单接触而在物体的内部产生的。在我们看来,这样的命题似乎完全没有明确的意义。一个接触面不可能是任何物理性质的原因;它既不受热,不变色,也无重量。当一个物体的某一部分把它的热传给另一部分时,第一部分有无数质点对第二部分的无数质点发生作用。这只需加上,在不透明物质内不是很近的点不可能直接传递它们的热就够了;它们所发出的热被中间分子所拦截。当接触中的这些薄层的厚度等于或者是超过从一点所发出的热在被完全吸收前所越过的距离时,这些薄层就只是直接传递它们热量的薄层。除了挨得极近的质点外,不存在直接作用,正是由于这个原因,热流量的表达式具有我们所赋予它的这种形式。这时热流量就由其效应被加起来的无数作用所产生;但是,即使它仅仅只由温度之间的一个极小的差所确定,也不能由此推出它的值在单位时间内是一个有限的可测值。
当一个受热物体在一种弹性介质中或者是在由一个固体壳所界定的不含空气的空间中失热时,这种向外的热流量的值无疑是一个积分;它也属于离表面很近的无数质点的作用,我们在前面曾证明过这种聚集决定外辐射定律 【47】 。但是如果温差没有有限的值,那么在单位时间内所发射的热量就是无穷小的。
物质内部的传导力比在表面所发生的这种力要无比地大。无论这个性质的原因如何,这个性质由我们最清楚地察觉到,因为,当棱柱达到它的不变状态时,在单位时间流过一个截面的热量就严格等于通过位于该截面之外、其温度比介质温度高一个有限量的那个受热面的所有部分所失去的热量。如果我们无视这个基本事实,省略热流量表达式中的这个因子,那么即使对于最简单的情况也不可能建立这个微分方程;更何况这会阻止我们研究一般方程了。
第五,此外,有必要知道棱柱的截面积对所得到的温度有什么影响。即使这个问题仅仅是线性运动问题,并且把一个截面的所有点都看做是有相同温度的,也不能由此得出我们可以忽视截面积,并把只属于某个棱柱的结论推广到其他棱柱上去。不表示这个截面的大小和在棱柱顶端所产生的这个作用之间的关系,就不可能建立精确的方程。
我们不打算进一步展开对引导我们得到这些微分方程知识的这些原理的考察;我们只补充,为了确信这些原理的有效性,还有必要考虑各种难题;例如我们即将指出的那些问题,以及正如我们早以注意到的,其解需要我们的理论的那些问题。这个问题在于建立一些微分方程,当和这些温度变化混合后所有分子由任一种力所移动时,这些微分方程就表示运动流体中的热分布。我们在1820年间所给出的这些方程属于一般流体动力学;它们完善了分析力学的这个分支 【48】 。
430 物理学家谓之为传导性(conductibity)或者是助导性(conducibility),即容热能力或者是在其物体内部传导它的能力,在不同的物体中有很不相同的性质。尽管这些名称在我们看来似乎不准确,但我们仍然这样用。这两个名称,特别是第一个,完全是根据类比,如其说它表示传导能力,倒不如说表示被传导的能力。
热,不论是进入还是逃逸出物体,都以或大或小的能力贯穿不同物质的表面,并且物体对这种元素的可穿透性是不等的,即它在它们之中以或大或小的能力从一个内部分子传导到另一个内部分子。我们认为这两种截然不同的性质可以用穿透性(penetrability)和渗透性(permeability)这两个名称来表示 【49】 。
重要的是,不能够忽视表面的穿透性由两种不同的性质决定,一种与外部介质有关,它表示由接触所产生的传导能力;另一种在于放射辐射热或者是容纳辐射热的性质。至于渗透率,它是每一种物质所固有的,并且与表面状态无关。至于其他的名称,尽管精确定义是理论的真正基础,然而就我们的问题而言,名称却没有这样高的重要性。
431 最后这句话不能用在记号上,记号对微积分科学的贡献极大。这些记号只能谨慎地提出,并且只有经过长期考验后方可接受。我们用了一个记号来指示积分符号∫的上下积分限;在这两个界限之间变化的量的微分紧写在这个符号之后。
我们还用符号∑表示由某个一般项所导出的一些数目不定的项的和,在一般项中,指标i是变化的。如果有必要,我们就把这个指标加到这个符号上,在这个符号的下面写i的第一个值,上面写最后一个值。这个记号的习惯用法使我们确信它的有效性。特别是当分析由一些定积分所组成并且积分限本身是研究的对象时尤其如此。
432 我们的理论的这些主要结果是那些在固体或者是液体中的热运动的微分方程以及那个与表面有关的一般方程。这些方程的正确性不以热效应的任何物理解释为基础。在我们为设想这种元素的性质所情愿采纳的任何方式中,不管我们把它看做是从空间的一部分传到另一部分的特殊物质材料,还是认为热仅仅是运动的传递,我们都总会得到同样的方程,因为我们所作的假定应当表示这个导出数学规律的一般和简单的事实。
由两个温度不等的分子所传递的热量依赖于它们的温差。如果这个差是无穷小的,那么所传递的热肯定与这个差成正比;所有实验都严格证明这个命题。现在,为了建立所说的这些微分方程,我们只考虑那些无穷近的分子的相互作用。因此,关于与物质内部有关的这些方程的形式不存在任何的不确定性。
如我们所说,不管我们是计算这些固体分子的相互作用,还是考虑介质对外壳所施加的作用,与表面有关的这个方程都表示在固体边界的法方向上的热流量肯定有相同的值。前一个值的分析式很简单并且完全已知;至于后一个值,当表面温度超过介质温度的超出量是一个充分小的量时,它明显与表面温度成正比。在其他情况下,我们则应当把第二个值看做是由一组观察所给定的;它取决于表面,压力和介质的质;这个观察值应当成为与表面有关的这个方程的右半边。
在几个重要的问题中,最后举出的这个方程由一个已知条件所取代,这个条件表示或不变、或可变、或周斯性变化的表面状态。
433 热运动的这些微分方程是与那些平衡和运动的一般方程相类似的一些数学结论,并且和它们一样,是从那些最常见的自然界的事实中导出的。
一般地,进入这些方程的系数c,h和k应当被看做是变量,这些变量取决于温度或者是物体的状态。不过在应用于我们所最感兴趣的那些自然界的问题时,我们可以赋予这些变量明显不变的值。
第一个系数c随温度的上升而非常缓慢地变化。这些变化在大约30℃的区间几乎察觉不出来。杜隆和珀蒂教授所作的一组有价值的观察表明,比容量(specific capacity)的值随温度而缓慢地增加。
计量表面穿透性的系数h是最可变的,它恰好与一种复合状态相联系。它表示或者是通过辐射或者是通过接触而传递给介质的热量。因此这个量的严格计算依赖于液态和气态介质中的热运动问题。但是当温度的超出量是一个充分小的量时,观察证明可以把这个系数值看做是常数。在其他情况下,不难从已知的实验得到使结果充分精确的校正值。
无疑,系数k,渗透性的量度,易发生明显的变化;然而在这个重要的问题上还没有一组实验能适当地告诉我们热传导的能力怎样随温度 【50】 和压力而变化。我们由观察看到,这个性质在很大一部分温标中可以看做是不变的。但是,同样的观察又告诉我们所说的这个系数值因温度的增加所引起的变化要比容量的值大得多。
最后,固体膨胀率,或者是增加体积的趋势,在所有温度下都是不相同的;不过在我们所讨论的这些问题中,这些变化不可能明显地改变结果的精度。一般地,在对由热分布所决定的那些主要自然现象的研究中,我们相信可以把这些系数值看做是不变的。首先,有必要从这个观点出发考虑这个理论的这些结论。其次,这些结果与那些很精确的实验结果的仔细比较将表明必须运用什么样的校正值,并且随着这些观察愈来愈多和愈来愈精确,这种比较会对这些理论研究给出进一步的扩展。那时我们会确定改变物体内部热运动的原因究竟是什么,这个理论会得到一种现在不可能得到的完整性。
光热,或者是伴随炽热体所放出的光线的热,贯穿透明的固体和液体,在经过相当长的一段距离以后逐渐在它们之中被吸收。因此,在这些问题的考察中不可能假定热的这些直接效应仅仅只被传递极短的距离。虽然当这个距离有一个有限的值时,这些微分方程呈现出一种不同的形式;但是,除非这部分理论建立在我们还没有得到的那些实验知识的基础之上,否则它就不能提供任何有效的应用。
实验表明,在中等温度上,很少一部分的暗热有和光热一样的性质;很可能,贯穿固体的这些热效应被传送的距离不完全是不可察觉的,它只是很小罢了:但是这样的情况在这些理论结果中不引起明显的差别,或者至少这种差别至今还没有被观察到。
注释
【1】 这句话英译本是错的。现依法文《文集》本翻译。——汉译者
【2】 参见黎曼,《偏微分方程》,§16,第34页。——A. F.
【3】 即 F(x)=-F(-x)。——A. F.
【4】 在x的极限值上,这个积分的值是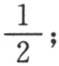 黎曼,§15。——A. F.
黎曼,§15。——A. F.
【5】 参见黎曼,§16。——A. F.
【6】 在这个方程中所需要的代换是用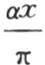 代替x,用dq代替
代替x,用dq代替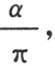 用q代替
用q代替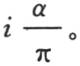 这样,对于在0到π之间的x值,我们有sinx等于一个与上面这个积分等价的级数,对于0到π之间的x值,原方程成立。——A. F.
这样,对于在0到π之间的x值,我们有sinx等于一个与上面这个积分等价的级数,对于0到π之间的x值,原方程成立。——A. F.
【7】 方法是简单运用表达式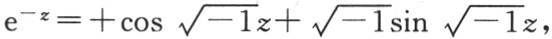 同时把u写在y2 ,以此变换a和b,并且重新合并
同时把u写在y2 ,以此变换a和b,并且重新合并 参见§407。——R. I. E.
参见§407。——R. I. E.
【8】 为了做到这一点,把 代入f(x)并相加,因此
代入f(x)并相加,因此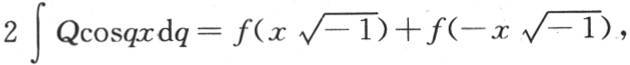 用-x代替x它仍然保持不变。因此
用-x代替x它仍然保持不变。因此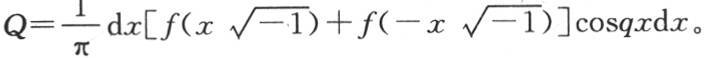 我们也可以相减并用正弦,不过处理虚量的困难会不断出现。——R. L. E.
我们也可以相减并用正弦,不过处理虚量的困难会不断出现。——R. L. E.
【9】 在“关于波的理论的论文”(Mémoire sur la Théorie des Ondes,载于《科学院研究报告》,第1卷,巴黎,1818年,第85—87页。)中,泊松首次对定理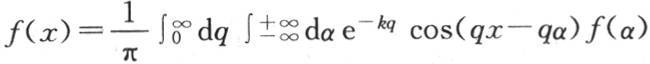 给出了一个直接证明,其中假定k是一个很小的正量,并且在积分后它等于0。
给出了一个直接证明,其中假定k是一个很小的正量,并且在积分后它等于0。
在“关于不连续函数的分析”〔On the Analysis of Discontinuous Functions,载于《爱尔兰皇家科学院学报》(Trans actions of the Royal Irish Academy),第21卷,都柏林,1848年,第126—130页。〕中,布尔引进不连续性的某些解析表示,并且把傅立叶定理看做是未证明的,除非它等价于上面的命题。
在“关于几个定积分的注记等”(Note sur quelques inté gralesdé finise & c.,载于《科学普及协会公报》,巴黎,1819年,第161—166页)一文的结尾,德弗勒斯指出傅立叶定理的一个证明,泊松以一个修改的形式重复了这个证明,见《综合工艺学校学报》(Journal Polytechnique),第19册,第454页。这个证明的具体困难为德·摩根所注意,《微积分计算》,第619,628页。
此处引证的这类证明的一个出色的讨论由格莱舍(J. W. L. Glaisher)在一篇文章中给出,“论sin∞和cos∞”(On sin∞ and cos∞),《数学通信》(Mesenger of Mathematics),系列1,第5卷,第232—244页,剑桥,1871年。——A. F.
【10】 黎曼在《偏微分方程》中给出了这一证明,并推出对应于F(x)=±F(-x)的情况的公式。——A. F.
【11】 就观点的清晰性而言,这些注记是必不可少的。能够导出(E)及其同族形式的这些方程可以在托德亨特的《积分学》(Integral Calculus)中找到,剑桥,1862年,§316,方程(3)和(4)。——A. F.
【12】 在英译本中,这里的u′被当做u,因此,这句话被说成:“我们应当为u找到一个满足方程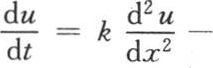
 由于傅立叶在前面作了代换u′=e-ht u,所以这会引起混乱。这里是依法文《文集》本订正的。——汉译者
由于傅立叶在前面作了代换u′=e-ht u,所以这会引起混乱。这里是依法文《文集》本订正的。——汉译者
【13】 《综合工艺学校学报》(Journal del Ecole Polytechnique),第8卷,第235—244页,巴黎,1809年。拉普拉斯还表明,这个方程的完全积分只含一个任意函数,不过在这方面泊松的工作比他更早。——A. F.
【14】 此方程右边的式子,在英译本中,没有前面的因子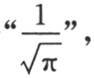 这里是按法文《文集》本订正的。——汉译者
这里是按法文《文集》本订正的。——汉译者
【15】 下面的文献由黎曼给出:
克朗普(Kramp),《地球和天文中的折射分析》(Analyse des réfractions astronomiques et terrestres),莱比西克和巴黎,1799—1800年,4开本,表I,末尾包含积分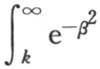 dβ从k=0.00到k=3.00的值。
dβ从k=0.00到k=3.00的值。
勒让德(Legendre),《椭圆函数及欧拉积分研究》(Traité des fonctions elliptiques et des intégrales Eulériennes),第二卷,巴黎,1826年,4开本,第520—521页。积分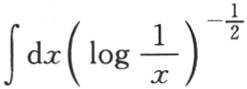 的取值表。第一部分为
的取值表。第一部分为 从0.00到0.50的值,第二部分为x从0.80到1.00的值。
从0.00到0.50的值,第二部分为x从0.80到1.00的值。
恩克(Encke),《作为1834年的天文学年鉴》(Astronomisches Jahrbuch für 1834),柏林,1832年,第8卷,表I,末尾给出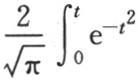 dt从t=0.00到t=2.00的值。——A. F.
dt从t=0.00到t=2.00的值。——A. F.
【16】 英译本中的表述与这里的有出入。两等号中间的式子中的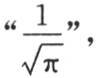 在那里是
在那里是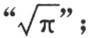 后一个等号右边的式子中e的指数
后一个等号右边的式子中e的指数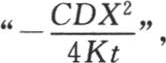 在那里是
在那里是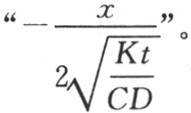 此处依法文《文集》本订正。——汉译者
此处依法文《文集》本订正。——汉译者
【17】 在英译本中,这个表述是这样的:“用ψ(R)表示从r=R取到r=x的积分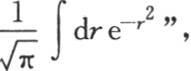 即
即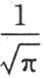 的位置刚好与这里的相反。此处依法文《文集》本订正。——汉译者
的位置刚好与这里的相反。此处依法文《文集》本订正。——汉译者
【18】 法文《文集》本在此方程后面还加了一个等式,即为: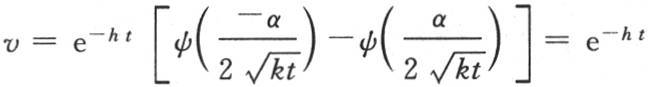
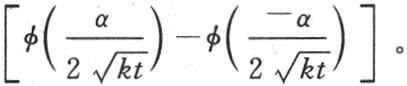 ——汉译者
——汉译者
【19】 参见黎曼,§18。
【20】 见汤姆森爵士的一篇文章,“论线性热运动”(On the Linear Motion of Heat),第1部分,《剑桥数学学报》,第3卷,第170—174页。——A. F.
【21】 这个值可以用托德亨特《积分学》(Integral Calculus)§375中的一种不同的方法求得。——A. F.
【22】 在像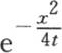 这样的量中。——A. F.
这样的量中。——A. F.
【23】 在英译本中,等式右边e的指数,是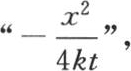 这显然与这里的叙述不符。此处是依法文《文集》本订正的。——汉译者
这显然与这里的叙述不符。此处是依法文《文集》本订正的。——汉译者
【24】 在英译本和法文《文集》本中,这句话都是“因而用kt或者是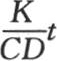 代替t”。但是这似乎与这里所要表达的意思相反,故作如上改动。——汉译者
代替t”。但是这似乎与这里所要表达的意思相反,故作如上改动。——汉译者
【25】 在英译本中,V的值不含“b”,即为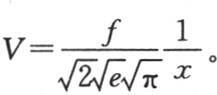 英译者弗里曼在此处对此给了一个脚注:“见第388目的方程(D)和(C),令b=1。”由此可推知,在1822年的法文本中,此式也不含“b”。但是,法文《文集》本中有。虽然弗里曼的“令b=1”没有错,因为前页已交待“b的长为一个计量单位”,但似乎不如直接在式中加上“b”更好。因此,此处从法文《文集》本译出。——汉译者
英译者弗里曼在此处对此给了一个脚注:“见第388目的方程(D)和(C),令b=1。”由此可推知,在1822年的法文本中,此式也不含“b”。但是,法文《文集》本中有。虽然弗里曼的“令b=1”没有错,因为前页已交待“b的长为一个计量单位”,但似乎不如直接在式中加上“b”更好。因此,此处从法文《文集》本译出。——汉译者
【26】 法文《文集》本的编者M. 加斯东·达布在此给出了如下一个脚注:
如果在这个精确表达式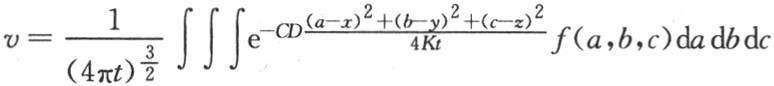 中,我们相对于t求导,那么我们得到
中,我们相对于t求导,那么我们得到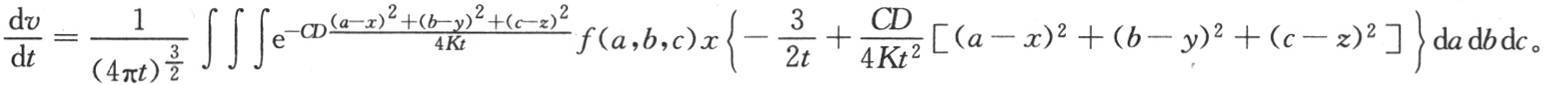 为了确定上述设想,假定初始温度f(a,b,c)总是正的。前面的积分不会为0,所以因式
为了确定上述设想,假定初始温度f(a,b,c)总是正的。前面的积分不会为0,所以因式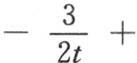
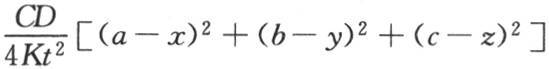 在这些积分区间内反号,因此,对于原来被加热的六面体内的一个内点(ξ,η,ζ),它们相互抵消。因此我们得到t的值
在这些积分区间内反号,因此,对于原来被加热的六面体内的一个内点(ξ,η,ζ),它们相互抵消。因此我们得到t的值 在点(x,y,z)是无穷远的情况下,它显然变得与x2 +y2 +z2 成正比。——汉译者
在点(x,y,z)是无穷远的情况下,它显然变得与x2 +y2 +z2 成正比。——汉译者
【27】 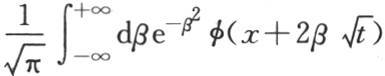 和
和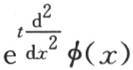 (见第401目)这两种形式的等价性的一个直接证明由格莱舍先生在1876年6月的《数学通信》(Messenger of Mathematics)第30页中给出。用泰勒定理展开
(见第401目)这两种形式的等价性的一个直接证明由格莱舍先生在1876年6月的《数学通信》(Messenger of Mathematics)第30页中给出。用泰勒定理展开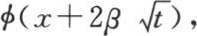 分别对每一项积分;含
分别对每一项积分;含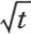 的奇次幂的项变成0,这样我们有第二种形式;因此第二种形式等价于
的奇次幂的项变成0,这样我们有第二种形式;因此第二种形式等价于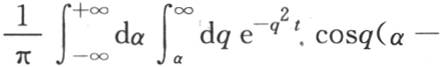
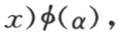 由此,第一种形式可如上导出。因此我们有第330页的傅立叶定理的一个稍微一般化的形式。—A. F.
由此,第一种形式可如上导出。因此我们有第330页的傅立叶定理的一个稍微一般化的形式。—A. F.
【28】 法文《文集》本的编者M. 加斯东·达布在此处加了一个如下的脚注:或者更好地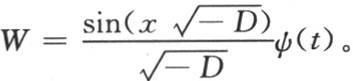 ——汉译者
——汉译者
【29】 法文《文集》本的编者在此处再次加了一个和前面类似的脚注:或者同样地 ——汉译者
——汉译者
【30】 法文《文集》本的编者在此处再次加了一个如下的脚注:或者再一次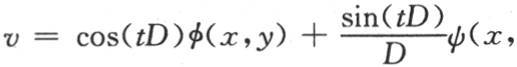
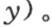 ——汉译者
——汉译者
【31】 在法文《文集》本中,此方程等号右边各项的符号是正负相间的,即m=ap2 -bp4 +cp6 -…。同样,在本目下面所给的v值中亦如此。——汉译者
【32】 就一根细弹性杆的横向振动而对一般方程所进行的研究,可以在唐金的《声学》第9章§§167—177中找到,(d)是其中的一个特例,它与无永恒内张力对应,同时还省略了杆的截面的角运动。——A. F.
【33】 从第360目所给出的已知结果,即——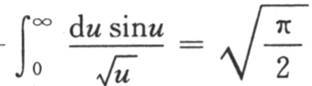 推出更容易。设
推出更容易。设 这时
这时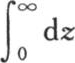
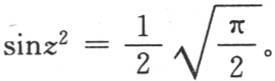 并且
并且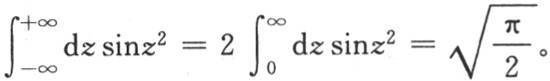 余弦亦可从
余弦亦可从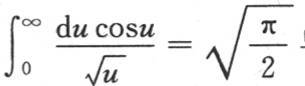 导出。——R. L. E.
导出。——R. L. E.
【34】 方程右边的系数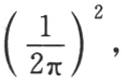 在法文《文集》本中,是
在法文《文集》本中,是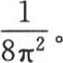 下面W的表达式中的这个系数,亦有这样的差别。——汉译者
下面W的表达式中的这个系数,亦有这样的差别。——汉译者
【35】 在法文《文集》本中,u的表达式是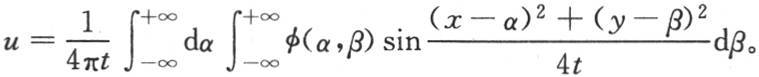 因为英译本中第二个积分式中有因子
因为英译本中第二个积分式中有因子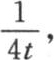 所以,两者相差
所以,两者相差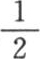 倍。——汉译者
倍。——汉译者
【36】 见W. 汤姆森爵士的论文“论线性热运动”(On the Linear Motion of Heat),第二部分,第1目,《剑桥数学学报》,第3卷,第206—208页。——A. F.
【37】 英译本是说“424”目。此处依法文《文集》本订正。——汉译者
【38】 此方程第二个等式右边的第二个积分号由两个项的差,在英译本中,是两个项的和,即: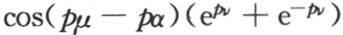
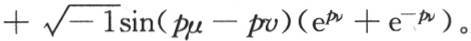 此处依法文《文集》本订正。相应地,我们也对下面ψ的值,也添加了负号。——汉译者
此处依法文《文集》本订正。相应地,我们也对下面ψ的值,也添加了负号。——汉译者
【39】 英译本中,u值的积分号前的常数是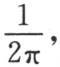 但根据前页φ和ψ的值,它应是
但根据前页φ和ψ的值,它应是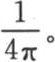 此处依法文《文集》本订正。事实上,把f(x)的值中的
此处依法文《文集》本订正。事实上,把f(x)的值中的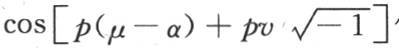 化积,并把化积后的
化积,并把化积后的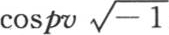 和
和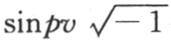 变换成指数式,则它们有一共同的因子
变换成指数式,则它们有一共同的因子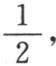 因而f(x)的值中原来的
因而f(x)的值中原来的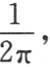 就变成
就变成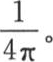 ——汉译者
——汉译者
【40】 这个日期不准确。这份研究报告是在1818年6月8日宣读的,根据它所给出的一个摘要,发表在《科学普及协会通报》上,1818年9月,第129—136页,标题为《关于波动和弹性表面振动的注记》(Note relative aux vibrations des surfaces élastiques et au mouvement des ondes),傅立叶先生著。研究报告的宣读还可以从《科学院1818年成果摘要》(Analyse des travaux de l'Académie des Sciences pendant l'année 1818)(第14页)上看到。根据泊松的一个注记,除摘要外,这份研究报告从未以别的形式发表过,泊松的这个注记在他的研究报告《偏微分方程》(Sur les équations aux différences)第150—151页上,此报告被收入《科学院研究报告》,第3卷(1818年),巴黎,1820年。傅立叶先生题为《论弹性表面的振动的研究报告》(Mémoire sur les vibrations des sur faces élastiques)在这个《摘要》的第14页给出。“对几个偏微分方程积分以及由这些积分导出这些方程所指的物理现象的知识”这一课题,在《通报》的第129页提到。——A. F.
【41】 在英译本中,此方程是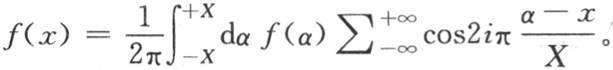 同第418目对方程(A)的订正一样,这里是根据法文《文集》本订正的。——汉译者
同第418目对方程(A)的订正一样,这里是根据法文《文集》本订正的。——汉译者
【42】 《科学院研究报告》,第10卷,巴黎,1831年,第119—146页,载有傅立叶的《关于超越方程代数分析原理应用的一般注记》(Remarques généralcs sur l'application des principes de l'analyse algébrique aux équations transcendantes)。作者表明:secx=0的虚根不满足方程tanx=0,因为对于它们, 方程tanx=0仅由sinx=0的根所满足,这些根都是实根。还可表明secx=0的虚根不满足方程x-mtanx=0,此处m小于1,不过这个方程恰好由方程f(x)=xcosx-msinx=0的根所满足,这些根都是实根。因为,如果fr+1 (x),fr (x),fr-1 (x)是f(x)的三个连续微分系数,那么,使fr (x)=0的x值就使fr+1 (x)和fr-1 (x)的符号相异。因此,根据与f(x)极其连续导数的符号变化数目有关的傅立叶定理,f(x)不可能有虚数。——A. F.
方程tanx=0仅由sinx=0的根所满足,这些根都是实根。还可表明secx=0的虚根不满足方程x-mtanx=0,此处m小于1,不过这个方程恰好由方程f(x)=xcosx-msinx=0的根所满足,这些根都是实根。因为,如果fr+1 (x),fr (x),fr-1 (x)是f(x)的三个连续微分系数,那么,使fr (x)=0的x值就使fr+1 (x)和fr-1 (x)的符号相异。因此,根据与f(x)极其连续导数的符号变化数目有关的傅立叶定理,f(x)不可能有虚数。——A. F.
【43】 参见作者在《科学普及协会通报》(1818年,第1—11页)中所给出的这个研究报告概要的第11节。——A. F.
【44】 参见第11页脚注5所指的研究报告。——A. F.
【45】 在英译本中,这个词是“This motion”(这个运动),但是在法文《文集》本中,则是“Cette notion”(这个概念,或者,这个观念)。按英译本,也可以译作“这个动机”,但更有可能的是,英译本误把“notion”当做了“motion”。——汉译者
【46】 牛顿在他的《热度温标》(Scala graduum caloris et frigoris)[《哲学会报》(Philosophical Transactions),1701年4月,或卡斯蒂略谬(Castillioneus)编,《作品》(Opuscula),第二卷]的文未暗示道,当一个铁盘在均匀流动的恒温气流中冷却时,在相等时间内有相等量的空气与这块金属接触,并且带走与这块铁的温度超过空气温度的超出量成正比的热;由此可推出这块铁的超出温度形成一个几何级数,如他所说,这个几何级数常常以算术级数出现。通过把不同物质放在这块受热的铁上,当这块铁冷却时,他得到这些物质的熔点。
阿蒙通在他的《关于从1701年的哲学会报上摘录的热度表的注记》(Rémarques sur la Table de degrés de Chaleur extraite des Transactions Philosophiques 1701,《科学院研究报告》,巴黎,1705年,第205—206页)中说,他沿一根一端加热至白热的铁棒把牛顿实验过的这些物质放在适当的点上面得到它们的熔点;但是他对温度沿棒而下降的定律作了一个错误的假定。
在《高温学》(Pyrometrie,柏林,1779年,第185—186页)中,兰贝特把牛顿计算的温度和阿蒙通测定的距离合并,发现一端受热的长棒中的温度的实验定律。兰贝特的著作包含对直至今日的热量测量进展的最完整的论述。
毕奥,《矿物学报》(Journal des Mines),巴黎,1804年,第17卷,第203—244页。拉姆弗德,《科学院研究报告》(数理科学),第6卷,巴黎,1850年,第106—122页。
埃里克森(Ericsson)在《自然》(Nature)第6卷第106—108页叙述了一些真空中的冷却实验,对于从华氏10℃到100℃的有限范围的超出温度,它表明非常接近于牛顿的气流中的冷却定律。这些实验不足以怀疑杜隆和珀蒂(《综合工艺学校学报》,第11卷,或者是《物理学和化学年鉴》,1817年,第7卷)从他们精心设计的更广泛的实验所导出的真空中的冷却定律。但是,埃里克森用设计精巧的量热计所做的关于铁水辐射力的一些其他实验(《自然》,第5卷,第505—507页)似乎表明,对于真空中的冷却,杜隆和珀蒂的定律完全不能应用于大气中辐射热的超高温物质,尽管对于这样的条件他们的定律简化成前一个定律。
傅立叶在他《关于辐射热的物理理论的若干问题》(Questions sur la théorie physique de la Chaleur rayonnante,《物理学和化学年鉴》,1817年,第6卷,第298页)中曾发表过一些关于牛顿冷却定律的注记。他区分了表面传导和向大气的辐射。
牛顿在《热度温标》中的原始论述是“Calor quemm ferrum calefactum corporibus frigidis sibi contiguis dato tempore communicat, hoc est Calor, quem ferrum dato tempore amittit, est ut Calor totus ferri”(加了热的铁在一定时间之后能把这热传给附近的物体,这就是说铁在一定时间之后会失热,而这失去的热好像是铁的全部热一样)。这假定这块铁是完全可导的。并且周围物质处于0度。和前面一样,这只能由他后来的解释来说明。——A. F.
【47】 《科学院研究报告》,第5卷,第204—208页。1811年提交。——A. F.
【48】 见《科学院研究报告》,第12卷,巴黎,1833年,第515—530页。
除一种不可压缩流体的运动的这三个普通方程和相对于在一个分子的温度为θ,在时间t经过点x,y,z的速度沿其方向为u,v,w的直交轴的连续方程之外,傅立叶还得到方程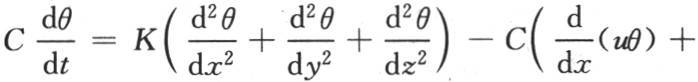
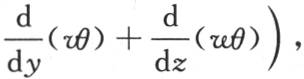 如下所述,其中K是热导率,C是每单位体积的比热。
如下所述,其中K是热导率,C是每单位体积的比热。
如果流体是静止的,那么由传导所流过下表面∆x∆y而进入其对顶隅角为(x,y,z),(x+∆x,y+∆y,z+∆z)的平行六面体的热量在时间∆t内就是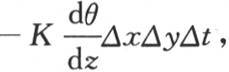 对流产生的增益是+Cw∆x∆y∆t;上表面∆x∆y有一个相应的损耗;因此整个增益呈负数,是
对流产生的增益是+Cw∆x∆y∆t;上表面∆x∆y有一个相应的损耗;因此整个增益呈负数,是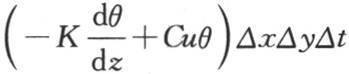 相对z的变分,即增益等于
相对z的变分,即增益等于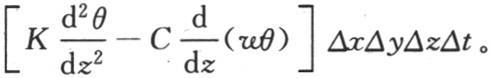 沿y和z方向的增益由两个类似的表达式表示;三个式子的和等于
沿y和z方向的增益由两个类似的表达式表示;三个式子的和等于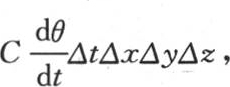 它是在时间∆t内在体积∆x∆y∆z中的增益:因此有上面的方程。
它是在时间∆t内在体积∆x∆y∆z中的增益:因此有上面的方程。
系数K和C随温度和压力而变化,不过它们通常被看做是常数。即使对于所谓的不可压缩流体,密度也服从于微弱的温度变分。
可以注意到,当速度u,v,w为0时,这个方程就转化成关于固体中的热流量的方程。
还可以注意到,当K小到足以可以忽略不计时,这个方程的形式和连续方程相同。——A. F.
【49】 穿透性和渗透性,在傅立叶的第一个例子中,对于铸铁的情况,由对环的永恒温度和对球的变化温度的实验来确定。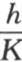 的值由第110目的方法确定,h的值由第297目的方法确定。《科学院研究报告》,第5卷,第165、220和228页。——A. F.
的值由第110目的方法确定,h的值由第297目的方法确定。《科学院研究报告》,第5卷,第165、220和228页。——A. F.
【50】 第78页的脚注给出了福布斯实验的文献。——A. F.
