第6章　非平衡涨落

大数定律的破缺

量子力学引起如此巨大兴趣的一个理由是在微观世界的描述中引进了概率的因素。如我们在第3章中所看到的，量子力学中的物理量是采用非对易算符来表示的。这就导致著名的海森伯测不准关系。很多人已经看到，这些关系证明了在量子力学所适用的微观水平上，决定论是不成立的。这是一个还需要作某些阐明的说法。

像我们在第3章的“量子力学中的时间变化”一节中强调的那样，量子力学的基本方程——薛定谔方程和经典运动方程一样是决定论的。在海森伯测不准关系有效的意义下，并不存在涉及时间和能量的不确定关系。一旦知道波函数在初始时刻的值，按照量子力学，我们能够计算出它在一切时刻（不论是过去或将来时刻）的值。然而量子力学在微观世界的描述中，的确引进了基本的概率要素。不过宏观的热力学描述通常只处理平均值，量子力学所引进的概率因素并不起作用。因此，特别有兴趣的是：在与测不准关系无关的宏观系统中，涨落和概率起着本质性的作用。这一情形可以期望在分支点附近得到，在那里，系统必须选取可能出现分支中的一支，这就是我们在这一章中将要较详细分析的统计因素。我们想要指出：在分支点附近实质上是处理大数定律的破缺（关于概率论的介绍见Feller，1957）。

在宏观物理学中，涨落一般起着较小的作用，因为当系统充分大时，它们作为可以忽略的小的修正而出现。然而在分支点附近，它们起着实质性的作用，因为在那里是涨落驱动平均值。这正是我们在第4章引进通过涨落达到有序的观念的意义。

有趣的是它导致化学动力学的未曾预料到的方面。化学动力学是一个有将近一百年历史的领域，通常是用我们在第四、第5章研究过的速率方程来陈述。它们的物理解释是十分简单的：热运动导致粒子间的碰撞，多数粒子是弹性的，即它们改变平移动能（如果考察多原子分子，还有旋转能和振动能）而不影响电子结构。然而这些碰撞的一部分是活性的，而且产生新的化学种类。

在这个物理图像的基础上，人们可能期望在X分子与Y分子之间的碰撞总数将正比于它们的浓度，并且非弹性碰撞数也是这样。自从这个观念形成以来，它一直统治着整个化学动力学的发展。然而，在随机发生碰撞的图像中出现的如此混乱的状态，为什么还能产生协调的结构呢？自然，某些新特征必须考虑，这个特征就是，反应粒子的分布在接近不稳定时不再具有随机性。这个新特征直到最近才被包括在化学动力学之中，不过可以期望在最近几年中将有更大的进展。

在我们谈论大数定律破缺之前，先简单地解释一下这个定律。为此我们考察一下泊松分布，它是在很多科技领域中具有巨大重要性的一个典型的概率分布。我们考察取整数值的变量X，X＝0，1，2，…。当X遵从泊松分布时，X的概率由

给出。这个规律在很多情形中是成立的，例如电话呼叫的分布，餐馆等待时间的分布，在给定浓度的媒质中粒子涨落的分布。在式6.1中，〈X〉表示X的平均值。

泊松分布的一个重要特征是分布中仅含一个参数〈X〉，概率分布完全由它的平均值决定。式6.2给出的高斯分布便不是这样，除了平均值〈X〉以外，它还包含弥散度σ，

由概率分布函数，我们容易得到所谓的“方差”，它给出相对于平均值的弥散度

泊松分布的特征是它的方差与平均值相等

让我们考察X，它是与（给定体积中）粒子数N或体积V本身成比例的广延量，于是得到相对涨落的著名的平方根律：

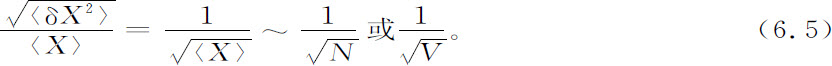
相对涨落的数量级反比于平均值的平方根。因此，对于数量级为N的广延量，它的相对偏差的数量级为N^-1/2 。这是大数定律的本质特征。作为它的结果，我们可以忽略大系统的涨落而用宏观描述。

对于其他概率分布，方差不再像式6.4那样等于它的平均值。但是只要大数定律能应用，方差的数量级仍然是一样的，并且有

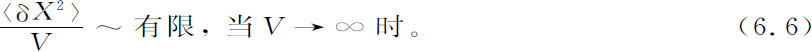
在式6.2中，我们也可以引进一个变量x，它是一个“强度”量，即它不随系统容量的增加而增加（例如压力、浓度或温度）。应用式6.6，这类强度变量的高斯分布就变成

这表明强度变量相对于它的平均值的最可能的偏差具有V^-1/2 的数量级，因而当系统扩大时，偏差将变小。反之，强度变量的大涨落仅能在小系统中发生。

这些议论将要通过今后考察的例子加以阐解。我们将看到自然界如何经常提供某些精妙的途径，通过适当的核化过程避免了分支点近旁的大数定律结果。

化学博弈

为了将涨落考虑在内，就必须离开宏观层次。然而进入经典力学或量子力学实际上是离开了这个问题。此时，每一化学反应将都变成复杂的多体问题。因此，考虑一种中间层次是有益的，这与第1章我们研究随机游动问题时所考虑的东西有些类似。

基本观念是单位时间的转移概率的存在。再次考查在位置k及时刻t找到布朗粒子的概率W（k，t）。引进转移概率ω_lk ，它给出（每单位时间内）在“态”k及l之间进行一次转移的概率。然后我们可以将W（k，t）对t的变化率表成由转移l→k决定的“得”项与由转移k→l决定的“失”项的差，这样我们得到基本方程

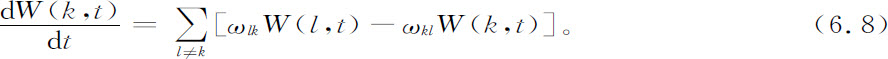
在布朗运动问题中，k相当于阵点的位置，而ω_kl 仅在k与l相差一单位时才不等于零。但方程6.8更为一般。事实上，它是马尔可夫过程的基本方程，在概率论的近代理论中起着重要的作用（Barucha-Reid，1960）。

马尔可夫过程的本质特征是转移概率ω_kl 仅包含两个态k及l。由k→l的转移概率不依赖于在占据态k以前曾经占据的态。在这个意义下系统是无记忆的。马尔可夫过程已经用来描述很多物理现象，而且也能用来描述化学反应。例如，考虑单分子反应的简单链

宏观动力方程在前面的第四、第5章已经引进过（在此我们写出动力常数），即

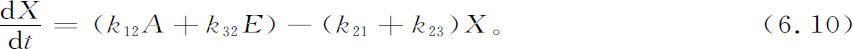
如前，假定A和E的浓度已给定，则相应于式6.10的定态是

在这个标准的宏观描述中，涨落被忽略了。为了研究它的影响，我们引进概率分布W（A，X，E，t）并且应用一般表达式6.8。结果是

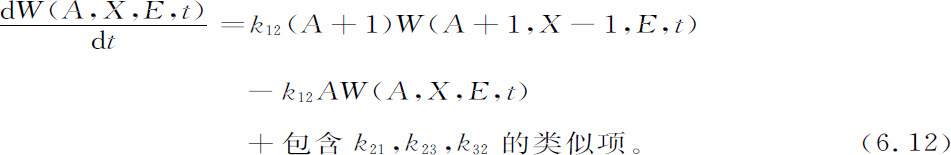
我们来讨论前两项。第一项是得项，它相应于由A粒子的个数是A+1而X粒子的个数是X-1的态到态A，X的转移，其中单个A粒子以速率k12进行分解。另一方面，第二项是失项，开始粒子处于A，X，E的态，通过一个A粒子的分解而达到新态A-1，X+1，E。所有其他的项有类似的意义。

这个方程对平衡态及非平衡态都能解出，结果是一个带有作为X平均值表达式6.11的泊松分布。

这个结果相当圆满，并且似乎是这样的自然，以致有时我们相信这个结果能推广到一切化学反应而无论反应的机制如何。但是却有一个新的意外因素出现了。如果考查更一般的化学反应，相应的转移概率是非线性的。例如，应用前面用过的证据，相应于反应步骤A+X→2X的转移概率正比于（A+1）·（X-1），它是非弹性碰撞以前的A粒子与X粒子的个数的乘积。于是相应的马尔可夫方程也是非线性的。非线性可以说是化学博弈的明显特征，这与转移概率为常数的随机游动形成了对照。使我们惊奇的是这个新的特性导致了对泊松分布的偏差。这个值得注意的结果已经引起广泛的兴趣，它是由我和尼科利斯证明的（Nicolis，Prigogine，1971；也可见1977）。由宏观动力论有效性的观点来看，这些偏差是很重要的。我们将看到宏观的化学方程仅当对泊松分布的偏差可忽略时才是有效的。

作为例子，假设有化学反应步骤2X→E，其速率常数为k。由马尔可夫方程6.8，可以导出X的平均浓度对时间的变化率。可以得到

事实上，我们不得不从X个分子中依次取两个分子。注意

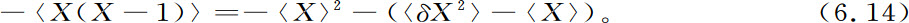
式中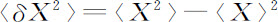 。对于泊松分布，按照式6.4，第二项应等于零，于是我们回到了宏观的化学方程。

这个结果是很一般的。我们看到，在微观层次与宏观层次之间的转换中，对泊松分布的偏差起着实质的作用。通常我们可以忽略它们，例如在式6.13中，我们看到第一项与〈X〉同量级，即它正比于体积。而第二项与体积无关。因此，在大体积的极限中，我们可以忽略第二项。但是如果对泊松分布的偏差不像由大数定律所预测的那样正比于体积，而是正比于体积的高阶量，那么整个宏观的化学描述就被破坏了。

有趣的是将化学动力学看成一定意义下的平均场理论，就像其他许多经典物理学和经典化学的理论，例如态方程理论（范德瓦耳斯理论），磁学理论（外斯场）等等那样。我们由经典物理学知道，除了相变区附近的情况以外，这种平均场理论都将得出自洽的结果。这个发端于卡丹诺夫（Kadanoff）、斯威夫特（Swift）、威尔逊（Wilson）等人的理论依据的是研究在相变临界点附近出现的长程涨落的巧妙思想（Stanley，1971）。涨落的标度变得如此之大，以致分子的细节不再起作用。我们考虑的情形与此颇为类似。

我们希望，通过取热力学极限（即粒子数和体积趋于无穷大，但密度保持有限）和给主方程以长标度不变性，找到宏观系统非平衡相变的条件。从这些条件出发，我们应该能明确地估计出相变区附近涨落变化的方式。对于非平衡系统来说，能做到这一点的目前还仅限于主方程的一个简单模型，即福克-普朗克方程（Dewel，Walgraef，Borckmans，1977）进一步的工作还在进行中。

现在我们来详细地考察大数定律不成立的简单例子。

非平衡相变

施勒格尔研究了下列化学反应序列（Schlögl，1971，1972；Nicolis，Prigogine，1978）：

按照常用的方法，容易得出宏观动力方程

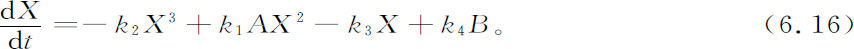
经过适当的标度并引进下列记号及假定：

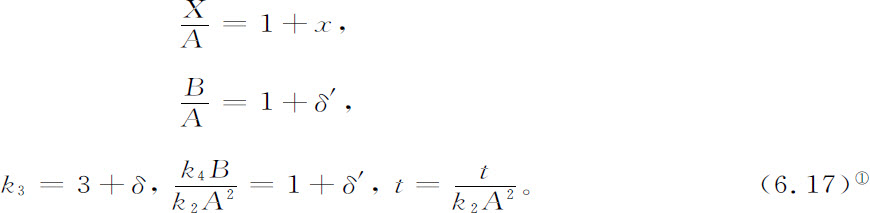
①　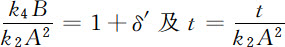 两式原书印刷时遗漏，现据作者手稿补正。——译者注。

方程6.16化成

于是定态由三阶代数方程

给出。有兴趣的是这个三阶方程与人们熟悉的另一方程同构，后者是用范德瓦耳斯理论描述平衡相变得到的。当沿直线δ＝δ′（图6.1）追随系统的演化时，我们看到对δ为正数的情形，方程6.19只有根x＝0而对δ为负数，有三个根

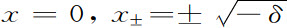
（记住x表示浓度，必须是实数）。这个模型足够地简单，以致能通过马尔可夫理论确切地得到方差（Nicolis，Turner，1977a和b）。当由正值趋于点δ＝0时，我们得到

该式两边当δ→0时均发散，这表明在由式6.6确定的含意下，大数定律的破缺。在系统可由根x₊ 跳到根x_- 的那些点上，这个破缺特别明显，正如在通常的相变中由液态变到气态那样。在这类点上，方差的量级变成V² 的量级，即

换句话说，在非平衡相变区附近不再与宏观描述相一致，涨落和平均值一样重要。

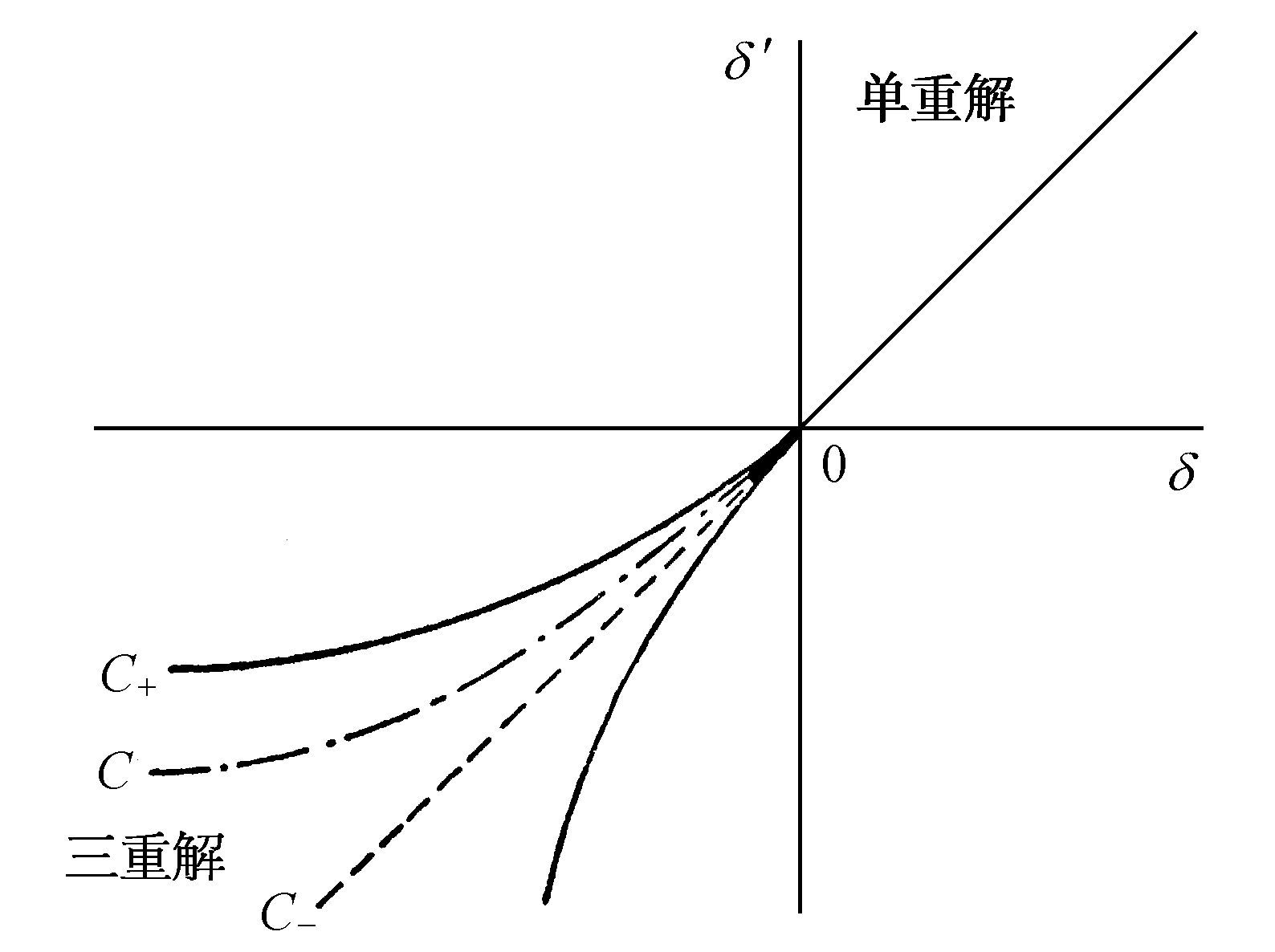
图6.1　用参数δ及δ′代表的方程6.19的解的性态C＝多重定态的共存线。

人们能够证明：在多定态的区域内，概率函数P（x）在V→∞时经历一个深刻的变化。对于任何有限的V，P（x）是一个双峰分布，而峰顶位于宏观的稳定态x₊ 及x_- 。对V→∞，双峰中的每一个都蜕化成δ函数（Nicolis，Turner，1977a和b）。因此，人们得到如下的平稳概率

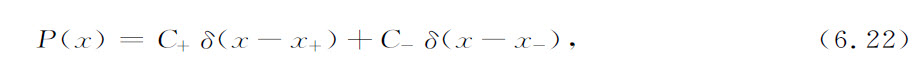
其中x是与X有关的强度变量，x＝X/V。权C₊ 与C_- 的和为1，且明显地由主方程决定。对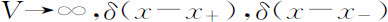 都独立地满足主方程。另一方面，它们的“混合”（式6.22）给出了定态概率分布的热力学极限，而这个定态是先对有限系统算出的。伊辛模型类型的平衡相变的类比是明显的：若x₊ ，x_- 是总磁化强度的值，则式6.22描述在零（平衡）磁化态的伊辛磁体。另一方面，如果在系统的曲面上施加适当的边界条件，“纯态”δ（x-x₊ ），δ（x-x_- ）描述两个持续任意长时间的磁化态。

结论并不像初看时那样使人惊愕。在某种意义上说，甚至连宏观值的概念也失去了它原来的含义。一般来讲，宏观值等于“最可能”值；如果涨落可以忽略，它就恒同于平均值。然而在相变区附近有两个“最可能”值，它们都不对应平均值，而在这两个“宏观”值之间，涨落就成为非常重要的了。

非平衡系统中的临界涨落

在平衡相变情形，临界点附近的涨落不仅有很大的幅度，而且延展到很远。莱默尚德和尼科利斯（Lemarchand，Nicolis，1976）研究了非平衡相变的同一问题。为了使计算成为可能，他们考虑一列箱子，在每个箱中，进行布鲁塞尔器型的反应（式4.57），而且在相邻箱之间有扩散。然后应用马尔可夫方法，他们计算在两个不同箱中X的占据数之间的相关。人们可能预期化学的非弹性碰撞连同扩散会导致一个混乱现象，但是结果并非如此。在图6.2及6.3中，示出了系统在临界态附近和低于临界态时的相关函数。显然可见，临界点附近有长程的化学相关。系统仍然是以一个整体行动而不管化学相互作用的短程特征如何，混乱给出了有序。

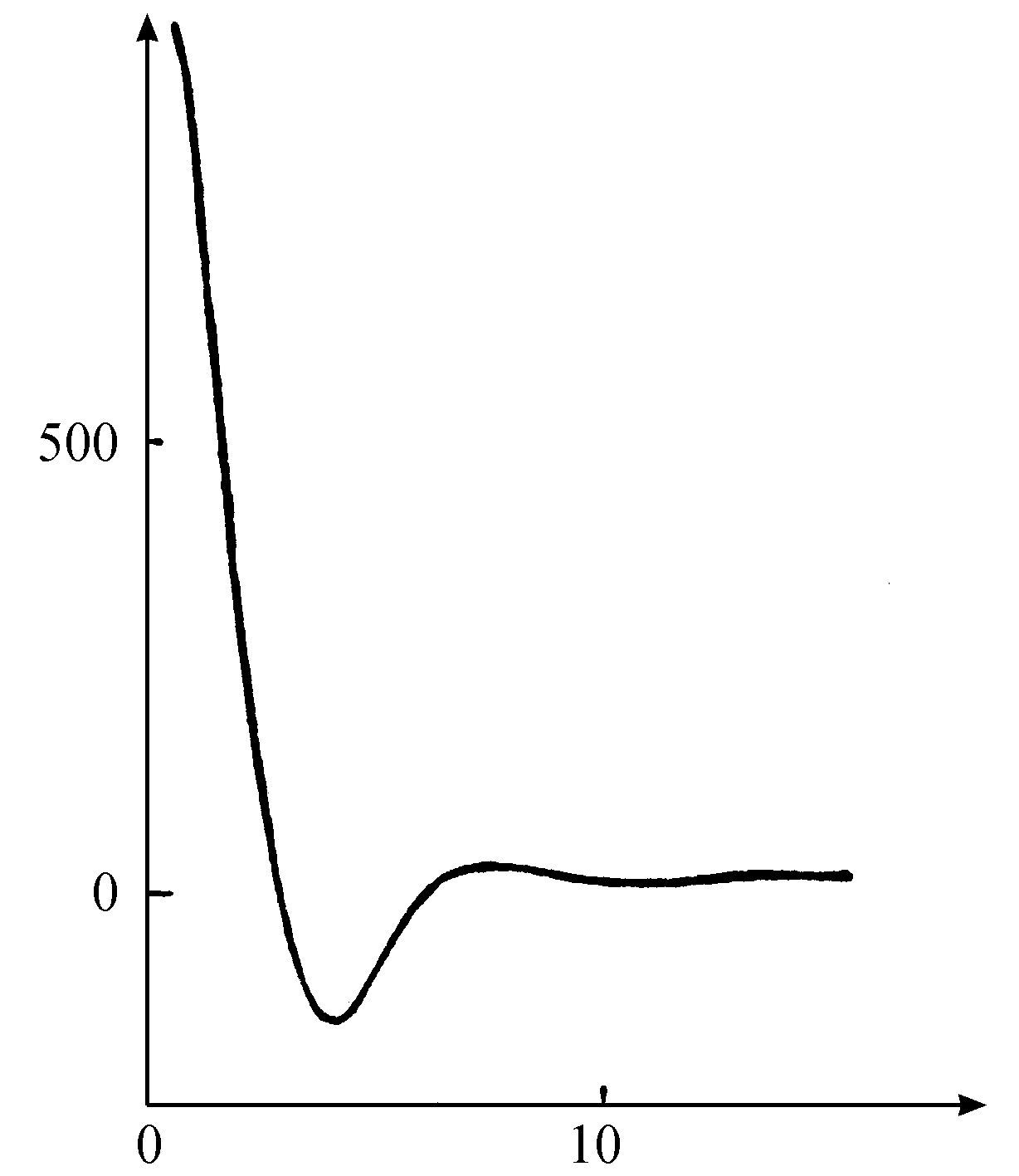
图6.2　相关函数G_ij

第i箱与第j箱的相关函数G_ij 被表示为从i到j的距离的函数。这些箱是被布鲁塞尔器方程控制的，其参数是A＝2，B＝3，D₁ /D₂ ＝1/4，且各箱之间的联系如正文所述。这些参数值使该系统低于临界点，形成一个空间耗散结构。

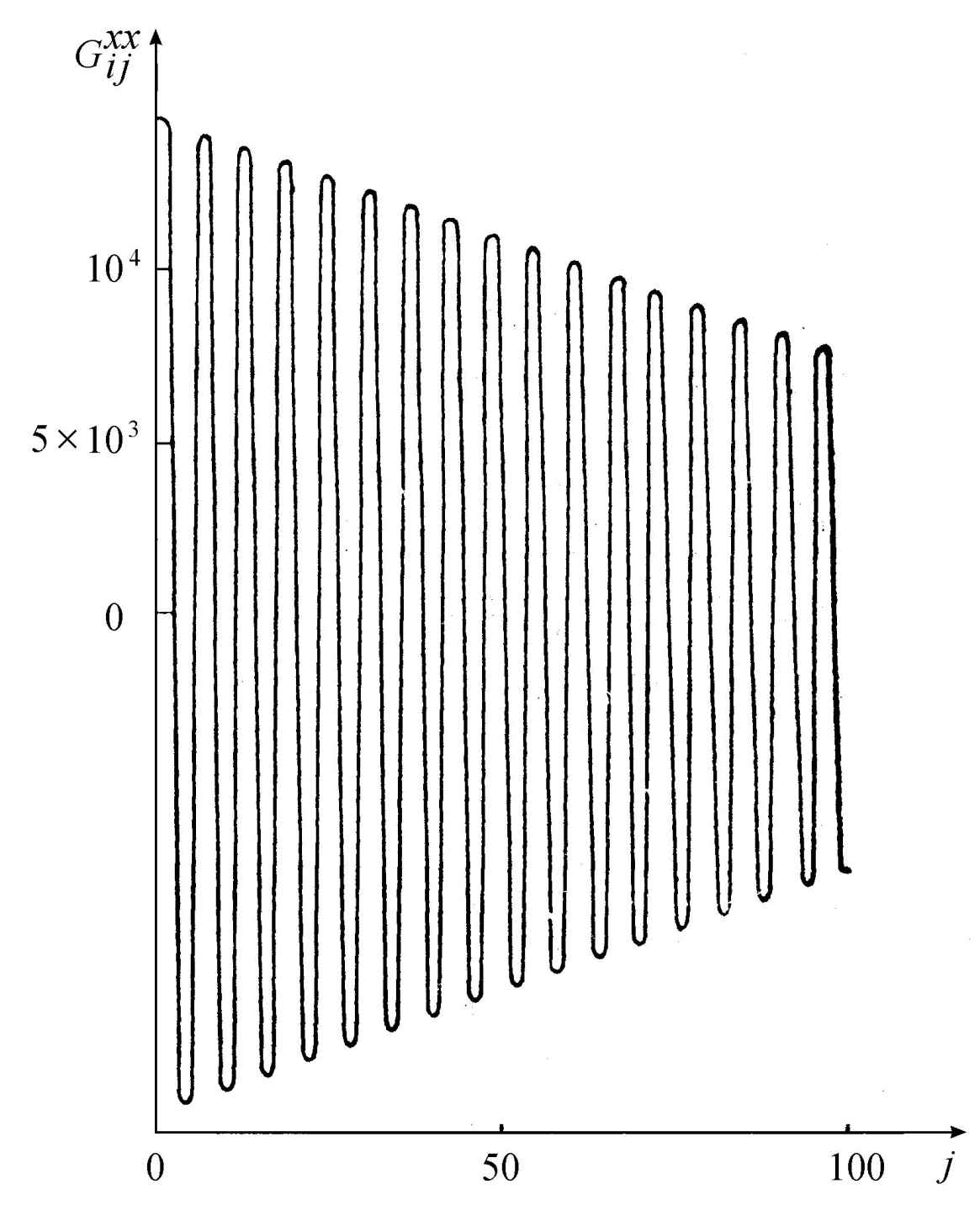
图6.3　空间相关函数的临界性态

参数值与图6.2中的相同，但B＝4。

在这个过程中粒子数起什么作用？这是一个实质性的问题，我们将用一个化学振荡的例子来考查它。

振荡及时间对称破缺

我们前面的考查也能应用到振荡的化学反应问题上。从分子的观点看，振荡的存在是十分出乎意料的。

人们可能首先猜测用少数粒子（比方说50个），比用阿伏伽德罗数10²³ （即通常在宏观实验中涉及的粒子数）可以更容易地得到一个相干振荡过程。但是电子计算机实验表明恰巧相反，仅在粒子数N→∞时，才趋于“长程”时间有序。

为了至少在定性上理解这个结果，让我们作与相变类比的考虑。当我们使顺磁物质变冷，到达居里点，该系统的性态发生变化并变得像一个铁磁体。高于居里点时，一切方向起着相同的作用。而低于居里点时，存在一个与磁化方向一致的优惠方向。

在宏观方程中，没有任何东西可以决定将取哪个磁化方向。在原理上，一切方向都是同样可能的。如果铁磁体包含有限个粒子，这个优惠方向最终将不再继续存在，它将会发生转动。然而，如果我们考虑一个无穷系统，那么没有任何涨落能变更铁磁体的方向，长程有序便一劳永逸地被建立起来。

这种情形非常类似于振荡化学反应。人们能够证明，当系统转向一个极限环时，平稳概率分布也经历一个结构上的改变。它由单峰分布转向集中在极限环上一个火山湖型的曲面上。像在式6.22中那样，当V增加时，火山湖变得越来越陡峭，而在V→∞时，就成为奇异的，而且这里有主方程的一族依赖于时间的解。对任何有限V，这些解导致阻尼振荡，以致唯一的长时间解保持为定态解。直观地看，意义如下：在极限环上的运动的相位起着与磁化方向相同的作用，它是由初始条件决定的。如果系统有限，涨落将逐渐加剧并破坏相位相干性。

另一方面，电子计算机模拟显示当V增加时，依赖时间的图式越来越衰减。因此，人们期望在V→∞时，主方程的依赖时间的整个解族沿极限环旋转（Nicolis，Malek-Mansour，1978）。再者，在直观图景中，这意味着在无穷系统中相位相干性可以保留任意长的时间，恰如特定的初始磁化方向能在铁磁体中保持那样。因此在这个意义上，周期反应的出现是时间对称破缺过程，恰如铁磁性是一个空间对称破缺一样。

对于与时间无关但与空间有关的耗散结构，可以作同样的考察。换句话说，仅当化学方程刚好有效（即当粒子数很大，大数定律可以应用时），我们可以有相干的非平衡结构。

对于第4章使用过的远离平衡条件，一个附加因素是系统的尺度。如果生命的确与相干结构联系着（每一件事都支持这个观点），生命必须是基于很大的自由度的相互作用的一种宏观现象。诸如核酸之类的分子确实起着举足轻重的作用，但是它仅能在具有很大自由度的相干介质中生成。

复杂性的限度

本章所概述的方法可以应用到很多情形。这个方法的一个有趣的特性是它表明涨落的定律显著地依赖标度，这一点十分类似于过饱和气体中的液滴的经典核化理论的情形。在临界尺度（称为“胚胎”尺度）以下，液滴是不稳定的，超过这个尺度，它将长大并使气体变为液体（图6.4）。

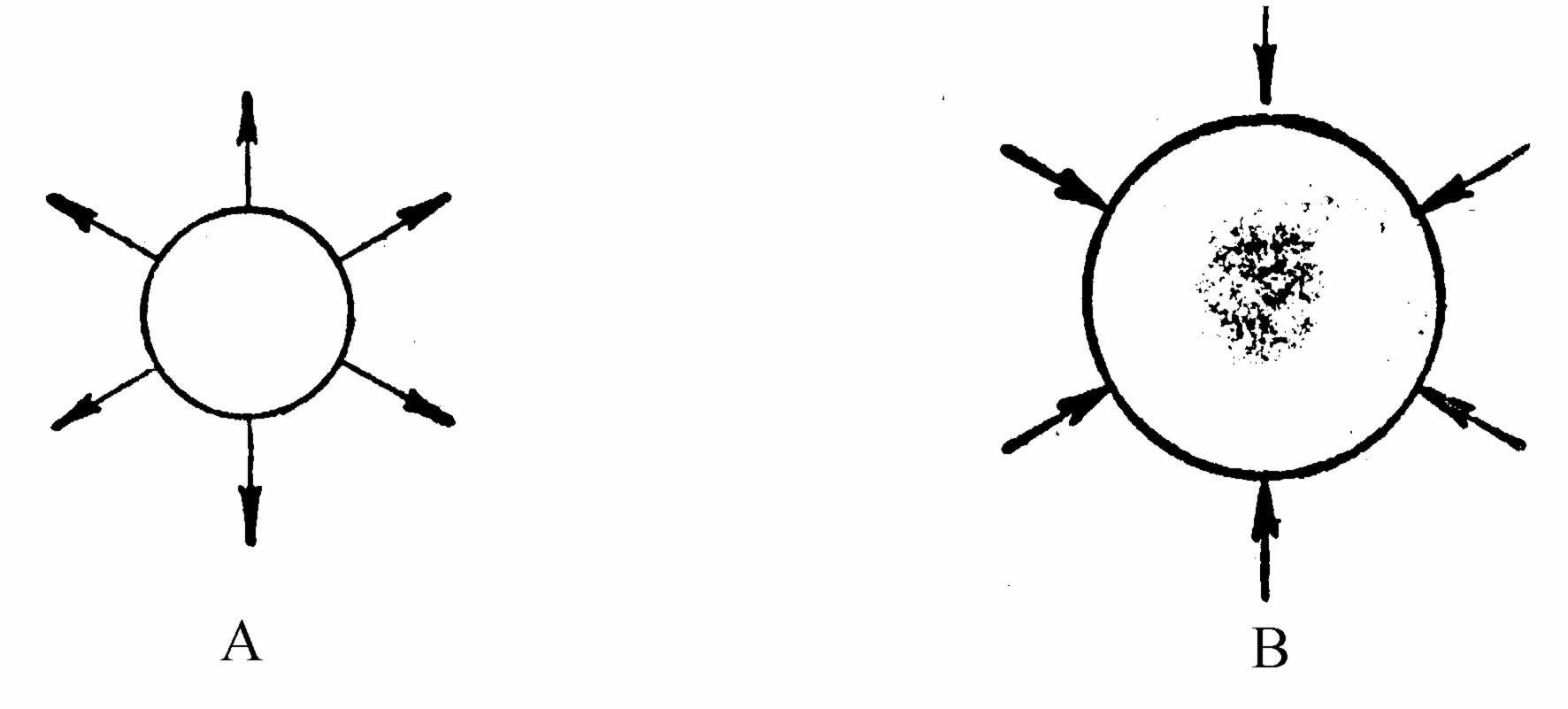
图6.4　过饱和气体中液滴的核化

（A）小于临界尺度的液滴；（B）大于临界尺度的液滴。

这样的核化效应也在任何一种耗散结构的形成中出现（Nicolis，Prigogine，1977）。我们可以写出其主方程

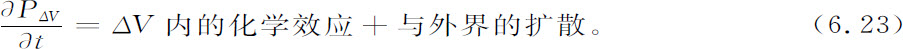
它既考虑到在某一容积ΔV内化学反应的效应，又顾及到通过与外界的交换而产生的粒子迁移。这个方程的形式是很简单的，当计算容积ΔV中平均值〈X² 〉时，人们由式6.2得到两项的和，简式如下：

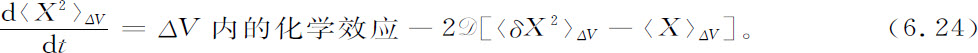
第一项是容积ΔV内的化学效应，第二项是由于与外界的交换，系数 随表面积与体积之比变大而增加。有趣之点是第二项正好包含均方涨落与平均值之差。对于充分小的系统，这将是一个优势项，按照式6.4，分布将变成泊松型的。换句话说，外界通常作为一个平均场而起作用，它通过在扰动区域的边界上发生的相互作用而减弱涨落，这是一个非常一般的结果。在小标度涨落的情形，边界效应将占优势，而涨落将衰退。然而对大标度涨落而言，边界效应可以忽略。在这些极端情形之间，存在着核化的实际尺度。

对于生态学家长期以来所讨论的一个非常普通的问题，即复杂性的限度问题（May，1974）来说，这个结果是有趣的。我们暂时回到第4章阐述过的线性稳定分析，这导致某种色散方程。方程的次数等于相互作用的物种的个数，因此在复杂介质中（例如，一个热带森林或一个现代文明社会）这样的方程的次数肯定是很高的。因此，至少存在一个导致不稳定增加的正根的机会是增大了。然而复杂系统究竟为什么可能存在呢？我相信我们在这里概括的理论给出了解答的开端。方程6.24中出现的系数量度了系统与其周围耦合的程度。我们可以期望：在一个很复杂（即有很多交互作用的物种或分量）的系统中，这个系数以及涨落的尺度都将大到足以引起不稳定。因此我们有如下结论：足够复杂的系统一般是处于亚稳态。阈值既依赖于系统的参数，也依赖外部条件。复杂性的限度不是一个单方面的问题。值得指出的是：在核化过程中通过扩散进行的这种传播作用已在最近进行的核化数字模拟中实现。

环境噪声的影响

至今我们只是讨论了内部涨落的动力学。我们看到由系统本身自发地产生的这些涨落往往变小，除了系统在分支点附近或者在同时稳定的态的共存域中以外。

另一方面，宏观系统的参数——包括大部分分支参数——是被外部控制的量，从而也受到涨落的控制。在很多情形下，人们遇到剧烈起伏的环境，因此可以预期这些被系统作为“外部噪声”接受的涨落能够深深地影响它的性态。这个观点最近在理论上（Horsthemke，Malek-Marsour，1976；Arnold，Horsthemke，Lefever，1977；Nicolis，Benrubi，1976）及在实验上（Kawakubo，Kabashima，Tsuchiya，1978）都建立起来了。看来，环境的涨落不但能影响分支，而且更惊人的是，可以产生不能由唯象的演化律预测的新的非平衡相变。

环境涨落的传统研究是起源于布朗运动问题的朗之万（Paul Langevin）的分析。他的观点是：描述一个可观察量（设为x）的宏观演化的速度函数［设为v（x）］仅给出x的瞬时速度部分。因为周围环境的涨落，系统还受一个随机力F（x，t）的作用，所以x作为一个涨落量而被观察，我们写出

如果在布朗运动中，F反映内部分子间相互作用的效应，人们就要求它依次所取的值在时空上都是无关的。因此，所获得的涨落方差与中心极限定理一致。另一方面，在一个非平衡环境中，涨落剧烈地改变系统的宏观性态。似乎出现这种性态的一个条件是外部噪声以乘法方式作用而不是加法方式作用，即它与态变量x的一个函数耦合着，使得如果x变为零，它就变为零。

作为一个解释，考察下列修改了的施勒格尔模型（见式6.15）：

令一切速率常数等于1，且

唯象方程是：

在γ＝2，有一个稳定的及一个不稳定的定态解，如图6.5所示。而且，x＝0永远是一个解，它在无穷小的扰动下是稳定的。

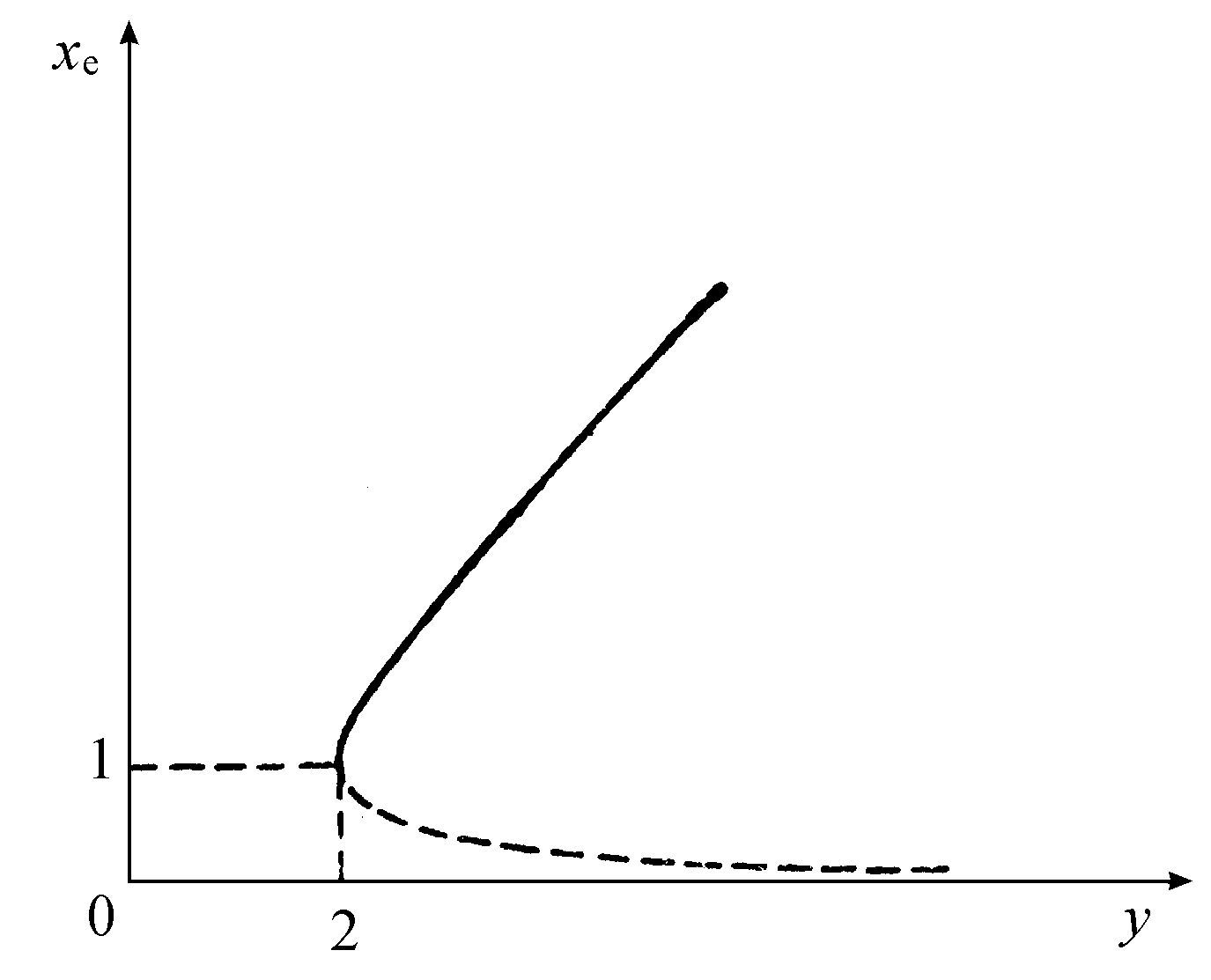
图6.5　方程6.28的平稳解x₀ 与γ的关系

实线表示稳定解，虚线表示不稳定解。

现在将γ看成是一个随机变量。最简单的假设是它对应一个高斯白噪声，正如像在布朗运动问题中一样，我们令

现在我们用一个随机微分方程（Arnold，1973）代替了方程6.28，它是郎之万方程（式6.25）的适当推广，消除了后者的通常陈述中的某些不明确之处。这个方程将噪声与状态变量的二次幂x² 耦合起来了。可以将它与一个福克-普朗克型的主方程联系起来，由此可以算出平稳概率分布。结果，在这个分布中，唯象描述的相变点γ＝2不出现，过程肯定达到零并且随后就停在那儿。

在本节开头所提及的噪声效应的实验工作（Kawakubo，Kabashima，Tsuchiya，1978）中，所作的安排与方程6.28表示的非常类似，只是噪声与一线性项耦合而且在方程6.28中还包括一个常数输入项。正如所证明的，对于方差σ² 的小值来说，系统（参数振荡回路）显示极限环性态。然而，如果方差超过阈限，则振荡性态消失而且系统转入定态体制。

结　　语

现在，我们已经概述了演化的物理学的主要部分。很多意外的结果已经得到，这些结果扩展了热力学的范围。如前所述，经典热力学与初始条件的被忘却以及结构的被破坏有关。我们现在看到存在另外一个宏观的领域，在那里（在热力学的框架之内）结构可以自发地出现。

宏观物理学中的决定论的作用必须重新评价。在不稳定区附近，我们找到导致概率论常用定律破缺的大涨落。化学动力学的一个新观点已经出现。这些发展的一个结果是经典的化学动力学作为一种平均场理论而出现，但是为了描述相干结构的出现，为了描述由混乱中形成有序，我们必须给出一个新的更精细的时间顺序的描述，这种时间顺序引出了系统的时间演化。然而，耗散结构的稳定还需要极大的自由度。这就是为什么决定论描述盛行于多级分支之间的理由。

在最近的几年中，无论存在的物理学还是演化的物理学都有了新的进展。我们可以用某种办法将这两种观点统一起来吗？毕竟大家是生活在同一个世界里，它们的各个方面初看起来尽管不同，但必定有着某种关系。这是我们下面将要讨论的问题。