附录Ⅰ

1977年诺贝尔化学奖颁奖词和讲演词

Appendix I

普里戈金的伟大贡献在于建立了远离平衡状态的非线性热力学理论，这一理论令人满意。他发现了全新类型的现象和结构，如今这种普遍的、非线性的不可逆热力学已奇迹般地在各种领域中得到了广泛的应用。

普里戈金与夫人、儿子在家中（普里戈金夫人提供）。

颁　奖　词

（瑞典皇家科学院斯蒂格·克莱桑教授致词）

曾国屏　译　沈小峰　校

（清华大学教授）　（北京师范大学教授）

伊利亚·普里戈金以他在热力学领域的发现，而荣获本年度的诺贝尔化学奖。热力学作为科学理论是最为错综复杂的一门分科，具有无穷无尽的现实意义。

热力学的历史可追溯到19世纪初叶。主要是由于道尔顿（Dalton）的工作，原子论获得了公认，人们开始普遍接受这样一种观点，即人们所称做热的东西，只不过是物质的最小组分的运动。后来，热机的发明使得人们越来越迫切要求对热和机械功之间的相互作用进行精确的数学研究。

许多卓越的科学家为19世纪热力学的发展作出了贡献，他们的名字不仅将永存于科学史中，而且已被用做重要的单位术语。除了道尔顿以外，还有瓦特（Watt）、焦耳（Joule）和开尔文（Kelvin），他们的名字分别被用来作为原子量、功率、能量和从绝对零点起计算的绝对温标的单位。亥姆霍兹（Helmholtz）、克劳修斯（Clausius）和吉布斯（Gibbs）也做了重要工作，他们采用统计方法探讨了原子和分子的运动，实现了热力学和统计学的综合——我们称做统计热力学。他们的名字已被用来称呼一些重要的自然定律。

这个发展过程在20世纪初叶获得了一些结论，热力学开始被看做其发展基本上已告完成的一门科学分支。不过，它仍然有某些局限，它在绝大部分情况下只能处理可逆过程，也就是通过平衡态而发生的过程。甚至对同时进行热传导和电传导的热偶这种简单的可逆系统，在昂萨格（Onsager）建立起倒易关系以前，也不可能得到满意的处理。昂萨格因而获得了1968年的诺贝尔化学奖。在不可逆过程的热力学的发展中，这个倒易关系是向前迈出的巨大一步，但是，其中预先假设了一种线性近似，只能运用于相对接近平衡的情形。

普里戈金的伟大贡献在于建立了远离平衡状态的非线性热力学理论，这一理论令人满意。他发现了全新类型的现象和结构，如今这种普遍的、非线性的不可逆热力学已奇迹般地在各种领域中得到了广泛的应用。

普里戈金一直着迷于解释这样的问题：有序结构——例如生物学系统——如何能够从无序发展而来。即使是利用昂萨格关系，热力学中经典的平衡原理仍然展示出，接近平衡态的线性 系统总是要发展成无序 状态，这种状态对于扰动是稳定的，无法解释有序结构 的出现。

普里戈金及其助手们却选择这样的系统进行研究，这些系统遵循非线性动力学定律，而且保持与其环境的接触以便能进行能量交换，换言之，就是开放系统 。如果这些系统被驱使而远离平衡，就形成了完全不同的情形，会形成新的系统，它们表现出在时间和空间上都有序，而且它们对于扰动是稳定的。普里戈金已把这些系统称做耗散系统 ，因为它们是通过耗散过程而形成并得以保持的，耗散过程的发生则是由于系统与环境之间的能量交换；这种交换一旦停止，耗散系统也就不复存在了。也可以这样认为，它们在与其环境的共生之中生存。

普里戈金用来研究这种耗散结构对于摄动的稳定性的方法，已引起了普遍的极大兴趣。它使得研究那些变幻无常的问题成为可能，这里仅略举几例，如城市交通问题、昆虫社会的稳定性、有序生物结构的发展以及癌细胞的生长。

在此，值得特别提到的还有三个人，他们协助普里戈金工作多年，其中首先是格兰斯多夫（P．Glansdorff），此外还有莱费尔（R．Lefever）和尼科利斯（G．Nicolis），他们重要的创造性贡献，推动了科学的发展。

这样一来，普里戈金对不可逆热力学的研究已从根本上改造了这门科学，使之重新充满活力；他所创立的理论，打破了化学、生物学领域和社会科学领域之间的隔绝，使之建立起了新的联系。他的著作还以优雅明畅而著称，使他获得了“热力学诗人”的美称。

普里戈金教授，我已尝试简要地勾画出您对非线性不可逆热力学的伟大贡献，现在我怀着愉快的心情，荣幸地向您表示瑞典皇家科学院的最高祝贺，并请您从国王陛下手中接过您的诺贝尔奖。

讲演词

时间、结构和涨落 ⁽¹⁾

伊·普里戈金

郝柏林　于渌　译

（中国科学院院士、第三世界科学院院士）（中国科学院院士）

物理学和化学中的时间（t）问题，与热力学第二定律的表述密切相关。因此，这一篇演说的另一个合适的标题是“热力学第二定律的宏观方面与微观方面”。

热力学第二定律在科学史上起过的基本作用远远超出了它原有的范围。只要指出玻尔兹曼关于气体运动论的工作，普朗克量子论的发现，以及爱因斯坦的自发辐射理论，就足以说明这一点，所有这些成就都是以热力学第二定律为基础的。

这篇演说的主题是我们才处于理论化学和理论物理学新发展的起点，其中，热力学概念将发挥更为基本的作用。由于本论题的复杂性，我在这里主要限于讨论概念问题。概念问题既有宏观方面，又有微观方面。例如，从宏观看，经典力学已经很好地说明了诸如晶体之类的平衡结构。

热力学平衡可由亥姆霍兹自由能的最小值来表征。通常的定义是

式中，E是内能，T是绝对温度，S是熵。是不是我们周围的“组织”形式大多数都具有这样的性质呢？谁只要提出这样一个问题，他就可以知道答案是“不”。显然在一个城市或活的机体中，我们面临着类型颇为不同的功能序。为了得到这类结构的热力学理论，我们必须说明非平衡可能是有序的根源，不可逆过程能导致物质的新型动力状态，我称之为“耗散结构”。我在后面关于熵产生，热力学稳定性和对化学反应的运用各节中，将讨论这类结构的热力学理论。

这类结构对于今天的化学和生物学具有特殊重要性。它们显示出一致的、超分子的特征，在诸如包含酶振荡的生物化学循环中有新奇的表现。

这类一致的结构是怎样作为反应碰撞的结果而出现的呢？后面关于大数定律的一节中将简要地讨论这个问题。我想强调指出，通常的化学动力学相当于“平均场”理论，这理论和范德瓦耳斯状态方程理论或外斯的铁磁理论十分相像。正像这些理论一样，平均场理论在产生新的耗散结构的不稳定点附近失效。这里（像在平衡态理论中的一样）涨落起着重要的作用。

在最后两节中，我将回到微观方面，并评述我们小组在布鲁塞尔自由大学近年来在这方面所完成的工作。这些工作导致了不可逆过程的微观定义。然而，这一步发展只有通过建立一种变换理论才可能实现。这个理论允许人们引入明显地展示出不可逆性和趋向热力学平衡的非么正的运动方程。

引进热力学因素导致（经典和量子）力学的重新表述。这是最令人惊异的一个特点。自从20世纪初以来，我们已经有能力在基本粒子的微观世界或者宇宙尺度的宏观世界中去发现新的理论结构。现在我们知道，甚至在与我们自身属于同一层次的现象中，引入热力学因素也导致新的理论结构。如果我们要建立一套理论方法，其中时间要具有与不可逆性甚至与“历史”相联系的全部涵义，而不仅仅是一个与运动有关的几何参数，那么，引进热力学因素就是必须付出代价。

熵产生

深入到热力学第二定律的核心，我们就看到“可逆”过程与“不可逆”过程的基本差别^[1] 。这最终导致了熵S的引进和热力学第二定律的表述。克劳修斯的经典表述是关于孤立系统的，这些系统与外界既不交换能量，也不交换物质。第二定律只是确认存在着一个函数S，它单调上升，直到处于热力学平衡态才达到最大值，

很容易把这个公式推广到对外界交换能量和物质的系统（图1）。这时我们就必须把熵的变化dS区分为两项，第一项是经过系统边界的熵转移d_e S，第二项是系统内部产生的熵d_i S。第二定律认为系统内部的熵产生总是正值（或零）

图1　系统内外的熵交换

这里在可逆过程和不可逆过程之间有基本差异。只有不可逆过程对熵产生有贡献。显然第二定律表现的正是这样一个事实，即不可逆过程导致时间的单向性。时间的正方向和S的增加相联系。我想强调指出，时间的单向性出现在第二定律中的这种顽强和特殊的方式。这个定律的表述就暗示着存在一个具有特殊性质的函数，即对于孤立系统来说，这个函数只能随时间增加。这类函数在李雅普诺夫（Lyapounov）的经典工作所开创的现代稳定性理论中有重要作用。因此它们被称为李雅普诺夫函数（或泛函）。

对于孤立系统来说，熵是一个李雅普诺夫函数。亥姆霍兹或吉布斯自由能这一类热力学势，也是其他“边界条件”（如给定温度或体积）下的李雅普诺夫函数。

这个系统在所有这些情形下演化到一个平衡态，是由热力学势的存在来表征的。这个平衡态是许多非平衡态的“汇聚点”（attractor）。这是最重要的一个方面，早就被普朗克^[1] 恰当地强调过了。

然而，热力学势只存在于一些例外情形中。方程（3）这个不等式并不包含一个函数的全微分，在一般情形下也就不容许人们作为李雅普诺夫函数的定义。在重新回到这个问题之前，我想着重指出：热力学第二定律建立150年以来，它看来仍然更像一个纲领，而不是在通常意义下解释得很周详的理论，因为关于熵产生没有说出任何明确的东西（除了它的正负号以外）。甚至这个不等式的适用范围仍未确定。这是热力学的应用范围基本上限于平衡过程的主要原因之一。

为了把热力学推广到非平衡过程，我们需要一个对于熵产生的准确表达式。由于假定了甚至在平衡态之外，S也只依赖于在平衡态时的同一些变量，因而在这一方向上取得了一些进展。这就是“局部”平衡假定^[2] 。一旦采纳这个假定，我们就得到单位时间内的熵产生P：

式中，J_ρ 是所包含的各种不可逆过程（化学反应、热流、扩散）的速率，而X_ρ 是相应的广义力（亲和力、温度梯度、化学势梯度）。方程（4）是不可逆过程宏观热力学的基本公式。

我使用了补充假定才推得熵产生的明显表达式（4）。这个公式只能在平衡态的某个邻域内建立^[3] 。这个邻域限定了局部平衡区，在后面关于非么正变换理论的一节中，我还要从统计力学的观点去讨论它。

在热力学平衡态，我们对全部不可逆过程同时有

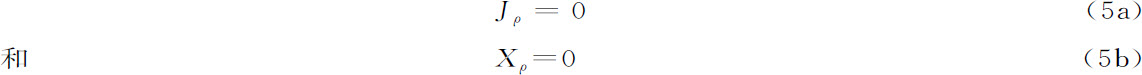
因此，很自然地可以假定，至少在平衡附近，各种流和各种力之间存在着线性齐次关系。这一方案自然而然地包括了许多经验定律，例如热流正比于温度梯度的傅里叶定律，或者扩散流正比于浓度梯度的斐克（Fick）扩散律。这样，我们就得到描述线性不可逆过程热力学^[4] 的以下关系式

线性不可逆过程热力学受到两项重要原理的支配。其一是昂萨格（Onsager）倒易关系^[5] ，它说明

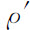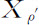当相应于不可逆过程ρ的流J_ρ 受到不可逆过程 的力 影响时，流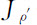 也受到力X_ρ 的影响，而且比例系数也是相同的。

昂萨格关系的重要在于它们的普遍性。它们被许多实验检验过。它们的适用性表明，非平衡热力学和平衡热力学一样，可以导致与任何特殊的分子模型无关的普遍结果。倒易关系的发现，在热力学史上确实是一个转折点。

另一项适用于平衡附近的重要原理是最小熵产生理论^[6] ，它说明对于足够接近平衡的稳态，熵产生达到最小值。与时间有关的态（相应于同样的边界条件）具有更高的熵产生。最小熵产生定理比线性关系式（6）要求更多的限制条件。它只在严格线性的理论框架内适用，这时对平衡态的偏离必须很小，使得唯象的系数L_ρρ 可以看做常数。

最小熵产生定理表达了非平衡系统的一种“惯性”。当规定的边界条件阻止系统达到热力学平衡（即熵产生为零）时，系统就在“耗散最小”的状态安定下来。

自从提出这个定理以后，已经明白，这一性质严格说来只适用于平衡态的邻域。多年来曾经作过很大努力，试图把这个定理推广到离平衡更远的情形。当最后证明远离平衡时热力学行为可能十分不同，事实上甚至与最小熵产生定理背道而驰时，人们才大为惊异。

值得一提的是，这类新型行为出现在早被经典流体力学研究过的一些典型情况中。首先根据这一观点来分析的一个例子是所谓“贝纳尔（Bénard）不稳定性”。考察恒定重力场中两个无穷平面之间的水平液体层。令下平面处于温度T₁ ，而上边界处于温度T₂ ，且T₁ ＞T₂ ，当“逆”梯度（T₁ -T₂ ）/（T₁ +T₂ ）的数值足够大时，静止状态变得不稳定，开始有对流。由于对流提供了新的热输运机制，熵产生也就增大。更有甚者，失稳后出现的流动状态比静止状态更有组织。事实上必须有宏观数量的分子在宏观时间内以一致方式运动，才能显出流动花纹。

这里有一个非平衡可以成为有序的根源这个事实的很好例子。在关于热力学稳定性理论，以及关于对化学反应的运用各节中，我们将看到这一情况并不限于流体力学的情况，而且还在化学系统中出现，可是要对反应律加上一些明确规定的条件。

有趣的是，由正则分布表达出来的玻尔兹曼有序原理，对于贝纳尔对流的产生所赋予的概率几乎是零。每当出现远离平衡的新的一致状态时，包含在组态计数中的概率论观念就要失效。就贝纳尔对流而论，我们可以设想，总有一些小对流作为平均状态附近的涨落出现；但是当温度梯度低于一定临界值时，这些涨落就逐渐衰减以至消失。然而在某个临界值以上，一定的涨落会被放大而引起宏观流动。这样就产生了新的超分子有序，它基本上对应一个由于和外界交换能量而稳定下来的巨大涨落。这就是由产生耗散结构来表征的有序。

在进一步讨论耗散结构的可能性之前，我想评论一下热力学稳定性理论中与李雅普诺夫函数理论有关的若干方面。

热力学稳定性理论

对应热力学平衡的状态，或是线性非平衡热力学中对应最小熵的产生的稳定态，自然都是稳定的。我已经引入了李雅普诺夫函数的概念。按照最小熵产生定理，在平衡周围的严格线性区域内，熵产生确实是这样一个李雅普诺夫函数。如果系统受到扰动，熵产生将增加，但系统的反应是回到熵产生的最小值。

与此类似，对应熵的最大值的封闭平衡态是稳定的。如果我们在平衡值附近扰动这一系统，就得到

式中S₀ 是平衡熵。然而，由于平衡态是最大值，一阶项消失，因而稳定性由二阶项δ² S的符号决定。

格兰斯多夫和普里戈金曾经证明^[3] ，δ² S是在平衡附近与边界条件无关的一个李雅普诺夫函数，用经典热力学可以明确地算出这个重要表达式。我们得到^[3]

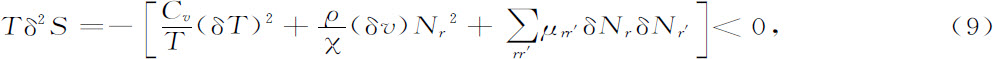
式中，C_v 是定容比热，ρ是密度，v＝1/ρ是比容，（下标N_r 表示v变分时组分保持不变），χ是等温压缩率，N_r 是组分r的克分子份数，而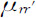 则是导数

式中，p是压力。

吉布斯最早提出的经典热力学基本稳定性条件如下：

这些条件表明δ² S是负二次函数。此外，用初等的计算就可以证明，δ² S的时间导数和P的关系是^[3] （见方程（4））

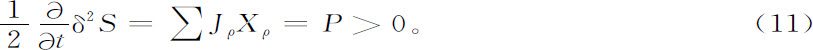
正是因为方程（9）和（11）中的不等号，δ² S才是李雅普诺夫函数。李雅普诺夫函数的存在保证了一切涨落的衰减。基于这种理由，对于平衡附近的大系统用宏观方法进行描述就足够了。涨落只能起次要作用，表现为对宏观定律的修正，而对于大系统则可忽略不计（图2）。

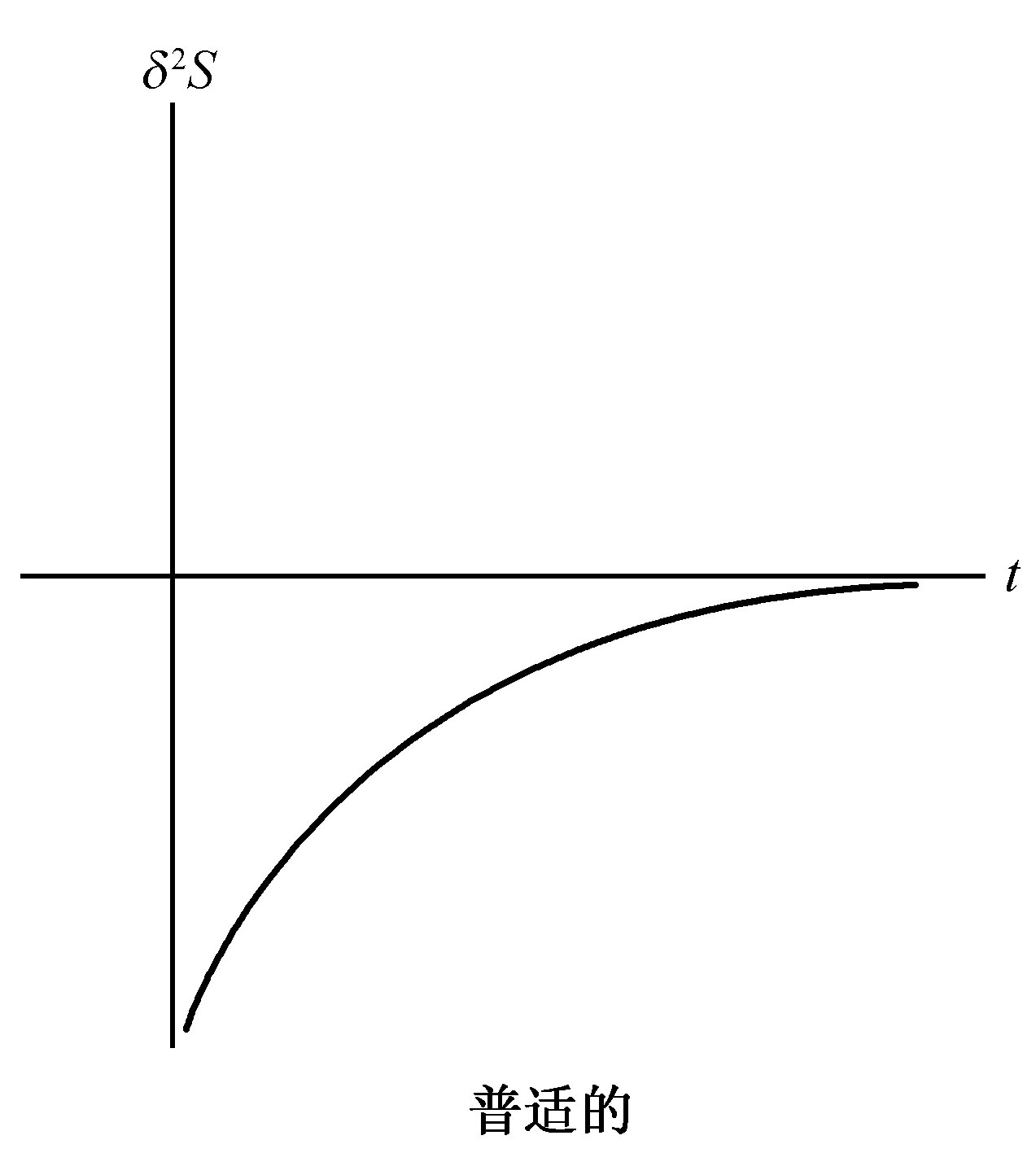
图2　平衡附近二阶盈余熵（δ² S）_eq 的时间演化。

我们现在准备研究下面的基本问题：能否把上述的稳定性外推到离平衡更远的情况？当我们考虑偏离平衡较大但仍然保持宏观描述的框架时，δ² S能否起李雅普诺夫函数的作用？我们围绕一个非平衡态再来计算扰动量δ² S。在宏观描述的范围内（9）式中的不等号仍然成立。然而，δ² S的时间导数不再如同（11）式那样与总的熵产生有关，而只是与这个熵产生的扰动相联系。换言之，我们现在有^[3]

（12）式等号右边就是格兰斯多夫和普利戈金称之为“盈余熵产生”的量。应当着重指出，δJ_ρ 和δX_ρ 是对在定态时的J_ρ 和X_ρ 值的偏离，而我们正通过扰动检验这个定态的稳定性。现在，与平衡或靠近平衡的情况相反，对应盈余熵产生的（12）式等号右边通常并不具有确定的符号。如果对一切t＞t₀ 的情况（t₀ 是扰动的开始时刻）都有

则δ² S确实是李雅普诺夫函数，而且稳定性是有保证的（图3）。在线性范围内，盈余熵产生和熵产生本身具有相同的符号，我们重新得到和最小熵产生定理一样的结果。然而，在远离平衡的区域，情况就改变了。这里化学动力学的形式起着主要的作用。

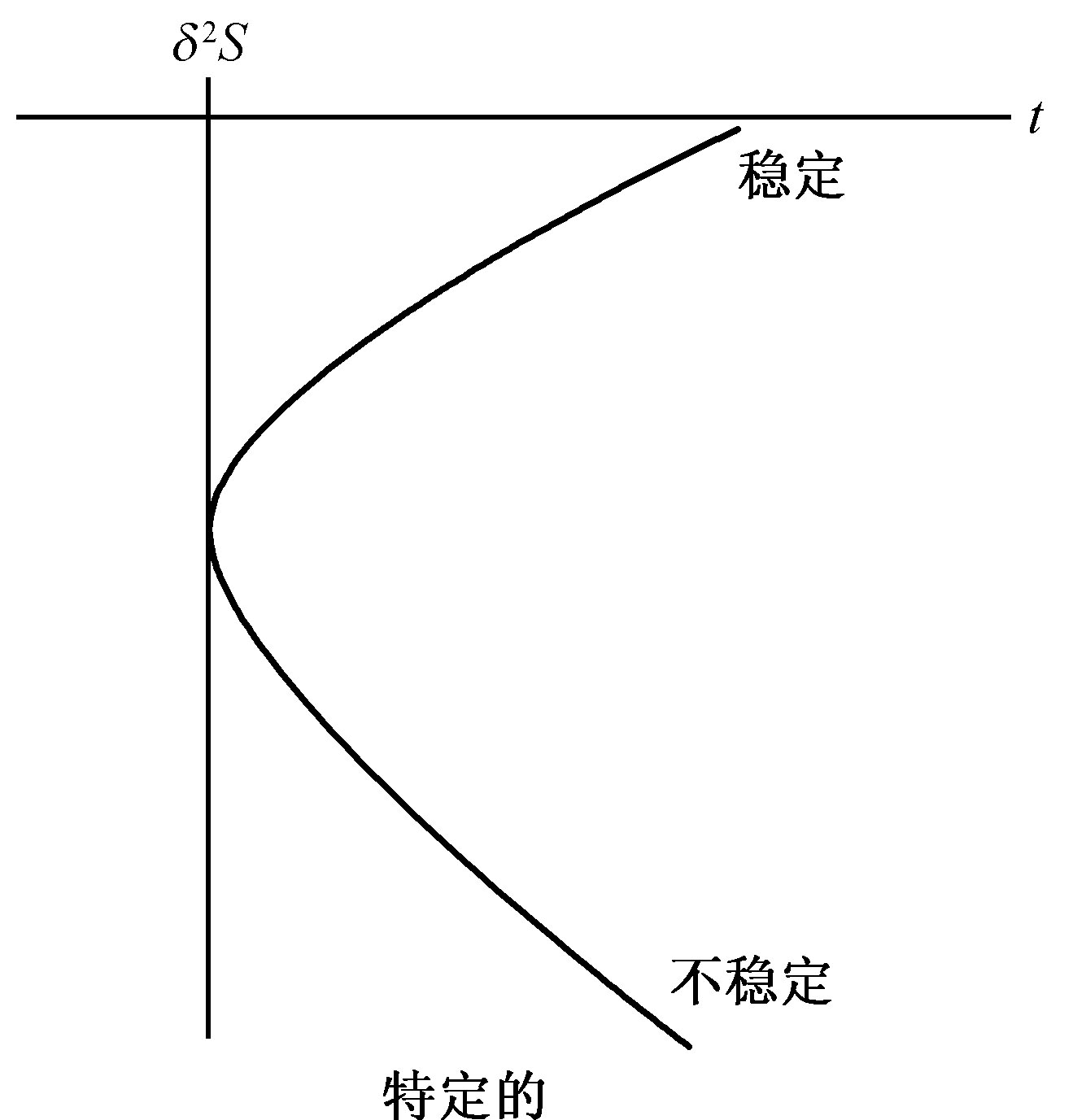
图3　渐近稳定，边缘稳定和不稳定情形下二阶盈余熵（δ² S）的时间演化。

在下一节中我将考察几个例子。对于适当类型的化学动力学，系统会变得不稳定。这一结果表明，平衡规律和远离平衡的规律之间有着本质上的差别。平衡规律是普适的。然而远离平衡的行为会变得极为特殊。这当然是一件好事，因为它允许我们引入各种物理系统的行为特征，而这在一个平衡的世界中是无法理解的。

所有这些考虑都是非常普通的。它们可以推广到可能产生宏观运动的系统中，推广到表面张力的问题中，或是推广到有外场的效应中^[7] 。例如，在我们引进了宏观运动的情形下，应当考虑如下表达式^[3]

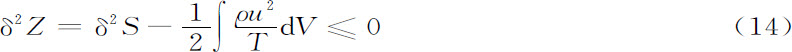
式中，Z是李雅普诺夫函数，它确定盈余熵，而u是宏观对流速度。这里对整个体积V积分，以便计入所有u的空间依赖性。我们可以再次计算δ² Z的时间导数，其形式将更为复杂。由于结果可在其他地方^[3] 找到，这里不再重复。我只想指出内部对流的自发激励不能从处于热力学平衡的静止状态中产生出来。作为特例，这当然也适用于贝纳尔不稳定的。

对化学反应的运用

现在回过来进化学反应的情况，一般的结论是，为了破坏（13）式的不等性，我们需要有自催化反应。更确切地说，自催化步骤是破坏热力学分支稳定性的必要（但非充分）条件。我们来考虑一个简单例子，即所谓“布鲁塞尔器（Brusselator）”，它对应以下反应式^[8] ：

初始反应物和最终产物是A、B、D和E，它们保持不变，而两种中间组分X和Y的浓度可以随时间变化。令反应常数等于1，我们得到方程组

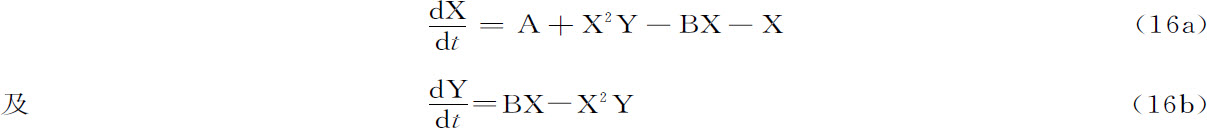
它容许有稳态

式中，X₀ 和Y₀ 是X和Y在稳态的浓度。利用热力学稳定性判据或利用正则模式分析，可以证明，只要

式（17）这组解就变得不稳定。

超过B的临界值B_c 之后，我们得到“极限环”，即X，Y空间中的任何始点都趋向同一个周期轨道。因此这里重要之点在于，与洛特卡－沃特拉（Lotka-Volterra）型的振荡化学反应不同。振荡频率是诸如浓度、温度等这些宏观变量的确定函数。化学反应导致相干的时间行为：它变成了一个化学钟。在文献中这通常称为霍夫（Hopf）分岔点。

计入扩散之后，不稳定的种类变得益发多了。因此，近若干年来许多学者研究了方程（15）所示的反应式。有扩散存在时，方程（15）中的反应式变成

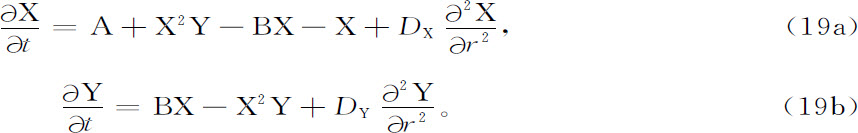
式中，D_X 和D_Y 是组分X和Y的扩散系数。除了极限环之外，现在还可能有不均匀的稳态。我们可以把它称为特林（Turing）分岔点，因为特林1952年在其关于形态发生学的经典论文^[9] 中，最先注意到化学动力学中有可能出现这类分岔点。有扩散存在时，极限环也可能与空间位置有关，并且引起化学波。

如果我们把对应热力学分支的解看做基本解，就可以把结果整理得有条理一些。其他的解可以作为从这个基本解相继产生的分岔而得到，也可以从一个非热力学分支作为高阶分岔而得到，这发生在离开平衡的距离更远的地方。

有意义的一个普遍特征是，耗散结构对于描述化学系统环境的整体特征很敏感，这包括它们的尺寸和形状、在表面上所加的边界条件等等。所有这些特性对于导致耗散结构的不稳定性的类型有着决定性的影响。

远离平衡时，在化学动力学和反应系统的“时空结构”之间出现意想不到的关系。确定有关的反应常数和输运系数的数值的相互作用，确实是短程相互作用（价力、氢键、范德瓦耳斯力）所造成的。然而，除此之外，输运方程的解还和系统的整体特征有关。在平衡附近，热力学分支上这种依赖性是很简单的，但在远离平衡的条件下，对化学系统就成为有决定意义的。例如，耗散结构的出现通常要求系统的尺寸超过某个临界值。临界尺寸是描述反应扩散过程的诸参数的复杂函数。因此，我们可以说：化学不稳定性包括长程序，系统通过长程序起着整体的作用。

耗散结构总有三个互相联系的方面：由化学方程表现出来的功能，由不稳定性引起的时空结构，以及触发不稳定性的涨落。这三个方面的相互影响，导致一些简直难以想象的现象，其中包括“通过涨落的有序”，下面我就要对此作分析。

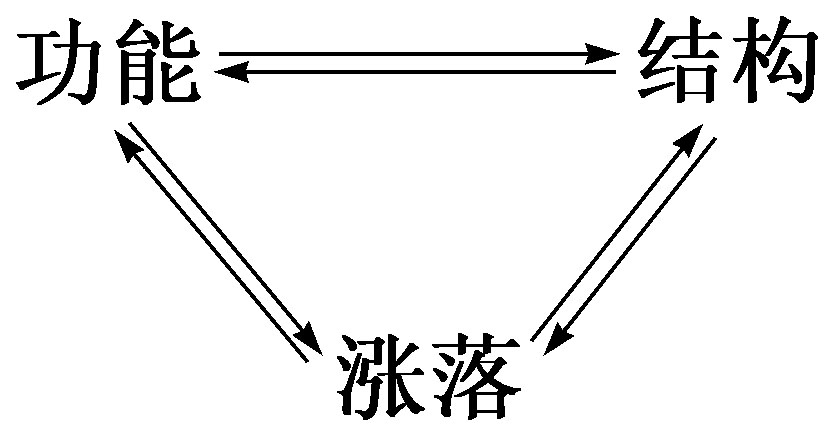
一般说来，当我们增加某个特征参数（例如布鲁塞尔器中的分岔参数B）的数值时，会相继出现分岔点。在图4中对于参数值λ₁ 只有单一解，而对λ₂ 值则有多重解。

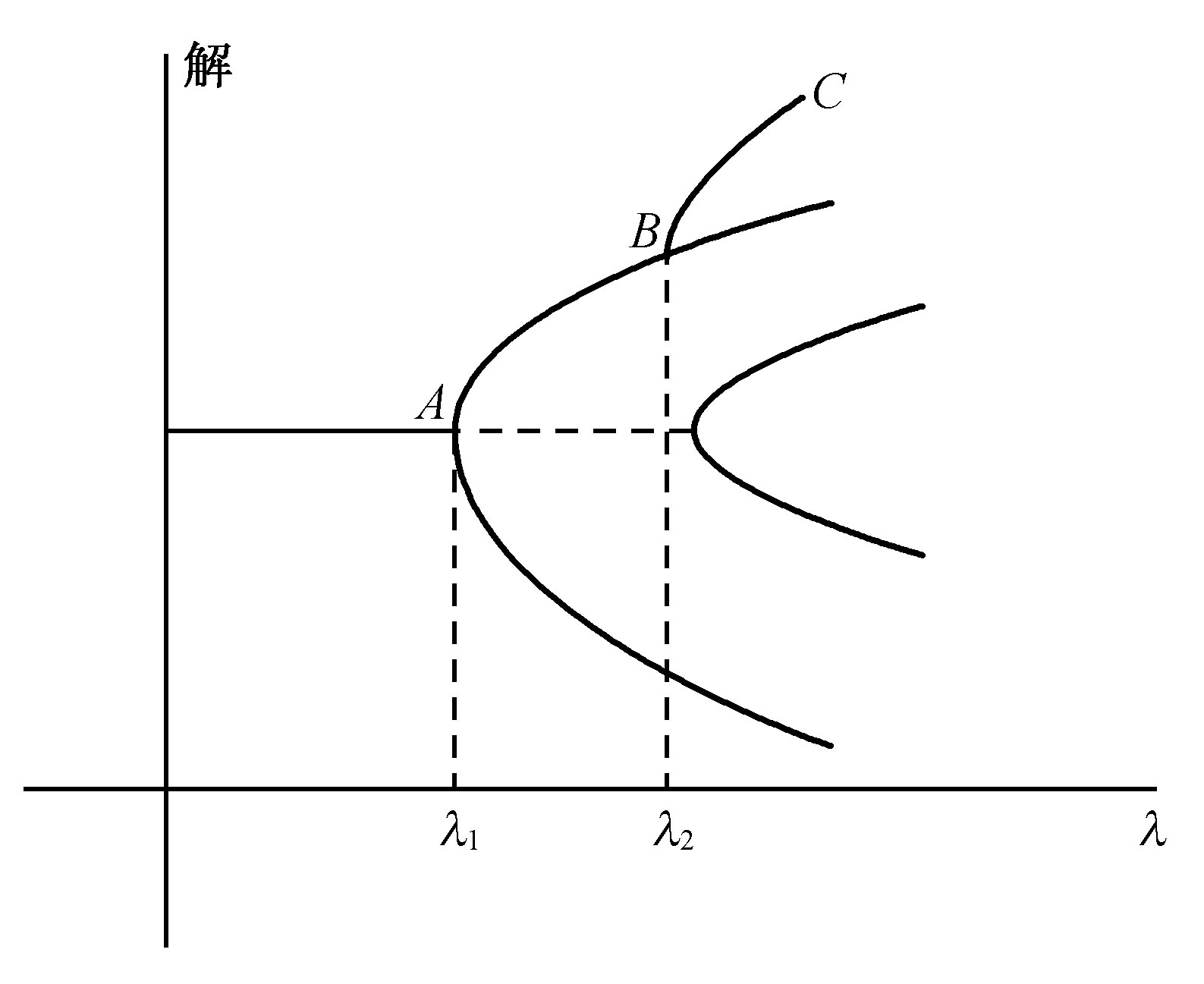
图4　相继分岔

饶有兴味的是，分岔在一定意义上把“历史”引进物理学中来了。假定观察结果向我们指出，一个具有如图4那样的分岔图的系统正处于状态C，而且是通过增加λ的值达到这个分岔状态的。对这个状态X的解释就暗示着关于这一系统过去历史的知识，因为它必须经过分点A和B。这样我们就在物理学和化学中引入了历史因素，而这一点似乎向来是专属于研究生物、社会和文化现象的各门科学的。

对具有分岔现象的系统的每种描述，都包含决定论和概率论两种因素。我们在下一节中将更详细地看到，在两个分岔点之间系统遵从决定论的规律，例如化学动力学的规律，而在分岔点领域，则涨落起本质作用，并且决定系统将走到那一分支上去。

我不准备在这里探讨分岔点理论和它的各种见解，例如托姆（Thom）提出的突变理论^[10] 等等。这些问题在尼科利斯和普里戈金最近的专著^[8] 中都有所讨论。我也不再列举化学和生物学中目前已知的一致结构的例子。许多实例都可以在文献^[8] 中找到。

大数定律和化学反应统计学

让我们现在转而讨论耗散结构形成的统计方面。通常的化学反应动力学是以碰撞平均数（更确切地说是反应碰撞平均数）的计算为基础的。这些碰撞是随机发生的。但是，这种杂乱行为如何能导致一致结构呢？显然，必须引入新的特征。简言之，这就是大数定律成立条件的失效；结果是反应粒子在不稳定附近的分布不再是随机分布。

首先，我得指出大数定律的含义。为此，我考察一个在许多科学技术领域中有重要意义的典型概率描述——泊松分布。这个分布包含变量X，它可取整数0，1，2，3……。根据泊松分布，X的概率分布是

等式（20）中的〈X〉是X的平均值。诸如电话叫号、饭店中的等待时间、给定浓度介质中的粒子数涨落等很多情形，都遵从这个规律。泊松分布的一个重要特点在于〈X〉是分布的唯一参数。概率分布完全由变量的平均值确定。

由等式（20）很容易得到所谓的“方差”，它规定平均值附近的离差

泊松分布的特点是离差等于平均值本身

我们来考察X是正比于粒子数N（在规定的体积中）或正比于体积V的广延量的情形。于是我们得出相对涨落的著名平方根定律

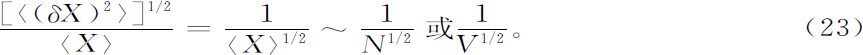
相对涨落的数量级与平均值的平方根成反比。因此，对于量级为N的广延量我们求得量为N^-1/2 的相对偏差。这就是大数定律的特点。因此，我们可以忽略大体系的涨落，并采用宏观描述。

对于其他分布，平均方差不再如（22）式那样等于平均值。但只要大数定律适用，平均方差的数量级仍然一样，即

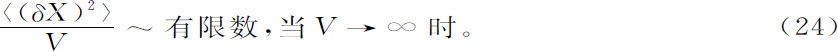
现在我们来考虑一个化学反应的随机模型。像过去通常的做法那样，将化学反应与“生灭”型的马尔科夫链联系起来是自然的^[11] 。这直接导致P（X₁ t），即种类X在时刻t的分子数为X的概率所满足的主方程：

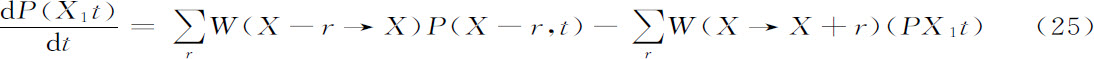
式中，W是种类X由（X-r）个分子变到X个分子的跃迁概率。在（25）式右端有得失两项的竞争。与经典的布朗运动的特征区别在于跃迁概率，W（X-r→X）或W（X→X+r），对占有数是非线性的。化学反应往往是非线性的，而这导致重要的区别。例如，很容易证明，对应于线性化学反

X的定态分布是泊松分布（对于给定的A和F的平均值）^[12] 。但是，当1971年尼科利斯和普里戈金证明^[13] 化学反应链

的中间物X的定态分布不再是泊松分布时，使人非常惊异。从宏观动力理论的观点看，这是非常重要的。实际上马来克－曼索尔和尼科利斯已证明^[14] ，一般说来，宏观化学方程必须考虑偏离泊松分布所引起的修正项。这就是为什么现在如此重视研究化学反应随机理论的基本原因。

例如，尼科利斯和图尔奈尔^[16] 广泛地研究了施洛格尔反应^[15]

他们证明，这个模型导致“非平衡相变”，与经典的范德瓦耳斯方程描述的情形非常类似。在临界点附近，以及在共存曲线附近，等式（24）所表述的大数定律失效，因为〈（δX）² 〉变得与体积的更高方次成比比。正如平衡态相变的情形，这种失效可通过临界指数表达出来。

对于平衡态相变的情形，临界点附近的涨落不仅幅度大，而且延伸距离广，雷马冒德和尼科利斯^[17] 对非平衡相变曾研究过同样的问题。为了使计算有可能进行，他们考察了一系列盒子。每个盒子里都进行（15）式所描述的“布鲁塞尔器”式反应。此外，不同盒子之间有扩散。他们利用马尔科夫方法计算了两个不同盒子X的占有数之间的关联。人们会预期，化学的非弹性碰撞和扩散结合起来将导致杂乱行为。但实际不是这样。在图5～7中表示出临界点以下和临界点附近的关联函数。十分清楚，在临界点附近有长程化学作用的关联。与我前面讨论过的系统类似，这个系统的行为有整体性，虽然化学相互作用是短程的。杂乱引起有序。此外，数值模拟表明，仅在粒子数N→∞的极限才趋向于“长程的”时间有序。

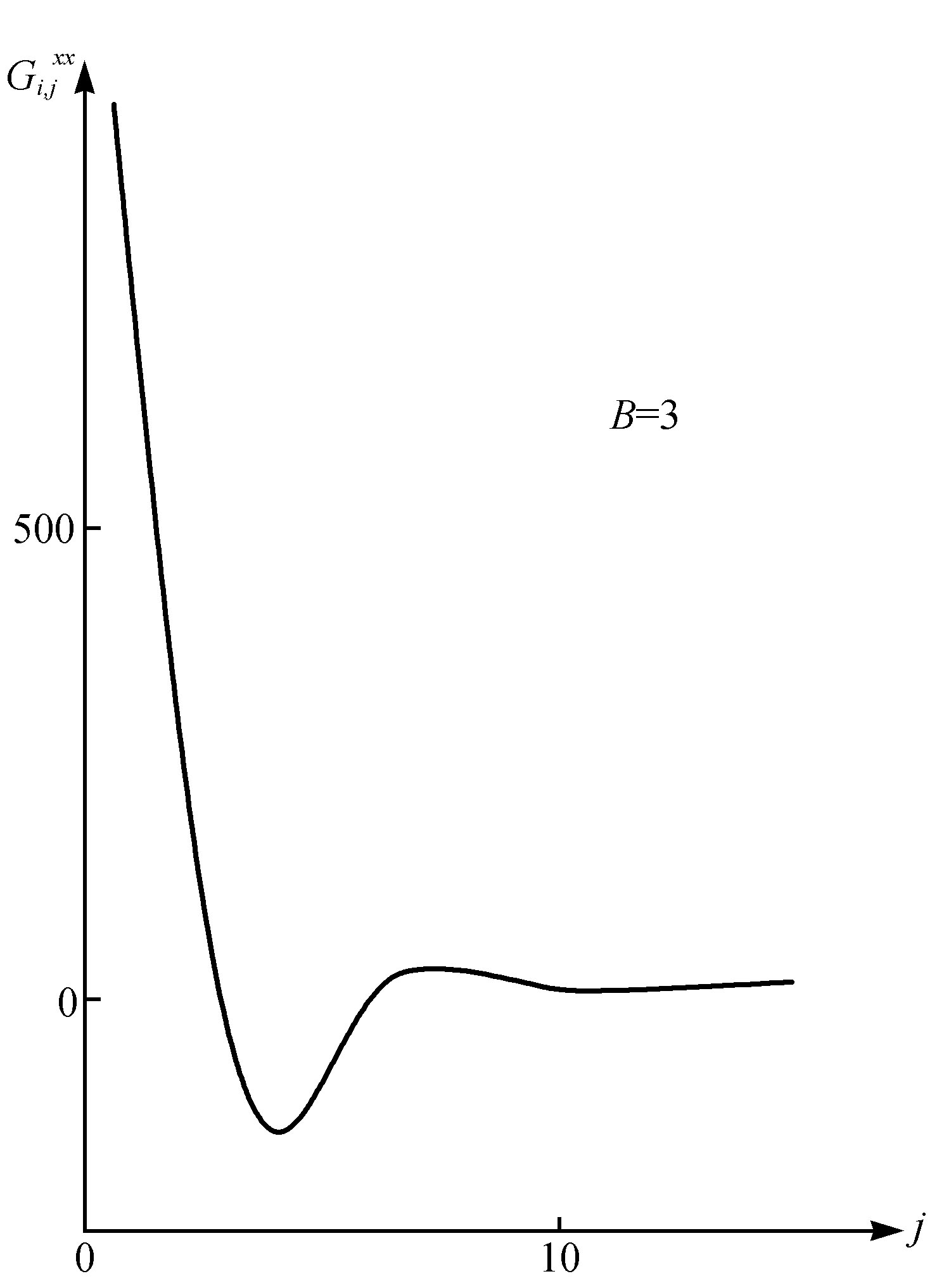
图5　远低于分岔参数B的临界值时，空间关联函数 随距离的变化

A＝2，d₁ ＝1，d₂ ＝4（d₁ 与d₂ 是A与B的扩散系数）。

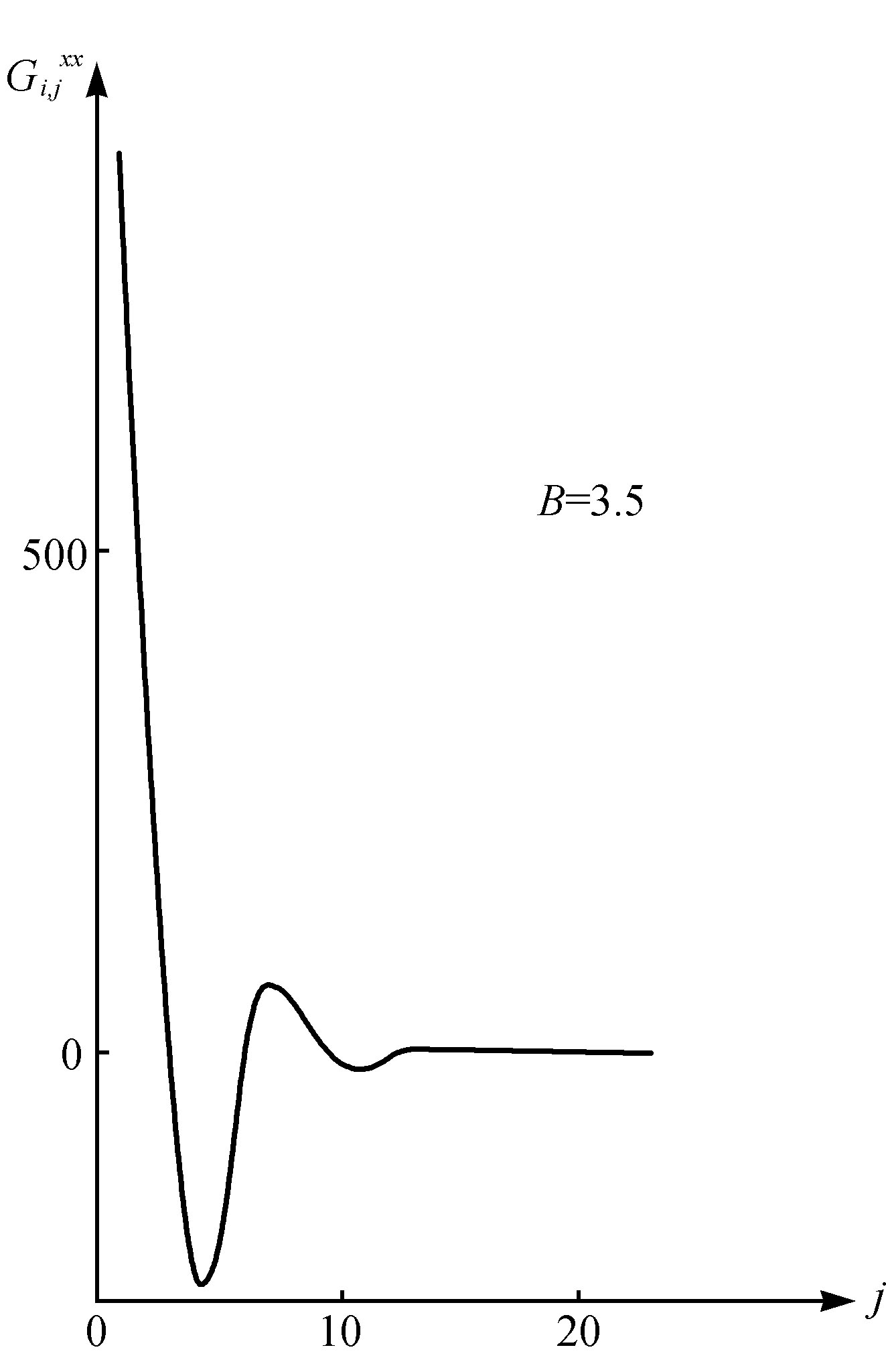
图6　当分岔参数B趋近临界值时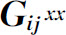， 的范围比图5所示稍有增加

图7　空间关联函数的临界行为

参数与图5中一样，关联函数同时表现出随距离的线性衰减和周期振荡，其波长与宏观浓度花纹的波长相同。

为了哪怕是定性地理解这一结果，让我们考察一下与相变的类比。当我们将顺磁物质冷却时，达到所谓的居里点，在这温度以下体系的行为像铁磁体，在居里点以上，所有的方向具有同样的作用。居里点以下有对应于磁化方向的特殊方向。

宏观方程中没有东西决定磁化所取的方向。原则上，所有方向同样可能。假若铁磁体只包含有限数目的粒子，这个特殊方向不可能永远维持下去。它会转动。但是，假使我们考察一个无限体系，涨落就不再能改变铁磁体的方向。长程序一旦产生，就永远保持。

铁磁体系和振荡化学反应的情形有惊人的相似之处。当远离平衡时，体系开始振荡。它将沿极限环运动。极限环上的相位是由初始涨落决定的，而且与磁化强度的方向起同样的作用。如果体系是有限的，涨落逐步取得优势，干扰转动。但如果体系是无限的，则可得长程时间有序，与铁磁体系的长程空间有序非常类似。由此可知，周期反应的出现是破坏时间对称的过程，正如铁磁性是破坏空间对称的过程一样。

李雅普诺夫函数的力学解释

我现在来更严密地考察熵的力学意义，更具体地说，是我前面引用过的李雅普诺夫函数δ² S的力学意义。

让我先简要地概括一下玻尔兹曼对这个问题的表达方法。即使到了今天，玻尔兹曼的著作仍然是一个里程碑。人所共知，玻尔兹曼推导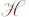 定理时的实质性的一条是用分子的速度分布函数f所满足的输运方程

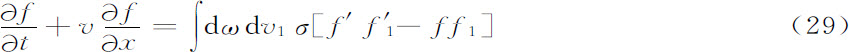
代替准确的运动方程（用我下面要谈到的刘维方程表示），式中dω是碰撞中的有效立体角，σ是截面，v是速度。

只要采纳这个方程，很容易证明玻尔兹曼的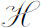 量

满足不等式

因此它起着李雅普诺夫函数的作用。

用玻尔兹曼方法得到的进展是惊人的。但是，还有许多困难^[18] 。首先有实际的困难，例如难于将玻尔兹曼的结果推广到更普遍的情形（如稠密气体）。气体运动论最近几年有了惊人的进展，但是，当你检阅气体运动论或非平衡统计力学的最新教科书时，你不会找到任何在更普遍的情形下成立的类似玻尔兹曼 定理的东西。因此，玻尔兹曼的结果仍旧是很孤立的，与我们所赋予热力学第二定律的普遍性适成截然不同的对照。

不仅如此，我们还有理论上的困难。最严重的可能是洛施密特的可逆佯谬。简言之，如果将分子速度反向，就回到初始态。在这个趋向初始态的过程中，玻尔兹曼的 定理（31式）被破坏。我们得到“反热力学行为”，这一结论可以进行检验，譬如说，用计算机模拟的办法。

玻尔兹曼 定理失效的物理原因在于速度反向所引入的长程关联。也许有人认为，这种关联是例外，可以忽略。但是，人们如何才能找到一个区分反常关联和正常关联的判据，特别是当考察稠密体系的时候？

如果我们不是讨论速度分布函数，而是考察相应于相空间密度ρ的吉布斯系综，情形就会变得更糟。它的时间演化得自刘维方程

式中，Lρ在经典力学中是泊松括号i{H，ρ}，在量子力学中是对易子［H，ρ］（H是哈密顿量）。如果我们考察如

这样的正凸泛函，式中q是坐标，p是与q共轭的动量，或在量子力学中

则容易证明

是刘维方程（32）的推论，方程（33）或（34）所规定的Ω不是李雅普诺夫函数，经典力学或量子力学的规律似乎妨碍我们构成一个李雅普诺夫泛函，使它能起熵的作用。

由于这个原因，常常有人说，不可逆性引用到力学中来只能通过力学规律以外的附加近似（如粗粒平均）的方法^[19] 。我总是难于接受这个结论，特别是鉴于不可逆过程的建设性作用。难道耗散结构是由于错误所造成的吗？

考查一下为什么玻尔兹曼的气体运动论可以导出 定理而刘维方程却不能，我们就可以得到关于从那个方向可能解决这一佯谬的启示。刘维方程（32）显然是Lt不变的。如果我们同时反转刘维算子L（经典力学中可通过速度反向作到）和时间t的符号，刘维方程仍旧不变。另一方面，很容易证明^[18] ，玻尔兹曼方程的碰撞项破坏Lt对称，因为它对L具有偶对称。因此，我们可以把问题换一个提法：怎样才能破坏经典力学和量子力学中固有的Lt对称呢？我们的观点一直是，力学和热力学的描述是在一定意义上“等价”的体系演化的表示，它们通过一个非么正变换相联系。让我扼要地指出我们应如何前进。我所遵循的方法是在布鲁塞尔和奥斯汀与同事们密切合作下发展起来的^[20-22] 。

非么正变换理论

既然（34）式已证明是不对的，我们从如下形式的李雅普诺夫函数

出发（这里M是正定算子），它具有非增长的时间微导数

可以肯定，这一点并不总是可能的。在简单的力学情形，如果运动是周期性的，不管是经典力学还是量子力学，都不可能有李雅普诺夫函数存在，由于过了一段时间后体系会回到原始状态。M的存在与刘维算子谱的类型有关。在经典遍历理论的范围内，密斯拉^[23] 最近已对这个问题进行了研究。这里我将追究一下（36）式中的M算子可能存在所导致的一些推论，这个量可看成“熵的微观表示”。由于这个量是正定的，一个普遍性的定理允许我们把它表示成一个算子的积，譬如说Λ^-1 和它的厄米共轭（Λ^-1 ）⁺ 的乘积

（这相应于取正定算子的“平方根”）。将此式代入（36）式，即得

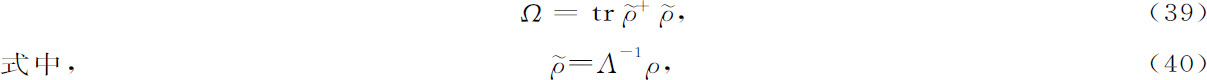
这是一个最有意思的结果，因为（39）式正是我们前面要找的那种类型的方程。但是，我们看到，这个表述式仅在新的表示中才存在，它通过变换（40）式与原来的表示相联系。

首先让我们写下新的运动方程。考虑到（40）式，求得

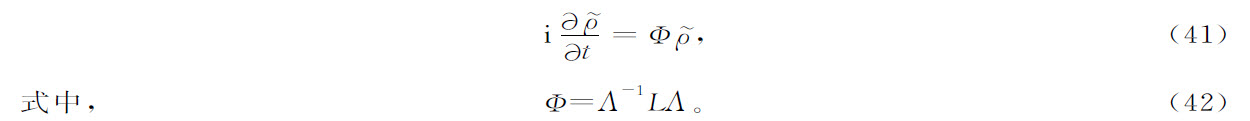
现在来利用运动方程（32）的解。可以用更准确的不等式

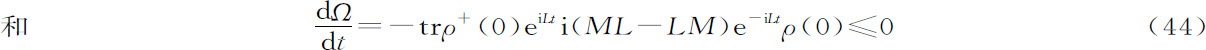
代替方程（36）和（37）因此微观“熵算子”M可能与L不对易。对易子正好表示可以叫做“微观熵产生”的量。

这使我们自然地想起海森伯的测不准关系和玻尔的互补原理。在这里也发现非对易性是非常有意思的，但现在是在通过算子L表示的力学与通过M表示的“热力学”之间的非对易。这样，我们得到了一种新的、非常有意思的，在具有轨道或波函数的力学与具有熵的热力学之间的互补性。

变到新表示后，求得熵产生方程（44）

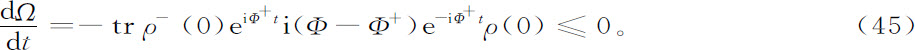
这一结果意味着Φ与其厄米共轭Φ^- 的差不为零，

因此，我们得到一个重要的结论，即变换了的刘维方程（41）中新的运动算子不再是厄米的，与刘维算子不一样。这表明，我们需要越出通常的么正（或反么正）变换类，去扩展量子力学算子的对称。幸亏这里很容易决定现在要讨论的变换类。既可用老的也可用新的表示来算出平均值。结果应该一样。换句话说，我们要求

而且，我们对那些明显依赖于刘维算子的变换感兴趣。实际上这是此一理论的非常具体的动机。我们已看到，玻尔兹曼型的方程具有破缺的Lt对称。我们希望通过这种变换来精确地实现这种新的对称^[20] 。这只有考虑与L有关的变换Λ（L），才可能做到。最后，利用密度矩阵ρ与可观察量具有同样的运动方程，只是将L变换成了-L，我们求得基本条件

这里，它代替通常加在量子力学变换上的么正条件。

不必惊讶，我们确实找到了一种非么正变换律。么正变换非常像坐标变换，它不影响问题的物理过程。不管用哪个坐标系，体系的物理过程还是不变的。但这里我们对付的是一个完全不同的问题。我们希望从一种类型的描述，即力学的描述，过渡到另一种“热力学”的描述。这正是我们需要在表示中作更剧烈的变化（如用新变换律方程（48）来表示）的原因。

我把这种变换称为“星－么正”变换，并引入记号

我把Λ^* 称为与Λ相联系的“星－厄米”算子（星总是意味着反演 ）。于是等式（48）表明，对于星－么正变换，逆变换等于其星－厄米共轭。

现在我们来考察（42）式。利用L，以及（48）、（49）式都是厄米算子的性质，得

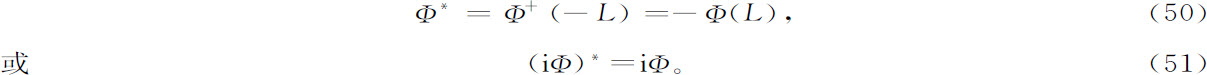
运动算子是“星－厄米”的，这是一个非常有意思的结果。为了具有星－厄米，算子可以是厄米的，且对L反演具有偶对称（即L→-L时不变号）。也可以是反厄米的，且具有奇对称（即L→-L时变符号）。因此，一般的星－厄米算子可写成

这里上标e和o分别表示新的时间演化算子Φ的偶对称和奇对称部分。表示存在一个李雅普诺夫函数Ω的耗散条件（46式），现在变为

这就是获得“熵产生”的偶对称部分。

让我来概括一下已得到的结果。我们得到了一种新型的微观方程（就像经典力学和量子力学中的刘维方程一样），它明显地显示出一个可与李雅普诺夫函数联系的部分。换句话说，方程

包含“可逆”部分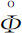 和“不可逆”部分 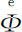。这个新方程的对称完全与玻尔兹曼唯象输运方程一样，因为在L反演下，流的项具有奇对称，而碰撞项具有偶对称。

这样，可逆过程与不可逆过程之间的宏观的热力学的差异转变为微观的描述。我们所得到的可以看成是微观可逆力学与宏观不可逆热力学之间的“缺少的环节”图式如下：

通过变换Λ来有效地构成李雅普诺夫函数Ω（36式），必须牵涉到对相应于刘维算子的预解式的奇异性作一番仔细的研究^[21] 。

对于稍微偏离热力学平衡的情形可以证明（如最近西奥多索普路等人^[24] 所作的那样），如果此外只保留守恒量的时间演化，则李雅普诺夫泛函Ω（36）式准确地归结为宏观量δ² S（9式）。因此，至少是在线性区域，我们已完全普遍地建立了非平衡热力学与统计力学的联系。这是在适用于稀薄气体的玻尔兹曼理论范围内早已取得结果^[25] 的推广。

结束语

通过非么正变换理论引进热力学不可逆性导致力学结构的深刻变化。它把我们从群引到半群，从轨道引到过程。这种进化与本世纪来我们对物理世界描写的某些主要变化是一脉相承的。

爱因斯坦的相对论的一个最重要方面是我们不能脱离限制信号传播速度的光速问题来讨论时间和空间的问题。同样，消去“不可观测量”在海森伯创始的量子理论基本方法中起了重要作用。

爱因斯坦和玻尔曾经常强调相对论和热力学的类比。我们不能以任意的速度传播信号，我们也不能造出一个为第二定律所禁戒的永动机。

从微观角度看，后一个禁戒意味着，如果体系满足热力学第二定律，从力学角度看可以明确规定的量是不可观测的。例如，体系的轨道作为整体是不可观测的。如果可观测，我们就能在每个时刻区分两个轨道，热平衡这个概念就失去其意义。力学和热力学互相制约。

有意思的是，现在有另外一些理由似乎表明，力学相互作用和不可逆性的关系会起到比迄今已意识到的更深刻的作用。在表述量子力学时曾如此重要的可积分的体系的经典理论中，所有的相互作用都可以通过相应的正则变换消去。如果真是要讨论的力学体系（特别是涉及基本粒子及其相互作用的情形）的正确原型吗？我们应该不应该先转到非正则表示，使我们在微观水平上区分可逆过程与不可逆过程，然后再消去可逆部分，得到可以明确规定的但仍然相互作用着的组成部分？

这些问题也许再过几年会搞清楚。但已有的理论进展已容许我们区分时间的不同水平：与经典力学或量子力学联系的时间，通过李雅普诺夫函数与不可逆性联系的时间，通过分岔与“历史”联系的时间。我相信，时间概念的这种多样化会使理论物理和理论化学与研究自然界其他方面的学科更好地结合。

参考文献

［1］M. Planck，Vorlesungen über Thermodynamik，（Teubner，Leipzing，1930；英译本，Dover，New York）

［2］I. Prigogine，Etude thermodynamique des phénomènes irréversibles，theiss，University of Brussels（1945）

［3］P. Glansdorff，I. Prigogine，Thermodynamics of Structure，Stability and Fluctuations，Wiley—Interscience. New York，1971）

［4］线性不可逆过程理论的标准参考书是S. R. de Groot 和P. Mazur的专著Non-Equilibrium Thermodynamics（North-Holland，Amsterdam，1969）

［5］L．Onsager，Phys. Rev．73，405（1931）．

［6］I．Prigogine，Bull. Cl．Sci．Acad. R. Belg. 31，600（1945）

［7］R. Defay，I. Prigogine，A. Sanfeld，J. Colloid Interface Sci. 58，598（1977）

［8］G. Nicolis & I. Prigogine，Self-Organization in Nonequilibrium Systems（Wiley-Interscience. New York，1977），第7章

［9］A. M. Turing，Phil. Trans. R. Soc. London Ser. B 237，37（1952）

［10］R．Thom，Stabilité Structurelle et Morphogénèse（Benjamin，New York，1972）

［11］标准参考书是A. T. Barucha-Reid，Elements of the Theory of Markov Processes and Their Applications（McGraw-Hill，New York，1960）

［12］G. Nicolis & A. Babloyantz，J. Chem. Phys. 51，2632（1969）

［13］G. Nicolis & I. Prigogine，Proc. Natl. Acad. Sci. U. S. A. 68，2102（1971）

［14］M. Malek—Mansour & G. Nicolis，J. Stat. Phys. 13，197（1975）

［15］F Schlögl，Z Phys，248，446（1971）；ibid，253，147（1972）

［16］G. Nicolis & J. W. Turner，Physica 89A，326（1977）

［17］H. Lemarchand & G. Nicolis，ibid. 82 A，521（1976）

［18］I. Prigogine，见 The Boltzmann Equation，E. G. D. Cohen，W. Thirring，Eds.（Springer—Verlag，New York，1973），p.401

［19］关于这一观点的精辟表述见G. E. Uhlenbeck，The Physicist's Conception of Nature，J. Mehra，Ed.（Reidel，Dordrecht，Holland，1973），501—513

［20］I. Prigogine，C. George，F. Henin，L. Rosen-feld，Chem. scr. 4，5（1973）

［21］A. Grecos，T. Guo，W. Guo，Physica 80 A，421（1975）

［22］I. Prigogine，F. Mayné，C. George，M. de Haan，Proc. Natl. Acad. Sci. U. S. A. 74，4152（1977）

［23］B. Misra，ibid. 75，1629（1978）

［24］M. Theodosopulu，A. Grecos，I. Prigogine，ibid. 75，1632（1978）；A. Grecos，M. Theodosopulu，Physica，出版中.

［25］I. Prigogine，physica 14，172（1949）；ibid. 15，272（1949）

［26］这篇演讲综述了我在布鲁塞尔和奥斯汀与同事们密切合作中取得的成果，不可能对他们一一致谢，但我想对G. Nicolis教授和J. Mehra教授在准备这一讲稿的最终文本时所给予的协助表示感谢。

————————————————————

(1) 本文考虑了热力学第二定律的宏观和微观方面所引起的基本概念问题；指出非平衡可以成为有序的根源，而不可逆过程能导致物质的新型的，称为“耗散结构”的动力状态；概述了这类结构的热力学理论。文中也提出了不可逆过程的一种微观定义，同时提出了一种变换理论，它允许人们引用非么正的运动方程，这些方程明显地展示出不可逆性和趋向热力学平衡。布鲁塞尔自由大学这个小组在这些领域中的工作也作了简要的评论。看来在理论化学和理论物理学的这一新发展中，热力学概念的作用将与日俱增。

（郝柏林、于渌译自Science，vol. 201，No. 4358，I September 1978）