第一编　波动力学的创立

·Part of The Establishment of Waoe Mechanics·

他熟悉人类思想和实践的许多领域，他的广博的知识像他的敏锐的思想和创造力一样是惊人的。……我没有能力描绘这位具有多方面才能的杰出人物的形象。他所涉足的许多领域我所知甚少——特别是在文学和诗歌方面。

——M. 玻恩

量子论的奠基人和量子力学的创建者

薛定谔

（E. Schrödinger, 1887—1961）

创建波动力学，提出薛定谔方程。

玻尔

（N. Bohr, 1885—1962）

将量子论用于原子结构理论研究的先驱，提出量子力学诠释的互补性原理，建立了哥本哈根学派。

普朗克

（M. Planck, 1858—1947）

量子理论的奠基人。

海森伯

（W. Heisenberg, 1901—1976）

创建矩阵力学，提出不确定性原理。

狄拉克

（P. A. M. Dirac, 1902—1984）

创立相对论量子力学，预言正电子、反粒子和磁单极子。

关于波动力学的四次演讲

·Four Lectures on Waoe Mechanics·

我的朋友，

生活中什么看起来至关重要？

无论它带来了沉重的压抑，

还是快乐和欣喜。

行动，思想和愿望，

相信我，没有任何意义比得上

在我们所设计的实验中

一个指针的波动。

看穿了自然：也无非只是分子的碰撞，

光疯狂的颤动也不能让你明白基本定律，

更不是你的快乐和战栗让生活有了意义。

世界之灵，如果

可能来自千次的实验，

最终得出了如下结果——

这真是我们所做的吗？

——E. 薛定谔

位于利马德河岸的苏黎世大学。这所瑞士最大的综合性大学创建于1833年。

第一次演讲

1．从通常的力学和几何光学间的哈密顿类比推导出波动力学的基本观念

当一质点m在一以势能V（x，y，z）描述的保守力场中运动时，假如你让它从定点A以已定的速度，即以已定的能量E开始运动，那么，只要适当地瞄准，即让它沿一个明确选定的方向开始运动，你就可以让它到达另一任意选定的点B。一般说来，对应于一个已定的能量，总有一条确定的从A到B的动力学轨道。这条轨道具有这样的特性：

图1

并由这个特性［莫培督（Maupertuis）形式下的哈密顿原理］所规定。这里T是质点的动能，而这个方程表示：考虑所有从A联到B并服从能量守恒定律（T＋V＝E）的轨道的簇，其中实际的动力学轨道具有这样的特点：对应于这条轨道和簇中所有同它无限接近的轨道， 基本上取相同的值，它们之间的差异为二阶无穷小（“无限接近”一词是用来规定一阶无穷小的）。令 为质点的速度，我们取

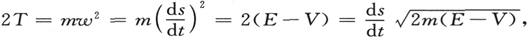
由此，方程（1）可以变换为

这个形式的优点在于变分原理是应用在一个纯粹几何积分上，它不包含时间变数，而且还自动照顾到能量守恒的条件。

哈密顿发现，将方程（2）同费马原理比较是有用的，费马原理告诉我们：在一不均匀的光学媒质中，实际的光线，即能量传播的径迹，是由（通常所称的）“最小时间定律”决定的。现在设同图1相关联的是一个任意不均匀的光学媒质，例如地球的大气；那么，如果在A点有一盏探照灯，射出一支轮廓分明的光束，只要将探照灯适当地瞄准，一般地就能够照亮任意选定的点B。有一条确定的光程从A联到B，它服从这样一条定律：

而这条定律也唯一地规定了这条光程，这里，ds同前面一样，表示路程元，而u是光速，是坐标x，y，z的函数。

如果我们假设：

则方程（2）、（3）分别表示的两条定律就变为等同的了，这里C必须不依赖于x，y，z，但可以依赖于E。这样，我们就做出了一幅关于光学媒质的假想图像，在这幅图像里，可能的光线簇和那个在V（x，y，z）力场中以已定能量E运动着的质点m的动力学轨道簇相重合。光速u不仅依赖于坐标，而且也依赖于质点的总能量E，这个事实是最重要的。

这个事实使我们能够把上面的类比推进一步，这只要将光速对E的依赖关系描述为色散，即描述为对频率的依赖关系就行了。为了达到这个目的，我们必须给我们的光线以一确定的频率，它是取决于E的。我们要（任意地）假设

E＝hν（h是普朗克常量），　　　　　　　　　　　　（5）

而不过多地去讨论这一对现代物理学家讲来是非常富有启示性的假设了。这样，这个不均匀的和色散的媒质就以它的光线提供出一幅关于粒子的一切动力学轨道的图像。现在我们可以再前进一步，提出这样的问题：我们能不能使一个小的“点状的”光信号完全像我们的质点一样运动呢？（到此为止，我们只注意到轨道的几何等同性，完全忽略了时间变率问题）乍看起来，这似乎是不可能的，因为质点（沿着路径，即以不变的能量E）的速度

是同光速u成反比的［见方程（4），C只依赖于E］。但我们必须记住，u当然是通常的相速度，而一个小的光信号却以所谓的群速度在运动，令群速度为g，它可以用下式求得

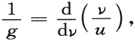
或者，在这里，根据方程（5），可以从下式求得

我们要试着使g＝w。要达到这个目的，我们可以使用的唯一办法是对C的适当选择，这C是方程（4）中出现的关于E的任意函数。根据（4）、（6）和（7），g＝w的假设变成为

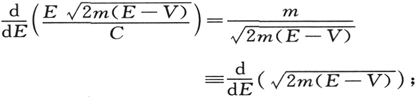
由此可知

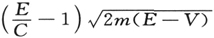
对于E来说是常数。既然V含有坐标，而C又必须只是E的函数，那么，显然只有使第一个因子等于零才能保证这个关系普遍成立。因此

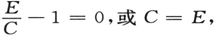
由此得出方程（4）的一个特殊形式：

关于相速度的这个假设是唯一能保证质点运动的动力学定律与我们想象的光传播中光信号运动的光学定律绝对符合的假设。值得指出的是：按照（8），

在u的这个定义中，仍然还有一种任意性，这就是说，显然可以用任意加上一个恒量的办法来改变E，如果在V（x，y，z）上加上一个同样的恒量的话。在非相对论性的处理中，这种任意性无法克服，而在这几次演讲中，我们是不准备探讨相对论性的处理的。

现在可把波动力学的基本观念归纳如下：我们以为在旧力学中用描述一个质点运动的方法（即令它的坐标x，y，z为时间变量t的函数）做了适当描述的现象，必须用描述一种确定的波运动的方法来正确地——按照这种新观念——加以描述，这种波运动发生在前面考察过的那类波中，这类波所具有的确定的频率和速度（从而也具有确定的波长），也就是我们认为前面我们称为“光”的那种东西所应该具有的。波运动的数学描述不能用一个变量t的有限几个函数来实现，而需要用比如这样一些函数的一个连续簇，即用一个（或者可能用几个）x，y，z和t的函数来实现。这些函数满足一个偏微分方程，即满足某种波动方程。

用描述波运动的方法正确地描述了真实的现象，这种讲法并不一定就完全等于说：真实存在的就是波运动。在后面我们将看到，在推广到任意力学系统的时候，我们将用广义坐标空间（q空间）中的波运动来描述这样一种系统中真实发生的事情。虽然后者具有完全确定的物理意义，然而把它说成是“存在”的，是不太恰当的；因此，即使是从通常的字面意义上来讲，也不能说这种空间中的波运动是“存在”的。这只是对现象做适当的数学描述。对于我们现在所探讨的单个质点的情况也是一样，波运动也不能过于死板地理解为是真实“存在”的，尽管在这种特别简单的情况中，位形空间和普通空间正好完全一致。

2．通常的力学只是一种近似，它对于非常微小的系统不再适用

在用波动力学描述来代替通常的力学描述时，我们的目的是要得到这样一种理论，它既能处理量子条件在其中不起显著作用的通常的力学现象，而另一方面，也能处理典型的量子现象。实现这个目的的希望就在下面的类比当中。以前面讨论的方法所建立的哈密顿波动图像包含了某些对应于通常力学的东西，这就是：光线对应于力学路径，而信号就像质点一样地运动。但是用射线来描述波运动只是一种近似（在光波的情况下称为“几何光学”）。只有碰巧当我们所要处理的波动现象的结构与波长相比甚为粗略而我们又只对它的“粗略结构”感兴趣时，这种近似才能成立。波动现象的精细结构绝不能用射线（“几何光学”）的处理来揭示，而且总是存在着这样的波动现象，它们都是那么细微，以至于射线方法是毫无用处，而且也提供不出任何知识的。因此，在用波动力学代替通常的力学时，我们可以指望，一方面把通常的力学作为一种近似保留下来，它只对于粗略的“宏观力学”现象才是有效的；而另一方面，又对那些精细的“微观力学”现象（原子中电子的运动）做出解释，关于这种现象，通常的力学完全不能给出任何知识。至少，如果不做非常人为的附加的假设，是不能做到这一点的，这些假设实际上构成了理论中比力学处理更重要得多的部分。 ^〔1〕

从通常的力学走向波动力学的一步，就像光学中用惠更斯理论来代替牛顿理论所迈进的一步相类似。我们可以构成这种象征性的比例式：

通常力学∶波动力学＝几何光学∶波动光学。

典型的量子现象就类比于衍射和干涉等典型的波动现象。

对于这种类比的概念来说，通常力学在处理非常细微的系统时遭到失败，这一事实是有重大意义的。我们能够立即掌握到可预料通常力学将遭到完全失败的那个数量级，并且将看出这个数量级是分毫不差的。这种波动的波长λ是［参见方程（5）和（8）］

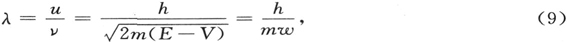
即普朗克常量除以质点的动量。现在，为简单起见，取氢模型的一个半径为a的圆形轨道，但不一定是“量子化”了的。那么，从通常的力学（没有应用量子法则）可得到

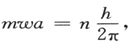
这里n是任意正实数（对于玻尔的量子化应该是1，2，3，…；后一方程中h的出现暂时只是一种表示数量级的便利方法）。合并上二方程，我们得到

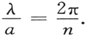
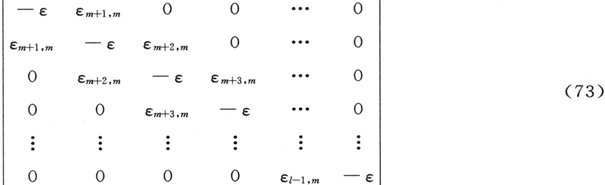
现在，为了使我们能够可靠地应用通常的力学，必须使这样算出来的路径的大小总是要比波长大得多。可以看出，当“量子数”n比1大得多时，就是这种情形。当n变得愈来愈小时，λ对于a的比率就变得愈来愈不利了。可预料通常力学将遭到完全失败的区域正是我们实际碰到这种情况的区域，即n具有1的数量级的区域，对于那些具有1个正常原子的大小（10^－8 cm）的轨道，情况就该是这样。

3．把玻尔的定态能级作为波的本征振动频率推导出来

现在让我们考察一下怎样用波动力学来处理一个通常的力学无法处理的情况；比如说，让我们专门来考察一下，如何用波动力学来处理通常的力学中称之为氢原子中的电子运动。

我们将用什么方法来解决这个问题呢？

啊，这同我们要解决那种求弹性体的可能运动（振动）的问题时所用的方法十分相像。只是，对于后者，因为存在着纵波和横波这两类波而使问题复杂化了。为了避免这种复杂化，让我们考察一种装在一个已定的包壳中的弹性流体。关于压力p，我们得到一个波动方程：

式中u是纵波传播的恒定速度，纵波是在流体的情况下唯一可能发生的波。我们必须尽力找到这个偏微分方程的满足容器表面一定边界条件的最普遍解。求解的标准方法就是试用

p（x，y，z，t）＝ψ（x，y，z）e^2πiνt

代入方程，由此得出关于ψ的方程

ψ和p服从同样的边界条件。这里我们遇到一个众所周知的事实，那就是，对于ψ的系数的一切数值，即对于一切频率ν，不是都能得到一个满足这个方程和这种边界条件的正则解的，而只对于分立的频率ν₁ ，ν₂ ，ν₃ ，…，ν_k ，…的无穷集才能得到正则解，这些频率称为这个问题或者这个物体的特性频率或者本征频率（Eigenfrequenzen）。我们称ψ_k 为属于ν_k 的解（如不考虑相乘的常数，通常总是唯一的），那么，——因为方程和边界条件都是齐次的——带有任意常数c_k ，θ_k 的

将是一个更普遍的解，而且如果量（ψ_k ，ν_k ）的集是完备的话，它确实是这个普遍解。［说到物理的应用，我们当然只用（11）式的实数部分］

在用波来代替我们想象中的电子运动的情况下，也必须有某个量p，它满足像方程（10）那样的波动方程，虽然我们还不能讲出p的物理意义。让我们暂时撇开这个问题。在方程（10）中，我们必须取（见前）

这不是一个恒量；因为：（1）它依赖于E，即在本质上依赖于频率ν（＝E／h）；（2）它依赖于坐标x，y，z，这些坐标包含于势能V中。与前述振动流体的简单情况相比较，这就有双重的复杂化了。但这两者都不严重。第一方面，从对E的依赖关系，我们受到这样的限制，就是我们只能把波动方程应用于这样的函数p，它对时间的依赖关系如下：

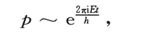
因此

我们用不着担心这一点，因为在任何情况下，在求解的标准方法中也都要做这样的假定（Ansatz）。将（12）和（8）式代入（10），并用ψ来代替p（要注意的是，我们现在同以前一样只研究坐标的函数），我们得到

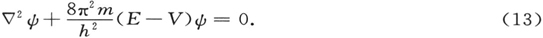
现在我们看到，第二种复杂化（u对V的依赖关系，即对坐标的依赖关系）只是产生了这样的结果，所得到的方程（13）同方程（10′）相比，多少具有更有意思的形式，这里ψ的系数不再是一个恒量，而是同坐标有关的了。这实在是可以预料到的，因为一个表达力学问题的方程不能不包含这一问题中的势能。这种“力学的”波动问题的简化（与流体问题相比）在于不存在边界条件。

当我最初接触这些问题时，我曾以为后一种简化是致命的。由于对数学的造诣不深，我就不能想象在没有边界条件的情况下怎能出现本征振动频率。后来，我认识到系数的更复杂形式［即V（x，y，z）的出现］好像起了通常由边界条件所起的作用，即对E的确定值的选择作用。

这里我不能进一步做冗长的数学讨论，也不准备多讲求解的详细过程，虽然求解法实际上同通常的振动问题完全相同，即：引入一组适当的坐标（例如按照函数V的形式，可选用球面坐标或者椭圆坐标）并令ψ等于几个函数的乘积，其中每个函数只包含一个坐标。我要直接说出关于氢原子问题的结果。这里我们必须令

r是电子与原子核的距离。那么，可以看出，不是对于E的一切值，而只是对于E的下列值，才能够找到正则的、单值的和有限的解ψ：

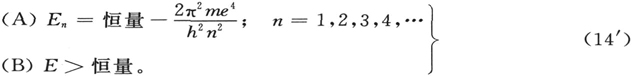
这个恒量同（14）中的相同，并且（在非相对论性波动力学中）除了我们不能很妥当地令它取通常为简便起见所取的那个值（即0）之外，它是没有什么意义的。因为，如取它为0，（A）式中所有的E值都将成为负的。而一个负频率，如果它终究还是意味着什么的话，它只能与绝对值相同的正频率意味着同样的东西。那么，为什么一切正频率都是可容许的，而负频率却只能是一组分立的值，这是不可思议的。但是这个恒量问题在这里是无关紧要的。

你们可以看到，我们的微分方程自动选择出来的容许的E值是：（A）按照玻尔理论量子化了的椭圆轨道的能级；（B）一切属于双曲线轨道的能级。这是很值得注意的。它表示，不管这种波动在物理上意味着什么，这个理论提供一种量子化的方法，这种方法绝对不需要任意假设这个或者那个量必须是一个整数。这里恰恰给出了整数如何发生的观念；例如，假如φ是一个方位角，而已知波幅总包含一个因子cosmφ，m是一个任意常数，那么，m必定应该取作整数，因为否则波函数将不是单值的了。

你们将会对于上述E值的波函数ψ的形式感到兴趣，并将追问是否可用它们来解释任何可观察的事实。事情正是这样，但是问题却颇为复杂。

第二次演讲

4．氢原子中波系的粗略描述。简并性。微扰

波幅函数的主要特性是：属于那组分立的E_n 值（椭圆轨道）的波幅函数随着离原子核的距离的增长而迅速递减，就是说像指数函数e^－const.r 那样，这实际上是将它们限制在这样一个区域之内，这区域的大小和对应的玻尔轨道具有完全相同的数量级。另一些属于双曲线能级的波幅函数递减得不太快，就是说只像r^－1 那样。

在上述区域中，“椭圆”函数的详细行为由于以下的理由不能很好地用唯一的方法来描述。属于一个E_n 值的一般不只有波动方程的一个解，却正好有n² 个独立解。从数学观点看来，这是一个例外，那是由于势能V的特殊形式，特别是它的球面对称性。属于一个本征值的解的多重性相当于著名的玻尔理论中属于同一能级的轨道的多重性。玻尔理论中称这为“简并性”，我们在波动力学中仍将保留这个名称。现在，既然方程是线性齐次的，任何带有完全任意系数的解的线性组合也是属于同一本征值的解。大家都知道，在这种情况下，如果另一组解是由第一组解的独立的线性组合形成的，其数目也和第一组解相同，那么，这两组解就无法区别开来。用这种构成线性组合的方法，我们能得到一些呈现出非常不同的行为的解。举例说吧，有这样一组解，它们的节面是：（1）同心球，（2）同轴锥，（3）通过锥轴的平面，你可以由这组解构成另一组解，在那里，同心球和同轴锥被两组共焦抛物面所代替。这还只是最简单的例子。一般说来，取任意的系数，节面系统将复杂得多。

属于各个本征值的解的这种多重性（这在通常的振动问题中已为大家所熟知）在原子问题中极为重要。如果没有多重性（例如，对于最低的频率，n＝1），那么，势能V的一个微小变化，例如相当于加上一个弱外电场，除了使本征值产生微小的位移和使本征解产生微小的变化以外，就不会再引起什么变化了——这就像将一小片金属附加到一个音叉上，只不过稍微改变它的音调和它的振动形式而已。但是一个多重的（比如说α重的）本征值在这种情况下却显示出这样一种实际的多重性，它分裂成α个稍有差异的不同本征值，其中每一个现在都有完全确定的本征函数，它稍稍不同于属于这多重值的本征函数的完全确定的线性组合。从理论上说来，这种分裂可为最微小的扰动所引起，并且可以由于两种性质不同的扰动而有很大的区别。举例说，一个均匀电场产生前述的抛物面节面，而磁场却产生球面和锥面。

几乎不需要说明，刚才所举两种情况下的分裂正相当于塞曼和斯塔克效应中氢光谱线的分裂。新理论对光谱线的位移所做的定量描述就像旧理论所描述的一样。但是，新理论能够描述更多的东西，那是旧理论所难以办到的，这就是：光谱线的偏振状态，它们的强度，特别是不存在许多这样的谱线，而要是我们考虑到能级分裂的一切可能的差异，我们本可以指望这些谱线是会出现的。我们将立即看到这一点。

5．波函数的物理意义。对于选择定则和光谱线的偏振定则的解释

微扰效应的高度重要性是在于这一事实：简并性一旦被消除，我们就必须立即同唯一地规定的本征函数ψ_k 打交道，对于所谓ψ这个量的物理意义所做的任何假说，现在就可以比较容易地加以检验了。

让我们称

E_k ＝hν_k 和ψ_k （x，y，z）

为问题的本征值、本征频率和本征函数，它的势能我们设想为是十分不对称的，由此足以消除一切的简并性。那么，带有任意常数c_k ，θ_k 的

将描述这系统的最一般的“振动”。 ^〔2〕 既然每个ψ_k 除了可乘以任意常数以外，它本身是唯一地规定了的，为了避免混乱起见，我们将使各个ψ_k 都满足归一化条件

∭ψ_k dx dy dz＝1．　　　　　　　（16）

或许这里值得一提，这些ψ_k 自动地具有一个非常重要的性质，那就是它们是相互“正交”的：

∭ψ_k ψ_ι dx dy dz＝0，当k≠ι，　　　　（17）

并且它们构成了一个完备的正交集；就是说，同它们全体都是正交的函数必然是0。（对于用这些ψ_k 来把任一函数展开为级数这件事来说，上述这些性质是十分重要的，但我们将不在这里讨论它，因为我们暂时还不需要）

现在回到一般的振动函数（15）。我们提出这样的问题：能否给ψ这个量以一定的物理意义，使得频率为

ν_kk′ ＝ν_k －ν_k′

的光的发射成为可理解的行，这是做得到的。但是，说来奇怪，这只有当我们利用复数的ψ函数而不是只利用它的实数部分时才能成立，而我们在通常振动问题中是习惯于只取实数部分的。

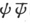必须接受的假说是很简单的，这就是令ψ的绝对值平方同电密度成比例，这个电密度按照通常电动力学定律引起光的发射。既然ψ的绝对值平方是ψ乘以共轭复数值的量（我们称它为 从（15）式立即可以看出，组成 的项是以所要求的频率ν_k －ν_k′ 的余弦因子这样的形式来包含时间的。更准确地说，让我们令电荷密度ρ为

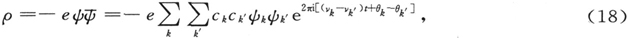
这里e表示电子电荷的绝对值。将此式对整个空间积分，并利用方程（16）和（17），我们得出总电荷为

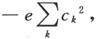
这表示我们必须假设

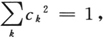
以便使总电荷等于电子电荷（我们有意要这样做）。

前面已说过，ψ实际上是限制在几个埃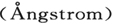 的非常小的区域内，因而ρ也是这样。既然频率为ν_k －ν_k′ 的光辐射的波长要比这个区域大得多，所以，大家都知道，起伏密度ρ的辐射同电矩的z分量为

M_z ＝∭zρ dx dy dz

（类似地可写出x和y分量）的电偶极子的辐射非常相近。从（18）式计算M_z ，在简单的演算之后，我们求得

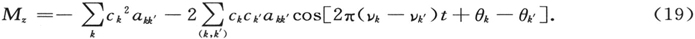
这里a_kk′ 是下面的恒量的缩写：

a_kk′ ＝e∭zψ_k ψ_k′ dx dy dz，　　　　（20）

而 表示对于所有的（k，k′）对求和。因此这些积分的平方（以及相应的关于x和y方向的积分）决定着频率为｜ν_k －ν_k′ ｜的发射光的强度。强度并不是由它们单独决定的；振幅常数c_k 当然也起作用。但这是十分令人满意的。因为积分a_kk′ 为系统的本性所决定，即为它的本征函数所决定，而不用考虑它的状态。a_kk′ 是相应的电矩的振幅，如果只有ψ_k ，ψ_k′ 这两个本征振动被激发，并且它们具有相等的强度 的话，a_kk′ 将由ψ_k ，ψ_k′ 这两个本征振动所产生。

（19）式中的第一个和式对我们研究的辐射没有意义，因为它表示电矩的一个不随时间变化的分量。

关于ψ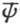 假说的正确性已经得到了验证，所用的方法就是在那些ψ_k 已被充分规定了的情况中，即在塞曼和斯塔克效应中计算出a_kk′ 。所谓选择定则、偏振定则和这些图样中的强度分布，都可用这些a_kk′ 以下述的明显方式来描述，而这种描述和实验完全符合。

一条预期会出现的谱线的不存在（“选择定则”）是用对应的a_kk′ 和另外两个关于x和y方向的恒量等于零来描述的。

一条谱线在一个确定方向上的线偏振是用这样一个事实来描述的：只有对应于这个方向的恒量a_kk′ 不等于零，而另外两个恒量都是零。类似地，比如xy^－ 平面上的圆偏振是这样来表示的：①z^－ 恒量等于零，②x^－ 和y^－ 恒量相等，以及③在方程（19）中相应的余弦函数之间有 的相差。

最后，氢的斯塔克图样和塞曼图像中那些不等于零的分量之间的强度关系是由这些a_kk′ 的平方值之间的关系来做正确的表示的；这种关系很能令人满意，因为，尽管我们缺乏关于c_k 的其他方面的知识，但是关于同一能级的精细结构的分量的各个c_k 是相等的这个假定是富有启发性的。

当然，不可能在这次演讲中把得出上述结论的任何计算都加以介绍；这样得耗费许多篇幅，虽然毫不困难，但却非常繁琐。但不管它们怎样繁琐，令人惊奇的是，一切人所熟知的但却不为人所理解的“定则”从非常平常而又基本的并且绝对令人信服的分析中一个接着一个地显示出来，这就像 除n＝m外都等于零这一事实一样。当人们一旦做出了关于ψ 的假说，就不需要也不能够做出任何附加的假说；如果这些“定则”不能正确地显示出来，那么谁也帮不了我们的忙。但是，很幸运，它们正是这样地显示出来了。

我想我应当提醒大家注意我只在开始时简略地提到过的另一个事实，即玻尔的非常基本的“频率定则”：

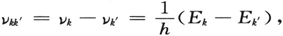
也可以说是为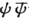 假说所解释。在原子中存在着确实以观测到的频率在振动着的某种东西，这就是电密度分布的某个部分，或者，如果你愿意，也可以是ψ 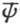的某个部分。

这可能引导我们去做这样的猜想：只有ψ函数的绝对值的平方才有实在的意义，而ψ函数本身则没有实在的意义。而这种设想又会引起这样一种愿望，即想用一个直接描述ψ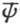 的行为的方程来代替波动方程。为了打消这种愿望，我要提醒你们回想一个事例，在这个事例中，由于完全类似的理由或许会引起类似的愿望；但你们全都会承认，要追求这种愿望是注定要失望的。

麦克斯韦方程描述电磁矢量的行为。但这些都不是真正能够观察到的。唯一可以观察到的是有质动力（ponderomotive forces）或者能（如果你愿意的话），因为这些力都是由虚能差所引起的。但所有这些量（能、麦克斯韦应力）都是场矢量的二次函数。因此，我们或许会期望用别的方程来代替麦克斯韦方程，这些方程可直接决定场矢量的可观察的二次函数。但是任何人都会同意，这无论如何意味着很大的麻烦，而且没有麦克斯韦方程实际上也就不能做到这一点。

6．含有时间的波动方程（就其本来的意义而言）的推导

我们用来研究氢原子的方程

仅仅提供振动振幅在空间中的分布，它对时间的依赖关系总是由下式表示：

频率的值E在方程中出现，所以我们实际处理的是一组方程，其中每一个方程只对一个特殊的频率成立。事情正如同在通常的振动问题中一样；我们的方程对应于通常所谓的“振幅方程”［见第3节，方程（10′）］

而不对应于

前面已讲过从后一方程导出前一方程的方法（即假设p是时间的正弦函数）。现在的问题是从相反的方向进行类似的推算，即要消去振幅方程中的参数E，而用时间导数来代替它。这很容易做到。取方程组（13）中的一个（具有一特殊的E值），然后，从（21），我们得到

利用这个关系，我们从（13）得到

不论E取什么值，都可以得到同样的方程（因为E已消去）。因此方程（22）对任何本征振动的线性组合都将成立，即对于那种作为这问题的解的最一般的波运动，这方程也是成立的。

我们可以进一步尝试在势能V明显地包含时间变数的情况下也利用这个方程。这究竟是不是一个正确的推广，并不是显而易见的，因为可能遗漏了那些包含 等等的项——从我们得到这个方程的方法看来，它们或许是有可能进入方程（22）的。但是成果会证明我们的做法是否正当。当然，要做出假定，说方程（13）中的V是明显地包含时间的，那是荒谬的，因为限制这个方程的条件（21），在一任意变化的V函数的情况下，会使这个假定不可能满足（13）。

7．受交变电场微扰的原子

这个推广使得我们能够解决这样一个重要问题：在交变外电场即入射光波的作用下，原子的行为是怎样的呢？这是一个非常重要的问题：因为它不仅包含次级辐射特别是共振辐射的机制，并且还包含在适当频率的入射辐射作用下原子态变化的理论，此外，还有折射与色散的理论；因为，众所周知，色散——我指的是一种折射率的现象——是由于初级辐射和所有次级子波的叠加而形成的，这些次级子波是物体的每单个原子在初级辐射的作用下发射出来的，它们和初级辐射同相。如果入射电矢量E使得每个原子发射一个次级子波，就像电矩偶极子所发射的一样：

M＝αE，　　　　　　（23）

式中α是一个恒量。如果单位体积中有Z个原子，那么，它们将使折射有一个增量

2πZα．　　　　（24）

因此，研究α的值（它通常依赖于频率）就意味着研究折射与色散的现象。

为了考察原子在交变电场作用下的行为，让我们设想方程（22）中的V是由两部分组成的，其中一部分描述原子内部静电场V₀ ，而另一部分描述光场Aez cos 2πνt；A，ν表示光场的振幅和频率，我们假定这光场是沿z方向而偏振的（电子电荷的负号已经考虑到了，这里的e是一个正数）。因此方程（22）成为

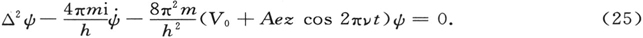
我们将设想A较内部场（用V₀ 表示）小得多，并用近似法解这个方程。如果A是零，我们将通过假设（21）而回到方程（13）（不同的仅仅是以记号V₀ 代替V）。我们将假设未受微扰的原子的问题已完全解决，它的归一化本征函数和本征值是

ψ_k 和E_k （＝hν_k ）．

因此，当A＝0时，（25）的最普遍解是

式中各个c_k 是任意复数值恒量。

我们将试用（26）去满足仍带有A的方程（25），但是（26）式中的c_k 现在要随时间做微小的变化（恒量变值法）。考虑到这一点，并考虑到ψ_k ，hν_k 是未受微扰方程的本征函数和本征值，将（26）代入（25），我们很容易得到

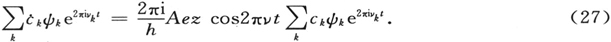
如果左端对于正交函数ψ_k 的完备系展开的全部系数和右端相应的展开系数恒等（对于任何时间都恒等），则这个方程将被满足。因此，乘以ψ_ι 并对整个空间积分。取缩写（见第5节）

a_kι ＝e∭ψ_k ψ_ι z dx dy dz．　　　　（20）

那么，由于各ψ_k 的归一性和正交性，我们得到

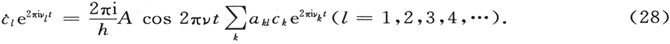
这个常微分方程的无穷集是和（27）等价的。分离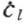 并将余弦分裂成指数函数，我们将它写成

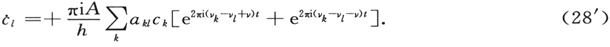
到这里为止，我们还没有利用任何近似方法。现在我们将用两种不同的方法来进行这一工作，一种方法导出了次级辐射理论（不包括共振的情况）和色散理论，而另一种方法则提供了共振的情况和原子态的变化。

第三次演讲

8．次级辐射理论和色散理论

在方程（28′）中，我们首先假设所有在指数上出现的组合

ν_k －ν_ι ±ν，

较

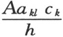
的数量级要大得多。这表示入射频率和任一个自发射频率的差要比原子从外场得到的势能所对应的频率大（完全共振或接近共振时除外）。从这个假设来看，方程（28′）表示c_ι 的全部时间导数都比指数函数的时间导数小。在说明了这一点之后，让我们在（28′）中的任何一个方程的右端取出任一指数函数。我们可以假设，在指数函数的一个周期中，它的系数c_k 是一个恒量。因此，这一项将只使c_ι （左端的）产生一个小的周期振荡，当指数函数经过一个周期以后，这个c_ι 将恢复到原状（或者差不多如此）。但是同样的情况对所有指数函数都成立。因此所有的c围绕它们的平均值进行很多的微幅振荡，当A消失时振荡当然也就消失。因此，我们可以用一些恒量来代替方程组（28′）右端的各个c，就是说用它们的平均值去代替各个c，因为略去微幅振荡以后，这里只省略了那些带有A² 的项。我们用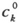 表示所说的恒量。现在这些方程很容易积分了。我们得到

因此，我们的解（26）中的第ι项将是

虽然我们还没有到达能和实验相比较的地步，但我们还是要用文字来描述那些在入射光波作用下按照方程（29）而发生的事件。不论每一个本征振动ψ_ι 本身是否一开始就是受激的，它都会被迫进行许多小的附加的受迫振荡，那就是，每一个被激发到相当程度的本征振动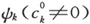 都给了它两份“赏赐”。如我们所说的：ψ_ι 因受到ψ_k 的“赏赐”而进行的两个受迫振荡的频率是ν_k ±ν，那就是入射频率同“赏赐”的本征振动频率的和与差。它们的振幅是同外场的振幅和“赏赐的”振动的振幅两者都成比例的；它们也包含一个因子a_kι ，这是一个恒量，它掌管着那个频率为｜ν_k －ν_ι ｜的自发射的强度。而且，在两个受迫振幅中出现了两个“共振分母”，当入射频率接近自发辐射频率｜ν_k －ν_ι ｜时，它们使得两个振幅中的一个急剧增大。

在从（26）和（29）得出完全解以前，我们不妨只限于处理最重要的情况，那就是只有一个自由振动（比如说是ψ_k ）受激的情况：

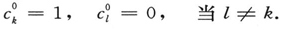
我们可以设想ψ_k 对应于正常状态。那么，在方程（29）的右端，第一项（除了ι＝k外）和连加号都可以略去，并且我们为了求完全解，得到［把方程（26）中的k用ι来代替］

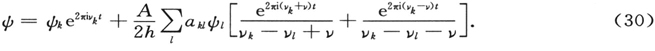
（注意现在指数已同求和指数ι无关；只有两个受迫振动的频率存在。）

为了得到次级辐射的知识，我们从（30）式构成合成电矩的分量 ^〔3〕 M_z 。在化简之后，省略二阶的微小项（同A² 成比例），我们得到

第一项－a_kk 同时间无关；它是由于自由振动ψ_k 的受激而形成的恒定电矩。我们在这里对它没有什么兴趣。第二项决定次级子波。它的频率与入射电力（Acos2πνt）的频率相同。它的相与入射电力相同或者相反，这要随ν≶ν_ι －ν_k 而定，就像在经典理论中一样［如果ψ_k 对应于正常态，所以ν_ι －ν_k 永远是正的，这个关系就成立；如果ν_ι －ν_k 是负的，则相反的关系成立；色散公式的克拉麦斯（Kramers）项］。从（31）式的右端第二项除去Acos2πνt就求得了方程（23）中的量α，根据表示式（24），它是决定对折射率的贡献的。分母（ν_ι －ν_k ）² －ν² 提供了所有那些包含ψ_k 的指数k（记住我们曾假定只有ψ_k 这一个自由振动被激发）的发射（或吸收）频率附近的反常色散现象。分子中的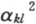 与那个决定自发射｜ν_k －ν_ι ｜的强度的量相同。在所有这些方面，这公式是亥姆霍茨老公式（为克拉麦斯的“负”项所补充）的完整的摹本，它被认为是同实验完全符合的。

另外两点也是值得提出的。你们都知道托马斯（Thomas）和库恩（Kuhn）提出了关于色散公式中全部系数的总和的假说，在我们这里是

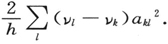
按照他们的见解，这应当等于有关一个受弹性束缚的电子的系数值，就是说，它必须等于

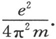
（在我们这里是乘以1，因为我们处理的是单电子原子；一般说来，应当乘以一个整数）

对于我们的色散公式，上述二量的相等是能加以证明的，但证明有点儿冗长，因此我要省略它。

第二个注意点如下：也许你们记得那个首先由斯梅卡（Smekal）提出的讲法：频率不同于入射辐射频率ν的次级辐射（因此没有相的关系，因此没有折射现象的影响）也应当是存在的。预期的频率是

ν±（ν_k －ν_k′ ）．

如果我们放弃只有一个自由振动是受激的这样的简单化的假定，而假设它们之中至少存在着两个，比如说ψ_k 和ψ_k′ ，那么现在的理论所给出的正是这些频率的次级辐射。

9．共振辐射理论，频率与自然发射频率一致或接近一致的入射辐射所引起的原子态变化的理论

在上节的开头，我们曾必须假设像

ν_k －ν_ι ±ν

那样的全部组合都有不可忽略的大小，这表示入射光的频率ν不能与所考察的原子的任何自然频率极其接近，现在我们要研究入射频率非常接近于一个自然频率的情形。为了集中我们的思想，设

ν_k －ν_ι ＋ν很小，而ν_ι ＞ν_k ．

（“很小”意味着数量级为Aa_kι ／h或者更小，也可能为零）

回到方程（28′），你们现在会发现方程组的右端有两个指数项都是缓慢地变化，这就是

前者出现在第ι个方程中，后者出现在第k个方程中。（我们将立刻看到）不管入射波的振幅A可能是多么小，这些项现在使c_k ，c_ι 两个量发生了很可观的“久期的”变化。而所有其他指数，如以前一样，只引起小的周期性扰动。因此，有理由略去它们，因为我们现在处理的是更为粗糙的现象（就是c_k 和c_ι 的可观的久期变化）。我们甚至可以设想，其他的c全都是零；这并没有什么关系，因为它们在我们所指望的准确度范围内都必然是恒量。为了决定c_k 与c_ι ，我们从（28′）得到两个简单的方程：

其中的简写为

①　严格地说，ε应等于2π（ν_k －ν_ι ＋ν）。——译者

为了解这两个方程，我们引入新的变数x，y，取

结果可改写为

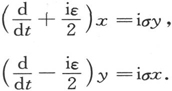
这些方程都有常系数，也都容易用熟悉的方法解出。解可以写成下列形式：

其中的简写是

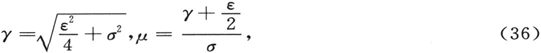
而ρ，ρ′，φ，φ′是任意的实恒量，如果你愿意，可以令它们不是负的。我们可以把（35）写成下列形式：

其中的简写

从（37）我们很容易得出x和y的绝对值的平方，也就是［由方程（34）］c_ι 和c_k 的绝对值的平方，从而我们得到问题中两个振动间变化着的强度分布的知识——这是主要的意义所在。我们得到

这些强度之和是恒量，正如所预期的一样。可以认为它是由三个部分所组成，其中有两个“部分”不变地固定在两个振动级上，第三“部分”（就是4μρρ′）在它们之间缓慢地振荡。为了集中我们的思想，让我们考察这样的一种情况，在这种情况下，全部强度在某一个时刻都集聚于一个振动（比如说下面的一个振动c_k ）。在选择适当的t值以使cosθ＝0的同时，这要求

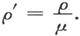
那么，我们就得到强度的振荡部分和总强度之比为

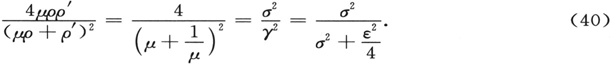
利用由（36）式可以明显看出的事实，即

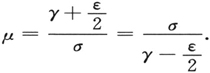
我们看到，当ε＝0时，总强度是振荡的。从（33）式可以看出，ε＝0意味着锐共振的情形。如果共振是不完全的，那么（40）表示只有某一部分强度在振荡，当缺少共振时，即当ε较（33）式规定的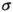 大得多时，振荡部分就变得微不足道了［ 的数量级是原子在光波的电场中由于第k个和第ι个振动方式的合作而形成的电矩所获得的势能（除以h）］。如果能够构成入射光振幅A的全面观念的话，量 在一定意义上会给出共振线的天然锐度的度量。我们不拟在这里讨论这个问题。

这里粗略地提出的理论既描述了由于适当的频率的辐射而引起的原子态的变化，也描述了共振辐射的出现。由于两个振动ψ_k 和ψ_ι 的存在，当然会引起它们的天然发射。值得指出的是，由于方程（34）中出现的指数，这种发射的频率不应该正好等于ν_ι －ν_k ，而是应该正好等于入射光波的频率ν。

10．波动力学向非单质点系的扩展

到此为止，我们只对一种很简单的系统应用了波动力学方法，这系统就是一个在不变的力场或随时间而变的力场中运动的单质点。现在我们要着手研究完全任意的力学系统。我们或许在以前就可以做到了这一点；对前面谈过的关于交变电场作用的一切，只要稍加修改，就可以应用到任意的系统上去，即多电子原子上去。但是我想，在我们的心目中有一个清晰而简单的实例，似乎更好。

在第一次演讲中所做的关于基本波动方程的推导很容易扩展到完全任意的系统，唯一的差别就是发生波传播的“空间”不再是通常的三维空间，而是“位形空间”。

让我们回忆一下曾作为我们的出发点的哈密顿－莫培督原理，就是

令

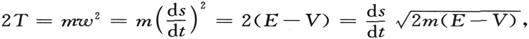
我们就将（1）变换为

然后我们将它同关于波传播的费马原理

作比较，这就使我们得到

现在，T一般不取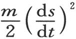 这种简单形式，而取

式中b_ιk 是广义坐标q_ι 的函数。我们现在用下式来定义广义的q空间中的线元ds：

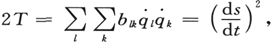
或者　　　　　

后式所描述的广义非欧几里得几何正是哈因利希·赫兹（Heinrich Hertz）在他的著名的力学中所应用的几何学，这种几何学使他在处理一个任意系统的运动时，在形式上可以像处理一个单质点的运动一样（在一非欧几里得的多维空间里）。将这种几何学引用到这里，我们很容易看出第一次演讲中导出基本波动方程的一切考虑都可以转换过来，甚至在形式上还稍有简化，就是说我们必须取m＝1。用完全像以前一样的方法，我们得到

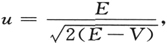
而最后得到的波动方程（或者比较恰当地说，是振幅方程）是

关于在本来意义上的波动方程，正和以前一样（第6节），我们得到

但是，∇² 现在既不能理解为三维空间中的初等拉普拉斯算符，也不能理解为多维欧几里得空间中的初等拉普拉斯算符（就是关于单个坐标的二阶导数之和），而应该把它理解为拉普拉斯算符在具有像（42）那样的广义线元的情况下的众所周知的推广。在处理广义的问题时，我们常能避免写出这种运算的明显的表示式；我们只需要知道它是一个二阶自伴（Self-adjoint）微分算符（不必介意你是否了解“自伴”的意义，此刻这并不重要）。但为了完满起见，我要写下∇² 的一般表示式。设a_ιk 是对应于b_ιk 的子行列式除以行列式∑±b_ιk 。令a表示a_ιk 的行列式。那么

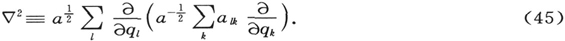
在笛卡儿坐标中处理质量为m的单质点的例子中，这个式子简化为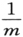 乘上初等∇² 算符（就是 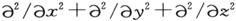）。或者，如果你选择任何别的坐标，例如极（polar）坐标或椭（elliptic）坐标来描述单质点的运动，你会得到 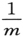乘以那个转换到这些坐标的初等∇² 的表示式。如果这系统是由n个自由质点组成，你可以把各个初等拉普拉斯算符除以相关质量，然后再加起来。

现在这种形式的理论可以应用到任意大于、等于、小于三个自由度的系统。我将很快地说明少数例子，如果它们没有什么物理意义，我将不做详细的计算。

11．例：振子，转子

举一维谐振子为例。在通常的力学中能量的表示式可以取为

（我们已将势能的系数用由它所引起的经典本征频率ν₀ 来表示）

由此很容易导出振幅方程：

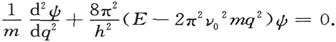
可以证明，只有对于下列E值，这个方程在沿实q-轴的解才是有限的：

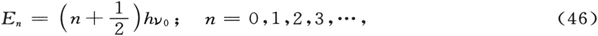
本征函数就是所谓正交厄米函数

其中

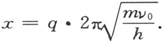
H_n （x）是所谓的n阶厄米多项式。（47）式的头5个函数的图形如下图2。

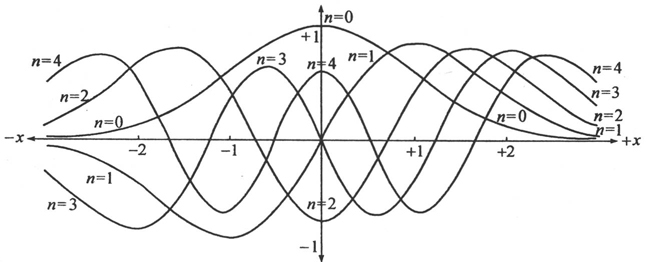
图2

虽然，理论上它们可以伸展到无穷远，实际上它们被指数函数限制在这样一个区域里，它的数量级与对应的经典力学质点的振幅的数量级相同（这很容易证明）。我们尚未讨论我们的广义ψ函数的物理意义。然而下面的陈述是颇有意思的：如果各ψ_n 是单电子问题的本征函数，而q是直角坐标之一，我们应当用积分

根据波动力学得出的普朗克振子的头5个本征振动。在本图中，在-3≤x≤+3区域之外，这五个函数全都单调地趋近x轴。

∫qψ_k ψ_n dq

的平方来估计（按照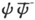 假说）频率为 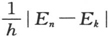在q方向偏振的发射的强度。如果在这里我们也试图这样做，我们就得到一个最令人满意的结果，就是说，积分等于零，除了

｜k－n｜＝1．

这意味着除了频率为1．ν₀ 以外，全部发射频率都是不许可的。后面我们将回到普遍情况下的ψ的物理意义问题。

用另一个一维问题作为第二个例子：其轴在空间中固定的简单转子。这里全部能量都是动能，就是

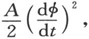
这里A＝转动惯量，φ＝转动角。振幅方程成为

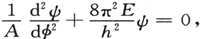
这方程有解：

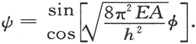
显然，必须限制ψ为以2π为周期的φ的周期函数。因此φ的系数必须是一个整数；这个条件提供了本征值

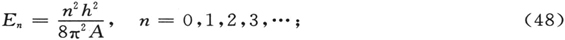
这同量子论的旧形式完全相符。现在让我们如前面一样地试图对辐射强度做一估计。在通常力学中，如果一个带电粒子固定在离转子重心距离为a的地方，它的直角坐标是

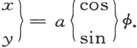
现在构成

既然头两个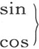 函数的乘积总是能用 的和或差来表示，那就容易看得出，除非｜n＋k｜或｜n－k｜等于1，或者，实质上也等于说，除非｜n－k｜＝1，上式中所包含的8个量都将等于0。这是众所周知的关于转子的选择定则。现在不假定转子的轴在方向上刚性地固定的，要处理这样的转子是颇有意思的。我们求得振幅方程为

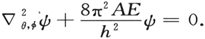
这里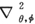 表示初等∇算符（当用极坐标表示时）中只包含着对θ，φ这些角微分的那个部分。已知上面的方程式只有当常数为两个相接连的整数的积：

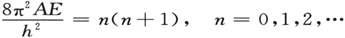
时，它的解才是有限的、单值的，而且此解是n阶的球面谐函数［本征值E_n 是（2n＋1）重简并的，因为有2n＋1个独立的n阶球面谐函数］。这给出了本征值

这主要意味着“经典”的公式（48）中的n应当由“半整数”来代替［因为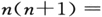 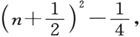而在所有E_n 中的一个共同常数在构成它们的差时被消去］。已经知道，带光谱的表示常常不得不使用“半整数”，并且它们似乎全都同新公式相符合［当然，在使用时，正确的公式是（49）式而不是（48）式，因为分子的轴绝不是刚性地固定下来的］。选择定则可用那个和前一例子中完全相同的方法得出，只是要通过更为麻烦的计算。

第四次演讲

12　关于氢原子中核运动的校正

在第一次演讲中，我们把氢原子当作一个单体问题来处理，就像它的核是固定于空间中的一样。在通常力学中，人们都熟知，如果我们从二体（质量为m和M）问题开始，我们可以把问题分离成为两个部分，就是：

①重心的匀速直线运动（惯性运动）。

②一个具有“并合质量”μ的物体绕一固定中心的开普勒运动，其中

按照玻尔的理论，对氢原子的这种精密的处理可以从He⁺ 谱线同那些氢谱线之间的频率的微小差异而得到定量的支持，如果原子核具有无穷大的质量，He⁺ 谱线就该同那些氢谱线完全重合（换句话说，只要考虑到核的微小运动，He⁺ 和H的里德伯恒量间的微小差异就可以定量地算出；索末菲）。

我们在波动力学中碰到完全相同的情形。二体问题的六维振幅方程是

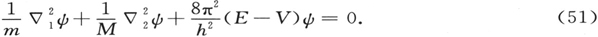
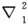和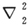 分别表示对于电子的坐标（x₁ ，y₁ ，z₁ ）和原子核的坐标（x₂ ，y₂ ，z₂ ）的初等拉普拉斯算符。关于V，我们只需假设它仅仅依赖于

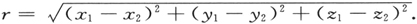
现在，引入重心的坐标（ξ，η，ζ）和m对M的相对坐标（设为x，y，z）来代替x₁ ，…，z₂ 。我们很容易证明

各∇² 的意义是很明显的；μ由（50）式给出。将此式代入（51），我们得到这样一个方程，只要假设ψ是一个只包含ξ，η，ζ的函数（设为φ）和另一个只包含x，y，z的函数（设为X）乘积，这个方程就可以分离成为两个部分。在分离时，引入这样一个恒量，它在下列方程中用E_t 表示。对于φ，我们得到

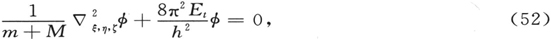
而对于X，我们得到

前一方程按照波动力学描述了不受力的重心的运动；常数E_t 对应于它的平动能量并且可以取任何正值。E－E_t 对应于内能。第二个方程正好是关于在固定场V中运动、具有质量μ的单体问题方程。因此，对应于内能的本征值同（14′）式只有一个区别，就是其中里德伯恒量中的m应由μ来代替。这样，前面提到的索末菲的重要结果在波动力学中得到了新的讲法。由于这种推导在分析上的简单性，在文献中关于这个问题未曾有过什么争论。但这实际上是多维波处理中必定有某些东西是正确的这一点的最直接证明之一——尽管起初多维波处理也许是令人不满的。

13．任意系统的微扰

和单电子原子的微扰理论相比，任意系统的微扰理论实际上并不显示什么新的特征。单电子原子微扰理论的一个特例已在第7—9节中做了讨论；但我们将重新用一种简明的方式来论述任意系统的微扰理论，以开阔我们的眼界。第10节的广义波动方程（44）可以写为

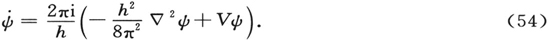
我们要用H来代表算符

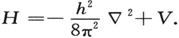
（V作为一个算符意味着“乘以V”）

那么，由第10节（43）式可以看出，本征函数正是那些受算符H作用后再现的函数，且不管一个作为本征值而同它们相乘的恒量：

H［ψ_k ］＝E_k ψ_k ．　　　　（55）

方程（54）可写成简单的形式：

现在，给V加上一个小的微扰场（它可以是也可以不是明显地含有时间），这意味着把算符H稍加改变（当然，也可以用其他方法引起H的变化，例如改变其中的一个质量，等等。而且也不妨把这种更加一般的情形包括在我们的处理中）。我们把这个改变后的算符叫做H＋H′，同时要记住H′必定是一个“小”算符。我们必须解

试代入带有缓慢变化的时间函数c_k 的

我们在最初得到

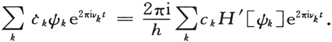
这个方程将得到满足，如果它和所有的ψ_ι 都正交的话。 ^〔4〕 乘以ψ_ι 并在整个位形空间中求积分：

这里　　　　　a_ιk ＝∫dqH′［ψ_k ］ψ_ι ，　　　　（60）

而∫dq总是表示在整个位形空间中求积分。各个a_ιk 都是微小的量。

我们要假设微扰是保守的。在这种情况下，a_ιk 就都是恒量，正如以前所处理的一些特例一样，只有指数为零的那些指数函数才使各个c_ι 有不可忽略的变化。首先，认为系统是非简并的。这样，略去只提供微小振荡的其他项，对于每个c_ι 你可以得到

如果你将它代入（58）式，这就不过是意味着频率稍有改变，其改变量是

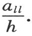
现在，考虑一个简并的例子。设振幅c_ι ，c_ι＋1 ，…，c_ι＋α－1 属于α个不同的本征函数，这些本征函数全都是属于同一个本征值E_ι 或本征频率ν_ι 的。那么在同它们有关的每一个方程中，你会得到不仅仅是一个而是α个等于零的指数，它们都是引起久期变化的。因此这α个振幅将由下面一组方程来决定：

这些方程表示，在很小的微扰的影响下，在属于同一本征值的简并振动方式之间，一般将有振幅的交换。说它是一种交换，那是正确的，因为从方程（62）容易证明

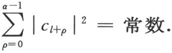
然而当想到这种交换时，我们必须记得本征函数组ψ_ι＋ρ （ρ＝0，1，2，…，α－1）是可以任意地进行行列式为1的正交线性变换的。这引导出振幅c_ι 的类似的变换。给定一个确定的微扰，即给定a_{ι＋λ，ι＋ρ} 这些量的确定的值，至少总能够找到各个ψ_ι＋ρ 的一种正交变换，它可以把方程（62）转化为非简并情形的简单形式（61）。这样，用一种适合微扰的这种特殊形式的方法所选定的这些特殊的本征函数，在微扰的作用下，会有恒定的振幅平方值，但它们一般将会属于稍有差别的本征频率。α重本征值已经被分裂为α个稍有差别的本征值；简并性为扰动场所消除，而这个简并问题中所特别选定的本征函数，都成为这样的一种非简并本征函数，它们同这微扰问题的各个本征值都是“零级近似”的。本征值的α个微小的改变量可以用“久期方程”

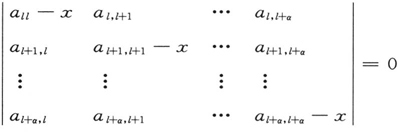
的α个根来表示。

当然，还可能碰到这些根并非全都不同的情形；这时，某种程度的简并性仍然保持着。我们或者可以说，一组任意选定的简并函数中的各个函数都以未受微扰的频率在振动，但交换它们的振幅；——或者可以说，这组适当的函数中的各个函数都有固定不变的振幅，但每个函数都有稍微不动的频率：这样两种说法当然是相同的。因为——我们可以说明——或者是：一个具有变动的振幅的振动并没有真正获得我们认为它该有的那个频率；或者是：两个或者更多个稍有不同的频率，在它们相互叠加时，就引起了“节拍现象”，就是说，引起了振幅的变化。

14．两个任意系统间的相互作用

现取起初没有相互作用的两个任意系统，其中之一是按照波动力学［参见方程（56）］由

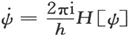
来描述，而另一个则由

来描述。将第一方程乘以φ，第二方程乘以ψ，然后将二者相加；你可得到

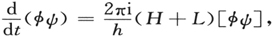
因为算符H并不影响φ，而算符L并不影响ψ。最后的方程是“并合系统”——即想象上把这两个系统合而为一——的波动方程。（所用的方法恰好和“分离”方程时所经常使用的方法相反，而分离方程时假设解是两个各自依赖于不同的单个变量的函数所形成的乘积。）并合系统的本征函数是第一个系统的任一本征函数和第二个系统的任一本征函数的乘积。不难看出，这样两个本征函数的乘积的本征值是各个本征值之和（这相当于通常力学中的能量的可加性）。单个系统即使是非简并的，但由于本征值的相加，在并合系统中却有可能出现新的简并性（为简单起见，让我们假设是前一种情形）。设E，E′是第一个系统的两个本征值，F，F′是第二个系统的两个本征值，并假设

E＋F′＝E′＋F＝G

或

E－E′＝F－F′．

由此可见，如果两个系统之间存在共同的本征值差，那就会出现并合系统的一个二重简并的本征值G。为简单起见，假设没有别的这一类的关系，现在再假设两个系统间发生一个微弱的相互作用，将算符H＋L改变为H＋L＋T，这里T当然会既包含第一系统的变量又包含第二系统的变量。那么，属于E＋F′和E′＋F的振幅会现出一种缓慢的、久期的交换，而所有其他振幅则基本上保持不变。所讨论的两个振幅的平方和也是常数。

图3

从这两个单个系统看来，这只能这样进行解释：F的振幅因F′的振幅的减少而增加，并且好像是用来补偿E′的振幅一样，而E′的振幅的增加又是以E的振幅的减少为代价的。这似乎是旧量子论中所谓一个能量子E－E′（＝F－F′）从一个系统传递到另一系统的适当的波动力学描述。

15．广义ψ函数的物理意义

以上那些结论或许会由于下面这个事实而显得暧昧难解了，这就是，迄今为止，我们没有对函数ψ（q₁ ，q₂ ，…，q_n ，t）的物理解释提出任何明确的假说，这个函数是有关这样一个系统的，它的位形依据通常力学是用广义坐标q₁ ，q₂ ，…，q_n 来描述的。这种解释是一个很微妙的问题。在一般力学系统的情况下，下述观点或许是把电子电荷按照相对密度函数ψ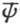 而扩展开来的这种做法（这种做法在单电子已提供了令人满意的结果，见第5节）的一种明显的推广：真实的自然系统的行为并不像通常力学为它（例如一个具有确定位形的点电荷系统）所建立的图像那样，而却像把这个系统（用q₁ ，q₂ ，…，q_n 来描述）按照相对密度函数ψ 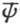在它的整个位形空间里扩展开来而得到的结果。如果一定要用到通常力学图像的话，那么，这就该意味着，实际系统的行为就像这样一幅通常力学的图像：在这图像中，这系统在同一时刻出现在它的一切可能的位形中，不过，在其中某些位形中要比在其他位形中表现得“更强”一些。

我曾在某一时期抱着这种观点。这种观点证明是很有用处的，这可由单电子问题（见第5节）中看出。没有任何别的关于ψ函数的解释能够使我们理解那些恒量a_kι 所提供的关于辐射强度和辐射偏振的大量知识。但是这种说明问题的方法肯定是十分不能令人满意的。因为，在以上那些句子中，“其行为像”什么的说法到底是什么意思呢？ψ函数的“行为”，即其随时间的发展，绝不是受经典力学定律这类东西支配的；它是受波动方程支配的。

有人提出了一个关于ψ函数的明显的统计解释，认为这种函数完全不和单个系统发生关系，而只是和一个系集（assemblage of systems）发生关系，ψ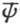 确定那些会出现在某一确定位形中的系统（在整个系集中所占的）比率。这种观点有点儿不能令人满意，因为它完全没有说明a_kι 这些量何以能够提供它们确实已提供的一切知识。关于这种统计解释，据说，对于任何一个按照原子的经典图像会有确定的物理意义，并且在原则上（principiell）是可以量度的物理量，都有一些确定的本征值是属于它的（例如有些本征值E_k 是属于能量的）；而且据说对这样一个量的量度结果，总是这一个或那一个本征值，而绝不会是介乎两个本征值之间的。在我看来，这种说法似乎包含着一种颇为模糊的概念，那就是对于一个量（例如能量或动量矩）的量度概念，这种概念和原子的经典图像有关，也就是和一种显然错误的图像有关。按照那种我们明知道是错误的图像来解释量度，岂不是有点冒失吗？按照我们终将被迫接受的图像，这些量度会不会具有一种完全不同的意义呢？例如：让一束电子射线穿过汞蒸气之前和之后来量度该电子束在一个电场和一个磁场中的偏斜。按照旧概念，这可以解释为关于汞原子能级差的量度。波动图像则提供了另一种解释，那就是：一部分电子波的频率减小了，其减小量等于汞的两个本征频率之差。说这两种解释不互相抵触，而旧解释是可以同新解释一起站得住脚的，难道这是完全可信的吗？说在宏观现象中不可缺少的能量概念，在微观力学现象中会具有任何别的不同于每h秒的振动次数的意义，难道这是完全可信的吗？

（本文是薛定谔1928年在英国皇家研究院所作的四次演讲的讲稿。——编注）

（范岱年　译）

作为本征值问题的量子化

·Quantisation as a Problem of Proper Values·

在理论物理学中，还有什么比他建立波动力学的最初六篇文章更为出色的呢？……他熟悉人类和实践的许多领域，他的广博的知识、敏锐的思想和创造力都是惊人的。……他的名字是物理学出版物中出现最多的。我们中谁没有把薛定谔方程或薛定谔函数写过无数次呢？或许以后几代人也将这么做，并生动地记住他的名字。

——M. 玻恩

奥地利格拉茨大学一角

第一篇

（《物理学年鉴》1926年第4期，第79卷）

§1．在本文中，我希望首先来考虑简单的（非相对论性的和未受扰动的）氢原子的情形，并且证明通常的量子化条件可以为另一个假设所取代，在这一假设中，无须再专门引入像“整数”这样的概念。而当整数的确出现时，其出现方式就像一根振动弦上的节点数出现时那样自然。我相信，这种新的观念是可以普遍化的，并且深刻地触及了量子规则的真正本质。

后者通常的形式是与哈密顿－雅可比微分方程相联系的

寻求这个方程的解，可以表征为函数的和，其中每个函数都是一个独立变量q的函数。

现在，我们用一个新的未知函数ψ来表示S，它将表现为单一坐标的相关函数的积，即我们令

S＝K logψ．　　　　（2）

出于量纲的考虑，必须引入常数K，其量纲为作用量的量纲。这样，我们得到

现在，我们并不着手寻求方程（1′）的解，而是按如下操作。如果我们忽略质量的相对论性变化，方程（1′）总可以转换成（ψ及其一阶导数的）等于零的二次方形式。（对于单电子问题，这甚至当质量变化不被忽略时也成立。）现在，我们寻找一个函数ψ，使得对于它的任意的变化，我们在整个坐标空间对于所说的二次形式的积分是稳态的，ψ是处处实在的，单值的，有限的，二阶连续可导的。 ^〔5〕 量子化条件为这一变分问题所取代。

首先，我们取H为开普勒运动的哈密顿函数，并证明ψ的如此选取适用于E的所有的正值，但当E小于零时，只适用于一组负的分立值。这就是说，上述变分问题有着分立的和连续的本征值谱。

分立的谱系对应于巴耳末项，而连续谱对应于双曲线轨道。为了数值上一致，K必须取值为h／2π。

变分方程的形成中，坐标的选取是任意的，让我们取笛卡儿直角坐标系。于是，在我们的情形中，方程（1′）变成

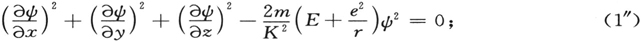
其中e＝电荷，m＝电子质量，r² ＝x² ＋y² ＋z² 。

我们的变分问题于是变为

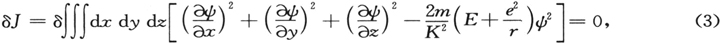
积分对于整个空间进行。由此，按通常方式，我们发现

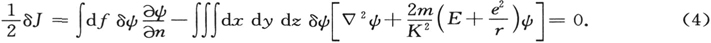
于是，我们必然首先有

并且其次有

df为所进行积分的无穷闭合面上的面元。

（以后将证明，这最后一个条件需要对我们的问题补充一个关于δψ在无穷大处行为的假定，以便确保上面提及的本征值的连续谱的存在。见后文。）

方程（5）的解的得出，例如，可通过极坐标r，θ，φ的形式，如果ψ被写作三个函数的乘积，其中每个函数仅为r，θ或φ的函数。这一方法已为人们所充分地熟知。角函数表明为面谐函数，如果r的函数被称为X，我们易于得到微分方程

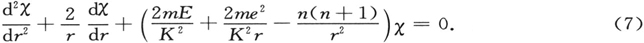
n＝0，1，2，3……

n必须限于整数值，以便面谐函数是单值的。我们要求（7）的解对于r的所有非负实数都是有限的。现在 ^〔6〕 方程（7）在复r平面上有两个奇点，位于r＝0处和r＝∞处，其中第二个对所有积分是“无穷点”（本性奇点），而反之，第一个（对所有积分）则不是。这两个奇点刚好构成了我们实区间的边界点。在此种情形中，我们现在知道假设X在边界点的有限性，等价于边界条件。方程一般不存在在两个端点都保持为有限的积分；这种积分仅对方程中某些特殊的常数值存在。现在的问题是确定这些特定的值。这是整个研究的突破点。 ^〔7〕

让我们首先来检查在r＝0处的奇点。确定在此点的积分行为的所谓指数方程是

ρ（ρ－1）＋2ρ－n（n＋1）＝0，　　　　（8）

其根为

ρ₁ ＝n，　ρ₂ ＝－（n＋1）．　　　　（8′）

因此，在此点的两个正则积分有指数n和－（n＋1）。由于n为非负数，二者中只有前者对我们是有用的。由于它拥有更大的指数，它可以由一个以rⁿ 开始的通常的幂级数表示。（另一个我们不感兴趣的指数，能包含一个对数，因为两个指标之间的差为一个整数。）下一个奇点位于无穷，因此上述幂级数总是发散的，并代表一个超越积分函数。由此，我们可以证明：

所需的解为（除了一个常数因子）一个单值有限的超越积分方程，它在r＝0处拥有指数n。

现在，我们必须研究这一函数在正实数轴上无穷远处的表现。在那一端，我们用代换

X＝r^α U，　　　　（9）

来简化方程（7），其中α如此选择，使得此项随着1／r² 衰减。此时，易于证明α必然具有n和－（n＋1）这两个值之一。方程（7）的形式于是变为

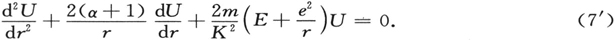
在r＝0处，其积分拥有指数0和－2α－1。关于α的值，对于这些积分中的第一个，α＝n，而对于第二个，α＝－（n＋1）。这些积分中的第二个是一个积分函数，按照（9），它导致所期望的单值的解。因此，如果我们限定自己于这两个α值中的一个，我们并不会失去任何东西。于是，取

α＝n．　　　　（10）

于是，我们的解U在r＝0处拥有指数0。方程（7′）被称为拉普拉斯方程。一般类型为

这里，常数的值为

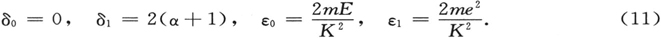
这一类型方程的处理相对而言是比较简单的，其原因是：通常会再导致一个二阶方程的所谓的拉普拉斯变换，这里给出了一阶中的一个。这使得（7″）的解可以由复积分来表示。这里，只给出这一结果。 ^〔8〕 积分

是（7″）对积分路径L的一个解，对此

常数c₁ ，c₂ ，α₁ ，α₂ 有下述值。c₁ 和c₂ 是二次方程

的根，并且

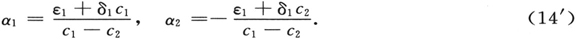
在方程（7′）的情形中，运用（11）和（10），这些变成

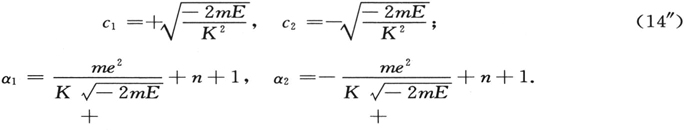
采用积分（12）的表示不仅允许我们考察当r以确定的方式趋于无穷时，解的总体的渐进行为，而且允许我们对于一个确定的解，给出这种行为的一种说明。这种说明始终是一个非常困难的任务。

首先，我们应当排除α₁ 和α₂ 为实整数的情形。当这种情形发生时，它会对两个量都同时发生，并且当且仅当

因此，我们假设（15）不被满足。

当r以确定的方式趋于无穷时（我们总是认为r通过正的实数值趋于无穷），解的总体的渐进行为由两个线性独立的解的行为来描写， ^〔9〕 我们称之为U₁ 和U₂ ，它们由下述积分L的路径的特征化而获得。在每种情形中，让z来自无穷，并沿同一路径回向那儿，其方向为

即zr的实数部分成为负的且无穷的。条件（13）由此得以满足。在一种情形中，让z沿点c₁ （解U₁ ）形成一个环路，而在另一个环路中，绕c₂ （解U₂ ）形成一个环路。

现在，对于非常大的r的正实数值，这两个解可由

所渐进地表示（在彭加勒的意义上），其中我们满足于取r的负整幂渐进级数中的第一项。

我们现在必须区分两种情形。

1．E≥0。这保证了（15）的不满足，因为它使得方程左首为一纯虚数。进一步，根据（14″），c₁ 和c₂ 也成为纯虚数。由于r为实数，（17）中的指数函数因而成为保持为有限的周期函数。来自（14″）的α₁ 和α₂ 的值表明，U₁ 和U₂ 二者都像r^－n－1 一样趋于0。因此，这必然对我们正研究其行为的超越积分解U是有效的，尽管它可能是来自U₁ 和U₂ 线性组合。进一步地，（9）和（10）表明函数X，即初始方程（7）的超越积分解，随着来自U的为rⁿ 所倍乘的增长，像1／r一样趋于0。这样，我们可以说：

我们的变分问题的欧拉微分方程（5）对每个正的E都有解，这种解处处单值，有限且连续；它在连续振荡下随着1／r在无穷处趋于零。表面条件（6）也已经被讨论。

2．E≤0。在这种情形中，可能性（15）因而并没有排除，而我们将暂时保持这样一种排除。于是由（14″）和（17），对于r→∞，U₁ 的增长将超越所有界限，而U₂ 将呈指数地消失。因此，我们的积分函数U（同样适用于X）将保持为有限的，当且仅当除了一个数量因子之外U与U₂ 相一致。然而，情形绝不可能如此，其证明如下：如果环绕c₁ 和c₂ 两点的闭合回路被选为路径L，则满足条件（13），因为回路确实被选在被积函数的黎曼曲面上。因为α₁ ＋α₂ 为一整数，因此易于证明积分（12）表征了我们的积分函数U。（12）可以展开为r的一个正幂级数，它对于所有事件都是收敛的，因为r足够得小，并且由于它满足方程（7），它必然是与U的级数相一致的。因此，如果L是环绕c₁ 和c₂ 的闭合回路，U即为（12）所表征。然而，这一闭合的回路可以如此地被扭曲，使得它看上去为来自上面所考虑的属于U₁ 和U₂ 的两个路径的相加组合；而且因子为非零的1和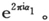 因此，U不可能与U₂ 相一致，而是必然也包含U₁ 。证毕。

因此，基于上述假说，我们的积分函数U（它单独地被看做是我们的问题（7）的解）对于大的r不是有限的。同时，保留完备性问题，即倘若我们的处理允许我们发现问题所有的线性独立的解，则我们可以说：

对于不满足条件（15）的E的负值，我们的变分问题没有解。

我们现在只需去研究那些满足条件（15）的负E值中的离散集。于是，α₁ 和α₂ 都是整数。（先前给我们以基本值U₁ 与U₂ ）的积分路径中的第一条，现在必定无疑地需要修改，以给出一个非零的结果。因为如果α₁ －1确实为正，点c₁ 既不是一个分支点，也不是被积函数的一个极点，而是一个寻常的零点。如果α₂ －1也是非负数，点c₂ 也可以成为规则的。然而，在每一种情形中，都易于发现两条合适的路径，积分也完全为已知函数所影响，因此，解的行为可以被完全地研究。

设

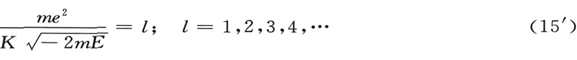
于是由（14″），我们有

α₁ －1＝ι＋n，　α₂ －1＝－ι＋n．　　　　（ ）

必须区分两种情形：ι≦n和ι＞n。

（1）ι≦n。于是c₁ 和c₂ 失去每一种奇异性质，而成为积分路径的起点或终点，以便满足条件（13）。这里的第三个特征点位于无穷（负的且实的）。每一条这三个点中的两个点之间的路径产生一个解，而在这三个解中有两个是线性独立的，如果我们计算出这积分的话，易于确认这一点。特别需要指出的是，超越积分解由从c₁ 到c₂ 的路径给出。这一积分在r＝0处为规则的这一点，可以即刻看出，而无须计算。我强调这一点，是因为实际的计算易于模糊这一点。然而，计算并没有表明对于r的正无穷大的数值，积分会趋于正无穷大。对于r的很大的值，其他两个积分保持为有限值，但对于r＝0，它变为无穷。

因此，当ι≦n，此问题无解。

（2）ι＞n。此时，由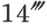（ ），c₁ 为零，而c₂ 至少为一阶积分的一个极点。于是获得两个独立的积分：一个来自从z＝－∞到0的路径，以避免极点；另一个来自这一极点的残数。后者是积分函数。我们将给出其计算值，但要为rⁿ 所乘，以便我们按照（9）和（10），获得起始方程（7）的解X。（常倍数是任意的。）我们发现：

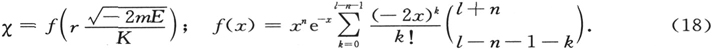
可以看出这是可被利用的解，因为它对于r的所有非负的实数值保持为有限。此外，它满足表面条件（6），因为它指数地消失于无穷。这样，归结关于E为负数的结果：

对于E为负数，当仅且当E满足条件（15），我们的变分问题有解。只有那些小于ι的值（在我们的安排中至少会有一个这样的值）才能被赋予整数n，后者标明了出现在方程中的面谐函数的阶数。解依赖于r的部分由（18）给出。

考虑到面谐函数中的常数（数值上已知为2n＋1），可以进一步发现：

对于任何允许的（n，ι）的组合，所发现的解正好有2n＋1个任意常数；因此对一个指定的ι的值，有ι² 个任意常数。

由此，我们可以确认对于变分问题的本征值谱，我们通常所论述的主要观点，但这里仍然存在着不足。

首先，我们需要关于上述汇集的本征函数系统的完备性信息，但我在本篇论文中没有论及这一问题。由类似情形的经验，可以假设本征值无一遗漏。

其次，必须记住对于E为正数所列出的本征函数，并没有如起初所假设的那样解决变分问题，因为它们仅随着1／r在无穷处趋于0，因此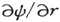 在一个无穷的球面上，只是随着1／r² 而趋于0。表面积分（6）依然与δψ_i 在无穷处为同一阶数。因此，如果想得到连续谱，则对此问题必须加上另一条件，δψ在无穷处将趋于0，至少趋于一个独立于所趋于无穷的方向的常数值。在后一种情形中，面谐函数导致表面积分趋于0。

§2．条件（15）得出

由此得出对应于巴耳末项的著名的玻尔能级。如果对（2）中为量纲原因引入的常数K，我们给出值

由此得出

我们的ι为主量子数，n＋1类似于角量子数。通过面谐函数的严格定义，这一数字的分离可以与角量子数分解为“赤道”和“极”量子数相比较。这些数字在这里，确定了球面上的节点线系统。“径向量子数”ι－n－1也精确地给出了“节点球”的数目，因为易于证明，（18）中的函数f（x）有着精确的ι－n－1个正实根。E的正值对应于双曲轨道的连续区，人们可以在某种意义上把径向量子数∞归之于它。与之相对应的事实，是在所讨论问题中，在连续振动下，函数的趋于无穷。

令人感兴趣的，是注意到这样一个范围，（18）中的函数在这范围中显著地不同于0，而在其外面它们的振动则衰减；在每种情形中，这一范围与椭圆的主轴具有一般的量级。径向矢量作为常自由函数f的自变量所乘的因子，自然地是一个长度的倒数，这一长度为

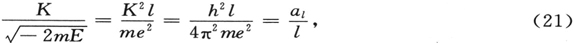
其中a_ι 为第ι个椭圆轨道的半轴。（来自（19）的方程加上已知的关系式E_ι ＝－e² ／2a_ι ）。

量（21）给出了当ι和n很小时，根的范围的量级；因为人们由此会设想f（x）的根为单位量级。当多项式的系数数值很大时，这当然不再成立。目前，我将不对根做更准确的估算，尽管我相信它会非常好地确证上述断言。

§3．当然，这会强烈地启示我们，应当尝试把函数ψ与原子中的某些振动过程相联系，这将比今日已遭到相当质疑的电子轨道更趋近于实在。起初，我想以这种更直观的方式发现新的量子化条件，但最终还是以上述更为中性的数学形式给出了它们，因为它揭示出了真正本质性的东西。在我看来，真正本质性的东西，在于“整数”假设无须再神秘地进入量子化规则，而是通过进一步回溯问题，从而发现“整数性”植根于某个空间函数的有限性和单值性。

在从新的出发点成功地计算出更复杂的情形之前，我不想进一步讨论这种振动过程的可能表征。尚不能确定这些结果是否仅为通常的量子理论结果的回响。例如，如果求解相对论性开普勒问题，发现会以一种引人注目的方式，得出半整数的部分（径向和角向）量子。

尽管如此，我想对于这种振动的表示做一些新的评论还是允许的。首先，我想说最初引导我走向这些思考的，是德布罗意的启发性论文 ^〔10〕 。通过反思那些“相波”的空间分布，他表明：度量电子的每个周期或类周期的路径，总存在着一个整数。主要的区别在于德布罗意考虑的是行进波，而我们导出的是稳态的本征振动，如果我们把我们的公式解释为代表了振动的话。我后面会表明 ^〔11〕 ，爱因斯坦的气体理论也能够建立在这种稳态本征振动的考虑上，德布罗意的相波色散定律已被应用于它。上述关于原子的反思，可以被表示为一种来自气体模型的推广。

如果我们取分离的函数（18），乘之以一个n阶的面谐函数，作为本征振动过程的描述，那么量E必须与相关的频率有关联。现在，在振动问题中，我们习惯于“参量”（通常称为λ）与频率的平方成比例。然而在我们的情形中，首先，这样的陈述对于负E值，会导致虚数的频率；其次，本能使我们相信，能量必然与频率本身，而不是它的平方成比例。

矛盾是这样得以解释的。对于变分方程（5）的“参量”E，并没有规定自然的零级别，特别是由于未知函数ψ的出现为一个r的函数所乘，而后者可以为一个常数所改变，以适应于E在零能级的对应的变化。因此，我们必须修正我们的预期，以便期待不是E本身（继续用同样的术语），而是为某一个常数所增加的E与频率的平方成比例。假设现在，这一常数与所有被允许的负E值（它已为（15）所限制）相比都非常大。于是首先，这频率将成为实数，其次，由于我们的E值只对应于相对小的频率差异，它们实际上将非常近似于与这些频率的差成比例。再一次地，这是我们的“量子本能”所全部能够要求的，只要能量的零级不是确定的。

振动过程的频率由

给出（其中C是一个与所有的E相比都非常大的常数）这一观点，还有另一个非常有价值的优势。它使得我们得以理解玻尔的频率条件。按照这一条件，辐射频率与E的差值成比例，由（22），因而也与那些假设的振动过程的本征频率ν的差值成比例。然而，比之于辐射频率，这些本征频率都非常大，它们彼此之间都非常接近。因此，这些辐射频率看上去像是本征振动自身的深层的“差音”。非常易于想象，在从一种常规振动向另一种的能量跃迁中，某种具有与每一个频率差相关联的频率的东西（我指的是光波），将使得它得以出现。人们只需设想，光波是与这样的拍在因果上相关联的，这些拍在能量跃迁中必然出现于空间中的每一点；这一种光的频率由每秒中拍过程的强度极值重复自身的次数来确定。

人们或许会反对说，这些结论建立在以一种近似的形式来表达（在平方根展开之后）的关系（12）的基础上，由此，玻尔频率条件本身似乎得到一种近似的性质。然而，这仅仅是表面如此；当相对论性理论发展起来，从而使一种深刻的洞见得以可能时，这种情形完全可以避免。很大的常数C自然地与电子的静止能量（mc² ）密切相连。频率条件中看上去新的并且独立引入的常数h（已由（20）所引进）也由相对性理论得以消除，或者说避免。但不幸的是后者的正确确立即刻遇到了某些困难，这一点我们已经间接地提及。

无须强调，想象在量子跃迁中，能量从一种振动形式变化到另一种形式，比起设想电子的跃迁来，要多么令人愉快。振动形式的变化能够在空间和时间中连续发生，而且它能像发射过程在经验上（W. Wien所做的关于极隧射线的实验）所能持续的时间一样地持久。然而，如果在此转换中，原子在一个相对短的时间里，被放到一个改变本征频率的电场中，那么只要这个场在运作，拍频率即刻会感应地改变。众所周知，这一实验上已确立的事实迄今为止已成为最大的困难。参见玻尔，克拉默斯和斯拉特（Bohr, Kramers and Slater）为解决此难题而提出的著名的尝试。

然而，我们不要忘记，在我们满足于我们在这些问题上的进展时，只要原子没有辐射，就只有一个本征振动被激发这一观念（如果我们必须坚持这一观念的话），已经偏离一个振动系统的自然图像很远了。我们知道一个宏观系统的表现并非如此，而一般产生的是其本征振动的杂汇（pot-pourri）。本征振动的杂汇对于单个原子也是允许的，因为与此相关联，拍频率的出现与依据经验，原子能够偶尔地发射并没有什么不同。事实上由同一个原子同时发射许多光谱线与经验并不相悖。因此，可以想象只有在标准状态（以及近似地在某种“亚稳态”），原子才以一个本征频率振动，也正是由于这一原因，即由于没有拍产生，才不再辐射。刺激可能由一个或几个其他的本征频率构成，拍频借此产生，并引起光的发射。

无论如何，我相信拥有相同频率的本征函数一般是同时受激的。用以往理论的语言说，即本征值的多重性对应于简并。简并系统的量子化的归约，或许对应于能量在拥有同一本征值的函数之间的配分。

1926年2月28日添加的对于证明的修正

在经典力学的保守系情形中，变分问题可以一种比前面所述的更为优雅的形式来表述，并且无须引入哈密顿－雅可比微分方程。由此，让T（q，p）为作为坐标和动量函数的动能，V为热能，而d_τ 为空间中体积元的“合理的量度”，即它并非dq₁ dq₂ dq₃ ……dq_n 的简单乘积，而是它除以二次形式的T（q，p）判别式的平方根（参见吉布斯的《统计力学》）。然后，让ψ以这种形式进行“哈密顿积分”

稳态的，同时满足归一化的附加条件

∫ψ² dτ＝1．　　　（24）

这样，这一变分问题的本征值是积分（23）的定态值，并且按照我们的论文，产生了能量的量子化能级。

值得注意的是在（14″）的量α₂ 中，我们本质上已经得到著名的索末菲表达式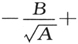 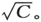（参见Atombau, 4^th (German) ed., p. 775）

苏黎世大学物理学研究所

（收稿日期：1926年1月27日）

第二篇

（《物理学年鉴》1926年第4期，第79卷）

§1．力学与光学之间的哈密顿类似

在进一步考察特殊系统的本征值问题之前，让我们来更好地理解存在于力学问题的哈密顿－雅可比微分方程和“相关的”波动方程，即第一部分的开普勒问题情形中的方程（5）之间的普遍对应。迄今为止我们只简略地描述了这种对应的外在的解析方面，通过第一部分中其自身也不好理解的变换（2），也通过同样不好理解的一种转换，即从某个表示式的等于零，到假设这一表示式的空间积分应当是稳态的。 ^〔12〕

哈密顿理论与波的传播之间的内在联系绝非什么新的观念。哈密顿不仅熟知它，而且还在他的《非均匀介质光学》中，用它作为发展起他的力学理论的出发点 ^〔13〕 。可以证明，哈密顿的变分原理对应于在位形空间（q空间）中波的传播的费马原理，哈密顿－雅可比方程表达了对于这种波的传播的惠更斯原理。不幸的是，在大多数现代重述中，哈密顿的这个强有力的和重要的观念的精髓被作为无足轻重的附饰物剥夺了，以有利于一种更为苍白的解析的对应表述。 ^〔14〕

让我们先来考虑经典力学中一般的保守系问题。其哈密顿－雅可比方程为

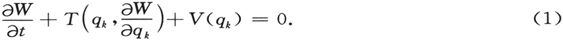
W是作用函数，即拉格朗日函数T－V沿着作为端点和时间的函数的系统路径的时间积分。q_k 为代表性的位置坐标，T为作为q和动量的函数的运动能，为后者的二次形式；如所规定的，动量被写作W对q的偏导数。V是势能。为求解这一方程，令

W＝－Et＋S（q_k ），　　　　（2）

得出

如所共知，E为任意积分常数，标示出系统的能量。与通常不同，我们让函数W保持为（1′）中的形式，而不是引入与时间无关的坐标函数S。这仅仅是一种表面性。

如果我们运用H. 赫兹（Heinrich Hertz）的方法，方程（1′）现在可以非常简单地表示。像所有位形空间（变量q_k 的空间）中的几何断言一样，如果我们通过系统的动能，把一种非欧几里得的度规引进这一空间，这一方程可以变得特别简单和清楚。

让T代表作为速度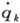 的函数的动能，而不是如上述那样作为动量的函数，然后把下式作为线元

现在方程右边只外在地包含dt，表示了（因为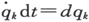 ）dq_k 的二次形式。

在此约定之后，诸如两个线元之间的角度，正交性，矢量的散度和旋度，标量的梯度，标量的拉普拉斯运算（＝div grad）及其他概念都可以如在三维的欧氏空间中一样简单地运用；我们若想在思维中运用欧氏三维空间而不造成损害，就必须使对这些概念的分析表达式变得非常简单，如线元（3）必须处处取代欧氏线元。我们规定：在这之后，所有q空间中的几何表述，都取此非欧几何中的意义。

对于计算的最为重要的一点修正，是我们必须仔细区分矢量或张量的协变和反变分量。然而，这种复杂性丝毫不比在笛卡儿坐标轴的倾斜组合情形中所发生的复杂。

dq_k 是协变矢量的原型。因此，形式2T的系数（它依赖于q_k ）具有协变的性质，并构成协变的基本张量。2T是属于2T的反变形式，因为已知动量为属于速度矢量q_k 的协变矢量，动量为协变形式的速度矢量。（1′）中的左边现在简化为反变的基本形式，其中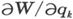 被引入作为变量。并区分矢量或张量的协变和抗变形式。后者构成了矢量gradW的分量，依其本性是协变的。

（于是，用动量而不是速度来表示动能，具有如此的意义：如果要导出的某样东西是可以理解的、即不变的，则协变矢量分量只能以反变的形式被引入。）

这样，方程（1′）等价于简单的表示

（grad W）² ＝2（E－V），　　　　（1″）

或

这一要求很易于分析。设想发现一个形式（2）的函数W满足它。于是，如果表面W的家族为常数，它被在q空间中描述，并且对其每一个成员，W被指定一个值，则这一函数在每个确定的t可以被清晰地表示。

现在，一方面，如下面马上要表明的，方程（ ）给出了如果已知表面家族的任一成员及其W值，要构造其他成员，并得出其W值的精确规则。而另一方面，如果用于构造的唯一的必要数据，即一个表面及其W值的给出相当任意，那么按照规则，它正代表了两种选择，从而完成了一个满足给定要求的W函数。时间暂时被看做是常数，因此构造规则穷尽了微分方程的内容；而它的每一个解，都可由适当选择表面和W的值来获得。

让我们来考虑这种构造规则。设在图1中，值W₀ 被给定为任一表面。为了找出表面W₀ ＋dW₀ ，取给定表面的任意一侧为正的一方，在它的每一点建立起法线，并且（对于dW₀ 的记号）切割出步幅

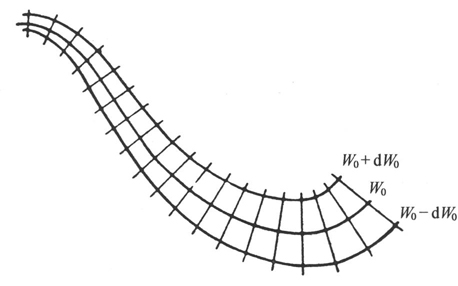
图1

步幅的终点的轨迹，就是表面W₀ ＋dW₀ 。类似地，表面家族可以成功地在两侧构造。

这一构造有着双重的解释，因为作为第一步，给定表面的另一侧也可以被取作是正的。这种含混对于后面这一步则不成立，即在这个过程的任何后面的阶段，我们都不再能任意改变我们已经获得的表面一侧的符号，因为一般这将在W的第一个微分系数中涉及一个不连续性。此外，在两种情形中得到的两个家族显然是相同的，只不过W的值是在相反的方向上。

现在，让我们来考虑非常简单的依赖时间的情形。对于这种情形，由（2）可知，对于任何以后（或以前）的时刻t＋t′，同一组表面说明了W的分布，尽管不同的W值是与单个成员相联系的，即对每个在时间t指定的W值，必定有被减去的Et′。W值依照一个确定和简单的定律，在表面之间徘徊，而正的E则在W增加的方向上。然而，我们还可以设想表面以这样一种方式徘徊，它们中的每一个连续地占据这样的位置和下述精确的形式，并总是带有它的W值与它一起。这种徘徊的定律由这样的事实给出：表面W₀ 在时间t＋dt必然总是抵达这样的地方，它在t为表面W₀ ＋Edt所占据。这可以由（4）获得，如果表面W₀ 的每一点被允许在正法线方向移动一个距离

即表面以垂直速度

移动，当常数E给定，它是纯粹的位移函数。

现在看来，表面W＝常数的系统，可以被看做是q空间中的一个渐进的然而却是定态的波运动的波面系统，其在空间中每一点的相速度的值由（6）给出。常规的构造可由基础的（半径为（5）的）惠更斯波结构，以及它们的闭合所清晰地取代。“折射率”与（6）的倒数成比例，依赖于位置，但与方向无关。这样，q空间是光学上不均匀的，但却是各向同性的。基本的波是“球”，尽管当然（让我们再次重申一下）是在线元（3）的意义上。

作用函数W在我们的波系统中扮演着相的角色，哈密顿－雅可比方程则是惠更斯原理的表示。现在，如果费马原理如此构造，

我们就直接导出了莫培督形式的哈密顿原理（这里时间积分有保留地取T＋V＝E，即使在变分中）。由此，“光线”（即与波表面正交的轨迹）为能量取E值的系统的路径，与著名的方程系

一致，这一方程说的是一组系统的路径能由每一个特殊的作用函数导出，就像流体的运动能由它的速度势导出一样。 ^〔15〕 （动量p_k 构成协变的速度矢量，方程（8）断言它等于作用函数的梯度。）

尽管在这些关于波面的考虑中，我们论及了传播速度和惠更斯原理，但我们必须把这种类似看做是力学与几何光学，而不是与物理光学或波动光学之间的类似。因为作为与力学相似的根本特征的“光线”的概念属于几何光学，它只能在后者中得到清晰的定义。同样，费马原理也能应用于几何光学，而无须超越折射率的观念。被看做波面的W表面系统与力学运动处于某种松散的关系中，因为力学系统的假想点并不沿着光线以波速u运动，相反，它的速度（对于常数E）与1／u成比例。这可由（3）中直接得出

这种不一致是明显的。首先，按照（8），系统的点速度当W的梯度很大时是很大的，即在那里W表面密集地拥挤在一起，亦即u是很小的。其次，由W的定义知，作为拉格朗日函数的时间积分，W在运动中（随着（T－V）dt在时间dt中）变化，因此，假想点不能连续地保持着与同一W表面的接触。

波动理论中的重要概念，如振幅、波长、频率（或者更一般地说，波形）都根本没有进入这种类似，因为不存在其力学对应物；甚至波函数本身也未被提及，除了W有波相的意义之外（而由于波形未加定义，这一点也是有些模糊的）。

如果在这整个对应中，我们发现的不过是一种令人满意的思考工具，那么这点缺陷就不会令我们困扰，而把任何弥补它的尝试看做是无足轻重的，相信这完全是与几何光学的一种类似，或至多不过是与某种非常初级的波动光学形式的类似，而不是与发展完善的波动光学的类似。几何光学仅仅是光的粗略近似，这因而也就无关紧要。而要沿着波动理论的路线，在q空间中光学的进一步发展中保持这种类似，我们就必须小心不明显地偏离几何光学的界限，即必须选择 ^〔16〕 波长足够的小，与所有路径的尺度相比很小。于是，这一补充就不会给我们什么新的教益，这一图景不过是添加了些无足轻重的装饰。

这样，我们可以开始我们的考察。但即使是发展这种相似到波动理论的第一步，就导致了如此惊人的结果，一个相当不同的疑虑产生了：事实上，我们今天都知道，我们的经典力学对于每个微小的路径尺度和很大的曲率都失效了。或许这种失效严格地类似于几何光学的失效，即“无穷小波长的光学的失效”；一旦障碍物或圆孔比之于真实的、有限的波长不再是很大时，这一点就是显然的了。或许我们的经典力学完全类似于几何光学，因而是错误的，与实在不符；一旦曲率半径和路径的尺度比之于某个被赋予q空间的实在意义的波长不再很大时，它就失效了。这样，问题就成为寻求 ^〔17〕 一种波动力学，而最明显的方式，就是从哈密顿相似出发，沿着波动光学的路线去求解。

§2．“几何”力学与“波动”力学

我们首先将假设，在扩展这一类似时，设想上述波动系统由正弦波构成是合理的。这是最简单和最明显的情形，而由这一设想的基本意义所产生的任意性也必须被强调。这样，波函数必须以因子sin（…）的形式包含时间，而波幅是W的线性函数。W的系数必须有作用量的倒数的量纲，因为W具有作用量的量纲，而正弦的相位是无量纲的。我们假设它是非常普遍的，即它不仅独立于E，而且具有力学系统的性质。于是，我们立即可以用2π／h表示它。时间因子则是

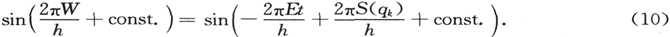
由此，波的频率ν由下式给出

这样，我们得到q空间波的频率以一种并非明显的人为的方式，正比于系统的能量。 ^〔18〕 当然，这一点的正确仅当E是绝对的，且如同在经典力学中一样，对于一个可加常数的范围并非不确定的。由（6）和（11），波长是独立于这一可加常数的，为

并且我们知道在根号下的项为动能的两倍。让我们把这一波长与由经典力学给出的氢的电子轨道的尺度初步作一粗略的比较，注意到q空间中的一“步”并非波长的尺度，而是由（3）得出的波长乘以质量的平方根。λ有着类似的尺度。因此，我们必须用轨道的尺度（比如说a cm）和m（电子的质量）的平方根除以λ。其商的大小的量级约为

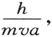
其中v代表的是此刻电子的速度（厘米／秒）。分母mva为力学的动量矩的量级，其大小至少对于开普勒轨道约为10^－27 的量级，这可由电荷和质量的值中计算得出，而独立于所有的量子理论。这样，我们就得出了经典力学的有效性的大约范围，如果我们能确定我们的h为普朗克作用量子的话——而这，只是一个初步的尝试。

如果在（6）中，E由以ν表述的（11）来表示，那么我们得到

这样，波速对于能量的依赖就变成了对于频率的特殊依赖，即它变成了关于波的散射定律。这个定律令人极感兴趣。我们已经在§1中表明徘徊的波面仅与系统点的运动有着松散的联系，因为它们的速度是不相等，也不可能相等的。按照（9），（11）和（6′），系统的速度对于波也有着具体的意义。我们立即可以确认

即系统点的速度，是一个波群的速度，包含在一个小范围的频率（信号速度）中。这里，我们再一次发现了关于电子的“相波”的定理，这是由德布罗意借助于相对论推导出来的，他的这些杰出研究 ^〔19〕 对于我的这一工作有着很大的启示。我们认为这一定理有着广泛的普遍性，它不仅起因于相对论，而且对于一般力学中的每个保守系都是有效的。

我们可以利用这一事实，在波传播和表征点的运动之间，建立比以往所可能的更加内在的联系。我们可以尝试构造一个在各个方向都有着相对小的尺度的波群，假设这种波群服从与力学系统中单个假想点同样的定律。这样，只要我们能把它看做近似地限定于一个点，即只要我们在比之于系统路径时，能忽略它的扩散，它就等价于一个假想点。这只有当系统路径的尺度，尤其是路径的曲率半径比之于波长很大时才适用。因为如上所说，类似于普通光学，显然不仅波群的尺度不能低于波长的量级，而且相反，如果它要近似地为单色波的话，波群在各个方向的扩散必须大于大数量的波长。然而，这点必须被假设，因为波群必须作为一个整体以确定的群速度运动，并对应于一个能量确定的力学系统（参见方程式11）。

就我所见，这样的波群可以建立在为德拜 ^〔20〕 和冯·劳厄 ^〔21〕 所采用的完全相同的原理上，他们用此原理来解决在普通光学中，对于光锥或光束给出精确的解析表征的问题。由此，出现一个在§1中未曾描述的非常有趣的与哈密顿－雅可比理论的关系，即著名的积分形式的运动方程的推导，通过哈密顿－雅可比方程的完全积分对于积分常数的微分。如我们即刻会看到的，用雅可比的名字命名的方程系统等价于这一表述：力学系统的假想点连续地对应于这一点，在此，某种波列的连续谱聚合在相等的相位。

在光学中，（严格地关于波动理论的）具有明确限定的有限截面的“光束”（它持续地聚焦，然后又发散）的表征，就这样由德拜实现了。它们被设想为平面波列的连续体，其中每一个都能填满整个空间。连续体的获得是通过让波面法线在整个给定的立体角中变化。于是，波通过在某个双锥外面的干涉，几乎完全彼此销毁。关于波理论，它们准确地代表了所期望的有限的光束，而衍射现象也必然由此限制引起。如果我们允许波群的波面法线仅在一个无穷小的立体角中变化，我们就可以用这种方式来把一个无穷小的光锥表示为就像是有限小的。冯·劳厄在他关于光束的自由度的著名论文中曾采用这种方法。 ^〔22〕 最后，如果我们不是用迄今为止都默认的纯粹的单色波，而是允许频率在一个无穷小间隔内变化，通过波幅和相位的适当分布，也限定扰动在经度方向的一个相对小的区域。这样，我们成功地给予一个相对小尺度的“能量包”以解析表示，它以光速运行，或是在发生色散时，以群速运行。如果详细的结构没有问题的话，由此可以以一种十分可能的方式，给出能量包的瞬间位置，就是空间中的这一点，在这儿所有叠加的平面波以精确一致的相位相遇。

现在，我们将把这些思考用于q空间的波。我们在一个确定的时间t，选择q空间中的一个点P，在这一时刻，波包沿着一给定方向R通过它。此外，让平均频率ν或是波包的平均E值也确定。这些条件精确地对应于在一给定时间，力学系统从一个确定的位形以一给定的速度分量出发。（能量加上方向等价于速度分量。）

为了扩展光学构造，我们首先需要一组具有所期望的频率的波面，即哈密顿－雅可比方程对于所给E值的一个解。这个解（比如说W）具有以下性质：在时间t通过P的这组表面，我们把它表示为

W＝W₀ ，　　　　（14）

它必定在P具有在规定方向R上的法线。但是这还不够。我们必须能以n折的方式（n为自由度数）使这组波W在一个无穷小的范围内变化，致使波面法线将清除掉P点的一无穷小的n－1维空间角，并使频率E／h在一个无穷小的一维区域中变化。由此，注意如何使无穷小的组波的n维连续体在时间t，在P点，在精确一致的相位上得以会聚。于是，在任何其他时刻，问题就在于要找出出现这种相位一致的点在何处。

要做到这一点，充分条件是我们能有一个哈密顿－雅可比方程的解W听由我们所使，这个解不仅依赖于常数E，这里标记为α₁ ，而且依赖于（n－1）个额外的常数α₂ ，α₃ ，…α_n ，依赖的方式是它不能被写成为少于n个由这n个常数构成的组合的函数。因为这样，我们就能首先，把规定于E的值给予α₁ ，然后其次，确定α₂ ，α₃ ，…α_n ，致使这个通过P点的表面集在P点有规定的法线方向。自此，我们由α₁ ，α₂ ，…α_n 来理解这些值，并取（14）为这组在时刻t通过点P的表面。然后，我们来考虑属于α_k 值的一个邻近的无穷小的α_k 区域的集合连续体。一些这种连续体，亦即对于数值为dα₁ ，dα₂ ，…dα_n 的确定的集和变化数值的连续体将给出为

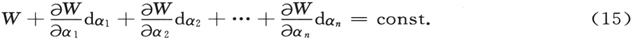
这一组的数目，亦即在时间t通过P的单个表面，将由下述常数的选择来确定，

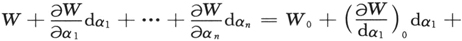
其中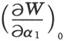 等为在微分系数中代入点P的坐标和时间t的数值所获得的常数（它后来确实只出现于 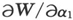中）。

对应于dα₁ ，dα₂ ，…dα_n 的所有可能值的集合的表面（15′），构成了它们自己的一个组。它们都在时间t通过点P，它们的波面法线持续地清除一个（n－1）维的小立体角；此外，它们的E参量也在一个小的区域中变化。表面（15′）的组如此形成，使得组（15）中的每一个都对（15′）提供一个代表，即这一成员会在时间t通过点P。

我们现在假设属于组（15）的波动函数的相位角刚巧与进入组（15′）的那些表示式精确一致。因此，它们在时间t在点P一致。

我们现在问：在任意时间，是否存在着这样一个点，组（15′）中所有的表面在此彼此截断，并且由此在这里，所有属于组（15）的波函数的相位都一致呢？回答是：确实存在一个相位一致的点，但它并非组（15′）中表面的共同交点，因为这样的交点在其后任意的时间并不存在。而且相位一致的点是以这样的方式产生的，组（15）持续地交换它们给予（15′）的代表。

证明如下。下列表式

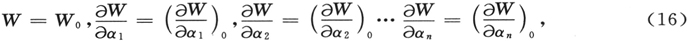
对于（15′）的所有成员的共同交汇点，必须在任何时间都同时成立，因为dα₁ 在一个小的区域内是任意的。在这n＋1个方程中，方程右边是常数，而左边的是n＋1个量——q₁ ，q₂ ，…q_n ，t——的函数。这些方程为初始数值系统所满足，即为P点的坐标和起始时间t所满足。对于t的另一任意值，它们在q₁ ，q₂ ，…q_n 将无解，但是要比这n个量的系统更为确定。

然而，我们可以如此操作。我们首先把第一个方程W＝W₀ 搁在一边，然后定义q_k 为这一时间和依据剩余的n个方程的这些常数的函数。让我们称这个点为Q。自然，由此第一个方程将不被满足，方程左边与方程右边将有某个值的不同。如果我们回到从（15′）到系统（16）的推导，我们刚才所说就意味着尽管Q对于（15′）这一组表面不是共同点，然而它对于从（15′）导出的一组却是共同点，如果我们对方程（15′）的右侧改变一个对于所有的表面都是常数的量。让这个新组为（15″）。因此，对于这组，Q为共同点。如上所述，这个新组来自于（15′），通过交换（15′）中的代表而得。这一交换由对于（15）中所有的代表，改变这一常数以相同的量而引起。因此对于所有的代表，相位角也改变了相同的量。这些新的代表，即我们称之为组（15″）的成员将会聚于Q点，如旧的组一样有一致的相位角。因此，这等于说：

由n个方程

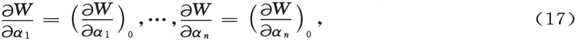
定义为时间的函数的点Q，对于整个波组（15）的集合继续为相位一致的点。

在所有n个表面中（由此Q由（17）表明为共同点），只有第一个是可变的；其余的保持为确定的（方程组（17）中只有第一个包含时间）。n－1个确定的表面决定了Q点的路径为它们的交线。易于证明，这条线为组W＝常数的正交轨道。因为按照假说，W在α₁ ，α₂ ，…α_n 总是满足哈密顿－雅可比方程（1′）。如果我们现在让哈密顿－雅可比方程对α_k （k＝2，3，…，n）微分，会得到这样一个表述：表面∂W／∂α_k ＝常数的法线，在它上面的每一点都正交于通过那点的表面W＝常数，亦即这两个表面中的每一个都包含另一个的法线。如果如通常情形，这n－1个确定的表面（17）的交线没有分支，那么这条交线的每个线元作为n－1个表面唯一的共同线元，与W表面的法线相一致，通过同样的点，即交线是W表面的正交轨迹。证毕。

我们可以以一种非常简短或者说速记的方式，对于使我们得以获得方程（17）的这些较为详细的讨论，总结如下：除了常数（1／h）之外，W表示了波函数的相位角。如果我们现在处理的不仅是一个，而是一个波函数系统的连续流形，并且如果这些是通过连续参量α_i 来连续地安排的，那么方程∂W／∂α_i ＝常数表达了这样一个事实：这一流形的所有无限邻近的个体（波系统）是相位一致的。因此，这些方程确定了相位一致点的几何轨迹。如果这些方程是充分的，这一轨迹将收缩到一点；于是这些方程确定了作为时间的函数的这个相位一致的点。

由于方程系（17）与已知的第二雅可比方程系一致，这样我们证明：

某个包含n个参量的无穷小的波动系统流形的相位一致点，按照与力学系统的假想点同样的定律运动。

我认为要精确证明这些波动系统的叠加，在一个围绕着相位一致的点的相对小的环境中，确实产生了显著的扰动，是非常困难的；而在所有其他地方，它们实际上都通过干涉彼此破坏，或者说上述陈述证明：至少对一个适当选择的振幅，并且或许对一个特别选择的波面形式是正确的。我将发展这一物理假说，它位列于有待证明理论之列，尚未尝试证明。后者仅当这一假说经受住了试验的检验，且其应用要求有精确的证明时，才是值得的。

另一方面，我们可以确定，微扰所被限定的区域依然在各个方向包含有大数量的波长。这一点是显而易见的，首先因为我们距相位一致点只有几个波长之遥，因此相位的一致是很少被扰乱的，就像干涉的稳定几乎就像在点自身一样。其次，只需看一眼普通光学的三维欧几里得情形，就足以确保这种一般的行为。

现在，我能明确地假设如下：

真正的力学过程，是以一种适当的方式，通过q空间的波动过程，而不是通过这种空间中的假想点来实现的。对作为经典力学对象的假想点的运动研究，仅仅是一种近似的处理，与真正的波动过程相比，其所需的辩护正如几何光学，或“光线”光学所需的辩护一样。宏观力学过程可以被描述为上述的波动信号，与路径的几何结构相比，它可以足够近似地视作限定于一点。我们已经看到，适用于这样的波信号或波群的定律，已在经典力学对于假相点的处理中发展出来。然而，当路径的结构与波长相比不再很大时，这种处理方式就失去了其全部的意义。此时，我们必须严格地按照波动理论来处理，即我们必须从波动方程出发，而不是从力学的基本方程出发，以形成可能过程的流形的图景。这些力学方程对于力学过程微观结构的无效，正像几何光学用于说明衍射现象时一样。

现在，作为经典力学的补充，已经成功地获得了对于这种微观过程的一种解释；尽管公认是在新的和相当任意的设定下，这种解释已经带来了最高意义上的实践上的成功。在我看来，非常重要的是这些理论（我指的是为索末菲、施瓦兹谢耳德、爱泼斯坦和其他人所推崇的量子理论形式）与哈密顿－雅可比方程及其解有着非常紧密的关系，即与这样一种已经非常清楚地指明了力学过程的波动特性的经典力学形式有着密切的联系。哈密顿－雅可比方程对应于（旧的简单形式的，而不是来自基尔霍夫的形式的）惠更斯原理。正像借助于一些在几何光学中不可理解的规则，可以在很大程度上说明衍射现象一样，通过作用函数理论，可以理解原子中的过程。但是，如果我们很自然地试图在这些过程中坚持系统路径的概念，我们就不可避免地卷入无法克服的矛盾；正如我们发现在衍射现象的邻近，追寻光线的路线是无意义的一样。

我们可以论证如下。然而，我不会对于实际过程给出结论性的图像，这种过程肯定不能由这一出发点，而只能由波动方程的研究来达到；我将限于定性地来说明问题。让我们想象一个其性质如上的波群，它以某种方式进入了一个小的封闭的“路径”，其尺度约为波长的量级，因而比之于波群自身的尺度是很小的。于是显然，经典意义上的“系统路径”，即精确的相一致点的路径将完全丧失了其特权，因为在特定点的前后周围存在着整个点的连续体，其中有着几乎完全的相一致，它们描述着全然不同的“路径”。换言之，波群不仅即刻填充了所有的路径区域，而且在各个方向都远远地伸展出这一区域。

我的确在如此的意义上来解释“相波”（按照德布罗意，这种波伴随着电子的路径）：这个意义就是不能赋予电子路径（在原子内部的任何意义上）自身以特定的含义，更不能给电子在此路径上的位置以任何意义。在此意义上我来解释如今已日趋明显的信念：首先，必须否认原子中电子运动的相有真实的意义；其次，我们决不能断言在一个确定的瞬间，电子会在量子路径的任何确定的地方被发现；第三，量子力学的真正定律不包含单一路径的确定规则，但在这些定律中，系统的整个路径流形的元素都被方程约束在一起，因此在不同的路径间存在着某种倒易关系。 ^〔23〕

不难理解，如果已知实验事实是如上表述的真实过程结构的后果的话，那么对于实验上已知量的仔细分析将导致这种断言。所有这些断言都系统地导向拒斥“电子的位置”和“电子的路径”这样的概念。如果不放弃这些，矛盾就会依然存在。这种矛盾是如此强烈，致使人怀疑原子中发生的事件究竟能否在时空框架中来描述。从哲学的观点看，我认为这样一种结论性的观点无异于完全投降。因为我们无法真的改变在空间和时间中思考的方式，我们不能在空间和时间中理解的东西，就是根本上不能理解的。会存在着这样的东西——但我不认为原子结构是这样的东西。然而，从我们的观点看，不存在这种怀疑的理由，尽管，或不如说因为它的出现是非常能理解的。因此，或许一个非常熟悉几何光学的人，在多次尝试用（在宏观光学中值得信赖的）光线的概念来说明衍射但无功而返后，至少会想到几何定律不适用于衍射，因为他持续发现他设想为直线运动和彼此独立的光线，现在突然甚至在单色媒介中，也表现出引人注目的弯曲，和明显的彼此相互依赖。我认为这种类似是非常严格的。即使对于无法说明的弯曲，原子中也不乏其类似——不妨想一想“非力学力”，它被设想出以说明反常塞曼效应。

现在，在那些必需的情形中，我们应如何着手力学的波动表述呢？我们必须不是从力学的基本方程出发，而是从Q空间中的波动方程出发，考虑依据它过程可能的流形会如何。在此篇论文中，波动方程尚未被清晰地运用，或甚至提出过，关于它的构造，仅有的相关数据是波速，它在（6）或（6′）中分别作为力学能量参量和频率的函数，而凭此数据，波动方程显然并未唯一地确定，甚至未决定它必须确定地为二阶。只不过因为对于简单性的追求，导致我们试图以此作为出发点。因此，对于波函数ψ，我们有

适用于所有通过一个因子e^2πiνt 依赖于时间的过程。这样，考虑（6），（6′）和（11），我们分别得出

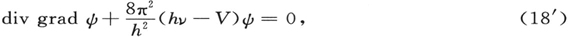
和

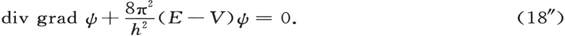
微分方程被理解为是关于线元（3）的。但是即使在二阶的假设下，上述方程也并非唯一与（6）一致的。因为有可能用

来取代div gradψ以加以概括，其中f可能是q的任意函数，它必然以某种可能的方式依赖于E，V（q_k ），以及线元（3）的系数。（例如，设想f＝u．）我们的假设再一次为对于简单性的追求所规定，而我认为在此例子中，一种错误的推演并非是不可能的。 ^〔24〕

在原子问题上，偏微分方程取代动力学方程这一步骤，由于这一方程所拥有的大量的解，因而初看起来是非常令人怀疑的。经典动力学已经导致了不止一个，而是相当大数量的解的流形，即导致了一个连续集，而全部的经验似乎都表明，其中只有一些分立的数目得以实现。按照流行的观点，量子理论的问题，就在于依据“量子化条件”，由按经典力学可能的连续路径集，来选择事实上的分立的路径集。对于在此方向上的新尝试而言，如果可能解的数目是增加了，而不是减少了的话，那似乎是一个不好的开端。

确实，经典力学也允许自身以偏微分方程的形式出现，即哈密顿－雅可比方程；但问题的解的流形并不对应于方程的解的流形。方程的一个任意的“完备”解，完全地解决了力学问题，任何其他完备的解产生了同样的路径——它们只是以另一种方式被包含在路径的流形中。

无论对于把方程（18）作为原子动力学的基础会表达出什么样的担心，我都不会断言对它无须要求进一步的附加定义。但这些或许不再会像“量子化条件”那样，其性质对于我们全然是陌生的和不可理解的，而是我们在物理学中，已习惯于作为偏微分方程的初始条件和边界条件而去发现的那一类东西。它们无论如何不会类似于量子化条件——因为在迄今为止我已讨论的所有经典力学的情形中，都证明方程（18）在自身中带有量子化条件。在某些情形中（而且的确在那些经验要求的地方），它辨别出自身，即某些频率或能级为仅凭自身对于稳态过程就是可能的，而无须任何不同于下述最明显要求的进一步的假设，这一要求就是：作为一个物理量，ψ必须在整个位形空间中是单值、有限和连续的。

这样，在任何涉及能级，或让我们说得更慎重些，涉及频率的情形中，所表达的担心转向了其反面。（对于它自身所坚持的“振动能”问题，我们必须不要忘记，仅在单电子问题中，解释为在真实的三维空间中的振动才是直接有启示意义的。）量子能级的定义在两个分别的阶段不再发生：（1）所有路径都是动力学上可能的定义；（2）通过特定的假设，来选择一些解，并抛弃更大部分的解。相反，量子能级被即刻定义为方程（18）的本征值，它在自身中带有其自然的边界条件。

至于在更为复杂的情形中，一种解析的简化在多大程度上能以这种方式行之有效，我现在还没有定论。然而，我期望如此。大多数解析研究有上述的两阶段过程中的感觉，必然会产生（1）一个更为复杂问题的解，对于最终结果确实是必要的：能量作为一个（通常）非常简单的量子数的合理函数。如已知情形，哈密顿－雅可比方程的应用创造了极大的简单性，因为力学解的实际计算被避免了。这足以估计一个代表了动量的积分，这一积分由于仅仅是对于一个闭合的复路径，而不是对一个变化的上限进行的，从而极大地减少了麻烦。哈密顿－雅可比方程的完备解依然必须真实地获取，即由求（面）积给出，这样力学问题的积分必须原则上对于任意的起始值有效。为寻求微分方程的本征值，通常我们实际上必须如此着手。首先，我们寻求方程的解，而不考虑边界条件或连续性条件；然后，由解的形式来挑选参量的值，使得解满足给定的条件。本文的第一篇提供了这样的一个例子。然而，我们也由这一例子——这是本征值问题的典型——看出，一般这种解只是以一种极为不能接受的解析形式给出的（在上述引文中的方程（12）），但它是对于那些属于“自然边界条件”的极为简化的本征值的。我并不是十分有把握说用于计算本征值的直接方法是否已发明出来。这种方法被认为适用于高阶的本征值的分布。但这种极限情形并非这里所感兴趣的，它对应于经典的宏观力学。对于光谱学和原子物理学，一般仅对前5—10项本征值感兴趣；甚至第一项本身已是伟大的成果——它定义了电离电势。从这一明确描述的观念，每一个本征值问题都允许自身被处理为极大和极小值之一，而无须直接指涉微分方程。在我看来，用于计算本征值（至少是近似）的直接方法非常有可能，只要有迫切的需求产生。至少应当有可能在单个的情形中加以检验，本征值（通过光谱学，数量上已达到所有所期望的精确度）是否满足这一问题。

这里我想提到，为消除量子困境，另一项研究也在由海森伯、玻恩、约旦和其他杰出的科学家同时进行， ^〔25〕 这种研究业已取得如此的成功，其中无疑包含着至少部分的真理。就其倾向而言，海森伯的尝试非常接近于我们已提及的当下的工作。但就方法而言，它们是如此的全然不同，我迄今还未能成功地发现两者间的联系。我显然希望，这两种理论进展间能不彼此抵触，而恰恰因为它们彼此出发点和方法的全然不同，它们能彼此补充，一方能在另一方失败的地方获得成功。海森伯纲领的优势，在于它允诺给出谱线强度这一事实，而这是我们现在还不能达到的。而我们这一尝试的优势——如果允许我就此做出评论——在于从物理学的观点看，它引导我们去创造沟通宏观与微观物理过程之间的桥梁，使得它们所要求的表面上不同的处理方式成为可以理解的。就我个人而言，在前一部分结尾所提到的把发射频率看做“节拍”的概念有着特殊的魅力，我相信它将导致对于强度公式的一种直观的理解。

§3．对于实例的应用

现在，我们将对第一部分所讨论的开普勒问题增添几个例子，但它们将具有非常简单的性质，因为我们暂时限定自己于经典的力学，不涉及磁场。 ^〔26〕

1．普朗克振子。简并问题

首先，我们将考虑一维振子。设坐标q为位移乘以质量的平方根。动能的两种形式于是为

势能将是

其中ν₀ 为力学意义上的本征频率。于是在这种情形中，方程（18）读作

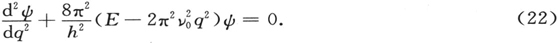
为简洁起见，写作

因此

引入独立变量

于是得到

这一方程的本征值和函数为已知。 ^〔27〕 借助于这里所用的符号，本征值为

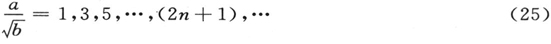
函数为厄米正交函数，

Hn（x）意味着第n阶厄米多项式，可被定义为

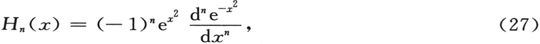
或展开为

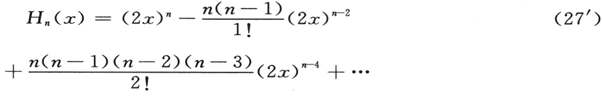
这些多项式的第一项为

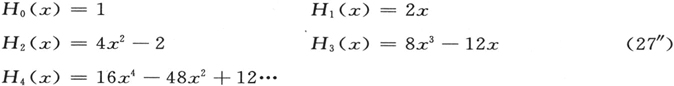
然后考虑本征值，我们从（25）和（23）得到

这样，作为振子的量子能级，就出现了奇特的“能量量子”的所谓“半整数”倍数，即hν₀ ／2的奇数倍。能级之间的间距（其本身对于辐射就是重要的）与在前面的理论中是一样的。值得注意的是我们的量子能级正是海森伯理论中的那些。在比热理论中，这一对于以往理论的背离不无重要性。其重要性首先在于当本征频率ν₀ 由于热的耗散而变化时。此前，它与产生于在普朗克理论的第一种和第二种形式之间作选择相关的老的“零点能”问题有关。顺便说，附加项hν₀ ／2也影响了能带边缘定律。

如果我们再次从（24）和（23）中引入原初的q，本征函数（26）变为

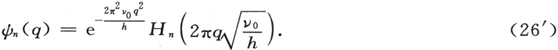
对（27″）的考虑表明，第一项函数是高斯误差曲线，第二项在原点为零，当x为正时对应于二维的“麦克斯韦速度分布”，当x为负时继续以一种奇函数的方式。第三项函数是偶函数，在原点处为负，而在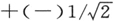 时，有两个对称的零，等等。曲线很容易被概略地绘出，可以看出连续多项式的根彼此分离。由（26′）也可看出被看做是数量级的本征函数的特征点（例如对于n＝0的半宽度，零点，以及最大值等）在经典的振子振动范围内。易于发现，经典的第n级振动的振幅由下式给出

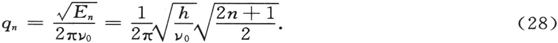
而在我看来，一般来说，对于本征函数的曲线图上经典的转折点的精确的横坐标，无法赋予什么确定的意义。然而，或许可以猜想，由于转折点对于相空间的波具有这种意义，因此，在这些点传播速度变为无穷，而在极大的距离上，则为负数。然而，在微分方程（22）中，这只是意味着Ψ的系数的消失，并导致没有奇点。

这里，我想指出的是（而且它是非常普遍有效的，而不仅限于振子）无论如何，传播速度的这种消失和成为虚数是某种非常典型的情形。它是仅仅通过函数应当保持为有限的这一条件，来选择确定的本征值的解析的理由。我想进一步地做一些说明。具有一个实传播速度的波动方程仅仅意味着：函数的值在所有那些其值低于邻近点的值的地方，都有着加速的增加，反之亦然。这样一种方程（如果不是如同在热传导方程中那样即刻且持久）在时间进程中，会导致最大值的拉平，而不允许在任何点有函数的过度增长。而具有虚传播速度的波动方程的意味则恰恰相反：高于周围的平均值的函数值经历了加速的增长（或更为迟缓的减少），反之亦然。因此，我们看到，为这种方程所代表的函数处于最大地超越了所有边界的增长风险中，从而我们必须熟练地操纵事物，以避免这种风险。正是明确确定的本征值使得这得以可能。确实，我们可以从第一部分中处理的例子中看出，一旦我们选择量E为正，对于明确确定的本征值的要求就即刻中止了，因为这使得波速在整个空间中全部为实数。

在这段离题的讨论之后，让我们回到振子，问一下当我们允许它有两个或三个自由度（空间振子，刚体）时，情况会有什么改变。如果不同的力学本征频率（ν₀ 值）属于分离的坐标，那么什么都没有改变。Ψ被看做是单一坐标函数的乘积；有多少个坐标出现，问题就分离成多少个上面所讨论类型的分离的问题。本征函数是厄米正交函数的积，整个问题的本征值被看做是那些分离问题的本征值的和，考虑其每一种可能的组合。（对于整个系统）没有本征值是多重的，如果我们假设在ν₀ 值之间没有合理的关系的话。

然而，如果有这样一种关系，同样的处理方式仍然是可能的，但它确实将不再是唯一的。会出现多重的本征值，“分离”当然会影响到其他的坐标，例如，球极坐标中的各向同性空间的情形。 ^〔28〕

然而，我们所得到的本征值确实是在每一种情形中都精确相同的，至少就我们（以一种方式获得的）所能证明的本征函数系统的完备性而言。这里，我们认识到一种与以往的量子化方法在简并情形中所遇到的著名关系的完全的类似。只是在一点上，有着并非不受欢迎的区别。如果我们应用索末菲－爱泼斯坦量子化条件，而无视可能的简并，那么我们总会得到同样的能级，但按照坐标的选择，却由于所允许的路径，而达到不同的结论。

现在，这并非这里的情形。确实，我们得到了一个完全不同的本征值系统，如果我们（例如说）所处理的这一振动问题，对应于未受扰动的抛物线坐标中的开普勒运动，而不是我们在第一篇中所用的极坐标的话。然而，这并非提供了可能的振动态的唯一的本征振动，而是这种振动的任意的，有限或无限的，线性的集合。而在其他方式中发现的本征函数也总是这样被描绘的，即它们被发现以一种任意的方式，被描绘为本征函数的线性集合，如果这些本征函数形成了一个完全系的话。

当然，迄今为止尚未考虑的能量如何在本征振动之间真实分布的问题，将会在某个时间被面对。依赖于以往的量子理论，我们将仅倾向于假定在简并情形中，属于一个确定的本征值的一组振动的能量，必须有某一指定的值；而在非简并情形中，这个值则属于一个单一的本征振动。我将仍然把这一问题留作未决，以及这样一个问题，即所发现的“能级”是否是真实的振动过程的能量台阶，抑或它们仅仅有着频率的意义。如果我们承认节拍理论，那么能级的意义对于说明锐发射频率就不再是必需的。

2．定轴转子

由于势能的缺乏和欧几里得线元，这是振动理论中可想象的最简单的实例。设A为转动矩，Φ为转动角，我们可清楚地得到振动方程

其解为

这里，辐角必须为Φ的整数倍，这是因为否则Ψ将既不是单值的，也不会在坐标Φ的整个范围内是连续的，如我们所知，Φ＋2π与Φ有着相同的意义。这一条件给出了著名的结果

这一结果与先前的量子化完全一致。

然而，对于带光谱应用的结果，却不能赋予任何意义。如我们一会儿就会知道的，这是一个特别的事实：我们的理论对于自由转子给出了另一个结果。这就一般而言，是正确的。在波动力学中这是不允许的，即设想系统运动的自由被比实际情形更为严格的限定，以便简化计算，即使我们从力学方程的积分中知道在某个单一的运动中，有些确定的自由没有被用上。对于微观力学，基本的力学方程系是绝对不合格的；它所处理的单一路径现在不再有单独的存在。一个波动过程填充了整个相空间。众所周知，即使是波动过程在其中发生的维度的数量也是十分重要的。

3．自由轴的刚体转子

如果我们引入从核出发的半径的极角θ和Φ为坐标，那么对于作为转矩的函数的运动，我们有

按照其形式，这是一个束缚在球面上运动的粒子的动能。这样，拉普拉斯算子不过是其空间拉普拉斯算子部分，依赖于极角，振动方程（18″）取如下形式

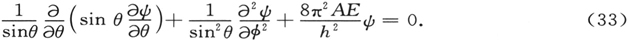
由假定ψ在球面上应当是单值的，连续的，得出本征值条件

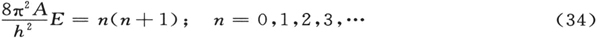
本征函数已知为球面谐函数。因此，能级为

这一定义不同于所有以前的表述（或许除了海森伯的以外）。然而，从来自实验的论证，我们被引向在公式（31）中将“半整数”值赋予n。易于看出实际上（34′）给出了如（31）一样的n的半整数值。因为

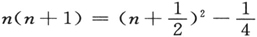
差异仅仅在于一个小的可加常数。（34′）中的能级差与从“半整数量子化”中所得的相同。这对于短波带的应用也同样正确，在这里，因为“电子跃迁”，转动矩在初始态和最终态不同。由于在能带的全部谱线中，至多不过有一个小的常数可加部分，它被淹没在很大的“电子项”或是“核振动项”中。此外，我们以往的分析不允许我们以（比如说）比下式更为确定的方式来说到这一小的部分

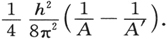
为关于电子运动和核振动的“量子化条件”所确定的转动矩概念，这里自然地追随着整个思想发展的线索。在下一节，我们将表明我们如何能通过综合第一小节：普朗克振子和第三小节：自由轴转子的情形，来至少近似地同时处理中心振动和双原子分子的转动。 ^〔29〕

我还愿意指出，值n＝0对应的不是波函数ψ的等于零，而是它的一个常数值，相对应的是一个在整个空间中振幅不变的振动。

4．非刚体转子（双原子分子）

按照第2节结束时的观察，我们必须论及最初具有转子所真实拥有的全部六个自由度的问题。对两个分子选择笛卡儿坐标系，即x₁ ，y₁ ，z₁ ；x₂ ，y₂ ，z₂ ，并设质量为m₁ 和m₂ ，r为它们之间的距离。势能为

其中　　　　　r² ＝（x₁ －x₂ ）² ＋（y₁ －y₂ ）² ＋（z₁ －z₂ ）² ．

而

可以被称为“合成质量”。由此，ν₀ 是中心振动关于连接中心，使之成为固定的线的力学本征频率，而r₀ 则是势能最小的相分离的距离。这些定义都与一般力学中的意义相同。

对于振动方程（18″），我们得到下列方程

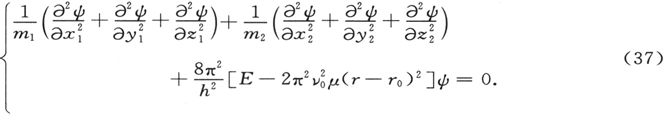
引入新的独立变量x，y，z，ξ，η，ζ，其中

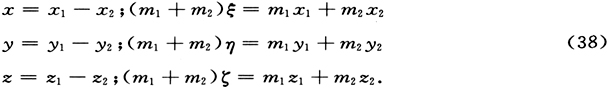
代换给出

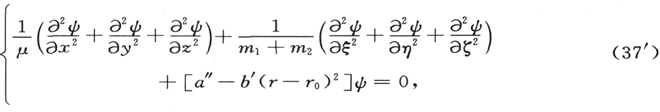
其中为简洁起见

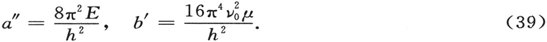
现在，我们可以认为ψ为相对坐标x，y，z的函数和质量中心的坐标ξ，η，ζ的函数的乘积

ψ＝f（x，y，z）g（ξ，η，ζ）．　　　　（40）

对于g，我们得到定义方程

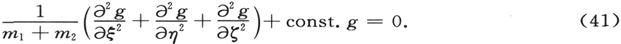
这与一个质量为m₁ ＋m₂ 的粒子在没有力作用情况下的运动方程形式相同。在这种情形下，常数的意义为

其中E_t 为所说粒子的平移能。设想把这个值插入（41）。关于可认可为本征值的E_t 的值的问题，现在依赖于这样一点：对于原初的坐标，以及对于引力中心的坐标而言，整个无限的空间是否是可利用的，而无须新的势能引入？在第一种情形中，每个非负值都是允许的，每个负的值都是不被允许的。因为当且仅当E_t 为非负的，（41）有非零解，并在所有空间中保持为有限。然而，如果分子被设置在一个“容器”中，那么后者必然为函数g提供边界条件；或者换言之，方程（41）由于引入了进一步的势能，将在器壁处突然地改变其形式，这样，一组分立的E_t 值被选为本征值。这是一种“平移运动的量子化”问题，其主要点我将在后面讨论，表明它导向爱因斯坦的气体理论。 ^〔30〕

关于依赖于相对坐标x，y，z的振动函数ψ的因子f，我们得到其定义方程

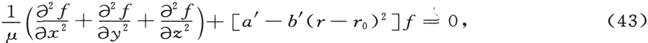
其中为简洁起见，我们令

现在我们不用x，y，z为坐标，而是引入球极坐标r，θ，φ（与先前r的运用相一致）。在用μ相乘后，我们得到

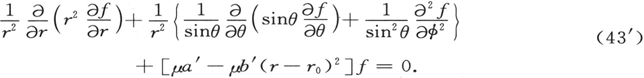
现在分解f。依赖于角的因子是一个面谐函数。设其阶数为n。被旋转的括号（curled bracket）为－n（n＋1）f。设想这一式被插入，为简单起见，让f现在代表依赖于r的因子。这样引入新的因变量

x＝rf，　　　　（44）

以及新的独立变量

ρ＝r－r₀ ．　　　　　　　　　　　（45）

代入得出

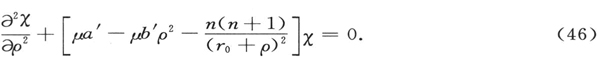
到这一点，分析都是精确的。现在我们来作一个近似（当然我知道，这需要比我在这儿所给出的更为严格的证明）。把（46）与前面讨论过的（22′）相比较。它们在形式上是一致的，不同之处仅在于以ρ₀ ／r₀ 的相对数量级来表示的未知函数的系数。这一点可由下面看出，如果我们这样展开

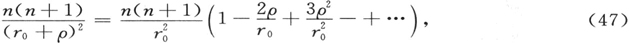
代入（46），并安排为ρ₀ ／r₀ 的幂形式。如果我们对ρ引入一个仅有一小常数之差的新变量，即

于是方程（46）的形式为

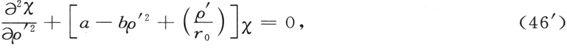
其中我们命

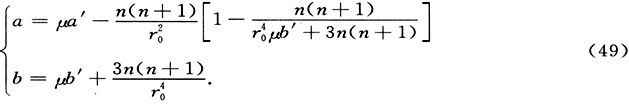
（46）中的符号 代表了与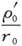 的级数残留相比较小的项。

现在，我们知道了方程（22′）的第一个本征函数。将其与（46′）相比，它在原点两侧的小区域中显著地不等于零。只有那些更高阶的函数逐渐会有进一步的展开。对于中等的阶数，如果我们忽略掉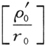 项，并记住分子常数的数量级，方程（46′）的区域比之于r₀ 确实是很小的。这样，我们得出结论（我再重复一次，并未做严格的证明），我们可以此种方式，在它们显著地不同于零处，得到第一本征函数（以及第一本征值）的一个有用的近似。由本征值条件（25）并忽略缩写（49），（39′）和（39），而引入一小量

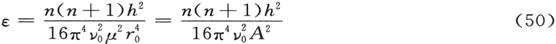
我们易于推出下列能级

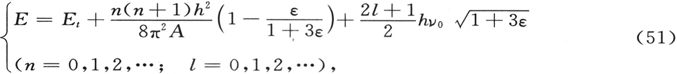
其中

仍然表示转动惯量。

按经典力学的语言，ε为转动频率对振动频率ν₀ 比率的平方；因此，当应用于分子时，它确实为一小量。除了这一小的修正和另一已提到过的不同外，公式（51）具有通常的结构。它是（25′）和（34′）的综合，其中所加的Et用以表示平移能。必须强调这一近似的有效不仅在于ε为一小量，而且在于ι不能太大。然而，实际上，对于ι只需考虑小的数量。

（51）式中ε的修正并不能用于说明中心的振动对于纯谐振类型的偏离。因此，与克拉策（Kratzer）的公式［参见索末菲（Sommerfeld）的前述引文］的比较和与实验的比较是不可能的。我只是想临时地提一下这一案例，作为一个例子，以表明这样一种直观的平衡结构的观念：核系统在波动力学中也保持其意义；并表明它这么做的方式，如果ψ的波幅实际上仅在平衡结构邻近的很小区域内不为零的话。这一三维空间中六个变量的波动函数的直接解释，起初无论如何都遇到了抽象本性的困难。

目前，当结合能中的非谐项被加以考虑时，双原子分子的转动－振动问题必须被重新处理。被克拉策巧妙地选来用于经典力学处理的方法，也适用于波动力学。然而，如果我们想把这一计算推进到对谱带结构的精细性是必需的，那么我们必须运用本征值和本征函数的微扰理论，这是当对一个微分方程中的一个未知函数的系数加上一个小的“扰动”时，这一方程的本征值和附属的本征函数所经历的变动。这一“微扰理论”是经典理论中的微扰理论的完全的配对，只是比起来更小些，因为在波动力学中，我们总是在线性关系的区域中。作为第一级近似，我们有这样一个表述：本征值的微扰等于微扰项对“未被干扰的运动”取平均。

微扰理论极大地拓宽了解析范围。作为一个重要的实践上的成功，我要说第一级的斯塔克效应在这里确实与爱泼斯坦公式完全相符，经过实验的确证，后者已经是无可怀疑的。

苏黎世大学物理学研究所

（收稿日期：1926年2月23日）

第三篇

微扰理论，借助于对巴耳末谱线的斯塔克效应的应用

（《物理学年鉴》1926年第4期，第80卷）

引言　摘要

如上篇论文结束时所说， ^〔31〕 通过比较基础性的方法，本征值理论的可应用范围能在“直接可解问题”的范围之外有可观的增加；因为对于这种与直接可解问题的足够密切相关的边界值问题，本征值和本征函数都易于近似地确定。类似于一般力学，我们把所讨论的方法称之为微扰方法。它基于本征值和本征函数所拥有的重要的连续性性质， ^〔32〕 而就我们的目的来看，它首先是基于它们对于微分方程系数的连续依赖，而较少地基于这一区域的范围和边界条件。因为在我们的情形中，这一区域（“整个q空间”）和边界条件（“保持有限”）对于未受扰动的和受微扰的问题基本上是相同的。

这一方法与瑞利勋爵在他的《声学理论》（Theory of Sound，第二版，第五卷，pp. 115—118，伦敦，1894年。）中用于研究带有微小不均匀性的弦振动的方法 ^〔33〕 本质上是相同的。这是一种特别简单的情形，因为未受扰动问题的微分方程有着不变的系数，只有扰动项为沿着弦方向的任意函数。一种完全的推广不仅对于这些点是可能的，而且对于这种有着几个独立变量的非常重要的情形，即对于偏微分方程也是可能的，其中多重本征值出现于未受扰动的问题，而附加的扰动项引起了这些值的分裂，这在著名的光谱学问题中有着极大的兴趣（塞曼效应，斯塔克效应，多重性）。下面第一节中所讨论的微扰问题对于数学家而言，确实没有什么新的东西，我并没有致力于把它推广到最为广泛可能的范围，而是以尽可能清楚的方式，给出非常简单的初步形式。而从后者出发，任何想要的推广都可在需要时几乎自动地浮现出来。在第二节，作为一个实例，用两种方法讨论了斯塔克效应，其中第一种类似于爱泼斯坦的方法，用这种方法他首先基于经典力学解出问题， ^〔34〕 辅之以量子化条件；而第二种则更为一般化，类似于通常的微扰方法。 ^〔35〕 第一种方法用于表明在波动力学中，微扰问题也能被在抛物线坐标中“区分开”，微扰理论将首先被应用于由起初的振动方程分裂而来的通常的微分方程。这样，这一理论将仅仅接管了在旧理论中移交给索末菲优美的复积分的任务，以计算量子积分。 ^〔36〕 按第二种方法，可发现在斯塔克效应中，相当偶然地，存在一种严格的坐标系统分离，对于微扰问题也同样如此，微扰理论被直接应用于偏微分方程。这后一步进展在波动力学中被证明是更为麻烦的，尽管它在理论上是优越的，且更有可能推广。

第二节也简略地讨论了斯塔克效应中分量的强度问题。表格的计算作为整体，甚至于要比克拉默斯借助于对应原理所作的著名计算与实验更为相符。 ^〔37〕

（尚未完成的）对于塞曼效应的应用，当然会更令人感兴趣。它看来与对于以波动力学语言来表述相对论性问题有着不可分解的联系，因为在四维表示中，矢势自动地等列于标量。在全文的第一部分中已经提到，相对论性的氢原子的确可以无须进一步的讨论就加以处理，但它导出了“半整数的”角量子数，与实验不符。因此“肯定还有某些东西未能发现”。自那以来，通过乌伦贝克和戈德施米特的最为重要的发现， ^〔38〕 其后又通过与巴黎（朗之万）和哥本哈根（泡利）的口头的和书面的交往，我知道了所缺少的是什么，即用电子轨道理论的语言，电子围绕其自己的轴的角动量，它给了它一种磁矩。这些研究者的见解与另两篇其重要性略逊一筹，由斯拉特， ^〔39〕 和由索末菲、翁泽耳德（Unsöld）撰写的讨论巴耳末光谱的文章一起， ^〔40〕 明确地证明了通过引入悖谬然而却又令人愉快的自旋电子的概念，轨道理论就能够克服那些后来积蓄起来的令人烦恼的困难（如反常塞曼效应，巴耳末谱线的帕邢－贝克效应，规则与不规则的伦琴双线，后者与碱金属双线的类似等）。我们必须把乌伦贝克和戈德施米特的概念吸收到波动力学中。我相信，后者对于这一概念会是非常肥沃的土壤，因为电子在这儿不是被设想为一个点电荷，而是连续地流过空间， ^〔41〕 从而避免了令人不快的“旋转的点电荷”的观念。然而在本篇文章中，尚未尝试吸收这一概念。

第三节作为“数学附录”，收集了一些不那么令人感兴趣的计算——主要是为第二部分所需要的本征函数的乘积。

第一节　微扰理论

§1．单个独立变量

让我们考虑一个线性的、均匀的、二阶的微分表式，不失一般性，我们假设它为自伴随形式，即

L［y］＝py″＋p′y′－qy．　　　　（1）

其中y为相关函数，p和p′为独立变量x的连续函数，且p≧0。一撇表示关于x的微分（因此p′表示p的微商，这是自伴随的条件）。

现在让ρ（x）为x的另一连续函数，它为非负的，一般也不为零。我们考虑斯图谟和刘维问题的本征值 ^〔42〕

L［y］＋Eρy＝0．　　　　（2）

首先，这是一个发现所有那些不变的E值（“本征值”）的问题，对于这些值而言，方程（2）有解y（x）；这些值是连续的，在某个区域内并不同等地消失，并且在边界点满足某些“边界条件”。其次要发现这些解（“本征函数”）本身。在原子力学所处理的情形中，区域和边界条件总是“自然的”。例如，当x表示径矢量或内在地为正的抛物线坐标的数值时，区域从0伸展到∞，而边界条件在这些情形中为：保持为有限的；或是当x表示方位角时，区域为从0到2π的积分，而边界条件为：在积分终端，重复y和y′的起始值（“周期性”）。

只有在周期性条件的情形中，对一个独立变量，才会出现多重的，即双值的本征值。由此，我们理解会有几个（其特殊情形是两个）线性独立的本征函数同属于同一个本征值。为简单起见，我们现在排除这种情形，因为它很容易与下述进展联系上。此外，为简化公式起见，我们将不考虑区域扩展到无穷时，会出现“带光谱”（即本征值的连续统）的可能性。

现在，让y＝u_i （x），i＝1，2，3，……为斯图谟－刘维本征函数系；于是本征函数系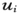 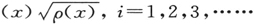构成这一区域的完全正交系，即如果在第一位，u_i （x）和u_k （x）为属于值E_i 和E_k 的本征函数，则

ʃρ（x）u_i （x）u_k （x）dx＝0　　　　i≠k．　　　　（3）

（没有上下限的积分是对整个这一论文所讨论的区域进行的。）表述“完全的”意味着原初任意的连续函数仅仅由于假设它必须与所有的函数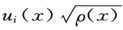 正交而宣告完全消失。（更简洁地说：“对于这一系统不存在进一步的正交函数。”）我们能够，并将总把所有一般讨论中的本征函数u_i （x）看做是“归一化的”，即我们想象在说明（2）的均匀性时，其中的每个依然是任意的常数因子，会以如此方式确定，使得积分（3）对于i＝k取单位值。最后，我们再次提醒读者，（2）的本征值当然都为实数。

现在，设本征值E_i 和本征函数u_i （x）为已知。让我们从现在起，把我们的注意力特别集中到一个确定的本征值，比如说E_k ，和相应的本征函数u_k （x）上，来看一看当我们不改变任何方面，而仅在（2）的左边添加一小的“扰动项”时，它们会如何变化。

设此扰动项起初的形式为

－λr（x）y．　　　　（4）

其中λ是一小量（扰动参量），而r（x）为x的一个任意连续函数。因此，这不过是微分表式（1）中系数q的微小变动。由引言中提到的本征量的连续性，我们现在知道改变后的斯图谟－刘维问题

L［y］－λry＋Eρy＝0　　　　（2′）

在任何情形中，对一个足够小的λ，都必须有邻近E_k 和u_k 的本征量，我们试着把它们写作

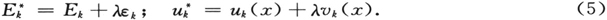
在代入方程（2′）时，记住u_k 满足（2）。忽略λ² 项，并消除λ因子，我们得到

L［v_k ］＋E_k ρv_k ＝（r－ε_k ρ）u_k ．　　　　（6）

为确定本征函数的微扰项v_k ，如（2）与（6）的比较所表明的，我们得出一个非齐次方程，它正属于为我们的未受扰动的本征函数u_k 所满足的齐次方程。（因为在（6）中，空间本征值E_k 占据了E的位置。）在此非齐次方程的右边所出现的，除了已知量外，有尚未知的本征值的微扰ε_k 。

ε_k 的出现用以在计算v_k 之前计算这个量。作为整个微扰理论的出发点，已知非齐次方程对一个齐次方程的本征值有解，当且仅当其右边与所有与其同源的本征函数正交（在多重本征值的情形中，与所有的同源函数正交）。 ^〔43〕 （对一个弦振动而言，这一数学定理的物理解释是如果这个力与一个本征振动相谐振，它必须以一种非常特殊的方式分布在整个弦上，使得它不进入所讨论的振动；否则振幅的变化会超出所有的限度，使得稳态条件成为不可能。）

因此，（6）的右边必须与u_k 正交，即

或

或者，如果我们设想u_k 已经归一化，则更简单地有

这一简单的公式表示了用微扰函数r（x）和未受扰动的本征函数u_k （x）来表述的（一阶的）本征值的微扰。如果我们认为我们问题的本征值意味的是机械能，或类似于它，而本征函数u_k 可比之于“以能量E_k 运动”，则我们在（7″）中所见到的与经典力学的微扰理论完全类似，即能量的微扰就一级近似而言，等于微扰函数对未受扰动的运动取平均。（或许可以顺便评论一下，作为一个明智的，或是美学的规则，在对整个区域所有积分的积分函数中，应当把因子ρ（x）大胆地映衬出来。如果我们这么做，那么在积分（7″）中，我们必须用r（x）／ρ（x）而不是r（x）作为微扰函数，并在表式（4）中做出相应的变化。然而，由于这一点并不那么重要，我们将仍然坚持用已选定的符号。）

我们还须定义来自（6）的本征函数的微扰v_k 。我们通过把v_k 作为本征函数的级数，来解此非齐次方程， ^〔44〕 即

并通过展开右边，除以ρ（x），类似于一个本征函数的级数，这样

其中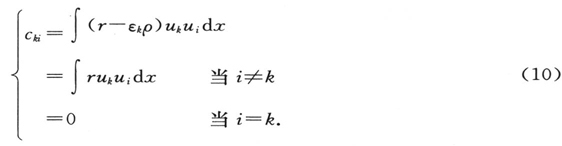　　　　　

最后的等式得自于（7）。如果我们把（8）和（9）代入（6），得到

由于现在u_i 以E＝E_i 满足方程（2），得出

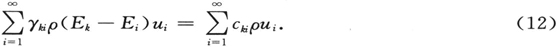
由方程两边的系数相等，除γ_kk 之外的所有γ_ki 都得以确定。从而

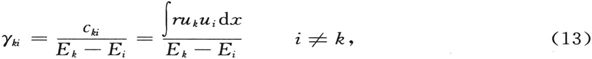
而如我们所理解的，γ_kk 保持为完全不确定的。这一不确定性对应于归一化假设对受扰动的本征函数仍然是可得到的这一事实。如果我们在（5）中应用（8），并主张u_k 的归一化对 也同样适用（忽略阶数为λ² 的量），则显然γ_kk ＝0。运用（13），我们现在得到微扰后的本征函数

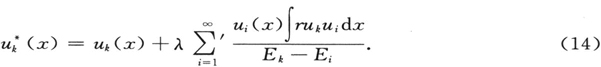
（∑符号上的一撇表示i＝k这一项未加在内。）由上可知，同源的微扰的本征值为

通过代入（2′），我们可以使自己相信，（14）和（15）的确满足了所提出的近似范围内的本征值问题。这一确证是必须的，因为（5）中所作的微扰参量的整数次方的假设并非连续性的必然推论。

这种在这个最简单的例子中解释得非常详细的程序，可以以多种方式推广。首先，我们当然能以一种相当类似的方式，考虑λ的二阶，然后是三阶的微扰，在每种情形中首先得到本征值的下一级近似，然后是本征函数的相应近似。在某些情形中，把微扰函数本身看做是λ的级数或许是明智的，正如在力学的微扰理论中那样，它的项一个接一个地在分立的阶段起作用。这些问题在赫尔E·菲斯（Herr E. Fues）的工作中有详尽的讨论，这些工作现在以与光谱带理论的应用相联系的方式出现。

其次，以相当近似的形式，我们也能考虑以（1）中微分算子y′来表示的微扰，正如我们已经考虑了以－qy来表示的微扰。这种情形的重要性在于塞曼效应无疑导致的是这种类型的微扰，尽管显然在一个方程中有着几个变量。这样，方程由于微扰，失去了它的自伴随形式；这在单个变量的情形中并非实质性的事情。然而，在一个偏微分方程中，这一失去有可能导致微扰的本征值不再是实数，尽管微扰项是实数；而自然地也是相反的，一个虚数的微扰项，却可能有一个实的、物理上有意义的微扰作为其结果。

我们也能进而考虑用y″来表示的微扰。一般而言，的确完全可能添加一个任意的“无穷小的”线性的 ^〔45〕 且均匀的、甚至比二阶更高的微分算子，以作为微扰项，并用于以与上述相同的方式来计算微扰。然而，在这些例子中，我们将运用这一优势，即事实上本征函数的二阶的和更高阶的微商，可以由零次或一次微商的微分方程自身来表示，由此这一一般的情形可以在某种意义上还原为两种特殊的首先被考虑的情形——以y和y′来表示的微扰。

最后，显然把方程拓展到高于二阶的情形是可能的。

然而，最为重要的推广无疑是推广到几个独立的变量，即推广到偏微分方程。因为这才的确是一般情形中的问题，并且只有在例外的情形中，才有可能通过引入适当的变量，把被扰动的偏微分方程分离为单独的每个只有一个变量的微分方程。

§2．几个独立变量（偏微分方程）

我们将用一个符号x，来在公式中作为几个独立的变量的符号表示，并简略地把对于一个多维区域展开的积分，写作ʃdx（而不是写作ʃ…ʃdx₁ dx₂ …）。这种类型的一个符号已经被用于积分方程的理论中，并且多少具有这样一种优势，即这一公式的结构并不随变量数目的增加而改变，而仅仅基本上随着那些可能与其相关的新的事件而变化。

因此，现在让L［y］表示一个二阶的自伴线性偏微分表达式，它的清晰的形式我们无须限定。进一步地，让ρ（x）再一次为独立变量的正函数，它一般不为零。假设“自伴”现在不再是不重要的，因为这一性质现在不再能如仅有单个变量的情形时那样，一般地通过适当地选择一个f（x）相乘而获得。然而，在波动力学的特殊的微分表示中，情形依然如此，如它由变分原理而产生的那样。

按照这些定义或约定，我们也可以把§1中的方程（2）

L［y］＋Eρy＝0，　　　　（2）

看做是几个变量情形中的斯图谟－刘维本征值问题的公式表示。当本征值为简单的时，如果我们运用与上述一致的简化的符号体系，则那里提到的关于本征值和本征函数的任何事，如它们的正交性，归一性等等，与那里发展的整个微扰理论一样（简言之，整个的§1）都保持其有效性不变。只有一件事并没有保持有效，即它们必须是简单的。

然而，从纯数学的立场看，在有几个变量时，根之间的彼此不同是通常的情形，而多重性则被看做是特殊性事件，它被承认为应用中的规则，以说明所出现的微分表式L［y］（及“边界条件”）的特别简单和对称的结构。本征值的多重性对应于条件周期性系统中的简并性，因而为量子理论所特别感兴趣。

当方程（2）对于E＝E_k 拥有不止一个，而是精确地有着α个线性独立的满足边界条件的解时，本征值E_k 被称为α重的。我们将用

u_k1 ，u_k2 ，…，u_ka ．　　　　（16）

来表示这些解。这样，这α个本征函数中每一个都是与属于另一个本征值的其他本征函数中的一个正交的（因子ρ（x）被包括在内，参见（3））。相反，这α个函数彼此之间通常不是正交的，如果我们仅仅假设它们是关于E_k 的α个线性独立的本征函数，而并没有其他假设的话。因为这样，我们可以用它们自身的α个任意的、线性独立的（具有常系数的）线性组合，来同样好地取代它们。我们由此可以用其他方法来表达这一点。函数（16）的级数对于一个（具有常系数的）线性变换的范围起初是无限的，包括了一个非零的行列式，这样的一个变换通常会破坏彼此的正交性。

然而，通过这样的一个变换，这种彼此的正交性总是能产生的，而且是以无穷数目的方式；后一种性质的产生，是由于正交变换并不破坏彼此的正交性。我们现在已经习惯于简单地把它包含于归一化中，由此得以对所有的本征函数确保其正交性，甚至对那些属于同一个本征值的本征函数。我们假定我们的u_ki 已经是以此种方式归一化的，并且当然是对于每一个本征值。于是我们必须有

于是，（对于常数k和变化的i而得出的）每一个本征函数u_ki 的有限级数，仅在此范围内仍然是无限的，它属于一个正交的变换。

现在，我们将首先用文字（而不是用公式）来讨论，当一个微扰项被加到微分方程（2）上会有什么结论。一般而言，微扰项的添加将会消除上面提及的微分方程的对称性，本征值的多重性（或是其中的一些）正起因于这种对称性。然而，由于本征值和本征函数是连续地依赖于微分方程的系数的，一个小的微扰会导致一组彼此相近，也相近于E_k 的本征值，并进入α重本征值E_k 的地域。后者由此分裂。当然，如果对称性并未为微扰整个破坏，分裂有可能是不完全的，相等的多重性的几个本征值大体上（仍然部分是多重的）仅仅出现在E_k 的位置（简并部分消除）。

关于受扰的本征函数（那属于产生于E_k 的α本征值的α个成员），由于连续性，显然也必须无穷趋近于未受扰动的属于E_k 的函数，即u_ki ，i＝1，2，3，…，α。而我们肯定还记得，如我们前述所确定的最后命名的函数级数，在任意正交变换的范围内是无限的。这种无限数量的函数中的一个（它或许适用于函数级数u_ki ，i＝1，2，3，…，α）将无穷趋近于这个受扰函数级数；并且如果值E_k 完全分裂，它将会是非常确定的。因为对于由值的分裂所产生的分离的简单本征值，都有着属于它们的完全单一地确定的本征函数。

这种对于未受扰本征函数的独特的特殊限定（或许可以恰当地称之为关于受扰函数的“零阶近似”），由扰动的本性所规定，自然通常是与我们在开始时所偶然采用的未受扰函数不一致的。后者中的每一组（属于一个确定的α重的本征值E_k ），在它能作为出发点，即对一个更为精确的扰动本征函数的“零阶近似”之前，将首先经受一个为扰动的类型所规定的正交代换。这些正交代换（每一个多重的本征值对应于一个）的确定，是由于变量数目的增加而产生（或是从多重本征值而来）的唯一本质上的新颖之点。这些代换的确定构成了在条件周期性系统理论中，对受扰运动发现一种近似的分离系统的精确对应。如我们即刻会看到的，代换的定义总是可以以一种理论上简单的方式进行的。对于每一个α重的本征值，它仅要求α个（因而是有限数目的）变量的二次形式的主轴变换。

一旦这种代换完成，第一阶近似的计算就几乎逐字逐句地与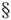 2中的情形相同了。唯一的不同在于在方程（14）中的∑上的一撇，必须意味着在加和中，所有属于值E_k 的本征函数，即所有其分母会消失的项，都必须被略去。或许可以顺便提及的是，在计算一阶近似时，根本没有必要对于所有的多重本征值完成正交代换，而只要对值E_k 这么做就足以了，我们感兴趣的是它的分裂。至于更高阶的近似，我们当然也需要。然而在所有的其他方面，对这些更高阶的近似的计算，从一开始就完全像简单的本征值一样。

当然，如上面所提及的，无论是一般的，还是在近似的起初阶段，值E_k 有可能没有完全分裂，因而仍然保留着多重性（“简并”）。这一点表现为这一事实：对于已经经常被提及的代换，仍然依附有某种不确定性，它或者总是保持着，或是在其后的近似中一步一步地被消除。

现在，让我们用公式来表示这些想法，考虑由前面§1中的（4）所导致的微扰

－λr（x）y　　　　（4）

即我们想象属于（2）所解决的本征值问题，现在来考虑其精确对应的问题（2′）

L［y］－λry＋Eρy＝0．　　　　（2′）

我们再一次地集中注意于一个确定的本征值E_k 。让（16）为一个属于它的本征函数的系统，并假设它在如上面所描述的意义上为归一化的和彼此正交的，但在所解释的意义上，尚未适合于特定的微扰，因为要发现能导致这种适合的代换，正是我们主要的任务！替代 1中的（5），我们现在必须提出下述的微扰量

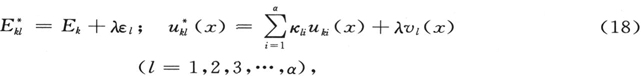
其中v_ι （x）为函数，而ε_ι 和κ_ιi 为有待确定的常数系统，但我们起初并不以任何方式加以限定，尽管我们知道系数系统κ_ιi 必然 ^〔46〕 形成一个正交代换。角标κ应当仍然被加诸于三种类型的被命名的量，以便表明整个讨论涉及未受扰问题的第κ个本征值。我们之所以没有这么做，是为了避免混淆角标的累加。角标κ在下面的整个讨论中被设想为固定的，直到相反的情形被说明。

让我们通过对（18）中的角标ι给予一个确定的值，来选择受扰本征函数和本征值中的一个，并且让我们把（18）代入微分方程（2′），安排为λ的幂级数。这样，完全如同§1中的情形，λ的独立项消失了，因为按照假说，未受扰的本征量满足方程（2）。只有包含λ的一阶幂的项保留下来，因此我们可以删去其余项。略去一个因子λ，得到

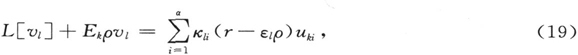
并且由此再次获得非齐次函数方程的微扰v_ι 的定义，与之相对应的作为齐次方程的，是具有特定值E＝E_k 的方程（2），即为函数集u_ki ，i＝1，2，3…，α所满足的方程。方程（19）左边的形式是独立于角标ι的。

这样，在方程右边出现的有待确定的常数ε_ι 和κ_ιi ，我们能够甚至在计算v_ι 之前，就估算出它们。因为只要是方程（19）有一个解，其充分和必要条件就是其右边应当正交于属于E_k 的齐次方程（2）的所有本征函数。因此，我们必须有

即由于归一化（17）

如果我们简略地写出常数的对称的矩阵，其计算可由求（面）积得出

则我们由

中得到用于计算这α个常数κ_ιm （m＝1，2，…，α）的α个线性齐次方程组，其中本征值的微扰ε_ι 依然出现在常数中，并且其本身是未知的。然而，在κ_ιm 的计算之前，这用于ε_ι 的计算。由于已知线性齐次方程组（21′）有解，当且仅当它的行列式为零。这就导致下述α阶关于ε_ι 的代数方程：

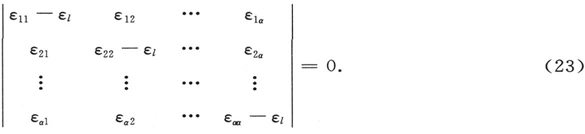
我们看出这一问题与具有系数ε_mi 的α个变量对于主轴的二次形式的变换完全相同。“特征方程”（23）产生出ε_mi 的α个根，“主轴平方的倒易”，它们通常是不同的，并且由于ε_mi 的对称性而总是实数。我们由此同时得到本征值的全部α个微扰（ι＝1，2，…，α），并且将推导出α重本征值会分裂成精确的α个通常不同的简单值，即使我们并没有假设这一点，它也是十分明显的。对这些ε_ι 中的每一个，方程（21′）给出一组量κ_ιi ，i＝1，2，…α，并且如果说所有的ε_ι 确实是不同的，那么作为已知的只有一个（除了一个一般的常数因子外）。此外，已知整个α² 个量κ_ιi 构成系数的正交系，如通常在主轴问题中一样，定义了相对于旧的坐标轴的新坐标轴的方向。我们会并且将采用刚刚提到的未确定因子把κ_ιi 完全归一化为“方向余弦”，而易于看出，按照（18），这使受扰本征函数 （x）再次归一化，至少在“零级近似”中（即除了λ项外）。

如果方程（23）有多重根，就会有前面提到过的微扰没有完全消除简并的情形。受扰方程于是也有多重的本征值，而常数κ_ιi 的确定部分是任意的。其后果不过是（如多重的本征值总是具有的情形）我们必须并且可以默许甚至在微扰被应用之后，在一个本征函数系统中，其许多方面仍然是任意的。

借助于这一对主轴的转换，主要的任务已经完成；我们将经常发现它足以应用于量子理论中，以确定一阶近似的本征值，和零级近似的本征函数。常数κ_ιi 和ε_ιi 的计算总是无法进行，因为它依赖于一个α次代数方程的解。但情况再差，总有一些方法， ^〔47〕 能通过一种理性的过程，给出任何所希望的近似度的计算。这样，我们现在可以把这些常数看做为已知的，并出于完备性的考虑，来对本征函数计算其一级近似。这一程序与在§1中完全相似。

我们必须解方程（19），为此，我们把v_ι 写作（2）的整个本征函数集的级数

对于k′而言，求和的范围从0到∞；而对每一个确定的k′值，i′的变化范围为属于E_k′ 的有限数目的本征函数。（现在，我们第一次考虑到不属于我们一直关注的α重本征值E_k 的本征函数。）其次，我们在本征函数的完备集的级数中，来变化被ρ（x）所除的方程（19）的右侧，

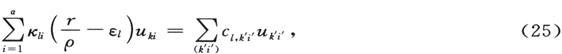
其中

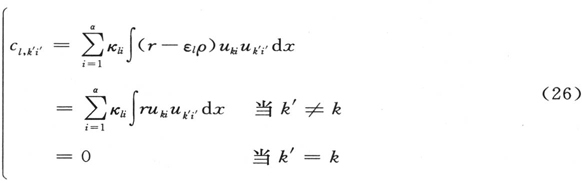
（最后两个等式分别来自方程（17）和（20）。）把方程（24）和（25）代入（19），我们得到

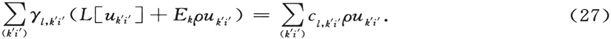
由于u_k′i′ 对于E＝E_k 满足方程（2），这就给出

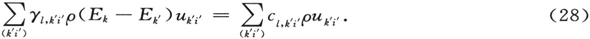
通过让等式左右两边的系数相等，除了那些其中k′＝k的项以外，所有的γ_{ι，k′i′} 被确定。由此

而那些k′＝k的γ则当然不能由（19）确定。这再次对应于这一事实：我们业已临时地将（18）中的受扰函数 （通过 的归一化）仅仅在零级近似上归一化。再一次地，我们易于意识到，必须让整个讨论中的γ量为零，以便导致 甚至在一阶近似中的归一化。通过把（29）代入（24），然后把（24）代入（18），我们最后得出受扰本征函数的一阶近似

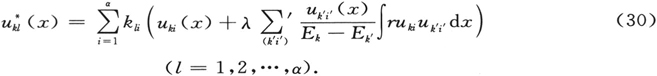
第二个∑符号上的一撇，表示所有具有k′＝k的项都被忽略。当这一公式应用于任意的k，可以观察到k_ιi 也与我们前面已经专门讨论过的本征值E_k 的多重性α一样，仍然依赖于指标k，尽管这一点在符号上并没有表现出来。这里让我们重申一下，k_ιi 是被作为方程（21′）的解的系统来计算的和归一化的，因此其平方和为一，其中方程的系数由（22）给出，而（21′）中的量ε_ι 取做（23）的根之一。由此，从方程

这个根给出相关的受扰本征值。公式（30）和（31）是§1中的（14）和（15）的推广。

毋庸置疑，在§1结束时所提到的扩展和推广在这里当然也是有效的。但进行这些一般化的推展通常是不值当的。我们的成功至多不过是在一些特殊的情形中，不是运用那些现成的公式，而是直接借助于那些在本文中或许已经被解释得过于详细的简单的基本原理。我愿意只去简略地思考在§1结束时已经提到的那种可能性，即如果说微扰项也包含未知函数的微商，方程（2）或许会失去（并且在多变量的情形中不可挽回地失去了）其自伴性质。由一般性定理，我们知道由此受扰方程的本征值无须再是实数。我们可以进一步说明这一点。通过这一段中的发展，我们易于看出，当微扰项包含微商时，行列式（23）的元素不再是对称的。已知在这种情形中，方程（23）的根无须为实数。

把某个函数展开为本征函数的级数，以便达到本征值或本征函数的一级或零级近似这种要求，会变得非常不方便，或至少使计算变得相当的复杂，在那些延展光谱与点光谱并存，以及点光谱在有限的距离有着极限点（累积点）的情形中。这正是在量子理论中出现的情形。幸运的是，经常（或许总是）有可能出于微扰理论的目的，把自己从这种通常非常麻烦的延展光谱中解脱出来，从一个不拥有这种光谱的方程去发展微扰理论，其本征值不累积在接近一个有限值处，而是随着增加的指标而超越所有界限地增长。在下一节我们将接触到这样的一个例子。当然，这种简化仅当我们对延展光谱的本征值不感兴趣时才是可能的。

第二节　应用于斯塔克效应

§3．借助对应于爱泼斯坦的方法计算频率

如果我们添加一项势能＋eFz到论文第一篇中的开普勒问题的波动方程（5），以对应于一个在正z方向上，场强为F的电场对一个电荷为e的电子的影响，这样，我们就得到下述对于氢原子的斯塔克效应的波动方程

它构成本篇剩余部分的基础。在§5中，我们将直接应用§2中一般的微扰理论于这一偏微分方程。然而现在，我们将通过下述方程，引入空间抛物线坐标λ₁ ，λ₂ ，φ来减轻我们的任务

λ₁ 和λ₂ 从0到∞；对应的坐标表面为两组回转的共焦抛物面，它们以原点为焦点，正的（λ₂ ）和负的（λ₁ ）z轴分别为轴线。φ的取值为从0到2π，属于它的坐标面为z轴所限定的半个平面的集合。坐标的关系是唯一的。对于函数行列式，我们得到

由此，空间元为

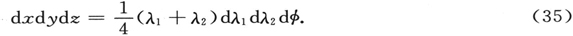
作为（33）的结果，我们注意到

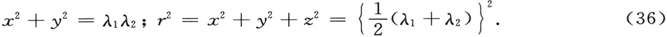
如果我们用（34） ^〔48〕 来相乘（以保证自伴形式），在所选择的坐标中（32）的表达式给出

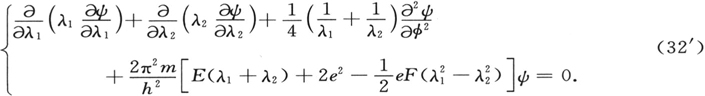
这里我们再次可以取函数ψ为三个函数的乘积（这是所有解线性偏微分方程“方法”的缘由），这样

ψ＝Λ₁ Λ₂ Φ，　　　　（37）

其中的每一个都只依赖于一个坐标。对于这些函数，我们得到通常的微分方程

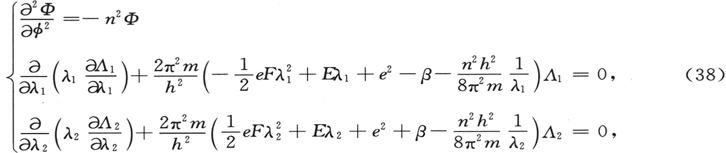
其中n和β为两个进一步的“类本征值”（除了E之外的）积分常数，仍有待确定。通过对其中的第一个选择符号，我们考虑到这一事实，如果Φ和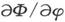 为方位角φ的连续和单值函数，则方程（38）中的第一个使它取整数值。我们于是有

并且如果我们不考虑n的负值，它显然是充分的。由此

n＝0，1，2，3，…　　　　（40）

在用于第二个常数β的符号中，我们遵循索末菲（Atombau, 4th edit., p. 821）以便易于进行比较。（类似的，下面用A，B，C，D。）我们对（38）的后两个方程一并处理，其形式为

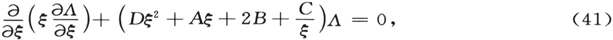
其中

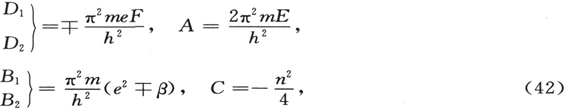
并且上面的符号适用于Λ＝Λ₁ ，ξ＝λ₁ ，而下面的适用于Λ＝Λ₂ ，ξ＝λ₂ 。（不幸的是我们不得不写作ξ以取代更为合适的λ，以避免与§1和§2中一般理论中的微扰参量λ相混淆。）

如果我们起初在（41）中忽略斯塔克效应项Dξ² （对这一所设想的微扰项在场强为零时的极限情形），那么这一方程与论文第一篇中的方程（7）有同样的一般结构，取值也同样为从0到∞。相应的讨论几乎逐字逐句地是相同的，并且表现出非零解，这种解与它们的导数一起，是连续的，并在取值范围内保持为有限的，仅存在于或者是A＞0（延展光谱，对应于氢轨道），或者是

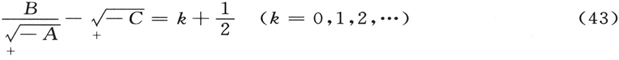
如果把它应用于方程（38）的最后两个，并且用下标1和2以区分两个k值，我们得到

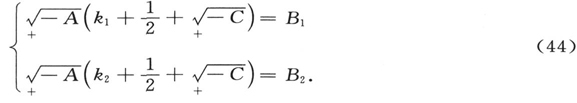
通过加和，平方和运用（42），我们发现

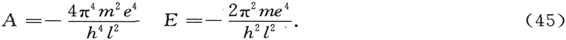
这是著名的巴耳末－玻尔椭圆能级，其中作为主量子数出现的

ι＝k₁ ＋k₂ ＋n＋1．　　　　（46）

我们以一种比应用在数学文献中已知的下述结果更为简单的方式，求得了分立光谱项及相关的本征值。我们通过使

首先变换因变量Λ，然后通过使

变换自变量ξ。我们发现对于作为μ的函数的u，有方程

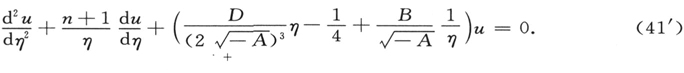
这一方程与拉盖尔多项式密切相关。在数学附录中，将表明e^－x／2 与（n＋k）次拉盖尔多项式的n阶导数的乘积，满足微分方程

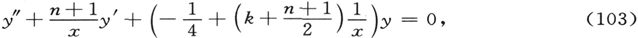
并且对一个固定的n，当k取所有非负整数时，所命名的函数构成了刚刚写出的方程的本征函数的完备系。由此得出，对于D为零时，方程（41′）拥有本征函数

并且其本征值

且无它值！（见数学附录中，由于显然无伤大雅的变换（48）所导致的延展光谱的明显的略去；由此微扰理论的处理变得非常容易。）

我们现在必须计算由包括（41′）中的D项在内，所导致的对§1一般理论的本征值的微扰（50）。如果我们乘上η^n＋1 ，方程成为自伴随的。这样，一般理论的密度函数ρ（x）变成ηⁿ 。作为微扰函数r（x）出现

（我们形式上让微扰参量λ＝1；如果我们期望，我们可以让D或是F与之相等。）现在公式（7′）对于第k项本征值的微扰给出

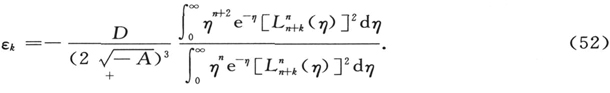
对于分母中的仅用于归一化的整数，附录中的公式（115）给出的值为

而在同样的地方，分子中的积分求值为

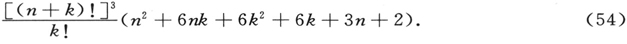
其结果是

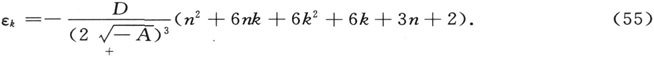
方程（41′）的第k项受扰本征值的条件，以及由此，自然地，对于原初的方程（41）第k项分立的本征值趋于

（ε_k 为简洁起见同时保留。）

这一结果被两次应用，即通过代入常数A，B，C，D数值的两个方程组（42），应用于（38）的最后两个方程；由此观察出n在两种情形中为相同的数，而两个k值如上所述，由角标1和2得以区分。首先我们有

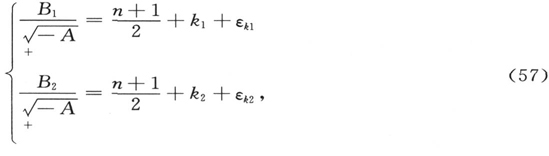
据此有

（应用缩略的主量子数表式（46））。为求近似，我们旨在对小量ε_k 展开，并得出

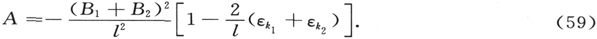
进一步，在这些小量的计算中，我们可以用近似值（45）于（55）中的A。这样，我们由（42）得出两个D值，

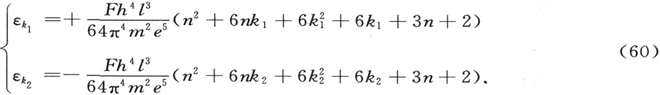
此外，在简单的化简后，得出

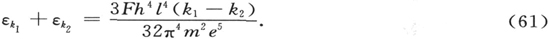
如果我们把这一结果，和（42）中的A，B₁ 和B₂ 代入（59），在化简后我们得到

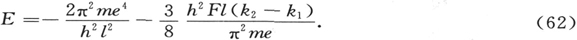
这是我们临时的结果。它就是著名的爱泼斯坦关于氢原子光谱的斯塔克效应项的求值公式。

k₁ 和k₂ 完全对应于抛物量子数，它们可以取值为零。同样，由（40）看出，明显与赤道量子数相关的整数n也可取值为零。然而，由（46）可知，这三个数的和还必须加上1才能得出主量子数。因此是n＋1而不是n对应于赤道量子数。由此，数值零对于后者（赤道量子数）自动地为波动力学所排除，正如为海森伯的力学所排除。 ^〔49〕 完全不存在本征函数，即没有振动态对应于这样一种子午轨道。这一重要的和令人满意的情形在论文的第一篇中计算角量子数时，已经通过不存在对应于穿核轨道的振动态而被注意到。然而，它的完全的意义，只是通过刚才引用的两位作者的评论才为我所完全明白。

关于再以后的应用，让我们关注“零阶近似”中的方程（32）或（32′）的本征函数系，它属于本征值（62）。它得之于陈述（37），得之于结论（39）和（49），得之于变换（47）和（48）的考虑，以及A的近似值（45）。为简洁起见，让我们称a₀ 为“氢的第一轨道半径”。于是我们得到

而本征函数（尚未归一化！）读作

它们属于本征值（62），其中ι的意义为（46）。对于每一组三元n，k₁ 和k₂ 的非负整数值，依据n＞0或是n＝0，有着（按照双重符号sin／cos）两个或是一个本征值。

§4．尝试计算斯塔克效应模式的强度和极化

我在以后会表明， ^〔50〕 从本征函数出发，通过微分和积分，我们可以计算在海森伯力学中与广义的位置和动量坐标相关的矩阵元素。例如，对于第（rr′）项矩阵元；按照海森伯，它属于广义坐标q本身，我们发现

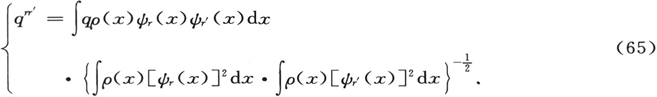
这里，对于我们的情形，每一个分离的指标代表了一个三元组n，k₁ 和k₂ ，此外，x代表了三个坐标r，θ，ψ。ρ（x）是密度函数；在我们的情形中为量（34）。（我们可以把自伴方程（32′）与一般形式（32）作比较。）（65）中的“分母” 必须加入，因为我们的函数组（64）尚未归一化。

现在，按照海森伯 ^〔51〕 ，如果q意味着一个笛卡儿直角坐标系，那么矩阵元（65）的平方就是从第r个状态到第r′个状态的“转换概率”的量度，或者更精确地说，是与这一转换相关的，在q方向上极化的辐射强度的量度。从这一点出发，我在上述论文中表明，如果我们对于“力学场标量”ψ的电动力学意义作某些简单的假定，则所讨论的矩阵元在波动力学中被容许有一个非常简单的物理解释，即实际上，它是电子周期性振动电矩幅度的分量。分量一词在这里有双重的意义：（1）在q方向上的分量，即在所讨论的空间方向上的分量；（2）只有这一空间分量的部分以一种时间正弦曲线的方式，精确地随着辐射光频率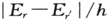 而变化。（由此，这是一种傅里叶分析的问题：不是以谐振频率的方式，而是以实际的辐射频率。）然而，波动力学的观念不是那种从一个振动状态到另一个突然转换的观念，而是如我将简单地提到的，一种涉及来自于两种本征振动同时存在的偏矩，持续时间与二者同时被激发一样长。

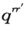此外，上述确认的 与偏矩成正比由此得以更精确的表达。例如， 与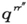 的比率等于当本征函数ψ_r 与 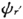和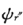 同时受激时产生的偏矩的比率，第一项具有任意的强度，而最后两项的强度彼此相等，即对应于归一化。要计算强度的比率，q的商必须首先被平方，然后为辐射频率的四次方所乘。然而，后者与斯塔克效应分量的强度比毫无关系，因为在这里，我们只比较了实际上有着同样频率的线的强度。

已知的关于斯塔克效应分量的选择定则和极化规则几乎无须计算，即可由（65）中分子的积分和（64）中本征函数的形式中获得。它们来自于对φ的为零或不为零的积分。我们通过在（65）中用来自（33）中的z取代q，获得其电矢量振动方向平行于场，即z方向的分量。对z的表达式（即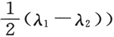 并不包含方位角φ。这样，我们由（64）即刻可看出：在对φ积分后的一个非零结果只能产生于如果我们组合本征函数，其第n项相等，从而其赤道量子数相等（事实上等于n＋1）。对于其垂直于场而振动的分量，我们必须使q等于x，或者是等于y（参见方程（33）。这里出现了cosφ或是sinφ，几乎像前面一样易于看出，如果对φ的积分要产生非零的结果的话，两个组合起来的本征函数的n值的差，必须精确地为一。因此，已知的选择定则和极化规则得以证明。进一步地，应当再次回忆起：我们无须在额外的反思后，排除任何n值，如在老的理论中所必需的那样，以便与经验一致。我们的n比赤道量子数小1，并且从一开始就不能取负值（非常相同于我们已知的在海森伯理论中所存在的事件状态） ^〔52〕 。

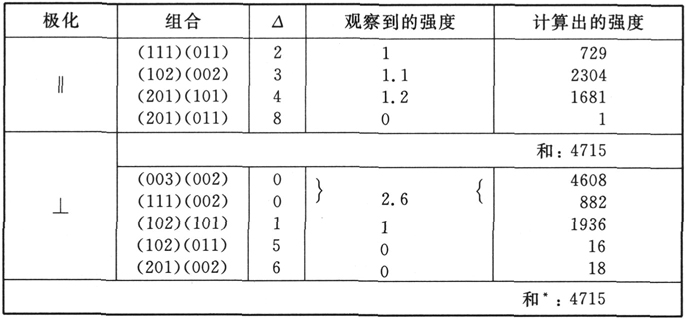
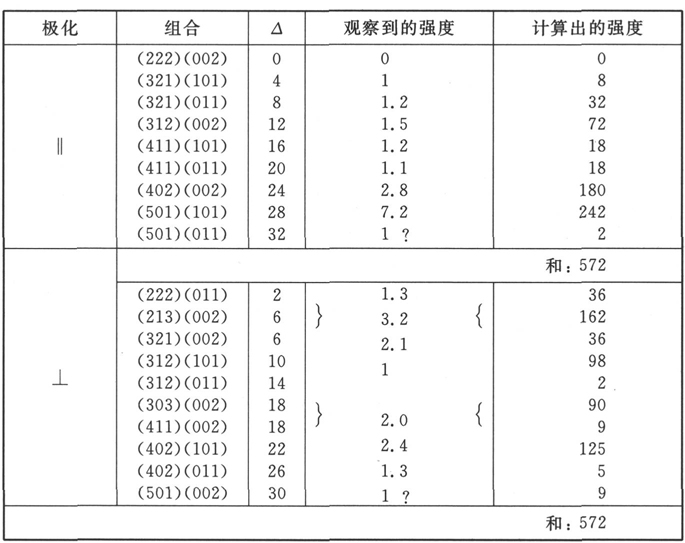
出现在（65）中的对于λ₁ 和λ₂ 积分的数值估算异常的冗长乏味，尤其是对分子的估算。同样的用于计算的估算在（52）的估值中已经发挥作用，只是问题更为详细一些，因为两个（一般化的）拉盖尔（Laguerre）多项式（它们的乘积正是要被积分的）没有同样的自变量。得益于好运，在我们所主要感兴趣的巴耳末线中，两个多项式之一的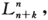 即与双重离散值状态相关的那一个要么是一个常数，要么是其自变量的线性函数。计算的方法在数学附录中有更完全的描述。下面的表格和图表给出了关于前四项巴耳末线的结果，以对比在每厘米10万伏的场强下，关于强度的测量和由斯塔克做出的估算 ^〔53〕 。第一栏表明极化的状态；第二栏给出了通常的描述方式下的项的组合，即在我们的符号中：两组三元数（k₁ ，k₂ 和n＋1）的组合，其中第一组指更高的离散态，第二组指双重离散态。第三栏以∆为标题，给出了在多重态3h² F／8π² me中项的分解（见方程（62））。下一栏给出为斯塔克所观察到的强度，而零表示未观察到。为斯塔克加上问号的线，或者是由于不相干的线，或者是由于可能的“幽灵”而不能得到保证。在斯塔克看来，由于在摄谱仪上两种极化状态的削弱不相等，对于振动的平行分量‖和垂直分量⊥他的结果是不能彼此相比较的。最后，这最后的一栏给出在相对数中我们的计算结果，它对于一条线，例如H_α 的分量集合（‖和⊥）是可比较的，但对于H_α 与H_β 的集合却是不可比较的，等等。这些相对数被还原为它们的最小的整数，即那些在这四个表中的每一个都是彼此中最基本的数字。

巴耳末线的斯塔克效应中的强度

表一

H_α

*　未被移动的分量减半

表二

H_β

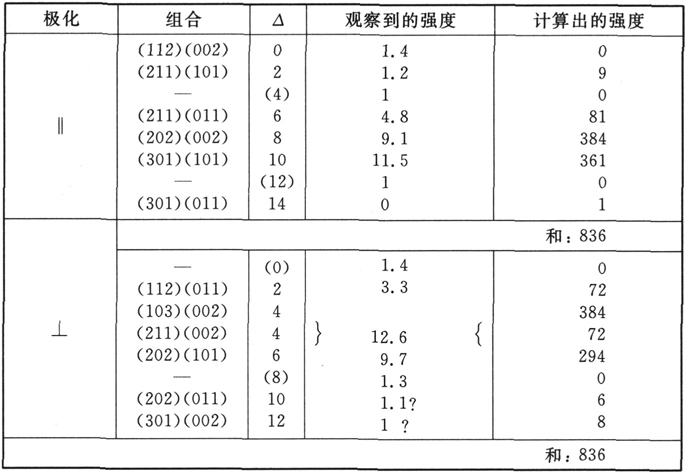
巴耳末线的斯塔克效应中的强度

表三

H_γ

*　未被移动的分量减半

表四

H_δ

从图表中可以注意到，由于理论强度中的巨大差异，有些理论强度无法真正在尺度上表征，因为它们实在太小。这些由小圆圈来表明。

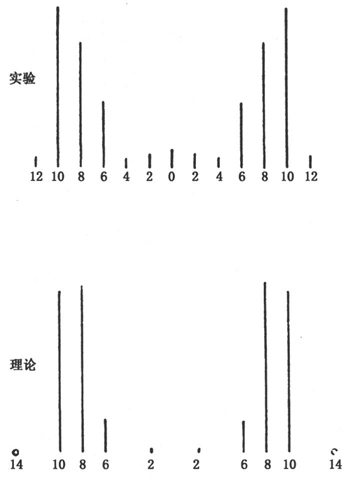
图3　H_β 的‖分量

图4　H_β 的⊥分量

对图表的思考表明，对于几乎所有的强分量，这种（理论与实验的）一致程度都是可以允许的，而且总体上考虑，它在某种程度上要好于由对应性考虑而演绎出的数值。 ^〔54〕 这样，例如，就消除了一个最为严重的矛盾，这一矛盾产生于按照对应原理给出的两个∆为4和6的强⊥分量的强度比，倒转且非常不符，事实上几乎达到了1∶2，而实验要求的是5∶4。一件类似的事出现于H_γ 的平均（∆＝0）⊥分量，它在实验上取决定性的压倒优势，但由对应原理给出的却太弱。在我们的图表中也是这样，人们承认这种为理论和实验所要求的强分量的强度比之间的“倒易”并非完全短缺的。H_α 的理论上最强的‖分量（∆＝3）跑出的最远，而按实验它应当位于强度上相邻的分量之间。H_β 的两个最强的‖分量和最强的两个⊥分量（∆＝10，13）也由理论“倒易地”给出。当然，在两种情形中，实验的和理论的强度比，都非常接近于1。

现在来看较弱的分量。我们首先注意到，对H_β 对选择定则和极化规则的某些被观察到的弱分量存在的矛盾，当然，仍然保留在新理论中，因为正是新理论给出了这些规则以与旧理论相一致。然而，那些理论上非常弱的分量大部分是不可观察的，或是观察是成问题的。弱分量之间的强度比，或是与更强的分量之间的比，几乎从未哪怕是近似正确地给出，尤其是参见H_γ 和H_δ 。这些严重的错误在谱线的实验确定中当然都不成问题。

图5　H_γ 的‖分量

图6　H_γ 的⊥分量

图7　H_δ 的⊥分量

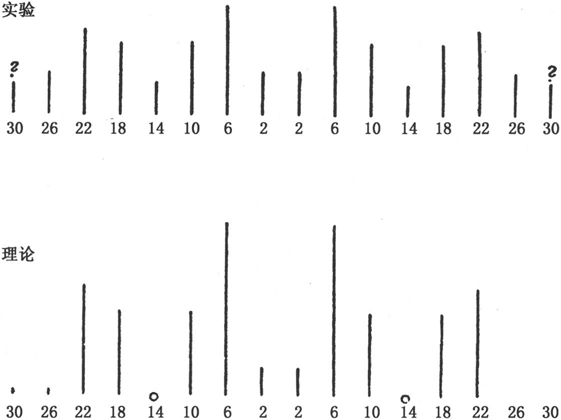
图8　H_δ 的⊥分量

考虑到所有这些，我们或许倾向于非常怀疑这一论题：积分（65）或是它们的平方是强度的量度。我绝非想把这一论题描绘成不可反驳的。依然有着许多可想象的选择，当理论被进一步拓展时，这些或许可以出于内在的理由是必需的。整个计算已经对未受扰动的本征函数，或更精确地说，对受扰函数的零级近似进行（参见上述§2）。因此，它代表了一个场强为零的近似！然而，正是对弱的，或是几乎消失的分量，我们应当期望随着场强的增强，理论上会有一个相当强的增长，其理由如下：如这一部分一开始所说明的，按照波动力学的观点，积分（65）描述了一个电子偏矩的幅度，它是由原子范围内绕核运动的电荷的分布产生的。当面对一个线分量时，我们作为零级近似，得到的是非常弱或甚至于为零的强度，这在任何方式上都与这样一个事实无关，即两个本征振动的同时存在仅对应于一个不重要的电运动，或甚至与之对应的什么也没有。振动的电物质（如果允许用这一含糊的说法的话）或许可以基于归一化，在所有的分量中同样被表述。这不如说是在电运动中发现高对称性程度情况下，线强度低的理由；通过它只有小的（甚或没有）偶极子运动产生（相反，例如只有一个四极运动）。因此，人们期望在任何种类的微扰呈现中，线分量的消失是相对不稳定的条件，因为对称性或许为微扰所破坏。这样，人们可以预期随着场强的增加，很快会得到弱的或者为零的分量。

这一点现在事实上已经被观察到，并且对于约一万高斯及以上的场强，强度比确实随着场强有相当大的变化；如果我理解得正确的话，变化的方式即为目前所讨论的一般方式。 ^〔55〕 某些关于这是否真正解释了分歧这一问题的信息，当然只能由对下一级近似的持续计算才能得出，但这是非常麻烦和复杂的。

当然，当前的分析不是别的，仅仅是语言的“转换”，转换到为人们已熟知的新理论的语言，正是玻尔 ^〔56〕 通过对应原理的方式，提出了与线强度相关的这一理论。

表中所给出的理论上的强度，同时满足了直觉和实验所确立的基本要求， ^〔57〕 即所有‖分量的和等于所有⊥分量的和。（在加和之前，未被移位的分量必须被减半，以作为其他分量发生在两侧的复制的补偿。）这造成了一种对于算法的非常受欢迎的“控制”。

同样令人感兴趣的，是通过运用表中给出的四个“和”，来比较四条线的总强度。为此，我将从我的数值计算中撤下四个因子，它们曾经被忽略，以使得在四组线中的每一级中，通过乘上它们，把强度比表现为最小的整数成为可能。此外，对这四个乘积，我乘以适当的辐射频率的四次幂。这样，我得到下述四个数字：

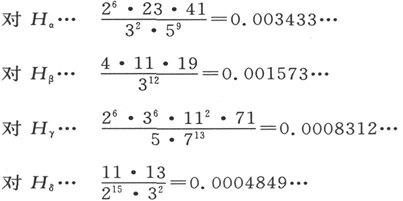
我以比前面更大的保留给出这些数字，因为在理论上，我对这一频率的四次幂并不确定。我后来发表的研究 ^〔58〕 似乎要求六次幂。上面的计算方法严格地对应于玻恩、约旦和海森伯的假设。 ^〔59〕 图表9是以图表的方式表示的结果。

实际测量到的辐射强度（已知它极大地依赖于激发条件）自然不能在这里用于与实验相比较。从其关于相邻的H_α 和H_β 的色散和磁旋转的研究中 ^〔60〕 ，R. 拉登堡（Ladenburg）与F. 赖歇（Reiche）一起 ^〔61〕 ，对这两条线的所谓“电子数”的比，计算了数值4·5（限度3和6）。如果我假设上述数字会与拉登堡表达式 ^〔62〕 成比例，

图9　总强度

那么通过用 相除，即分别为

所除，它们可以被还原为（相对的）“电子数”。

这样，我们得到四个数字

1.281，　0.2386，　0.08975，　0.04418．

第一个对第二个的比值为5.37，这与拉登堡的数值能足够好地相符。

§5　用与玻尔相对应的方法来处理斯塔克效应

主要是为了给出§2中一般理论的一个例子，我想概述对方程（32）的本征值问题的处理，如果我们没有注意到受扰方程在抛物坐标中也是精确地“可分离的”话，它必定是适用的。因此，我们现在仍然用极坐标r，θ，Φ，并因而用rcosθ取代z。我们也通过变换

对r引入新的坐标η.（它非常类似于对于抛物坐标ξ的变换（48））。对一个未受扰本征函数（45），我们由（66）得到

其中a₀ 为与在（63）中一样的常数。（“氢原子最内层轨道的半径”。）如果我们把这个变换和未受扰的值（45）引入待处理的方程（32），则我们得到

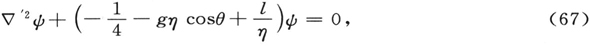
其中为简洁起见

拉普拉斯算符上的一撇，仅用于表示在其中，字母η被写作径矢量。

在方程（67）中，我们设想ι为本征值，g中的项为微扰项。微扰项包含本征值这一事实在一级近似中无须让我们烦恼。如果我们忽略掉微扰项，方程具有像自然数这样的本征值

ι＝1，2，3，4，…　　　　（69）

并且没有其他值。（延展光谱再次由技巧（66）所删除，这对于更接近的近似是有价值的。）相关的本征函数（尚未归一化）为

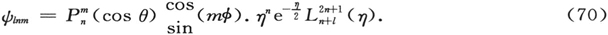
这里 表示n次勒让德函数的第m个“相关”项，而 为（n＋ι）次勒让德多项式的第（2n＋1）次导数。 ^〔63〕 所以，我们必然有

n＜ι，

否则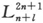 将会为零，因为微分数将会大于幂次数。关于这一点，球面谐函数的计数表明ι为一未受扰方程的ι² 重本征值。现在我们来研究假设如下所述，由于微扰项的加入，ι的一个确定值的分裂。

按照§2，要这么做，我们首先必须把我们的本征函数（70）归一化。从一个令人厌倦的计算中（借助于附录中的公式 ^〔64〕 ，它可以轻易地进行），我们得到如果m≠0，则归一化的因子为

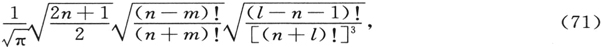
但是对m＝0，则要用 乘上这一值。其次，按照（22），我们必须计算常数ε_im 的对称矩阵。那儿的r等于我们的微扰函数－gη³ cosθsinθ，那儿称为u_ki 的本征函数等同于我们的函数（70）。刻画本征值的固定的下标k对应于ψ_ιmn 的第一个下标ι，而u_ki 的另一个下标i现在对应于ψ_ιmn 中的另一对下标n和m。在我们的情形中，常数矩阵（22）的形式为一个ι² 行和ι² 列的正方形矩阵。运用附录中的公式，求积分非常容易，并得出下列结果。只有这样一些矩阵元不为零，它们在两个本征函数ψ_ιmn 和ψ_{ι′m′n′} 结合时，同时满足下列条件：

1．“连带勒让德函数”（associated Legendre function）的上标必须相一致，即m＝m′。

2．两个勒让德函数的阶数的差必须精确地为1，即｜n－n′｜＝1。

3．对于每一组三元指标ιmn，如果m≠0，按照（70），则有着两个勒让德函数，因而也有着两个本征函数ψ_ιmn ，彼此的不同仅在于一个包含因子cosmΦ，而另一个包含因子sinmΦ。第三个条件读作：我们只能用正弦与正弦组合，或是余弦与余弦组合，而不能让正弦与余弦组合。

所想要的矩阵剩余的非零矩阵元，必须用两个指标对（n，m）和（n＋1，m）来刻画。（我们拒绝任何明确地表明指标ι的想法。）由于矩阵是对称的，一个指标对（n，m）就足以了，如果我们规定了第一个指标，比如说n，这在任何地方都意味着两个阶数n和n′中更大的那个。

于是，计算给出

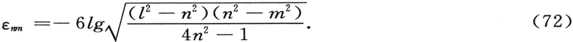
我们现在必须从这些矩阵元中形成行列式（22）。基于下列原理，像排列它的列一样，来排列它的行是有利的。（为了确定我们的想法，让我们说列，然后来说刻画两个勒让德函数中第一个的指标对。）这样，首先是对于所有m＝0的项，然后是所有m＝1的项，接着是m＝2的项，等等，最后，直到所有m＝ι－1的项，这是m（像n一样）所能取的最大的值。在这些组中的每一个中，让我们这样来排列这些项：首先是所有具有cosmΦ的项，然后是所有具有sinmΦ的项。在这些“半组”中，让我们按照n的阶数增加来排列它们，其值从m，m＋1，m＋2，…直到ι－1，即所有（ι－m）的值。

如果如此操作，我们会发现（72）的非零矩阵元仅限定于两条第二级对角线，它们紧靠着主对角线。在主对角线上的是有待发现的微扰的本征值，但是是以负数的形式，而其他各处的矩阵元都为零。此外，这两条二级对角线在这些地方为零所中断，在这儿，它们以非常便捷的形式，突破了所谓“半组”之间的边界。由此，整个行列式分解为正如“半组”所呈现出的那么多的更小的行列式的乘积，即（2ι－1）。我们只需考虑其中之一就足够了。我们把它写在下面，用ε（没有下标）来表示所要求的本征值的微扰：

如果我们用ε_nm 的公因子6ιg（参见（72））来除每一项，并在眼下看做为未知的

上述（ι－m）次的方程的根为

k^* ＝±（ι－m－1），　±（ι－m－3），　±（ι－m－5），　…　　　　（75）

其中级数依据次数ι－m是偶数还是奇数而中断于±1或是0（含在内）。遗憾的是这一点的证明在附录中没有，因为我尚未能成功地获得它。

如果我们对于每一个值m＝0，1，2，…（ι－1）求得了级数（75），那么我们在数目上就有了

ε＝－6ιgk^* 　　　　（76）

主量子数ι的微扰的完备集。为了找出方程（32）的受扰本征值E（项－层级），我们只需把（76）代入

其中考虑了缩写g和a₀ 的意义（分别见（68）和（63））。

对此式化简之后，得出

与（62）相比表明，k 是抛物线量子数的差k₂ －k₁ 。记住上述提及的m的取值范围，我们由（75）看出k 可能也与刚刚提及的差取同样的值，即0，1，2，…（ι－1）。同样，如果我们不怕麻烦把它算出来，我们会发现多重性，其中k 与差k₂ －k₁ 出现同样的值，即ι－｜k ｜。

这样，我们也从一般理论获得了一阶的本征值微扰。下一步将是对κ量求解一般理论的线性方程组（21′）。于是，按照（18）（暂时令λ＝0），这些将产生零阶的受扰本征函数；这不过是本征函数（64）的表征，作为本征函数（70）的线性形式。在我们的情形中，因为根ε可观的多重性，（21′）的解自然不会是唯一的。如果我们注意到方程分解成如上述研究的包含像（73）这样的因子行列式一样多（即（2ι－1））具有完全分离的变量的组，或保留前面的半组的表述，解会变得简单得多；而如果我们进一步注意到，在我们选择了一个确定的ε的值后，它会允许我们只把一单一的半组变量κ看做为在此半组中不为零，而事实上对于它，行列式（73）对于所选的ε值为零。于是，变量的此一半组的定义是唯一的。

但是我们的目标，即通过一个例子说明§2的一般方法，已经充分地实现了。由于对继续计算并无特别的物理上的兴趣，我没有费心去求出行列式的值，我们可以立即以一种更清楚的形式，对于系数κ得出这一值，或是以任意其他方式，得出对于主轴的转换。

大体上，我们必须承认在目前的情形中，长期微扰的方法（§5）要比对分离系统的直接应用（§3）麻烦得多。我相信在其他情形中也会是这样。如我们所知，在普通力学中，情况通常是相反的。

第三节　数学附录

序注：此处并非旨在提供论文中被略去的所有计算的连续性细节。没有这些，目前的论文也已经太长了。一般来说，只有那些他人可以在类似的工作中有效地利用，且无其他更好的方法，将被简略地描述，因为它可以容易地做到。

§1．一般化的拉盖尔多项式和正交函数

k次拉盖尔多项式L_k （x）满足微分方程 ^〔65〕

xy″＋（1－x）y′＋ky＝0．　　　　（101）

如果我们首先用n＋k取代k，然后微分n次，我们得出（n＋k）阶拉盖尔多项式的n次导数，我们总是用 来表示它，满足方程

xy″＋（n＋1－x）y′＋ky＝0．　　　　（102）

此外，通过一个简易的转换，我们发现对于 下述方程成立

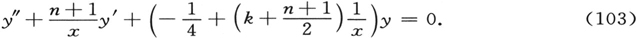
这可以应用于§3中的方程（41′）。相关的一般化的拉盖尔正交函数为

顺便注意到，它们的方程是

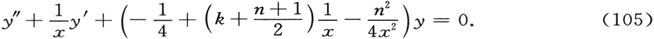
让我们回到方程（103），考虑n是一个固定的（实）整数，而k是本征值参量。这样，按照前述，在x≥0的区域，无论如何，方程会有本征函数，

属于本征值

k＝0，1，2，3，…　　　　　　　（107）

文中坚持它不再有其他值，而且首先是不拥有连续谱。这对于方程

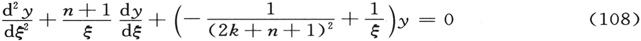
似乎是悖谬的，方程（103）通过代换

转变为它，而它确实拥有一个连续谱，如果说在其中我们把

看做是本征值参量，即所有E的正值是本征值（参见第一篇，方程（7）的分析）。为什么（103）的本征值k不能对应于这些正E值的理由，在于按（110），所讨论的k值将是复数，而这依据一般定理是不可能的。 ^〔66〕 按照（110），（103）的每一个实的本征值引出（108）的一个负的本征值。此外，我们知道（参见第一篇）（108）拥有不同于这些引出的绝对非负的本征值，如（110）中来自于级数（107）的那些值。这样，只剩下一种可能性，在级数（107）中某些负的k值缺失，这出现于对于k的解（110），由于当求根时的双值性。但这也是不可能的，因为所讨论的k值被证明在代数上小于 并且因此，按一般定理， ^〔67〕 不可能是方程（103）的本征值。数值级数（107）因此是完备的。证毕。

上述补充表明，函数（70）是（67）与本征值（69）相关的本征函数（具有被抑制的微扰项）。我们只能把（67）的解写作θ，φ的函数与η的函数的乘积。η的方程易于表现为（105）的形式，唯一的不同在于我们目前的n在那儿总是奇数，即在那儿发现的总是（2n＋1）。

§2．两个拉盖尔正交函数的乘积的定积分

拉盖尔多项式可以以下述方式获得：在展开为一个所谓的“生成函数” ^〔68〕

的级数中，作为辅助变量t的幂的系数。如果我们用n＋k取代k，然后对x微分n次，就得到我们的广义多项式的生成函数

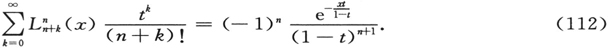
为了借助于它来评估诸如在论文的表达式（52）中首次出现的积分，或者说更一般的，例如在§4（同样在§5中）为计算（65）所必需的积分，我们以如下方式进行。我们重新以假设固定的下标n和可变的下标k′为条件，写出方程（112），并且用s取代未定义的t。然后，这两个方程相乘，即左边乘左边，右边乘右边。接着，我们进一步用

x^p e^－x 　　　　（113）

乘，并对x积分，x取值范围为从0到∞。p为一个正整数——这对于我们的目标来说已经绰绰有余了。积分在方程右边采用基本的方法是可行的，我们得到

现在，我们在方程左边，有了所期望的积分，就像一条线上的珍珠一样，我们只需依据我们偶尔的需要，通过在右边寻找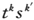 的系数即可取出一个。这一系数总是一个简单和，并且事实上在文中所发生的情形中，总是一个只有很少几项（上限为3）的有限和。一般而言，我们有

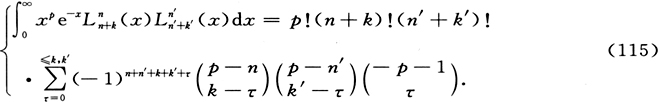
和中止于两个数k和k′中较小的之后。在实际情形中，它经常起始于τ的一个正值，随着二项式系数（其较低的数比上面的数更大）而消失。例如，在（52）式分母中的积分中，我们令p＝n＝n′，且k′＝k。于是τ仅能取一个值k，并且我们能确定文中的表述（53）。在（52）的分子的积分中，只有p有另一个值，即p＝n＋2。现在τ取值为k－2，k－1和k，经简单的化简，我们得到论文中的公式（54）。以非常相同的方式，出现在§5中的积分由拉盖尔多项式得以评估。

因此，我们现在可以把（115）这一类型的积分看做为已知，而只需让自己去关注出现在§4中的强度计算的积分（参见表达式（65）和在那儿必须被代换的函数（64））。在这一类型中，两个拉盖尔正交函数（它们的积被积分）没有相同的自变量，然而，例如在我们的情形中，却有着自变量λ₁ ／ιa₀ 和λ₁ ／ι′a₀ ，其中ι和ι′为我们所组合的两个能级的主量子数。作为典型，让我们考虑积分

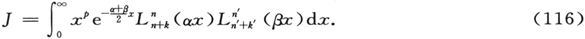
现在，我们可以以一种表面上不同的方式来进行。首先，前述程序依然平稳地进行，只是在（114）的右边一侧出现了多少更为复杂的表达式。在分母上出现了二次二项式的幂，而不是前述的二项式。这使得问题有些混乱，因为它使得（114）的右边一侧成为五重的而不是三重的，这样使（115）的右边成为三重的，而不是一个简单的和。我发现下述代换可使得事情更清楚：

因此

在把两个多项式展开为它们的泰勒级数后（它们是有限的，并且有着类似的作为系数的级数），运用缩写

我们得到下述结果

由此，J的计算化简为较为简单的积分类型（115）。在巴耳末线系的情形中，（120）中的双重求和相对而言，对于两个k值中的一个是易于处理的，即指涉两个量子能级的那一个，绝不会超过1，由此λ或许至多有两个值，并且如所证明的，μ至多只有4个值。来自指涉两个量子能级的情形表明，没有其他值，而只有

L₀ ＝1，　L₁ ＝－x＋1，　 ＝－1，

出现，允许做进一步的简化。不过，我们必须计算出一些表格，而非常抱歉地是，论文的这些表格中表示强度的数字无法让它们的一般结构被看出。幸运地是在平行分量‖和垂直分量⊥之间的可加关系保持得很好，由此我们可以有某种可能，感觉自己至少在代数上并没有犯什么大错。

§3．对勒让德函数的积分

在相关的勒让德函数之间，有三个积分关系，对于§5中的计算是必须的。为了他人的方便，我在这儿来表述它们，因为我在论文中的其他地方无法找到合适的地方。我们用惯常的定义

于是，下式成立

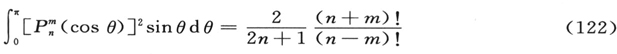
此外，

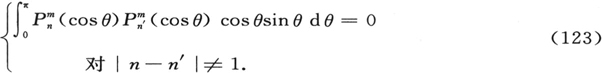
另一方面，

最后两个关系决定了［即（73）——译注］上行列式的“选择”。此外，它们对于光谱理论有着基本的重要性，因为显然，关于角量子数的选择原理依赖于它们（以及依赖于其他两个关系式，它们在这两个关系式中为cosθsinθ的地方，有着sin2θ）。

附加的对于证明的修正

沃尔夫冈·泡利告诉我，通过对于在附录第二部分中所给出方法的修正，他已经得到下述用于计算赖曼（Lyman）和巴耳末线系总强度的闭合公式。对于赖曼系，它们是

对于巴耳末线系，它们是

总的辐射强度（频率的四次方的幅度的平方）在所讨论的级数内，正比于这些表达式。对巴耳末系，由这些公式获得的数值与（§4结束处——译注）给出的数据完全相符。

苏黎世大学物理学研究所

（收稿日期：1926年5月10日）

第四篇

（《物理学年鉴》1926年第4期，第81卷）

摘要：§1．从振动方程中消去能量参量。实波动方程。非保守系。§2．把微扰理论推广到明显包含时间的微扰。色散理论。§3．补充第二节。激发态原子，简并系统，连续光谱。§4．讨论谐振情形。§5．推广到任意扰动。§6．基本方程推广到相对论性和带有磁场情形。§7．关于场标量的物理意义。

§1．从振动方程中消去能量参量。实波动方程。非保守系统

第二篇中的波动方程（18）或（18″），即

或

构成了在这一系列论文中重建力学的基础。但它的缺陷是它所表达的“力学场标量”ψ的变化规律既不统一，也不普遍。方程（1）包含了能量（或是频率）参量E，并且如在第二篇中所明确地强调的，其对于插入的一个确定的E值的有效，适用于那些仅通过一个确定的周期性因子

而依赖于时间的过程。这样，方程（1）实际上并不比方程（1′）普遍，后者考虑到了上面所提到的情况，并且根本不包含时间。

这样，当我们在不同的情形中，把方程（1）或（1′）标示为“波动方程”时，我们实际上是错了，或许称之为“振动”方程或“振幅”方程更为准确。然而，我们发现这样称呼也足够了，因为与其相联系的是斯图谟－刘维本征值问题，而不是真实的波动方程，正如数学上严格类似的弦和膜的自由振动问题。

关于这一点，我们迄今为止已经假设势能V为一坐标的纯函数，而不明显地依赖于时间。然而，这就产生出一个急迫的要求，把这一理论推广到非保守系，因为只有以这种方式，我们才能研究系统在规定的外力，如光波或一个经过的外部原子的影响下，所表现出的行为。一旦V明显地包含了时间，显然方程（1）或（1′）就不可能为函数ψ所满足，这里函数ψ对时间的依赖方式由（2）所给定。于是，我们发现振幅方程不再是充分的，而必须寻找真正的波动方程。

对于保守系，后者是很容易找到的。（2）等价于

我们可以通过微分从（1′）和（3）中消去E，得到下述方程，它以易于理解的符号方式写出：

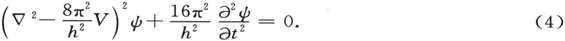
这一方程必定为每一如（2）那样依赖于时间的ψ所满足，尽管其中E是任意的；因而也能为每一对于时间展开为傅里叶级数的ψ所满足（自然也为以作为系数的坐标函数所满足）。这样，方程（4）显然是关于场标量ψ的均匀的和一般的波动方程。

显然，这不再是来自振动膜的简单类型，而是一种四阶的，类似于许多出现于弹性理论中的问题的类型。 ^〔69〕 然而，我们无须害怕这一理论过于复杂，或是必须修改与（1′）相联系的前述方法。如果V不包含时间，我们可以从（4）出发，应用（2），然后把算子分解如下：

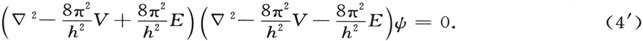
借助于尝试的方法，我们能把这个方程分解为两个“二中择一的”方程，即分解为方程（1′）和另一个方程，其与（1′）的不同仅在于其本征值参量被称作负E，而不是正E。按照（2），这并不导致新的解。（4′）的分解并非绝对令人信服的，因为“乘积仅当至少其一个因子为零时为零”的定理对于算子并不有效。然而，这种说服力的缺乏，正是所有偏微分方程解法的共同特征。这种程序可由随后的这一事实得到证明，即我们可以证明所发现的本征函数作为坐标函数的完备性。这种完备性与（2）中的虚部与实部同样满足方程（4）这一事实相结合，允许任意的起始条件为ψ和 所满足。

这样，我们看出其自身包含了色散定律的波动方程（4），确实可以作为前面所发展的关于保守系的理论的基础。然而，对于势能函数随时间变化的情形则须小心，因为此时会出现含V的时间导数的项，而方程（4）由于我们获取它的方式而不能给我们以相关信息。事实上，如果我们试图应用方程（4），就像它能适用于非保守系那样，我们就会遇到看来产生于 项的麻烦。因而，在下述讨论中，我将采取稍许不同的途径，它很易于计算，并且我认为它原则上是业已被证明的。

我们无须把波动方程的阶数提到4，以便摆脱能量参量。ψ对时间的依赖（如果（1′）成立，则它必然存在）可表示为

就像由（3）表示一样。这样，我们就得到两个方程中的一个

我们将要求复波动函数ψ满足这两个方程中的一个。由于共轭复函数ψ将满足另一个方程，我们可以取ψ的实数部分作为实波动函数（如果我们需要它）。在保守系情形中，（4″）本质上等价于（4），因为实算子可以被分解为两个共轭复算子的乘积，如果V不包含时间的话。

§2．把微扰理论推广到明显包含时间的微扰。色散理论

我们主要的兴趣不在于那些其势能的时间和空间变化处于同一量级的系统，而是那些其本身为保守系，却为势能所附加的一个小的给定依时（及坐标）函数所微扰的系统。因此，让我们写出

V＝V₀ （x）＋r（x，t），　　　　（5）

其中，如前面所经常的那样，r代表整个位形坐标。我们把未受扰动的本征值问题（r＝0）看做为已经解决的。于是微扰问题可以通过求积来解决。

然而，我们不是立即去处理一般的问题，而是从大量有关这一论题的重要应用中，挑选出色散理论问题，由于其显著的重要性，它确实在任何情形中，都需要一种独立的处理。在这一问题中，微扰力起源于一个变动的电场，它在原子的区域中是均匀的，同步振动的；这样，如果我们必须面对的为一频率为ν的线性极化的单色光，写作

r（x，t）＝A（x）cos2πνt，　　　　（6）

并且因此

V＝V₀ （x）＋A（x）cos2πνt．　　　　（5′）

这里，A（x）是光振幅与坐标函数的负乘积，而按照一般力学，后者表示了在电－光矢量方向上，原子电矩的分量（比如说－F∑e_i z_i ，其中F为光幅，e_i 与z_i 为粒子的电荷和z坐标，光在z的方向上被极化）。我们像从前一样（如在开普勒问题中），尽量少地从一般力学中借来势函数的时间变量部分，我们借的是常数部分。

运用（5′），方程（4″）变成

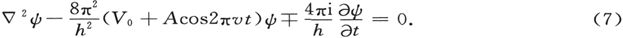
对于A＝0，这些方程通过代换

（现在这只是一种字面意义的代换，而并不意味着真实的代换）变为未受扰问题的振幅方程（1′），而且我们知道（参见§3）未受扰问题的解的总体是以这种方式发现的。让

E_k 和u_k （x）；　k＝1，2，3，…

为未受扰问题的本征值和归一化的本征函数，我们把它们看做为已知的，并且将假设它们为分立的和彼此不同的（不具有连续谱的非简并系统），这样我们就无须卷入需要特殊考虑的次生的问题。

正如在独立于时间的微扰势中的情形，我们必须在未受扰问题的每一个可能解的邻近，也就是在有着常数系数的u_k 的一个任意线性组合的邻近（由（8）知，u_k 将与一个适当的时间因子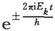 组合），来寻找受扰问题的解。位于一个确定的线性组合邻近的受扰问题的解，将有着下述物理意义。如果当光波抵达时，这一首次出现的解，正是一确定的自由本征振动的线性组合被呈现（或许在“激发”中有不重要的变化）。

然而，由于受扰问题的方程也是齐次的（让我们着重强调这一与声学中的“受迫振动”类比意图的表达），在每一个分别的

的邻近寻找受扰解显然是充分的，我们于是会任意地线性组合它们，正如对未受扰的解所做的一样。

因此，为了解（7）中的第一个方程，我们现在令

［下面的符号，即（7）中的第二个方程且暂放一边，因为它并无什么不同。］附加项w（x，t）可被看做一小量，它与受扰势的乘积被忽略。记住这一点，把（10）代入（7），并且记住u_k （x）和E为未受扰问题的本征函数和本征值，我们得到

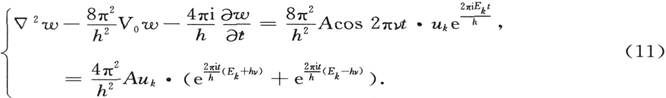
这一方程易于为，并且确实也仅仅为下一代换所满足

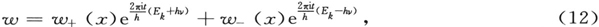
其中两个函数w_± 分别服从两个方程

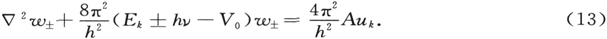
这一步本质上是独特的。初看起来，我们显然可以对（12）加上一个未受扰本征振动的任意集合。但这一集合必须假设为一小量，并且是一阶的（因为这是对w的假设），因此在眼下不引起我们的兴趣，因为它至多只会产生二阶的扰动。

在方程（13）中，我们最终有了那些我们所期望遇到的非齐次方程，尽管如前所强调的，缺少与真实受迫振动的类比。这一类比的缺乏是极端重要的，并且在方程（13）有下述两点特殊的表现。首先，作为“第二成员”，（“激发力”），扰动函数A（x）并不单独出现，而是为一个已经呈现的自由振动的幅度所倍乘。如果适当地考虑物理事实，这一点是不可避免的，因为原子对于入射光波的反应，几乎完全依赖于原子在那一时刻的状态；而已知一个膜（或是片等）的受迫振动是相当地独立于叠加于它们之上的本征振动的，因此，这将会产生对我们例证的一个错误表示。其次，要取代（13）左边的本征值，即“激发频率”，我们并未发现扰动力自身的频率ν，而只是在不同情形中，对已经呈现的自由振动频率有所加减而已。这也同样是不可避免的。否则，对应于项－频率的本征频率本身，将作为谐振点而起作用，而不是如所要求并由方程（13）所真正给出的，作为本征频率的差。此外，我们满意地看到后者给出的仅仅是事实上被激发的本征频率与所有其他频率之间的差，而不是那些没有成员被激发的本征频率对之间的差。

为了更严密地考察这一点，让我们完成这一解。运用著名的方法， ^〔70〕 我们发现方程（13）的简单解

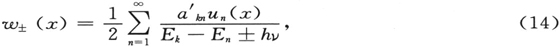
其中

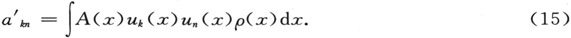
ρ（x）是“密度函数”，即位置坐标函数，方程（1′）必须乘上它以成为自伴的。u_n （x）被假设为归一化的。进一步的假设是hν并不精确地与任何本征值E_k －E_n 的差相符。这一谐振的情形将在后面处理（参见§4）。

如果我们现在运用（12）和（10），从（14）形成整个受扰振动，我们得到

这样在受扰的情形中，与每一个自由振动u_k （x）一起，对那些 的项，出现了所有那些振动u_n （x）的小的振幅。后者正是这样的振动，如果它们作为自由振动存在，与引起辐射的u_k （x）一起，其极化将（整个或部分地）与入射波的极化方向一致。因为除了一个因子，a′kn正是原子电矩（在这个极化方向上）的分量振幅，按照波动力学，它以频率（E_k －E_n ）／h振动，并且当u_k （x）和u_n （x）一起存在时出现。 ^〔71〕 然而，同时振动既不与那些本征频率为E_n ／h的特殊振动一起发生，也不与光波频率ν一起发生，而是与ν和E_n ／h（即一个激发自由频率）的和与差一起发生。

（16）的实的或虚的部分可以被考虑为实的解。然而，在下面，我们着手处理复数解本身。

要认识我们的结果在色散理论中的重要性，必须考察由受激强迫振动与原已呈现的自由振动的同时存在而产生的辐射。为此目的，按照我们前面已经采用的方法 ^〔72〕 （在§7中有一个批评），我们构成了复波函数（16）与它的共轭的乘积，即复波函数ψ的模方。我们注意到扰动项较小，因此其平方和乘积可以被忽略。经简单的变形， ^〔73〕 我们得到

按照关于场标量ψ的电动力学意义的启示性假说，如果x仅仅代表三维空间坐标，即我们处理单电子问题的话，目前的量（除了一个多重性系数外）代表了作为空间坐标和时间的函数的电流密度。我们记得，同样的假说把我们引向了正确的选择和极化规则，在我们讨论氢的斯塔克效应时，引向了非常令人满意的强度关系表示。通过对这一假说的自然的推广（在§7中会有更多），我们把下述看做是表征了电流密度的一般情形，它是与经典力学中的一个粒子“相关联的”，或是它“起源于其中”，或是它“在波动力学中对应于它”： 对系统的所有那些坐标的积分（在经典力学中，它确定了剩余粒子的位置），乘上某一个常数，第一个粒子的经典的“荷”。得出的在空间中任意点的荷密度，于是由这种对所有粒子的积分的和来表征。

由此，为了发现作为时间函数的总体波动力学偶极矩的无论什么空间分量，我们必须基于这一假说，用作为点系统的位形函数，在经典力学中给出了特定偶极矩分量的坐标函数，来乘以表达式（17），例如，如果我们正处理的是y方向上的偶极矩分量的话，则乘以

M_y ＝∑e_i y_i ，　　　　（18）

这样，我们必须对全部位形坐标积分。

让我们来对此作出计算，用缩写

b_kn ＝∫M_y （x）u_k （x）u_n （x）ρ（x）dx．　　　　（19）

让我们进一步来澄清 的定义（15），通过回忆如果入射电光矢量是由

给出，则

如果我们类比于（19），让

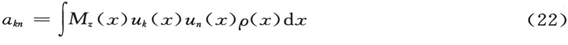
则 通过算出所设想的积分，我们发现

对所导致的电矩，由入射波所产生的二次辐射将归之于它。

当然，这一辐射仅依赖于第二（时间变量）部分，而第一部分代表的是时间不变的偶极矩分量，它可能与原初存在的自由振动相关联。这一变量部分似乎很有希望，可以满足所有我们通常对“色散公式”所提出的要求。首先，让我们关注那些所谓“负”项的出现，它在通常的措辞中对应于向一个较低能级（E_n ＜E_k ）的转换概率。克拉默斯（Kramers）首先从一种对应的观点关注到它。 ^〔74〕 一般而言，尽管思考和表达的方式非常不同，我们的公式确实可以在形式上描画得与克拉默斯的次级辐射公式一样。A_kn 和b_kn 之间的重要联系，次级辐射和自发辐射的系数得以表明，而且确实次级辐射也针对其极化条件得以精确描述。 ^〔75〕

我愿意相信，散射辐射或诱发的偶极矩的绝对值也由公式（23）正确地给出，尽管显然在可能性的边界内，在应用上述引入的启发性假设时，可能会出现数值因子上的错误。无论如何，物理量纲是正确的，来自（18），（19），（21）和（22）的A_kn 和b_kn 是电矩，因为本征函数的平方积分被归一化为单一的。如果ν远为偏离了正讨论的发射频率，诱发偶极矩与自发偶极矩的比率，与附加的势能Fa_kn 对“能级”E_k －E_n 的比率就在同一个数量级上。

§3．补充第二节。激发态原子，简并系统，连续光谱

为明晰起见，我们在前面的章节中做出了一些特别的假定，把许多问题放在一边。这些现在必须通过补充的方式来加以讨论。

首先，当光波遇到原子，而后者处于并非迄今为止所假定的仅仅一个自由振动u_k 被激发，而是几个，比如说两个，u_k 和u_ι 的状态时，会发生些什么呢？如上面所提到的，我们在提供它们以常（可能是复数）系数（对应于所假设的自由振动的强度，和它们的刺激相位关系）后，在受扰情形中，简单地以加和的方式来组合两个对应于下标k和ι的受扰解（16）。在实际操作这一计算前，我们看出在 的表达式和用于导出电矩的表达式（23）中，产生的不仅仅有前面获得的项，即表达式（17）或是（23）中用k，然后用ι写出的项的相应的线性聚集，我们此外还得到了“组合项”，即首先考虑量的最高级，在

中的一个项，它再次给出了与两个自由振动的同时存在密切相关的自发辐射；其次是一阶的微扰项，它与微扰场的振幅成正比，对应于属于u_k 的受迫振动与自由振动u_ι 之间的相互作用，以及属于u_ι 的受迫振动与自由振动u_k 之间的相互作用。这些出现在（17）和（23）中的新的项的频率不是ν，而是

这一点仍然无须计算，而可以轻易地看出。（然而，新的“共振分母”不在这些项中出现。）这样，我们在这里必须面对次级辐射，其频率既不与激发光频率一致，也不与系统的自发频率相同，而是这二者频率的组合。

这种引人注目的次级辐射的存在，首先为克拉默斯和海森伯出于对应原理的考虑所假设（见前引文），然后为玻恩、海森伯和约旦出于海森伯量子力学的考虑所假设。 ^〔76〕 据我所知，这尚未为实验所证明。目前的理论也清楚地表明，这种散射的辐射依赖于特殊的条件，它要求特别地依据目的来安排研究。首先，两个本征振动u_k 和u_ι 必须被很强地激发，由此所有对处于常规态的原子所做的实验（绝大部分情形都是如此）都被拒斥。其次，至少三分之一的本征振动态必须存在（即必须是可能的——它无须被激发），当与u_k 以及同样与u_ι 相组合时，它们将导致有力的自发辐射。有待发现的非常散射辐射与所讨论的自发发射系数的乘积（a_kn b_ιn 和a_ιn b_kn ）成比例。组合（u_k ，u_ι ）自身不必引发一个强发射。用旧的理论语言来说，如果这是一种“禁戒跃迁”，这并不重要。而实际上，我们必须也要求这条线（u_k ，u_ι ）在实验中被很强地发射出来，因为这是唯一的手段，使我们自己确信下述两条：本征振动在同样的单个原子中被激发，以及在足够大数目的原子中被激发。现在，如果我们反思，在那些被考察最多的有力的项－线中，即在通常的s线，p线，d线和f线中，关系通常是这样的：与第三项很强地组合的两个项，彼此之间却并不如此，因此，如果我们期望所要的散射辐射具有任何确定性的话，一个特殊的对于研究对象和条件的选择似乎是必需的。特别是由于它的频率并非激发光的频率，这样，它不能产生色散或极化平面的旋转，而只有当光向所有侧面散射时被观察到。

在我看来，上面提及的海森伯、玻恩和约旦的色散理论尽管在形式上与眼前的理论有极大的相似性，但并不允许作我们所做的这样的反思。因为它只考虑了一种原子对入射辐射做出反应的方式。它把原子想象为永恒的实体，迄今为止仍不能用自己的语言表述这一确定无疑的事实：原子在不同的时间能处于不同的状态，由此，如已经证明的，可以不同的方式对入射的辐射做出反应。 ^〔77〕

现在，让我们转向另一个问题。在§2中，集体的本征值被假定是彼此不同的和分立的。现在，我们不讨论第二个假说，而是问：当产生多重本征值，或是简并出现时会有什么改变？或许我们预期会出现一些复杂的情形，类似于我们在时间为常数的微扰情形中所遇到过的（第三篇，§2），即一个（适用于特定的微扰的）未受扰原子的本征函数系统，必须被定义为一个“久期方程”的解，然后应用于微扰计算。在任意微扰情形［在方程（5）中，由r（x，t）所代表］中的确如此，但在由入射所产生的微扰（方程（6））情形中，情况并非如此——无论如何，就我们通常的一阶近似而言，并且只要我们设想光频率ν并不与所考虑的任何自发发射频率相一致。于是，双重方程（13）中关于受扰振动幅度的参数值就不是一个本征值，这一对方程总是有明确的一对解（14），其中即使当E_k 为一多重值，也不会有为零的分母出现。值得注意地是通过这些项（如果其中一项真的出现，即具有非零的a_kn ），频率ν＝0也出现在共振频率中。当然，这些项对“寻常的”散射并没有贡献，如我们从（23）中所看到的，因为E_k －E_n ＝0。

当微扰函数的时间平均值为零，或是同样的，当后者的按时间的傅里叶展开式不包含常数项，即独立于时间的项，简化总是可获得的 ^〔78〕 （至少在一个一级近似中，我们不要求特别地考虑任何可能的简并出现）。光波就是这样一种情形。

当我们关于本征值的第一个假设（它们应当是简单的）就此证明自身确实是过分谨慎了时，未加讨论的第二个假设（它们绝对应当是分立的）尽管在原则上不导致变化，但在计算的外观上，却带来了相当可观的变化，就对方程（1′）的连续谱所取的积分，被加到（14），（16），（17）和（23）中的分立的和上而言。这样的由积分表征的理论业已由外尔（H. Weyl）所发展， ^〔79〕 尽管它只适用于寻常的微分方程，但对于偏微分方程的拓展是允许的。为简明起见，这一情形也是如此。 ^〔80〕 如果属于非均匀方程（13）的均匀方程，即未受扰系统的振动方程（1′），在点光谱之外还拥有一个连续光谱，这一连续光谱（比如说）从E＝a延伸到E＝b，那么一个任意的函数f（x）自然不能如下这样，仅仅展开为归一化的分立本征函数u_n （x），

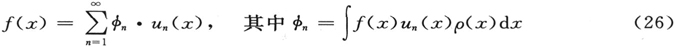
而必须加上一个按本征函数u（x，E）展开的积分，它属于本征值a≤E≤b，这样我们有

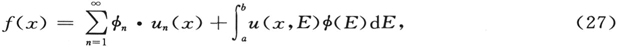
这里要强调，我们有意识地选择地同一字母来表示“系数函数”φ（E），来类似于分立系数φ_n 。如果现在我们通过把它与一个合适的E的函数相连，一次性对本征解u（x，E）归一化，以如下的方式

按照E是否属于区间E′和E′＋∆，于是在（27）中，在积分的标记下，我们代入

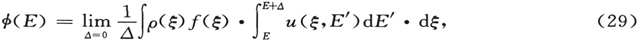
其中第一个积分符号所指的总是变量群x的区域。 ^〔81〕 假设（28）得以满足，展开式（27）得以存在（这一表述为外尔证明对通常的微分方程成立），来自（29）的“系数函数”的定义几乎与著名的傅里叶系数一样显明。

在任何具体情形中，最重要也是最困难的任务，是进行u（x，E）的归一化，即发现E的函数，再乘上（由于尚未归一化）连续谱的本征解，以便条件（28）得以满足。上面所引用的外尔的工作，包含了对这一实际任务的非常有价值的指导，以及一些已经完成的例证。一个关于带谱线强度原子动力学的案例是由Herr E. Fues在最近一期的《物理学年鉴》（Annalen der Physik）上的一篇论文中完成的。

让我们把它应用于我们的问题，即应用于受扰振动的振幅w的方程对（13）的解，其中一如以往，我们假设有一个受激的自由振动u_k 属于分立的点光谱。我们按照（27）的框架来展开（13），这样

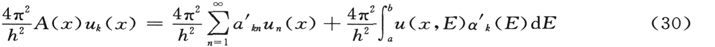
其中 由（15）给出，而a′_k （E）来自（29），通过

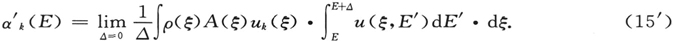
如果我们想象展开（30）放入（13），然后类似地按照本征函数u_n （x）和u（x，E），展开所欲求的解w（x），并注意对（13）中左边最后命名的函数取值

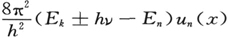
或是

然后通过“系数比较”，我们得到作为（14）的推广的

进一步的程序完全类似于§2中的程序。

最后，作为（23）的附加项，得到

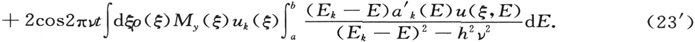
这里，或许我们不能总是未经进一步的考察，就改变积分的次序，因为对于ξ的积分可能不是收敛的。然而，作为一种通往极限的严格通道（它在这里可以免去）的直观上的权宜之计，我们能把积分分解成许多小的部分，每一个都有一范围∆，它足够地小，以至于我们可以把所有所讨论的E的函数看做在每一部分中是不变的，除了u（x，E）是一例外，因为我们从一般的理论知道，它的积分不能通过这样一种固定的分割来获得，它是独立于ξ的。于是，我们能从部分积分中取出剩余的函数，并且作为次级辐射的电偶矩（23）的附加项，获得最后的结果，除了下述

其中

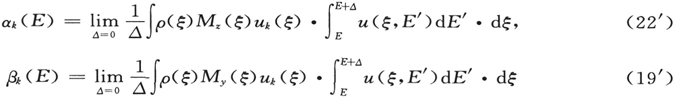
（请注意，与§2中没有撇的同样数字的公式完全类似。）

当然，前述的计算仅仅是一种一般的概观，以表明已经有着许多讨论的、实验似乎已证明的 ^〔82〕 连续光谱对于色散的影响，是精确地为目前的理论以预期的形式所需要的，并且概述了问题的计算得以解决的方式。

§4　讨论谐振情形

迄今为止，我们总是假设光波的频率ν与任何必须考虑的发射频率都不一致。我们现在假设，比如说

hν＝E_n －E_k ＞0，　　　　　　　　　　（31）

此外，为简单起见，我们改变§2中的极限条件（简单的、分立的本征值，单一的受激自由振动u_k 。）。因此，在方程对（13）中，本征值参数取值

即对上面的记号，出现了一个本征值，即E_n 。有两种可能的情形。第一种，方程（13）的右侧为ρ（x）所乘，可以正交于对应于E_n 的本征函数u_n （x）。即我们有

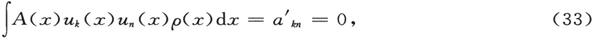
这在物理上意味着：如果u_k 和u_n 共同作为自由振动存在，它们将不会产生自发辐射，或极化会正交于入射光极化的方向。在这一情形中，临界方程（13）再一次也有一个解，这个解一如此前，由（14）给出，其中灾难性的项消失了。这在物理上意味着（用旧的术语来说）“禁戒跃迁”不可能通过共振来激发，或是一个即使并不被禁戒的“跃迁”，也不能为其振动垂直于将“自发跃迁”所发射的光的极化方向的光所导致。

第二种则不同，（33）不被满足。因此，临界方程没有解。假设了一个与原初存在的自由振动有微小不同（大约在光的振幅F的量级）的表述（10），并且在这一假设下是有着最一般可能的，由此将不能达到其目标。因此，不存在与原始的自由振动仅有F量级差异的解。这样，入射光对于系统的状态，具有一种变化着的影响，它与光的振幅大小并不相关。这会有什么影响呢？我们仍然可以无须进一步的计算，而是从共振条件（31）并没有被精确满足，而只是近似的满足的情形出发，来评价这一影响。于是，我们由（16）看到，U_n （x）由于一个小的分母的缘故，在一个非同寻常强的受激振动中被激发，并且并非不重要的是，这些受激振动的频率，已经接近于本征振动U_n 的自然本征频率E_n ／h。［确实，所有这些非常类似于（当然也有着自己的不同）在其他地方所遇到的共振现象，否则我不会如此详细地讨论它。］

在对于临界频率的逐渐趋近中，先前并未激发的本征振动u_n （其可能存在引起了这一危机）被刺激到一种愈来愈强的程度，并且具有一种愈来愈接近自身本征频率的频率。与通常的共振现象形成对比，而呈现不同的是会有这么一个点，甚至在到达临界频率之前，即使是假设我们明显的“无阻尼的”波严格有效的条件下，我们的解也不再能正确地表现这种情形。因为我们事实上把受激振动w看做与存在的自由振动相比是很小的，并且忽略了平方项［在方程（11）中］。

我相信目前的讨论已经足够清晰地表明，在共振情形中，理论事实上将给出它应当给出的结果，以便与伍德（Wood）的共振现象一致：导致了危机的本征振动u_n 增加到一个有限的尺度，与原始存在的振动u_k 可比较时，由此，当然就导致了光谱线（u_k ，u_n ）的自发发射。然而，我并不期望试图在这儿完全去计算出这一共振情形，因为如果不考虑对发射系统的发射辐射的反作用，这一结果的值会很小。这样的反作用必然存在，不仅仅因为原则上根本没有依据以区分外来的入射光波和为系统自身发现的波，而且因为如果只有一个系统自身，几个本征振动被同时激发的话，自发辐射将无限地持续下去。这要求反馈耦合必须起作用，使得在这一情形中，随着光的辐射，更高的本征振动逐渐衰退，最终只留下对应于系统常规状态的基本振动。反馈耦合显然完全类似于经典电子理论中的辐射反作用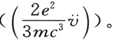

这一类比也缓解了我们由先前忽略了这一反馈耦合而导致的忧惧。波动方程中的（或许不再是线性的）相关项一般会比较小，正如在电子中，辐射的反压一般而言，与惯性力和外部的场强相比非常小一样。然而，在共振情形中，正如在电子理论中一样，如果要正确计算不同本征振动之间的“平衡”（其确定有赖于辐照）的话，由于与本征光波的耦合与同入射光的耦合处于同一量级，因此必须加以考虑。

然而，让我们对此作一明确的评论：反馈耦合项并非为避免共振灾难所必需的！它可能在任何情形中都不会发生，因为按照下面的§7中所提供的归一化的持续性定理， 的位形空间积分即使在任意的外界力的影响下，也总是保持归一为相同的值；而且作为波动方程（4）的结论，确实是很自动地这样做的。因此，ψ振动的振幅不可能无限地增长；它们“平均”总是保持同一个值。如果有一个本征振动增加，那么另一个必须因而减弱。

§5．推广到任意扰动

如果所讨论的一个任意微扰如§2中开始时的方程（5）中所假设的那样，我们就要把微扰能量r（x，t）展开为傅里叶级数，或是对时间的傅里叶积分。于是这一展开的项具有光波的微扰势的形式（6）。我们立即可以看出，在方程（11）的右边一侧，我们简单地得到e的两个虚的幂级数（或者可能是积分），而不仅仅是两项。如果激发频率与临界频率不相符，我们会以与§2中所描述的完全相同的方式得到解，但是当然，是关于时间的傅里叶级数（或者可能是傅里叶积分）。在这里，写出它的形式表达式，与我们的目标无关；更精确地分别计算出这些问题，也超出了本文的范围。然而，这里必须说到在§3中已经提到过的重要的一点。

在方程（13）的临界频率中，由E_k －E_k ＝0而得出的频率ν＝0也出现了。因为在这一情形中只有一个本征频率，即E_k 作为本征值参量出现在方程左边。这样，如果频率0，即一个独立于时间的项出现在微扰函数r（x，t）的傅里叶展开式中，我们就不能用与以前相同的方法达到我们的目标。然而，易于看出它必须如何修改，因为一个时间为常数的微扰在先前的工作中已经得知（参见第三篇论文）。于是，我们必须同时考虑受激自由振动的本征值的一个小的变动和可能的分裂，即在方程（10）右边第一项中e的幂指数中，我们必须用E_k 加上一个小的常数，本征值的微扰，来取代E_k 。与在论文第三篇中的§1和§2中完全相同，这一微扰由下述假设得以确定：我们的方程（13）中的临界傅里叶分量的右边，正交于u_k （或可能正交于所有属于E_k 的本征函数）。

属于目前这一节所讨论的特殊的问题，为数众多。通过把由不变的电场或是磁场产生的微扰与光波所产生的相叠加，我们得到了磁和电的双重折射，和极化平面的磁旋转。磁场中的共振辐射也出现在这一标题下，但为此目的，我们必须先获得§4中所讨论的共振情形的精确解。此外，我们可以处理一个α粒子或是电子飞经原子时的作用， ^〔83〕 这种经过是以这样的方式，其相遇不会太近，以便两个系统中的一个的微扰，可以由另一个的未受扰运动来计算。一旦未受扰系统的本征值和本征函数成为已知，所有这些问题都不过是计算问题。因此，人们期望对于重原子，我们也可以成功地（至少是近似地）确定这些函数，就像是近似地确定属于不同类型项的玻尔电子轨道一样。

§6．基本方程推广到相对论性和有磁场情形

作为对刚才提到的物理问题（其中迄今为止，在这一系列论文中完全被忽略的磁场起着一个重要的作用）的补充，我愿意简略地给出基本方程（4″）对于相对论性－有磁场情形的可能的推广，尽管其间我只能对单电子情形这么做，并且有着最大可能的保留——这种保留出于两个理由。首先，这一推广暂时还基于一个纯形式的类推。其次，如在第一篇论文中提到的，尽管它确实形式上，在开普勒问题中导出了索末菲的精细结构公式，事实上带有“半整数的”角向和径向量子，这在今天一般被看做是正确的，但仍然缺乏补充，以说明它是为确保数值上正确的氢线的分裂图形所必需的，而在玻尔理论中，这已由戈德斯密特和乌伦贝克（Goudsmit and Uhlenbeck）的电子自旋给出。

关于洛伦兹电子的哈密顿－雅可比偏微分方程，可以容易地写出：

其中的e，m，c是电子的电荷、质量和光速；V和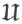 为电子所处位置外部电磁场的电磁势，而W是作用函数。

现在，从经典（相对论性）方程（34），我尝试从下述纯形式的程序，推导出电子的波动方程；易于验证，它如果应用于一般力学中，粒子运动于任意力场中的哈密顿方程，将导出方程（4″）。在方程（34）中，在取平方后，我用分别的算符，

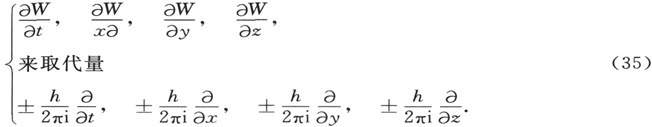
由此获得的双重的线性算子被应用于波动函数ψ，令结果为零，得出

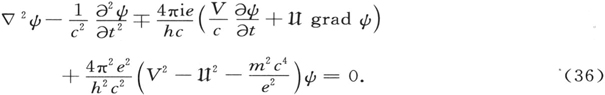
（这里的∇² 和梯度符号具有基本的三维欧几里得空间的意义。）方程对（36）是方程（4″）对于单电子情形的相对论性－有磁场情形的推广，因而类似地，意味着复波函数必须满足方程对中的这一个，或是另一个。

从（36），用与第一篇论文中所描述的完全相同的方法，可以获得关于氢原子的索末菲的精细结构公式，并且我们也可导出（忽略掉 ² 中的项）正常塞曼效应，同样可获得著名的选择和极化规则，以及强度公式。它们来自于在第三篇论文结尾处引入的勒让德函数之间的积分关系。

出于在本节第一段中给出的理由，我在这里不再给出这些计算的详尽过程；同样在下一节中，也只涉及理论的“经典”版本，而不讨论尚不完善的相对论性－有磁场情形。

§7．关于场标量的物理意义

场标量ψ的电动力学意义的启发性假说，过去曾用于单电子问题，被立即推广到§2中荷电粒子的任意系统，并在那儿许诺了对这程序的更为彻底的描述。我们已经计算了在如下空间中任意点的电荷密度。我们选择一个粒子，确定在一般力学中描述其位置的三元坐标组；用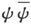 对系统所有剩余的坐标积分，并对结果乘以一个常数，所选电子的“电荷”；我们对每个粒子（三元坐标组）作相同的事，在每一情形中给所选电子以相同的位置，即我们想知道电荷密度的空间那点的位置。这一密度等于部分结果的代数和。

这一规则现在等价于下述概念，它允许ψ的真实意义更清楚地突现出来。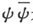 是系统的位型空间中的一种权重函数。系统的波动力学位型，是许多（严格地说是所有运动学上可能的点的力学）位型的叠加。这样，每一个点的力学位型对真正的波动力学位型贡献某种权重，它正是由 给出的。如果我们喜欢悖谬的说法，我们可以说系统存在于所有运动学上可以想象的位置，但并非在各处都有同等强度的可能性。在宏观运动中，权重函数实际上集中于一个很小的不能辨别的位置区域内。这一区域在位型空间中的引力中心运行的距离是宏观上可觉察的。在微观运动问题中，我们在所有情形中感兴趣的也都是（在某些情形中甚至主要是）区域中变化着的分布。

这种新的解释起初可能会令我们震惊，因为我们以前经常以这么一种直观具体的方式，把“ψ振动”说成仿佛是某种相当真实的东西。但在目前的概念背后，也有着某种确实真实的东西，即非常真实的、电荷空间密度的电动力学上有效的涨落。ψ函数所起的作用，恰恰在于允许这些涨落的总体，能以单个偏微分方程从数学上把握和考察。我们已经反复强调 ^〔84〕 了这一事实：ψ函数本身不可能，也不可以直接以三维空间的语言来解释，无论单电子问题如何趋向于把我们误导向这一点，因为它一般而言是一个位型空间中，而不是真实空间中的函数。

关于在上述意义上的这么一种权重函数，我们希望它对整个位型空间的积分，保持其归一化为同一不变的值，最好是单位值。我们很容易证实：如果系统的总电荷在上述条件下保持不变，这就是必然的。即使是对非保守系，显然也必须假设这个条件。因为很自然，系统的电荷在下述这样的过程中并没有改变，例如光波落于系统上，持续了一段时间，然后中止的过程。（注意：这对于电离过程也有效。一个粒子的瓦解仍然被包含在系统内，直到分离逻辑上也（通过位形空间的分解）完成。）

现在出现的问题是：是否所假设的归一化的持续，事实上为以ψ为对象的方程（4″）所保证。如果情形并非如此，我们的整个概念将实际上会破产。幸运的是，情形并非如此。让我们形成

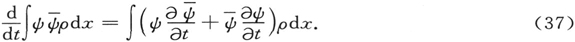
现在，ψ满足两个方程（4″）中的一个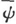， 满足另一个。因此，除了一个倍增常数外，这一积分变成

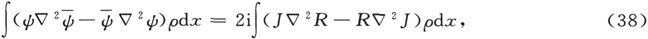
其中目前，我们令

ψ＝R＋iJ.

按照格林定理，积分（38）必然为零；而对此，函数R和J所唯一必须满足的必要条件（在足够大的无穷时为零）的物理意味，不过是所考虑的系统实际上应限定于一个有限的区域。

我们以一种稍许不同的方式来提出这一点，不是对整个位形空间积分，而是仅仅通过格林变换，把对权重函数的时间求导，改为求散度。通过这一变换，我们得到的是一种权重函数流，进而是电流的问题。两个方程

分别乘上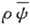 和ρψ后相加。由此有

为了进行方程右边的转换，我们必须记得我们的多维非欧拉普拉斯算子的明确表达式 ^〔85〕

通过一个小的变换，我们易于得出

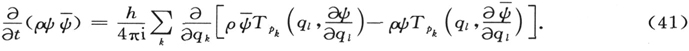
右边一侧出现的，是作为多维实矢量的散度，它显然可以被解释为位形空间中权重函数的流密度。方程（41）是权重函数的连续性方程。

由此，我们可以获得电流的连续性方程，而且确实，这样的一个单独的方程适用于“由每个单独的粒子产生的”电荷密度。例如，让我们确定第α个粒子。设它的“电荷”为e_α ，质量为m_α ，为简单起见，它的坐标空间由笛卡儿坐标x_α ，y_α ，z_α 表示。我们用dx′来简略表示其余坐标的微分的乘积。我们固定x_α ，y_α ，z_α 不变，让方程对后者积分。其结果，方程右边除了三项之外全部为零，我们得到

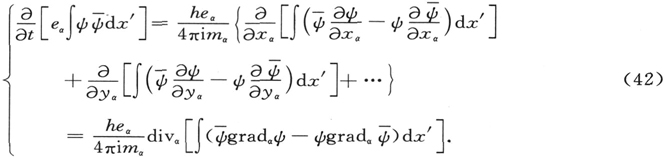
在此方程中，散度和梯度有着通常的三维欧氏意义，而x_α ，y_α ，z_α 被解释为实空间的笛卡儿坐标。方程是“产生于第α个粒子的”那个电荷密度的连续性方程。如果我们以类似方式形成其他粒子的方程，并把它们加总，我们就得到了总的连续性方程。当然，我们必须强调，把方程右边的积分解释为电流密度的分量，像其他所有这类情形一样，并非绝对必需的，因为此外，一个无散度矢量也是可加的。

为给出一个例证，在单电子保守系中，如果ψ由下式

给出，我们对流密度J得到

这对一般保守系都有效。我们看到，如果只有单一的本征振动被激发，电流分量消失，电流的分布在时间中为常数。这一点也可由ψ 对于时间而言成为常数这一事实，而即刻成为显然的。即使当有几个本征振动被激发时，如果它们都属于同一个本征值，情形也仍然如此。而另一方面，电流密度由此不再需要为零，而是呈现为（通常一般也是）一种稳态的流分布。由于在任何情况下，这一点或是其他都发生在未受扰的常态下，我们在某种意义上可以说回复到电磁的原子模型。以这种方式，通常状态中辐射的缺失确实找到了一处惊人简单的说明。

我希望并且相信，眼下这种陈述将被证明为对于原子和分子的磁性质的说明是有用的，并且对于进一步说明固体中的电流也是有用的。

同时，在对复波函数的应用中，无疑仍然有着某种不成熟。如果这是原则上不可避免的，而不仅仅是计算上的简单化方式，这可能意味着在原则上有着两种波函数，它们必须一起应用，以获得系统状态的信息。我相信：这一多少有些不可接受的推论会承认，系统状态的最为合适的解释，是由一个实函数和它的依时导数给出的。我们对于这一点之所以不能给出更为精确的信息，是与下述事实密切相关的：在方程对（4″）中，我们面前只有一个或许是四阶的实波函数的（确实非常便于计算的）替代品，然后，对非保守系情形，我还不能成功地构造它。

苏黎世大学物理学研究所

（收稿日期：1926年6月23日）

（本文节选自薛定谔在1926年发表在德国《物理学年鉴》的六篇论文。论文的发表标志着波动力学理论的创立。——编注）

（胡新和　译）

位于月球的南极附近的“薛定谔坑”

维也纳大学校徽

钱币和邮票中的薛定谔

《生命是什么——活细胞的物理学观》（剑桥大学出版社，1948年出版）。书中薛定谔试图用热力学、量子力学和化学理论来解释生命的本性，引进了非同性晶体、负熵、遗传密码、量子跃迁式的突变等概念。此书引导人们用物理学和化学方法去研究生命的本性，使薛定谔成了今天蓬勃发展的分子生物学的先驱。

量子力学中著名的薛定谔方程，它揭示了微观世界中物质运动的基本规律。

洪堡大学的艾尔文·薛定谔中心

薛定谔在爱尔兰毗邻克朗塔夫城堡的故居。1939—1956年，薛定谔居住于此。在此期间，他创建了都柏林高等研究院。

德国洪堡大学。1927年薛定谔接替普朗克成为德国洪堡大学理论物理所所长。

各种形象有趣的薛定谔猫。1935年薛定谔写下了《量子力学的现状》一文，在这篇文章中出现了著名的薛定谔猫的悖论。这是科学史上的一个著名的思想实验。

如何解释和理解量子力学的成果是学界，尤其是科学哲学上的热门话题。爱因斯坦和玻尔为之争论了一辈子，“薛定谔猫”则被爱因斯坦认为是最好地揭示了量子力学的通用解释的悖谬性。“薛定谔猫”佯谬假设了这样一种情况：将一只猫关在装有少量镭和氰化物的密闭容器里。镭的衰变存在概率，如果镭发生衰变，会触发机关打碎装有氰化物的瓶子，猫就会死；如果镭不发生衰变，猫就存活。根据量子力学理论，由于放射性的镭处于衰变和没有衰变两种状态的叠加，猫就理应处于死猫和活猫的叠加状态。显然，既死又活的猫是荒谬的。薛定谔提出这一悖论，想要阐述的物理问题是：宏观世界是否也遵从适用于微观尺度的量子叠加原理。“薛定谔猫”佯谬巧妙地把微观放射源和宏观的猫联系起来，旨在否定宏观世界存在量子叠加态。然而随着量子力学的发展，科学家已先后通过各种方案获得了宏观量子叠加态。

1900—1926年是量子力学的酝酿时期，此时的量子力学是半经典半量子的学说，称为旧量子论，开始于普朗克对黑体辐射的研究。他因有关量子理论方面的发现而获1918年诺贝尔物理学奖。

普朗克（左）和爱因斯坦（右）。爱因斯坦第一个意识到普朗克量子假设的革命性意义，即能量量子化与牛顿力学和麦克斯韦电磁场理论是不相容的，还进一步发展了能量子概念，并大胆地提出了光量子假设。利用光量子假设，提出了光电效应定律，为此，他获得了1921年的诺贝尔物理学奖。

1911年卢瑟福提出原子核模型。

1911年10月29日，在能斯特的组织下，主题为“辐射理论与量子”的第一届索尔维会议在布鲁塞尔召开，各国的物理学家们共同讨论了恼人的量子问题。此次会议使量子思想声名远播，并使更多的人投入到量子问题的研究中。

前排坐者从左至右依次为：能斯特　布里渊　索尔维　洛伦兹　瓦尔堡　佩兰　维恩　居里夫人　庞加莱

后排立者从左至右依次为：戈德施米特　普朗克　鲁本斯　索末菲　林德曼　德布罗意　克努森　哈泽内尔　奥斯特莱　赫尔岑　金斯　卢瑟福　开默林·昂内斯　爱因斯坦　朗之万

第一届索尔维会议合影

玻尔与爱因斯坦对量子问题的最早论战。爱因斯坦主张完备的光理论必须以某种方式将波动性和粒子性有机地结合起来，并且波和粒子这两个侧面可以因果性互相联系起来，而玻尔却坚持光的经典波动理论，否认光量子假设的有效性。

玻尔是量子力学中著名的哥本哈根学派的领袖。他们不仅创建了量子力学的基础理论，并给予合理的解释，使量子力学得到许多新应用，如原子辐射、化学键、晶体结构、金属态等。更难能可贵的是，玻尔与他的同事在创建与发展科学的同时，还创造了“哥本哈根精神”——这是一种独特的、浓厚的、平等自由地讨论和相互紧密地合作的学术气氛。

1930年出席在哥本哈根理论物理研究所召开的一次会议的代表。前排左起第二、三、四为玻尔、海森伯、泡利。

1916年，密立根通过光电效应实验，证实了爱因斯坦的理论工作，也证明了普朗克常数独立于黑体辐射。

1921年，在玻尔的倡议下成立了哥本哈根大学理论物理学研究所。它在量子力学的兴起时期是全世界最重要、最活跃的学术中心。图为当时的理论物理学研究所。

1923年，当旧量子论面临困境时，德布罗意在《哲学研究》上发表论文，提出了物质波的概念和理论，把量子论发展到一个新的高度，并最终导致了量子力学的波动形式——薛定谔方程的发现。德布罗意因发现电子的波动性而获得1929年诺贝尔物理学奖。

海森伯和玻恩、约旦第一次提出了一种系统的量子理论。在这个理论中，经典的牛顿力学方程被矩阵形式的量子方程所代替，此理论就是矩阵力学。

1924年，玻色提出了一种新的方法来解释普朗克辐射定律。他把光看做一种无（静）质量的粒子（现称为光子）组成的气体，这种气体遵循全同性性质的统计理论。爱因斯坦立即将玻色的推理应用于实际的有质量的气体，从而得到一种描述气体中粒子数关于能量的分布规律，即玻色－爱因斯坦分布。

佛罗里达州立大学科学图书馆的狄拉克塑像。狄拉克和薛定谔分享了1933年诺贝尔物理学奖，他们获奖的工作是“因为发现原子理论新的有效形式”。

1926年，费米推导出服从泡利不相容原理气体的统计性质。

1927年10月24日到29日，由洛伦兹主持召开了第五届索尔维会议。在这次会议上，薛定谔被认为是理论物理界的世界领袖之一，被重金聘请在会上做演讲。薛定谔的报告题目为“波动理论”。他解释了依赖于时间的波动方程对理解光谱跃迁的重要性。

前排坐者：朗缪尔　普朗克　居里夫人　洛伦兹　爱因斯坦　朗之万　古伊　威尔逊　里查森

中排坐者：德拜　克努森　布拉格　克莱默　狄拉克　康普顿　德布罗意　玻恩　玻尔

后排立者：皮卡尔德　亨利厄特　埃伦费斯特　赫尔岑　德唐德　薛定谔　费尔夏费尔特　泡利　海森伯　富勒　布里渊

玻尔和海森伯、泡利在哥本哈根讨论量子问题。

薛定谔与伦敦在柏林（1928）。1927年，伦敦和海特勒将海森伯的共振理论应用于氢分子的共价键。结果证明了电子自旋函数的稳定性，并否定了相同氦键的稳定性。

玻恩和儿子在德国格丁根（1924）。尽管玻恩是矩阵力学的创建者之一，但他对薛定谔的波动力学情有独钟，1926年6月他首次提出了量子力学的概率波解释。

1938年，泡利（左）与狄拉克（右）在一起。

海森伯（左）和狄拉克（右）在一起。

1932年，冯·诺伊曼利用希尔伯特空间等数学工具，严格证明了矩阵力学和波动力学之间的数学等价性。

电子的波粒二象性示意图。在宏观世界里，将球投过前一块板的狭缝，球必定会击中后一块板正对着狭缝的位置。但在微观世界里，电子却不一定击中后一块板正对着狭缝的位置，而是出现衍射现象。

1962年，玻尔去世，他的工作室的黑板上还画着当年爱因斯坦那个光子盒的草图。

注　释

〔1〕 　举一个例：虽然对于无条件周期系统，世界上从来没有人知道该怎样去表明它的量子化法则，但说也奇怪，这件事并不妨碍我们把量子化法则实际应用到多电子问题上去。我们简单地把多体问题当成是有条件周期性的，尽管完全知道它并不是这样的。我认为，这说明通常的力学的应用方式并不是很严格的，否则，上述应用会像把刑法应用到行星的运动上一样。

〔2〕 　这里我们没有考虑到那种对应于双曲线轨道的“连续谱”。我们或者可以设想这些振动方式不存在，或者认为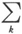 包括一个作为极限情形的积分，为了适当地估计到本征值的连续区域，这个积分是必须加上的。然而，我总希望避免公式的不必要的累赘。

〔3〕 　一般说来，对于各向异性的原子，还有M_y 和M_x （与入射辐射的偏振正交）。这里我们不想讨论它们。

〔4〕 　就本征函数的完备性和正交性说来，一般的情况是同简单的氢原子的情况一样的，这一点我们认为是理所当然的。这是十分可靠的。我们也同以前一样，不明显地考虑本征值的连续谱，以避免公式的过分累赘。

〔5〕 　我知道这一表述并非完全明确的。

〔6〕 　关于对求解（7）的指导，我要感谢赫尔曼·外尔（Hermann Weyl）。

〔7〕 　对于下面未加证明的部分，请见L. Schlesinger的Differential Equations（Collection Schubert, No. 13, Goschen, 1900，特别是第三章和第五章）

〔8〕 　参见Schlesinger. 此理论来自H. Poincare和J. Horn.

〔9〕 　如果（15）被满足，至少文中描述的两条积分路径中的一条不能被使用，因为它产生为零的结果。

〔10〕 　L. deBroglie, Ann, de Physique (10) 3, p. 22, 1925. (Thèses, Paris, 1924.)

〔11〕 　Physik, Ztschr. 27, p. 95, 1926.

〔12〕 　这一过程在本文中将不作进一步的讨论。这里只打算对于波动方程和哈密顿－雅可比方程之间的外部联系作一临时的、快速的考察。ψ实际上并非论文第一部分方程（2）所述关系中的确定运动的作用函数。另一方面，波动方程与变分问题之间的联系则当然是十分真实的；定态积分的积分函数是波动过程的拉格朗日函数。

〔13〕 　参见例如E. T. Wittaker的Anal. Dynamics, chap. Xi. .

〔14〕 　从1891年起，Felix Klein在他关于力学的演讲中，从一个在更高阶的非欧几里得空间中的类光思考，一再地发展了雅可比的理论。参见F. Klein, Jahresber, d. Deutsch, Math, Ver. 1, 1891, and Zeits. f. Math. U. Phys. 46, 1901 (Ges. Abh. ii. pp. 601 and 603). 在第二个注解中，Klein责备地论及他十年前在哈勒的演讲，在其中他已经讨论过这一对应，并强调了哈密顿的光学工作的重要性“尚未得到他所曾期待的普遍重视”。我要感谢索末菲教授在他的友好的通信中，向我提及F. Klein的工作。也可见Atombau, 4^th ed., p.803.

〔15〕 　特别是见爱因斯坦，Verh. d. D. Physik. Ges. 19, pp.77—82, 1917. 在所有旧的尝试中，量子化条件的制定是与目前的这一尝试最为类似的，德布罗意已经回到这一点。

〔16〕 　对于光学的情形，参见A. 索末菲和Iris Runge, Ann. d. Phys. 35, p.290, 1911. 那儿（在P. 德拜的口头评论中说明）表明了关于相的一阶和二次方程（“哈密顿方程”）如何能在波长消失的极限情形中，从关于波动函数的二阶和一次方程（“波动方程”）中精确地推导。

〔17〕 　参见爱因斯坦，Berl. Ber. p. 9 et seq., 1925.

〔18〕 　在第一部分中，这仅仅是作为一个近似方程出现的，由纯粹的猜测推导得出。

〔19〕 　L. de Broglie, Ann, de Physique (10) 3, p.22, 1925. (Theses, Paris, 1924.)

〔20〕 　P. Debye, Ann. D. Phys. 30, p.755, 1909.

〔21〕 　M. v. Laue, idem 44, p.1197 (§2), 1914.

〔22〕 　Loc. cit.

〔23〕 　尤其是参见海森伯、玻恩、约旦和狄拉克此后引用的论文，进一步的文章见N. 玻尔：Die Naturwissenschaften, January 1926.

〔24〕 　f（q_k ）的引入意味着不仅“密度”，而且“弹性”也要随位置变化。

〔25〕 　W. Heisenberg, Ztschr. F. Phys. 33, p. 879, 1925; M. Born and Jordan，出处同上，34, p. 858, 1925; M. Born, W. Hensenberg, and P. Jordan，出处同上，35, p. 557, 1926; P. Dirac, Proc. Roy. Soc., London, 109, p. 642, 1925.

〔26〕 　在相对论中并考虑磁场，哈密顿－雅可比方程的表述将变得更为复杂。在单电子情形中，它断言作用函数的四维梯度（为一个给定矢量所减，四维势）具有一不变值。这一表述转换成波动理论的语言，呈现出更多的困难。

〔27〕 　参见Courant-Hilbert, Methods of Mathematical Physics, i, (Berlin, Springer, 1924), v. §9, p. 261, eqn, 43，和进一步的ii. §10. 4, p. 76.

〔28〕 　这样，我们就导出了一个r中的方程，它可用本文第一部分中开普勒问题里所采用的方式来处理。此外，如果取q² 为变量，一维振子将导出相同的方程。我起初直接按这种方式来解决这一问题。关于这是一个厄米多项式问题的提示，我必须感谢赫尔·菲斯（Herr E. Fues）。出现在开普勒问题中的厄米多项式（第一部分中的方程18）是第n＋1级Laguerre多项式的（2n＋1）阶微分系数，如我随后所发现的。

〔29〕 　参见A. Sommerfeld, Atombau und Spektrallinien, 4^th edit., p. 833. 这里，我们不考虑势能中额外的非谐项。

〔30〕 　Physik. Ztschr. 27, p. 95, 1926.

〔31〕 　第二篇的最后两节。

〔32〕 　Courant-Hilbert, chap. vi. ξξ 2, 4. p. 337.

〔33〕 　Courant-Hilbert, chap. v. ξ 5, 2,. p. 241.

〔34〕 　P. S. Epstein, Ann. d. Phys. 50, p. 489, 1916.

〔35〕 　N. Bohr, Kopenhgener Akademic (8), Ⅳ., 1, 2, p. 69 et seq., 1918.

〔36〕 　A. Sommerfeld, Atombau, 4^th ed., p. 772.

〔37〕 　H. A. Kramers, Kopenhgener Akademic (8), Ⅲ., 3, p. 287, 1918.

〔38〕 　G. E. Uhlenbeck and S. Goudsmit, Physica, 1925; Die Naturwissenschaften, 1926; Nature, 20^th Feb., 1926；也可见L. H. Thomas, Nature, 10^th April, 1926.

〔39〕 　J. C. Slater, Proc. Acad. 11, p. 732, 1925.

〔40〕 　A. Sommerfeld and A. Unsöld, Ztschr. f. Phys. 36, p. 259, 1926.

〔41〕 　参见前述论文的最后两页。

〔42〕 　参见Courant-Hilbert, chap. v. ξ 5, 1, p. 238及以下等等．

〔43〕 　参见Courant-Hilbert, chap. v. ξ 10, 2, p. 277.

〔44〕 　参见Courant-Hilbert, chap. v. ξ5, 1, p. 240，和ξ10, p. 279.

〔45〕 　甚至于“线性的”限制也并非绝对必需的。

〔46〕 　这来自于这一一般性理论：如果微扰完全消除了简并，受扰函数系统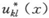 必须为正交的；而尽管情形并非如此，也可假设为正交的。

〔47〕 　Courant-Hilbert, chap. i. ξ3.3, p. 14.

〔48〕 　就所涉及的事实上的分析细节而言，最简单的得到（32′）的方式，或更一般的，得到任何特定坐标的波动方程，不是转换波动方程本身，而是转换相应的变分问题（参见论文第一篇，第11页），由此重新得到作为欧拉变分问题的波动方程。这样，我们就免除了二次求导赋值的麻烦。参见Courant-Hilbert, chap. iv. §7, p. 103.

〔49〕 　W. Pauli, jun., Ztschr. F. Phys. 36, p. 336, 1926; N. Bohr, Die Nature. 1, 1926.

〔50〕 　这本文集中正在进行中的文章。

〔51〕 　　W. Heisenberg, Ztschr. F. Phys. 33, p. 879, 1925; M. Born and P. Jordan, Ztschr. F. Phys. 34, p. 867, 886, 1925.

〔52〕 　W. Pauli, jun., Ztschr. f. Phys. 36, p. 336, 1926.

〔53〕 　J. Stark, Ann. d. Phys. 48, p. 193, 1915.

〔54〕 　H. A. Kramers, Dänische Akademie (8), iii. 3, p. 333 et seq., 1919.

〔55〕 　J. Stark, Ann. d. Phys. 43, p. 1001, et seq., 1914.

〔56〕 　N. Bohr, Dänische Akademic (8), iv., 1, 1, p. 35, 1918.

〔57〕 　J. Stark, Ann. d. Phys. 43, p. 1004, 1914.

〔58〕 　这本论文集的前一篇论文（On the Relation between the Quantum Mechanics of Heisenberg, Born, and Jordan, and that of Schrödinger）结束时的方程（38）。四次幂适用于这一事实，即辐射是加速度的平方的问题，而不适用于电矩本身。在方程（38）中出现的显然是另一因子（E_k －E_m ）／h。这是由于表述（36）中的 面引起的。对于证明的附加修正：现在我意识到，这一 是不正确的，尽管我希望它能使后面的相对论性概括更容易。上述引文中的表述（36）将为 所代替。由此，关于四次幂的疑问烟消云散了。

〔59〕 　参见M. Born and P. Jordan, Ztschr. F. Phys. 34, p.887, 1925.

〔60〕 　R. Ladenburg, Ann. d. Phys. (4), 38, p. 249, 1914.

〔61〕 　R. Ladenburg and F. Reiche, Die Naturwissenschaften, 1923, p.584.

〔62〕 　R. Ladenburg and F. Reiche，见上述引文，第二栏中的第一个公式，p.584．上述表达式中的因子ν₀ 来自这样一个事实：“转换概率”a_ki 仍须为“能量子”所乘，以给出辐射强度。

〔63〕 　我后来给出本征函数（70）（见论文第一篇），但没有注意到它们与拉盖尔多项式的联系。关于上述表征的证明，见“数学附录”第一小节。

〔64〕 　注意通常被表示为ρ（x）的密度函数，在方程（67）中读作ηsinθ，因为方程必须乘上η² sinθ，以获得自伴形式。

〔65〕 　Courant-Hilbert, chap. ii. §11, 5, p.78，方程（72）．

〔66〕 　Courant-Hilbert, chap. iii. §4, 2, p.115．

〔67〕 　Courant-Hilbert, chap. v. §5, 1, p.240．

〔68〕 　Courant-Hilbert, chap. ii. §11, 5, p. 78，方程（68）。

〔69〕 　例如，对一个振动板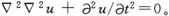， 参见Courant-Hilbert, chap. v. §8, p. 256．

〔70〕 　参见论文第三篇，§1和§2，方程（8）和（24）附近的文章。

〔71〕 　参见下述和§7。

〔72〕 　参见海森伯等人量子力学论文的结尾，也可参见本系列论文的第三篇中斯塔克效应中强度的计算。在第一篇被引证的论文中，提出的是ψψ的实数部分，而不是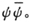 这是一个错误，在本文第三篇得以纠正。

〔73〕 　如前面一样，为简单起见，我们假设本征函数u_n （x）为实的，但注意到有时它若是实本征函数的复集合更为方便得多，或是必须如此，例如在开普勒问题中，我们用e^±mφi ，而不是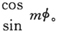

〔74〕 　H. A. Kramers, Nature, May 10, 1924；同上，August 30, 1924; Kramers and W. Heisenberg, Ztschr. F. Phys. 31, p. 681, 1925. 在后一篇文章中由对应原理所描述的散射光的极化（公式27），几乎形式上与我们的完全一致。

〔75〕 　几乎无须说为简单起见我们称之为“z方向”和“y方向”的两个方向不需要精确地彼此正交。一个是入射光的极化方向；另一个是我们特别感兴趣的次级波的极化分量。

〔76〕 　Born, Heisenberg, and Jordan, Ztschr. f. Phys. 35, p. 572, 1926.

〔77〕 　特别是参见海森伯关于其论文的最新说明中的结论性文字，与理解时间中的一个事件过程的这种困难有关，见Math. Ann. 95, p. 683, 1926。

〔78〕 　进一步的讨论在§5中。

〔79〕 　H. Weyl, Math. Ann. 68, p. 220, 1910; Gött. Nachr. 1910. 也可参见E. Hill, Sitz.-Ber. d. Physik. Mediz. Soc. Erlangen, 43, p. 68, 1911; Math. Ann. 71, p.76, 1911. 我必须谢谢Herr Weyl，不仅为了这些参考文献，而且为了非常宝贵的对于这些并不十分简单的问题的口头解说。

〔80〕 　对这一说明，我必须感谢Herr Fues。

〔81〕 　如Herr E. Fues所告诉我的，我们会非常经常地忽略实际中的极限过程，而把内部积分写成u（ζ，E），即总是当∫ρ（ξ）f（ξ）u（ξ，E）dξ存在。

〔82〕 　K. F. Herzfeld and K. L. Wolf, Ann. d. Phys. 76, p. 71, 567, 1926; H. Kollmann and H. Mark, Die Nw. 14, p. 648, 1926.

〔83〕 　一个非常有趣和成功的比较飞行荷电粒子与光波的作用的尝试（通过它们的场的傅里叶分解），可以见Fermi的一篇论文，Ztschr. f. Phys. 29, p. 315, 1924.

〔84〕 　第二篇的结尾（原书第39页）；关于海森伯量子力学的论文（原书第60页）。

〔85〕 　参见关于海森伯理论的论文中方程（31）。那儿标示为 的量为我们的“密度函数”ρ（x）（例如，在球坐标中为r² sinθ）。T表示的是作为位置坐标和动量函数的动能，T的下标标示出对动量的区分。在上述引文中的方程（31）和（32）中，很遗憾下标k被错误地用了两次，一次用于加和，然后也被用在函数的自变量的表征性下标中。