《笛卡儿几何》导读

袁向东

（中国科学院数学与系统科学研究院）

Chinese Version Introduction

笛卡儿是第一位杰出的近代哲学家，是近代生物学的奠基人，是第一流的物理学家，但只偶然是个数学家。不过，像他那样富于智慧的人，即使只花一部分时间在一个科目上，其工作也必定是有重要意义的。

笛卡儿著作中的插图

“纸上得来终觉浅，绝知此事要躬行”——理性实践家笛卡儿

笛卡儿这个名字因解析几何对科学的巨大贡献而家喻户晓。笛卡儿的“我思故我在”的哲学绝唱，成了唯物与唯心论者唇枪舌战的一个永恒主题。这位17世纪的绅士到底是个什么样的伟人呢？《古今数学思想》（Mathematical Thought from Ancient to Modern Times ）的作者克莱因（Morris Kline）说：“笛卡儿（1596—1650）是第一位杰出的近代哲学家，是近代生物学的奠基人，是第一流的物理学家，但只偶然是个数学家。不过，像他那样富于智慧的人，即使只花一部分时间在一个科目上，其工作也必定是有重要意义的。”

为了更好地了解笛卡儿的《几何》的来龙去脉，读读他的简要生平不无好处。

一、笛卡儿的简要生平

1596年3月31日，笛卡儿出生在法国图赖讷（Touraine）地区的莱依镇（La Haye）。

笛卡儿的父亲约阿希姆•笛卡儿（Joachim Descartes）是布列塔尼省伦诺地方法院的评议员，按现代术语讲，他既是律师又是法官。当时涉及法律事务的职位在很大程度上是世袭的；从事这一职业的人在社会上有相当的独立性和一定的特权，属于所谓的穿袍贵族阶层，其地位介于贵族和资产者之间。其母让娜•布罗沙尔（Jeanne Brochard）出身同一社会阶层，1597年去世，给笛卡儿留下一笔遗产，使他在此后的一生中有了可靠的经济保障，得以从事自己喜爱的工作。

有关笛卡儿早年生活的资料很少，只知他幼年体弱，丧母后由一位保姆照料；他对周围的世界充满好奇心，因此父亲说他是“小哲学家”。8岁（1604）时入拉弗莱什镇的耶稣会学校读书，校方出于对他健康的关心，特许他不受校规约束，早晨可躺到愿意去上课时为止。据说他因此养成了清晨卧床长时间静思的习惯。几乎终生不变。该校的教学大纲规定，学生在前五年学习人文学科（即拉丁语、希腊语和经典作家的作品）、法语（包括写作诗歌与散文）、音乐、表演和绅士必备的技艺——骑马和击剑。后三年课程的总称是哲学，包括逻辑学［亚里士多德（Aristotle）的三段论演绎法］、一般哲学（对亚里士多德的《尼各马克（Nicomach）的伦理学》的详尽分析）、物理、数学、天文学及形而上学［指托马斯•阿奎那（Thomas Aquinas）的哲学和天主教学者对此所作的注释］。在涉及科学的课程中，只有数学和天文学含有较新的研究成果。笛卡儿曾对诗歌怀有浓厚的兴趣，认为“诗是激情和想象力的产物”。人们心中知识的种子犹如埋在燧石中，哲学家“通过推理”使之显露，“而诗人靠想象力令其迸发火花，因而更加光辉。”（见于他的早期著作《奥林匹克》）笛卡儿后来回忆说，这所学校是“欧洲最著名的学校之一”，但他对所学的东西颇感失望，因为教科书中那些看来微妙的论证，其实不过是些模棱两可甚至前后矛盾的理论，只能使他顿生怀疑而无从得到确凿的知识，唯一给他安慰的是具有自明推理的数学。这所学校对笛卡儿的另一个影响是使他养成了对宗教的忠诚。他在结束学业时暗下决心：一是不再在书本的字里行间求学问，而要向“世界这本大书”讨教，以“获得经验”；二是要靠对自身之内的理性的探索来区别真理和谬误。

1612年他从拉弗莱什的学校毕业；1616年获普瓦提埃大学的法律学位。此后，笛卡儿便背离家庭的职业传统，开始探索人生之路。当时正值欧洲历史上第一次大规模的国际战争——30年战争时期（1618—1648），他从1618年起开始了长达10年的漫游与军旅生活。他曾多次从军，在一些参战的王公贵族麾下听命。他从戎的目的主要是为了弥补学校教育的不足，并无明显的宗教或政治倾向。1618年，他参加了信奉新教的奥伦治王子的军队，一年半后又到对立的信奉天主教的巴伐利亚公爵手下服务。笛卡儿自己评论这段生活的用词是“太空闲，太放荡”。看来，他不大可能实地参战，因而有足够的时间思考。在这期间有几次经历对他产生了重要影响。1618年他与荷兰哲学家、医生兼物理学家I．贝克曼（Beeckman）相识；据说因笛卡儿在短时间内独立解决了几道公开求答的数学难题而引起贝克曼对他的注意。他向笛卡儿介绍了数学的最新进展，包括法国数学家F．韦达（Viète）在代数方程论方面的工作；给了他许多有待研究的问题，特别是有关声学与力学类似于数学证明的方法，严格区分真正的科学知识和那些仅仅为可能成立的命题，从而驳倒一位与会者的“一种新哲学”。贝吕勒深有感触，专门召见笛卡儿，以上帝代表的身份劝导他应献身于一项神圣的事业，即用他的充分而完美的方法去研究医学和力学，为顺应天意，笛卡儿决定避开战争、远离社交活动频繁的城市，寻找一处适于研究的环境。1628年秋，他移居荷兰，开始长达20年的潜心研究和写作生涯，这期间除短期出访外一直在荷兰各地隐居。

1628—1630年间，他撰写了第一篇方法论的论文：《探求真理的指导原则》（未最终完稿，1701年刊于他的选集中）；1630—1633年间，他从事多个学科的研究，涉及光的本质、折射现象、物质的性质与结构、数学、生理学与解剖学。他的目标在于用他的方法建立一个包罗万象的知识框架，为此他准备出版一本定名为《论世界》（Le monde ）的书，计划写“论光”（Le lumièse）和“论人”（L'homme）两部分。1633年初稿即将告罄之际，梅森写信告诉他G．伽利略（Galilei）因宣传N．哥白尼（Copernicus）的学说而遭天主教宗教裁判所的审判；笛卡儿遂取消了出版该书的打算，因为书中显然含有哥白尼的观点，他甚至未按惯例把手稿全部寄给梅森。其实笛卡儿并没有放弃自己的基本主张，其后三年中，他专心论证他的新方法具有坚实的哲学基础，相信自己的形而上学原理最终能被神学家所接受。1637年，笛卡儿发表了《方法谈》（原名是Discours de la méthode pour bien conduire sa raison，et chercher la vérité dans les sciences ，可译为《更好地指导推理和寻求科学真理的方法论》）。这部著作一反当时学术界的常规，用法文而不用拉丁文撰写，以便普通人也能阅读。该书正文占全书篇幅的约七分之一，包含了未发表的《论世界》中的重要内容，简要阐述了他的机械论的哲学观和基本研究方法，以及他的经历。书的其余部分给出了三个应用实例，现一般称为三个“附录”，它们都可独立成篇，是笛卡儿最主要的科学论著，它们是《折光》（La dioptrique ），其中提出了折射定律；《气象》（Les météores ），用于阐释与天气有关的自然现象，提出了虹的形成原理；《几何》（La géometrie ），用于清晰地表明他的方法的实质，包含了解析几何的基本思想。这部著作的出版引起了一些学者（包括费马）和他的争论。1638—1640年间，笛卡儿进一步探究其学说的哲学方面，用拉丁文撰写了《第一哲学沉思集》（meditationes de prima philosophia ），其论点大体在《方法谈》中出现过，只是有的观点更激烈。梅森收集到不少对该书的批评［包括来自英国哲学家T．霍布斯（Hobbes）和法国数学家兼哲学家P．伽桑狄（Gassendi）的］。1641年，笛卡儿正式发表此书，并加进了各种批评意见和他的简要的辩驳。这本书使笛卡儿作为哲学家的名声大震，也招致了涉及宗教的纷争。他被谴责为无神论者；地方行政当局甚至要传讯他。后经有势力的朋友斡旋，才使事态平息。其后9年间，笛卡儿试图把他的哲学与科学理论完善化、系统化，以期获得神学界的支持。1644年，他的《哲学原理》（Principiae philosophiae ）问世，该书除重述其哲学信条外，还试图把一切自然现象（包括物理的、化学的和生理的）纳入一种符合逻辑的机械论模式。其历史功绩在于排除科学中的神学概念和目的论解释。他的研究纲领是用力学概念解释一切物理和生理现象，同时将力学与几何相联系，这种借助某种力学模型研究自然的方式，体现了现代科学的精神。但由于机械论的局限，书中的具体结论不少是错误的，或者很快就过时了。

笛卡儿的《哲学原理》题献给伊丽莎白公主——信奉新教的波希米亚国王腓特烈五世的女儿。他们在1643年相识后成了好友，经常通信，内容涉及从几何到政治学，从医学到形而上学的广阔领域，特别谈到人的机体与灵魂的相互作用问题以及笛卡儿的一种并不系统但已初具轮廓的伦理学观点。这些通信的价值不亚于笛卡儿跟梅森神父，以及跟法国神学家A．阿尔诺（Arnauld）之间的通信。

1649年，笛卡儿出版了一本小书《激情论》（Traité des passions de l'âme ），探讨属于心理生理学的问题，他认为这是他的整个知识体系中不可或缺的部分。同年秋天，笛卡儿很不情愿地接受了23岁的瑞典女皇克里斯蒂娜（Christina）的邀请，到斯德哥尔摩为女皇讲授哲学。晨思的习惯被打破了，每周中有三天他必须在清晨五点赶往皇宫去履行教师的职责。1650年2月1日，他受了风寒，很快转为肺炎，10天后便离开了人世。他的著作在生前就遭到教会指责，他死后的1663年，更被列入梵蒂冈教皇颁布的禁书目录之中。但是，他的思想的传播并未因此而受阻，笛卡儿成为17世纪及其后的欧洲哲学界和科学界最有影响的巨匠之一。

二、《几何》的主要内容

1637年，笛卡儿的名著《方法谈》问世，其中有三个附录：《折光》、《气象》、《几何》，作为他的一般方法论的应用实例。就是这本《几何》所阐发的思想，被弥尔（John Stuart Mill）称做“精密科学进步中最伟大的一步”。

《几何》共分三编，笛卡儿在里面讨论的全是关于初等几何的作图问题，这些都是从古希腊起一直在研究的，新颖之处就在于他使用的方法。在笛卡儿看来，希腊人的几何方法过于抽象，欧几里得几何中的每个证明，总要求某种新的奇妙的想法，由于证明过多地依赖图形，它束缚了人们的思想；笛卡儿也不满意当时流行的代数，说它完全从属于法则和公式，以至不成其为一门改进智力的科学。他在《方法谈》中回忆了他曾学习过的逻辑、几何、代数之后说：“我想，我必需寻找某种别的方法，它将把这三方面的优点组合在一起，并去掉它们的缺点。”让我们以《几何》第一编为例，勾画一下笛卡儿新方法的轮廓。

《几何》第一编的标题是“仅需直线和圆的作图问题”。笛卡儿认为，在这类问题中，“只要知道直线段的长度的有关知识，就足以完成它的作图。”为了尽可能地把线段和数量联系在一起，就要定义线段的加、减、乘、除、开根。为此，他引进了单位线段的概念。他写道，“为了更加清晰明了，我毫不犹豫地把算术语言引进几何。例如，令AB 单位线段，求BC 乘BD 的积。我只要联结A 与C 点，引DE 平行于CA ；则BE 即是BD 和BC 的乘积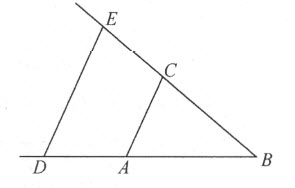。（图1）

图1

若求BD 除BE ，我连接E 和D ，引AC 平行DE ；则BC 即为除得的结果。

若想求GH 的平方根，我沿该直线加上一段等于单位长的线段FG ；然后平分FH 于K ；我再以K 为圆心作圆FIH ，并从G 引垂线延至I ，那么，GI 就是所要求的平方根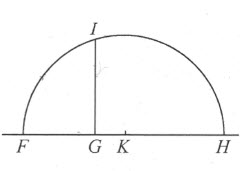”。（图2）

图2

接着，笛卡儿阐明了解这类几何作图题的一般原则。“当要解决某一问题时，我们首先假定解已经得到，并给为了作出此解而似乎要用到的所有线段指定名称，不论它们是已知的还是未知的。然后，在不对已知和未知线段作区分的情况下，利用这些线段间最自然的关系，将难点化解，直至找到这样一种可能，即用两种方式表示同一个量。这将引出一个方程。”斯霍滕（Van S chooten）曾用例子给这段话一个注解：已知线段AB ，C 是AB 上任意给定的一点，要求延长AB 至D ，使得边长为AD 和DB 的矩形面积等于边长为CD 的正方形面积。

解：令AC ＝a ，CB ＝b ，BD ＝x 。则AD ＝a ＋a ＋x ，CD ＝b ＋x 。据面积定义得

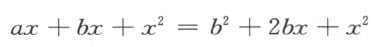
（图3）。得到这个方程后，经过合并同类项，得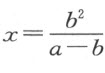 。根据对线段进行代数运算的定义，就可以用几何办法画出x 。

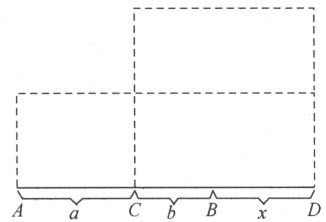图3

笛卡儿在《几何》第一编中讨论的是二次方程的情形。他说，“如果所论问题可用通常的几何来解决，即只使用平面上的直线和圆的轨迹，此时，最后的方程要能够完全解出，其中至多只能保留有一个未知量的平方，它等于某个已知量与该未知量的积，再加上或减去另一个已知量。于是，这个根或者说这条未知线段能被容易地求得。例如，若我得到z 2 ＝az ＋b 2 ，我便作一个直角三角形NLM ，其一边为LM ，它等于b ，即已知量b 2 的平方根；另一边LN ，它等于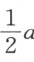 ，即另一个已知量——跟我假定为未知线段z 相乘的那个量——的一半。于是，延长MN ，整个线段OM 即所求的线段z （图4）。它可用如下方式表示：

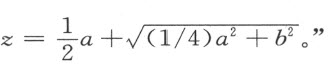
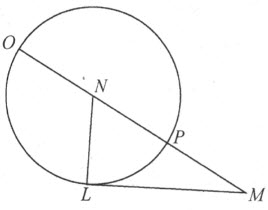图4

笛卡儿还指出当方程形如z2 ＝－az ＋b 2 及z 2 ＝az －b 2 时，如何用简单的几何作图画出z 。应该注意，这最后的一步，笛卡儿给出的是二次代数方程的几个解法。

从上面的介绍，我们看到笛卡儿是多么热衷于几何与代数的结合，目的是寻找作图问题的统一解法。但上述内容并没有涉及解析几何的精华——用代数方程表示并研究几何曲线。如果他就此歇手，数学史上就不会留下他显赫的大名。他是这样继续前行的：从解代数方程的角度出发，提出“我们必须找出跟假定是未知线段的数目一样多的方程，”但“若……得不到那样多的方程，那么，显然该问题不是完全确定的。一旦出现这种情况，我们可以为每一条缺少方程与之对应的未知线段，任意确定一个长度。”在《几何》第二编中，笛卡儿在讨论著名的帕普斯（Pappus）问题时，大大地发展了这一思想。

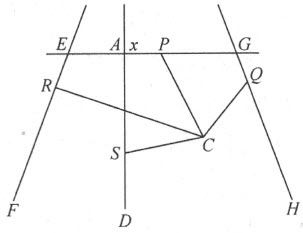图5

帕普斯问题是这样的：设给定四条直线AG ，GH ，EF 和AD ，考虑点C ，从点C 引四条线各与一条已知直线相交，交角的大小是预先给定的（但四个角不一定相同），记所引的四条线段为CP ，CQ ，CR 和CS 。要求适当地选取C 点的位置，使得CP •CR ＝CS •CQ （图5）。

笛卡儿仍用他的新方法解这个题。他假定C 点已经找到，令AP 为x ，CP 为y 。经过寻找各线段之间的几何关系，他用已知量表示出CR ，CQ 和CS 。代入CP •CR ＝CS •CQ 就得到

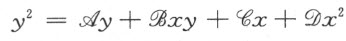
其中，A ，B ，C ，D 是由已知量组成的简单代数式。根据这个不定方程，任给一个x 的值，按《几何》卷Ⅰ中的方法，就立即可以用直线和圆规画出一个y 。由于x 的值可以任取，直线段y 的一个端点C 就相应画出了一条曲线。在这个具体问题中，为了确定点C 的位置，笛卡儿选直线AG 为基线（相当于一根坐标轴），点A 为起点（相当于坐标原点），x 值是从起点量起的一根线段的长度，y 值是另一根线段的长度，该线段从基线出发，与基线交成固定角（这可以看成另一根坐标轴，随x 的不同而改变位置，但与基线AG 的交角始终不变）。笛卡儿在我们面前展现的就是这样一个斜角坐标系。

笛卡儿顺着用代数方程表示曲线的思路，又提出了一系列新颖的想法：曲线的次数与坐标轴的选择无关；坐标的选取应使曲线相应的方程尽量简单；几何曲线是那些可以用一个唯一含x 和y 的有限次代数方程来表示出的曲线；根据代数方程的次数将几何曲线分类。

《几何》的第三编讨论了一些纯代数理论。他把方程中所有的项移至等号的一侧，另一侧为0。相当于把方程记作p （x ）＝0的形式。他经由归纳得出如下结论：每一个n 次方程皆可表示成（x －a ）（x －b ）…（x －s ）＝0，其中a ，b ，…，s 是方程的根。由于每个根必出现在其中的某个二项式因子中，为使x 的最高次幂为n ，就要求有n 个这样的因子。笛卡儿在这里相当于提出并直观论证了代数基本定理——n 次方程有n 个根［A．吉拉尔（Girard）首先于1629年叙述过该定理］。他还首次给出了一般形式的求代数方程正根和负根个数的法则（现称笛卡儿符号法则）。在一系列的例子中，他说明如何能改变一个方程的根的符号，怎样使方程增根或减根，并给出消去n 次方程中x n －1 项的方法。

笛卡儿的《几何》中虽然没有我们现在所称的笛卡儿坐标系——平面上的直角坐标系，但他的思想和方法确实体现了解析几何的精髓。笛卡儿的《方法谈》1637年问世时，另一位法国数学家也已经完成了用代数方程研究几何曲线的大作《平面和立体的轨迹引论》（Introduction aux Lieux Plans et Solides ），据称该文于1629年完稿（1679年正式发表），此人即赫赫有名的费马（Fermat，1601—1665）。“优先权问题，在一切科学史中都构成了不幸的一章”。这两位大师也被卷进过这种不幸的争论。但我们乐于称笛卡儿和费马同为解析几何之父。科学史上从来就不乏两人甚至多人几乎同时获得一项重大发现或创见的例证！

三、笛卡儿的数学观

笛卡儿儿的数学观跟他的哲学观是相辅相成的。这里主要就他对欧几里得的《几何原本》的体系及内容（以下简称为欧氏几何）的看法作一分析。

1．笛卡儿儿是否喜欢欧氏几何。

1）欧氏几何是以构造方法为基础的公理体系。

对欧几里得《几何原本》（以下简称《原本》）作为公理体系的特色，已有大量著述，不再赘言，此处只简要提一提其构造方法的特征。

应该说，人类早期发展起来的几何、算术和代数，都以其研究对象的直观性存在或构造性存在为基础。《原本》的基础仍在于几何对象的构造性存在：①它的5条（公设）是为作图而设的；②它只讨论可规、尺作图的图形。他规定的工具（不带刻度的直尺和离开作图平面即失效的原始圆规）虽使人感到一种浓烈的公理味（使工具尽量简单，但不虑及作图的方便，所引起的麻烦见《原本》卷Ⅰ命题2：“过一已知点作一直线（段），使它等于一已给定的直线（段）”）。但欧几里得的目的可能是为了作图的规格化、统一化。用现代的观点看，《原本》中的作图过程，大都可看成一种简单的algorithm（可译作算法 ）——使用一组特定的数学工具去解决一类给定问题的一个程序。在讨论平面几何的卷Ⅰ，Ⅱ，Ⅲ，Ⅳ和Ⅵ中，共有基本作图题48个，每个都给出一种简单算法，典型的如卷Ⅱ命题Ⅱ：“分割给定直线（段），使得整段与其中一分段所作的矩形等于所余另一分段上所成的正方形。”为了指出这种算法不是太平凡的，只消说明它相当于代数中求解x 2 ＋ax ＝a 2 这类方程。

值得注意的是，《原本》中涉及图形间关系的不少命题，也是通过直接作图再加全等公理来证明的，如卷Ⅱ中的命题1，2，3，4，5，6，7，8。

2）笛卡儿对《原本》的公理形式和几何内容分而治之，各作取舍。

在笛卡儿的著作中，我们尚未找到他对欧氏几何的系统评价，但从他建立他的哲学体系的方法，可以看出他在如下意义上，并不排斥由定义、公理到定理的这种形式的知识结构，即认为它是证明各种知识的确实性（或者说真理性）的唯一可靠的方法。他也确实把他的哲学体系全部建立在“我思故我在”这条“第一原理”之上了。在《哲学原理》的序言中，笛卡儿写道：“要寻找第一原因和真正的原理，由此演绎出人所能知的一切事物的理由。”

同时，笛卡儿也指出了这种综合的、演绎的数学体系的局限，说它虽“给出了大量真理”，但无法使人明白“事情为什么会是这样，也没有说明这些真理是如何发现的。”（参见《探求真理的指导原则》）。因此，在具体的研究工作中，笛卡儿明显喜欢分析的几何而不是综合的几何。

对于《原本》的具体几何内容，笛卡儿的态度是矛盾的，他觉得这种几何只研究一些非常抽象而看来无用的问题，这跟他的强调实用的科学观相悖；但那些几何命题确实具有最大的简明性，而又不必求助经验，这正是他所追求的具有确实性的知识的典范（参见《探求真理的指导原则》）。不过，笛卡儿最终对远离常识的推理作了这样的评价：“我觉得，我在一般人对切身的事所作的推理中，比在一个读书人关在书房里对思辨所作的推理中，可以遇到多得多的真理。一般人如果判断错了，他的推论所产生的后果就会立刻来处罚他，而一个读书人所作的关于思辨的推理，则不产生任何后果，这些推理所带给他的，只不过是推理离常识愈远，他从中获得的虚荣就愈大，因为要力求使这些推理显得近乎真实，必须运用更多的心机和技巧”（参见《方法谈》），他显然不满足于书斋式的研究，而强调几何与自然的结合，在《哲学原理》第4章中，他明确提出：“关于物质事物的明白而清晰的概念有形相、体积、运动及其变化的各种法则，这些法则就是几何和机械学的法则。”

3）笛卡儿取消了欧氏几何对构造性存在的苛刻限制，为扩大几何的研究对象，从而为几何研究自然现象开辟了道路。

笛卡儿在《几何》中分析了古希腊人在作图问题上的局限性，首次提出“几何的精确性最终依赖于推理，”因此比欧氏尺、规复杂的工具，只要在机械学中允许使用，就应视为跟尺、规有同样的精确性，它们作出的图形，应该和圆与直线一样有资格作为几何的对象。他在给贝克曼的信（1619.3.26）中说，算术问题根据各自的特点加以解决，“有的问题用有理数解，另一些仅用到无理数，还有一些仅可以想象而无法解出。”在涉及连续量的问题中，“某些仅用直线和圆就可解决，其他的要由别种曲线来解，不过要求它们由单一的运动给出，因此，可用新形式的各种作图规画出（我想这些新作图规在几何上的精确性不会亚于通常用来画圆的圆规）。”为此，他提议增加一条用于作图的假定：两条或更多的直线可以一条随一条的运动，每一条的运动由它们跟其余直线的相交情况决定。笛卡儿还真的设计了一种带滑槽和活动轴的作图工具（参见《几何》）。

更有甚者，笛卡儿主张尚无法用当时的工具画出的曲线，也应被接纳入几何。他说：“还有另一些问题可以仅用各种互不从属的运动产生的曲线来解，这些曲线肯定只能想象（如著名的割圆曲线），我想不出还有什么问题不能用这样的曲线来解决。”（见致贝克曼的信，1619.3.26）笛卡儿如此热衷于扩大几何曲线的领域，目的是明确的，他说：“我想，提出更广的曲线来研究是恰当的，这将为实践提供巨大的机会”。（参见《几何》）他本人就花了很大努力，利用几何来研究光学现象。

笛卡儿能突破直到韦达为止人们一直坚守的以尺、规作图决定几何对象存在的防线，跟他的哲学思维似有联系。他在《沉思集》第6部分中，提出所谓“想象”和“纯粹理解（或理会）”之间的区分：“当我想象一个三角形时，我不仅理会到这是一个由3条线组成的形相，而且同时直观到可以说由我的心智的能力或内视力提供出来的3条线……可是如果我要去思想一个千边形，我虽然明白地理会到这是一个由一千条边组成的形相……可是无论如何不能想象出千边形的一千条边，即不能用我的心灵的眼睛看到那一千条边。”这说明即使最简单的直线图形，有些也是无法想象的，当然也不能具体地作图了。那么笛卡儿放弃尺、规作图的限制是顺理成章的了。

2．由传统的几何、算术到笛卡儿的普遍的数学。

凡论及解析几何发生历史的著作都必讨论这个主题，我们想强调以下几点：

1）他对古希腊数学家流传下来的著作，表示了普遍的不满。在《探求真理的指导原则》中，他写道：“我曾特别注意算术和几何，因为据说它们是最简单的……是达到所有其他知识的通道。不过没有一个作者能使我真正满意……忙忙碌碌地去研究干巴巴的数和虚构的图形，满足于这些小事，使用很肤浅的论证——常常是靠机会而非技巧，靠眼睛而非理解，没有比这更无用的了。在某种意义上它取消了运用人的理性。”

2）但他觉得即使在古代也已萌发了一种真正的数学。在同一著作中他写道：“在帕普斯和丢番图（Diophantus）的著作中，我似乎认出了这种真正的数学的踪迹……他们可能想象许多发明家一样……害怕他们的方法如此容易和简单，一经泄漏就会丧失身价。因此，他们为赢得人们的赞美，宁肯展示贫乏不毛的真理和能充分表现才智的演绎论证，作为他们这门技艺的成果，而不顾揭开真正使用的方法——它也许会把能获得的赞美化为乌有。”

笛卡儿发现在他的同时代的人中，正有人在复兴这门技艺，“它具有真正的数学所必备的清晰性和简单性。”他说他的这些考查使他从带特殊性的算术和几何走向一种具有普遍性的数学。

3）笛卡儿的普遍的数学的目标是直接指向科学研究的。他提出数学应研究“一切事物的次序与度量性质”，不管它们“来自数、图形、星辰、声音或其他任何涉及度量的事物。”数学应该阐明“有关次序与度量的完整的原理”。（参见《探求真理的指导原则》）笛卡儿实际提出了科学数学化的任务。

4）帕普斯问题是笛卡儿打开“普遍的数学”大门的敲门砖。

恩格斯说笛卡儿使变量进入数学，使数学成为研究运动的武器。而笛卡儿做到这一点的直接原因却归于一个纯粹的几何问题——所谓的帕普斯问题。在这里讲一下笛卡儿对实验以及哲学的功效的观点，来跟上述事实对照是颇有意思的。

跟一般人以为的不同，笛卡儿非常重视科学实验。在《哲学原理》的序言中，他讲了他的宏图大志，讲了已完成和尚未完成的工作，接着，他不无遗憾地说：“假如我能做一切必要的实验来论证和支持我的理论，我一定会努力去完成整个计划的，因为我并不觉得自己很老，也不怀疑自己的精力，离要达到的知识又不算遥远。不过，做这些事（指实验）费用浩大，若无公家资助，以我个人的家产实在难以实现。可是，公家之助既然不可期，我想今后的研究只能满足于自我教诲了。我想我因此而未能为后人的直接利益效力，他们是会原谅我的。”这是他1644年发出的叹息，时年48岁。此前，在他力所能及之处，他确实做过不少实验，包括磨制光学镜片，解剖从屠宰场买来的动物器官等。

不少人也不了解笛卡儿的理性主义哲学的目的却是相当讲究实际的。他把全部哲学比喻成一棵树：根是形而上学，干是物理学，枝条是其他科学（包括医学、机械学、伦理学等）。他说：“不过，我们不是从树根、树干而是从树的枝梢采集果实的。”“我一向怀着一种热忱，愿对公众稍有贡献，所以我在10年或12年前就印行了一些论说，发表我认为是一得之见的一些学说”（参见《哲学原理》），这显然是指他的光学、气象学和几何学。

尽管有以上背景，他却并不是从当时科学界热烈讨论的运动问题为数学引入变量的观念，而是从纯几何的帕普斯问题出发，为研究运动问题提供了有效的方法。

笛卡儿达到解析几何真谛的过程大致如下：①在学生时代，对几何、算术和代数产生了浓厚的兴趣，认为是他所学知识中最明白和确实的⇒②在发展他的哲学体系时，提出由怀疑为先导的理性方法，因而对希腊数学进行了深刻的反思；③与此同时，他对科学的兴趣，使他产生了要寻找一种普遍适用的数学的强烈愿望⇒④在批判希腊数学著作时，在帕普斯的《数学汇编》中发现了“轨迹问题”［欧几里得和阿波罗尼奥斯（Apollonius）都研究过但未解决］。这一适合发挥“分析”论证优点的问题引起了笛卡儿极大的兴趣，在给友人的信中说，他在《几何》发表前4年，花了5到6周的时间解决了这个问题。笛卡儿正是在解这个问题时踏进了我们称做解析几何的大门。

3．笛卡儿对数学对象的客观性的解释。

在《沉思集》中，笛卡儿有一段对数学对象本性的论述：“我想象一个三角形的时候，虽然在我以外的世界的任何地方也许没有这样一种形相，甚至从来没有过，但是这种形相毕竟具有明确的本性、形式或本质，这种本性是不变的、永恒的，不是我捏造的，而且不以任何方式依赖我的心灵。”接着他点出了三角形的几个性质：三内角和等于两直角，大边对大角等，并说他初次想象一个三角形时并没想到这类性质。他不同意这样的解释：“由于我曾经见过三角形的物体，于是关于三角形的观念通过感官进入我的心灵。”因为“我可以在心中形成无数其他根本无法认为是感官对象引起的形相，而我仍旧能推证出各种涉及它们本性的特征。”它们是“如此清楚，因此不是纯粹的虚无，而具有真实性。”“上帝的存在至少与我在这里认为真实的全部（仅涉及数和形相的）数学真理同样确实。”

应该指出，在笛卡儿早年为外部世界的事物（他称为感官对象）所深深吸引时，就曾把算术、几何以及一般纯粹数学中的形相、数目等能清楚明白理会到的东西当成是真实的。经过多年的哲学考察后才转向上述接近柏拉图的数学客观性观念的。