《希尔伯特几何基础》导读

李文林

（中国科学院数学与系统科学研究院）

Chinese Version Antronduction

“建立几何的公理和探究它们之间的联系，是一个历史悠久的问题；关于这问题的讨论，从欧几里得以来的数学文献中，有过难以计数的专著，这问题实际就是要把我们的空间直观加以逻辑的分析。”“本书中的研究，是重新尝试着来替几何建立一个完备 的，而又尽可能简单 的公理系统；要根据这个系统推证最重要的几何定理，同时还要使我们的推证能明显地表出各类公理的含义和个别公理的推论的含义。”

——希尔伯特

希尔伯特画像

希尔伯特1862年1月23日生于德国柯尼斯堡（今俄罗斯加里宁格勒），1943年2月14日卒于格丁根。

希尔伯特出生于东普鲁士的一个中产家庭。祖父大卫·菲尔赫哥特·勒贝雷希特·希尔伯特（David Fürchtegott Leberecht Hilbert）和父亲奥托·希尔伯特（Otto Hilbert）都是法官，祖父还获有“枢密顾问”头衔。母亲玛丽亚·特尔思·埃尔特曼（Maria Therse Erdtmann）是商人的女儿，颇具哲学、数学和天文学素养。希尔伯特幼年受到母亲的教育、启蒙，8岁正式上学，入皇家腓特烈预科学校。这是一所有名的私立学校，哲学家康德（E. Kant）曾就读于此。不过该校教育偏重文科，希尔伯特从小喜爱数学，因此在最后一学期转到了更适合他的威廉预科学校。在那里，希尔伯特的成绩一跃而上，各门皆优，数学则获最高分“超”。老师在毕业评语中写道：“该生对数学表现出强烈兴趣，而且理解深刻，他用非常好的方法掌握了老师讲授的内容，并能有把握地、灵活地应用它们。”

1880年秋，希尔伯特进柯尼斯堡大学攻读数学。大学第二学期，他按当时的规定到另一所大学去听课，希尔伯特选择了海德堡大学，那里富克斯（L. Fuchs）教授的课给他印象至深。在柯尼斯堡，希尔伯特则主要跟从韦伯（H. Weber）学习数论、函数论和不变量理论。他的博士论文指导老师是赫赫有名证明π超越性的林德曼（F. Lindemann）教授，后者建议他做代数形式的不变性质问题。希尔伯特出色地完成了学位论文，并于1885年获得了哲学博士学位。

在大学期间，希尔伯特与比他年长3岁的副教授赫维茨（A. Hurwitz）和比他高一班的闵可夫斯基（H. Minkowski）结下了深厚友谊。这种友谊对各自的科学工作产生了终身的影响。希尔伯特后来曾这样追忆他们的友谊：“在日复一日无数的散步时刻，我们漫游了数学科学的每个角落”；“我们的科学，我们爱它超过一切，它把我们联系在一起。在我们看来，它好像鲜花盛开的花园。在花园中，有许多踏平的路径可以使我们从容地左右环顾，毫不费力地尽情享受，特别是有气味相投的游伴在身旁。但是我们也喜欢寻求隐秘的小径，发现许多美丽的新景。当我们向对方指出来，我们就更加快乐”。（见研究文献［1］。）

大学毕业后，希尔伯特曾赴莱比锡、巴黎等地作短期游学。在莱比锡，他参加了克莱因（F. Klein）的讨论班，受到后者的器重。正是克莱因推荐希尔伯特去巴黎访问，结识了庞加莱（H. Poincaré）、约当（C. Jordan）、皮卡（E. Picard）与埃尔米特（C. Hermite）等法国著名数学家。在从巴黎返回柯尼斯堡途中，希尔伯特又顺访了柏林的克罗内克（L. Kronecker）。希尔伯特在自己早期工作中曾追随过克罗内克，但后来在与直觉主义的论战中却激烈地批判“克罗内克的阴魂”。

1886年6月，希尔伯特获柯尼斯堡大学讲师资格。除教课外，他继续探索不变量理论并于1888年秋取得突破性结果——解决了著名的“果尔丹问题”，这使他声名初建。1892年，希尔伯特被指定为柯尼斯堡大学副教授以接替赫维茨的位置。同年10月，希尔伯特与克特·耶罗施（Käthe Jerosch）结婚。1893年，希尔伯特升为正教授。1895年3月，由于克莱因的举荐，希尔伯特转任格丁根大学教授，此后他始终在格丁根执教，直到1930年退休。

在格丁根，希尔伯特又相继发表了一系列震惊数学界的成果：1896年他向德国数学学会递交了代数数论的经典报告“代数数域理论”（Die Theorie der algebraischen Zahlkörper）；1899年发表著名的《几何基础》（Grundlagen der Geometrie）并创立了现代公理化方法；同年希尔伯特出人意料地挽救了狄利克雷原理而使变分法研究出现崭新转机；1909年他巧妙地证明了华林猜想；1901—1912年间通过积分方程方面系统深刻的工作而开拓了无限多个变量的理论。这些工作确立了希尔伯特在现代数学史上的突出地位。1912年以后，希尔伯特的兴趣转移到物理学和数学基础方面。

希尔伯特典型的研究方式是直攻重大的具体问题，从中寻找带普遍意义的理论与方法，开辟新的研究方向。他以这样的方式从一个问题转向另一个问题，从而跨越和影响了现代数学的广阔领域。

代数不变量问题 （1885—1893）

代数不变量理论是19世纪后期数学的热门课题。粗略地说，不变量理论研究各种变换群下代数形式的不变量。古典不变量理论的创始人是英国数学家布尔（G. Boole）、凯莱（A. Cayley）和西尔维斯特（B. Sylvester）。n 个变元x ₁ ，x ₂ ，…，x _n 的m 次齐次多项式j （x ₁ ，…，x _n ）被称为n 元m 次代数形式。设线性变换T 将变元（x ₁ ，…，x _n ）变为（X ₁ ，…，X _n ），此时多项式J （x ₁ ，…，x _n ）变为J （X _l ，…，X _n ），J 的系数a ₀ ，a ₁ ，…，a _q 变为J 的系数A ₀ ，A _l ，…，A_q 。若对全体线性变换T 有J ＝J ^* ，则称J 为不变式，称在线性变换下保持不变的J 的系数的任何函数I 为J 的一个不变量。凯莱和西尔维斯特等人计算、构造了大量特殊的不变量，这也是1840—1870年间古典不变量理论研究的主要方向。进一步的发展提出了更一般的问题——寻找不变量的完备系，即对任意给定元数与次数的代数形式，求出最小可能个数的有理整不变量，使任何其他有理整不变量可以表成这个完备集合的具有数值系数的有理整函数。这样的完备系亦叫代数形式的基。在希尔伯特之前，数学家们只是对某些特殊的代数形式给出了上述一般问题的解答，这方面贡献最大的是果尔丹（P. Gordan）。果尔丹几乎毕生从事不变量理论的研究，号称“不变量之王”。他最重要的结果是所谓“果尔丹定理”，即对二元形式证明了有限基的存在性。果尔丹的证明冗长、繁复，但其后二十余年，却无人能够超越。

希尔伯特的工作从根本上改变了不变量理论研究的现状。他的目标是将果尔丹定理推广到一般情形，他采取的是崭新的非算法的途径。希尔伯特首先改变了问题的提法；给定了无限多个包含有限个变元的代数形式系，问在什么条件下存在一组有限的代数形式系，使所有其他的形式都可表成它们的线性组合？希尔伯特证明了这样的形式系是存在的，然后应用此结果于不变量而得到了不变量系有限整基的存在定理。希尔伯特的证明是纯粹的存在性证明，他不是像果尔丹等人所做的那样同时把有限基构造出来，这使它在发表之初遭到了包括果尔丹本人在内的一批数学家的非议。果尔丹宣称“这不是数学，而是神学！”但克莱因、凯莱等人却立即意识到希尔伯特工作的价值。克莱因指出希尔伯特的证明“在逻辑上是不可抗拒的”，并将希尔伯特的文章带到在芝加哥举行的国际数学会议上去推荐介绍。存在性证明的意义日益获得公认。正如希尔伯特本人阐明的那样：通过存在性证明“就可以不必去考虑个别的构造，而将各种不同的构造包摄于同一个基本思想之下，使得对证明来说是最本质的东西清楚地突显出来，达到思想的简洁和经济，……禁止存在性证明，等于废弃了数学科学”。对于现代数学来说，尤为重要的是希尔伯特的不变量理论把模、环、域的抽象理论带到了显著地位，从而引导了以埃米·诺特（Emmy Noether）为代表的抽象代数学派。事实上，希尔伯特对不变量系有限基的存在性证明，是以一条关键的引理为基础，这条关于模（module，指多项式环中的一个理想）的有限基的存在性引理，正是通过使用模、环、域的语言而获得的。

希尔伯特最后一篇关于不变量的论文是“论完全不变量系”（Über die vollen Invariantensysteme，1893），他在其中表示“由不变量生成的函数域的理论最主要的目标已经达到”，于是他在致闵可夫斯基的一封信中宣告：“从现在起，我将献身于数论。”

代数数域 （1893—1898）

希尔伯特往往以对已有的基本定理给出新证明作为他征服某个数学领域的前奏。他对代数数论的贡献，情形亦是如此。在1893年慕尼黑德国数学学会年会上，希尔伯特宣读的第一个数论结果——关于素理想分解定理的新证明，即引起了与会者的重视，数学学会遂委托希尔伯特与闵可夫斯基共同准备一份数论进展报告。该报告最后实际上由希尔伯特单独完成（闵可夫斯基中间因故脱离计划），并于1897年4月以“代数数域理论”为题正式发表（以下简称“报告”）。远远超出数学学会的期望，这份本来只需概述现状的报告，却成为决定下一世纪代数数论发展方向的经典著作。“报告”用统一的观点，将以往代数数论的全部知识铸成一个严密宏伟的整体，在对已有结果给出新的强有力的方法的同时引进新概念、建立新定理，描绘了新的理论蓝图。希尔伯特在“报告”序言中写道：

“数域理论是一座罕见的优美和谐的大厦。就我所见，这座建筑中装备得最富丽的部分是阿贝尔域和相对阿贝尔域的理论，它们是由于库默尔关于高次互反律的工作和克罗内克关于椭圆函数复数乘法的研究而被开拓的。更深入地考察这两位数学家的理论，就会发现其中还蕴藏着丰富的无价之宝，那些了解它们的价值，一心想试一试赢得这些宝藏的技艺的探索者，将会得到丰富的报偿。”

“报告”发表后的数年间，希尔伯特本人曾努力发掘这些“宝藏”，这方面的工作始终抓住互反律这个中心，并以类域论的建立为顶峰。

古典互反律最先为欧拉（L. Euler，1783）和勒让德（A. -M. Legendre，1785）发现，它描述了一对素数p ，q 及以它们为模的二次剩余之间所存在的优美关系。高斯（C. F. Gauss）是第一个给二次互反律以严格证明的人（1801），他把它看做算术中的“珍宝”，先后作出了七个不同证明，并讨论过高次互反律。

将互反律推广到代数数域情形，是代数数论的一个重要而困难的课题，希尔伯特的工作为此种推广铺平了道路。希尔伯特从二次域的简单情形入手，将二次剩余解释为一个二次域中的范数，将高斯剩余符号解释为范数剩余符号。利用范数剩余符号，古典互反律可以被表示成简单漂亮的形式

此处p 跑遍无限及有限素点。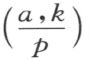 即范数剩余符号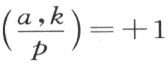： ，若a 是二次域k 中的p -adic范数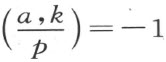； ，若a 不是p -adic范数。这样的表述可以被有效地推广，使希尔伯特猜测到高次互反律的一般公式（虽然他未能对所有情形证明其猜测）。

希尔伯特在1898年发表的纲领性文章《相对阿贝尔域理论》（Ueber die Theorie der relativ Abelschen Zahlkörper）中，概括了一种广泛的理论——类域论。“类域”，是一种特别重要的代数数域：设代数数域k 的伽罗瓦扩张为K ，若K 关于k 的维数等于k 的类数，且k 的任何理想在K 中都是主理想，就称K 为k 的类域。希尔伯特当初定义的“类域”，相当于现在的“绝对类域”。作为猜想，希尔伯特建立了类域论的若干重要定理：（1）任意代数数域k 上的类域存在且唯一；（2）相对代数数域K／k 是阿贝尔扩张，且其伽罗瓦群与k 的理想类群同构；（3）K／k 的共轭差积为1；（4）对于k 的素理想p ，如果f 是最小正整数使p ^f 成为主理想，则p 在K 中分解为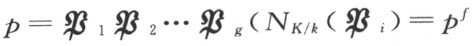 ，f _g ＝h ）；（5）（主理想定理）设K／k 为绝对类域，则将k 的任意理想扩张到K 时，就都成为主理想。希尔伯特在某种特殊情形下给出了上述定理的证明。类域论后经高木贞治和E．阿廷（Artin）等人进一步发展而成完美的现代数学体系。

希尔伯特关于代数数域的研究同时使他成为同调代数的前驱。“报告”中有一条相对循环域的中心定理——著名的“定理90”，包含了同调代数的基本概念。

“相对阿贝尔域理论”的发表标志了希尔伯特代数数域研究的终结。希尔伯特是属于这样的数学家，他们竭尽全力打开一座巨大的矿藏后，把无数的珍宝留给后来人，自己却又兴趣盎然地去勘探新的宝藏了。1898年底，格丁根大学告示：希尔伯特教授将于冬季学期作“欧几里得几何基础”的系列讲演。

几何基础 （1898—1902）

韦尔（H．Weyl）曾指出：“不可能有比希尔伯特关于数域论的最后一篇论文与他的经典著作《几何基础》把时期划分得更清楚了。”在1899年以前，希尔伯特唯一正式发表的几何论述只有致克莱因的信“论直线作为两点间的最短联结”（Über die gerade Linie als kürzeste Verbindung zweier Punkte，1895）。但事实上，希尔伯特对几何基础的兴趣却可以追溯到更早。1891年夏，他作为讲师曾在柯尼斯堡开过射影几何讲座。同年9月，他在哈雷举行的自然科学家大会上听了H．维纳（Wiener）的讲演“论几何学的基础与结构”（Üher Grundlagen and Aufbau der Geometrie）。在返回柯尼斯堡途中，希尔伯特在柏林候车室里说了以下的名言：“我们必定可以用‘桌子、椅子、啤酒杯’来代替‘点、线、面’。”说明他当时已认识到直观的几何概念在数学上并不合适。以后希尔伯特又先后作过多次几何讲演，其中最重要的有1894年夏季讲座“几何基础”、1898年复活节假期讲座“论无限概念”（Über den Begriff des Unendlichen），它们终于导致了1898—1899年冬季学期讲演“几何基础”中的决定性贡献。

欧几里得几何一向被看做数学演绎推理的典范。但人们逐渐察觉到这个庞大的公理体系并非天衣无缝。对平行公理的长期逻辑考察，孕育了罗巴切夫斯基（Н．И．Лобачевский）鲍耶（J．Bolyai）与高斯的非欧几何学，但数学家们却并没有因此而高枕无忧。第五公设的独立性迫使他们对欧几里得公理系统的内部结构作彻底的检查。在这一领域里，希尔伯特主要的先行者是帕施（M. Pasch）和皮亚诺（G. Peano）。帕施最先以纯逻辑的途径构筑了一个射影几何公理体系（1882），皮亚诺和他的学生皮耶里（M. Pieri）则将这方面的探讨引向欧式几何的基础。但他们对几何对象以及几何公理逻辑关系的理解是初步的和不完善的。例如帕施射影几何体系中列出的公理与必须的极小个数公理相比失诸过多；而皮亚诺只给出了相当于希尔伯特的部分（第一、二组）公理。在建造逻辑上完美的几何公理系统方面，希尔伯特是真正获得成功的第一人。正如他在《几何基础》导言中所说：

“建立几何的公理和探究它们之间的联系，是一个历史悠久的问题：关于这问题的讨论，从欧几里得以来的数学文献中，有过难以计数的专著，这问题实际就是要把我们的空间直观加以逻辑的分析。”“本书中的研究，是重新尝试着来替几何建立一个完备 的，而又尽可能简单 的公理系统；要根据这个系统推证最重要的几何定理，同时还要使我们的推证能明显地表出各类公理的含义和个别公理的推论的含义。”

与以往相比，希尔伯特公理化方法的主要功绩在于以下两个方面。

首先是关于几何对象本身达到了更高的抽象。希尔伯特的公理系统是从三类不定义对象（点、线、面）和若干不定义关系（关联、顺序、合同）开始的。尽管希尔伯特沿用了欧式几何的术语，其实是“用旧瓶装新酒”，在欧氏几何的古典框架内提出现代化公理化的观点。欧氏几何中的空间对象都被赋予了描述性定义，希尔伯特则完全舍弃了点、线、面等的具体内容而把它们看做是不加定义的纯粹的抽象物。他明确指出欧几里得关于点、线、面的定义本身在数学上并不重要，它们之所以成为讨论的中心，仅仅是由于它们同所选诸公理的关系。这就赋予几何公理系统以最大的一般性。

其次，希尔伯特比任何前人都更透彻地揭示出公理系统的内在联系。《几何基础》中提出的公理系统包括20条公理，希尔伯特将它们划分为五组：

Ⅰ．1～8．关联公理

Ⅱ．1～4．顺序公理

Ⅲ．1～5．合同公理

Ⅳ．　　　平行公理

Ⅴ．1～2．连续公理

这样自然地划分公理，使公理系统的逻辑结构变得非常清楚。希尔伯特明确提出了公理系统的三大基本要求，即相容性（consistency）、独立性（independency）和完备性（completeness）。

相容性要求公理系统不包含任何矛盾。这是在公理基础上纯逻辑地展开几何学时首先遇到的问题。在希尔伯特之前，人们已通过非欧几何在欧氏空间中的实现而将非欧几何的相容性归结为欧氏几何的相容性。希尔伯特贡献的精华之一，是通过算术解释而将欧氏几何的相容性进一步归结为算术的相容性。例如，将平面几何中的点与实数偶（x，y ）对应起来，将直线与联比（u，v，w ）（u，v 不同时为0）对应起来，表达式ux ＋vy ＋w =0就表示点落在直线上，这可以看做“关联”关系的算术解释。在对每个概念与关系类似地给出算术解释后，希尔伯特进一步将全部公理化成算术命题，并指出它们仍能适合于这些解释。这样，希尔伯特就成功地证明了：几何系统里的任何矛盾，必然意味着实数算术里的矛盾。

希尔伯特处理独立性问题的典型手法是构造模型：为了证明某公理的独立性，构造一个不满足该公理但满足其余公理的模型，然后对这个新系统证明其相容性。希尔伯特用这样的方法论证了那些最令人关心的公理的独立性，其中一项重大成果是对连续公理（亦叫阿基米德公理）独立性的研究。在这里，希尔伯特建造了不用连续公理的几何学——非阿基米德几何学模型。《几何基础》用了整整5章篇幅来实际展开这种新几何学，显示出希尔伯特卓越的创造才能。

如果说独立性不允许公理系统出现多余的公理，那么完备性则意味着不可能在公理系统中再增添任何新的公理，使与原来的公理集相独立而又与之相容。《几何基础》中的公理系统是完备的，但完备性概念的精确陈述则是由其他学者如亨廷顿（E．Huntington，1902）、维布伦（O．Veblen，1904）等给出的。

《几何基础》最初发表于1899年6月格丁根庆祝高斯-韦伯塑像落成的纪念文集上，它激起了对几何基础的大量关注，通过这部著作，希尔伯特不仅使几何学本身具备了空前严密的公理化基础，同时使自己成为整个现代数学公理化倾向的引路人。其后，公理化方法逐步渗透到几乎所有的纯数学领域。正因为如此，人们对《几何基础》的兴趣历久不衰，该书在希尔伯特生前即已6次再版，1977年纪念高斯诞生200周年时发行了第十二版。

变分法与积分方程 （1899—1912）

希尔伯特在代数和几何中留下了深刻印记后，接着便跨入数学的又一大领域——分析。他以挽救狄利克雷原理（1899）的惊人之举，作为其分析时期的开端。

狄利克雷原理断言：存在着一个在边界上取给定值的函数u ₀ ，使重积分

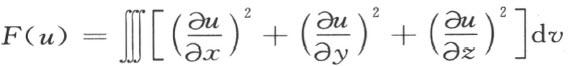
达极小值，这个极小化函数u ₀ 同时是拉普拉斯方程Δu ＝0的满足同一边界条件的解。该原理最早出现在格林（G．Green，1835）的位势论著作中，稍后又为高斯和狄利克雷独立提出。黎曼（G．F．B．Riemann）首先以狄利克雷的名字命名这一原理并将其应用于复变函数。然而，魏尔斯特拉斯（K．T．W．Weierstrass）1870年以其特有的严格化精神批评了狄利克雷原理在逻辑上的缺陷。他指出：连续函数下界存在并可达，此性质不能随意推广到自变元本身为函数的情形，也就是说在给定边界条件下使积分F （u ）极小化的函数未必存在。他的批判迫使数学家们闲置狄利克雷原理，但另一方面数学物理中许多重要结果都依赖于此原理而建立。

希尔伯特采取完全不同的思路来处理这一难题。他通过边界条件的光滑化来保证极小化函数的存在，从而恢复狄利克雷原理的功效。具体做法是：设F （u ）的下界为d ，选择一函数序列u _n 使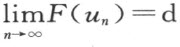 ，此时u _n 本身不恒收敛，但可用对角线法获得一处处收敛的子序列，其极限必使积分达极小值。希尔伯特的工作不仅“复活”了具有广泛应用价值的狄利克雷原理，同时大大丰富了变分法的经典理论。

希尔伯特对现代分析影响最为深远的工作是在积分方程方面。积分方程与微分方程一样起源于力学与物理问题，但在发展上却比后者迟缓。它的一般理论到19世纪末才由意大利数学家沃尔泰拉（V．Volterra）等开始建立。在希尔伯特之前，最重要的推进是瑞典数学家弗雷德霍姆（E．I．Fredhölm）作出的。弗雷德霍姆处理了后以他的名字命名的积分方程：

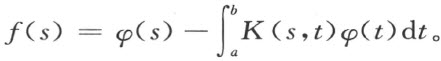
他将积分方程看做是有限线性代数方程组当未知数数目趋于无限时的极限情形，从而建立了积分方程与线性代数方程之间的相似性。希尔伯特于1900—1901年冬从正在格丁根访问的瑞典学者霍尔姆格伦（E．Holmgren）那里获悉弗雷德霍姆的工作，便立即把注意力转向积分方程领域。

一如以往的风格，希尔伯特从完善和简化前人工作入手。他首先严格地实现了从代数方程过渡到积分方程的极限过程，而这正是弗雷德霍姆工作的缺陷。如果希尔伯特停留于此，那他就不可能成为20世纪领头的分析学家之一了。希尔伯特随后便越出了弗雷德霍姆的线性代数方程理论，而开辟了一条独创的道路。他研究带参数的弗雷德霍姆方程

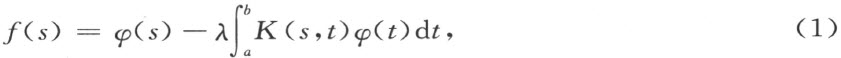
参数λ在希尔伯特的理论中具有本质意义。他将重点转到与方程（1）相应的齐次方程的特征值和特征函数问题上，以敏锐的目光看出了该问题与二次型主轴化理论的相似性。希尔伯特首先对二次积分型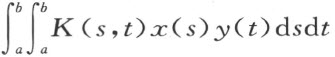 建立了广义主轴定理：设K （s ，t ）是s ，t 的连续对称函数，φ ^p （s ）是属于方程（1）的特征值λ _p 的标准化特征函数，则对任意连续的x （s ）和y （t ）如下关系成立：

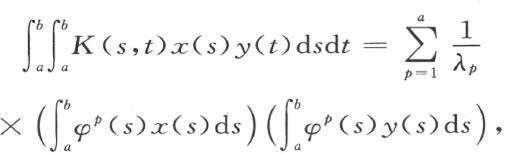
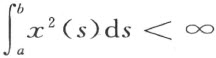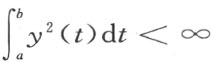其中α 有限或无限，在无限情形，级数对满足 与 的所有x （s ），y （t ）绝对一致收敛。

利用上述结果，希尔伯特证明了著名的展开定理（后称希尔伯特-施密特定理），即形如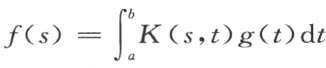 的函数成K的标准正交特征函数｛φ _p ｝的一致收敛级数 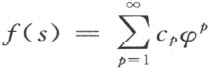，其中 为展开式的傅里叶系数。

希尔伯特接着又将通常的代数主轴定理推广到无限多个变量的二次型，这是他全部理论的关键之处。他证明：存在一个正交变换T ，使得对新变量x ′＝Tx ，全连续有界二次型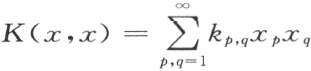 ，可化为平方和形式 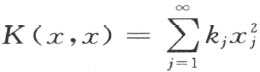（k _j 为特征倒数），其中“全连续”和“有界”性都是希尔伯特为保证主轴定理在无限情形的推广而特意引进的重要概念。

正是在这里，希尔伯特创造了极其重要的具有平方收敛和的数列空间概念。他将二次型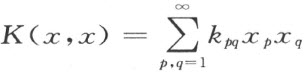 中无限多个实变量组成的数列（x ₁ ，x ₂ ，…）看做可数无限维空间中的一个向量x ，考虑具有有限长度 的x 全体，它们构成了现在所谓的希尔伯特空间，它具有发展积分方程论所必需的完备性。

希尔伯特应用上述无限多个变量的二次型理论而获得了积分方程论的主要结果。首先是证明了具有对称核的齐次方程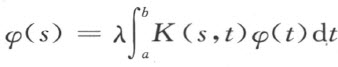 至少存在一个特征值及相应的特征函数。希尔伯特还利用展开定理证明了齐次方程除特征值λ _p 以外没有非平凡解。这就重建了弗雷德霍姆的“择一定理”。虽然希尔伯特的结果有许多并不是新的，但正如我们已经看到的那样，他彻底改造了弗雷德霍姆的理论，其意义远远超出了积分方程论本身。他所引进的概念与方法，启发了后人大量的工作。其中特别值得提出的是：匈牙利数学家里斯（F．Riesz）等借完备标准正交系确立了勒贝格平方可积函数空间与平方可和数列空间之间的一一对应关系，制定了抽象希尔伯特空间理论，从而使积分方程理论成为现代泛函分析的主要来源之一。希尔伯特关于积分方程的一般理论同时渗透到微分方程、解析函数、调和分析和群论等研究中，有力地推动了这些领域的发展。

希尔伯特关于积分方程的成果还在现代物理中获得了意想不到的应用。希尔伯特在讨论特征值问题时曾创造了“谱”（spectrum）这个术语，他将谱分析理论从全连续二次型推广至有界二次型时发现了连续谱的存在。到20年代，当量子力学蓬勃兴起之时，物理学家们发现希尔伯特的谱分析理论原来是量子力学的非常合适的数学工具。希尔伯特本人对此感触颇深，他指出：“无穷多个变量的理论研究，当初完全是出于纯粹数学的兴趣，我甚至管这理论叫‘谱分析’，并没有预料到它后来会在实际的物理光谱理论中获得应用。”

希尔伯特关于积分方程的研究，被总结成专著《线性积分方程一般理论基础》（Grundzüge einer allgemeiner Theorie der linearen Integralgleichungen）于1912年正式出版，其中收进了他1904—1910年间发表的一系列有关论文。

物理学 （1912—1922）

希尔伯特对物理学的兴趣起初是受其挚友闵可夫斯基的影响。闵可夫斯基去世后，1910—1918年，希尔伯特一直在格丁根坚持定期讲授物理学。从1912年开始，他更将其主要的科学兴趣集中到物理学方面，并为自己配备了物理学助手。

与物理学家不同的是，希尔伯特研究物理学的基本途径是“借助公理来研究那些在其中数学起重要作用的物理科学”。遵循这一路线，希尔伯特先是成功地将积分方程论应用于气体分子运动学，随后又相继处理了初等辐射论与物质结构论；受狭义相对论应用数学的鼓舞，他于1914—1915年间大胆地将公理化方法引向当时物理学的前沿——广义相对论并作出了特殊贡献；1927年，他与冯·诺依曼（von Neumann）和诺德海姆（L．Nordheim）合作的文章《论量子力学基础》（Über die Grundlagen dei Quantenmechanik）则推动了量子力学的公理化。

希尔伯特所提倡的公理化物理学的一般意义，至今仍是需要探讨的问题。值得强调的是他在广义相对论方面的工作，确实提供了物理学中运用公理化方法的成功范例。希尔伯特在1914年底被爱因斯坦（A．Einstein）关于相对性引力理论的设想和另一位物理学家米（G．Mie）试图综合电磁与引力现象的纯粹场论计划所吸引，看到了将二者联系起来建立统一物质场论的希望，并立即投入这方面的探讨。他运用变分法、不变式论等数学工具，按公理化方法直接进行研究。1915年11月20日，希尔伯特在向格丁根科学会递交的论文《物理学基础，第一份报告》（Die Grundlagen der physik，erste Mitteilung）中公布了基本结果。他在这份报告中这样概括自己的贡献：

“遵循公理化方法，事实上是从两条简单的公理出发，我要提出一组新的物理学基本方程，这组方程具有漂亮的理想形式，并且我相信它们同时包含了爱因斯坦与米所提出的问题的解答。”

希尔伯特所说的两条简单公理是：

公理Ⅰ（世界函数公理）。物理定律由世界函数H 所决定，使积分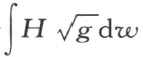 对14个位势g _μv ，、q _s 的每个变分皆化为零。

公理Ⅱ（广义协变公理）。世界函数H 对一般坐标变换皆保持不变。

由公理Ⅰ，Ⅱ，希尔伯特首先通过取世界函数H 对引力势的变分并经适当变换后获得10个引力方程：

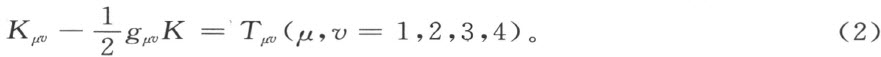
可以证明，方程组（2）与爱因斯坦的广义协变引力场方程等价。爱因斯坦是在同年11月25日发表其结果的，比希尔伯特晚了5天。希尔伯特引力场方程的推导是完全独立地进行的。不过两位学者之间并没有发生任何优先权的争论，希尔伯特把建立广义相对论的全部荣誉归于爱因斯坦，并在1915年颁发第三次鲍耶奖时主动推荐了爱因斯坦。

除了引力场方程，希尔伯特还同时导出了另一组电磁学方程（广义麦克斯韦方程）：

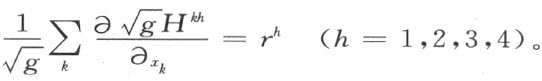
特别重要的是，在希尔伯特的推导中，电磁现象与引力现象被相互关联起来，前者是后者的自然结果，而在爱因斯坦的理论中，电磁方程与引力方程在逻辑上是完全独立的。这样，希尔伯特以数学的抽象推理而预示了统一场论的发展。他后来在《物理学基础，第二份报告》中进一步阐述了统一场论的设想。沿着希尔伯特的路线前进而建立起第一个系统的统一场理论的是他的学生韦尔（规范不变几何学，1918）。而包括爱因斯坦在内的物理学家们对希尔伯特的思想最初却并不理解。爱因斯坦1928年在反驳量子力学相容性的企图失败后转而寄厚望于统一场论，并为此而付出了后半生的精力。统一场论至今仍是数学家和物理学家们热烈追求的目标。

数学基础 （1917年以后）

希尔伯特对数学基础的研究是他早期关于几何基础工作的自然延伸。他在几何基础的研究中已将几何学的相容性归结为算术的相容性，这就使算术的相容性成为注意的中心。1904年，希尔伯特在海德堡召开的数学家大会上所作“论逻辑与算术的基础”（Über die Grundlagen der Logik und Arithmetik）的讲演，表明了他从几何基础向一般数学基础的转移。这篇讲演勾画了后来被称为“证明论”（Beweistheorie）的轮廓，但这一思想当时并未得到进一步贯彻，在随后十余年间，希尔伯特主要潜心于积分方程和物理学研究而把海德堡计划暂搁一边。直到1917年左右，由于集合论 论和直觉主义的发展日益紧迫地危及古典数学的已有成就，他又被迫回到数学基础的研究上来，这年9月，希尔伯特向苏黎世数学学会作了题为“公理化思想”（Axiomatisches Denken）的讲演，再次公布了证明论的构想。此后他又在一系列讲演和论文中明确展开了以证明论为核心的关于数学基础的所谓形式主义纲领。

按照希尔伯特的纲领，数学被形式化为一个系统，这个形式系统的对象包含了数学的与逻辑的两个方面，人们必须通过符号逻辑的方法来进行数学语句的公式表述，并用形式的程序表示推理：确定一个公式—确定这公式蕴涵另一个公式—再确定这第二个公式，依此类推，数学证明便由这样一条公式的链所构成。在这里，从公式到公式的演绎过程不涉及公式的任何意义。正如希尔伯特本人所说的那样，数学思维的对象就是符号自身。一个命题是否真实，必须也只须看它是否是这样一串命题的最后一个，其中每一条命题或者是形式系统的一条公理，或者是根据推理法则而导出的命题。同时，希尔伯特的形式化方法重点不在个别命题的真实性，而是整个系统的相容性。这种把整个系统作为研究对象，着眼于整个系统相容性证明的研究，就叫做证明论或“元数学”（metamathematics）的研究。

形式化推理的进行要求保留排中律。为此希尔伯特引进了所谓“超限公理”：

A （τA ）→A （a ），

其意思是：若谓词A 适合于标准对象τA ，它就适合于每一个对象a 。例如，阿里斯提得斯（Aristides，古希腊政治家）是正直的代表，若此人被证明堕落，那就可以证明所有的人都堕落。此处τ 称为超限函子。超限公理的应用保证了公式可以按三段论法则来进行演绎。

超限公理还使形式系统的相容性证明得到实质性缩减。为要证明形式系统无矛盾，只要证明在该系统中不可能导出公式0≠0即可。对此，希尔伯特方法的基本思想是：只使用普遍承认的有限性的证明方法，不能使用有争议的原则诸如超限归纳、选择公理等等，不能涉及公式的无限多个结构性质或无限多个公式操作。希尔伯特这种所谓的有限方法亦由超限公理加以保障：借助超限公理，可将形式系统的一切超限工具（包括全称量词、存在量词以及选择公理等）都归约为一个超限函子τ ，然后系统地消去包含τ 的所有环节，就不难回到有限观点。

希尔伯特的形式化观点是在同以布劳韦尔（L．Brouwer）为代表的直觉主义针锋相对的争论中发展的。对直觉主义者来说，数学中重要的是真实性而不是相容性。他们认为“一般人所接受的数学远远超出了可以判断其真实意义的范围”，因而主张通过放弃一切真实性受到怀疑的概念和方法（包括无理数、超限数、排中律等）来摆脱数学的基础危机。希尔伯特坚决反对这种“残缺不全”的数学。他说：“禁止数学家使用排中律就等于禁止天文学家使用望远镜和禁止拳击家使用拳头一样。”与直觉主义为了保全真实性而牺牲部分数学财富的做法相反，希尔伯特则通过完全抽掉对象的真实意义、进而建立形式系统的相容性来挽救古典数学的整个体系。希尔伯特对自己的纲领抱着十分乐观的态度，希望“一劳永逸地解决数学基础问题”。然而，1931年奥地利数学家哥德尔（K．Gödel）证明了：任何一个足以包含实数算术的形式系统，必定存在一个不可判定的命题S （即S 与～S 皆成立）。这使形式主义的计划受到挫折。一些数学家试图通过放宽对形式化的要求来确立形式系统的相容性，例如，1936年希尔伯特的学生根岑（G．Gentzen）在允许使用超限归纳法的情况下证明了算术公理的相容性。但希尔伯特原先的目标依然未能实现。尽管如此，恰如哥德尔所说：希尔伯特的形式主义计划仍不失其重要性，它促进了20世纪数学基础研究的深化。特别是，希尔伯特通过形式化第一次使数学证明本身成为数学研究的对象。证明论已发展成标征着数理逻辑新面貌的富有成果的研究领域。

希尔伯特的形式主义观点，在他分别与其逻辑助手阿克曼（W．Ackermann）和贝尔奈斯（P．Bernays）合作的两部专著《数理逻辑基础》（Grundzüge der Theoretischen Logik，1928）和《数学基础》（Grundlagen der Mathematik，1934，1939）中得到了系统的陈述。

数学问题

卡拉西奥多里（C．Caratheodory）曾引用过他直接听到的一位当代大数学家对希尔伯特说过的话：“你使得我们所有的人，都仅仅在思考你想让我们思考的问题”，这里指的是希尔伯特1900年在巴黎国际数学家大会上的著名讲演“数学问题”（Mathematische Probleme）。这篇讲演也许比希尔伯特任何单项的成果都更加激起了普遍而热烈的关注。希尔伯特在其中对各类数学问题的意义、源泉及研究方法发表了精辟见解，而整个讲演的核心部分则是他根据19世纪数学研究的成果与发展趋势而提出的23个问题，数学史上亦称之为“希尔伯特问题”。这些问题涉及现代数学的大部分领域，它们的解决，对20世纪数学产生了持久的影响。

1．连续统假设。1963年，科恩（P．Cohen）在下述意义下证明了第一问题不可解，即连续统假设的真伪不可能在策梅罗（Zermelo）-弗伦克尔（Fraenkel）公理系统内判明。

2．算术公理的相容性。1931年哥德尔“不完备定理”指出了用元数学证明算术公理相容性之不可行。算术相容性问题至今尚未解决。

3．两等高等底的四面体体积之相等。这问题1900年即由希尔伯特的学生德恩（M．Dehn）给出肯定解答，是希尔伯特诸问题最早获得解决者。

4．直线作为两点间最短距离问题。在构造各种特殊度量几何方面已有许多进展，但问题过于一般，未完全解决。

5．不要定义群的函数的可微性假设的李群概念。1952年由格里森（A．Gleason）、蒙哥马利（D．Montgomery）、齐宾（L．Zippin）等人解决，答案是肯定的。

6．物理公理的数学处理。在量子力学、热力学等部门，公理化方法已获得很大成功。概率论的公理化则由柯尔莫哥洛夫（А．Н．Колмогоров，1933）等完成。

7．某些数的无理性与超越性。1934年，盖尔芳德（А．О．Гелъфанд）和施奈德（T．Schneider）各自独立地解决了问题的后一半，即对任意代数数α ≠0，1和任意代数无理数β ≠0证明了α^β 的超越性。此结果1966年又被贝克（A．Baker）等大大推广。

8．素数问题。一般情形的黎曼猜想仍待解决。哥德巴赫猜想目前最佳结果属于陈景润，但尚未最后解决。

9．任意数域中最一般的互反律之证明。已由高木贞治（Takagi Teiji）（1921）和阿廷（1927）解决。

10．丢番图方程可解性的判别。1970年，马蒂雅谢维奇（Ю．Н．Матиясевич）证明了希尔伯特所期望的一般算法是不存在的。

11．系数为任意代数数的二次型。哈塞（H．Hasse，1929）和西格尔（C．L．siegel，1951）在这一问题上获得了重要结果。

12．阿贝尔域上的克罗内克定理推广到任意代数有理域。尚未解决。

13．不可能用只有两个变数的函数解一般的七次方程。连续函数情形1957年由阿诺尔德（В．Арнолвд）否定解决，如要求解析函数则问题尚未解决。

14．证明某类完全函数系的有限性。1958年永田雅宜（Nagata Masayosi）给出了否定解答。

15．舒伯特计数演算的严格基础。舒伯特演算的合理性尚待解决。至于代数几何基础已由范德瓦尔登（Van der Waerden，1940）与魏依（A．Weil，1950）建立。

16．代数曲线和曲面的拓扑。问题前半部分近年来不断有重要结果，至于后半部分，彼得罗夫斯基（И．Т．Петровскнй）曾声明他证明了n ＝2时极限环个数不超过3。这一结论是错误的，已由中国数学家指出（1979）。

17．正定形式的平方表示式。已由阿廷解决（1926）。

18．由全等多面体构造空间。带有基本域的群的个数的有限性已由比贝尔巴赫（L．Bieberbach，1910）证明；问题第二部分（是否存在不是运动群的基本域但经适当毗连可充满全空间的多面体）已由赖因哈特（Reinhardt，1928）和黑施（Heesch，1935）分别给出三维和二维情形的例子。

19．正则变分问题的解是否一定解析。问题在下述意义下已解决：伯恩斯坦（С．Ъернщтейн，1904）证明了一个变元的解析非线性椭圆方程其解必定解析。此结果后又被推广到多变元和椭圆组的情形。

20．一般边值问题。偏微分方程边值问题的研究正在蓬勃发展。

21．具有给定单值群的线性微分方程的存在性。已由希尔伯特本人（1905）和勒尔（H．Röhrl，1957）解决。

22．解析关系的单值比。一个变数情形已由克贝（P．Koebe，1907）解决。

23．变分法的进一步发展。

希尔伯特无疑是属于20世纪最伟大的数学家之列。他生前即已享有很高声誉。1910年荣获匈牙利科学院第二次鲍耶奖（该奖第一次得主是庞加莱）；从1902年起一直担任有影响的德国《数学年刊》（Mathematische Annalen ）主编；他是许多国家科学院的荣誉院士。德国政府授予他“枢密顾问”称号。

希尔伯特同时是一位杰出的教师，他在这方面与不喜欢教书的高斯有很大的不同。希尔伯特讲课简练、自然，向学生展示“活”的数学。他乐于同学生交往，常常带着他们在课余长时间散步，在融洽的气氛中切磋数学。希尔伯特并不特别看重学生的天赋，而强调李希登堡（Lichtenberg）的名言“天才就是勤奋”。对学生们来说，希尔伯特不像克莱因那样是“远在云端的神”，在他们的心目中，“希尔伯特就像一位穿杂色衣服的风笛手，用甜蜜的笛声引诱一大群老鼠跟着他走进数学的深河”。（见研究文献［1］。）这位平易近人的教授周围，聚集起一批有才华的青年。仅在希尔伯特直接指导下获博士学位的学生就有69位，他们不少人后来成为卓有贡献的数学家，其中包括韦尔（H．Weyl，1908）、柯朗（R．Courant，1910）、施密特（E．Schmidt，1905）和布鲁门萨尔（O．Blumenthal，1898）等（详细名单及学位论文目录参见［1］）。曾在希尔伯特身边学习、工作或访问而受到他的教诲的数学家更是不计其数，最著名的有埃米·诺特（Emmy Noether）、冯·诺依曼（von Neumann）、高木贞治、卡拉西奥多里（C．Caratheodory）、策梅罗（E．Zermelo）等等。

希尔伯特的学术成就、教学活动以及其个性风格，使他成为一个强大的学派的领头人。20世纪初的30年间，格丁根成为名副其实的国际数学中心。韦尔后来回忆当年格丁根盛况时指出：希尔伯特“对整整一代学生所产生的如此强大和神奇的影响，在数学史上是罕见的”。“在像格丁根那样的小城镇中的大学，特别是在1914年前平静美好的日子里，是发展科学学派的有利场所，……一旦一帮学生围绕着希尔伯特，不被杂务所打扰而专门从事研究，他们怎能不相互激励……。在形成科学研究这种凝聚点时，有着一种雪球效应。”（见研究文献［1］，［2］。）

然而，在第二次世界大战中，希尔伯特的学派不幸遭到打击。他的大部分学生在法西斯政治迫害下纷纷逃离德国。希尔伯特本人因年迈未能离去，在极其孤寂的气氛下度过了生命的最后岁月。1943年希尔伯特因摔伤引起的各种并发症而与世长辞。葬礼极为简单，他的云散异国的学生都未能参加，他们很晚才获悉噩耗。战争阻碍了对这位当代数学大师的及时悼念。

希尔伯特学派的成员后来纷纷发表文章和演说，论述希尔伯特的影响。韦尔认为：“我们这一代数学家还没有能达到与他相比的崇高形象。”除了具体的学术成就，希尔伯特培育、提倡的格丁根数学传统，也已成为全世界数学家的共同则富：希尔伯特寻求“精通单个具体问题与形成一般抽象概念之间的平衡”。他指出数学研究中问题的重要性，认为“只要一门科学分支能提出大量的问题，它就充满着生命力，而问题缺乏则预示着独立发展的衰亡或中止”。这正是他在巴黎提出前述23个问题的主要动机。希尔伯特强调数学的统一性——“数学科学是一个不可分割的有机整体，它的生命力正是在于各个部分之间的联系。……数学理论越是向前发展，它的结构就变得越加调和一致，并且这门科学一向相互隔绝的分支之间也会显露出原先意想不到的关系”，“数学的有机的统一，是这门科学固有的特点”；希尔伯特将思维与经验之间“反复出现的相互作用”看做数学进步的动力。因此，诚如柯朗所说：“希尔伯特以他感人的榜样向我们证明：……在纯粹和应用数学之间不存在鸿沟，数学和科学总体之间，能够建立起果实丰满的结合体”。

卡拉西奥多里指出：“指导希尔伯特一生的最高准则是绝对的正直和诚实。”这种正直、诚实，不仅表现在科学活动上，而且表现在对待社会和政治问题的态度上。希尔伯特憎恶一切政治的、种族的和传统的偏见，并敢于挺身抗争。第一次世界大战初，他冒着极大的风险，拒绝在德国政府起草的为帝国主义战争辩护的“宣言”上签名，并表示不相信其中编造的事实是“真的”；战争期间，他又勇敢地发表悼词，悼念交战国法国的数学家达布（G．Darboux）的逝世；他曾力排众议，为女数学家埃米·诺特争取当讲师的权利，而不顾当局不让女性任职的惯例；他对希特勒的“排犹运动”也表示了极大的愤慨。

希尔伯特出生于康德之城，是在康德哲学的熏陶下成长的。他对这位同乡怀有敬慕之情，却没有让自己变成其不可知论的殉道者。相反，希尔伯特对于人类的理性，无论在认识自然还是社会方面，都抱着一种乐观主义。在巴黎讲演中，希尔伯特表述了任何数学问题都可以得到解决的信念，认为“在数学中没有ignorabimus（不可知）”。1930年，在柯尼斯堡自然科学家大会上，希尔伯特被他出生的城市授予荣誉市民称号。在题为“自然的认识与逻辑”的致辞中，他批判了“堕入倒退与不毛的怀疑主义”，并在演说结尾坚定地宣称：“Wir müssen wissen．Wir warden wissen！”（我们必须知道，我们必将知道！）柯朗在格丁根纪念希尔伯特诞生100周年的演说中指出：“希尔伯特那有感染力的乐观主义，即使到今天也在数学中保持着他的生命力。唯有希尔伯特的精神，才会引导数学继往开来，不断成功。”

文献

原始文献：

［1］D. Hilbert. Gesammelte Abhandlungen, Ⅰ, Ⅱ, Ⅲ. Springer: Berlin, 1932—1935．《全集》共3卷，其中包括1900年巴黎讲演“数学问题”，并附有希尔伯特的学生0．Blumenthal所写希尔伯特传略和希尔伯特学派其他成员对其工作的评述（Van der Waerden：代数；H．Hasse：代数数论；A．Schmidt：几何基础；E．Hellinger：积分方程；P．Bernays：数学基础）。

［2］D. Hilbert. Grundlagen der Geometrie.初版．Teubner: Leipzig, 1899；第十二版．Teubner: Stuttgart, 1977.（中译本：D．希尔伯特．几何基础．上册（第二版）．北京：科学出版社，1987．）

［3］D. Hilbert. Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. Teubner: Leipzig and Berlin, 1912.

［4］D. Hilbert & R. Courant. Mathematischen Physik, Ⅰ, Ⅱ. Springer: Berlin, 1924, 1937.（中译本：R．柯朗、D．希尔伯特．数学物理方法，Ⅰ，Ⅱ．北京：科学出版社，1958，1977．）

［5］D. Hilbert & W. Ackermann. Grundzüge der Theoretischen Logik. Springer: Berlin, 1928.（中译本：D．希尔伯特等．数理逻辑基础．北京：科学出版社，1958．）

［6］D. Hilbert & S. Cohn-Vossen. Anschauliche Geometrie. Springer: Berlin, 1932．（中译本：D．希尔伯特，S．康福森．直观几何，上，下．北京：人民教育出版社，1959，1964．）

［7］D. Hilbert & P. Bernays. Grundlagen der Mathematik, Ⅰ, Ⅱ. Spriner: Berlin, 1934, 1939.

研究文献：

［1］H. Weyl. David Hilbert and his mathematical work. Bulletin of American Mathematical Society，50（1944），pp. 612—654.（中译本：赫尔曼·外尔. 大卫·希尔伯特及其数学工作. 数学史译文集，pp. 33—59，上海：上海科学技术出版社，1981．）

［2］C. Reid. Hilbert. Springer: Berlin, 1910.（中译本：康斯坦西·瑞德．希尔伯特．上海：上海科学技术出版社，1982.）

［3］H. Freudenthal. Hilbert, Dictionary of scientific biography, Ⅵ. Charles Scribner's Sons: New York, 1972.

［4］P. Bernays. Hilbert. Encyclopedia of philosophy. Ⅲ. MacMillan: New York. 1967.

［5］F. Browder (ed.). Mathematical developments arising from Hilbert problems. Proceeding of Symposia in Pure Mathematics of American Mathematical Society. vol. 21. 1976.