第二章　公理的相容性和互相独立性

Chapter II. The Consistence … of the Axioms

§9　公理的相容性

第一章里所提到的五组公理中的公理是有相容性的（即不互相矛盾的）；这就是说，不可能从所提到的这些公理出发，用逻辑推论得到和其中一条公理相矛盾的事实。我们现在就是要说明这些公理的相容性，我们的方法是用实数作成一组对象，指出这一组对象满足这五组公理中的全体公理。

首先考虑数域Q ，其中的数都是从1这个数出发，作有限次下列五种运算得来的代数数：加，减，乘，除和第五种运算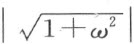 ，这里的ω 每次都表示运用这五种运算业已得来的某一个数。

然后把数域Q 中的任意一个数偶（x ，y ），看做是一个点；把Q 的任意三个数的比（u :v :ω ），在u，v 不都等于零的时候，看做是一条直线；而且在方程

ux ＋vy ＋w ＝0

成立的时候，就把（x ，y ）这个点看做是在（u ：v ：w ）这条直线上。我们很容易知道，公理Ⅰ_1～3 和Ⅳ都将满足^【35】 。数域Q 中的数都是实数；考虑到它们可以按大小来排列，我们就能很容易地对我们的点和直线，作出规定，使得第二组的顺序公理也全体成立。事实上设（x ₁ ，y ₁ ），（x ₂ ，y ₂ ），（x ₃ ，y ₃ ），…是一条直线上的点。在数列x ₁ ，x ₂ ，x ₃ ，…或y ₁ ，y ₂ ，y ₃ …是单调递减的或单调递增的序列的时候，我们就把这些点的这里写下的顺序，看做是这些点在这直线上的顺序。为了再满足公理Ⅱ₄ 的要求，我们只需要规定：所有的点（x，y ），使ux ＋vy ＋w 大于零的，在（u：v ：w ）这直线的一侧；而使ux ＋vy ＋w 小于零的，在这直线的另一侧。我们很容易看出，这个规定和关于共线点的顺序的规定是符合的^【36】 。

我们根据解析几何里的方法，规定线段的迁移和角的迁移。下述类型的一个变换

给定线段的平移和角的平移，而

这个变换给定对于直线y ＝0的一个反射。再用O 表示点（0，0），E 表示点（1，0），C 表示任意一点（a，b ）（图28）。考虑以O 为固定点，以∠COE 为旋转角的这个旋转。经过这旋转，任意一点（x ，y ）换成（x′ ，y′ ），其中

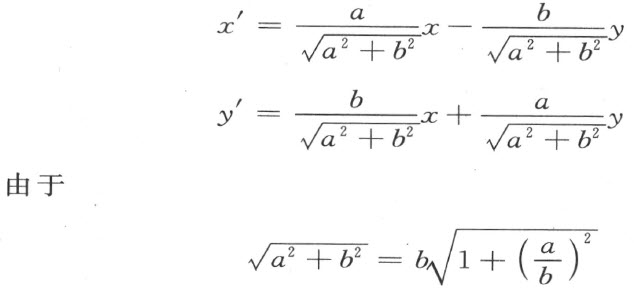
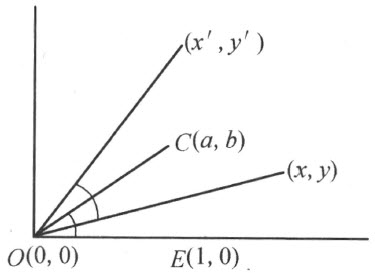
图　28

这个数仍然属于数域Q ，所以，在我们的规定下合同公理Ⅲ_1-4 也成立，而且显然三角形合同公理Ⅲ₅ ^【37】 和阿基米德公理Ⅴ₁ 也是满足的。完备公理Ⅴ₂ 是并不满足的。

所以直线的和平面的公理Ⅰ～Ⅳ，Ⅴ₁ 的推论中，若有矛盾，则每一个矛盾必定也在数域Q 的算术中出现 ^（1） 。

若在上文中我们用的不是数域Q ，而是所有的 实数所成的数域，我们所得到的就是通常的平面笛卡儿几何。在这种几何里，不只是公理Ⅰ_1～3 ，Ⅱ，Ⅲ，Ⅳ，Ⅴ₁ 满足，而且完备公理Ⅴ₂ 也满足，现说明如下：

在笛卡儿几何里，我们只要用顺序的和线段合同的定义，就知道：每一线段都能分成n 个合同的部分，n 是预先任意给定的一个数；若线段AB 短于线段AC ，则AB 分成n 份中的一份也短于AC 分成n 份中的一份。

现在假设平面笛卡儿几何不满足完备公理，即假设一条直线g 上可增加点，而在g 上还不破坏公理Ⅱ_1～3 ，Ⅲ_1～3 ，Ⅴ₁ ，和定理5或迁移线段的唯一性。把增加的点中的一个叫做N 。N 把g 分成两条射线。根据阿基米德公理，每一条射线都含有在扩充之前就存在的点。我们把这种点叫做旧 点。所以N 把g 上的旧点分成两条射线。设直线g 是用参数方程

x ＝mt ＋n

y ＝pt ＋q

表出的，在用点N 扩充之前，这个参数t 就已经可以取遍全体实数。因此，由于N 把直线分成两条射线，我们也就有了实数的一个戴德金（Dedekind）的分割。关于戴德金的分割的两组，我们知道：或者第一组有一个最后的元素，或者第二组有一个最先的元素。设这个元素在直线g 上所决定的旧点是A 。那么A 和N 之间没有旧点。

但是有一个旧点B ，使N 在A 和B 之间。根据阿基米德公理，还有若干个不同的点，姑且说n -1个，C ₁ ，C ₂ ，…，C _{n -2} ，D，使AN ，NC ₁ ，C ₁ C ₂ ，…，C _{n -2} D这n 条线段互相合同，而且使B 在A 和D 之间（图29）。把线段AB 分成n 个合同的部分。全体分点都是旧点；把其中离A 最近的那一个叫做W 。根据本证明之前所提到的直线顺序和合同的要求，因为线段AB 短于AD ，所以线段AW 短于AN 。所以W 这个旧点在A 和N 之间。因此我们的假设-g 上可以增加新点而不破坏直线公理的假设，就引起了矛盾。

图　29

所以在平面笛卡儿几何里，全体 直线的和平面的公理Ⅰ～Ⅴ都成立。

关于立体几何：相应的讨论毫无困难。

所以公理Ⅰ～Ⅴ的推论中若有矛盾，则每一个矛盾必定也在实数系的算术中出现。

众所周知，满足公理Ⅰ～Ⅳ，Ⅴ₁ 的几何有无限多种，而同时还满足完备公理V₂ 的几何只有一种 ，即笛卡儿几何。

§10　平行公理的独立性（非欧几里得几何） ^（2）

我们知道了公理有相容性之后，另一个有趣的问题是研究它们全体是否互相独立。实际上，我们的五组公理的每一个组成部分，都不能够是在它之前的诸组的逻辑推论。

首先，前三组公理中的个别公理，我们很容易证明：同一组中的诸公理基本上是互相独立的。

在我们的叙述中，第一组公理和第二组公理是其余的公理所根据的。所以我们还只要进而证明：第三组、第四组和第五组中的每一组公理都与其余的公理互相独立。

平行公理Ⅳ和其他公理互相独立；这可以按熟知的方式最简单地证明如下：在§9中所建立的通常的（笛卡儿）几何中，取一固定的球，并考虑使这个球不变的所有的一次变换，用这几何里所有在这个球以内的点和在这个球以内的那部分的直线和平面，而且只限于这些，当做一种空间几何的元素。并通过上述一次变换来定义这种几何的合同关系。我们知道，再加上适当的规定之后，这“非欧几里得 ”几何里，除去欧几里得公理Ⅳ之外，其他全体公理都满足了，既然§9中的通常的几何已经证明了是可能的，所以这种非欧几里得几何也是可能的^【38】 。

有些定理特别有趣，它们不依赖平行公理，也就是说，它们在欧几里得几何和非欧几里得几何里都成立，最重要的例子是勒让德（Legendre）的两条定理。第一条的证明，除去公理Ⅰ～Ⅲ之外，还需要公理Ⅴ₁ ，我们先证明一些辅助定理。

定理33 　已知一个直角三角形OPZ ，角P 是直角，若X ，Y 是线段PZ 上的两点，使（图30）

∠XOY ＝∠YOZ

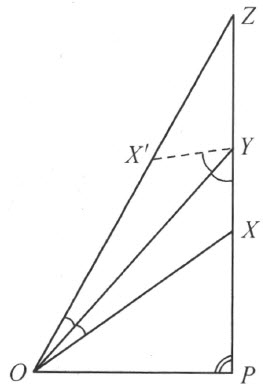
图　30

则

XY ∠YZ

证明 　迁移线段OX 到OZ 上，以O 为起点：

根据定理22和定理23，X′ 在线段OZ 上，利用定理22和公理Ⅲ₅ ，得

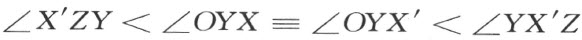
从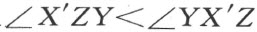 这个关系，利用定理12和定理23，得到本定理的结论。

定理34 　对于任意两个角α 和ε ，恒能找到一个自然数r ，使

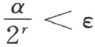
这里的 表示，从角α 起始，继续r 次作二等分角后所得到的角。

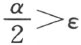证明 　给定了两个角α 和ε 。根据所假设的公理，角的二等分是可能的。考虑 这个锐角，若是 ，r ＝2时，定理34就成立了，现在设 ，从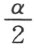 的一边上的一点C ，作另一边的垂线，交另一边于点B （图31）。把 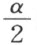的顶点叫做A 。迁移ε 到沿着边AB ，而且在 的内部，根据所假设的不等式，ε 迁移后的另一边交线段BC 于一点D 。阿基米德公理Ⅴ₁ 说：有一个自然数n ，使

n ·BD >BC

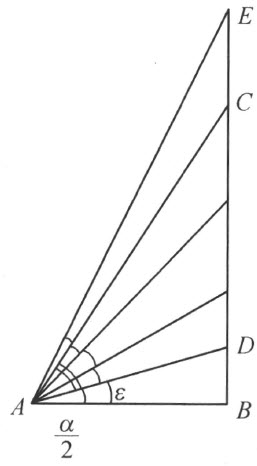
图　31

把角ε 迁移n 次；每次迁移到沿着ε 前一次迁移后的另一边。

可能至迟在最后一次，那第n 次迁移后，ε 的另一边不再和射线BC 相交。在这种情形下，设第m 次的迁移是最初的一次，使ε 的另一边不再和射线BC 相交。既然在前一次迁移时，ε 的另一边还和射线BC 相交，角（m -1）ε 是锐角。因此显然，经过m 次迁移所作成的角mε 的内部在直线AB 的点C 的那一侧，而且射线AC 在角mε 的内部，即

另一种可能是，在n 次迁移中的每一次时，角ε 都在射线BC 上截下一条线段。根据定理33，这条线段长于或等于线段BD 。设ε 第n 次迁移后的另一边交射线BC 于点E 。在射线BC 上截下的n 条线段的和BE 长于n ·BD ，从而更加长于BC ，因此

现在，相当于m （或n ），定一个自然数r ，使m <2^r-1 （或n <2^r-1 ）。用μ 表示角mε （或nε 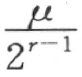）。 和 这两个角都能作。因为角的大小能比较，显然，一方面从不等式2^r-1 >m ，得到不等式 而另一方面从不等式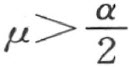 ，得到不等式 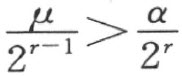。因此，根据大小比较的传递性，得

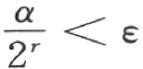
利用定理34，可以证明勒让德第一定理。

定理35（勒让德第一定理） 　三角形的三个内角的和，小于或等于两直角。

证明 　设一个已知的三角形的三个内角中的任意一个用∠A ＝α 表示；其余的两个用∠B ＝β 和∠C ＝γ 表示，而且β ≤γ （图32），根据定理26，线段BC 有一个中点D 。延长线段AD 到E ，使D 是线段AE 的中点。因为对顶角合同，公理Ⅲ₅ 能够应用到ADC 和EDB 这两个三角形，而根据定理15，我们可以明白易懂地定义角的和，这样对于三角形ABE 的内角α ′，β ′，γ ′，就有下列关系：

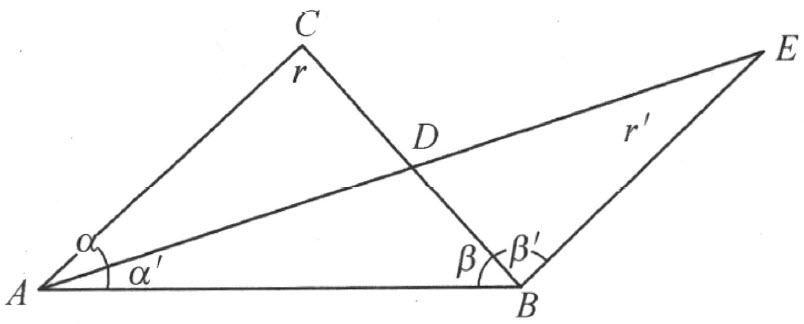
图　32

因此，三角形ABE 的内角的和等于三角形ABC 的内角的和。

根据定理23和定理12，从不等式β ≤γ ，即有

于是有

给定了一个三角形ABC ，和它的某一个角α ，于是恒可以作出一个三角形，它的内角和和三角形ABC 的相等，而且它的一个内角小于或等于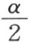 。因此，在另外给定了一个自然数r 的时候，恒可以作出一个三角形，它的内角和和三角形ABC 的相等，而且它的一个内角小于或等于 。

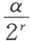现在假设勒让德第一定理不成立，假设给定了的三角形的内角和大于两个直角。

从定理22，我们知道：一个三角形的两个内角的和小于两个直角。给定了的这个三角形的内角和可表示成下述形式：

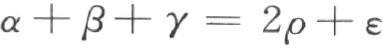
其中，ε 表示某一个角，ρ 表示一个直角。根据定理34，我们能找到一个自然数r ，使

现在再用前述的方法作一个三角形，它的内角α ，β ，γ ^* 适合下述关系：

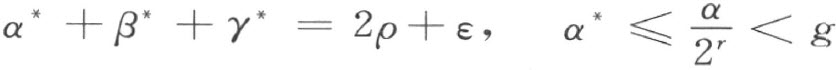
这三角形的两个内角的和

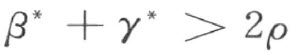
和定理22矛盾。因此，勒让德第一定理得证。

定理36 　若四边形ABCD （图33）的两个角A 和B 是直角，而且两条对边AD 和BC 合同，则∠C 和∠D 也就合同。再者，边AB 的在中点M 处的垂线，交对边于一点N ，使四边形A MND 和B MNC 合同。

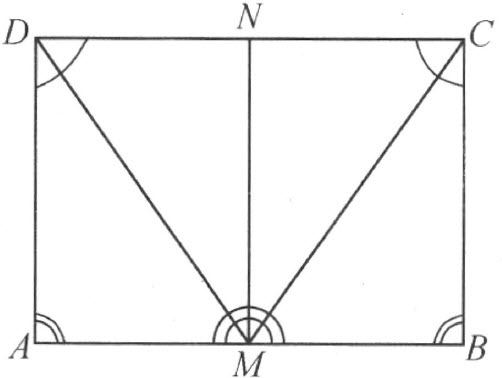
图　33

证明 　根据定理21和定理22，AB 的在点M 处的垂线是在∠DMC 内，而且，因此利用本书中所提到的一条定理，这垂线交线段CD 于一点N 。从定理12，定理21和定理15，即知三角形MAD 和MBC 合同，从而三角形MDN 和MCN 也合同。然后利用定理15，得

四边形A MND 和BMNC 所以合同。

定理37 　若四边形ABCD （图34）的四个角都是直角，则每一条从直线CD 的一点E 所作的对边AB 的垂线E F，也垂直于CD 。

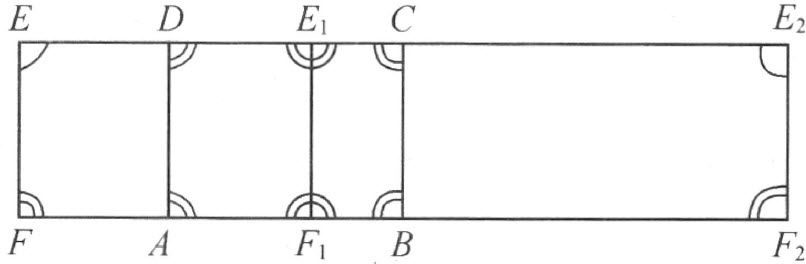
图　34

证明 　我们引进对于一条直线a 的反射的概念如下：从某一点P 作直线a 的垂线；延长这垂线到点P ′，使垂足是线段PP ′的中点。P ′就叫做P 的反射点。

对于直线AD 和BC ，反射这条线段EF 。从定理36的第二部分，反射所得的线段E ₁ F ₁ 和E ₂ F ₂ 都和EF 合同^【39】 。如同F 一样，F ₁ 和F ₂ 也在直线AB 上；如同E 一样，E ₁ 和E ₂ 也在直线CD 上。四边形EFF ₁ E ₁ ，EFF ₂ E ₂ 和E ₁ F ₁ F ₂ E ₂ 都满足定理36的第一部分的假设，因此在E ，E ₁ 和E ₂ 处的四个角都相等。在这三点中之一的地方出现两个相等的邻补角（在图34中的点E ₁ 处）；即这四个角都是直角。

定理38 　如果某一个四边形的四个角都是直角，那么每一个 有三个直角的四边形的第四个角，也是直角。

证明 　设A ′B ′C ′D ′是一个四边形，它的四个角都是直角，而且ABCD （图35）是任意一个四边形，它的三个角A，B ，D 是直角。我们作一个和A ′B ′C ′D ′合同的四边形AB ₁ C ₁ D ₁ ，它的直角A 和四边形ABCD 的重合。

在点B 和B ₁ 重合，或者点D 和D ₁ 重合的情形，本定理和定理37相同。且设B 在A 和B ₁ 之间，而且D ₁ 在A 和D 之间。如同在定理36的证明中，利用外角定理，我们知道，线段BC 和线段C ₁ D ₁ 相交于一点F 。定理37于是告诉我们，点F 处有一个直角，从而点C 处也有一个直角。

在点A，B ，B ₁ 和A ，D ，D ₁ 有其余可能的顺序时，本定理也同样成立。

利用定理38，可以证明勒让德第二定理。

定理39（勒让德第二定理） 　若某一个 三角形的三个内角的和等于两直角，则每一个 三角形的三个内角的和就等于两直角。

证明　给定了一个三角形ABC ，它的内角和是2w 。对于每一个这种的三角形，我们能作一个对应的四边形，它的三个角是直角，第四个角等于w 。为此，连接边AC 和BC 的中点D 和E （图36），而且从点A，B 和C 作这条连线DE 的垂线AF ，BG 和CH 。因为三角形AFD 和CHD 合同，又三角形BGE 和CHE 合同，不管这给定了的三角形ABC 的∠A 或∠B 是否为钝角，都有

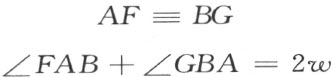
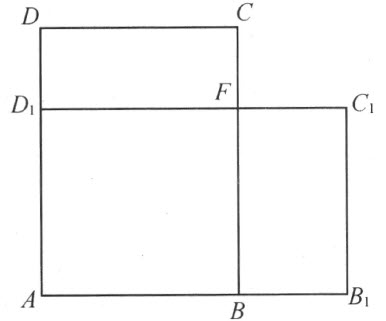
图　35

图　36

在线段FG 上作中点处的垂线JK 。从定理36的第二部分，四边形AKJF 和BKJG 合同，所以，这两个四边形各有三个直角，而且第四个角相等，即

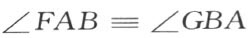
因此，

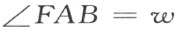
AKJF 就是所需要的，和这给定了的三角形相对应的四边形。

现在设某一个三角形D ₁ 的内角和等于两直角，而且给定了另一个三角形D ₂ 。作D ₁ 和D ₂ 的相应的四边形V ₁ 和V ₂ ，V ₁ 有四个直角，而V ₂ 有三个直角。根据定理38，V ₂ 的第四个角也是直角，勒让德第二定理得证。

§11　合同公理的独立性

关于合同公理的独立性，我们要证明下述的特别重要的事实：公理Ⅲ₅ 不能够是其余公理Ⅰ，Ⅱ，Ⅲ_1～4 ，Ⅳ，Ⅴ的逻辑推论。

我们仍用通常几何的点、直线、平面当做新空间几何的元素，而且和在通常几何中一样，例如§9中所说明的。规定角的迁移；但是线段的迁移，我们却另下定义。设A ₁ ，A ₂ 两点，在通常几何中的坐标是x ₁ ，y ₁ ，z ₁ 和x ₂ ，y ₂ ，z ₂ 。然后用下述式子

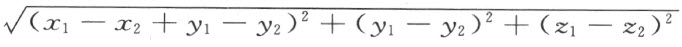
的正值当做线段A ₁ A ₂ 的长度；任意两条线段A ₁ A ₂ 和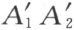 若是在这么规定的意义下有相等的长度，就说它们是互相合同。

在这样建立的空间几何里，公理Ⅰ，Ⅱ，Ⅲ_1～2 ，₄ ，Ⅳ，V（而且还有利用公理Ⅲ₅ 所证明的定理14，15，16，19，21）显然成立。

要证明公理Ⅲ₃ 也成立，我们取任意一条直线a ，而且取其上的三个点A ₁ ，A ₂ ，A ₃ ，其中的A ₂ 在A ₁ 和A ₃ 之间。设直线a 上的点x ，y ，z 是用下列方程

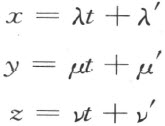
给定的，其中的t 表示一个参变数，λ ，λ′ ，μ ，μ′ ，ν ，ν′ 表示常数。若t ₁ ，t ₂ （<t ₁ ），t ₃ （<t ₂ ）分别是点A ₁ ，A ₂ ，A ₃ 的参变数的值，A ₁ A ₂ ，A ₂ A ₃ 和A ₁ A ₃ 这三条线段的长度就分别是

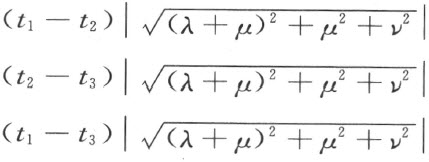
从而，A ₁ A ₂ 和A ₂ A ₃ 这两条线段的长度的和等于线段A ₁ A ₃ 的长度，所以公理Ⅲ₃ 成立。

在我们的几何里，关于三角形的公理Ⅲ₅ ，不是在任何情形下都成立的。例如，在平面z ＝0上，取下列四个点：

O ，以x ＝0，y ＝0　为坐标

A ，以x ＝1，y ＝0　为坐标

B ，以x ＝-1，y ＝0　为坐标

C ，以x ＝0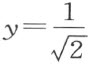， 　为坐标

线段OA ，OB ，OC 的长度都等于1。因此，在AOC 和COB 这两直角三角形里（图37），有下列合同式：

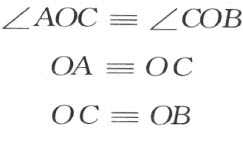
图　37

但是∠OAC 和∠OCB 不合同，公理Ⅲ₅ 不满足。同时，这个例子也不满足（三角形的）合同定理1；因为AC 的长度是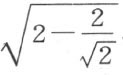 ，而BC 的长度是 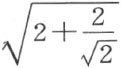。再者，对于AOC 和COB 这两个等腰三角形，定理11也不成立。

下述的例子，表明一种平面 几何，它满足除去公理Ⅲ₅ 之外的全体公理，但不满足公理Ⅲ₅ ：设在一个平面α 上除去线段合同的概念之外，其余在公理中出现的概念都有通常的定义。取一个平面β ，它和α 构成一个适当的锐角。现在却规定：平面α 上的一条线段的长度，就是这线段在平面β 上的投影的通常长度。

§12　连续公理的独立性（非阿基米德几何）

要想证明阿基米德公理V₁ 的独立性，我们必须建立一种几何，它满足除去公理V之外的全体公理，但公理V却不满足 ^（3） 。

为此，我们作出代数函数域Q （t ），其中的代数函数都是从t 出发，用下列五种运算得来的：加，减，乘，除和第五种运算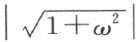 ，这里的ω 表示运用这五种运算业已得来的某一个函数。Q （t ）的元素的集合，如同§9中的Q 的一样，是可数的。这五种运算都是单值的运算，而且不产生虚数；所以域Q （t ）是只含有t 的单值的实函数。

设c 是域Q （t ）中的任意一个函数，既然c 是t 的一个代数函数，只有有限个t 的值能使c 等于零；所以，在t 的值是适当大的正值的时候，c 的值或者恒是正的，或者恒是负的。

现在，我们把域Q （t ）中的函数看做是一种在下一节§13的意义下的复数。显然，在这样规定的复数系中，通常的运算规律全体成立^【40】 。我们再进而规定大小。设a 和b 是这复数系中的任意两个不同的数。按照在t 的值是适当大的正值的时候，c ＝a -b 这个t 的函数恒取正值或恒取负值。我们就说a 大于或小于b ，用记号a >b 或a <b 表示。有了这个规定，我们的复数系中的数就能按照大小而有顺序，和实数的顺序类似；而且很容易看出，对于我们的复数，下列定理成立：若是不等式的两端加以同一个数或者乘以同一个大于零的数，不等式仍然成立。

设n 表示任意一个正整数，对于域Q （t ）中的n 和t 这两数，由于差n —t ，作为t 的函数，在t 的值是适当大的正值的时候，恒取负值，所以当然n <t 。这事实可叙述如下：域Q （t ）中的1和t 这两个大于零的数，具有下述的性质：前一个数的任意一个倍数恒小于后一个数。

我们现在利用复数域Q （t ），建立一种几何，犹如在§9中根据代数数域Q 所作的那样。把域Q （t ）中的任意一组三个数（x ，y ，z ）看做是一个点；把Q （t ）的任意四个数（u ：v ：w :r ），在u ，v ，w 不都等于零的时候，看做是一个平面，在方程：

ux ＋vy ＋wz ＋r ＝0

成立的时候，就把（x ，y ，z ）这个点看做是在（u :v :w :r ）这个平面上，而且把两个具有不同的u :v :w 的平面的全体公共点看做是一条直线。然后，如同在§9中一样，规定元素的顺序，线段的迁移和角的迁移。这样就产生了一种“非阿基米德 ”几何；正如复数系Q （t ）的上述的性质所表明的，在这种几何里，除去连续公理之外，其余公理都满足。实际上，迁移线段1到线段t 上，不管连续迁移多少次，线段t 的终点都是不会超过的；这和阿基米德公理所要求的矛盾。

完备公理Ⅴ₂ 也和在它之前的全体公理（公理Ⅰ～Ⅳ，Ⅴ₁ ）互相独立。这是§9中最先建立的那种几何所表明的；因为在那种几何里阿基米德公理是满足的。

非阿基米德几何和非欧几里得几何，都具有重大的意义。特别是，阿基米德公理在勒让德定理的证明中的地位也极有兴趣。戴恩（M.Dehn） ^（4） 遵照我的建议，对于这一点加以研究；他的结果把这个问题彻底澄清，戴恩的研究从公理Ⅰ～Ⅲ出发，不过他所用的顺序公理Ⅱ比本书中所说的更为普通，因此黎曼几何（椭圆几何）^【41】 也包括在他的研究范围之内。他的顺序公理Ⅱ略述如下：

一条直线上的四个点A，B ，C ，D ，恒能分为两个点偶A ，C 和B ，D ，使A ，C 和B ，D 互相分离 ；其逆也成立。一条直线上的五个点恒能如是选择它们的名称为A，B ，C ，D ，E ，使A ，C 被B ，D 分离，也被B ，E 分离，A ，D 被B ，E 分离，也被C ，E 分离，等等。

戴恩只从公理Ⅰ～Ⅲ出发，因此不利用连续性，首先证明勒让德第二定理（定理39）的推广。

若某一个三角形的三个内角的和大于 、等于或者小于两直角 ，则每一个三角形的三个内角的和必也都如此 ^（5） 。

在上文所引的论文里，还证明了勒让德第一定理（定理35）的下述的补充：

假设通过一点的 ，而且和一直线平行的直线 ，有无穷多条 ，根据这个假设 ，若是不用阿基米德公理 ，还不能推证一个三角形的三个内角的和小于两直角 。但是一方面有一种具有下述性质的几何 （非勒让德几何 ）：通过一点的和一直线平行的直线 ，既有无穷多条 ，而且黎曼几何 （椭圆几何 ）的定理平成立 ；另一方面也有一种具有下述性质的几何 （半欧几里得几何 ）：通过一点的和一直线平行的直线 ，既有无穷多条 ，而且欧几里得几何的定理还成立 。

假设通过一点的和一直线平行的直线不存在 。根据这个假设 ，一个三角形的三个内角的和恒大于两直角 。

最后，我们提一提下述事实：若引进阿基米德公理 ，则平行公理就能用下面的定理替代：一个三角形的三个内角的和等于两直角。

————————————————————

（1） 关于算术公理的相容性，参看我的关于数的概念的报告（Berichte der Deutschen Mathematiker-Vereinigung, 1900），以及1900年我在国际数学家会议中的讲演“数学问题”（Mathematische Probleme, Göttinger Nachr, 1900）特别是其中的问题2。

（2） 此外设一种几何里只有公理Ⅰ～Ⅲ和Ⅴ₁ 。我们容易证明：在这几何里，平行公理或者对于每一个包含直线a 和a 外一点A 的组都成立，或者对于任一个这样的组都不成立，参看巴尔都斯，非欧几何（Nichteuklidische Geometrie, Berlin, 1927）。

（3） 费罗尼斯（G. Veronese）在他的深奥的著作《几何基础》（Grundzüge der Geometrie，谢卜（A.Schepp）的德译本，Leipzig，1894）里，也作了建立一种独立于阿基米德公理的几何的尝试。

（4） “关于三角形的内角和的勒让德定理”（Die Legendreschen Sätze über die Winkelsumme im Dreieck, Math. Ann．卷53，1900）。

（5） 后来舒尔（F.Schur，Math. Ann．卷55）和希姆斯来夫（Hjelmeslev，Math. Ann．卷64）都前后证明了本定理，值得特别重视的是，后者极短的论证引出本定理中间部分的证明。也参看舒尔，几何基础（Grundlagen der Geometrie Leipzig und Berlin，1909）§6。