第五章 德沙格定理
Chapter V. Desargues Theorem
§22 德沙格定理和在平面上用合同公理的证明
在第一章所列举的公理中,第Ⅱ~V组全体公理的一部分是直线公理,一部分是平面公理,只有第Ⅰ组公理的4~8是空间公理。为了解这些空间公理的意义,我们设想已有了一种平面 几何,而要普遍地研究在什么条件下,这平面几何可以看做是一种空间几何的一部分;在这空间几何中,这平面几何中所假设的公理和空间关联公理Ⅰ1~8 全体都成立。
在本章和下一章中,一般不用合同公理,因而现在必须采用平行公理Ⅳ的一个较精确形式作为依据:
Ⅳ* (较精确形式的平行公理 )设a 是任一直线,A 是a 外的任一点,则由a 和A 所决定的平面上必有且只有一条直线 ,它通过A 而不和a 相交【57】 。
我们都知道,用第I,Ⅱ,Ⅳ* 组的公理作根据,就能够证明所谓德沙格定理【58】 。这是平面上的一条有关交点的定理,我们特别突出两个三角形的对应边的交点所应共的直线作为所谓“无穷远直线”,并把如此得到的定理和它的逆定理合并起来,简单地称为德沙格定理。这定理如下(图63):

图 63
定理53(德沙格定理) 若平面上的两个三角形的每两条对应边互相平行,则对应顶点的连线或者通过同一个点,或者互相平行;而且,反过来:
若平面上的两个三角形的对应顶点的连线通过同一个点或者互相平行,而且这两个三角形的两对对应边互相平行,则这两个三角形的第三对对应边也互相平行。
我们已经提起过,定理53是公理Ⅰ,Ⅱ,Ⅳ 的推论;由于这事实在一种平面几何中德沙格定理的成立是下述事实的必要 条件:这平面几何可以看做是一种空间几何的一部分,而且在这空间几何中,第Ⅰ,Ⅱ,Ⅳ 组的公理全体都成立。
如同在第三章和第四章中,我们来考虑一种平面 几何,在这几何中公理Ⅰ1~3 ,Ⅱ~Ⅳ都成立,而且设想在这几何中已经遵照§15引进了线段计算,然后如同§17中所说的,对于这平面的每一点,有一对线段(x ,y )和它对应;对于每一直线,有三条线段(u :v :w )的比和它对应,其中的u,v 不全是零,使得一次方程
ux +v y +w =0
表示点和直线关联的条件,几何中的线段全体,由于§17,组成一个数域,它具有§13中所列举的性质1~16,因而如同在§9或§12中利用数系Q 或Q (t )所做的,我们能用这个数域来构造一种空间几何。为着这个目的,规定一组三个线段(x ,y ,z )表示一个点,四条线段(u :v :w :r )的比,其中的u ,v ,w 不全是零,表示一个平面,而直线由两个平面的公共点规定;因而一次方程
ux +u y +w z +r =0
表明点(x ,y ,z )在平面(u :v :w :r )上。最后,对于一直线上的点的顺序,平面上的点对于这平面上的一直线而言的顺序,和最后空间中的点对于一平面而言的顺序,都如同在§9中平面的情形所作的那样,可以用线段的不等式来确定。
既然令值z =0时,我们就重得到原来的平面几何,所以,平面几何能够看做是一种空间几何的一部分。根据上文所说的,德沙格定理的成立是这种可能性的一个必要条件,所以在我们的平面几何中德沙格定理也成立。因此,德沙格定理是公理Ⅰ1~3 ,Ⅱ~Ⅳ的一个推论。
我们注意上文所得到的事实,也不难从比例论中的定理42,或者从定理61直接推证。
§23 在平面上不用合同公理时,不能证明德沙格定理
我们现在研究,在平面几何中,不用合同公理时,能否证明德沙格定理问题,以达到下述结果:
定理54 有一种平面几何存在,在这种几何里公理Ⅰ1~3 ,Ⅱ,Ⅲ1~4 ,Ⅳ* ,V,即除去合同公理Ⅲ5 之外的全体直线和平面公理都满足,而德沙格定理(定理53)不 成立。因此德沙格定理不能 从所提到的这些公理推证 ;它的证明或者需要空间公理,或者需要关于三角形的合同公理Ⅲ5 。
证明 (1) 通常的平面笛卡儿几何能够建立,已经在第二章§9中证实了。直线的和角的定义如下。取笛卡儿几何的任一直线当做轴,决定这轴上的一个正向和一个负向,而且决定对于这条轴来说的一个正半平面和一个负半平面。
把下列种种当做新几何中的直线(图64):这条轴;在笛卡几何中轴的每一条平行线;笛卡儿几何中的每一条直线,若它的在这半平面上的射线和轴的正向作成一个直角或者钝角;最后笛卡儿几何中具有下述性质的每两条射线h ,k 的组;h 和k 的公共端点在轴上,在正半平面上的射线h 和轴的正向作成一个锐角α ,而且在负半平面上的射线k 的延长线k′ 和轴的正向作成一个角β ,使得下列关系
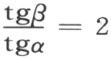
在笛卡儿几何中成立。
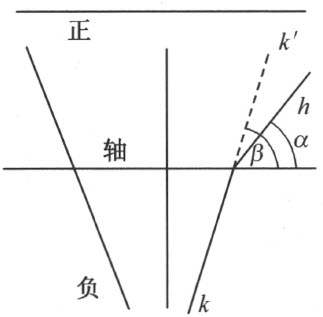
图 64
即便在由笛卡儿几何中的两条射线所表出的那些直线上,点的顺序和线段的长度也可同通常一样地很显然地规定出来。容易知道,公理Ⅰ1~3 ,Ⅱ,Ⅲ1~3 ,Ⅳ* 在这样规定的几何中成立【59】 ;例如立即可以看出,通过一点的诸直线不重复地盖满平面。此外,在这几何中公理V也成立。
若一个角没有具有下述性质的一条 边:从轴出发到正半平面而且和轴的正向作成一个锐角,这个角就如同通常在笛卡儿几何中【60】 一样来度量,否则,若一个角ω 至少有一条边是一条具有上述性质的射线h ,则用相当的k ′替代h (参看图64)作边,便得到另一个角ω′ ;然后规定笛卡儿几何中角ω′ 的量作为新几何中角ω 的量。图65说明这样定义的两对邻补角。根据角的定义,公理Ⅲ4 也成立;特别是对于每一个∠(l ,m );
∠(l ,m )≡∠(m ,l )

图 65
另一方面,如从图66立刻可以看出,而且容易用计算来证实的,在这个新的 平面几何中德沙格定理不成立。同样的容易作一个图,表明巴斯噶定理也不成立。

图 66
这里所说明的平面“非德沙格”几何,同时也是下述的一种平面几何的例子:一种平面几何,其中公理Ⅰ1~3 ,Ⅱ,Ⅲ1~4 ,Ⅳ* ,Ⅴ都成立,但它仍不 能看做是一种空间几何的一部分 (2) 。
§24 不用合同公理,用德沙格定理作根据,引进一种线段计算 (3)
为着要完全了解德沙格定理(定理53)的意义,我们从一种平面几何出发,其中公理Ⅰ1~3 ,Ⅱ,Ⅳ* (4) 都成立,即除合同公理和连续公理之外的全体公理都成立;而且在这种几何中,不依赖合同公理 ,而用下列方式引进一种新的线段计算。
在平面上取两条固定的,相交于一点O 的直线(图67)。此后,我们只考虑具有下述性质的线段,它们的起点是O ,而且它们的终点是这两条直线的一条上的任意点。点O 这单独一个点我们称为线段0,用
OO =0 或 0=OO
表示。

图 67
设E 和E′ 是这两条通过O 的固定直线上的定点,而且不在同一条直线上;这两条线段OE 和OE′ 都称为线段1,用
OE =OE′ =1
或
1=OE =OE′
表示。直线EE′ 简单的称为单位直线。若A 和A′ 分别是直线OE 和OE′ 上的点,而且连线AA′ 平行于EE′ ,我们就说线段OA 和OA′ 相等,用
OA =OA′ 或OA′ =OA
表示。
首先为着要规定在OE 上的线段a =OA 同b =OB 的和,作AA′ 平行于单位直线EE′ ,通过A′ 作直线平行于OE ,通过B 作直线平行于OE′ 。这后两条直线相交于一点A″ 。最后通过A″ 作直线平行于EE′ ,交固定的直线OE 和OE′ 分别于点C 和C′ 。线段c =OC =OC′ 叫做线段a =OA 同b =OB 的和,用
c =a +b 或a +b =c
表示。
我们首先证明,在德沙格定理(定理53)成立的假设下,两条线段的和能够用更普遍的方式得到。在A 和B 所在的直线上的、决定和a +b 的点C ,不依赖于所根据的单位直线EE′ 的选择;即点C 可由下列作图法得到:
在直线OA′ 上取任一点 (图68),通过B 作平行于
(图68),通过B 作平行于 的直线,通过
的直线,通过 作平行于OB 的直线。这两条直线交于一点
作平行于OB 的直线。这两条直线交于一点 。现在作通过
。现在作通过 而且平行于
而且平行于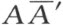 的直线,交直线OA 于点C ,即决定和a+b 的点。
的直线,交直线OA 于点C ,即决定和a+b 的点。
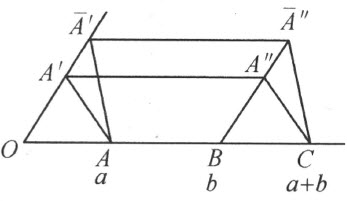
图 68
为了证明,我们假设点A′ 和A″ ,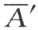 和
和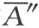 都按所说的方式得到,而且在OA 上的点C 是由平行于AA′ 的直线CA″ 所决定。那么要证明,
都按所说的方式得到,而且在OA 上的点C 是由平行于AA′ 的直线CA″ 所决定。那么要证明, 也平行于
也平行于 。在三角形
。在三角形 和
和 中,对应顶点的连线平行;而且,此外还有两对对应边
中,对应顶点的连线平行;而且,此外还有两对对应边 和
和 ,AA′ 和CA″ 平行,所以根据德沙格定理的第二部分,第三对对应边
,AA′ 和CA″ 平行,所以根据德沙格定理的第二部分,第三对对应边 和
和 也平行。
也平行。
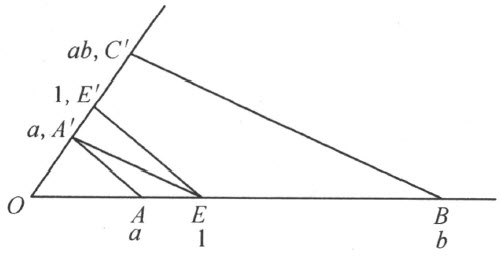
图 69
要规定一条线段a =OA 乘以一条线段b =OB 的积,完全可用§15中的作图,只要把那里的直角的两边改为现在的两条固定直线OE 和OE′ 。因而作图如下(图69):在OE′ 上求点A′ ,使得AA′ 平行于单位直线EE′ ,连接E 和A′ 而且通过B 作EA′ 的平行线;这条平行线交固定直线OE′ 于一点C′ ;然后把C =OC′ 叫做线段a =OA 乘以线段b =OB 的积。用
c =ab 或ab =c
表示。
§25 新的线段计算中,加法的交换律和结合律
我们容易证明,对于新的线段计算,§13中所列举的关联定理都成立;若我们所根据的是一种平面几何,其中公理Ⅰ1~3 ,Ⅱ,Ⅳ* 满足,而且德沙格定理成立 ,现在我们要研究,§13中所列举的运算律还有哪些是正确的。
首先要证明,对于§24中所定义的加法交换律
a +b =b +a
成立。设
a =OA =OA′ ,b =OB =OB ′
这里的AA′ 和BB′ ,按照我们的规约,平行于单位直线(图70)。现在作A′A ″,B′B ″平行于OA ,又作AB ″和BA″ 平行于OA′ ,这样求得点A″ 和B ″。我们立刻看出,论断所说的是连线A″B ″平行于AA′ 。根据德沙格定理(定理53)来证实这个论断如下:用F表示AB ″和A′A″ 的交点。用D表示BA″ 和B′B ″的交点;那么三角形AA′ F和BB′ D的对应边平行。应用德沙格定理,我们就可以断定O ,F ,D 这三点共线。因为这事实,在三角形OAA′ 和DB ″A″ 中,对应顶点的连线都通过同一个点F ;而且,因为还有两对对应边OA 和DB ″,OA′ 和DA″ 平行,所以,根据德沙格定理(定理53)的第二部分,第三对对应边AA′ 和B ″A″ 也平行。
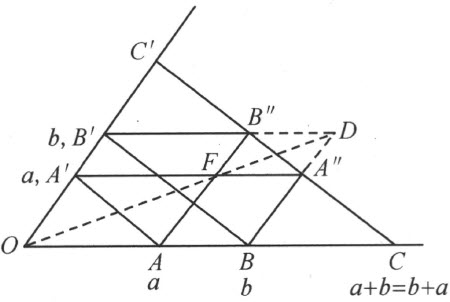
图 70
这证明同时说明了,在作两条线段的和时,不管从这两条固定直线中的哪一条出发,都是一样的。
其次,加法的结合律 成立:
a +(b +c )=(a +b )+c
设直线OE 上给定了线段
a =OA ,b =OB ,C =OC
根据上一节相加的规则,下列的和
a +b =O G,b +c =OB′ ,(a +b )+c =OG′
可以作图如下(图71):在直线OE′ 上任取一点D ,作连线DA 和DB 。作通过B 而平行于OD 的直线,和通过C 而平行于OD 的直线;它们与通过D 而平行于OA 的直线分别交于点F 和D′ 。通过F 而平行于AD 的直线,和通过D′ 而平行于BD 的直线,分别交直线OA 于上文所说的点G和B′ ;而且,通过D′ 而平行于GD 的直线,交直线OA 于上文同样说到的点G′ 。最后,要得到和a +(b +c ),首先作通过B′ 而平行于OD 的直线,交直线DD′ 于一点F′ ,再作通过F′ 而平行于AD 的直线。因此,问题是要证明G′F′ 和AD 平行。用H 表示直线BF 和GD 的交点。用H′ 表示直线B′F′ 和G′D′ 的交点。在三角形BDH 和B′D′H′ 中,对应边平行;而且,直线BB′ 和DD′ 还平行,所以,根据德沙格定理,直线HH′ 也和这两条直线平行。因而能应用德沙格定理的第二部分到GFH 和G′F′H′ 这两个三角形,证实G′F′ 平行于GF ,因而事实上也平行于AD 。

图 71
§26 新的线段计算中,乘法的结合律和两条分配律
在我们的假设下,线段的乘法结合律
a (bc )=(ab )c
也成立。
设在通过点O (图72)的两条固定直线的一条直线上给定了线段
1=OA ,b =OC
c =OA′
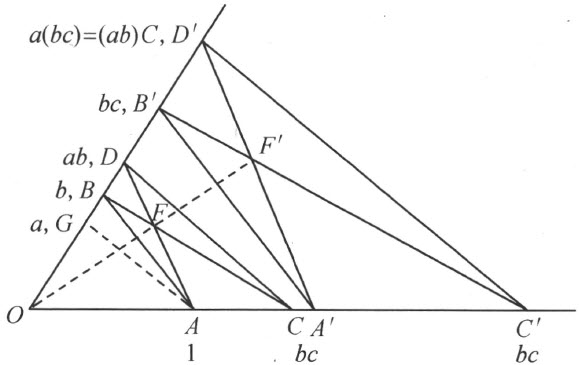
图 72
而且,在另一条直线上给定了线段
a =OG 和b =OB
根据§24中的规则,依次作线段
bc =OB′ 和bc =OC
ab =OD ,(ab )c =OD′
我们作A′B′ 平行于AB ,B′C′ 平行于BC ,CD 平行于AG ,而且A′D′ 平行于AD ;我们立刻得出,CD 也平行于C′D′ 。把直线AD 和BC 的交点叫做F ,直线A′D′ 和B′C′ 的交点叫做F′ ;三角形ABF 和A′B′F′ 中对应边都互相平行;根据德沙格定理,所以O ,F ,F′ 三点共线,由于这种情形,对于三角形CDF 和C′D′F′ 能应用德沙格定理的第二部分,从而得知CD 确实平行于C′D′ 。
最后,根据德沙格定理可以证明,在线段计算中,两条分配律
a (b +c )=ab +ac
(b +c )a =ba +ca
都成立。
首先证明第一条分配律
a (b +c )=ab +ac
设在两条固定直线的一条直线上给定了线段(图73)
1=OE ,b =OB ,c =OC
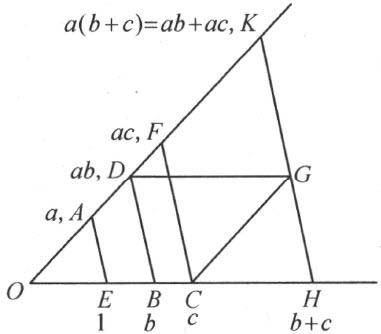
图 73
而且,在另一条直线上给定了线段
a =OA
通过B 和C 所作的直线EA 的平行线,分别交直线OA 于点D 和F 。根据§24中乘法的规则,得
OD =ab ,OF =ac
根据§24中更普遍的加法规则,得到
OH =b +c
此处点H 的作图如下:通过C 作OD 的平行线,通过D 作OC 的平行线,再通过这两条直线的交点G 作BD 的平行线;这平行线交OC 于所说的点H ,交OD 于一点K 。既然OH =b +c ,根据乘法规则,有
OK =a (b +c )
根据更普遍的加法规则,以及本书上所证明的关于和的作图中固定直线OE 和OE′ 的可换性,和ac +ab 终于可以如下作图:通过OE 的任意一点,姑且说C ,作OD 的平行线CG ,再通过D 作OC 的平行线DG ,最后通过G 作CF 的平行线GK 。因此得
OK =ac +ab
然后从加法的交换律就得第一条分配律。
最后证明第二条分配律 。设在这两条固定直线的一条直线上给定了线段(图74)
1=OE ,a =OA

图 74
而且,在另一条直线上给定了线段
b =OB ,C =OC
EB 的平行线AB′ 和EC 的平行线AC′ 分别决定线段
OB′ =ba ,OC′ =ca
在固定的直线OB 上,根据更普遍的加法规则,作线段
OF =b +c ,OF′ =ba +ca
如下:通过C 作OE 的平行线,通过E 作OC 的平行线;它们交于一点D 。通过D 作EB 的平行线,交OA 于上述的点F 。再者,通过A 作OC′ 的平行线。通过C′ 作OA 的平行线,它们交于一点D′ 。通过D′ 作AB′ 的平行线,交OB 于所说的点F′ 。
根据线段的乘法规则,若证明AF′ 平行于EF ,则第二条分配律成立。
在三角形ECD 和AC′D′ 中,对应边互相平行;从德沙格定理,O ,D ,D′ 三点共线。于是对于三角形EDF 和AD′F′ 能够应用德沙格定理的第二部分,从而得知AF′ 确实平行于EF 。
§27 以新线段计算作根据的直线的方程
根据§24中所援引的公理和德沙格定理的正确性的假设,在§24到§26中引进了平面上的一种线段计算,对于这种计算,除去§13中所列举的关联定理外,加法的交换律,加法和乘法的结合律,以及两条分配律都还成立。至于乘法的交换律不一定成立,我们将在§33中得知。在本节中,我们要表明,如何能够根据这种线段计算得到点和直线的解析表示。
定义 把平面上通过点O 的两条取定的直线叫做X 轴和Y 轴。设P 是平面上的任意一点。若通过P 作这两条轴的平行线,而在X 轴和Y 轴上所得到的线段分别是x 和y ,就把P 看做是由x ,y 所决定的。线段x ,y 叫做点P 的坐标 。
根据新的线段计算,利用德沙格定理,我们得到下述事实:
定理55 任一直线的点的坐标x ,y 恒满足下述形式的线段方程
ax +by +c =0
在这方程里线段a ,b 必须在坐标x,y 的左边 ;线段a ,b 不同时是零,而且c 是一条任意的线段。
反过来:每一个这种形式的线段方程恒表示所讨论的平面几何中的一条直线。
证明 Y 轴或它的平行线上的点P 的横坐标x 都不依赖于P 在这直线上的位置,这就是说,这样的一条直线可用下述形式的方程表出:

对于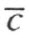 ,有一条线段c 存在,使得
,有一条线段c 存在,使得
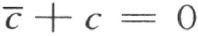
因而
x +c =0
这方程具有所要求的形式。
现在设l 是一条直线,交Y 轴于一点S (图75),通过这直线的任一点P ,作Y 轴的平行线,交X 轴于一点Q 。线段OQ =x 是P 的横坐标。通过Q 作与l 的平行线在Y 轴上截下一条线段OR ;按照线段乘法的定义有
OR =ax

图 75
其中,a 是一条线段,它只依赖于l 的位置,而不依赖于P 在l 上的选择。设P 的纵坐标是y 。根据本书上所给的更普遍的和的定义,而且由于本书上证明了的从Y 轴入手的求和的可能性,得知线段O S是和ax +y 。线段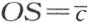 是一条仅由l 的位置而决定的线段。从等式
是一条仅由l 的位置而决定的线段。从等式

得
ax +y +c =0
其中,c 还是由 所决定的线段。这最后的方程具有所要求的形式。
所决定的线段。这最后的方程具有所要求的形式。
容易证明,不在l 上的点的坐标不适合这个方程。
同样地,容易证明定理55的第二部分成立。事实上设线段方程
a′x +b′x +c′ =0
给定了,其中a′ 和b′ 不同时是零。在b′ =0时,用从关系aa′ =1所决定的线段a ,左乘这个等式的两端;在b′ ≠0时,用从关系bb′ =1所决定的线段b 左乘。然后,根据运算律得到上文所推出的直线方程的一个,而且能在所讨论的平面几何中,作出适合这方程的一条直线。
我们还特别声明,在我们的假设下,凡形如
xa +yb +c =0
的一个线段方程其中的线段a ,b 在坐标x,y 的右边 ,一般不 表示一条直线。
在§30中,有定理55的一个重要的应用。
§28 线段集合当做复数系
我们已经提到,对于在§24中建立的新的线段计算,§13中的定理1~6满足了。
其次,我们利用德沙格定理,在§25和§26中看到了,对于这线段计算,§13中的运算律7~11成立;因此,除去乘法交换律之外,所有的关联定理和运算律在这线段计算中都正确。
最后,为了要使线段能够排成顺序,我们作以下的规定:设A ,B 是直线OE 的任意两个不同的点;那么根据定理5,我们可将O ,E ,A ,B 这四个点排成一个顺序,其中E 在O 之后【61】 。若在这个顺序中B 在A 之后,我们就说线段a =OA 小于 线段b =OB ,用记号
a <b
表示;若相反的,在这个顺序中A 在B 之后,我们就说线段a =OA 大于 线段b =OB ,用记号
a >b
表示。
容易看出,根据公理Ⅱ,在线段计算中,§13中的运算律13~16都满足了【62】 ;从而,所有不同的线段全体组成一个具有下述性质的复数系,§13中的规则1~11,13~16都成立;这就是说,除去乘法的交换律和连续定理之外 ,所有的规则都成立 。此后,我们把这样的一个数系叫做一个德沙格数系 。
§29 利用德沙格数系建立空间几何
设已有了一个德沙格数系D ;它使我们能够建立一种空间几何满足全体公理Ⅰ ,Ⅱ ,Ⅳ * 。
为了要表明此事,设想德沙格数系D 中的一组任意三个数(x,y ,z )是一个点,D 中的一组任意四个数(u :v :w :r )(其中,u ,v,w 不同时是零)是一个平面;而且当a 是D 中任意非零的数时,(u :v :w :r )和(au :av :aw:ar )这两组表示同一个平面。等式
ux +vy +w z +r =0
的成立表明点(x,y ,z )在平面(u :v :w :r )上【63】 。最后用两个平面(u′:v′:w′:r′ )和(u″:v″:w″:r″ )来规定一条直线,若D 中没有一个非零的数a ,使得
au′ =u″ ,av′ =v″ ,aw′ =w″
若一个点(x,y ,z )是(u′:v′:w′:r′ )和(u ″:v ″:w ″:r ″)的一个公共点,这个点就说是在这直线
[(u′:v′:w′:r′ ),(u ″:v ″:w ″:r ″)]
上。两条直线若含有完全相同的点,就看做是同一条直线。
按照假设,§13中的运算律1~11对于D 中的数都成立。应用这些运算律,不难达到下述结果:在刚才上文所建立的空间几何中,公理I和Ⅳ* 都得到满足【64】 。
要使顺序公理Ⅱ也满足,作如下规定:设
(x 1 ,y l ,z 1 ),(x 2 ,y 2 ,z 2 ),(x 3 ,y 3 ,z 3 )
是一条直线
[(u′:v′:w′:r′ ),(u ″:v ″:w ″:r ″)]
的任意三点。若下列六对不等式
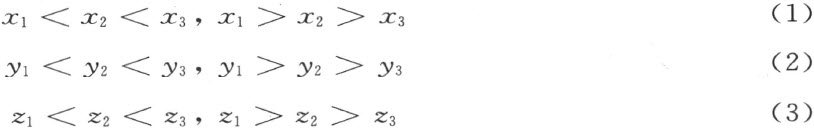
中至少一对满足,就说点(x 2 ,y 2 ,z 2 )在其他两个之间。若两对不等式(1)中的一对成立,就很容易得出:第一,或者y l =y 2 =y 3 ,或者两对不等式(2)中的一对必然满足,而且第二,同样的,或者z 1 =z 2 =z 3 ,或者两对不等式(3)中的一对必然满足。事实上,用D 中适当的非零的数左乘下列方程
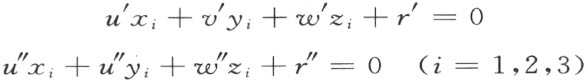
再把所得到的方程相加,就得到下述形式的一组方程
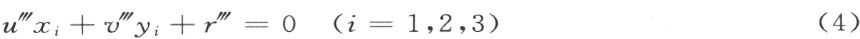
此处的系数 断然不是零,因为否则x 1 ,x 2 ,x 3 这三个数就要相等,和假设矛盾。在
断然不是零,因为否则x 1 ,x 2 ,x 3 这三个数就要相等,和假设矛盾。在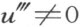 时,就得到
时,就得到
y 1 =y 2 =y 3
若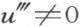 ,从
,从

得到另一对不等式
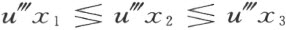
从而根据(4)得到
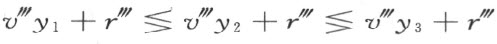
所以
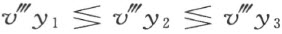
而且,既然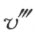 不是零,得到
不是零,得到
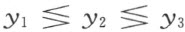
在这些不等式的每一对中,或者完全取上面的不等号,或者完全取下面的不等号。
从上文的讨论得知,在我们的几何中直线顺序公理Ⅱ1~3 是成立的。现在需要证明,在我们的几何中平面公理Ⅱ4 也是成立的【65】 。
为此,设给定了一个平面(u :v :w :r )和其中的一条直线[(u :v :w :r ),(u ′:v ′:w ′:r ′)]。我们规定,所有在这平面(u :v :w :r )中的点(x,y ,z ),使得式子u ′x +v ′y +w ′z +r ′小于或大于零的,分别在那直线的一侧或另一侧;然后必须证明,这种规定具有确定的意义,而且和本书上的一致,这个证明是不难的。
由此可知,在从德沙格数系D 用上述的方式所产生的空间几何中,公理Ⅰ,Ⅱ,Ⅳ* 都完全满足了。
既然德沙格定理是公理Ⅰ1~8 ,Ⅱ,Ⅳ* 的推论,所以我们认识到:
对于一个德沙格数系 D ,可以用上述的方式建立一种平面几何,在这几何中数系D 的数【66】 组成根据§24所引进的线段计算中的元素,而且公理Ⅰ1~3 ,Ⅱ,Ⅳ* 都满足了;所以,在这种平面几何中,德沙格定理 也恒成立。
这个事实是我们在§28中所得到的结果的逆,在§24中的结果可如下表述:
若在一种平面几何中,不但公理Ⅰ1~3 ,Ⅱ,Ⅳ* 都成立,而且德沙格定理 也成立,那么,在这几何中可以按照§24中所述的方式引进线段计算;在适当的规定顺序之后,这线段计算的元素恒组成一个德沙格数系 。
§30 德沙格定理的意义
若在一种平面几何中公理Ⅰ1~3 ,Ⅱ,Ⅳ 都满足了,而且,除此之外,德沙格定理还成立,那么,根据上节最后一条定理,恒能在这几何中引进一种线段计算,具有§13中的运算律1~11,13~16。然后再把这些线段的集合看做一个复数系,而且,根据§29中的说明,用这个数系建立一种空间几何,使得满足公理Ⅰ,Ⅱ,Ⅳ 。
若只考虑这空间几何中的(x,y ,0)这种点,和那些只含有这种点的直线,就得到一种平面几何;若再考虑§27中所推证的定理55,显然可见,这平面几何必定和原来所讨论的平面几何一致,换句话说,这两种平面几何的元素间可以在保持关联和顺序不变的条件之下,建立一个一一对应【67】 。于是我们得到下述定理,它可以看做是本章的整个研究的最终目的:
定理56 设在一种平面几何中,公理Ⅰ1~3 ,Ⅱ,Ⅳ 都满足;在这情形下,德沙格定理的成立是下述事实的充分必要条件:这平面几何可以看做是满足全体公理Ⅰ,Ⅱ,Ⅳ 的一种空间几何的一部分。
对于平面几何来说,德沙格定理可以说是标志着消去空间公理的结果。
从所得到的结果我们可以知道,每一种满足全体公理Ⅰ,Ⅱ,Ⅳ* 的空间几何,恒可以看做是一个“任意高维的几何”的一部分;这里所说的任意高维的几何,是指点、直线、平面以及别种元素的集合,而且满足相应的扩充了的关联公理、顺序公理以及平行公理。
————————————————————
(1) 本书的前几版在这里采用了第一种“非德沙格几何”;现在替代这种几何,我们要说明一种比较简单的,源于莫尔敦(Moulton)的非德沙格几何,可参看莫尔敦“一种简单的非德沙格平面几何”(A simple non-desarguesian plane geometry, Trans. Math. Soc., 1902)。
(2) 莫尔曼(H.Mohrmann)还给出了非德沙格几何的一些有趣的例子。参看题献给希尔伯特的一本出版物(Festschrift David Hilbert)* Berlin,1922,181页。
* 即“自然科学”(Die Naturwissenschaften)第10卷中的一期。——译者注
(3) 赫森堡在他的论文“关于一种几何计算”(Über einen geomet rischen Kalkul,Acta.Math.,29卷,1904)中,运用有关位置几何的概念,推导出这种线段计算。若先用德沙格定理作根据,在平面上制定向量加法,则推导的一些部分可以更为容易。参看霍尔德尔(Hölder)“线段计算和射影几何”(Strecken kennechnurg und projektive Geometrie,Leipz.Ber.,1911)。
(4) 甚至不用平行公理Ⅳ* ,而用德沙格定理的射影形式,也可以引进一种新的线段计算,关于去掉顺序公理的可能性,则可参见补篇Ⅳ。
