附录Ⅰ 直线作为两点间的最短距离 (1)
(转载自Mat h.Ann.,卷46)
(给克莱因(F.Klein)先生的一封信)
如果将点、直线和平面取作元素,则下面的公理能够作为一种几何学的基础:
1.说明元素间相互结合的公理 ,简单地叙述如下:
任意两点A 和B 恒定一直线a 。——任意不共线三点A ,B ,C 恒定一平面α 。——如果一直线a 上两点A ,B 在一平面α 上,则直线a 将全部位于平面α 上。——如果两个平面α ,β 有一公共点A ,则它们至少还有另一公共点B 。——每一直线上至少有两点,每一平面上至少有三个不共线点,空间至少有四个不共面点。
2.顺序公理 即说明赖以引入真线上线段的概念和点学列概念的公理 ;这些公理首先由M。帕士(M.Pasch) (2) 所引入并系统地加以研究。它们可基本归纳如下:
直线上两点A ,B 之间恒至少有这直线上的一个第三点C 。——一直线上三点中恒有一个且仅有一个点在另两个点之间。——如果A ,B 在一直线a 上,则在同一直线a 上恒有一点C 使B 在A 和C 之间。——直线a 上任意四点A 1 ,A 2 ,A 3 ,A 4 可以这样排列,即当下标h 小于i ,而k 大于i 时,则Ai 将落于Ah 和Ak 之间。——在一平面a 上每一直线a 将这平面上的点分成两个区域,且具有下面的性质:一个区域中任意点A 和另一个区域中任意点A′ 决定线段AA′ ,在线段AA′ 内有直线a 上的点;另一方面,同一区域中任意两点A ,B 所决定的线段不含有直线a 上任何一点。
3.连续公理 这个公理我以下述形式给出:
如果A 1 ,A 2 ,A 3 …是直线a 上的无穷点列,而B 是a 上另一点,使得当下标h 小于i 时,点A i 落在A h 和B 之间,则存在点C 具有下述性质:无穷点列A 2 ,A 3 ,A 4 ,…的所有点将落在A l 和C 之间。当C′ 是另一点时,则有同样论断,即C 将落于A 1 和C′ 之间。
由这些公理就可完全严格地论证调和点列的理论。利用类似于F。林德曼(F.Lindemann) (3) 所曾作过的,则我们可得出下面的定理:
对于空间内每个点,总有三个有限实数x,y ,z 和它相对应。而且对于每个平面就有三个这样的实数间的线性关系和它相对应使得满足线性关系的x,y ,z 所对应的全部点都在这个平面上;反过来,这个平面上的点所对应的三个数x,y ,z 都将适合这个线性关系。再者如果将x,y ,z 理解为通常欧几里得空间中一点的直角坐标,则原空间的点就对应着欧几里得空间里某个无处是凹的体的内部的点;反过来,无处是凹的体的内部所有点将对应着原空间的点。这样一来,原空间映射到欧几里得空间中无处是凹的体的内部。
无处是凹的体系指具有下述性质的一个体:假如在其内部两点用一直线相连,则此直线介于这两点的部分将整个位于这个体的内部。
请您注意这里所研究的无处是凹的体在闵可夫斯基(H.Minkowski) (4) 的数论研究中起着很大的作用。同时也请注意闵可夫斯基曾给它一个简明的解析定义。
反过来说,如果在欧几里得空间给出任意一个无处是凹的体,则它将确定一种几何学(下面称为广义几何学)。在这种几何里,适合开始所提的全部公理。无处是凹的体内的每一个点与广义几何学中的一个点相对应。在体的内部所作欧几里得空间的每条直线和每个平面将分别对应着这种广义几何学的直线和平面,而在体的边界或外部的欧几里得空间的点以及全部位于欧几里得空间外部的直线和平面将不与这种广义几何中的任何元素相对应。
这样,从上面所建立广义几何中的点到欧几里得空间中无处是凹的体的内部的点所建立映射的定理,说明广义几何元素中的一个性质:即这种广义几何从内容说完全等价于开始所给的全部公理。
现在我们来确定广义几何中长度的概念。为达到这个目的,将原空间中两点A 和B 所对应的欧几里得空间两点仍用相同的字母A 和B 来表示。然后将欧几里得空间中直线AB ,沿点A 和点B 向外延长与无处是凹的体的边界分别交于X 和Y 。欧几里得空间中任意两点P 和Q 的欧几里得距离一般用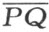 表示。于是实数值
表示。于是实数值

称为广义几何中线段AB 的长度。因为
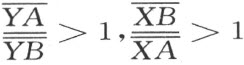
所以长度恒为正数。
利用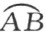 的表示式容易列举出长度概念的性质,但为了这封信不使您过于疲倦,我将这些略去。
的表示式容易列举出长度概念的性质,但为了这封信不使您过于疲倦,我将这些略去。
在所给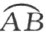 的公式中,同时说明这个量是如何依赖于无处是凹的体的形状。令A 和B 在体内固定,而仅将体的边界变动,使得边界点X 和Y 分别向A 和B 运动,显然两个商
的公式中,同时说明这个量是如何依赖于无处是凹的体的形状。令A 和B 在体内固定,而仅将体的边界变动,使得边界点X 和Y 分别向A 和B 运动,显然两个商
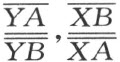
中的每一个都将增大,因此 之值也将增大。
之值也将增大。
现在给定无处是凹的体内的三角形ABC (附图1)。此三角形所在的平面α 这个体成一无处是凹的卵形线。其次将三角形的三边AB ,AC ,BC 中的每条边从两端点向外延长和卵形线的边界相交,令交点分别是X 和Y ,U 和V ,T 和Z ,作直线U Z 及T V 且延长它们相交于W 。此二直线和直线XY 的交点分别用X′ 和Y′ 来表示。现在考虑以三角形UW T 代替平面α 上的无处是凹的卵形线。容易看出,这种由三角形UW T 所定的平面几何中长度 和
和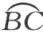 将与原几何中所定的长度完全一样,而边AB 将增大。设边AB 的新长度用不同于原长度
将与原几何中所定的长度完全一样,而边AB 将增大。设边AB 的新长度用不同于原长度 的
的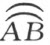 来表示,于是
来表示,于是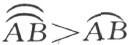 (5) 。
(5) 。
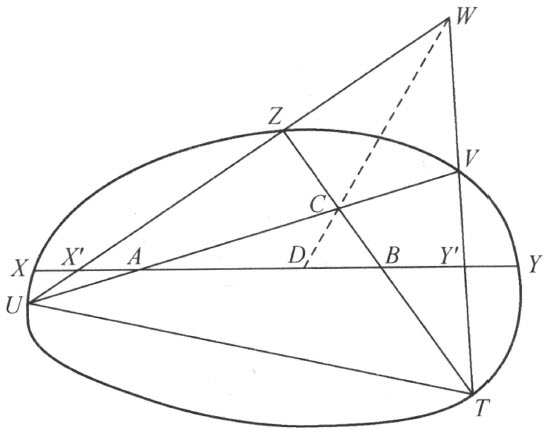
附图 1
由是三角形ABC 各边之间,存在一个简单关系

为了证明,联结W 和C 并延长之与AB 相交于D ,由于两个点列X′,A,D,Y′ 和U,A,C,V 具有透视位置,则由周知的交比定理得:
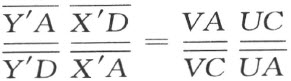
又由于两个点列Y′,B,D,X′ 和T ,B,C, Z 具有透视位置,故得
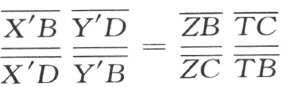
将此两等式相乘即得

这个等式即可证明上面的论断。
从上面的研究您可看出:仅仅在此信开始所列举的公理的基础上,利用已给的长度定义及其简单性质,下述的一般定理一定成立。
在每个三角形中两边之和大于或等于第三边。
同时显见相等的情况恰于三角形ABC 所在平面α 与这无处是凹的体的边界交成两个直线段 U Z 和T V 时方能出现。至于上面所提的条件不借助于无处是凹的体也可以表示出来。如果在原几何中给出某一平面α 上的两条直线a 和b 并且它们交于某点C ,那么,一般说来,平面α 分成以C 为顶点的四个平面角形区域,在每个区域中可能存在与两直线a 和b 无一相交的直线。特别地,如果两个相对的平面角形区域里不存在这样的直线,那么前述问题的情况就可以出现,也就是:恒存在着三角形,它的两边和等于第三边。 在这种情况下,在两点A 和B 之间用两条直线段所作的路径的总长度等于由A 直接到B 的距离是可能的,因此不难证明:在利用相同性质(方法)联结两点A 和B 的路径的所有路径中,总有全长较其他路径全长为大的路径。 对于进一步研究较短路径的问题是容易做到的。当无处是凹的体的边界取作四面体的情况时将是特别有趣的。
最后我请您注意下面的事实:在以前所展开的讨论中,常假设无处是凹的体位于欧几里得空间的有限部分。假如在开始所给的公理所建立的几何中存在一直线和一点且经过这点仅能作一条平行线的性质,则上述假定即不能成立。容易看出,我的论断必须予以修改。
关于这个附录所提问题的近代发展可以参看下列著作:
1.布兹曼(H. Busemann),《短程线几何》(Geometry of Geodesics 1955)。
2.布兹曼,《问题Ⅳ,德沙格空间》(Problem IV, Desarguesian Spaces, Math. Development Arising from Hilbert problems., Proceedings of Symposia in Pure Math. Vol. 28, 1976)。
3.鲁斯贴尔尼克(L. A. Lysternik),《最短线,变分问题》(The Shortest Lines, Variational Problems, 1976, 1983 2nd. Printing, Mir publishers, Moscow)。
4.普格芮娄夫(A. V. Pogorelov),《希尔伯特第四问题》(Hilbert's Fourth Problem, 1979, John Wiley and Sons, N. Y.)。——译者注
————————————————————
(1) 关于这个问题更一般的说明,可参看1900年在巴黎国际数学会议上我的报告“数学问题”(Mathematische Probleme),见Cöttinger Nachr. 1900, NO. 4,以及G.Hamel 1901年在格丁根的就职论文报告和他的文章“论直线为最短的几何学”(Über die Geometrien,in denen die Geraden die Kürzesten sind),见Math.Ann.,卷57,1903。
(2) 参看帕士《新几何学讲义》(Vorlesungen über neuere Geometrie,Teubner,1882)。
(3) 参看克来伯士-林德曼(Clebsch-Lindemann)《几何学讲义》(Vorlesungen üuber Geometrie),第2卷第1分册433页以后。
(4) 参看《数的几何》(Geometrie der Zahlen,Teubner,1896和1910)。
(5) 由于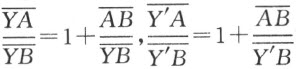 故
故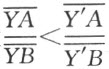 ,同理可得
,同理可得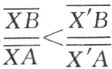 ,将此二不等式相乘,即得证。——译者注
,将此二不等式相乘,即得证。——译者注
