附录Ⅲ　鲍雅义-罗巴切夫斯基几何的新基础

（转载自Math. Ann.，卷57）

在我的献礼《几何基础》（Grundlagen der Geometrie） ^（1） 一书第一章中，我曾归纳出一组欧几里得几何公理，然后证明了仅用这组中的平面公理，甚至不用连续公理就可能建立平面欧几里得几何。在下面的讨论中，我将平行公理用与鲍雅义-罗巴切夫斯基几何中所相应需要的公理来代替，于是证明专用平面公理，而不用连续公理即可作为鲍雅义-罗巴切夫斯基几何的基础 ^（2） 。

这里所论到的鲍雅义-罗巴切夫斯基几何的新基础从简练方面来说并不亚于我所见到的，大家熟知的鲍雅义-罗巴切夫斯基同时所用的极限球法和克来因所用的射影法。但是那些方法实质上用到了空间以及连续性。

为了便于理解，按照我的献礼《几何基础》列出以后用到的平面几何公理于下 ^（3） ：

Ⅰ．关联公理

Ⅰ₁ ．已知两点A 和B ，恒有一直线a ，它与两点A ，B 中的每一点相关联。

Ⅰ₂ ．已知两点A 和B ，至多有一直线，它与两点A ，B 的每一点相关联。

Ⅰ₃ ．每一直线上恒至少有两点，至少有三点不在同一直线上。

Ⅱ．顺序公理

Ⅱ₁ ．若一点B 在一点A 和一点C 之间，则A ，B 和C 是一直线上的不同三点，而且B 也在C 和A 之间。

Ⅱ₂ ．已知两点A 和C ，在直线AC 上恒至少有一点B ，使得C 在A 和B 之间。

Ⅱ₃ ．一直线的任意三点中，至多有一点在其他两点之间。

定义 　两点A 和B 之间的点也叫做线段AB 或BA 的点。

Ⅱ₄ ．设A ，B 和C 是不在同一直线上的三点；且a 是平面A ，B ，C 上的一直线，但不通过A ，B ，C 三点中的任一点，若直线a 通过线段AB 的一点，则它也必通过线段BC 的一点，或线段AC 的一点。

Ⅲ．合同公理

定义 　每一直线被它上面的任一点分成两条半线（射线）或者说分成两侧。

Ⅲ₁ ．设A ，B 是直线a 上的两点，A ′是直线a ′上的一点，则在直线a ′上由A ′所确定的一侧，总可找到一点B ′，使得线段AB 和线段A ′B ′合同或相等；用记号表示，即

AB ≡A ′B ′

Ⅲ₂ ．若两线段A ′B ′和A ″B ″都和另一线段AB 合同，则这两线段A ′B ′和A ″B ″也合同。

Ⅲ₃ ．设AB 和BC 是同一直线a 上，无公共点的两线段，而且A ′B ′和B ′C ′是在此直线上或另一直线a ′上亦无公共点的两线段。若AB ≡A ′B ′，BC ≡B ′C ′，则AC ＝A ′C ′。

定义 　自一点A 作两条不在同一直线上的半线h 和k ，我们把它叫做一个角，且用

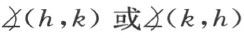
来表示。

在公理Ⅱ的基础上，我们可以规定面上的一条直线来规定它的两侧的概念。一平面的点与k 均位于h 的同侧，同时它与h 又均位于k 的同侧，这些点叫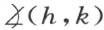 的内点；它们形成这个角的角形区域。

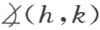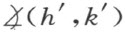Ⅲ₄ ．设给定了一个角 ，一直线a ′和a ′的一侧，设h ′是直线a ′上，从一点O ′发出的一条半线，则恰有一条半线k ′使角 与角 合同或相等，用记号表示：

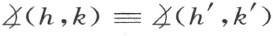
并且角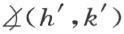 的全部内点同在a ′的已知一侧。

每一个角和它自己合同，即

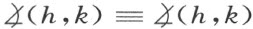
Ⅲ₅ ．两个三角形ABC 和A ′B ′C ′若有下列合同式：

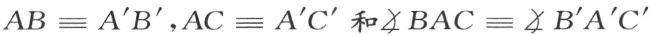
则必有合同式

从公理Ⅰ～Ⅲ容易推出三角形合同定理以及等腰三角形定理，且同时可以理解自线上一点或线外一点作垂线以及平分一个已知线段或一个已知角的可能性。

特别是，每个三角形两边之和大于第三边定理的推出恰如在欧几里得情况下一样。

Ⅳ．相交线和不交线的公理

在鲍雅义-罗巴切夫斯基几何中与欧几里得几何的平行公理相当的公理可叙述如下：

Ⅳ．如果b 是任一直线，且A 是不在这直线上的一点，则过A 存在两条半线a ₁ ，a ₂ 它们不在同一条直线上且与直线b 都不相交，而在a ₁ ，a ₂ 所成角形区域内，从A 所射出的每条半线与b 相交（附图9）。

附图　9

定义 　若直线b 由它上面一点B 分成两条半线b ₁ ，b ₂ 且a ₁ ，b ₁ 在直线AB 的一侧，a ₂ ，b ₂ 在直线AB 的另一侧。于是半线a ₁ 称为与半线b ₁ 平行，且类似地，半线a ₂ 称为与半线b ₂ 平行。同理半线a ₁ ，a ₂ 将称为与直线b 平行，并且两半线a ₁ 和a ₂ 所在直线也分别称为与直线b 平行。

自此立即推出下面两个命题的正确性：

如果一直线或一半线平行于另一直线或半线，则后者也将永远平行于前者 ^（4） 。

如果两半线均与第三半线平行，则它们也彼此平行。

定义 　每一半线确定一个端点。彼此平行的所有半线将确定同一个端点。一般来说，从A 点射出的端点是α 的半线，用记号（A ，α ）来表示。一直线有两个端点。具有两个端点α 和β 的直线一般用记号（α ，β ）来表示。

如果A ，B 和A ′，B ′是两对点，且α 和α ′是两个端点而线段AB 和A ′B ′相等且AB 及半线（A ，α ）所成的角等于A ′B ′及半线（A ′，α ′）所成的角。于是容易看出，BA 与（B ，α ）所成的角也等于B ′A ′与（B ′，α ′）所成的角。这两个图形ABα 和A ′B ′α ′称为互相合同。

最后用熟知的方法规定反射下的映象于下：

定义 　自一点向一直线作垂线，并自垂足延长到一点，使其距离等于原垂线长，则所得点叫做已知点关于这直线的反射映像。

一直线上所有点的映像仍在一直线上，这直线叫做已知直线的反射映像。

§1　引理

现在依次证明下面的引理：

引理1 　如果两直线与第三直线相交成相等的错角，则此两直线不互相平行。

证明 　假设结论不成立，即这两直线沿某一方向平行。如果沿第三直线所截成的线段的中点来将整个图形作半个旋转，即在这个线段的另一侧形成一个合同三角形，于是，已知两直线将沿另一方向平行，此与公理Ⅳ相矛盾。

引理2 　已知两直线a 和b ，它们既不相交，也不互相平行，则存在一条直线同时与这两直线垂直。

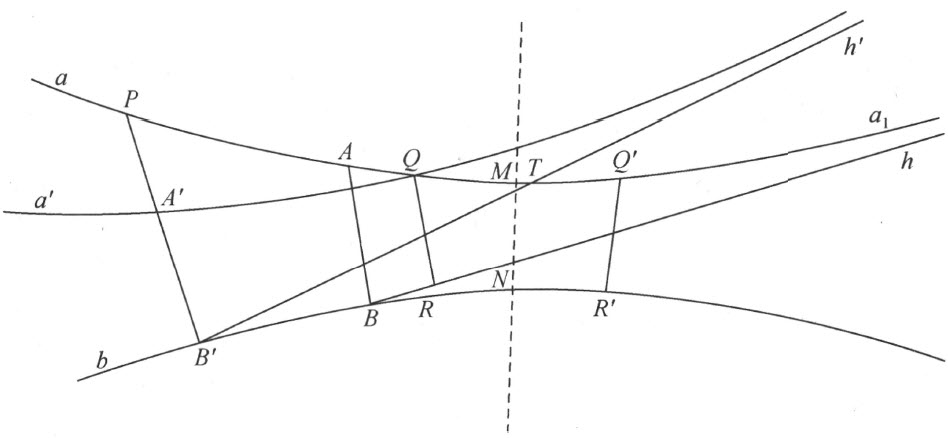
证明 　自直线a 上任意两点A 和P 作直线b 的垂线AB 和PB ′（附图10），设垂线段PB ′大于垂线段AB 。于B ′P 上自点B ′取点A ′使A ′B ′等于AB ，于是A ′落在P ′和B 之间。过A ′作直线a ′与B ′A ′交于A ′，使它们所成之角连同方向等于直线a 与垂线BA 交于A 点处所成之角。下面将证明直线a ′必须与直线a 相交。

附图　10

为了达到这个目的，直线a 于P 点分成两条半线，其中含有A 者为a ₁ ，过B 作半线h 平行于a ₁ 。再者设h ′是由B ′所射出的半线而使这半线与b 所成之角连同方向等于自B 所射出半线h 与b 所成之角。这样，由引理1，半线h ′不与h 平行，因此也不与a ₁ 平行。且一定不与h 相交，自公理Ⅳ，它必与a ₁ 相交。设h ′与a ₁ 的交点是T ，由作图a ′既与h ′平行，自公理Ⅱ₄ ，直线a ′必须经过边PT 离开三角形PB ′T 。再用下面所论即得到所要求的证明。设直线a 与a ′的交点为Q 。

自Q 作b 的垂线QR ，于b 上取R ′使BR ′＝B ′R ，且B 到R′的方向与B ′到R 的方向相同。同理于a 上自A 作线段AQ ′使其连同方向与自A ′所作线段A ′Q 相同。分别取线段QQ ′和RR ′的中点M 和N ，则连线MN 即是a 与b 的公垂线。

事实上，自四角形A ′B ′Q ′R 和ABQR ′的合同得出线段QR 和Q ′R ′必相等且Q ′R ′与b 垂直。由是可得：四角形QRMN 及Q ′R ′MN 的合同以及所要求的论证。因之引理2得以完全证明。

引理3 　已知任两条彼此不平行的半线，则必存在一条直线与这两条半线平行，亦即存在一条直线它具有两个预先给定的端点α 和β 。

证明 　自任意点O 作已知两半线的平行线，并在这两半线上自O 点到A 和B 截取相等线段（附图11），则有

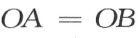
且自O 过A 所作半线的端点为α ，自O 过B 所作半线的端点为β 。

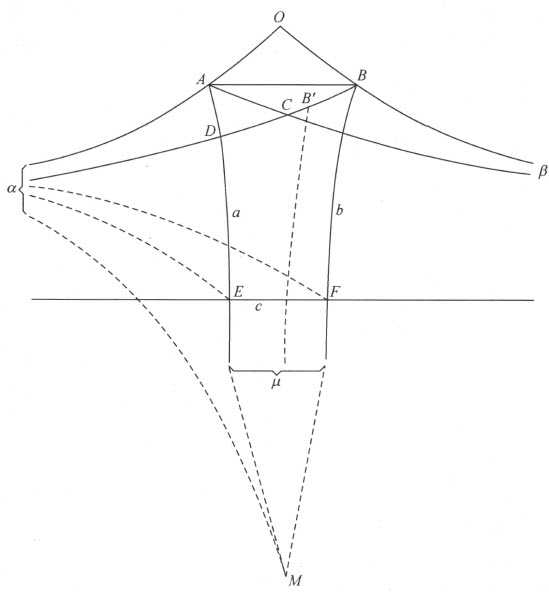
附图　11

OA ＝OB

于是联结点A 和β 并平分过A 所引的两条半线所成的角，同样联结B 和β 并平分过B 所引的两条半线所成的角。这两条平分线中的第一条和第二条分别用a 和b 来表示。由图形OAβ 和OBα 的合同得出

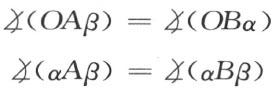
从后面一个等式以及角的平分性质得到下面角的公式

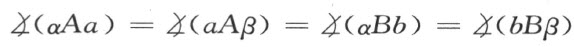
首先要证明两个角平分线a 和b 既不相交也不互相平行。

若a 和b 相交于点M ，则由作图OAB 是等腰三角形，而有

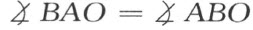
并利用前面方程

因此

AM ＝BM

今用半线联结M 与端点α ，自上面线段的相等和角 及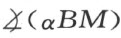 的相等得知图形αAM 和αBM 合同。自此合同将得出角 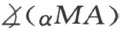和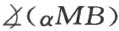 （αMB ）的相等。由于这个结论显然不成立，因之角平分线a 和b 相交的假定必须除掉。

其次，假设a 与b 互相平行。且将它们的端点用μ 表示，假设自B 射出过α 的半线与自A 射出过β 的半线交于点C 且与a 交于点D 。今证明线段DA 和DB 将相等。事实上，假定不相等，于DB 上取B ′使DB ′＝DA ，然后用半线联结B ′与μ ，自图形DAα 与DB ′μ 的合同将推出两角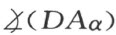 和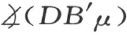 的相等，这样两角 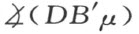和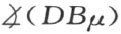 必相等。由引理1，此为不可能：

两线段DA 和DB 相等产生两角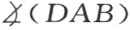 和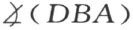 的相等。由前可知两角 及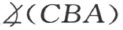 亦必相等，因此推出两角 及 也相等。但这结论显然不成立，故a 和b 平行的假设也必须除去。

由于这些论断，知两直线a ，b 既不相交也不平行。于是按照引理2，存在a 和b 的公垂线c 分别与它们交于E 和F 。可以断定直线c 就是两已知端点α 和β 的连线。

假如这个结论不成立，设c 不含有端点α ，则将E 和F 分别与端点α 相连，再连接线段AB 和EF 的中点。甚易得出EA ＝FB 。又自两图形αEA 和αFB 合同可以得出两角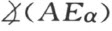 和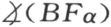 相等，这样自E 与F 所作半线将与c 成相等的角。这个结论显与引理1相矛盾。同理也可证明c 含有端点β ，本引理得以完全证明。

引理4 　设a 和b 是两条平行线，且O 是在a 和b 所成平面区域内部的一点。且设O _a 和O _b 分别是O 关于a 和b 的反射映象，又M 是O _a O _b 的中点，于是自M 所作与a 和b 均平行的半线将是O _a O _b 于点M 处的垂线。

证明 　假如结论不成立（附图12），就在O _a O _b 的同一侧，自点M 作O _a O _b 的一条垂线。设O _a O _b 与a 和b 分别交于P 和Q 。由于PO <PQ ＋QO ，故有PO _a <PO _b ，以及QO _b <QO _a 。因之M 必须在a 和b 所成平面区域的内部，则在点M 所作的垂线必与a 或b 相交。如果它与a 相交于A 点，则将推出AO _a ＝AO 以及AO _a ＝AO _b ，因之AO＝AO _b ，即A 也是b 上一点，此与定理的假设相矛盾 ^（5） 。

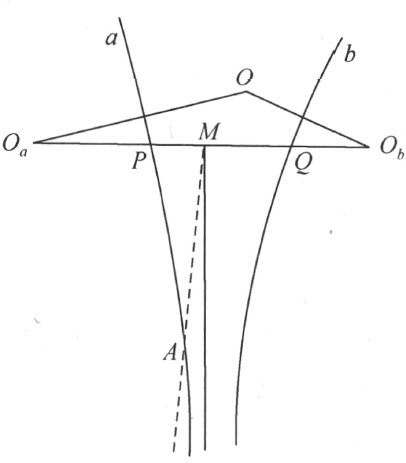
附图　12

引理5 　如果a ，b 和c 是三条直线，它们有公共端点ω ，且关于此三直线的反射分别用S_a ，S_b 和S_c 来表示。于是存在具有端点ω 的一直线d ，而使关于a ，b ，c 陆续所作反射的结果与关于d 所作反射S _d 相同，亦即

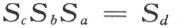
证明 　首先假设直线b 位于直线a 与c 所成平面区域的内部，设O 为b 上一点且O 关于a 和c 的反射映像分别记作O _a 和O _c 。联结线段O _a O _c 的中点与端点ω 的直线d ，于是自引理4，O _a 和O _c 是关于d 的反射映像，这样运算S _d S _c S _b S _a 将使点O _a 不动，同时也使O _a 与ω 所连直线不动。因为这个运算包含四个反射，合同定理证明它是一个恒等式，故得断言。

其次，当直线c 与a 互相重合时，引理5的正确性亦可立即得出。设直线b ′是直线b 关于a 的反射映象，且关于b ′的反射用S _{b ′} 来表示，于是公式

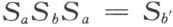
的正确性能立即看出。

最后，如果直线c 位于直线a 和b 所成平面区域的内部，则由本证明的第一部分，存在一直线d ′而有公式

设用d 表示d ′关于a 的反射映象，则由证明的第二部分

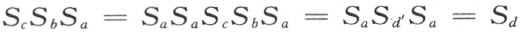
因之，引理5得以完全证明。

§2　端点的加法

已知一直线，它的端点用0和∞来表示，在这直线（0，∞）上取一点O ，并于此点作垂线。又此垂线的端点用＋1和-1来表示（附图13）。

附图　13

今规定两个端点的加法于下：

定义 　设α ，β 是任意两个与∞不同的端点。并设O _α 为O 点关于直线（α ，∞）的反射映像，O _β 为O 点关于直线（β ，∞）的反射映像。联结线段O _α O _β 的中点和端点∞。这样所作直线的另一端点叫做两端点α 和β 之和，且用α ＋β 来表示。

如果以α 为端点的半线关于直线（0，∞）作反射，则结果所得半线的端点将用-α 表示。

甚易看出下列等式的正确性：

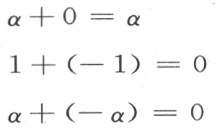
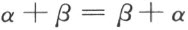
最后一个等式表示端点加法的交换律。

为了证明端点加法的结合律，今用S ₀ ，S _α ，S _β 分别表示关于直线（0，∞），（α ，∞）和（β ，∞）的反射；自§1引理5，存在一直线（σ ，∞）使得公式

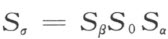
成立，其中S _σ 是关于这条直线的反射。由于运算S _β S ₀ S _α ，点O _α 变成点O _β ，因此O _β 必是O _α 关于直线（σ ，∞）的反射映象。故有σ ＝α ＋β ，亦即

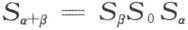
成立。

如果γ 也表示一个端点，则重复利用前面所推出的公式，即得

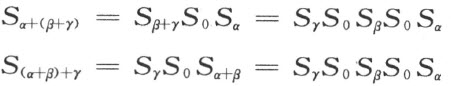
故有

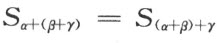
因此，

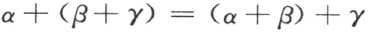
上面所推导的公式

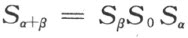
同时还指出所给的两个端点和作图与直线（0，∞）上点O 的选择无关。因此，如果O ′表示直线（0，∞）上与点O 不同的任何点，且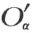 和 分别表示点O ′关于直线（α ，∞）和（β ，∞）的反射映像，则线段 的中垂线就是直线（α ＋β ，∞）。

这里我们将引入研究§4所必需的其他结果。

如果直线（α ，∞）关于直线（β ，∞）作反射，则所得反射直线是（2β -α ，∞）。

事实上，如果P 是直线（α ，∞）关于直线（β ，∞）反射所得直线上的任一点，则连续经过反射

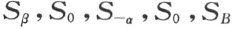
P 点显然不变。然而由于上面公式

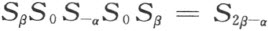
即，复合运算相当于关于直线（2β -α ，∞）的一个反射，因此P 点必在这最后一直线上。

§3　端点的乘法

我们规定两个端点的积如下：

定义 　如果一个端点与端点＋1位于直线（0，∞）同侧，则称为正；如果一个端点与端点-1位于直线（0，∞）同侧，则称为负。

现在设有与（0，∞）不同的任意两个端点α 和β 。两直线（α ，-α ）和（β ，-β ）将与直线（0，∞）垂直（附图14），它们与直线（0，∞）分别交于A 和B ，于直线（0，∞）上取线段BC ＝OA ，且使O 到A 的方向与B 到C 的方向相同，于C 点作直线（0，∞）的垂线，并依据两端点α ，β 均是正以及均是负或者一正和一负而分别称这垂线的正端点或负端点为两端点 α 和 β 之积 αβ 。

最后假设

附图　14

自线段合同公理Ⅲ_1～3 立即得知下面公式

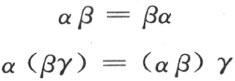
成立。即端点乘法交换律和结合律均成立。

容易看出公式

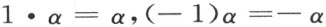
也成立。并且一直线的端点α ，β 适合方程

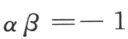
则此直线必过点O 。

除法的可能性立即变得明显。再者，对于每个正端点π常存在一个正端点（并且也存在一个负端点），它的平方等于端点π，故此端点能用 表示。

为了证明端点运算的分配律，首先从端点β 和γ 利用§2的方法作出端点β ＋γ （附图15）。其次，再按照上面所说的方法确定端点αβ ，αγ 和α （β ＋γ ）。可以看出上面的作图恒同于平面到自身的一个合同映射，它是由线段OA 沿直线（0，∞）所产生的一个平移。

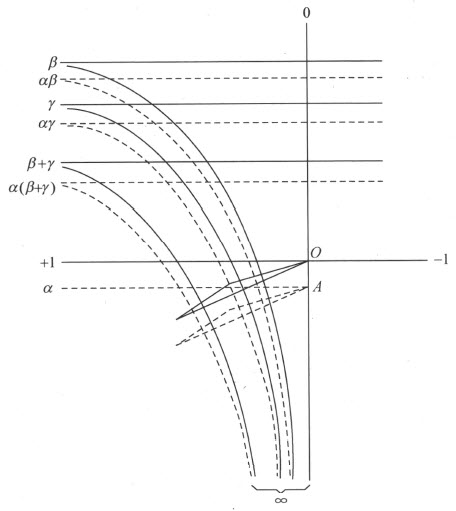
附图　15

从§2的注意，自点A 代替点O 作两个端点αβ 及αγ 之和的作图是允许的。于是可得这个和实际上就是端点α （β ＋γ ），即公式

是正确的。

§4　点的方程

自§2～§3我们已看出端点的运算律与寻常数的运算完全相同，因而几何学的建立并无多大困难，这可用下面的方法来完成。

如果ξ ，η 是任意直线的端点，并且将端点

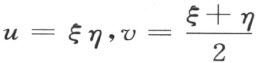
叫做这直线的坐标，于是下面的基本命题成立：

设α ，β ，γ 是三个端点，且具有端点4αγ -β ² 为正的一个特性，则坐标u ，v 适合方程

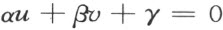
的所有直线将过同一点。

证明 　按照§2～§3，我们作端点

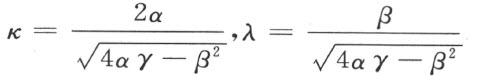
于是由坐标u ，v 的意义和在α ≠0的情况下，上面的方程可以写作如下形式

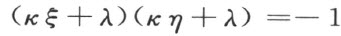
今考虑一个任意变动端点ω 的变换

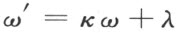
为了作这个变换，首先考虑两个变换

关于第一个变换，即动端点ω 和一个常端点κ 的乘法，由§3它恒同于平面内由一个与κ 有关的线段沿直线（0，∞）所作的平移。

至于第二个变换，亦即常端点λ 和一个动端点ω 的加法。它对应着仅与λ 有关的，平面到自身的一个运动，也就是平面关于端点∞的旋转。

为了证明，按照§2的结论，直线（ω ，∞）关于直线（0，∞）的反射是直线（-ω ，∞）。再者，它经过关于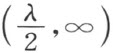 的反射变为直线（ω ＋λ ，∞）。于是端点λ 和动端点ω 的加法恒等于就两直线（0，∞）和 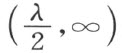连续所作的两次反射。

由上面所证可以看出：如果ξ ，η 是一直线的两个端点，则经过与κ ，λ 有关的平面的运动，所产生直线的端点将由

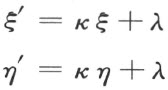
来表示，于是由上面方程

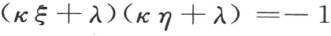
将得到关于端点ξ ′，η ′的方程

由§3的一个注记，这个关系表示已知直线经过点O 的条件，于是可见适合原方程

的所有直线（ξ ，η ）将过同一个点。所提定理得以完全证明。

已经看出在线坐标系下点的方程是一次的，容易导出关于一对直线的巴斯噶定理的特殊情形和成透视位置的三角形的德沙格定理以及射影几何的其他定理。鲍雅义-罗巴切夫斯基几何中一些熟知的公式也可无困难地导出。于是仅借助公理Ⅰ～Ⅳ这种几何学即可完全建立 ^（6） 。

————————————————————

（1） 指本书第一版，见第十二版的中译本序言。——译者注

（2） 同时也曾就不用公理Ⅳ来表示鲍雅义-罗巴切夫斯基几何特性的相应问题进行研究。其次，德恩（M. Dehn）在他的文章“论球面三角形的面积”（Über den Inhalt sphärischer Dreiecke, Math Ann. Bd. 60）就曾不用连续公理展开平面椭圆几何的面积理论的研究。以后海森伯格（G. Hessenberg）在他的文章“椭圆几何的基础”（Begründung der elliptische Geometrie, Math. Ann. Bd. 61）中，于同样假设下成功地给出平面椭圆几何交点定理的证明。最后杰尔姆斯勒（J. Hjelmslev）在他的文章“平面几何的新基础”（Neue Begründung der ebenen Geometrie, Math. Ann. Bd. 64）中不用连续公理甚至不用交线和不交线的任何假设即可建立平面几何。

（3） 公理Ⅰ～Ⅲ系按目前这一版的形式列出。

（4） 这个证明可以由高斯所给的方法得出，参看薄罗那-李勃曼（Bonola-Liebmann）《非欧几何》（Die nichteuk-lidische Geometrie. Leipzig, 1908和1921, §32）。

（此书有卡斯罗（H. S. Carslaw）英译本。——译者注）

（5） 此结论本质上与罗巴切夫斯基的一个结果相一致。可参看他的《利用平行线完备理论的几何新原理》（Neue Anfangsgründe der Geometrie mit einer vollständigen Theorie der Parallellinen）一书。

（此书有哈尔斯泰（G. B. Halsted）的英译本。——译者注）

（6） 作为本附录开始（参见此处 ）所提文献的补充，今列出下列较新的教材：

巴赫曼（F. Bachmann）《由反射概念所建立的几何》（Aufbau der Geometrie aus dem Spiegelungsbegriff, Berlin-Göttingen-Heidelberg, 1959）；

伯尔苏克和斯兹密尔鲁（K. Borsuk und W. Szmielew）《几何基础》（Podstawy Geometrii），此书有英译本，见玛尔魁（E. Marquit）《几何基础》（Foundations of Geometry, Amsterdam, 1960）。

下述文章也可作参考：

皮夹士（W. Pejas）“绝对几何的希尔伯特公理体系的模型”（Die Modelle des Hilbertschen Axiomensystems der absoluten Geometrie, Math. Ann., Bd. 143, 212—235（1961））。

巴赫曼“平行问题”（Zur Parallelenfrage, Abh. Math. Seminar University Hamburg. Bd. 27, 173—192（1964））。