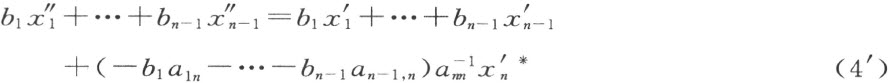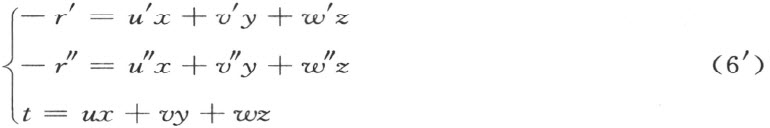德文第七版的俄译本注解
Index
以希尔伯特命名的数学名词多如牛毛,有些连希尔伯特本人都不知道,比如有一次,希尔伯特曾问系里的同事:“请问什么叫做希尔伯特空间?”

本书第二译者朱鼎勋(1921—1985)教授
【1】在德文原书中,这一段和以后某些段开始时,有一个标题“Erklärung”,这个字的意义是“说明”或“声明”。我们将按照以后每一段的意义,在译本中或者译成“定义”或者译成“说明”。
【2】这里和此后所说的平面几何,它的平面是看做独立存在 的。这几何只有点和直线作为它的元素,而且只有对应于它们的(即谈到有关于平面的组成的)一部分公理被规定了。
【3】“Verknüpfung”这个德文名词,一般译作“关联”或“结合”。有时也译成“从属”或“属于”。
如同前面(第xix~xx页)已经指出的,我们把某种关系了解为存在在点和直线之间的,和在点和平面之间的(我们还不加以区别地说:“一点同一直线相关联”,或“一直线同一点相关联”等等)。
这种关系的直接定义并没有给出,只是在第一组公理中说明了这种关系的所有的性质。因此,可以把第一组公理看做是关联概念的间接定义。
我们还没有提到的直线同平面相关联,原文中对此给出了一条直接的 定义:若一直线a 的每一点同一平面α 相关联,则直线a 同平面α 相关联。
【4】我们来指出,如何只从公理推出定理1和定理2中的所列举的五个命题。
定理1的证明
1.用反证法(利用Ⅰ2 )
2.若两平面有一个公共点A ,则还有另一个公共点B (Ⅰ7 );然后存在直线AB (Ⅰ1 ),并且这直线和它的所有的点都同这两平面的每一个相关联(Ⅰ6 ),这两平面在AB 外不能再有公共点,因为否则它们就将是同一个平面(Ⅰ5 )。
3.用反证法(利用Ⅰ6 )。
定理2的证明
1.给定了一直线a 和线外的一点A 。在a 上取B 和C (Ⅰ3 ),并且作平面ABC (Ⅰ4 )。直线a 和它的所有的点都同平面ABC 相关联(Ⅰ6 )。这平面是唯一的(Ⅰ5 )。
2.给定了有一公共点C 的两直线a 和b ,在a 上再取一点A ,在b 上再取一点B (Ⅰ3 )。作平面ABC (Ⅰ4 )。直线a 与b 同平面ABC 相关联(Ⅰ6 )。这平面是唯一的(Ⅰ5 )。
【5】在希尔伯特的原书中,图没有编号码,我们在译文中编上号码。将来援引图时,把引进的号码放在圆括弧里。
【6】我们来证明,直线a 不可能通过那分别在线段AB ,BC 和CA 内的L,M,N 三点。若假设可能,则得到矛盾如下:
L,M,N 三点中,必有一点在其他两点之间(参看定理4,§4)。设这一点是M (注图1)。然后考虑三角形ALN 和直线a′ =BC 。因为a′ 通过在L 和N 之间的点M ,那么它应该或者通过线段AL 的一个点,或者通过线段AN 的一个点(公理Ⅱ4 )。但是根据公理Ⅱ3 ,a′ 和直线AL 的交点B 在线段AL 外(因L 在A 和B 之间)。这就是说,a′ 通过线段AN 的一点,即C 在A 和N 之间。因此(公理Ⅱ3 ),N 不在A 和C 之间,与假设矛盾。
注图 1
我们只援引第二组公理来完成证明,第二组公理包含关于“在…之间”这概念的所有应有的知识,因而在说明的过程中完全避免了利用我们对于直线上的点的顺序的直观。
【7】对于三角形AEC 和直线BF 应用公理Ⅱ4 ;因为B 在A 和C 之间,而F 在EC 之外(从公理Ⅱ3 ),所以直线BF 交线段 AE 于一点G 。再对于三角形BFC 和直线AE 应用公理Ⅱ4 ;因为A 在BC 之外(从公理Ⅱ3 ),而E 在C 和F 之间,所以G 在B 和F 之间,即在线段BF 内。因此(从公理Ⅱ3 ),F 在GB 之外。再对于三角形BDG 和直线CF 应用公理Ⅱ4 ;因为F 在BG 之外,而C 在B 和D 之间,所以直线CF 和线段GD 有一公共点H 。
【8】对于三角形AGD 和直线EH 应用公理Ⅱ4 。
【9】对于三角形AGD 和直线CF 应用公理Ⅱ4 ,得知H 在线段GD 内。直线FH 交三角形BGD 的边GD ,而不交边GB ,是已经证明了的。因此,它交边BD ,即C 落在B 和D 之间。
【10】事实上,最后一种情形是不可能出现的。1)Q 在P 和R 之间,2)S 在P 和R 之间,3)P 在Q 和S 之间,从这三个排列法,是要产生矛盾的。因为从1)和3),根据论断1,即得P 和Q 在S 和R 之间,但这和2)矛盾。
【11】在证明定理6之前,我们先把定理叙述得更加明确:一直线上的给定了的任意n 个点,能够编起号码1,2,…,n 来,使得它们中的任意一点在其他两点之间,当且仅当前一点的号码在后两点的号码之间。
n =4时的定理已经证明了(定理5)。要用数学归纳法来证明n 是任意值时的定理,我们假设n -1时的定理已经证明了。
1.从给定了的n 个点中,恒能挑选出两个点,使得其余的n-2个点都在这两个点之间。理由如下。我们先从给定了的n 个点中,挑选出具有下述性质的两个点A 和C :它们之间含有尽可能多的其余的点。我们断定,所有的其余的n-2个点都在A 和C 之间。
否则,设这n 个点中的一点D 在AC 之外,根据定理4,或者A 在C 和D 之间,或者C 在A 和D 之间。为确定起见,设是后者。然后,从定理5的证明中的项2,在A 和C 之间的每一点B 也在A 和D 之间。结果,A 和D 之间含有在A 和C 之间的所有的点,而且此外还含有C 。这指出给定了的n 个点中的点,在A 和D 之间的比在A 和C 之间更多;这与我们所挑选的A 和C 矛盾。
这矛盾证明了我们的论断。
2.它们从给定了的n 个点中挑选出两个点A 和C ,使得他们之间含有所有的其余的点。我们断定,若B 和D 是其余的点中的任意两个点,则A 和C 都在BD 之外。理由如下。根据定理5,能够指出所考虑的四个点的确定顺序,而且现在因为B 和D 在A 和C 之间,这顺序只能写成ABDC 或ADBC (或者颠倒的写)。在这两种情形下,A 和C 都在BD 之外。
3.设A 和C 是这给定了的n 个点中的两点,而且它们之间含有所有的其余的点。因为假设n -1时的定理6已经证明了,就能够把所有的给定了的、除C 之外的点,编上号码,使得它们满足定理的要求。设编了号码的点是A 1 ,A 2 ,…,A n -1 我们断定,点A 或者和A l 重合,或者和A n -1 重合。因为,否则它就要在两个编了号码的点之间,和上文的论断2矛盾。
可以认为A ≡A 1 ;因为,否则只要把号码颠倒过来。现在把C 编上号码n ,令C =A n ;而且证明这样的编号满足定理的要求:对于任意三点来说,一点的号码在其他两点的号码之间时,这点也在其他两点之间。若所取的三点中没有C ,这是成立的,因为定理的要求是被编号的A 1 ,A 2 ,…,A n -1 满足了的。若所取的三点是A i ,A j ,A n (A n ≡C ),其中i <j <n ,则必须证明A j 在A i 和A n 之间。在i =1时,显然;因为A l ≡A ,A n ≡C 。若>1,则A i 在Ai 和A j 之间;此外,A j 在A 1 和A n 之间;因此,从定理5的证明中的论断2,得知A j 在A i 和A n 之间。
定理6证明了。定理6是严格地从公理系统推证出来的;而它所表出的直线上的点的性质,按照直观的说法,也就是说:直线上的点沿着直线一个跟着一个排列着。所以定理6可以说是总结了直线上的点的顺序关系。
【12】我们来证明,一直线上任意两点(用A 0 和 表示)之间有无限多个点。按照定理3,A 0 和
表示)之间有无限多个点。按照定理3,A 0 和 之间有A l 。根据同一条定理,A 1 和
之间有A l 。根据同一条定理,A 1 和 之间有点A 2 ,A 2 和
之间有点A 2 ,A 2 和 之间有点A 3 ,等等,A n 和
之间有点A 3 ,等等,A n 和 之间有点A n +1 。从点A 1 的求法,A 1 在A 0 和
之间有点A n +1 。从点A 1 的求法,A 1 在A 0 和 之间。为了使我们看出所有的其余的点A k (k =2,3,…)都在A 0 和
之间。为了使我们看出所有的其余的点A k (k =2,3,…)都在A 0 和 之间,只要证明下述论断:若点A n 在A 0 和
之间,只要证明下述论断:若点A n 在A 0 和 之间,则点A n +1 也在A 0 和
之间,则点A n +1 也在A 0 和 之间。从定理5证明中的论断2,得知现在的论断的正确性。
之间。从定理5证明中的论断2,得知现在的论断的正确性。
【13】我们固定定理中所谈到的两个区域如下:在平面α 上取不在直线a 上的任意一点A 。平面α 上所有的不在直线a 上的点M 分成两组。把使得线段MA 不和直线a 相交的,列入第一组;把所有的其余的点列入第二组。
现在,定理8的证明简化为下列两条论断的证明:
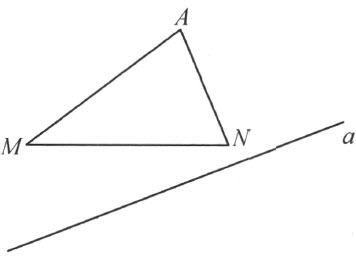
1.同一个区域的任意两点 M 和 N 所决定的线段 MN 不和直线 a 相交 (注图2)。
注图 2
实际有两种可能:
a)点M 和N 都在第一区域中;即直线a 既不交线段MA ,又不交线段NA (当两点中的一点,例如N ,特别和A 重合时,即当我们所讨论的只是一条线段时,我们的论断显然正确)。然后从公理Ⅱ4 ,立刻得知:只要点A,M,N 不在一直线上,则线路MN 不交a 。
若A,M,N 在一直线上,则从定理1得知;这直线或者不交直线a ,或者交直线a 于一个确定的点P 。在前者情形下,我们的论断已经证明了。在后者情形下,根据假设,点P 即不在A 和M 之间,又不在A 和N 之间。所以,若根据定理5把这四个点按照它们在直线上的排列顺序写出来,则点P 必定在极端,即不在M 和N 之间。
b)点M 和N 都在第二区域中,即直线a 既交线段AM ,又交线段AN 。若点A,M,N 不在一直线上,根据公理Ⅱ4 的推论(注解[6]所证明的),则线段MN 不交直线a 。若点A,M,N 在一直线上,而且P 是这直线和a 的交点,则P 在A 和M 之间,又在A 和N 之间。所以这四点在直线上的排列顺序(定理5)必定如此:P 把A 从M 和N 隔开,即APMN 或AP NM。因为P 在线段MN 外,线段MN 显然和直线a 不交。
2.连接不同区域的两点 M 和 N 的线段 ,和直线 a 相交 。
实际上,设M 是和A 在同一个区域中的点(注图3;当点M 和A 重合时的情形,因为简单,从略)。设点M,N ,和A 不在一直线上。因为直线a 交线段AN ,而不交线段AM ,从公理Ⅱ4 ,则直线a 交线段MN 。
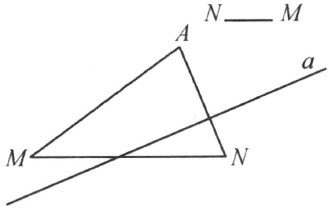
注图 3
现在设点A,M,N 在一直线上。直线a 和线段AN 的交点P 在A 和N 之间,而且在AM 之外,要按照这四个点在直线上先后顺序把它们写出来的时候(定理5),应该把A 和M 放在P 的同侧,而把A 和N 放在P 的异侧。这只有两种可能:AMPN 和MAPN ;在这两种情形下,P 都在M 和N 之间。
我们的论断都已经证明了。我们用下述简单的定理来做补充:若M 和N 在a 的同一侧,则线段MN 的每一点L 都在a 的这一侧。若不然,则直线MN 上有a 的一点P ,既在M 和L 之间,又在N 和L 之间。所以点的顺序是LPMN ,或LPNM ;二者都和L 在M 和N 之间矛盾。
【14】设直线a 上给定了一点O 。在直线a 上取任意另一点A ,并且把直线a 上的所有的点(点O 以外的)分成两组如下:若一个点和A 所作成的线段不含有点O ,我们就把这个点列入第一组;把所有的其余的点,即它们和A 所作成的线段含有点O 的,列入第二组。我们来证明下面两个论断:
1.若点 M 和 N 属于同一组 ,则点 O 不在线段 MN 内 。
这里能有两种情形。a)点M 和N 属于第一组。那么,根据定理5所建立的顺序,写下点A,M,N,O 的排列的时候,点O 应该放在端上;因为否则点O 将要或者在A 和M 之间,或者在A 和N 之间,都和假设相反。因此,在这种情形下,点O 应该在线段MN 外。b)点M 和N 属于第二组,即点O 既在A 和M 之间,又在A 和N 之间。在这种情形下,从定理5,点的排列只可能如下:AOMN ,AONM ,即点O 必定不在线段MN 内。
2.若线段 MN 的两端点不属于同一组 ,则点 O 在线段 MN 内 。
为确定起见,设M 属于第二组,即点O 在M 和A 之间。因为点O 不在N 和A 之间,则从定理5这四个点的排列可以是下列两种之一:MOAN ,MONA 。这都证明了我们的论断。
这些论断指出:点的分成两组完全被点O 决定了,和点A 的选择绝对无关。每一组叫做一条射线。因此,直线上的任意一点O 分直线(除去点O )成两条射线。我们说:在同一条射线上的点是在点O 的一侧。
【15】在定理9的证明中,我们要利用角的概念,而且要援引本书上正文中的注解[14]中所证明的论断。虽然在正文中,角的定义和所提到的论断都放在合同公理Ⅲ3 之后,但是这定义和这些论断的证明都未用合同公理(如同希尔伯特在原文中所指出的)。所以,我们用角的概念时,并未超出第一组公理和第二组公理的范围。
为简便起见,在本条注解中将要用“折线段”和“多边形”等名词,把它们了解作简单的折线段和简单的多边形。
在证明定理9的论断之前,我们先提出一些引理。
引理Ⅰ 凡平面α 中的,而不属于多边形β 的点,被这多边形分成两组如下。一组的点具有下述性质:从这组的任一点出发的每一条射线都穿过β 偶数次;另一组的点具有下述性质:从这组的任一点出发的每一条射线都穿过β 奇数次。
按照下列规律来计算一射线或直线穿过多边形的次数:所谓穿过一次是指:
1)射线和作为多边形的一条边的线段的一个交点;或者
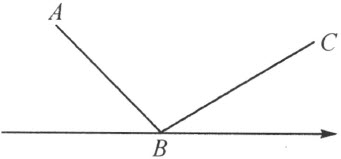
2)射线穿过多边形的一个顶点B ,而且同时多边形的从这顶点出发的两条边BA 和BC 在这射线的异侧(注图4,但非注图5);或者
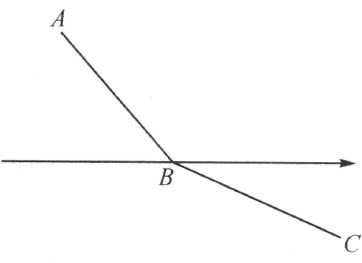
注图 4
注图 5
3)射线穿过多边形的两个相邻的顶点F 和G ,而且多边形的紧接着这两个顶点的其他两条边在这射线的异侧(注图6,但非注图7)。
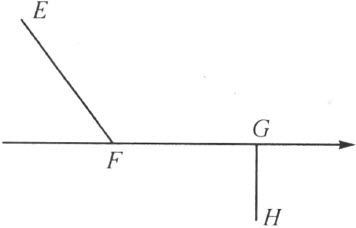
注图 6
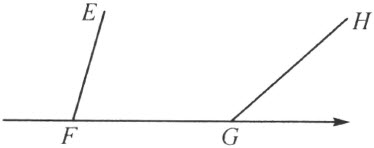
注图 7
在证明这引理时,我们将用“角”这个名词。所谓角,是指从同一个(不在β 上的)点O 出发的射线偶,也包括两条射线和点O 作成一条直线的情形,即“平”角的情形。所谓这种角的内点,是指角的边所在的那直线的确定的一侧(无论那一侧)的点。
从“射线穿过多边形”这名词的定义,即得下列结果:若角∠(h ,k )的一边,例如h ,穿过多边形β ,那么多边形的两条边(情形2和情形3),或者多边形的一条边上的两条线段(情形1),紧接着多边形上的而又在射线h 上的点(或边)的,落在直线h 的异侧。从多边形上消去射线h 或k 穿过多边形处所有的点(情形1和情形2),和所有如同FG (注图6)那类的线段(情形3)。多边形因而分解成若干个片段;而每一片段或者整个的在∠(h ,k )内(片段可能有一些部分在边上),或者整个的在∠(h ,k )外(片段可能有一些部分在边上)。同时,邻近的两个片段之中,恒有一个在∠(h ,k )内,一个在该角外,因为多边形是封闭的,片段的总数只能够是偶数。所以射线偶h 和k 穿过多边形β 的次数也应该是偶数。因此得:按照射线k 穿过多边形偶数次或奇数次,射线k 也分别穿过这多边形偶数次或奇数次。
这样,引理1得证。
若从一点出发的射线穿过给定了的一个多边形奇数次,这样的点就叫做这多边形的内点。平面上所有的其余的点,当然除去这多边形本身上的点,都叫做这多边形的外点。我们采用的这个定义是从卡岗(B. Φ. Κaгaн)的《几何基础》(Oδecca, 1905)里得来的。现在要证明的本定理,在卡岗的书里也用一些不同的方式证明了。
现在注意下述事实。设从一点O (不在多边形β 上的)出发的某一射线h 穿过多边形β 有n 次。再设射线h 和多边形β 上的共点和共边如下:多边形的边和射线h 相交的k 个交点(情形1);多边形的ι 个顶点,而且在其中每一个顶点处的多边形的两条边在射线的异侧(注图4);多边形的p 个顶点,而且在其中每一个顶点处的多边形的两条边在h的同一侧(注图5);多边形的m =n -ι -k 条边,而且其中每一条边和它的相邻两条边的位置如同注图6中所表出的;最后,多边形的q 条边,而且其中每一条边和它的相邻两边的位置如同注图7中所表出的。考虑由下列的点所组成的点集μ :点O ,在射线h 上的多边形β 的m +q 条边的2m +2q 个端点,多边形β 和射线h 所共有的k 个交点和ι +p 个顶点。根据定理6,点集μ 的N =k +ι +p +2(m +q )+1个点按完全确定的顺序分布在射线h 上。取定其中最靠近点O 的点(即在点O 和点集μ 的任意另一点之间的点),作第一个点之后,就能够把这N 个点编上号码。完全一样地,能够把射线h 穿过多边形β 的所有的n 次编上号码。若射线h 穿过多边形β 的第i 次处是一条线段。即β 的一条边(注图6),则F 和G 是第i 次穿过的端点;若第i 次的穿过只是一个点,则这个点就还用两个字母F 和G 表出(注图8)。设点集μ 已在射线h 上如此排好了顺序,使得点F 1 紧靠在点F 之前,而点G 1 紧跟在点G 之后。于是我们得到下述结论:
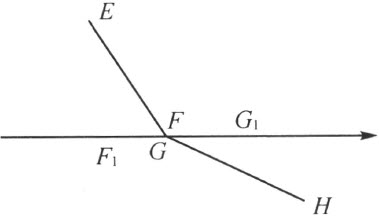
注图 8
引理Ⅱ 在射线h 上,紧靠在它穿过多边形的每一次之前,和紧跟在每一次之后,都各有一条线段(分别是F 1 F 和GG 1 ),不含有多边形的点。
我们还指出下述事实:
推论1 F 1 F 和 GG 1 这两条线段中的每一条的所有的点 ,即和多边形无公共点的线段的所有的点 ,或者都都在多边形内 ,或者都在多边形外 。
推论2 或者线段 F 1 F 的点都在 β 内 ,而线段 GG 1 的点都在 β 外 ,或者反之 。
我们来证明这些推论。任意在线段F 1 F 上取两个点M 和N ,在线段GG 1 上取一点P ,并且考虑分别从这三个点出发的射线MG 1 ,NG 1 和PG 1 。因为线段MN 不含有β 的点,射线MG 1 穿过β 的次数等于射线NG 1 穿过β 的次数;这就证明了第一条推论。因为在线段MP 上的线段FG 的点相当于射线穿过β 一次,又因为,除了线段FG 的点和它的端点之外,线段MP 上不再含有多边形β 的点,那么射线MG 1 比射线PG 1 显然多穿过β 一次;这就证明了第二条推论。
现在易证:多边形 β 的平面上有 β 的内点 ,也有 β 的外点 。为了证明,考虑交多边形的一条边于一点G 的一条直线a 。根据刚才的证明,直线a 上有两条线段F 1 F 和GG 1 ,其中一条的点在β 内,另一条的点在β 外。
引理Ⅲ 一条直线或者不穿过一个三角形,或者穿过两次。
实际上,任意一条直线不能交三角形的每一条边的直线多于一次。所以一条直线穿过一个三角形的次数不能大于三。然而,当用任意一点(不在三角形上的)把直线分成两条射线时,我们就看出这穿过次数应该是偶数,即只能够是0或2。因此,从三角形的内点出发的射线应该恰好穿过这三角形一次。
引理Ⅳ 一点在一个三角形内,当且仅当这点在通过这三角形的任意一个顶点的一条贯线上。
若一条线段连接一个三角形的任意一个顶点和对边上的一点,这线段就叫做三角形的一条贯线 (注图9)。
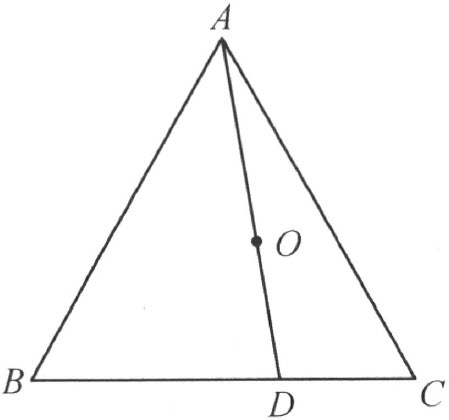
注图 9
必要条件。实际上,设点O 在三角形ABC 内。考虑连接点O 和三角形的一个顶点(为确定起见,见A 表示)的直线OA 。从引理Ⅲ得知直线OA 应该穿过三角形ABC 两次;因为若它不穿过这三角形,则它的所有的点,包含点O 在内,将都不在这三角形内,这是和假设矛盾的。直线每穿过三角形一次时,它至少交三角形的一条边。直线OA 穿过点A 时,就是它交直线AB 和AC ,而且不能和后两直线的任意一条重合;因为否则它就一次都不穿过三角形。所以直线OA 第二次穿过三角形ABC 时,它应该交线段BC 。设交点是D 。点O 应该在贯线AD 上,因为否则射线OA 上将含有点A 和D ,将穿过三角形两次,也就是说,点O 将在三角形外。
充分条件。实际上,若点O 在贯线AD 上(贯线AD 是连接任意一个用A 表示的顶点和对边BC 上的一点D 的线段),则点A 和D 在O 的异侧,所以从点O 出发的射线OD 穿过三角形ABC 只一次,即点O 在三角形ABC 内。
推论 在三角形 ABC 中作一条贯线 AD 。在三角形 ABD (或 ACD )内的任意一点 ,也必在三角形 ABC 内 (注图10)。
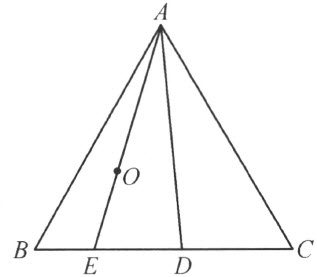
注图 10
实际上,设点O 在三角形ABD 内。由于引理Ⅳ,点O 现在应该在某一条贯线AE 上,此外的点E 在线段DB 上。由于定理5,点C,D,E,B 的排列顺序应该像这里所写下的(或者相反的顺序),即点E应该在线段BC 上;因而线段AE 也是三角形ABC 的一条贯线。所以,由于引理Ⅳ,点O 在三角形ABC 内。
若点O 在三角形ACD 内,命题的证明相似。
引理V 若点A 在多边形β 内(外),而且线段AB 和多边形β 无公共点,则这线段的所有的点都在β 内(外)。这线段的端点B 可以在β 内(外),也可以在这多边形上。
设射线BA 第一次(参看引理Ⅰ后所提的注意)遇多边形β 于点M ,而射线AB 第一次遇β 于点N 。若这两条射线的某一条,例如BA 不遇多边形β ,则在这射线上取任意一点当做点M ,只要使得A 在线段BM 内。点N 特别可以和点B 重合。由于定理5,线段AB ,点A ,不和N 重合时的点B ,都在线段MN 内。由于引理Ⅱ的推论Ⅰ,线段MN 的点或者都在β 内,或者都在β 外。它们究竟在那里,由它们之中的一点的位置,例如A 的位置来确定。
引理Ⅵ 若点A 在多边形β 内(外),而且可能除点N 之外,折线段ABC …MN 和这多边形无公共点,则这折线段的点没有一个在多边形β 外(内)。
对于线段AB ,BC ,…,MN ,继续地应用引理V,就得到本引理的证明。
现在考虑具有下述性质的任意一条封闭折线段б 和一个三角形ABC ;若折线段б 的某一条线段PQ 上有点在三角形内,则线段PQ (端点计算在内)和三角形的公共点只能在边AC 上(顶点A 和C 计算在内)。在这情形下,下述论断成立:
引理Ⅶ 只要三角形ABC 内含有折线段б 的一点O ,而非端点,则这三角形内也至少含有这折线段б 的一个端点。
引理Ⅷ 在这三角形ABC 的边AB 上能找得一点P ,使得在三角形PBC 内和在它的边PC 上没有折线段б 上的点。
证明引理Ⅷ 设折线段б 的一点O 在三角形ABC 内,而且设这点属于这折线段的线段PQ 。若线段PQ 和三角形ABC 无公共点,则由于引理V,折线段б 的端点P 和Q 或者在三角形ABC 内,或者在三角形本身上,因而在边AC 上。但是P 和Q 这两个端点显然不能都在AC 上,因为否则点O 将也在AC 上。因而至少P 和Q 这两个端点的一个在三角形内。现在设线段PQ 和三角形ABC 有公共点(注图11)。根据引理的条件,线段PQ 只能和这三角形的边AC 相交。用字母R 表示这交点。因为R 在P 和Q 之间,由于定理5,它不能同时在PO 和OQ 这两条线段内。设点R 在线段PO 内。在这种情形下,由于引理V,折线段б 的端点Q 在三角形ABC 内。
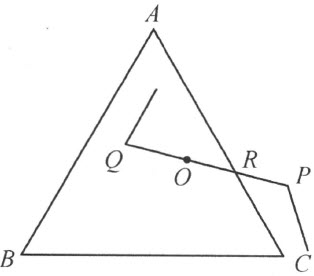
注图 11
证明引理Ⅷ 设折线段б 有k 个端点在三角形ABC 内和它的边AC 上。用M 1 ,M 2 ,…,M k 来表示这些顶点(注图12)。从点C 作射线CM l ,CM 2 ,…,CM k 。这些射线中有些可能互相重合。有的也可能和射线AC 重合,而其余的因为通过三角形ABC 的内点,由于引理Ⅳ,必交线段AB 。设交点是D,E,F, …,K 。点A,B 和点D,E,F, …,K 都在直线AB 上,所以由于定理6,它们有一定的先后顺序,其中一个极端是点A ,另一个是点B 。作在K 和B 之间的一点P ,此处设K 是最邻近B 的点。因为A,D,E,F, …,K 都在线段PB 外,点M i 中没有一个能在三角形PCB 的从顶点C 到边PB 的贯线上,因而没有一个能是三角形PCB 的内点(引理Ⅳ)。而三角形PCB 的每一个内点O ,由于引理Ⅳ的推论,也是三角形ABC 的一个内点。所以折线段б 没有一个顶点在三角形PCB 内。
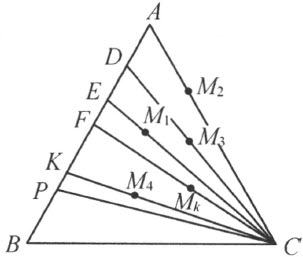
注图 12
三角形PCB 有一条边BC 和三角形ABC 的相同;另一条边PB 是三角形ABC 的边AB 的一部分。应用引理Ⅶ到三角形PBC (同时PC 替代AC 的地位),即知在这三角形内没有折线段б 的点。要证实在边PC 上也没有折线段б 的点,只要同样地考虑三角形P′CB ,此处的P′ 在K 和P 之间。
引理Ⅸ 若PQ 是多边形β 的一条边,C 是线段PQ 内的一点,A 和B 或者都是多边形β 的内点,或者都是外点,而且线段AC 和BC 都和β 无公共点,则线段AC 和BC 在直线PQ 的同一侧。
假设结论不对(注图13)。延长线段AC 到相反的一侧。由于引理Ⅱ,在延长线上能取一线段CA′ ,不含有β 的点;而且若线段AC 的点在β 内,则线段CA′ 的点在β 外,或者反之(引理Ⅱ的推论2)。由于我们的假设,射线CA′ 和CB 在直线PQ 的同一侧。应用引理Ⅷ到三角形A′BC ,而且用边A′B 替代[注图12中的]AC 的地位,在线段CA′ 上能求得一点D ,使得线段BD 不交多边形β ,因而点B 和D 或者都在β 内,或者都在β 外(引理V)。所以,若点A 在β 内(外),则点D (引理Ⅱ的推论2),而且因而点B ,应该在β 外(内),这与引理的条件矛盾。于是引理证毕。
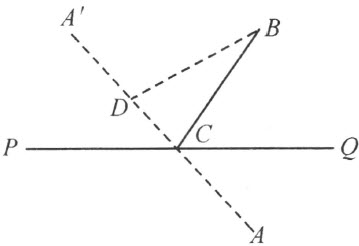
注图 13
此后,我们总把任意一条非封闭的折线,连接一点A 到任意一点B 的,叫做从点A 引到点B 的一条道路 。
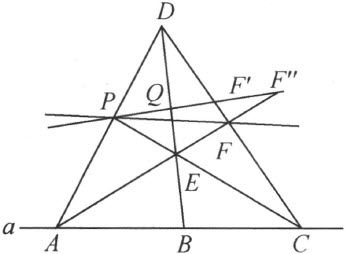
引理 Ⅹ 从不在一条(封闭的或非封闭的)折线б 上的任意一点A 到这折线上的任意一点B ,恒能引一条和折线б 无公共点的道路。
从点A 作任意一条射线,穿过折线б 。设M 是这射线和折线б 相遇的第一个点。线段AM 是不交б 的,而且是连接点A 和M 的一条道路。我们需要修改这条道路,把它修改成引到点B 去的道路。设PM 和QM 是两条线段,它们都在折线б 上,而且无公共点(PM 和QM 可以在б 的同一环节上)。首先,我们把我们的道路和折线б 的第一个相遇的点从点M 移到点Q 去。现在可能出现下列两种情形之一:或者射线MP 交线段AQ,即穿进到三角形AMQ 的内部;或者射线MP 在三角形AMQ 的外部。在第二种情形下(注图14),由于引理Ⅷ,线段AM 上能找得一点T ,使得折线段б 上没有一个点在三角形TMQ 内,而且除Q 之外也没有一个点在它的边TQ 上。用线段TQ 替代线段TM ;我们得到的道路ATQ ,按照前面的证明,除点Q 之外,不含有б 的点。在第一种情形下(即射线MP 穿进到三角形AMQ 内,注图15),在射线MP 的补射线(射线MP 和它的补射线和点M 组成一条直线)上取一点P′ ,使得P′ 在M 和这补射线与折线段б 中的第一个交点之间(若这补射线不交б ,则取这射线上的任一点当做P′ )。然后利用引理Ⅷ,在线段MP′ 上如此选取一点U ,使得在三角形UMQ 内和在它的边MQ 上没有折线段б 的点;再在线段AM 上如此选取(再利用引理Ⅷ)点F ,使得在三角形FMU 内和在它的边FU 上没有折线段б 的点。最后,用折线段FUQ 替代线段FM 之后,在这情形下我们得到道路AFUQ ,除点Q 之外,不含有б 的点。

注图 14
注图 15
显然,使用这方法,能够把我们的道路和折线段б 的第一个相遇的点移到折线段б 的对应的线段的任意一点,甚至于端点,而且如此继续进行,能够移到这折线的任意一点B 。
得到引理I至引理X之后,我们转到定理9。
我们首先来证明定理9的第一条论断。设多边形β 由一条非封闭的折线段б 和一条线段PQ 组成,而P 和Q 是这折线段和这线段的仅有的公共点(注图16)。由于引理X,从β 内的点A 能够用一条道路连接到β ,第一次交β 于线段PQ 的一点R 。从β 内的点B 也能够用同样的道路同样的连接到R 。设UR 和VR 是所取的两条道路的最后线段。因为点A 和B 都在β 内,由于引理Ⅵ,这两条道路的所有的点,除点R 之外,都在β 内。由于引理Ⅸ,线段UR 和VR 在PQ 的同一侧,即线段RP 和RQ 都不穿进三角形URV 。因而,多边形的通过R 的边不穿进三角形URV ;线段UR 和VR 上没有β 的点。所以能应用引理Ⅷ到三角形URV ,即在它的边RU 上能找得如此的一点W ,使得线段WU 和β 无公共点,所取的两条道路所组成的一条折线段,乃是从点A 到点B 的一条道路。若这道路的URV 这一部分用折线段UWV 替代,则得到从点A 到点B 的一条道路,不交多边形β 。
注图 16
总之,我们已经证明,若A 和B 都是多边形β 的内点,则(在多边形的平面上)恒有一条道路,连接这两点,而且和多边形β 无公共点。对于两个外点,证明完全类似。另一条论断说,多边形β 的平面上的,连接这多边形的一个外点到它的一个内点的每一条折线段,至少和β 有一个公共点;这论断是引理Ⅵ的直接推论。
这定理的证明的基本观念属于文特尔尼兹(A. Winternitz)“关于约当曲线定理以及拓扑学中有关的定理”(Üeber den Jordanschen Kurvensatz und verwandte Sätze der Analysis Situs, Math. Zeitschr.卷1,第329—340页,1918) (1) 。
现在要证明下述论断,并无困难。没有直线完全在一个多边形内,即任意一条直线若含有一个多边形的一个内点,则也含有这多边形的外点。事实上,设直线a 的点O 在β 内。那么这直线上的,从点O 出发的一条射线a ,至少穿过β 一次。按照引理Ⅱ,这条射线a 上有一条线段紧跟在这一次穿过之后,这线段的点对于多边形β 来说都是外点。
我们再转回来证明这定理的推论:多边形的平面上有和这多边形无公共点的直线。
首先证明:平面上给定了任意n 个点,恒有这样的一条直线,使得所有的给定了的点,除了在这直线本身的若干个之外,就都在它的同一侧。
先取任意一条不通过给定了的点的直线a 。若给定的点分布在a 的两侧,则如下进行。用线段把直线a 的一侧的每一个给定的点连接到另一侧的每一个给定的点,把这些线段和a 的交点按照在a 上分布的顺序写出如下:
A 1 ,A 2 ,…,A k
取直线MN ,此处的M 和N 是两个给定的点,在a 的异侧,而且线段MN 交a 于点A k 。我们断定,MN 就是我们所求的直线。事实上,用d 表示直线MN 所决定的,而且含有点A 1 ,A 2 ,…,A k -1 的半平面。现在设L 是给定的点的任意一个,而且和N 在A 的异侧(否则用M 替代N )。那么线段LN 含有某一点Ai (i ≤k ),因而N 在线段LAi 之外。由此得到:若i ≠k ,则L 和Ai 在直线MN 的同一侧,即L 属于d ;若L =K ,则L 在MN 上。论断得以证明。
现在再证:我们能够再进一步,选取如此的一条直线,使得所有的给定的点真正的都在这直线的一侧。为此,通过每一个给定的点作两条线段,然后在上述的基础上,作如此的一条直线,使得给定的n 个点连同这些线段的4n 个顶点,除了若干个在这直线本身上之外,都在它的同一侧。显然,给定的n 个点不会在这直线上,只能在它的同一侧,若取多边形的顶点作为给定了的n 个点,则我们得到所要证的论断。
【16】本定理是定理8在空间中的推广。取不在平面α 上的一点A 。把所有的点M ,使得线段MA 不含有平面α 的点的,列入一个区域;把空间中的其余的点(不属于平面α 的)列入另一个区域。我们来证明下列和注解[13]和[14]中所给出的论断相类似的三条论断:
1)若点M 和N 在第一区域中,则线段MN 不含有平面α 的点。
2)若点M 和N 在第二区域中,则线段MN 不含有平面α 的点。
3)若点M 和N 在不同的区域中,则线段MN 含有平面α 的点。
这三条论断可以用同一方式证明。若A ,M ,N 不在一直线上,根据公理I4 和I5 ,它们决定某一平面β 。若平面α 和β 无公共点,则线段AM ,AN 和平面α 也无公共点,即合于情形1)的条件;情形1)中的论断一定正确,因为线段MN 也和平面α 无公共点。设正面α 和β 有公共点,那么根据公理I7 和I6 ,它们交于一直线,用α 表示这直线。若线段AM ,AN ,MN 的任意一条和平面α 有公共点,则这公共点同时属于平面α 和β ,所以应该在直线A 上。容易看出,现在整个的问题化为平面β 上的线段AM ,AN ,MN 和直线A 相交(或不相交)的研究,而A 也在平面β 上,也即是重复定理8的证明。
若点A ,M ,N 在一直线b 上,则或者这直线和平面α 无公共点(又是情形1)的条件,那么本定理显然正确;或者直线a 交这平面,那么容易看出,只需要一字不改地重复注解[14]中所引进的证明。
【17】确切的意义如下:给定了两条线段,其中一条恒或者和另一条有我们用名词“合同”所表出的某种关系,或者没有。这种关系我们没有直接给出定义,只由第三组公理在下述的意义下间接地给出定义:第三组公理中列举了这关系的所有的此后我们认为是属于这关系的性质。
【18】事实上,根据公理Ⅲ2 从合同式A ′B ′≡A ′B ′和AB ≡A ′B ′,得A ′B ′≡AB。
【19】我们来证明这一段中所有的论断。
1.设H 是射线h 上的任一点,K 是射线k 上的任一点。取线段HK 上的任一点M 。因为M 在H 和K 之间,点H 不在线段MK 上,而且点K 不在线段HM 上。因而点H ,M 在直线 的同侧,即点M 和射线h 在直线
的同侧,即点M 和射线h 在直线 的同侧。同样地得到,M 和射线k 在
的同侧。同样地得到,M 和射线k 在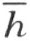 的同侧。结果是M 在∠(h ,k )内。现在如此取点N ,使得H 在K 和N 之间。点K 和N 在直线
的同侧。结果是M 在∠(h ,k )内。现在如此取点N ,使得H 在K 和N 之间。点K 和N 在直线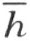 的异侧,即点N 和射线k 在
的异侧,即点N 和射线k 在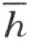 的异侧,因而N 在∠(h ,k )外。这就证明了下述论断:
的异侧,因而N 在∠(h ,k )外。这就证明了下述论断:
若 H 和 K 各在 ∠(h ,k )的一边上 ,则在直线 HK 上且在 H 和 K 之间的点必在 ∠(h ,k )内 ,而在线段 HK 之外的点必在 ∠(h ,k )外 。
2.设点M ,N 在∠(h ,k )内。这就是说,这两点都和射线h 在直线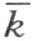 的同侧,因此(参看注解[13]的末尾),线段MN 的所有的点和射线h 在直线
的同侧,因此(参看注解[13]的末尾),线段MN 的所有的点和射线h 在直线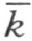 的同侧。这里所说的还成立,若在论证时把射线h 都用射线k 替代,把直线
的同侧。这里所说的还成立,若在论证时把射线h 都用射线k 替代,把直线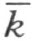 都用直线
都用直线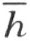 替代。可见,连接∠(h ,k )内两点的线段,完全在这个角内。
替代。可见,连接∠(h ,k )内两点的线段,完全在这个角内。
3.设从 ∠(h ,k )的顶点 O 出发的一条射线 l 的任一点 M 是在这个角内 。若N 是这同一射线的任意另一点,则点O 不在线段MN 上(参看射线的定义),然后根据注解[13],点N 和M 既在直线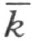 的同侧,也在直线
的同侧,也在直线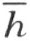 的同侧。所以,点N 和射线h 的点在直线
的同侧。所以,点N 和射线h 的点在直线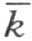 的同侧,也和射线k 的点在直线
的同侧,也和射线k 的点在直线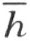 的同侧,即点 N 也在 ∠(h ,k )内 ;因此,在这种情形下,射线l 的所有的点都在∠(h ,k )内。同时容易证实:若从点 O 出发的一条射线 l 的一点 M 在 ∠(h ,k )外 ,则这同一条射线上的任意另一点也在这角外 (用反证法)。
的同侧,即点 N 也在 ∠(h ,k )内 ;因此,在这种情形下,射线l 的所有的点都在∠(h ,k )内。同时容易证实:若从点 O 出发的一条射线 l 的一点 M 在 ∠(h ,k )外 ,则这同一条射线上的任意另一点也在这角外 (用反证法)。
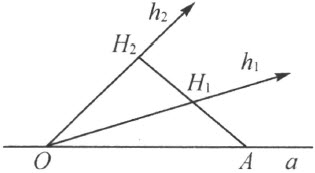
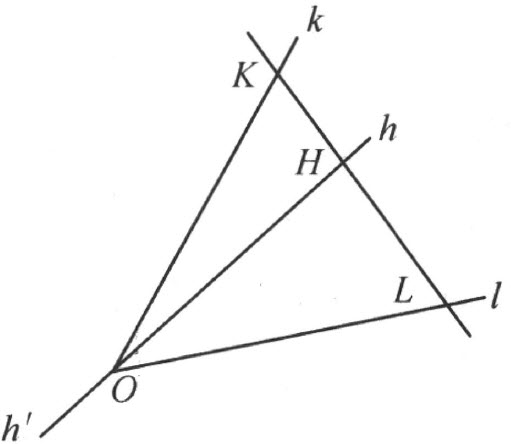
4.现在我们来证明,在∠(h ,k )内的一条射线 l 必定交线段 HK ,此处的 H 在 h 上 ,而 K 在 k 上 。
考虑在直线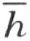 上的、不在射线h 上的、而且非点O 的任一点M (注图17)。直线
上的、不在射线h 上的、而且非点O 的任一点M (注图17)。直线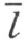 交三角形MHK 的边MH ,而同时不通过三角形的顶点。因此它必须交另一边HK 或MK 我们来证明,直线
交三角形MHK 的边MH ,而同时不通过三角形的顶点。因此它必须交另一边HK 或MK 我们来证明,直线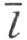 不能交边MK 。直线
不能交边MK 。直线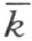 的点O 在M 和H 之间,即M 和射线h 的点在直线
的点O 在M 和H 之间,即M 和射线h 的点在直线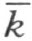 的异侧。设N 是线段MK 的任一点。直线MK 交直线
的异侧。设N 是线段MK 的任一点。直线MK 交直线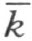 于一点K ,不在线段MN 上。因此,点N 和点M 在直线
于一点K ,不在线段MN 上。因此,点N 和点M 在直线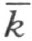 的同侧,即1)点 N 和射线 h 在直线
的同侧,即1)点 N 和射线 h 在直线 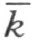 的异侧 ;另一方面,直线MK 和直线
的异侧 ;另一方面,直线MK 和直线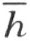 的交点M 在线段NK 之外,而这是说:2)N 和 K 在直线
的交点M 在线段NK 之外,而这是说:2)N 和 K 在直线  的同侧 ,即 N 和射线 i 在直线
的同侧 ,即 N 和射线 i 在直线  的同侧 。
的同侧 。
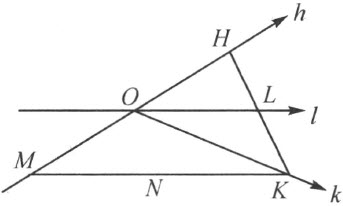
注图 17
直线 由射线l 、补射线l′ 和点O 组成的。射线l 在∠(h ,k )内,因此和射线h 在直线
由射线l 、补射线l′ 和点O 组成的。射线l 在∠(h ,k )内,因此和射线h 在直线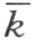 的同侧。所以射线l 上不能含有线段MK 的点N (论断1)。射线l ′和射线l 在直线
的同侧。所以射线l 上不能含有线段MK 的点N (论断1)。射线l ′和射线l 在直线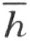 的异侧。因为在角内的射线l 和k 都在
的异侧。因为在角内的射线l 和k 都在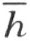 的同侧,l′ 在
的同侧,l′ 在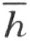 的另一侧。这就是说,射线l′ 上不能含有线段MK 的点N (论断2)。因此,我们所引的直线
的另一侧。这就是说,射线l′ 上不能含有线段MK 的点N (论断2)。因此,我们所引的直线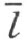 不能交线段MK ,而必定交线段H K。同时这交点即属于射线l (而不属于射线l′ ),因为线段HK 在角内。
不能交线段MK ,而必定交线段H K。同时这交点即属于射线l (而不属于射线l′ ),因为线段HK 在角内。
5.我们看到,从此得到若干很重要的论断:从同一点 O 出发的三条射线之中 ,只能有一条在其他两条所作的角内 。事实上,设射线l 在∠(h ,k )内。根据所证明的,它交线段HK 于某一点L 。因为L 在线段HK 上,从公理Ⅱ3 ,点H 不在线段LK 上;因此不交线段LK 的射线h 不能在∠(l ,k )内。在这里的论断中互换h 和k ,就证明了,射线k 也不能在∠(h ,l )内。
若射线 l 在 ∠(k ,m )内 。而射线 k 在 ∠(h ,m )内 ,则射线 l 在 ∠(h ,m )内 (注图18)。
注图 18
设点H 在射线h 上,而点M 在射线m 上。根据第4种情形中所证明的,射线k 交线段HM 于点K ,而且,射线l 交线段KM 于点L 。根据定理5,点H ,K ,L ,M 在直线HM 上的顺序或者和这里所写下的相同,或者相反,即点L 在线段HM 内。因此,由于第1种情形中所证明的,射线l 在∠(h ,m )内。
若 n 条射线 h 1 ,h 2 ,…,hn 和直线  上的射线都从直线
上的射线都从直线  上的一点出发 ,且射线 h 1 ,h 2 ,…,hn 在
上的一点出发 ,且射线 h 1 ,h 2 ,…,hn 在  的同侧 ,则在这后 n 条射线中有而且只有一条射线 ,它和射线 a 作成的角内含有所有其余的 n -1条射线 。
的同侧 ,则在这后 n 条射线中有而且只有一条射线 ,它和射线 a 作成的角内含有所有其余的 n -1条射线 。
首先证明这论断在n =2时正确。设射线h 1 在∠(h 2 ,a )内;那么,根据上文所证明的,射线h 2 在∠(h 1 ,a )外(注图19)。现在设射线h 2 在∠(h 1 ,a )外。我们来证明射线h 1 在∠(h 2 ,a )内。因为射线h 2 在∠(h 1 ,a )外,而且因为射线h 1 和h 2 在直线 的同侧,由此得出射线h 2 和a 在直线
的同侧,由此得出射线h 2 和a 在直线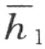 的异侧,即直线
的异侧,即直线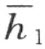 交每一条线段H 2 A (端点在射线h 2 和a 上)于某一点H 1 。同时,线段H 2 A 的点H 1 和点H 2 必定在直线
交每一条线段H 2 A (端点在射线h 2 和a 上)于某一点H 1 。同时,线段H 2 A 的点H 1 和点H 2 必定在直线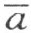 的同侧,即和射线h 2 同侧,这就是说和射线h 1 同侧。这就证明了点H 1 在射线h 1 上;否则它就在直线
的同侧,即和射线h 2 同侧,这就是说和射线h 1 同侧。这就证明了点H 1 在射线h 1 上;否则它就在直线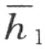 的补射线上,而且那就是说在
的补射线上,而且那就是说在 另一侧。但是点H 1 在∠(h 2 ,a )内(参看第1种情形),因此(第3种情形),射线h 1 也在这角内。
另一侧。但是点H 1 在∠(h 2 ,a )内(参看第1种情形),因此(第3种情形),射线h 1 也在这角内。
注图 19
现在假设我们的论断对于n -1条射线h 1 ,h 2 ,…,h n -1 正确,即假设这些射线中的n -2条,例如,h 1 ,h 2 ,…,h n -2 ,在∠(h n -1 ,a )内。我们证明这条论断对于n 条射线也正确。事实上,由于这条论断对于两条射线的正确性,所以或者射线h n 在∠(h n -1 ,A )内,因而这角内含有n -1条射线h 1 ,h 2 ,…,h n -2 ,h n ;或者射线h n -1 在∠(h n ,a )内。在后一情况下所有其余的射线h i (i=1,2,…,n -2)由假设在∠(h n -1 ,a )内,而由于上文所证明的,也在∠(h n ,a )内。
6.现在证明:若点 A 属于 ∠(h ,k )分平面 α 所成的两个区域中的一个 ,而点 B 属于另一个 , 则平面 α 中的连接 A 和 B 的每一 条折线段或者通过顶点O ,或者和h 或k 有公共点。
显然,能够假设点A 在∠(h ,k )内,而且点A 和B 在直线 的异侧,而不失论证的普遍性。现在证明,连接点A 和点B 的折线段ACDE …MB 交直线
的异侧,而不失论证的普遍性。现在证明,连接点A 和点B 的折线段ACDE …MB 交直线 。事实上,若折线段ACDE …MB 不交直线
。事实上,若折线段ACDE …MB 不交直线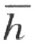 ,则点A 和C ,C 和D ,因而A 和D ,D 和E ,因而A 和E 等等,最后,A 和B 都在直线
,则点A 和C ,C 和D ,因而A 和D ,D 和E ,因而A 和E 等等,最后,A 和B 都在直线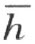 的同侧,这和我们的假设矛盾。然而折线段ACDE …MB 可能不交射线h ,而交直线
的同侧,这和我们的假设矛盾。然而折线段ACDE …MB 可能不交射线h ,而交直线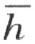 上的补射线h ′(我们设想这折线段不通过点O ;否则,我们的命题显然成立)。我们证明,在这种情形下折线段ACDE …MB 交射线k 。设P 是折线段ACDE …MB (折线段以A 为起点)和直线
上的补射线h ′(我们设想这折线段不通过点O ;否则,我们的命题显然成立)。我们证明,在这种情形下折线段ACDE …MB 交射线k 。设P 是折线段ACDE …MB (折线段以A 为起点)和直线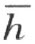 的第一个交点。设点P 在折线段ACDE …Q S…MB 的线段Q S上,而且同时它或者与折线段的端点S 重合,或者不重合,但决不和端点Q 重合。如同上文所说,我们知道折线段ACDE …QP (不包含点P 在内)的所有的点都和点A 在直线
的第一个交点。设点P 在折线段ACDE …Q S…MB 的线段Q S上,而且同时它或者与折线段的端点S 重合,或者不重合,但决不和端点Q 重合。如同上文所说,我们知道折线段ACDE …QP (不包含点P 在内)的所有的点都和点A 在直线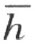 的同侧,因此在射线k 同侧。点A 和射线h 在直线
的同侧,因此在射线k 同侧。点A 和射线h 在直线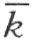 的同侧。点P 和射线h 在直线
的同侧。点P 和射线h 在直线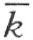 的异侧;因此,点P 和A 在直线
的异侧;因此,点P 和A 在直线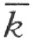 的异侧。所以根据上文所证明的,折线段ACDE …QP 必定交直线
的异侧。所以根据上文所证明的,折线段ACDE …QP 必定交直线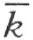 。交点F 既然属于折线段ACDE …QP ,必和射线k 在直线
。交点F 既然属于折线段ACDE …QP ,必和射线k 在直线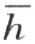 的同侧。因此,它在射线
的同侧。因此,它在射线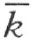 上。
上。
7.我们现在来证明,若点 A 和点 A ′属于同一个区域 ,则平面 α 中恒存在一条折线段 ,连接点 A 和 A ′,不通过点 O 。而且也和射线 h 和 k 无公共点 。
若点A 和点A ′在∠(h ,k )内,则这论断的正确性显然;因为能够取线段AA ′作为所说的折线段。若点A 和点A ′在∠(h ,k )外,而且即使在直线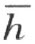 和
和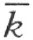 之一的同侧,例如在
之一的同侧,例如在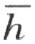 的同侧,则仍旧能够用线段AA ′把它们连接起来。事实上,在这情形下,线段AA ′和
的同侧,则仍旧能够用线段AA ′把它们连接起来。事实上,在这情形下,线段AA ′和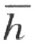 无公共点;此外,它和射线k 也无公共点——否则,点A 和点A ′将要和射线k 在
无公共点;此外,它和射线k 也无公共点——否则,点A 和点A ′将要和射线k 在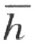 的同侧,而且点A 和点A ′中的一个将要和射线h 在k 的同侧,即在∠(h ,k )内。
的同侧,而且点A 和点A ′中的一个将要和射线h 在k 的同侧,即在∠(h ,k )内。
现在设点A 和点A ′既在直线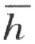 的异侧,也在直线
的异侧,也在直线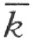 的异侧。同时,为确定起见,设A 和h 在
的异侧。同时,为确定起见,设A 和h 在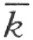 的同侧;那么A 和k 在
的同侧;那么A 和k 在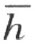 的异侧(否则,A 将要在角内),这就是说A ′和k 在
的异侧(否则,A 将要在角内),这就是说A ′和k 在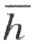 的同侧;最后,A ′和h 在
的同侧;最后,A ′和h 在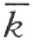 的异侧(否则,A ′将要在角内)。
的异侧(否则,A ′将要在角内)。
现在再在∠(h ′,k ′)内取任意一点N ,即点N 和射线h 在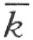 的异侧,而且和射线k 在
的异侧,而且和射线k 在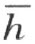 的异侧。显然,N 在∠(h ,k )外,而且同时和点A 在
的异侧。显然,N 在∠(h ,k )外,而且同时和点A 在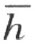 的同侧,也和点A 在
的同侧,也和点A 在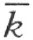 的同侧。那么根据刚才所证明的,线段AN 和NA ′都不交射线h 和k ,因而ANA ′是所求的折线段。
的同侧。那么根据刚才所证明的,线段AN 和NA ′都不交射线h 和k ,因而ANA ′是所求的折线段。
【20】希尔伯特所谓角的“迁移”不应当了解为利用某种仪器角的作图;例如利用直尺和圆规,而应当了解为(决定和已知角合同的角的)射线的存在这个事实。相应地,所谓迁移的唯一性,应当了解为只有一条这样的射线存在。
【21】事实上,若三角形AB C的边AB 和B C合同,则能写下
AB ≡BC ,BC ≡AB ,∠ABC ≡∠CBA
(根据公理Ⅲ4 的第二部分)。所以,根据公理Ⅲ5 ,
∠BAC ≡∠BCA
(应用公理Ⅲ5 时把同一个三角形一次看做是三角形ABC ,一次看做是CBA )
【22】事实上,只需要证明AC ≡A′C′ 。设此合同式不成立,在射线A′C′ 上作如此的一点D ′,使得AC ≡A ′D ′。那么,从公理Ⅲ5 ,∠ABC ≡∠A ′B ′D ′;此外,从定理的假设,∠ABC ≡∠A′B′C′ 。这和公理Ⅲ4 矛盾(∠ABC 所合同的∠A′B′D ′和∠A′B′C′ ,是从两种不同的方式迁移而得到的)。
【23】在所有的论证中,并没有假设角的合同的对称性,即没有认为∠ABC ≡∠A′B′C′ 和∠A′B′C′ ≡∠ABC 有相同的意义。因此,在讨论三角形合同时也如此。特别在刚才所引进的论证中,所有的合同式都应从图的上部读到下部。对称性是后来从定理19推证出来的。
【24】定理 设 k ,h ,L 是从一点 O 出发的射线 ,而且 k 和 h 在 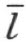 的同侧 (这里的
的同侧 (这里的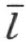 是含有射线l 的直线),那么或者 k 在∠(l ,h )内 ,而 h 在 ∠(l ,k )外 ,或者 k 在 ∠(l ,h )外 ,而 h 在 ∠(l ,k )内 。
是含有射线l 的直线),那么或者 k 在∠(l ,h )内 ,而 h 在 ∠(l ,k )外 ,或者 k 在 ∠(l ,h )外 ,而 h 在 ∠(l ,k )内 。
证明 设k 在∠(l ,h )外(注图20)。那么k 和l 在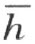 的异侧(否则,既然我们所考虑的只是k 和h 在
的异侧(否则,既然我们所考虑的只是k 和h 在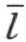 的同侧的情形,k 将要在∠(h ,l )内)。所以用线段连接k 上的任一点K和l 上的任一点L 时,这线段交直线
的同侧的情形,k 将要在∠(h ,l )内)。所以用线段连接k 上的任一点K和l 上的任一点L 时,这线段交直线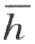 于某一点H 。因为H 在K和L 之间,则L 在KH 外。因此,点K和H 在l 的同侧;因为K 是在k 上取的点,K 和H 在
于某一点H 。因为H 在K和L 之间,则L 在KH 外。因此,点K和H 在l 的同侧;因为K 是在k 上取的点,K 和H 在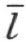 的k 侧,也就是射线h 侧(根据定理的假设)。由此得点H 既然在直线
的k 侧,也就是射线h 侧(根据定理的假设)。由此得点H 既然在直线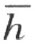 上,又在
上,又在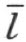 的射线h 侧,它必定在射线h 上(而不在补射线h ′上)。
的射线h 侧,它必定在射线h 上(而不在补射线h ′上)。
注图 20
因为点H 在∠(l ,k )内(参看注解[19],1),射线h 在∠(l ,k )内(参看注解[19],3)。
因此,k 在∠(l ,h )外,且h 在∠(l ,k )外,这种情形是不可能的。
k 在∠(l ,h )内和h 在∠(l ,k )内,这种情形也是不可能的;在这种情形下,连接k 上的任一点K 和l 上的任一点L 的线段KL ,必定交h 于某一点H (注解[19],4)。但是,同理,线段HL 必须交射线k ,即同时H 在L 和K之间,而且K在L 和H 之间。这是不可能的(公理Ⅱ3 )。
【25】我们证明下列情形:h 和k 在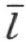 的异侧,而且h ′和k ′在
的异侧,而且h ′和k ′在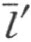 的异侧。
的异侧。
考虑h 的补射线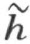 (在同一条直线上),和h ′的补射线
(在同一条直线上),和h ′的补射线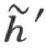 。
。
射线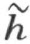 和k 在
和k 在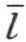 的同侧,因为它们都和射线h 在
的同侧,因为它们都和射线h 在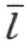 的异侧。
的异侧。
射线h ′和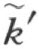 同样的在
同样的在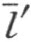 的同侧。因为已知∠(h ,l )≡∠(h ′,l′ )。根据定理14,
的同侧。因为已知∠(h ,l )≡∠(h ′,l′ )。根据定理14,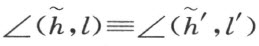 。
。
此外,还已知∠(k ,l )≡∠(k ′,l′ )
应用在已经证明的情形下的定理15(到射线L ,k , ),得
),得

因此根据定理14,得
【26】引理 设已知两条合同线段AC ≡A ′C ′。那么,对于AC 上每一点B ,能求出A ′C ′上的如此一点B ′,使得AB ≡A ′B ′,BC ≡B ′C ′。
证明 在射线A ′C′上,从点A ′起始,作线段A ′B ′,使得A ′B ′≡AB (注图21)。点B ′因此唯一的决定了(参看公理Ⅲ5 的推论)。再者,从点B ′开始作线段B ′C ″,使得B ′C ″≡BC ,而且使得C ″和A ′在B ′的异侧。那么,从公理Ⅲ3 ,AC ≡A ′C ″。因此,从公理Ⅲ2 ,A ′C ′≡A ′C ″。由此得点C ′和C ″重合(C ′和C ″在A ′的同侧:由作图法,B ′取在A ′的C ′侧,而且C ″如此选取,使得B ′在A ′和C ″之间;这就是说,A ′在B ′C ″之外,而且,因此,C ″在A ′的B ′侧)。点B ′显然就是所求的点。
注图 21
定理16的证明 在射线h 和k 上任取点H 和点K ,而在射线h ′和k ′上取点h ′和点K ′,使得(公理Ⅲ1 ):
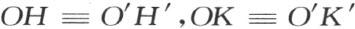
(这里的O 和O ′是角的顶点)。
从定理12,三角形OHK 合同于三角形O′H′K′ ,特别HK ≡H′K′
在∠(h ,k )内的射线l ,交线段HK 于某一点L (参看注解[19],4)。利用引理,在线段H ′K′上取如此的一点L′ ,使得
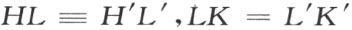
射线O ′L′ 满足定理的要求。第一,它在∠(h ′,k ′)内,因为L′ 在∠(h ′,k ′)内(注解[19],3)。第二,三角形OHL 合同于O′H′l′ ,因为
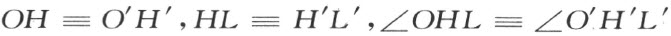
(最后一个合同式由三角形OH K和O ′H ′K′的合同得来)。因此∠HOL ∠H ′O ′L′ 。完全同样地得∠KOL ≡∠K′O′L′ 。
【27】要想应用定理15,必须预先证明:若射线Z 1 X 和Z 1 Y 在直线Z 1 Z 2 的异侧,则射线Z 2 X 和Z 2 Y 也在直线Z 1 Z 2 的异侧;而且在同侧的情形时也类似。
事实上,射线Z 1 X 和Z 2 X 恒在直线Z 1 Z 2 的同侧,属于它们的点X 所在的一侧;而射线Z 1 Y 和Z 2 Y 也在同侧,点Y 所在的一侧。所以当X 和Y 在Z 1 Z 2 的异侧时,射线Z 1 X 和Z 1 Y 也如此,而且射线Z 2 X 和Z 2 Y 同样也如此。
当X 和Y 在Z 1 Z 2 的同侧时,这两对射线中的每一对也同样如此。
【28】丝毫不改变定理20的证明,就能够把这定理陈述得更广泛些:设射线k ,l 在h 的同侧,射线k ′,l′ 在h ′的同侧,而且∠(h ,l )≡∠(h ′,l′ ),∠(h ,k )≡∠(h ′,k ′)。那么,若k ′在∠(h ′,l′ )内,则k 在∠(h ,l )内;反过来也正确。
这样的提法即是说,当迁移角到沿着任一射线(而且在它的给定了的一侧)时而不改变结果时,能够比较角的大小。论断2)现在立刻可以从下述的情形得到。若把角β “叠置”在角α 上来比较角α 和β ,我们就可以把β 换成和它合同的角r ,而不引起任何改变。完全同样地,在论断3)中,我们应该认为:是利用把β “叠合”在r 上的方法,来比较β 和r ;作这样运算时,把β 换成和它合同的α ,结果一点也不改变。
论断1)我们验证如下。把角α 和r “叠置”在β 上;那么,若r ,β ,α 分别和角∠(h ,k 1 ),∠(h ,k 2 ),∠(h ,k 3 )重合,则如同所给定了的,k 2 将在∠(h ,k 3 )内,而k 1 在∠(h ,k 2 )内。现在需要证明k 1 在∠(h ,k 3 )内;这就是说α >r 。但是,这是在注解[19],第5种情形证明了的。
至于线段长短的比较,那只是加以简化的重复一次角的对应的理论。首先在把线段AB 迁移到沿着射线CD 上,而且从点C 起始时,按照所得的线段超过线段CD 或落在CD 内,我们就分别说AB >CD 或AB <CD 。
其次,对于线段也能够提出定理20,而且一字不改地重复它的证明(所不同的,只是不援引定理16,而援引注解[26]中的引理)。如同对于角而言,这定理使我们能够肯定:AB >CD 和CD <AB 有相同的意义。
最后,对于线段大小关系的传递性的证明,就是上文对于角所引进的论证的重复(加以一些简化)。
我们还来证明一条简单的定理:
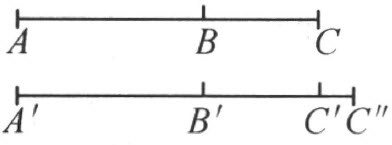
若在直线α 上依次给定了三点A ,B ,C ,而在直线a ′上依次给定了A ′,B ′,C ′,而且AB ≡A ′B ′,BC <B ′C ′,则AC <A ′C ′。
事实上(注图22),在射线B ′C ′上,从点B ′起始,作线段B ′C ″合同于BC ;那么,从关系BC <B ′C ′的定义,C ″落在B ′和C ′之间。显然,A ′上的点顺序只能是A ′B ′C ″C ′。从公理Ⅲ3 ,AC ≡A ′C ″;而因为C ″在A ′和C ′之间,则AC <A ′C ′。
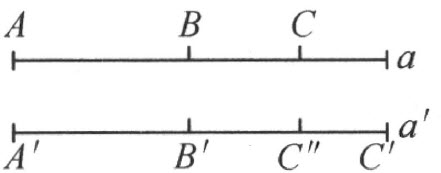
注图 22
推论 若定理的条件改变为AB <A ′B ′和BC <B ′C ′,则仍旧AC <A ′C ′。
为了证明AC <A ′C ′,只要在任一条直线a 0 上引进三个辅助点,依次为A 0 ,B 0 ,C 0 ,使得A 0 B 0 ≡AB ,B 0 C0 ≡B ′C′。那么,根据传递性,B 0 C 0 >BC ,A 0 B 0 <A ′B ′
从第一个不等式推知A 0 C 0 >AC ,而从第二个不等式推知A ′C ′>A 0 C 0 ,故得A ′C ′>AC 。
总之,粗糙地说,加项增大时,线段的和也增大。
【29】若l ″在角α 内,则从定义,l ″和h 在l 的同侧,而且,因此,l ″和k 在l 的异侧,也就是l″在角β 外。因为l ″和l 在k 的同侧(从作图)。而且l ″在∠(k ,l )外,则从注[24]的证明,l 在∠(k ,l ″)内。由此推得∠(k ,l )<∠(k ,l ″),也就是β <∠(k ,l ″)
至于谈到上述的论断:l ″或在α 内,或在β 内,可证明如下。从作法,l ″与l 在h 的同侧,也在k 的同侧(那是一样的)。其次,不论l ″在l′ 的那一侧,它或者将要和h 在同侧,或者和k 在同侧。从角的内部的定义,前者表示l ″在α 内,而后者表示l ″在β 内。
【30】用反证法来证明本定理。设有一对不合同的三角形ABC 和A ′B ′C ′,具有定理25的条件中所说的性质。这两个三角形中,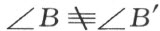 ,因为否则,根据定理13,这两个三角形将合同。为确定起见,假设∠B ′<∠B 。在射线BA 上而且在直线AB 的点C 侧,作角β =∠B ′。根据角的不相等的定义,射线BC ″在∠ABC 内(注图23),而根据注解[19],4,它交线段AC 于某一点,我们用字母D 表示。根据定理13,△ABD ≡△A ′B ′C ′。因此∠ADB ≡∠A ′C ′B ′≡∠ACB 。但是,根据定理22,∠ADB >∠ACB 。如是,我们的假设(定理25不正确)引出了矛盾。
,因为否则,根据定理13,这两个三角形将合同。为确定起见,假设∠B ′<∠B 。在射线BA 上而且在直线AB 的点C 侧,作角β =∠B ′。根据角的不相等的定义,射线BC ″在∠ABC 内(注图23),而根据注解[19],4,它交线段AC 于某一点,我们用字母D 表示。根据定理13,△ABD ≡△A ′B ′C ′。因此∠ADB ≡∠A ′C ′B ′≡∠ACB 。但是,根据定理22,∠ADB >∠ACB 。如是,我们的假设(定理25不正确)引出了矛盾。
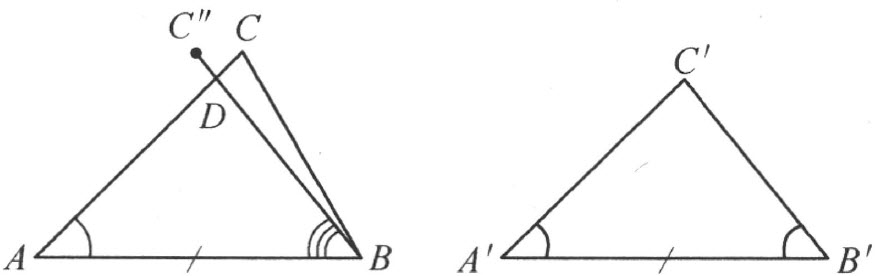
注图 23
【31】我们来证明,若两个合同点列中的一个的点都排成顺序,使得点Q 在点P 和R 之间,则和它们对应的点也应该依次为P ′,Q ′,R ′。假设这论断不正确,那么或者点P ′在点Q ′和R ′之间,或者点R ′在点P ′和Q ′之间。我们来证明第一个假设不可能。为了证明,在直线A 上,从点P 起始,在射线PR 相反的一侧。作线段PQ ″合同于线段PQ ,因而,根据公理Ⅲ2 合同于Q ′P ′(注图24)。线段Q ′P ′和P ′R ′也无公共点。如同线段Q ″P 和PR 无公共点一样。所以,根据公理Ⅲ3 ,Q ″R ≡Q ′R ,而根据我们所考虑的点列的合同性,Q ′R ′≡QR ,由此,按公理Ⅲ2 ,Q ″R ≡QR 。但是,按照定理5,直线A 上的点能够写下的顺序,一定是Q ″PQR (其他顺序将和作图矛盾),即点Q 和Q ″在点R 的同侧,所以合同式Q ″R ≡QR 与线段迁移的唯一性矛盾。

注图 24
同样的论证完全否定另一假设(点R ′在点P ′和Q ′之间)。
【32】为了证明定理28,我们需要一条众所周知的定理。
定理 在三角形中,每一边恒小于其他两边的和。
证明 需要证明:若A ,B ,C 不在一条直线上,则AB <AC +CB 。
在直线AC 上,从点C 开始,作线段CB ′合同于CB ,使得B ′和A 在C 的异侧(注图25)。因为点C 在A 和B ′之间,则C 落在∠ABB ′内,因此射线BC 也在∠ABB ′内(参看注解[19])。
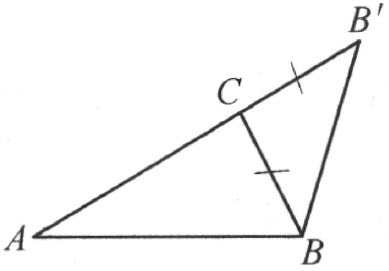
注图 25
由此得
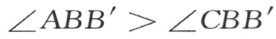
但是,从定理11,∠CBB ′≡∠CB ′B ,因此
∠ABB ′>∠CB ′B
从定理23,AB ′>AB ,这就证明了。
定理28的证明
1.首先考虑下述情形:P 和图形的两点,例如A 和B ,在一条直线上。
若所求的点P ′存在,则它只能在直线A ′B ′上。事实上,否则,线段A ′B ′,A ′P ′,B ′P ′的每一条将小于其他两条的和。根据图形的合同性,线段AB ,AP ,BP 的每一条也将小于其他两条的和;事实上,它们中的一条一定等于另两条的和,因为点A 、B 、P 在一条直线上。
其次,点A ′,B ′,P ′的顺序应该完全像点A ,B ,P 的顺序一样。这是定理27的结果。所以,若 点P ′存在 ,则将由下述的唯一 方式决定:若P 和B在A 的同侧,则从点A ′开始,作线段A ′P ′合同于AP 在点B ′的那一侧;若P 和B 在A 的异侧,则从点A ′开始作线段A ′P ′合同于AP 不在点B ′的那一侧。
现在来证明,按照这个方法恒能作出的点,一定是所求的点P ′,即所求的点P ′恒存在 。
设C 是图形(A ,B ,…,L )的任一点,而且C ′是图形(A ′,B ′,…,L′ )的对应的点。
那么,根据图形的合同性,
∠CAB ≡∠C ′A ′B ′
由此得
∠CAP ≡∠C ′A ′P ′
因为下一行的角或者和上一行的角重合(若P ,B 在A 的同侧,而且P ′,B ′,在A ′的同侧),或者上一行的角和下一行的角相邻补(若P ,B 在A 的异侧,而且P ′,B ′在A ′的异侧;参看定理14)。
根据定理12,三角形CAP 和C ′A ′P ′合同,由此得
CP ≡C ′P ′
在论证中,我们都假设了(没有明确指出),C 不在直线AB 上(因而C ′也不在直线A ′B ′上)。当C在直线AB 上,而且C ′在A ′B ′上时,证明更简单。留给读者自证。
总之,用点P 和P ′扩充了的图形中,所有的对应线段还合同。
按照定理18,不难得到对应角的合同性。
2.设P 不和图形(A ,B ,…L )的任意两点在同一条直线上,而且A ,B ,…,L 不全在一条直线上。
这时,能指出两条不同的直线,例如AB 和AC ,各连接图形的一对点(注图26)。点A 分直线AC 成两条射线,其中的一条和P 在AB 的异侧。在这条射线上取任意一点P 1 ;那么直线PP 1 交AB 于某一点P 2 。
注图 26
于是,点P 在直线P 1 P 2 上,这里的P 1 是在A C上取的,而P 2 是在AB 上取的。
按照第1种情形的证明。在直线A ′C ′和A ′B ′上能够(唯一的)指出点 和
和 ,使得扩充了的图形(A ,B ,…,L ,P 1 ,P 2 )和(A ′B ′,…,L′ ,
,使得扩充了的图形(A ,B ,…,L ,P 1 ,P 2 )和(A ′B ′,…,L′ , ,
, )合同。
)合同。
再把第1种情形应用到扩充了的合同图形和在P 1 P 2 上的点P 。那么,在P' 1 P' 2 上能够指出点P ′,使得图形(A ,B ,…,L ,P 1 ,P 2 ,P )和(A ′,B ′,…,l′ , ,
, ,P ′)合同。
,P ′)合同。
我们来证明点P ′是唯一确定的。设还有这样的一点P ″,使得图形(A ,B ,…,L ,P )和(A ′,B ′,…,L′ ,P ″)合同,那么,按照第1种情形,能够找到点 和
和 ,使得(A ,B ,…,L ,P ,P 1 ,P 2 )和(A ′,B ′,…,L′ ,P ″,
,使得(A ,B ,…,L ,P ,P 1 ,P 2 )和(A ′,B ′,…,L′ ,P ″, ,
, )合同。若从这两个图形消去P 和P ″,所得的图形更应该合同;但是由于刚才所说的条件,点
)合同。若从这两个图形消去P 和P ″,所得的图形更应该合同;但是由于刚才所说的条件,点 和
和 已经唯一地被决定了;因此
已经唯一地被决定了;因此 和
和 重合,而且
重合,而且 和
和 重合。
重合。
总之,图形
(A ,B ,…,L ,P 1 ,P 2 ,P )
和
(A ′,B ′,…,L′ ,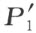 ,
,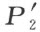 ,P ″)
,P ″)
合同。根据第1种情形中点P ′的作法的唯一性,比较这两个所得的合同式时,我们断定P ″和P ′重合。
3.设图形(A ,B ,…,L )的所有的点在一条直线上,而且P 在这直线外。
那么,根据第1种情形(证明的开始),点A ′,B ′,…,L′ 也在一条直线上,而且(定理27)有对应的顺序。
以射线A ′B ′为边,作角合同于∠PAB ,而且在这角的另一边上作线段A ′P ′合同于AP 。于是
∠PAB ≡∠P ′A ′B ′,AP ≡A ′P ′
我们断定,点P ′就是所要求的点。事实上,设C 是第一图形的任一点。∠PAC 和∠PAB 或者重合,或者相邻补。在前者情形下,∠P ′A ′C ′和∠P ′A ′B ′重合,而在后者情形下,相邻补;因为,若C 和B 在A 的同侧;侧C ′和B ′也在A ′的同侧,等等。
因为
∠PAB ≡∠P ′A ′B ′
由此得,在任一情形下,
∠PAC ≡∠P ′A ′C ′
此外还有
AP ≡A ′P ′,AC ≡A ′C ′
从定理12,得
PC ≡P ′C ′
这已证明了图形(A ,B ,…,L ,P )和(A ′,B ′,……,L′ ,P ′)的合同(在所考虑的情形下,点P ′并没有唯一的被决定;因为能够不用它,而用和它对于直线A ′B ′…L′ 对称的点替代)。
【33】定理28对于平面的几何,和定理29对于空间的几何,它们的深刻的原则性的意义在于建立了合同和运动 这两个概念间的联系。
在物理实验的领域里,这两个对应的概念已经彼此密切的联系着。如同想要 比较两条轴的长度,我们总是移动 一条,把它叠置在另一条上。就是这个样子,实际经验中两个物体的合同,首先就表现为借助于运动而使它们互相叠合的可能性。
在数学的领域里,这种联系仍旧保持着,而且这里有两种进行方式:或者用公理建立运动,以运动为基础,然后如前所说的方式通过运动,来规定合同;或者,如希尔伯特所作的,以由公理所建立的合同作基础,再在这基础上规定运动。
现在规定运动。所谓一个运动(广义的,这里包含镜面反射)就是把空间的点集换到它自身的、而且恒使得
AB ≡A ′B ′
的一个一对一的映射(双射),这里的A ,B 是空间中的任意点,而A ′,B ′分别是它们在这映射下的像点。
于是,运动的特征是把每一个图形(A ,B …)换成合同的图形(A ′,B ′…)。由此特别容易得到(重复注解[32]的论证,定理28的证明的开始),共线的点仍旧换成共线的点,即直线换成直线。因此,平面换成平面,等等。
在这联系中,定理29的作用在于证明了运动的可能性和确定了运动任意性的限度 。
设ABC 和A ′B ′C ′是两个任意给定了的彼此合同的三角形。再在平面ABC 外取一点D 。然后,从定理29,能够令点D ′和点D 成对应,使得图形
(A ,B ,C ,D )和(A ′,B ′,C ′,D ′)
合同。
从这同一条定理29,对于空间中的每一个点P ,恰有一个 对应点P ′,使得图形
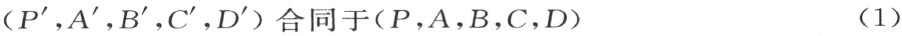
我们断言,这样的把任意一点P 换成它的对应点P ′的变换是一个运动 。
事实上,再利用这同一条定理29,能令点Q ′和某另一点Q 成对应,使得图形
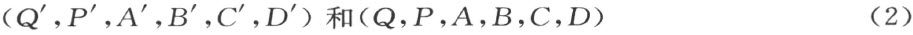
合同。
因为合同性保持,若从图形中消去点P 和P ′,则

比较(1)和(3),即见到,在我们从合同的四面体ABCD 和A ′B ′C ′D ′出发所建立的同一个变换下,Q 换成Q ′,而且P 换成P 。同时,根据(2),PQ ≡P ′Q ′。
总之,我们的变换是一个运动 。
至于谈到选择运动时任意性的限度,情形如下。
设给定了一点A ,从A 出发的一条射线a ,和以射线a 为边缘的一个半平面α 。设A ′,a ′,α ′,表示类似的一个结构,由任意另一方式取定的。在a 上任取一点B ,在α 上任取一点C ,作三角形ABC 。
其次,我们不难作到,作三角形A ′B ′C ′合同于ABC ,使得B ′在A ′上,C ′在α ′上。然后,如同上文所证明的,有一个运动存在,把ABC 移到A ′B ′C ′,因此,把结构(A ,a ,α )移到结构(A ′,A ′,α ′)。
稍加考虑,就能够证明,这样的运动只能由两个方式实现(两重性可从下列事实得出:实现了一个运动之后,还能接着作对于平面α ′的一个反射)。
于是,若暂不管这种两重性,则只要给定了一个结构(A ′,a ′,α ′)而使原给定的结构(A ,a ,α )应该移到它上面去,一个运动就被确定了。
直接从运动的定义就可以知道,所有的运动组成一个群,即
1)恒等变换是一个运动。
2)一个运动的逆变换是一个运动。
3)两个运动继续实施的结果还是一个运动。
如同所熟知的,对于把某一集合换到自身的一组一对一的映射来说,这些条件的满足即是说这一组是一个群。
我们不给出定理29的证明;因为能够按照类似定理28证明的方式进行定理29的证明,只要在后者中改用平面,替代前者中的直线。而且第一步必须先证,在合同的图形中共面的点的对应点也共面。
【34】事实上,公理I~V规定了三维的欧几里得空间的几何;这空间能够安置在一个四维的欧几里得空间中,作为一个三维的平面。我们现在看这四维空间的(而非只属于它的一个三维的子空间的)全体点、直线和二维的平面。不难验证,在这个扩充了的领域中,全体公理除去公理I7 之外,都满足了;四维空间中的两个二维的平面能够只交于一点(而且这甚至于是普遍的情形)。
于是,扩充元素的集合,而保持公理I7 之外的全体公理,是可能的。
【35】这里必须处理的是我们的公理系统的一些解释 。首先说明解释这概念本身。
1.用公理方法来建立几何时,我们有基本对象“点”、“直线”、“平面”和基本关系“关联”、“介于”和“合同于”(后者应用到后来引进的对象:线段和角)。基本概念并不包含超出公理对于它们所说的任何内容;应用纯粹逻辑推理来建立几何时,所需要的一切都包含在公理之中。
现在对于基本概念 ,改变我们的观点 :把这些基本概念了解为某一个数学领域某些完全确定的对象和关系 ,而这个领域是我们认为已经建立了的和有基础的 。
这就叫做“给公理系统一个解释”。在解释的结果中,每一条公理变成我们利用来作解释的已经有基础的数学领域中的一条完全确定的命题。
即使如此得到的命题中的一条不真实,我们的解释就失败了,这就是说在基本概念的这个具体解释(这是一个解释的主要部分)中,公理没有满足。
然而从这种情形,还不可能作出关于这抽象的公理系统的价值的任何结论,因为失败的原因可能是在于解释的选择不适当。
在解释的结果中,若公理变成的所有命题都是真实的,则解释实现了;而且,由此得到重要的结论说,原来的公理系统有相容性。
事实上,公理系统的所有的定理都是公理的纯粹逻辑推论。在解释的结果中,公理是真实的命题;这就是说,从它们逻辑地推出的定理也是真实的命题(在用作解释的领域的意义下)。所以,若在抽象的公理系统中得到两条定理,互相矛盾,则在解释中也要得到两条真实的命题,互相矛盾。但是这是不可能的,因为解释的领域是已经认为有基础的而且无矛盾的。
2.我们转到具体的例子,即转到原文中解析的解释 的讨论时,解释的概念就显得更清楚了。
选择算术的数域Q 作为解释的领域,而这数域是认为已经建立了的。此后,所谓“数”,永远是指“域Q 的数”。
现在对于点和直线(只限于平面几何的解释),和关系“属于”、“介于”和“合同”,我们改变观点如下:我们不把它们了解为抽象的概念,只受公理系统的节制,而把它们了解为这解释领域中的完全具体的概念:
点,了解为一对数(x ,y )
直线,了解为三个数(u :v :w ) (2)
而且u ,v ,w 除去可以相差同一个不等于零的因子之外完全确定了(因此(ρu :ρV :ρw )是同一条直线,若ρ 是不等于零的一个数)。加之,u 和v 不应该同时是零。
“点(x ,y )和直线(u :v :w )相关联”这关系,了解为等式
ux +vy +w =0
的成立。
公理Ⅰ1~2 显然变成命题:
“若给定了不同的两对数(x 1 ,y 1 )和(x 2 ,y 2 ),则恰存在一组三个数(u ,v ,w ),这组数除去可以相差一个不等于零的公因子外完全确定了,而且满足条件:
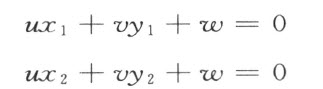
而且u 和,v 不同时为零。”
我们得到解释领域中的,即算术数域Q 中的一条命题,而能够证明它是否真实,但是,只要深入考虑这条关于存在的命题,即只要研究一对三元u ,v ,w 的一次方程,我们就相信这命题的正确性。
同样,很容易写出公理I3 和公理Ⅳ所变成的命题,而且证明它们的正确性。我们把这些留给读者。
【36】考虑属于直线(u :v :w )的点(x ,y ),那么等式
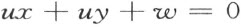
成立。
因为x 和y 的关系是线性的关系,x 的单调的改变引出y 的单调的改变,而且反过来也对(若不是两变数x 和y 中的一个保持常值)。
我们继续建立解析的解释。所谓“点(x 2 ,y 2 )在点(x 1 ,y 1 )和(x 3 ,y 3 )(在给定了的直线上)之间”这关系,是指下列算术的关系至少出现一个:
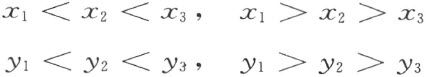
(如同刚才所提到的,上一行的一个关系的出现必引出下一行的一个关系的出现,若y 不是沿着直线保持常值;而且反过来也对)。
然后,第二组公理变成数域Q 的领域中的不等式理论的命题。所有这些命题都是正确的,特别是对于公理Ⅱ1~3 的证明是显然的。
所以我们只需论证公理Ⅱ4 。
首先说明下述论断在解释中有什么意义:点(x 1 ,y 1 )和(x 2 ,y 2 )在直线(u :v :w )的异侧。从定义,就是说存在一点(x ′,y ′),在线段(x 1 ,y 1 ),(x 2 ,y 2 )上,又同时在直线(u :v :w )上;即使得
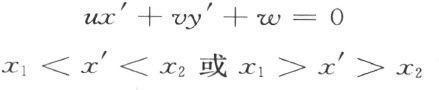
(或者同样对于y 的不等式)。
因为从(x 1 ,y 1 )出发,通过(x ′,y ′)而到(x 2 ,y 2 )的过程中,x 单调的改变,而且因为式子ux +vy +w 连同y 都线性地依赖x ,因而也单调的改变,所以ux ′+vy ′+w 等于零即和下述事实等价:u x1 +v y1 +w 和ux 2 +vy 2 +w 的符号不同。
在解释中,公理Ⅱ4 变成下述命题:
“设给定了三点(x 1 ,y 1 ),(x 2 ,y 2 ),(x 3 ,y 3 )(不属于同一直线),和不通过这三点的任一点的一直线(u :v :w )即
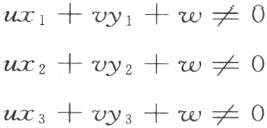
设这直线有点(x ′,y ′)在线段(x 1 ,y 1 ),(x 2 ,y 2 )内,即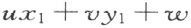 和
和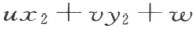 的符号不同。那么直线(u :v :w )或者有点在线段(x 1 ,y 1 ),(x 3 ,y 3 )内,或者在线段(x 2 ,y 2 ),(x 3 ,y 3 )内,即
的符号不同。那么直线(u :v :w )或者有点在线段(x 1 ,y 1 ),(x 3 ,y 3 )内,或者在线段(x 2 ,y 2 ),(x 3 ,y 3 )内,即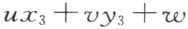 的符号或者和
的符号或者和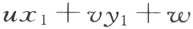 的符号不同,或者和
的符号不同,或者和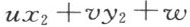 的符号不同”。
的符号不同”。
这论断显然正确,因为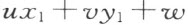 的符号和
的符号和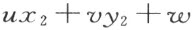 的符号不同,所以这两个符号之一应该和
的符号不同,所以这两个符号之一应该和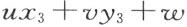 的符号不同。
的符号不同。
【37】要完成解释的构造,我们还必须说明“合同”概念。希尔伯特采用的说明如下:
两线段 (角 )的 “合同 ”,是了解为借助于运动 ,一条线段从另一条得到的可能性 。
同时,一个运动,是了解为原文中直接用公式给定的变换(三种类型)继续施行而成的,把平面换成它自身的任意一个变换[(x ,y )应该了解为平面的任一点,而(x ′,y ′)是它所变成的点]。
于是在解释中,合同性 的确定是通过运动 的,而运动的确定是纯粹解析方式的(由于所供给的公式的任务),对应于解释的解析特征。
若干初等的计算,从外表看来完全和通常的解析几何中的对应的计算相同。现在指出运动的下列性质:
1.由于变换的线性,(x ,y )间的线性相关引出(x ,y )间的线性相关:直线变成直线。
2.由于相同的原因,x 跟随着直线上点列而单调的改变,必引出x ′跟随着变换成的直线上点列而单调的改变:直线上的点的顺序保持不变。
3.两个运动的继续施行仍给出一个运动。
由此得到,在解释中公理Ⅲ2 满足了。
4.存在着一个互换一个给定了的角的两条边的运动,而且存在一个互换一条给定了的线段的两端点的运动。
这容许我们能通过运动使得两个合同角中的一个角的预先给定了的一条边和另一个角的预先给定了的一条边重合;对于线段也同样如此。
5.恰存在着一个运动,把一条给定了的射线l 移动到和另一条给定了的射线l ′重合,使得l 的直线所规定的一个给定了的半平面变成l ′的直线所规定的一个给定了的半平面。
由此立刻得到,公理Ⅲ4 ,Ⅲ1 所变成的那些命题的正确性。
6.若在第5种情形中只要求l 和l ′重合,则能由两个方式实现那个运动,但是在这两种情形下,l 的直线的点都同样地变换。
由此立刻得到,公理Ⅲ5 和Ⅲ3 在这解释中所得到的解释的正确性。
【38】这里所谈的是罗巴契夫斯基的非欧几里得几何的射影解释 。这解释的实质在于把罗巴契夫斯基空间中的几何形和关系,看做是通常空间中的椭球的内部中的一定的几何形和关系(最好是用射影的观点);还可以取椭球的特殊情形——球——替代椭球。在克莱茵(F. Klein)的书《非欧几里得几何》中能找到这问题的说明。
【39】这里援引定理36,是不恰当的,例如EF ≡E 1 F 1 这事实立刻容易看出。事实上,根据定理12,三角形ADE 和ADE 1 合同;由于定理15,还得到∠EAF ≡∠E 1 AF 1 ,而且再根据定理12,由此推得三角形AEF 和AE 1 F 1 合同,因而线段EF 和E 1 F 1 也合同。
【40】换句话说,领域Q (t )是一个域;事实上,对于领域的元素如同对于t 的代数函数一样,加、减、乘和除的运算连同它们通常的性质都是确定的,而且运算的结果仍旧是这个领域的元素。
【1】可从 的《黎曼的非欧几里得几何引论》(
的《黎曼的非欧几里得几何引论》(
 ,1934),认识椭圆几何。
,1934),认识椭圆几何。
【42】在所研究的平面上,不但假设关联公理I1~3 ,顺序公理II和合同公理Ⅲ满足了,而且平行公理Ⅳ也满足了。所以这里所援引的所有的定理(特别,任意一个三角形的内角和等于两直角)。都完全如同在通常平面几何一样的证明了。
在阅读本章时要想有正确的看法,必须记着,同通常的平面几何比较起来,我们现在只缺少了连续公理,首先是阿基米德公理 。而这就是说,我们失掉了把线段的比的概念当做数的概念来引进的办法,因为两条取定的线段中的一条,和另一条比较起来,可以是无穷大。没有这样的线段的比的概念,我们便不能形成相似形的概念 ,如同在通常的平面几何那样。顺便说明,关于弦c ,股a 和它相邻的角α (在直角三角形中),正文中所断定的只是说,a 是c 和α 的函数:a =αc ,而不是说,a :c 是α 的函数。这种情形一般地说明了缺少相似理论和线段的比的概念。
第三章的基本目的是解除因缺少阿基米德公理而造成的困难,建立一个也适用于非阿基米德几何的相似理论 。为此,希尔伯特建立所谓线段的计算法,这种计算法使得有可能引进两线段的比的办法;把两线段的比不当做是一个数,而当做是这种新计算法的一个元素(还参看§15,§16)。
【43】证明在这里有漏洞,因为从合同式(6)只能得到,垂足或者重合,或者对于点O 对称。还必须证明后者不可能。
两条通过点O 的直线中的每一条都被点O 分成两条射线;用1,2表示一条直线上的两条射线,用3,4表示另一条上的两条射线。对于线段l ,l * ,…的每一条,我们规定以和它对应的一个置换如下:若给定了的这条线段的端点在射线1,3上或2,4上,这置换就
是(13),(24);若端点在射线1,4上或2,3上,是置换是(14),(23)。让读者证明,对应于平行线段的置换必定是同一个(因为平行线段,对于通过点O 的平行直线来说,或者在这直线的同侧,或者在这直线的异侧)。
因为道路AC ′BA ′CB ′A 从开始的射线OA 回到这同一条射线,所指出的这些置换的乘积
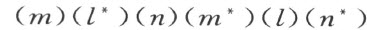
只能是单位元(这里的(m )表示对应于线段m 的置换,等等)。但是在所考虑的置换群[(12)(34),(13)(24),(14)(23)]中,两个置换的乘积是群的单位元,只当这两个置换恒等。所以 。由于m 和m 平行,而且l 和l 平行,置换(m )即(m ),而且(l )即(l )。由此得
。由于m 和m 平行,而且l 和l 平行,置换(m )即(m ),而且(l )即(l )。由此得

换句话说,n * 的两端点或者在n 所在那同一个角的边上,或者在对顶角的边上。
所以,若通过点O 作直线n 0 平行于n ,则线段n 或者整个地和n 在n 0 的同侧,或者整个的在另一侧。通过点O 作n 的垂线(因而,也是n 0 的垂线)。从n 的两端点,作前一条的两条垂线。这两条垂线都平行于n 0 ,这就是说,每一条都在n 0 的同侧。因为n * 的两端点在n 0 的同侧,则这两条垂线在n 0 的同侧,而且它们的垂足也在n 0 的同侧。
因此,这些垂足不可能对于点O 对称,这就是所需要证明的。
【44】这第三个证明假设A ,B ,C 在同一条从点O 出发的射线上,但不假设OA ′≡OC 。所以现在的情形比第一个叙述特殊,而比第二个普遍。
注意,从A ,B ,C 在点O 的一侧,即得A ′,B ′,C ′也在点O 的一侧(这事实在第一和第二情形的证明中都默认了)。事实上,从CA ′和AC ′的平行,推得:对于通过点O 而又平行于它们的一条直线,这两条线段或者在这直线的一侧,或者在两侧。但第二命题不可能,因为线段AC 不含有点O 。在这种情形下,第一命题成立,这就是说,线段A ′C ′也不含有点O ,即A ′,C ′在点O 的一侧。
同样地,从CB ′和BC ′的平行,推得B ′,C ′也在点O 的一侧。总之,若A ,B ,C 在一条射线上,A ′,B ′,C ′也如此。
【45】明确地说,若首先限定作线段ab (非线段ba ),然后连接ab 的端点和角的第一条边上线段a 的端点,则由于巴斯噶定理,所得到的直线平行于连接角的第一条边上线段1的端点和角的第二条边上线段b 的端点的直线(正文中的图46)。而这就是说,线段ab 同时也是线段ba。
【46】我们记着,在本章里假设我们的几何里除连续公理之外的全体公理都存在;所以我们没有理由“利用圆规”,即利用当做是连续不断的曲线的圆。
因为这个缘故,在我们的几何里还可能有下述情形:一条直线既有点离圆心比圆半径长,也有点离圆心比圆半径短,但是这直线不和圆相交(好像这直线趁我们几何中缺少连续性时,“穿进”圆里去了)。
【47】由于定理42,我们应该特别注意下述事实。线段计算还有一些任意性;一条作为1的线段是任意选取的,而且乘法运算就依赖于这种选取。另一方面,比例的概念虽然也根据于线段的计算法,但是和这种任意性无关。这是能够从比例的几何意义(定理42)看出的。
因此,相似性理论不含有任意性,并且是完全由几何系统推演出来的。
【48】这里说到扩充了的线段计算时,我们的运算不只是对于正线段,而且也对于负线段和零线段。
首先,必须注意到,在§15中线段(现在可以叫做正线段)的计算法,只对于不考虑在平面上的位置和端点的顺序 的线段作运算。现在作运算的线段,我们了解作是端点有固定顺序的线段,而且是在有固定指向的直线上的。端点重合的线段(零线段)也允许是有的。
现在只在下述的意义下两条线段才认为相等;它们既合同又同指向(即它们同在它们的直线的正向,或同在负向)。
现在,两条线段的加法确定第三条线段,它的起点是第一条的起点,而它的终点是第二条的终点;而且在下列条件之下:它们都在同一条直线上,而且第一条的终点和第二条的起点重合。
线段的乘法形式完全如同§15中一样的确定(和§15中只有下列差别:负线段不在给定了的角的边上,而在对顶角的边上)。
对于扩充了的线段计算法,性质1~16的验证不会再呈现任何原则上的困难。
【49】我们来明确这里所下的定义。我们说,多边形P 剖分成多边形P 1 +P 2 +P 3 …+P k (处处都只考虑简单多边形,参看定理9),若是:
1。多边形P 1 ,P 2 ,…,P k 的每两个没有公共内点;
2。多边形P 1 ,P 2 ,…,P k 的内点也都是P 的内点;
3。反之,P 的每一个内点或者是P 1 ,P 2 ,…,P k 中一个多边形的内点,或者至少是属于P 1 ,P 2 ,…,P k 中一个多边形的边界(在后一种情形时,能够证明,这点至少还属于这些多边形中的另一个的边界)。
设一条简单折线,只通过P 的内点,而且它的端点在P 的边界上。正文中断定:每一条这样的折线剖分多边形P 成两个多边形。这个论断,严格地说,是一条需要证明的定理。我们不在这里证明这个论断,而且,在本章中我们基本上不贪图用注解来引进每一个证明。理由如下:凡是有关用多边形的周界来剖分平面成几部分的问题,若要在顺序公理的基础上,毫无缺陷地严格地阐明它们,都特别繁难。这事实,已经能够从最简单的命题,例如定理9中,看出来了。
所以,在本章的范围内,依照需要我们和希尔伯特采取一些二元论的观点。我们不放弃证明,正文中缺少的证明我们要在注解中加以补充;但是同时,关于剖分平面成若干部分这个事实,我们常常把它看做是足够明显的,从而省略掉从顺序公理出发的严密推证。“明显”这个词,不但是说显然无疑,还说:若愿意时,严密的证明总是能够实行的。
当然,读者应该了解,从很严密的观点来说,每一个这样情形下的证明,是存在着缺陷的。例如在正文中定理43的证明里,因为明显而承认下列事实;对于多边形P 3 的两个剖分,其中一个的诸线段使另一个中的每一个三角形得到一个剖分,反之亦然;其次,如此再剖分所得到的多边形,在这两种情形下,都完全相同;最后,每一个多边形能分成三角形。
诸如此类的事项,几乎在本章每一个证明中都可能发现。在合同性概念这方面,证明仍然是严格的。
【50】证明“拼补相等”这个概念的传递性,就是证明:若是多边形P 和Q 之中的每一个都和多边形S 拼补相等,则它们就彼此拼补相等。
首先注意,希尔伯特关于多边形拼补相等这个概念的定义和下述的定义等价:两个简单多边形P 和Q 拼补相等,若存在着有限对合同的三角形
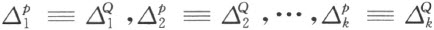
能把它们连接到P 和Q 上去(不互相叠盖),使得如此合并成的多边形

剖分相等。以后我们通常只说一个三角形△,用这种说法来替代一对合同的三角形△ P =△Q 。
于是,我们能够连接诸三角形 到P 和S上去,使所得到的多边形
到P 和S上去,使所得到的多边形

剖分相等。完全照样地,能够同时连接这样的诸三角形 到Q 和S上去,使所得到的多边形
到Q 和S上去,使所得到的多边形

变成剖分相等。
若是现在正如把三角形 连接到S 上去一样的,同时也把三角形
连接到S 上去一样的,同时也把三角形 ,这样联接到S 上去,那么,一般说来,若干三角形△′会叠盖着若干三角形△″。设这些三角形的公共部分是多边形
,这样联接到S 上去,那么,一般说来,若干三角形△′会叠盖着若干三角形△″。设这些三角形的公共部分是多边形
S 1 ,S 2 ,…,S m
再设在去掉这两组三角形△′和△″的这些公共部分之后,剩下的分别是两组多边形

这样一来(注图27)
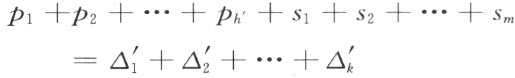
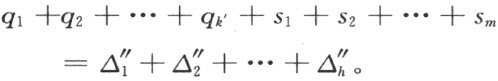
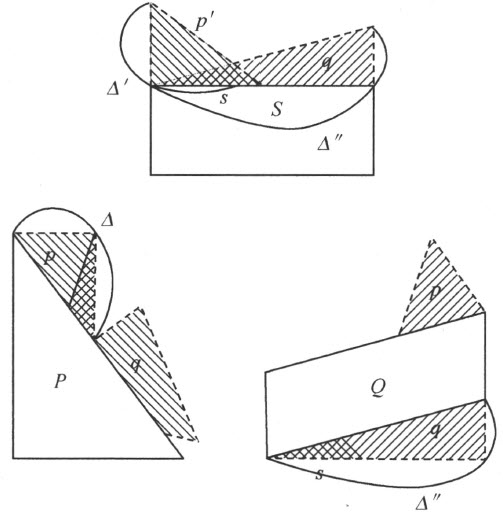
注图 27
把所有的多边形p i ,q i ,S i 都连接到S 上去;这样从S 得到的多边形用S 表示。把多边形q 1 ,q 2 ,…,q k ′ 连接到多边形p ′上去。结果我们得到的多边形P 和多边形S * 剖分相等,因为
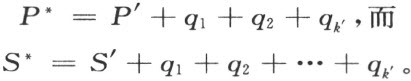
现在把多边形p 1,p 2,……,P h ′ 连接到多边形Q ″上去。结果我们得到多边形Q ,也和多边形S 剖分相等。多边形P 和Q 中的每一个都和多边形S * 剖分相等,所以它们应该剖分相等。
因为
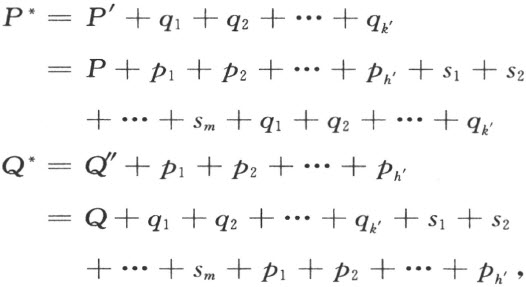
那就表出了下述事实:若相同的多边形p i ,q i ,si 都连接到多边形P 和Q 上去,我们就得到剖分相等的多边形;而这正是说:多边形P 和Q 拼补相等。
当多边形si 的集合是空集时,就是当△′这一组三角形中没有一个能叠盖着△″这一组三角形中的一个时,我们的全部证明显然还保持有效。
现在证明“拼补相等”这个概念的可加性 ,就是证明:若是多边形A ′和B′分别拼补相等于A 和B ,则由多边形A 和B 不互相叠盖而拼成的多边形(用A +B 表示)拼补相等于由A ′和B ′也不相叠盖而拼成的多边形A ′+B ′。
设按照确定的方式把三角形a 1 ,a 2 ,…,a h 连接到A 和A ′的每一个上去时,所得到的多边形剖分相等。设对于多边形B 和B ′,把它们的每一个连接上三角形b 1 ,b 2 ,…,b k 之后,也有了同样的结果。现在取多边形A +B 和A ′+B ′,而且把它们之中的A 和A ′连接上三角形a 1 ,a 2 ,…,a h ,B 和B ′连接上三角形b 1 ,b 2 ,…,b k ;正如同在建立多边形A 和A ′、B和B′拼补相等时所作的一样。
考虑多边形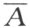 和
和 :
:
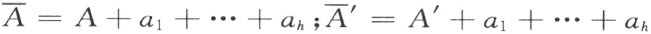
和多边形 和
和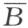
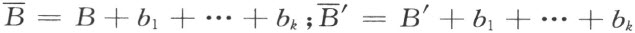
按照定理的条件,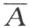 和
和 剖分相等。就是能够把它们剖分成相同的(在合同的意义下)三角形
剖分相等。就是能够把它们剖分成相同的(在合同的意义下)三角形
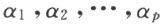
同样地,能够剖分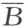 和
和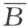 成相同的三角形
成相同的三角形

处理三角形a i 中的每一个如下:考虑多边形 中的α i 。剖分
中的α i 。剖分 成A +a 1 +…+a h 的诸线段能够穿过三角形α i ,而且把它剖分成若干部分。现在再考虑三角形α i 在
成A +a 1 +…+a h 的诸线段能够穿过三角形α i ,而且把它剖分成若干部分。现在再考虑三角形α i 在 中所占的位置;同样地,在α i 上有剖分
中所占的位置;同样地,在α i 上有剖分 成A′+a1 +…+a h 的诸线段。同时把这两个位置中的、落在α i 上的所有的分割线段都画在α i 上。一般说来,α i 中的每一个都被分成更细小的部分。这些部分用
成A′+a1 +…+a h 的诸线段。同时把这两个位置中的、落在α i 上的所有的分割线段都画在α i 上。一般说来,α i 中的每一个都被分成更细小的部分。这些部分用
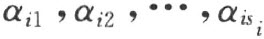
表示,而且在再加以剖分之后,都可以看做是三角形。
显然,从α ij 的全体可以拼成所有的α i ,因此也能够拼成 和
和 。同时,根据α ij 的作法,
。同时,根据α ij 的作法, 中的多边形A ,a 1 ,a 2 …,a h 和
中的多边形A ,a 1 ,a 2 …,a h 和 中的多边形A ′,a 1 ,a 2 ,…,a h ,每一个显然都能恰好分为若干个三角形α ij 。
中的多边形A ′,a 1 ,a 2 ,…,a h ,每一个显然都能恰好分为若干个三角形α ij 。
我们用完全类似的方法,作成三角形β ij 的全体,使得由它们既能拼成 ,也能拼成
,也能拼成 ,而且
,而且 中的多边形B ,b 1 ,…,b k 和
中的多边形B ,b 1 ,…,b k 和 中的多边形B ′,b 1 ,…,b k 的每一个都能恰好分为若干个三角形β ij 。
中的多边形B ′,b 1 ,…,b k 的每一个都能恰好分为若干个三角形β ij 。
现在考虑诸三角形a ij 如何拼成 ,和诸三角形β ij 如何拼成
,和诸三角形β ij 如何拼成 。
。
在A 中的这些α ij ,简略地用α * 表示;那些不在A 中的,即那些在a 1 +a 2 …+a h 中的α ij ,用α 表示。
同样地,用β * 表示在B 中的那些β ij ,用β 表示那些不在B 中的,即那些在b 1 +b 2 +…+b k 中的β ij 。
α 和β 显然不能交叠起来;而α 和β ,α 和β ,α 和β 能够交叠起来。
取三角形α 和β 的公共部分,β 和α 的公共部分,以及α 和β 的公共部分,而且把它们(即是,和它们合同的多边形)添加到 和
和 上去,添加时使它们不交叠在
上去,添加时使它们不交叠在 上,也不交叠在
上,也不交叠在 上,而且它们自己也不彼此交叠起来。所得到的图形
上,而且它们自己也不彼此交叠起来。所得到的图形 显然剖分相等于多边形
显然剖分相等于多边形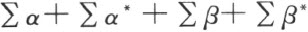 ,而后者是由所有的三角形
,而后者是由所有的三角形 (即由所有的α ij 和所有的β ij )按照某种方式拼成的,而且不交叠起来的。同时,图形
(即由所有的α ij 和所有的β ij )按照某种方式拼成的,而且不交叠起来的。同时,图形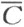 的、在A 和B 以外的部分,显然剖分相等于多边形
的、在A 和B 以外的部分,显然剖分相等于多边形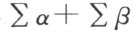 ,而后者是由所有的三角形α 和β ,按照某种方式拼成的,而且不交叠起来的。所以前者剖分相等于多边形
,而后者是由所有的三角形α 和β ,按照某种方式拼成的,而且不交叠起来的。所以前者剖分相等于多边形
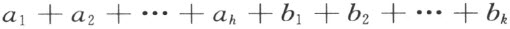
这是由a i 和b j 按照某种方式拼成的,而且不交叠的多边形。
对于多边形A ′和B ′重复同样的作法。图形 将和
将和 剖分相等,因为它们都剖分相等于由所有的α ij 和所有的β ij 不交叠起来而拼成的同一个多边形(在这两种情形下,α ij 和β ij 都是公有的,虽然它们分开成α 和α ,β 和β 可能有区别)。
剖分相等,因为它们都剖分相等于由所有的α ij 和所有的β ij 不交叠起来而拼成的同一个多边形(在这两种情形下,α ij 和β ij 都是公有的,虽然它们分开成α 和α ,β 和β 可能有区别)。
其次,在A ′+B ′之外的部分 ,剖分相等于在A +B 之外的部分
,剖分相等于在A +B 之外的部分 ,因为它们两个都剖分相等于由a 1 ,a 2 ,…,a h ,b 1 ,b 2 ,…,b k ,不交叠起来而拼成的多边形。
,因为它们两个都剖分相等于由a 1 ,a 2 ,…,a h ,b 1 ,b 2 ,…,b k ,不交叠起来而拼成的多边形。
定理证毕。
【51】预先证明下述论断:连接三角形的一个顶点(A )和对边(B C)上的任意一点(M )的线段,恰短于其他两条边的一条(AB 或A C)。
理由如下(参看注图28)。因为点M 在线段B C上,所以线段BM 和M C在直线AM 的两侧,而且∠AMB 和∠AM C是邻补角。因而其中的一个,例如∠AMB ,必须是直角或钝角,而另一个(∠AM C)是直角或锐角(定理11)。所以,由于定理22,∠BAM 和∠ABM 都是锐角,因为它们都小于∠AM C。应用定理23到三角形ABM ,就得到
AM <AB

注图 28
现在证明:完全在三角形之内的线段KL 短于三角形的三条边的一条(注图29)。根据注解[15]中的引理Ⅲ,任意一条从三角形内点出发的射线,穿过三角形一次。设直线KL 上的两条射线中,从K 出发的而不含有L 的那条射线,交三角形于一点P ;而且设同一条直线上的两条射线中的、从L 出发的而不含有K 的那一条射线,交三角形于一点Q 。K 和L 是显然都在P 和Q 之间。
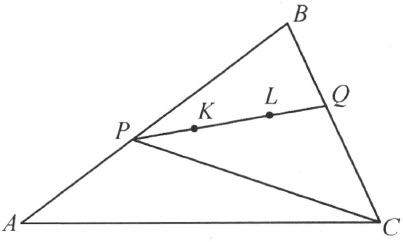
注图 29
P 和Q 两点中的一个,姑且说是Q ,应该在三角形的一边上,例如在边BC 上;另一点或者在其他边上,例如AB ,或者和顶点A 重合。从线段的不等的定义,得

用线段连接P 和C ,而且应用上述的论断的证法两次:一次对于三角形BPC 和线段PQ ,一次对于三角形ABC 和线段CP 。我们得到

和

(当直线KL 通过顶点,即当点P 和点A 重合时,等号成立)。从不等式(1),(2),(3)和不等式

得知下述三个不等式
KL <AB ,或KL <AC ,或KL <BC
中的一个成立。
【52】从定理46推知:恒能求得一个直角三角形,拼补相等于一个已知三角形ABC 。要想证明后者和一股等于1的一个直角三角形拼补相等,在边CA 上取C E=1,并且从点A 引直线AM 平行于BE (注图30)。根据定理46,三角形BEM 和BEA 拼补相等。因为三角形ABC 由BC E和BEA 拼成,而三角形CEM 由BCE 和BEM 拼成,从可加性定理(注解[50]),三角形ABC 和CEM 拼补相等。
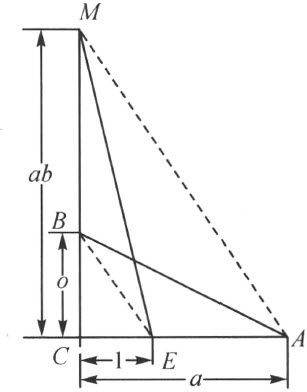
注图 30
在CA <1时,图将会不同。
【53】这里的意思是要作一个新的直角三角形,它的一股等于1,而另一股等于原先的诸直角三角形中不等于1的诸股之和。取这新三角形的第二股作为它的底边,因而它就是原先的诸直角三角形的诸底之和。用连接新三角形的顶点C 和底的分点的诸线段,分割这新三角形。所分成的诸三角形,根据定理46,和原先的诸三角形拼补相等,因而(定理43)也和原来的简单多边形所分成的诸三角形拼补相等。
根据可加性定理(注解[50]),原来的多边形和我们所作成的直角三角形拼补相等。
【54】我们来明确全部的叙述。
一条直线称为有向的 ,若指出了它的任意两点A ,B 的先后顺序,这个顺序应该满足下述要求:
若B 在A 之后,而且C 在B 之后,则1)C 在A 之后,2)B 在A 和C 之间。
我们断定,若在直线上指出任意两点,例如L 和M ,而且要求M 在L 之后,则唯一地规定了在上述意义下直线的一个方向。
若再取任意两点A ,B ,则根据定理6,点A ,B ,L ,M 能够依次写出,使得顺序的写法符合于几何的排列顺序(在“介于”这关系的意义下)。再者,还要求在这种写法中,点M 在L 之后。那么这种写法是完全的、唯一的决定了,因而我们就把在这种写法中点A ,B 的先后顺序作为这些点在直线上的先后顺序。
满足要求1)和2)是不难证实的。为了证实,只要对于五个点A ,B ,C ,L ,M 引进相似的写法,而且运用根据定理6而知道的这种写法的性质。应该注意的是,若从这个写法删去一个点,例如C ,则所得到的是先前的对于四个点的那个写法,因而点A ,B 的先后顺序在这两个写法中完全一样。
在有向的直线的一定点O 之后的点,显然组成一条半线(射线)。此后,凡是说直线 ,都了解为有向的直线 。
现在能够实行引进平面的定向如下。对于平面的每一条直线,我们把由它所形成的两个半平面的一个称为“左”半平面,而另一个称为“右”半平面。而且,在把直线的方向改为相反方向时,我们就互换这两个名称。
我们说,平面有了定向 ,若“左”和“右”半平面的选择,在下述的意义下是协调的;对于任意两条交于一点O 的直线a ,b ,若在点O 之后的半直线a 在b 的“右侧”时,则在点O 之后的半直线b 就在a 的“左侧”,而且反过来也对(注图31)。
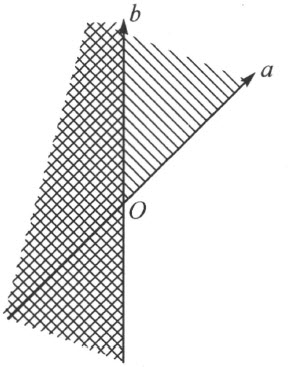
注图 31
我们简略地说,两条相交的直线a ,b 是“协调的”,若对于它们来说,“右”半平面和“左”半平面的选择满足所指出的要求。在把这两条直线中的一条的方向改为相反方向时,“协调性”显然保存而不被破坏(此时,应当记着“右”侧和“左”侧已互相调换)。
我们的任务如下:我们要证明,在对于任意一条直线a 任意的取定了“左”和“右”半平面之后,对于所有的其他每一条直线,都能够取定“右”和“左”半平面,使得任意两条相交的直线“协调”。
设从直线a 开始,对于它我们任意取定了“右”和“左”半平面。对于所有的其他和a 相交的直线b ,我们再规定“左”和“右”半平面,使得a 和b 都协调(若在点O 之后的半直线b 在a 的“左”侧,那么我们把b 所决定的两个半平面中的一个、含有在点O 之后的半直线A 的,称为b 的“右”半平面)。
不和直线a 相交的那些直线c ,一定和一些直线b 相交。对于这种c ,我们利用和它相交的任意直线b 的协调来规定c 的“左”侧和“右”侧。
为了证实任意两条相交的直线“协调”,只需要证明“协调性”是可传递的;若两条直线和第三条“协调”,前两条就互相“协调”。
理由。从“协调性”的传递性,立刻就得到,任意两条相交的直线b 互相“协调”;其次得到,若直线c 和交它的诸直线中的一条b “协调”,c 就和交它的任意一条直线b 2 “协调”[若必要时,首先指出c 和一条辅助直线b 3 “协调”,然后就得到和b 2 “协调”(注图32)]。最后,任意两条相交的直线c 1 和c 2 互相“协调”。理由。设c 1 和b 1 “协调”,c 2 和b 2 “协调”,那么c 1 和b 3 ,c 2 和b 4 “协调”(注图33)。因为b 3 和b 4 恒互相“协调”,c 1 和c 2 也“协调”。
注图 32
注图 33
于是,我们来证明“协调性”的传递性。
设三条直线 a ,b ,c 两两相交 。若 a 和 b 协调 ,a 又和 c 协调 ,那么 b 和 c 互相协调 。
第一种情形:a ,b ,c 组成三角形 ABC (注图34)。为明确起见,设a ,b ,c 的方向就由 表出(“协调性”不因改换直线的方向而被破坏)。设点A 在a 之“左”,那么在c 之后的半直线b 也在a 之“左”,而这就是说(根据“协调性”),在c 之后的半直线a ,在b 之右。同理,a 上的在c 之前的点B 是在直线a 的另一条半直线上,既在b 之“左”。同理 ,在 A 之后的半直线 c ,即
表出(“协调性”不因改换直线的方向而被破坏)。设点A 在a 之“左”,那么在c 之后的半直线b 也在a 之“左”,而这就是说(根据“协调性”),在c 之后的半直线a ,在b 之右。同理,a 上的在c 之前的点B 是在直线a 的另一条半直线上,既在b 之“左”。同理 ,在 A 之后的半直线 c ,即  ,在 b 之左 。
,在 b 之左 。
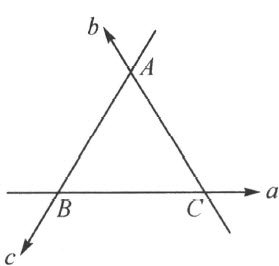
注图 34
现在再运用同样的论证,从在B 之后的半直线c 出发,因而是从在a 之后的半直线c出发。根据“协调性”,在B 之后的半直线a 是在c 之“左”,点C 也在c 之“左”,而且在 A 之后的半直线 b 在 c 之 “右 ”。
比较上文强调指出的结果,无疑地得到直线b 和c 的“协调性”。
第二种情形:a ,b ,c 三线共点 ,(注图35)。
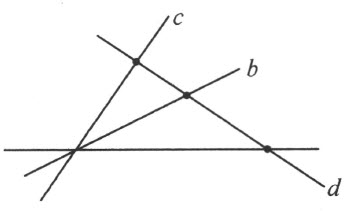
注图 35
取第四条直线d ,交a ,b ,c ,但不通过它们的公共点,而且使直线d 和a “协调”。根据第一种情形,d 既和b “协调”,也和c “协调”;因此b 和c也互相“协调”。
【54a 】在§17的开始,曾经指出过线段(连带它们的符号)的演算要服从§13中的规则1~16,特别是那加法的交换律与结合律。应用这些规则,可将右端的各加项重新组合,使得只有符号不同的线段先加起来,其结果它们都在和中消去了。
如同证明中所提到的。引用分配律,使我们能断定下述事实:当一个三角形的底边是另两个三角形的底边的和,而所有三个三角形的高线都合同时,则第一个三角形的面积——底边与高线的乘积的一半——是另两个三角形面积的和。
【55】事实上,若是我们有了已知多边形P 分为三角形的两个剖分,那么如同定理43的证明中所曾指出过的,可以作分为三角形的第三个剖分,那就是前两个剖分中的每一个的剖分。取第三个剖分的诸三角形面积度量的和,并且把所有的加项分成组,使得每一组的诸三角形都属于第一个(第二个)剖分的同一个三角形。按定理50,每一组的加项给出了第一个(第二个)剖分的一个三角形的面积度量,而全体的和给出了第一个(第二个)剖分的诸三角形面积度量的和。这样看起来,第一个与第二个剖分的诸三角形面积度量的和都等于同一个线段。
【56】援引定理50是多余的,直接从定义就能推得剖分相等的多边形的面积度量相等。
从多边形面积度量的定义,也直接推得;由若干多边形拼成的一个多边形的面积度量(参看注解[49])等于各组成部分的面积度量的和。由于这个结果,等式
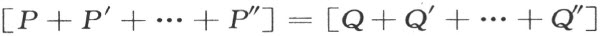
可以改写成:
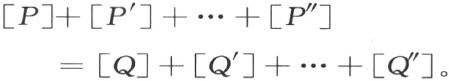
这就是正文的下一段所需要的。
【57】读者注意公理Ⅳ与Ⅳ 之间的区别,公理Ⅳ和Ⅳ 都一样地否定下述的可能性:通过已知点A 能作多于一条直线,不与一条已知直线(总是在已知平面α 上的)相交。但公理Ⅳ* 除此以外还断定恒可能作这样的一条直线;公理Ⅳ没有包含这样的论断。问题是在于早先我们有合同公理时,这论断已经被证明了 ;而现在不可能证明这个论断,必须把它当做公理。
【58】整个的第五章属于建立在公理Ⅰ,Ⅱ,Ⅳ* 上的几何,按照作者的意见,那其实就是只是取消了连续公理的射影几何 。我们应该在这里表出所讨论的几何的射影性质,因为否则就不能充分地说明德沙格定理出现的理由。
首先注意,从公理Ⅳ* 推出下述事实:若两条直线与第三条直线平行,则前两条直线相互平行(这里的平行直线所指的是在一个平面上而无公共点的直线)。
引理1 设三条直线a ,b ,c 中的二直线a 与b 在平面γ 上,二直线b 和c 在平面α 上,c 和a 在平面β 上(其中α 和β 是不同的平面)。那么,若a 和b 有公共点C ,则这点C 必在c 上。
首先,γ 和α 不同,又和β 不同:假若γ 和α 相同,那么γ 上就会含有直线a 和c ,就要和β 相同(由定理2)。
直线a 和b 的公共点C 在所有的三个平面α ,β ,γ 上;但平面α ,β 有公共的直线c ,并且除 C 以外 ,平面 α , β 没有其他的公共点 (定理1)。因此,点C 属于c 。
引理2 若三直线a ,b ,c 。中a ∥b ,a ∥c ,则也有b ∥c 。
用γ 表示平面(a ,b ),β 表示平面(a ,c )。若γ 和β 相同,则b 和c 在同一个平面上并且无公共点——否则,违反公理Ⅳ* ,通过这个公共点可作两条平行于a 的直线。因此b ∥c 。
若γ 和β 不同,则通过b 上的任一点B 和C 作一平面(定理2),并且α 表示(B 点不在C 上——否则由公理Ⅳ* ,b 和c 就重合)。平面α 和γ 不同(否则C 就在γ 上而β 就和γ 重合)。就b ′表示α 和γ 的公共直线(因为α 和γ 有公共点B ,它们就有公共直线(定理1))。
假若b ′和b 不同,那么,由公理Ⅳ* (平行的唯一性),b ′就和a 有公共点;然后,由引理1,这个点就在c 上,但这是不可能的,因为a ∥c 。
于是,b ′和b 重合,而这就是说,b 和c在一个平面α 上。假若b 和c相交,那么,由于引理1,直线a 就通过这交点,但这是不可能的。因而b ∥c。
空间中平行于一条已知直线的全体直线,叫做一个平行把 ;由于引理2,平行把中所有的直线,都相互平行。
我们不再停下来阐述平面和直线之间与两平面之间的平行理论了,因为如同在平常的立体几何中一样,我们能毫无困难地推出这些理论,而且由于引用公理Ⅰ和Ⅳ* 的结果,这种推证还是十分严格的。现在转到射影空间 的建立。把每一个平行把对应空间中的一个新元素,叫做一个假点 。当且只当两个平行把相同时,它们所规定的两个假点才认为相同。
定义 我们说一个假点属于一条给定的直线,当且仅当这给定的直线是对应的平行把中的一条。
这样看来,现在可以说,一个平行把中的所有的直线都有一个公共的假点。
定义 我们说一个假点属于一个给定的平面,当且仅当这个平面平行于对应的平行把中的诸直线(即是平面上有一平行束,属于这平行把)。
这样看来,因为平面上的每一个平行束有一个假点,在一个给定的平面上就有无穷多个假点。
定义 一个给定的平面上的全体假点的集合叫做这平面上的一条假直线 (3) 。
显然,平行平面的所有的假点都是这些平面的公共点,因而平行平面有公共的假直线。
定义 全体假点的集合叫做一个假平面 (于是,假平面是唯一的)。
射影空间的建立已完成了,我们把点、直线和平面,无论是原来有的(真的)或是新引进的(假的),都看成彼此之间毫无区别。
下列诸基本命题在射影空间中是正确的:
1.两点决定一条并且只一条属于该两点的直线。
2.两平面决定一条并且只一条属于该两平面的直线。
3.点和不属于该点的一条直线决定一个并且只是一个,属于该点及该直线的平面。
4.一个平面和不属于该平面的一条直线决定一个并且只是一个属于该平面和直线的点。
5.不属于一直线上的三点决定一个并且只是一个属于该三点的平面。
6.不属于一直线的三平面,决定一个并且只是一个属于这三平面的点。
特别重要的情形是:命题2,4,6在射影空间中是无条件地正确的,而在原来的空间中它们却例外(平行的情形)。射影空间的优越性就在于达到了完全的普遍性,而元素——假元素——的引进,正是为了这个目的。
至于命题1~6的验证,在下列的基础上都可以完成:在原来的空间中成立的公理Ⅰ,Ⅳ* 和根据于这些公理的平行理论,自然也根据被我们用来引进假元素的定义。验证时,我们分别处理所有的可能情形。例如验证命题4时,平面和直线必须分为下列诸情形:1)相交的,真的,2)平行的,真的,3)假平面,真直线和4)真平面,假直线 (4) 。
根据这些命题就可以证明德沙格定理(平面的)——有价值的射影定理的第一条。这定理叙述如下:
设ABC 和A ′B ′C ′是同一个平面上的两个三角形,它们既不共顶点也不共边(这里所谓边了解为直线 ,不是线段)。
然后,若是1)连接对应顶点的三条直线共点,那么2)三对应边的三个交点在一条直线上,并且反过来,从2)得1)。
这定理在射影空间中是正确的,那就是说,不论所考虑的点和直线是真的或假的,这定理是正确的 (5) 。
我们来考虑德沙格定理的特别情形。
设有性质1),并且除此以外,设两对应边平行,换句话说,两个交点在给定平面的假直线上。由于德沙格定理,应有性质2),即第三对对应边的交点应该在那同一条(假)直线上,就是说第三对对应边也应该平行。
设反过来,所有三对对应边都平行;即有性质2),其中对应边的三个交点都在假直线上。然后,根据德沙格定理,有性质1),那就是说,连接对应顶点的三条直线共点,这公共的点或者是真点,或者是假点(即三直线平行)。
这就是定理53(在希尔伯特的正文中)。
若是在射影空间的结构中我们希望终于消失真假元素间性质的区别,那么我们应该对于直线上的点规定新的顺序关系,照顾到直线上的假点。这一点我们不讲了(对于德沙格定理来说,顺序关系是不起什么作用的);我们只是指出来,点在直线上的射影顺序是循环的,并且虽然在建立射影顺序时,在真点区域中 的“介于”概念和公理Ⅱ都应该利用,但在射影的(用假点扩充了的)直线上,“介于”概念是失去了意义的。
现在我们总结这个注解中所说的:建立在公理 Ⅰ,Ⅱ,Ⅳ* 上的几何 ,实质上是取消了一部分自己的元素的射影空间的几何 。用假元素来扩充原来的空间 ,应该看做是恢复这些取消了的元素 。所得到的,实际就是通常的射影几何,不过取消了连续公理 。德沙格定理的特别地位是说明了几何的射影特征。
【59】取笛卡儿几何中直角坐标x ,y 的OX 轴作为这个非德沙格几何的轴。对于公理I1 和I2 的满足,只在下列情形中有可怀疑的地方:当给定的点A (x 1 ,y 1 )和B (x 2 ,y 2 )在不同的半平面上,同时连接这样两点的普通直线在正半平面上和轴的正方向作成锐角。换句话说,若A (x 1 ,y 1 )在正半平面上,则y 1 >0,y 2 <0,x 1 >x 2 ,若非德沙格直线AB 存在,用C (x ,0)(注图36)表示它和轴的交点,从非德沙格直线的定义推知,

或者
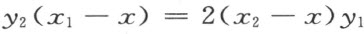
由此

注图 36
由此可见,因为y 1 >0,-y 2 >0,x 在x 1 和x 2 之间,所以射线CA 和射线CB 在正半平面上的延长将和轴的正向作成锐角。非德沙格直线AB 的存在和唯一性证明了。
公理I3 ,Ⅱ1~3 ,Ⅲ1~3 ,Ⅳ* ,Ⅴ的满足是完全显然的。甚至于公理Ⅱ4 的证明都不困难;唯一复杂的地方是必须考虑三角形的位置的所有可能情形。
【60】换句话说,这里所指的角是下述情形之一:1)它的顶点在轴外,2)它的顶点在轴上,而它的两条边的任一条都不是既在正半平面上,又和轴的正方向作成锐角(的射线)。
【61】这里不要求点E 紧跟在 点O 之后;OABE ,AOBE 等等排列顺序都可能。我们还能够不管点O 跟在点E 之后的相反的情形,由于定理5,可以把排列顺序反转过来,因而可以用反转过来的排列顺序替代。
【62】作为例子,我们来证明§13中规则15和规则16在德沙格数系中的正确性。在证明之前我们做一些说明。
设在平面α 上给定了两直线a 和a′,又设直线a 上的点A ,B ,C ,…,K ,L 有某种排列顺序。通过这些点,我们作相互平行但不与a ′平行的直线(并且不与a 重合)。这些平行线与直线a ′的交点A ′,B ′,C ′,…,K ′,L′ 叫做点A ,B ,C ,…,K ,L 的(平行的)射影。
引理I 从公理Ⅰ1~3 ,Ⅱ和Ⅳ* 推知,直线a 上的点的排列顺序和这些点在直线a ′上的射影的排列顺序相同。换句话说,若是在直线a 上取三个点A ,B 和C ,而且点B 在A 和C 之间,那么在a ′上的点B ′在A ′和C ′之间(注图37)。
注图 37
证明 因为点C 在线段AB 外,所以,点A 和B 在直线CC ′的同一侧。因为直线AA ′和BB ′都平行于CC ′,所以,点A 和A ′,B 和B ′都应该在CC ′的同一侧(参看注[13]),而点A ′和B ′都在直线CC ′的同一侧(参看同一个注),那就是说,点C ′在线段A ′B ′之外。因而,点A ′,B ′,C ′的排列顺序与A ,B ,C 的排列顺序相同。
推论 设直线a 上的线段AB 不和直线a ′相交,那么,点A ,B 在直线a ′上的射影A ′,B ′在a 的同一侧。
当直线a 和a ′平行时,这个推论的正确性是显然的,因为若是A ′和B ′在直线a 的异侧,那么直线A ′B ′,也即是直线a ′,将会和a 相交。若是直线a 和a ′交于某一点O ,而且点B 在线段AO 上(注图37),那么,由于引理Ⅰ,点B ′在线段A ′O 上,即线段A ′B ′不和直线a 相交,因此,点A 和B 在a 的同一侧。
引理Ⅱ 设把直线a 上的点A 和B ,利用一个平行束射影到直线a 上的点A ′和B ′又利用另一个平行束射影到同一直线a 上的点A ″和B ″。若是线段AB 上没有直线a 和a 的交点(其中包括这二直线平行的时候),那么点A ′,A ″,B ′,B ″在a 上的位置如下:只要是A ″跟着A ′,B ″就跟着B ′。
根据引理I的推论,射影偶A ′,B ′和A ″,B ″或者都在直线AB 的同一侧,或者在它的两侧。考虑第一种情形,并且先设点A ″和B ′在A ′的同一侧。假设引理不正确,那就是说,点B ″和A ′在B ′的同一侧(注图38)。由公理Ⅳ* ,直线AA ″交BB ′于某一点,设点P 。因为点B ′和A ″在A ′的同一侧,那么射线AA ″和直线BB ′在AA ′的同一侧,因此,点P 在射线AA ″上。属于射线AA ″的点P 应该在AB 的点A ″所在的一侧,因而,在所考虑的情形下,在点B ′所在的那一侧;这样一来,点P 在射线BB ′上。在这种情形下B ′和B ″在AB 的同一侧,并且B ″在BB ′的A ′所在的一侧。也就是说,A 所在的一侧。所以点B ″,因而射线BB ″,都在角ABB ′内,而角的两边上分别含有线段AP 的端点A 和P ;因此,射线BB ′应该和平行直线AA ′上的一条线段相交。我们得到了矛盾。
注图 38
现在设点A ″和B ′在A ′的两侧。在这情形下,引理Ⅱ的不正确就是表示着:点A ″,A ′,B ′,B ″可以在直线a * 排列成所说的顺序。但是在这样排列时(注图39),直线BB ″的射线BQ (射线BB ″的补射线)在BB ′的直线AA ′所在的一侧,而直线AA ″的射线AP (射线AA ″的补射线)在AA ′的直线BB ′所在的一侧。用完全类似上文的讨论,我们证明在这情形下直线AP 和BQ 相交,即引出矛盾。
注图 39
在第二种情形时,点偶A ′,B ′,和点偶A ″,B ″被直线AB 分开了,因而,直线a 和a * (注图40)交于点C ,则引理的正确性是显然的。
注图 40
我们现在来证明,若b >a ,则b +c>a +c。进行下面的作图(注图41)。在角xOy 的边Ox 上取线段OE =1,OA =a ,OB =b ,OC =c。在同一角的另一边Oy 上取线段OE ′=1,并作直线AA ′∥BB ′∥EE′,CN ∥OE ′,和E ′P ∥A ′Q ∥B ′R ∥OE。设直线E ′P ,A ′Q ,B ′R 分别交直线CN (它们都不和CN 平行,由于公理Ⅳ* )于点M 1 ,M 2 ,M 3 。从点M 1 ,M 2 ,M 3 作直线平行于EE ′。设这些直线交OE 于点H ,K ,L 。按照加法定义,我们将有:

注图 41
我们约定把轴Ox 上的点总写成如下的顺序:点E 在点O 之后。因为b >a ,所以按照定义(并且由于上面的约定),B 在A 之后。按照引理Ⅰ,点C,H ,K ,L 在直线OE 上的排列顺序,应该和点C ,M 1 ,M 2 ,M 3 在直线CN 上的排列顺序相同,这就意味着和点O ,E ′,A ′,B ′在直线OE ′上的排列顺序相同,也意味着和点O ,E ,A ,B 在直线OE 上的排列顺序相同。最后的论断所表明的是,例如,若点E 在点O 和点A 之间,那么点H 就在点C 和点K 之间;但是当所有的在轴Ox 上所取的点按约定的顺序写下来时(即E 在O 之后),从这个论断还绝对不能断定点H 在点C 之后。这个结论可以从引理Ⅱ推出。其实,直线E ′P 平行于OE ,所以对于作为点E ′和M 1 的射影的诸点O ,E ,C ,H ,可以应用引理Ⅱ,因而得到,H 在C 之后。
现在已经证明了:点C ,H ,K ,L 在轴Ox 上的先后顺序和点O ,E ,A ,B 的完全一样,用不着把一组中的四个点反转过来(曾在上面证过)。因为B 在A 之后,所以L 在K 之后,这就是需要证明的。
现在我们来证明,若a >b 和c >0,则ac >ba (注图42)。
注图 42
取线段OE =OE ′=1,OA =OA ′=a ,OB =OB ′=b (因而AA ′∥′BB ′∥EE′)和OC =c ,因而点O 不在线段EC 上(那就是说c >0)。再者,从点C 作平行于EA ′和EB ′的直线。设这些直线分别交OE ′于点K ′和L′ 。按照乘法定义,OK ′=ac 和OL′ =bc 。因为在线段EC 上没有直线OE ′的点。所以根据引理Ⅱ,若B ′在A ′之后,则L′ 在K ′之后;实际上这就是需要证明的。
【63】在所有的这些规定之中应该注意乘数的顺序。例如,(u :v :w :r )和(ua :va :wa :ra )这两组不表示同一个平面。
【64】我们要有一个方法来验证公理I和Ⅳ* 。
设在某个数系中§13的规则1~11都满足了,换句话说,这数系是一个域(一般说来,非交换的)。我们必须先建立这个域的代数的某些关系。
考虑域中的任意元素x 1 ,x 2 ,…,xn 变到某些新元素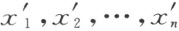 的由下列规律所定的线性变换:
的由下列规律所定的线性变换:
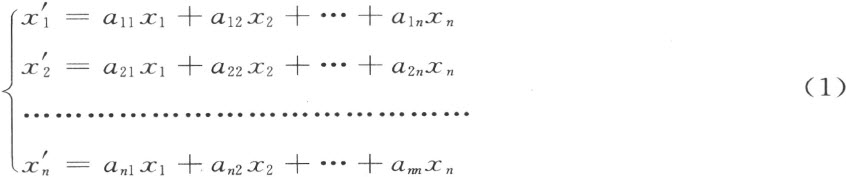
变换的系数(属于同一个域)写在左边,这对于非交换的域是重要的。关于同一类型的逆变换 的存在问题,即关于x l ,…,x n 的这一组联立方程的解的问题,是我们感觉有兴趣的问题。在无交换律的时候,不能搬用行列式的理论,所以我们应该重新解决这个问题。
定理 下列命题等价:
1)不存在这样的值x 1 ,x 2 …,x n (其中至少有一个不是零),使得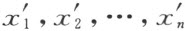 同时为零;
同时为零;
2)不存在这样的元素b 1 ,b 2 …,b n (其中至少有一个不是零),使得对于任意选择的值x 1 ,x 2 ,…,x n 有

3)变换(1)有逆变换。换句话说,对于变换(1)可以求出一个下述形式的、以这样的 为系数的变换
为系数的变换
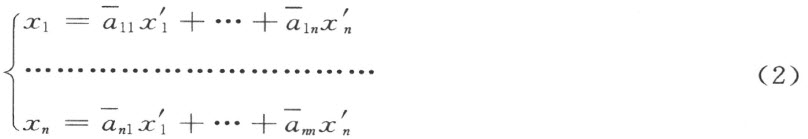
使得组(1)和组(2)等价,即当一组满足时,另一组也满足。
在这里我们顺便来指出:论断1)是说矩阵(1)的列右 线性无关,而论断2)是说矩阵(1)的行左线性无关。
在可交换的情形下,论断1),2)和3)等价于同一个事实:变换的行列式不为零。
当n =1时,变换的形式是: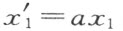 ,并且要求1),2),3)的每一个都显然意味着同一个事实:a ≠0。我们注意,对于a ≠0,由于§13的规则5,就存在着这样的数——我们记之为a -1 ——使得aa -1 =1,这等式右乘以a 时得(规则6)∶(aa -1 )a =a 或者(规则9):a (a -1 a )=a 。
,并且要求1),2),3)的每一个都显然意味着同一个事实:a ≠0。我们注意,对于a ≠0,由于§13的规则5,就存在着这样的数——我们记之为a -1 ——使得aa -1 =1,这等式右乘以a 时得(规则6)∶(aa -1 )a =a 或者(规则9):a (a -1 a )=a 。
比较这等式和a ·1=a ,由于规则5(除法的唯一性)我们得:
a -1 a =1
即a -1 和a 不论什么次序的乘积都是1。
在论断3)的意义下,变换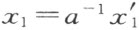 显然是
显然是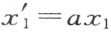 的逆变换。
的逆变换。
设对于所有小于给定的值n ,定理都已经证明了。我们来证明对于给定的值n 时的定理。
我们将认为,变换(1)的系数中至少有一个不是零(否则定理失去意义)。为确定起见,设这个不为零的是a nn 。
现在我们用下列公式规定新元素 :
:
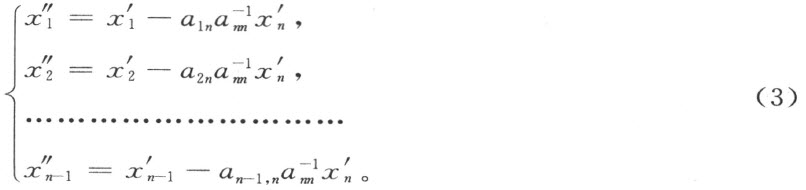
显然,若 换成它们在(1)中的式子,则
换成它们在(1)中的式子,则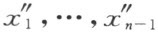 的式子中就只有
的式子中就只有 而没有x n 。这样一来,我们有类型(1)的变换,但是元素的个数较少。这个从
而没有x n 。这样一来,我们有类型(1)的变换,但是元素的个数较少。这个从 到
到 的变换,简称为变换(3)。我们现在有如下论断:
的变换,简称为变换(3)。我们现在有如下论断:
若性质1)对于变换(1)成立,则它对于变换(3)也成立,并且反过来也对。
只要能证明,若性质1)对于(1)不成立,则它对于(3)也不成立,并且反过来也对,这就足够了。于是,设存在了这样的值x 1 ,……,x n (其中至少有一个不等于零),使得所有的 为零。但是从公式(3)可见,此时
为零。但是从公式(3)可见,此时 都变为零,就是说对于(3)性质1)就不成立。[重要的是,x 1 ,…,x n -1 不可能同时为零——否则方程(1)的最后一个会引向矛盾,因为a nn ≠0。]
都变为零,就是说对于(3)性质1)就不成立。[重要的是,x 1 ,…,x n -1 不可能同时为零——否则方程(1)的最后一个会引向矛盾,因为a nn ≠0。]
反过来,若存在着这样的x 1 ,…,x n -1 使得所有的 为零,则我们还要求方程(1)的最后一个中的
为零,则我们还要求方程(1)的最后一个中的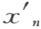 变为零;从方程(1)的最后一个,我们将毫无困难地找出对应的值x n (因为a nn ≠0)。我们现在有值x 1 ,x 2 ,…,x n 使得
变为零;从方程(1)的最后一个,我们将毫无困难地找出对应的值x n (因为a nn ≠0)。我们现在有值x 1 ,x 2 ,…,x n 使得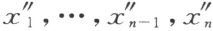 变为零,而且,使得
变为零,而且,使得 也如此。
也如此。
其次我们断定:若性质2)对于变换(1)成立,则它对于变换(3)也成立,并且反过来也对。
再只要证明,若性质2)对(1)不成立,则它对(3)也不成立,并且反过来也对。
设对于任意的x 1 ,…,x n ,存在着b 1 ,b 2 …,b n (其中有一个不等于零),使得
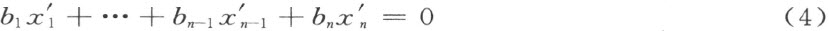
利用(3),能写下
我们可以用b n a nn 替代括弧中的和;为了证明这个,只要在特殊情形
x 1 =x 2 =…=x n-1 =0,x n =1
时,把(4)写出来就足够了。
结果是(4′ )的右端都和(4)的左端重合,因而,变为零。因此,对于变换(3)性质2)也不成立(所有的b 1 ,…,b n -1 不可能都等于零,因为,否则b n ≠0,并且从(4)会推得对于任意的x 1 ,…,x n 有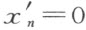 ;但这是不可能的,因为a nn ≠0)。
;但这是不可能的,因为a nn ≠0)。
反过来,若存在着这样的b 1 ,…,b n -1 (不是所有的都等于零),使得对于任意的x 1 ,…,x n -1 ,
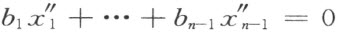
则再把式(3)替入这方程,就得到形式(4)的 之间的相关。
之间的相关。
最后我们证明,若性质3)(可逆性)对于变换(1)成立,则它对于变换(3)也成立,并且反过来也对。
在由公式(3)所规定的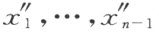 等元素之外再用下述公式
等元素之外再用下述公式

补充一个元素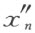 。
。
从 到
到 的变换显然是可逆的;只要在(3)中用
的变换显然是可逆的;只要在(3)中用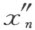 替代
替代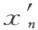 ,并且表示出
,并且表示出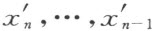 就足够了。
就足够了。
由此推得,从x 到x ′的变换的可逆性等价于从x 到x ″的变换的可逆性(因为两个可逆的变换的继续施行,显然给出一个可逆的变换)。
设x″ 依赖于x 的关系为可逆。我们知道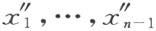 能用x 1 ,…,x n -1 线性地表示出来;
能用x 1 ,…,x n -1 线性地表示出来; (7) 能用x 1 ,…,x n -1 线性地表示出来。设后一个变换有逆变换,我们断言,在这逆变换中x 1 ,…,x n -1 能只用
(7) 能用x 1 ,…,x n -1 线性地表示出来。设后一个变换有逆变换,我们断言,在这逆变换中x 1 ,…,x n -1 能只用 表示出来。事实上,若在表示x 1 (例如)的式子中
表示出来。事实上,若在表示x 1 (例如)的式子中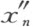 的系数不为零,则在假设
的系数不为零,则在假设
x 1 =…=x n-1 =0,x n =1
我们会得到矛盾。
因为此时,按照(3)
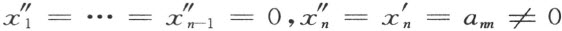
于是表示x 1 的式子简化成为含有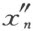 的而非零的一项,而这是和x 1 =0矛盾的。
的而非零的一项,而这是和x 1 =0矛盾的。
于是,若从x 1 ,…,x n 到 的变换的逆变换存在:则从x 1 ,…,x n -1 到
的变换的逆变换存在:则从x 1 ,…,x n -1 到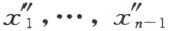 的变换的逆变换也存在。
的变换的逆变换也存在。
完全显然,逆定理也正确。
于是,从x 1 ,…,x n -1 到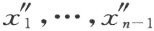 的变换的可逆性等价于从x 1 ,…,x n 到
的变换的可逆性等价于从x 1 ,…,x n 到 的变换的可逆性,而后者,如同上面曾证明过的,等价于从x 1 ,…,x n 到
的变换的可逆性,而后者,如同上面曾证明过的,等价于从x 1 ,…,x n 到 的变换的可逆性。
的变换的可逆性。
论断得以证明。
现在,因为论断1),2),3)的每一个对于变换(1)的正确性引起了它对于变换(3)的正确性,并且反过来,又因为对于变换(3)这三个论断是等价的(假设当n -1个元素时,定理已经证明),所以,对于变换(1)这些论断也是等价的。
定理证毕。
转回到非交换的解析几何 。
如同正文中所指出的,德沙格数系D 的三个数(x ,y ,z )叫做点,而直线上的所有的点由下述形式的一对方程:

确定,其中附有条件:矩阵
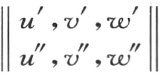
的行左线性无关。
再取德沙格数系D 的三个数u ,v ,w ,使所有的三行都左线性无关(不难证明这样的可能性)。用t 表出线性式ux +vy +wz ,并且写成:
我们可以认为,这里有一个线性变换在x ,y ,z 上进行,并且遵循性质2)。在这个情形下,性质3)就成立,并且我们能够把写下来的方程组(6′)代以和它等价的 方程组,其中x ,y ,z 都将通过(6′)的左端线性地表示出来,因为r ′和r ″都是常数,所以,我们合并含有r ′和r ″的诸项作为自由项x 0 ,y 0 ,z 0 ,而得到:

显然在不失去回到方程组(6′)的可能性时,(7)里的t 可以给任意值。因此,我们证明了每一条直线能够有参数表示(同时a ,b ,c 不同时是零——否则,把(7)中的x ,y ,z 代入(6′) (9) 时,我们会得到t =常数)。
反之,每一个参数表示(7),其中a ,b ,C 不同时是零,定义一条直线:若a ≠0,则从第一个方程:
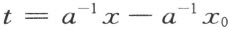
把这个式子代入第二和第三个方程,就回到(6)形式的方程组。
让我们从事验证公理I1 和I2 。我们要求暂且含有未定的a ,b ,c ,x 0 ,y 0 ,z 0 的直线(7)通过两个给定的点M 1 (x 1 ,y 1 ,z 1 )和M 2 (x 2 ,y 2 ,z 2 )。若是这样的直线存在,我们恒能够假设,在M 1 处的参数t 取值0——否则,若t 1 是参数t 在M 1 处的值,我们就引进t —t 1 作参数。再者,能够认为在M 2 处的参数t 取值1——否则,若t 2 是参数t 在M 2 处的值,我们就引进参数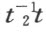 。因为参数的这些替换,(7)中的系数虽然不同了,(7)的形式可不改变。
。因为参数的这些替换,(7)中的系数虽然不同了,(7)的形式可不改变。
把值t =0和t =1代入(7),应该得到

因而x 0 ,y 0 ,z 0 ,a ,b ,c 立即决定了,并且同时唯一地决定了。
公理I1 和I2 验证完了。公理I3 显然成立:在(7)中令t =0和t =1,就足够了。
我们来验证公理I4 和I5 。设M 1 (x 1 ,y 1 ,z 1 ),M 2 (x 2 ,y 2 ,z 2 ),M 3 (x 3 ,y 3 ,z 3 )是三个给定的点。需要求出这样的u ,v ,w ,r ,使得

这里u ,v ,w 中至少一个不是零,把x i ,y i ,z i 看做系数,而u ,v ,w 看做未定的、要经过线性变换的元素。在上文证明过的代数定理中,系数都是假设在左边,而这里它们在右边。显然,在现在的情形下,定理仍正确,只要把在所有的叙述中的左乘用右乘替代,且反之。
可能有两种情形。若性质1)成立,则性质3)也成立,并且可以把方程组(8)改写成和它等价的形式,用左端-r ,-r ,-r 线性地(系数在右)表出u ,v ,w 来。
把r 拿在括弧外面来,我们得到:

其中a ,b ,c 是只依赖于x i ,y i ,z i 的某些系数[并且不同时为零——否则从(8)不可能推出(9)]。这样一来,若r 是任意取的(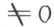 ),而u ,v ,w 是按照(9)定义的,则所得的元素将满足组(8),并且反过来也对。因此,u ,v ,w ,r 存在,并且完全确定了,到左乘任一不等于零的乘数为止(若选取另一个元素r′ 替代r ,则结果将是u ,v ,w ,r 左乘以r ′r -1 )。所求的平面存在,并且是唯一的。
),而u ,v ,w 是按照(9)定义的,则所得的元素将满足组(8),并且反过来也对。因此,u ,v ,w ,r 存在,并且完全确定了,到左乘任一不等于零的乘数为止(若选取另一个元素r′ 替代r ,则结果将是u ,v ,w ,r 左乘以r ′r -1 )。所求的平面存在,并且是唯一的。
若性质1)不成立,则这就是说可以选取值u ,v ,w 不全等于零,而使得
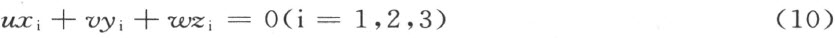
即仍存在一个平面,通过M 1 ,M 2 ,M 3 。
现在我们证明这平面是唯一的。设还另有一个平面,通过这些点。因而有
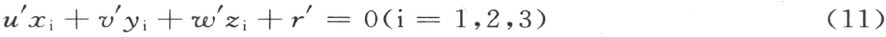
若是u ′,v ′,w ′是用同一数ρ 左乘u ,v ,w 而得到的,那么用ρ 左乘(10)并和(11)加以比较时,即得到r′ =0,因而第二个平面完全和第一个相同(参看正文中平面的定义)。
设为相反的情形,那么按照正文中所给的直线定义,所有的三点M 1 ,M 2 ,M 3 都在直线[(u ∶v ∶w ∶0);(u ′∶v ′:w ′:r ′)] (10) 上。这和公理I4 和I5 的条件矛盾。
其余的公理都能立刻验证。设给定了任一直线(7)和一平面:

把方程(7)中的x ,y ,z 代入(12);在左边我们得到t 的一次式。设给定的直线和平面有两个公共点;恒可能把这两个公共点看做是t =0和t =1。把t =0代入(12),我们就看出了不含t 的数项是零;而把t =1代入时,我们就看出了t 的系数是零。因而,把(7)代入(12)就成了恒等式,而且直线(7)上所有的点都在平面(12)上,这证明了公理I6 。
其次,设给定了有公共点(x 0 ,y 0 ,z 0 )的两个平面(公理I7 )是:
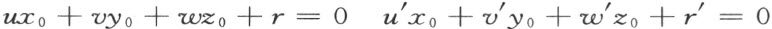
若u ′,v ′,w ′是从u ,v ,w 左乘以同一个数ρ 得来的,则用ρ 左乘第一个等式再和第二个等式比较时,我们会发现r ′是用ρ 左乘r 得来的。换句话说,这两个平面会是同一个平面,和我们的假设相反。
若这样的一个乘数ρ 不存在,则按照正文中所下的直线定义,写下的这一对方程就规定直线的点,这些点显然都同时在这两个平面上。
最后,验证公理IV (11) 。首先指出,在我们的空间中变换坐标之后,任意平面可以看做是平面
z =c
其实,设给定的平面
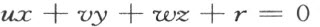
在行u ,v ,w 外还任意地选取两行u ′,v ′,w ′和u ″,v ″,w ″,使得在这些横行系数左线性无关。对于任意的x ,y ,z ,按照下述规律
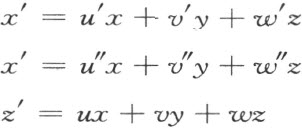
引进和它们相对应的x′ ,y′ ,z′ 。
按照假设,对于这个变换性质2)成立,因此,性质3)成立,即变换可逆。这两个三数组(x ,y ,z )和(x′ ,y′ ,z′ )彼此间一对一地对应,并且不难验证,由于系数在左边的变换的线性特征,平面和直线的方程,在新坐标中保持上述形式(系数当然有所改变)。在原来的平面上z ′也显然保持常值。
于是,只要证明在平面z =0上的公理IV* 就足够了。设在这平面上给定任意一条直线

和在这直线外的一个点(x 1 ,y 1 ),设通过这个点作一条暂时不确定的直线
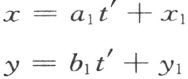
求这两条直线的交点,即求,这样的t 和t ′,满足
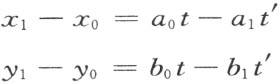
把写下的这公式看做在t ,t ′上的变换(性质1的特殊情形)有两种可能的情形。
设性质3)成立,那么变换是可逆的,能由左边唯一地求得值t ,t ′,因而交点存在。
现在设性质3)不成立;这就是说性质1)也不成立,可以选取这样的不等于零的值t 0 ,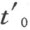 ,使得
,使得

换句话说,a 1 ,b 1 是从a 0 ,b 0 右 乘以同一个数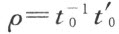 得到的。
得到的。
若是ρt ′用t 表示,并且看成是参数,那么第二条直线的方程有下述形式:

这样一来,在所考虑的情形下,第二条直线的方程可以化成完全确定的形式(14),因而,这样的直线是唯一的。
剩下还要证明方程(14)给出平行于(13)的直线(平行线的存在)。事实上,若这些直线有一个公共点,则它们是同一条直线;因为相当于参数的一个增量Δt ,在这两直线上,x 和y 一样的分别有增量a 0 Δt 和b 0 Δt 。而其实,(x 1 ,y 1 )在第二条直线上,不在第一条上。
公理I3 ,I8 (12) 的验证完全显然。
【65】若我们利用上一个注解中的直线(7)的参数表示:
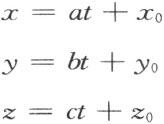
情形是十分明白的。
由于§13中的规则15和规则16,在德沙格数系中成立的,相当于参数t 的单调改变,坐标x ,y ,z 每一个也对应地单调改变(除去那些一般保持不变的:例如,在a =0时的x )。这样一来——如同在正文中所证明的——沿着直线坐标总是同时单调改变。
按照正文,一个点称为在其他两点(在给定的直线上)之间,若它的每一个坐标在其他两点的对应坐标之间(这里所讲的是关于不是沿着直线不变的坐标)。这个定义可以同样的用参数t 表示出来,因为参数的和坐标的单调改变是同时发生的。
于是,点t 2 在t 1 和t 3 之间,则是t 1 <t 2 <t 3 或者t 1 >t 2 >t 3 。
现在公理II1~3 的验证已经完全显然了。谈到公理II4 的验证,我们总可以把公理II4 中所说的平面看做是z =0(参看上一个注解,公理IV* 的验证)。
相应的论证,差不多是逐字逐句地重复注解[36],区别只在于:现在的坐标x ,y 和方程的系数不是交换域Q 的元素,而是德沙格数系的元素;特别是乘数的次序——还如同在注解[36]的公式中一样——是极其重要的。其余的论证只需要重复,无须改变。
【66】线段计算和原来的数系D 一致,严格地说来,这个事实还需要验证,但是验证并不困难。
【67】换句话说:由于定理55,原先给定的平面几何在一个德沙格数系的基础上,成为解析几何。
再者,所建立的点(x ,y ,0)的平面几何,按照它本身的建立方式,在同一个德沙格数系的基础上,也成为解析几何。
在这两种几何中,有相同坐标(x ,y )的点加以比较时,就得到所求的一一对应,保持着元素间所有的关系不变。
【68】这样一来,第六章是第五章的继续,同时实质上还带有射影性质。就是要在所考虑的空间(由公理I,II,IV* 确定的)中添加假元素,把这空间变成射影空间(参看注解[58]);相反的,最自然的是把原来的空间看成是这个射影空间的一部分,从后者取消一个平面(被取作假平面的);剩下的就是原来的空间。
如同第五章一样,所有的讨论都是根据§24所建立的德沙格的线段计算。
第六章的特征是引进在第五章中所不提出的阿基米德公理,和阐明它的作用。但是阿基米德公理的叙述要求迁移给定的线段到给定的点处;由于没有合同概念,必须给予这种迁移以新的意义。在有了德沙格的线段计算的情形下,对于分布在一条直线上的诸线段,这是能作得到的。作法是,取已知直线作为线段计算的两条轴的一条,并且O 表示两轴的交点。设A 是这轴上的任意一点(§24)。现对线段OA 建立运算。
为了要在线段计算的意义下 ,迁移线段AB 到点A ′处,我们如下进行(所有的作图都取在作为计算轴的一条直线上)。求线段OB 和OA 的差,即这样的线段OC ,使得
OB =OA +OC
从加法计算的显明的逆运算推知线段OC 的存在和唯一性。
现在作线段OB ′:
OB ′=OA ′+OC
关于线段A ′B ′,我们说它在线段计算的意义下和 AB 相等 。
从表面看来,这样的迁移线段不只依赖于给定直线上的线段本身的选取,和线段应该迁移到什么点处,而且也依赖于运算的第二条轴的选取,尤其是点O 的选取。但是能够证明,在给定的轴上的线段的加法运算(依照§24所规定的)不依赖于点 O 和第二条轴的选择 ,所以这样在给定的直线上线段的迁移是完全唯一的确定的作法。证明时需要利用德沙格定理。
【69】作者想说,若两个不能交换的数a ,b (即ab ≠ba )中的a <0,则必须考虑把a 换成(-a ),即从下列方程所规定的数。
(-a )+a =0
然后按照§13中的规则15,从a <0推知
a +(-a )<0+(-a )=0,即0<(-a )
从(-a )+a =0推知(规则10和11):
b (-a )+ba =0和(-a )b +ab =0
而且从ab ≠ba 推知(反证法)
(-a )b ≠b (-a )
同样地,若b <0,我们考虑换成(-b )>0。
于是,若对于D 系中的某两个数交换律不成立,则可以指出这规则对于两个正数也不成立。
【70】阐明在正文中所提示的证明。首先注意,式子T (连同0)的集合是一个域。
设给定了式子:

我们着重指出下述事实:所表出的幂级数,没有任何关于它们的收敛性的假设。合并T 和T ′中同类项所得到的式子,我们定义为和T +T ′。
我们用下述式子来规定乘积:
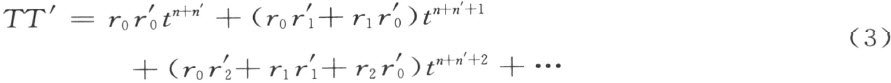
注意:在n =0,r 0 =1,r 1 =r 2 =…=0,式子(1)是单位元素。
我们来证明除法的可能性和唯一性(§13中的其余的规则1~4和6~11的验证,都完全显然)。事实上,若给定了
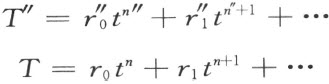
则恒能够求得——同时唯一的求得——这样的T ′
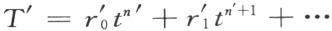
使得
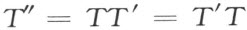
如同(3)所指出的,这是充分的。取n ′=n ″=n ″-n ,然后依次用下列公式决定 :
:
因为r 0 ≠0,所以这不会有任何困难的。
现在考虑具有形式S 的式子。它是——若是把T 0 ,T 1 ,…用它们的式子替代——写下的无穷级数,由rS μ t v 形式的项组成的,其中r 是有理数,而μ 和v 是整数( 0),并且μ ≥m ,而v ≥nμ 在μ 给定的 时候(这里nμ 是级数
0),并且μ ≥m ,而v ≥nμ 在μ 给定的 时候(这里nμ 是级数 的最小的指数)。
的最小的指数)。
把两个具有形式S 的式子的同类项合并起来,即把两个级数中同样的S μ t v 的系数r 加起来,来决定这两个式子的和。
在讨论具有形式S 的式子的积之前,我们规定两个具有形式rs μ t v 的积。这个积将由下述公式定义:
不难看出,这式子可从规则
ts =2st
得到,但是,我们宁愿把这个公式当做定义,为的是避免有关这结论的严密论证的那种繁琐的讨论。显然,ts =2st 这规则是公式的特殊情形,所以,公式给出了在一切情形下我们所需要的。
对于如此定义的式子rs μ t v 的乘法,结合律的验证没有任何困难。
设给定了式子S 和S ′,如我们所知道的,由具有形式rs μ t v 的项组成的。S 乘以S ′的积叫做S ″,它是由S 的每一项乘以S ′的每一项所得到的项组成的(乘之后还要合并同类项:容易看出,每一种的同类项只有有限数个)。换句话说,若
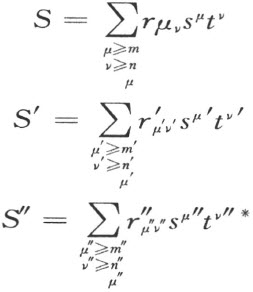
则关系S ″=SS '指的是
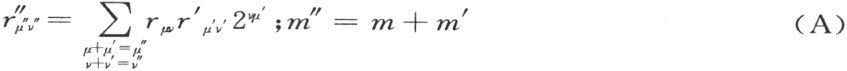
在式子S 的定义域中,所有的规则1~4和6~11的验证都完全显然;我们只讨论规则5,即除法的可能性和单一性。要讨论的正是:若把式(A)中的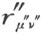 和r μv 看做是已知的,则我们能够从它们依次定义
和r μv 看做是已知的,则我们能够从它们依次定义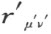 。
。
首先,必须取m′ =m ″-m 。用μ ″是最小值时的式(A),即μ ″=m ″时的公式(A)。然后在右端必须令μ =m ,μ′ =m ′。在依次令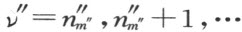 时,在
时,在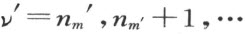 (令
(令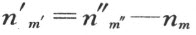 )的情形下,我们依次从式(A)定义
)的情形下,我们依次从式(A)定义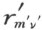 。
。
其次,用μ″ =m ″+1和令 时的(A),依次规定,在
时的(A),依次规定,在
 时的
时的 。
。
在μ″ =m ″+2等等时,我们同样地处理。所有的系数 都唯一决定了。
都唯一决定了。
【71】定理61在射影几何的解释中具有最自然的形式。设我们所考虑的平面几何是满足公理I1~3 ,II,IV (13) 的,而且补充了假点(和平行束一一对应的新元素)和假直线(所有假点的集合)的。这就成为射影几何(没有连续公理)。射影几何中的两直线恒有一个公共点(平行时就是假点)。
在今后不区分真点和假点时,我们给出巴斯噶-巴卜定理的射影说法如下:
若点A 1 ,A 3 ,A 5 在同一条直线a 上,而点A 2 ,A 4 ,A 6 在另一条直线a ′上,则直线:A 1 A 2 和A 4 A 5 ,A 2 A 3 和A 5 A 6 ,A 3 A 4 和A 6 A 1 ,这三对的交点都在同一条直线上。
特别的,若直线a 和a ′有真的公共点,而所说的交点中有两个在假直线上,则根据定理,第三个交点也在假直线上。我们显然,回到定理40了,即回到如同在正文中所了解的意义下的巴斯噶定理。
现在设在我们的几何中巴斯噶-巴卜定理的射影说法成立。我们断定德沙格定理,然后能够证明,这就是定理61的射影说法。
对于德沙格定理我们在这里也取一般的射影说法(参看注解[58])。
我们必须懂得定理61的字面上的意义,在正文中和在射影说法中不同,因为我们既加强了定理的条件,又加强了定理的结论。
至于证明,现在更简单了。首先,德沙格的正定理和逆定理变成一样的,因为它们都化简为同一个说法:若给定了10个点和10条直线,并且是德沙格构形所具有的点和直线的关联关系,可能除去一个之外都成立,则这最后一个也成立。
由于德沙格构形中的所有的点和直线的完全平等地位,不难看出,从德沙格正定理推得这个说法,也从逆定理推得这个说法(从它们推出来的这些命题是一样的)。
要想证明德沙格定理,而不改变正文中的名词,我们能够假设把新考虑的构形中的诸直线之一叫做假直线 ,而所有和它有同一个交点的直线叫做平行线 。然后我们能够重复正文中的讨论并且利用图77,把图中的构形了解为有一条假直线,而且把图中和假直线有同一个交点的直线了解为平行线。
在证明时,可以如下的简化,A ′C 不和OB ′平行,现在有了充分的保证。其余的限制原来需要附加上的原因,是为了使得:在证明过程中援引巴斯噶定理时,所得到的直线A 1 A 3 A 5 和A 2 A 4 A 6 不平行而相交于真点(在定理40中所假设的)。但是在我们的射影说法中,这些情形没有区别,而相应的附加条件是多余的。论证A ′C ′和OB ′不平行,那是总能够达到的,因为可以把A ′B ′和OC ′,或者把B ′C ′和OA ′当做A ′C ′和OB ′(在最后的情形下,必须考虑三角形ABC ″,替代考虑三角形ABC ,其中BC ″//B ′C ′,而且C ″在OC ′上;实行证明后,就知道原来A ′C ′//AC ″,因而,C ″和C 重合)。容易证明,在所有三种情形中都同时平行是不可能的。
【72】这里粗枝大叶地谈到实数。事实上,这里只是某一个可交换的、但是(在所作的假设是公理I1~3 ,II,IV* 和巴斯噶定理的情形下),一般说来,是非阿基米德的数系的元素(例如,式子T 。§33)。
【73】计算的元素的定义域已经是无穷的,因为它含有单位,而且同时——遵循运算律——既含有所有的整数,又含有所有的有理数(顺序的存在排斥了非零模域的情形)。由此推出,若是在数p 1 ,…,p r 用任意的运算的元素替代(特别是用任意的有理数替换)时,有理式R (p 1 ,…,p r )(以有理数为系数时)变为零,R (p 1 ,…,p r )就恒等于零。
于是,设关于交点的定理是正确的。这与下述事实等价:一系列的式子R (P 1 ,…,P r )恒等于零。这样一来,定理的证明化为诸式子R (P 1 ,…,P r )恒等于零的验证。同时,重要的是,要注意到:式子R (P 1 ,…,P r )的产生,是对于P 1 ,…,P r 继续进行一系列的、不管它是多么复杂的有理运算的直接结果。为了验证R (p 1 ,…,p r )恒等于零,我们应该引进一系列的计算:展开括弧,同类项化简等等。换句话说,我们应该运用计算规则1~12;但是这些规则的运用,如同上面曾经指出过的,在几何上,是化为巴斯噶定理的应用。
总起来说,交点定理的证明的过程是化为巴斯噶定理的运用(当然还有公理I1~3 ,IV* )。
【74】首先我们回忆,根据第I~IV组公理的几何中,巴斯噶定理是正确的,因而,可以在这几何中引进线段计算,如同§15中所作的,并且证明定理41和定理42。
我们来证明施泰因纳尔的命题。令PF 不和a 平行(注图43):设PQ 是和a 平行的直线,并且分别交AE ,BD ,CD 于点F ″,Q ,F′ (必然有交点,因为AE ,BD 和CD 都不和a 平行)。然后从相似三角形ABD 和PQD 有:
PQ ∶AB =DQ ∶DB
注图 43
但从相似三角形BCD 和QF ′D 推知
QF ′∶BC =DQ ∶DB
因为AB=BC ,因此得

从相似三角形ABE 和F ″QE 以及三角形BCE 和QPE ,我们有
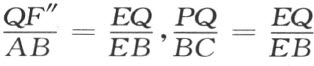
因为AB =BC ,因此推知

比较(1)和(2),可得
QF′ =QF ″
这就是说,F ″和F ′重合,与我们的假设直线PQ 平行于a 而不通过F 是相矛盾的(注意:F′ 和F ″不能够在Q 的两侧,因为否则其中之一会和P 重合,那是不可能的)。
【75】所谓由一些给定的数和变数所产生的域R ,我们了解为由这些数和变数经过四种有理运算所作成的所有可能的式子。
因此,这个域的元素是原来的,独立的参数p 1 ,…,p r 的有理函数,并且这些函数的系数是原来的数的有理式。
还要注意到,从§37开始,在正文中只考虑实数和取实数值的变数,这就是说,在普通的几何的范围中。
【76】更确切地说,在以后的正文中,所谓一个完全实数是具有下述性质的一个代数数:它是由有理运算和开平方得来的,并且它和它的共轭数都是实的。
我们特别是要来明确和上文讨论中有关的一系列的事实。
1.大家都知道:从给定的点出发,并且利用直尺和圆规 ,我们能够作而且只能够作具有下述性质的所有的点:它们的坐标能够用给定的点的坐标经过四种有理运算和开平方表示出来。这个证明是很初等的,它的根据在下面:求两个圆的交点,或者圆和直线的交点,都是求解二次方程,而且这方程的系数是两圆的、或者圆和直线的方程的系数的有理式;反过来,利用直尺和圆规,求任意一个由已给线段所表出的数的平方根,在几何上不难实现。
这问题的详细的阐述可查看阿得列尔(A.Aдлep)《几何作图的理论》一书。
2.令给定的点的坐标是r 个任意的参数p 1 ,…,p r 的有理函数。
考虑一个由给定的点的坐标所产生的p 1 ,…,p r 的有理函数的域:R (p 1 ,…,p r )。给定的点的坐标属于这个域。由R 开始,作一序列的域,使得每一个后项包含前一项:
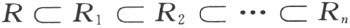
并且每一个后项是由它的前一项增加一个平方根而得来的。更确切地说:若R i 已经作好(R 看做R 0 ),则R i +1 就这样作成:从R i 选出具有下述性质的任意一个元素f i ,使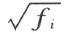 不在R i 中出现,并且把
不在R i 中出现,并且把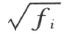 和R i 的系数所组成的全体有理式作为R i +1 ,因为在这里
和R i 的系数所组成的全体有理式作为R i +1 ,因为在这里 的偶数次幂能够归入系数(或者自由项),所以
的偶数次幂能够归入系数(或者自由项),所以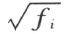 的多项式能够化为线性式;R i +1 的元素的一般形式是:
的多项式能够化为线性式;R i +1 的元素的一般形式是:
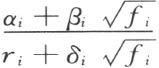
其中α i ,β i ,γi ,δi ,都是R i 的元素。用通常的方法有理化分母,我们最后得到R i +1 元素的一般形式:

其中a i 和b i 都是R i 的任意元素。
显然,这过程使我们能得出域R n ,它包含任意的事先指出的一些点(能从给定的点出发用直尺和圆规作出来)的系数。
定理64的意义是:若所论述的特别是关于利用直尺和迁线器 的作图,因为这种作图的可能性比较利用直尺和圆规 的作图的可能性更狭窄,所描写的过程的任意性也对应的受限制。正就是:每一个域R i 扩张到域R i +1 时,域R i 的元素f i 不能任意的选取,而只能是R i 的一些元素的平方的和。
3.回到一般情形,取域R n 的任意的一个元素a n ,R n 是序列(1)的最后一个域。
应用公式(2),得
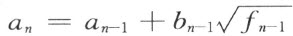
对于元素a n -1 ,b n -1 应用公式(2),得
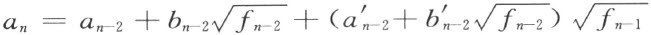
继续这个过程,最后我们得到a n 的表示式,它对于下列的根式的每一个

都是线性的,而它的系数都属于原来的域R (1,p 1 …,p r ) (14) 。
我们把它写出如下:
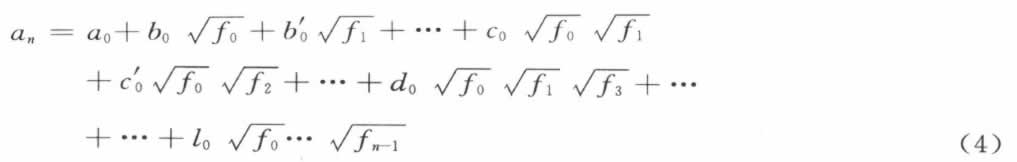
需要注意的是,每一个根式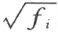 的根号下的f i ,是利用根式
的根号下的f i ,是利用根式

所组成的同样的式子。
式(4)的项数的个数是2 n ,是容易计算出来的:2 n 个系数都是域R (1,p 1 ,…,p r )的元素。
现在要把原来的诸点的坐标 认为不依赖于任何参数 ,特别是,认为p 1 ,…,p r 得到了实数值。然后在作诸域(1)的过程中,每一个根式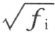 所指的是它的两个值中完全确定的一个;上边所写出的式子a n ,所以也将是完全确定的数。原来的域R 只包含实数。
所指的是它的两个值中完全确定的一个;上边所写出的式子a n ,所以也将是完全确定的数。原来的域R 只包含实数。
假设现在容许在式子(4)中任意的取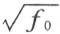 的符号;在取定之后,根号下的f 1 就完全确定了。我们再同样的任意地取
的符号;在取定之后,根号下的f 1 就完全确定了。我们再同样的任意地取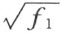 的符号;在取定之后,根号下的f 2 就完全确定了。我们再任意地取
的符号;在取定之后,根号下的f 2 就完全确定了。我们再任意地取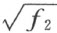 的符号等等。
的符号等等。
这样一来,我们显然得到2 n 个式子,因为每一个根式有两个可能的值。我们认为,这样得到的数是彼此都不相同的,因为,否则只要增加少于n 个平方根就达到元素a n 。
这2 n 个数中含有a n ,我们把它们叫做对于域R 说的和 a n 共轭的数 。

我们断言:这些数都是同一个代数方程的根,而这方程的次数是2 n ,系数属于原来的域 R 。
我们把式子(4)中出现的根式的每一个的值,看做任意的在两个可能的情形中取定了;但是,在这个根式出现的所有情形中,不管它是否在其他的根式下,当然都取同样的值。然后(4)不仅能够表出a n ,但也表出任一个和它共轭的数。
把(4)平方起来。一个根式的平方是一个含有较少个数根式的式子。把一个根式的平方用它的式子代入(这代入的方式是完全确定的)之后,我们得到和(4)同样形式的式子。它的系数也是原来的域的一些元素(显然,完全不依赖于根式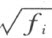 的符号的选择)。
的符号的选择)。
关于式子(4)的任意幂也是如此。
我们来考虑下列诸式子

它们都是形式(4)的式子。因为它们的个数比每一个式子的项数多1个,所以能够从原来的域R 中选择这样的乘数β i ,使得线性组合
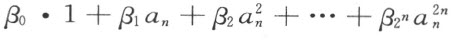
恒等于零。这就是说,在这个线性组合中,把它看做形式(4)的一个式子时,2 n 个系数的每一个都是零。结果是,a n 以及所有和它共轭的数都满足同一个2 n 次的、系数属于原来的域R 的方程:

我们注意,这个方程将不会引出下述情形,即a n 不适合任何一个低次的、系数属于R 的方程(在相反的情形下,把式子(4)代入这样的方程后,这方程对于

应该是一个恒等式,因为这些根式的任何一个也不能用在它以前[按号码说]的有理的表示出来;但是,这就是说,这方程应该被所有和a n 共轭的数适合;那是不可能的,因为它的次数<2 n )。
若域R 就是有理数域(p 1 ,…不出现),则a n 是代数数,而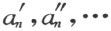 都是和它共轭的数。
都是和它共轭的数。
4。设域的序列(1)特别是与利用直尺和迁线器的作图相适应的;这意味着每一个根式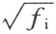 的根号下的式子是对应域R i 的元素的平方的和。
的根号下的式子是对应域R i 的元素的平方的和。
作成了域R n 的某个元素a n 后,我们来研究那些和它共轭的元素的形式。因为f 0 是平方和,所以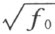 是实数。不论
是实数。不论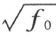 的符号是怎样取的,式子f 1 代表着域R 1 的元素的平方和,是非负的,并且
的符号是怎样取的,式子f 1 代表着域R 1 的元素的平方和,是非负的,并且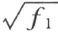 以及和它一起的域R 2 全体都是实数。不论
以及和它一起的域R 2 全体都是实数。不论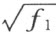 的符号是怎样取的,式子f 2 反正是域R 2 的元素的平方和,非负的,所以
的符号是怎样取的,式子f 2 反正是域R 2 的元素的平方和,非负的,所以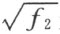 是实的;而和它一起的域R 3 的所有的元素都是实的等等。
是实的;而和它一起的域R 3 的所有的元素都是实的等等。
结果是,域 R n 的每一个元素 a n 以及所有的和它共轭的元素都是实的 。显然,这意味着:若我们从域
R (P 1 ,…,P r )
出发,其中的p 1 ,…,p r 是固定的参数,则在p 1 ,…,p r 取实数值时,被方程(6)所规定的,对应的参数p 1 ,…,p r 的代数函数值,也只取实数值(在p 1 ,…,p r 是有理数时,按照同样理由,这些函数的实数值将完全是实数)。
【77】关于利用直尺和圆规来作一个正p 角形的问题,其中P 是一个质数,大家知道,只有当p 是这样的形式:
p =2 n +1
这个作图问题才能解决。同时必须开平方n 次。
设问题是这样:已知圆的半径,我们取它的一端作为圆心,另一端作为所求的内接于圆的正多边形的一个顶点。还需要作多边形的另一个顶点。
显然这个问题有2 n 个实数解,因为多边形总共有2 n +1个顶点。我们实际是处在定理65的条件下。
【78】马耳发提问题如下:已知三角形ABC ;需要作这样的三个圆,使得其中的每一个和其他二个相切,并且也和三角形的两条边相切。
这问题的利用直尺和圆规的解法参看阿得列尔《几何作图的理论》,1909年,第9~11页;阿达玛(J. Hadamard)《初等几何》,卷I,平面几何 (15) ,1938。
【79】亚波隆尼亚问题如下:作一个圆与三个定圆相切。这个问题利用直尺和圆规的解法,参看切特维鲁辛( )《几何作图法》,1938,第134~136页;阿来克桑卓若夫(
)《几何作图法》,1938,第134~136页;阿来克桑卓若夫( )《几何作图问题》 (16) ,阿得列尔,《几何作图的理论》;阿得玛,《初等几何》,卷I,平面几何。
)《几何作图问题》 (16) ,阿得列尔,《几何作图的理论》;阿得玛,《初等几何》,卷I,平面几何。
————————————————————
(1) 原俄译本误为第330~332页。——译者注
(2) 俄译本写作(u ,v ,w )与正文及后面(注63)均不一致,今均改成(u :v :w )。—译者注
(3) 假直线就是正文中的无穷远直线。——译者注
(4) 命题1~6的验证可见于别的书中,例如,切特维鲁辛第二章。
(5) 证明见切特维鲁辛的书中,也可参考任一本射影几何教程。
(6) (4′)是中译者加的。——译者注
(7) 原俄文误为x n 。——译者注
(8) 原俄文为(6)。——译者注
(9) 原俄文为(6)。——译者注
(10) 原俄文为[(u ,v ,w ,0);(u ′,v ′,w ′,r ′)]。——译者注
(11) 原俄文为[(u ,v ,w ,0);(u ′,v ′,w ′,r ′)]。——译者注
(12) 此处不该再提到公理I8 ,因为前面已经提到了。——译者注
(13) 在式子S ″中,原文误印为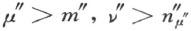 。——译者注
。——译者注
(14) 原文将p r 误印为p n 。——译者注
(15) 有朱德祥的中译本。——译者注
(16) 有丁寿田的中译本。——译者注